Open Journal of Discrete Mathematics
Vol.2 No.3(2012), Article ID:21127,4 pages DOI:10.4236/ojdm.2012.23020
An Entertaining Example of Using the Concepts of Context-Free Grammar and Pushdown Automation
Faculty of Mathematics and Natural Sciences, South-West University, Blagoevgrad, Bulgaria
Email: yordzhev@swu.bg
Received April 13, 2012; revised May 10, 2012; accepted June 4, 2012
Keywords: Context-Free Grammar; Context-Free Language; Pushdown Automation; Hanoi Towers; Discrete Mathematics Learning
ABSTRACT
A formal-linguistic approach for solving an entertaining task is offered in this paper. The well-known task of the Hanoi towers is discussed in relation to some concepts of formal languages and grammars. A context-free grammar which generates an algorithm for solving this task is described. A deterministic pushdown automation which in its work imitates the work of monks in solving the task of the Hanoi towers is built.
1. Introduction
Task 1 (The Task of the Hanoi Towers [1]). The Hanoi Towers are made up of three vertical pins. A series of N discs is hung on the first pin. The discs are all different, but ordered by size with the largest being on the bottom and the smallest on top. The task is to move the discs from the first to the third pin, using the second pin as an assistant. There are several conditions to completing this exercise: only one disc may be moved at one time and while one disc is being moved, all other discs must be on one of the pins and also, during this time, it is prohibited for a larger disc to be placed on a smaller one.
The task of the Hanoi Towers is a classic example used to teach recursion in programming [1-4]. In this paper, we will look at this Task from the standpoint of mathematical linguistics, i.e. as a part of the discipline of “discrete mathematics” and “mathematical linguistics” studies by students in Informatics and Computer courses at university [2,5-9].
There are three interesting approaches associated with the task of Hanoi towers in terms of mathematical linguistics:
1) To generate the Hanoi moves using a finite automaton;
2) To generate the Hanoi moves using a context-free grammar;
3) To generate the Hanoi moves using a pushdown automation.
The first approach is described in [10] and an equivalent version (with morphisms) in [11]. In this paper we will consider the second and third tasks. These tasks have been formulated in a Bulgarian in the textbook [12].
The algebraic properties of context-free grammars and languages are discussed in [5,8,13,14]. Several applications of formal grammars and languages and pushdown automata are considered in [8,15].
2. Context-Free Grammars and Languages
Let V be a finite and non-empty set. The elements of this set are called letters, and the whole set V—alphabet.
We will call a word over the alphabet V each finite string of letters from V. A word that does not contain any letter is called an empty word, which we will mark with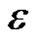 .
. 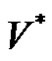 denotes the set of all words over V, including empty set. The term length of a word refers to the number of letters in it. The length of the word
denotes the set of all words over V, including empty set. The term length of a word refers to the number of letters in it. The length of the word 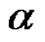 will be expressed by
will be expressed by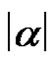 .
.
Let  and
and  be two words over the Alphabet V. By concatenation (multiplication)
be two words over the Alphabet V. By concatenation (multiplication) 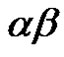 of both words we will mean the word obtained by successive completion of the letters of
of both words we will mean the word obtained by successive completion of the letters of 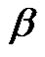 after the last letter of
after the last letter of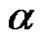 .
.
Let V be an alphabet. Each subset L of  is called formal language (or only language) over alphabet V.
is called formal language (or only language) over alphabet V.
By generative grammar (or only grammar) , we will understand the four ordered tuples
, we will understand the four ordered tuples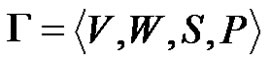 , where V is a finite set (Alphabet) of terminal symbols, W—a set of nonterminal symbols, S—a start symbol of the grammar, which is an element of W, and P is a set of ordered pairs
, where V is a finite set (Alphabet) of terminal symbols, W—a set of nonterminal symbols, S—a start symbol of the grammar, which is an element of W, and P is a set of ordered pairs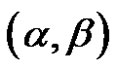 , where
, where , with at least there one non-terminal symbol in
, with at least there one non-terminal symbol in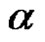 . In a number of sources (see references at the end), an additional condition is placed for sets W and P to be finite. For our needs this condition is not necessary. It is enough that these sets are countable. The elements of P are called productions. If
. In a number of sources (see references at the end), an additional condition is placed for sets W and P to be finite. For our needs this condition is not necessary. It is enough that these sets are countable. The elements of P are called productions. If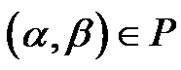 , then it means
, then it means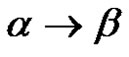 , as the symbol “
, as the symbol “ ” does not belong to
” does not belong to .
.
Let  and
and 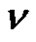 be two words from
be two words from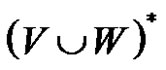 . We will say that
. We will say that  is derived directly from
is derived directly from  in the grammar
in the grammar  and will write
and will write  (or only
(or only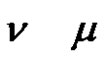 , if
, if 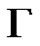 is understandable), if there exists words
is understandable), if there exists words 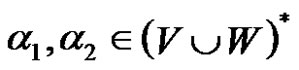 and a production
and a production 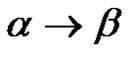 in
in  so that
so that 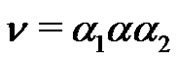 and
and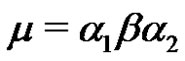 .
.
If  is a word over
is a word over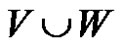 , for which
, for which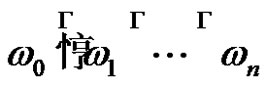 , we will say that the number of words is the derivation of
, we will say that the number of words is the derivation of 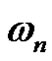 from
from 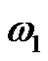 in
in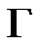 , which we denote by
, which we denote by 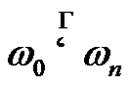 or only
or only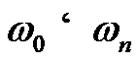 , if
, if 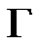 is default. The count n of the immediate derivations
is default. The count n of the immediate derivations  will be called the length of derivation.
will be called the length of derivation.
The Set 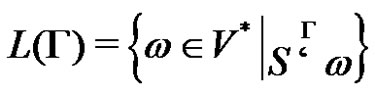 is called formal language over V, generated by the grammar
is called formal language over V, generated by the grammar . The Grammars
. The Grammars  and
and  are equivalent if
are equivalent if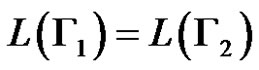 .
.
A grammar 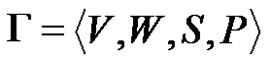 is context-free, if all the productions are of the type
is context-free, if all the productions are of the type
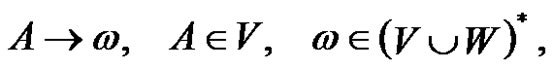
where V and W are alphabets, respectively with terminal and nonterminal symbols.
Task 2. For a given positive integer N a context-free grammar  should be built with a terminal alphabet encoding possible displacements and if
should be built with a terminal alphabet encoding possible displacements and if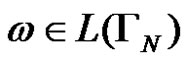 , then
, then 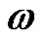 describes the algorithm that solves the Task 1. Prove that for each positive integer N language
describes the algorithm that solves the Task 1. Prove that for each positive integer N language 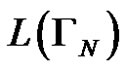 is not empty, i.e. for each positive integer N there is an algorithm that solves the task of the Hanoi towers1.
is not empty, i.e. for each positive integer N there is an algorithm that solves the task of the Hanoi towers1.
Solution. Let’s consider context-free grammar 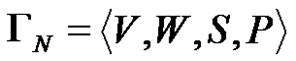 where
where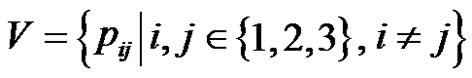 . The meaning of
. The meaning of  is “Move top disk from the i-th pin of the j-th pin”. In this way, if
is “Move top disk from the i-th pin of the j-th pin”. In this way, if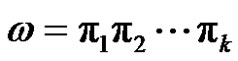 , where
, where 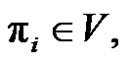
 , then
, then 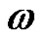 describes the algorithm for the consecutive moving of
describes the algorithm for the consecutive moving of  discs in the three pins.
discs in the three pins.
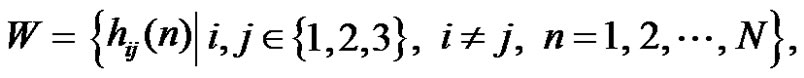 the start symbol
the start symbol ,
, 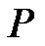 consists of productions
consists of productions and
and 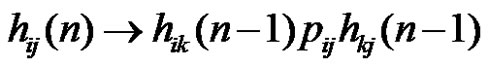 for
for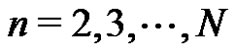 , where
, where 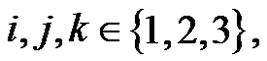

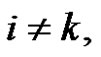
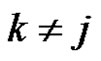 . Apparently, the grammar
. Apparently, the grammar 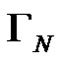 constructed in this manner is context-free.
constructed in this manner is context-free.
Let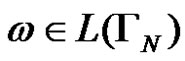 , i.e. we assume that the derivation
, i.e. we assume that the derivation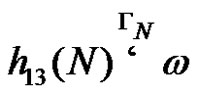 exists and let the length of the derivation is equal to
exists and let the length of the derivation is equal to . If
. If , then obviously this is possible if and only if the number of discs
, then obviously this is possible if and only if the number of discs 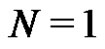 and there is a direct derivation
and there is a direct derivation 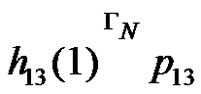 and in the presence of a single disc,
and in the presence of a single disc,  describes an algorithm for solving Task 1. Similarly
describes an algorithm for solving Task 1. Similarly 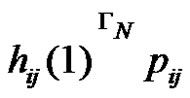 is a derivation with length 1 with start symbol
is a derivation with length 1 with start symbol  and
and  describes the algorithm for moving a single disc from pin
describes the algorithm for moving a single disc from pin 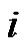 to pin
to pin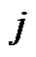 , where
, where  and
and . Let
. Let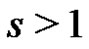 . We assume that if a derivation exists with length less than
. We assume that if a derivation exists with length less than 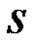 of type
of type , where
, where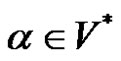 ,
,  then
then 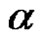 describes the moving of n discs from pin
describes the moving of n discs from pin 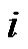 to pin
to pin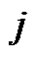 , using pin k as assistant according to the constraints in Task 1, where
, using pin k as assistant according to the constraints in Task 1, where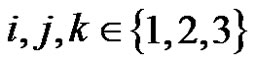 ,
,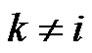
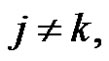
 . When s < 1 obviously derivation
. When s < 1 obviously derivation  with length s (if existing) will be of the type
with length s (if existing) will be of the type 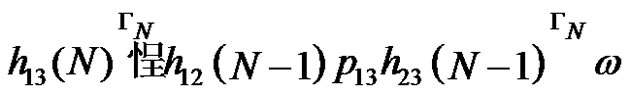 then the next derivations
then the next derivations 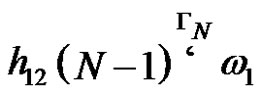 and
and exist with lengths less then s, where
exist with lengths less then s, where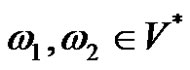 and
and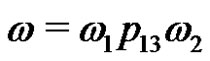 . According to the induction assumption,
. According to the induction assumption,  describes the algorithm for moving of
describes the algorithm for moving of 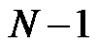 discs from the first to the second pin, using the third one as assistant, and
discs from the first to the second pin, using the third one as assistant, and 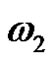 describes the algorithm for moving
describes the algorithm for moving  discs from the second to the third pin, using thr first one as assistant. Then
discs from the second to the third pin, using thr first one as assistant. Then 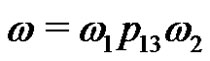 describes the following algorithm: first under the constraints of Task 1 we move the top number
describes the following algorithm: first under the constraints of Task 1 we move the top number  of discs from the first pin to the second, then we move the largest bottom disk from the first pin of the empty third and finally, we move
of discs from the first pin to the second, then we move the largest bottom disk from the first pin of the empty third and finally, we move 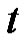 number of discs from the second pin to the third one. Therefore
number of discs from the second pin to the third one. Therefore  (if existing) describes the solution of the task of the Hanoi towers.
(if existing) describes the solution of the task of the Hanoi towers.
Let’s prove for each positive integer N that language 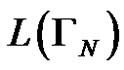 is not empty. When
is not empty. When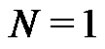 , the only production of
, the only production of  which can be applied is
which can be applied is 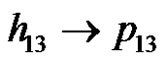 and therefore
and therefore , i.e.
, i.e.  is not an empty language. Let’s assume that for each positive integer
is not an empty language. Let’s assume that for each positive integer 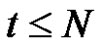 the languages
the languages 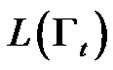 are not empty and put
are not empty and put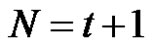 . Let’s consider the context-free grammars
. Let’s consider the context-free grammars and
and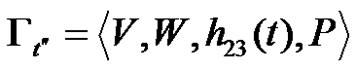 . Apparently
. Apparently 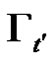 and
and 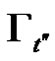 work by analogy of
work by analogy of  and according to the above proven if
and according to the above proven if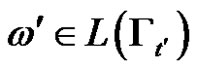 , then
, then  describes the algorithm for moving
describes the algorithm for moving 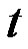 discs from the first tos the second pin, using third one as assistant under the constraints described in Task 1, and if
discs from the first tos the second pin, using third one as assistant under the constraints described in Task 1, and if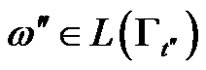 , then
, then  describes the algorithm for moving t discs from the second pin to the third one using the first one as assistant. According to the induction assumption
describes the algorithm for moving t discs from the second pin to the third one using the first one as assistant. According to the induction assumption 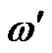 and
and  there exists. Then in
there exists. Then in  derivation exist
derivation exist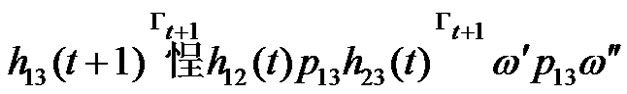 , where
, where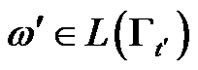 and
and . Therefore
. Therefore , i.e.
, i.e. 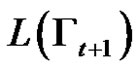 is a non empty language.
is a non empty language. 
When  the following word is produced
the following word is produced 
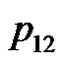
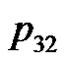
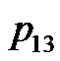
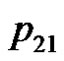
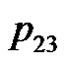


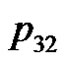

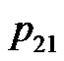
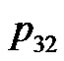

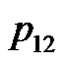
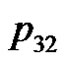
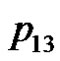
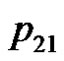
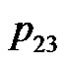
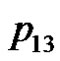
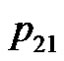
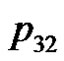
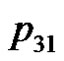

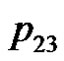
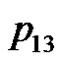
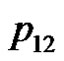

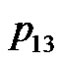
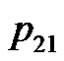
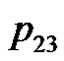
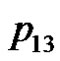 . We can verify the correctness of the algorithm using the example of the five consecutive playing cards.
. We can verify the correctness of the algorithm using the example of the five consecutive playing cards.
The following is easy to prove (e.g. using induction):
Proposition 1. Let N be a positive integer, and 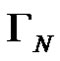 be defined as the solution of Task 2 context-free grammar, then
be defined as the solution of Task 2 context-free grammar, then
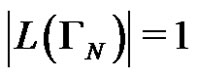
and if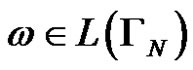 , then
, then
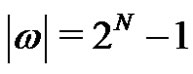
In other words, for each positive integer N, grammar 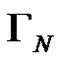 generates exactly one word that describes an algorithm for solving the task of the Hanoi towers with exactly
generates exactly one word that describes an algorithm for solving the task of the Hanoi towers with exactly 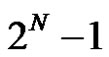 displacements of the disks from one pin to another.
displacements of the disks from one pin to another.
3. Pushdown Automata
By nondeterministic pushdown automation one will understand each ordered septuple
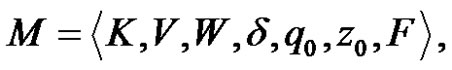
where:
- K is a finite set of states of automaton;
- V is a finite set of entry letters (entry alphabet);
- W is a finite, non empty set of stack symbols (stack alphabet);
- 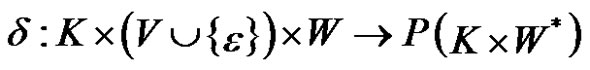 is a transition function;2
is a transition function;2
-  is a start state of automaton;
is a start state of automaton;
- 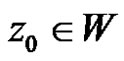 is a start stack symbol;
is a start stack symbol;
-  is a set of accepting states.
is a set of accepting states.
The ordered triple 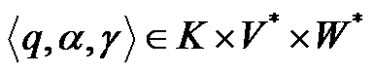 will be called configuration of nondeterministic pushdown automaton M.
will be called configuration of nondeterministic pushdown automaton M.
Let 
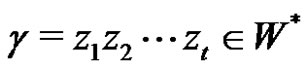 . Then the transition function
. Then the transition function  defines a transition configuration
defines a transition configuration 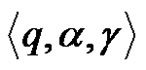 to the next configuration in the following way:
to the next configuration in the following way:
1) For each pair 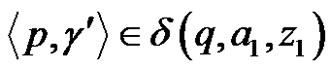 the configuration
the configuration 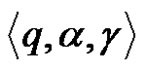 passes in the configuration
passes in the configuration , where
, where 
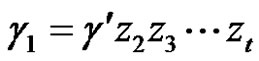 , which we denote by
, which we denote by .
.
2) For each pair 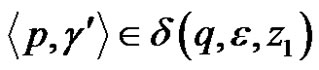 the configuration
the configuration 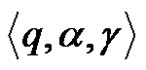 passes in the configuration
passes in the configuration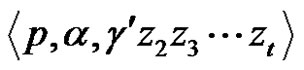 , which we denote by
, which we denote by .
.
If the nondeterministic pushdown automation is initially given the word 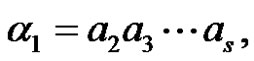 then, according to the start configuration
then, according to the start configuration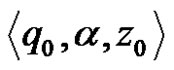 , the following possible configurations are obtained by using a function of transitions
, the following possible configurations are obtained by using a function of transitions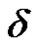 . For each new configuration using
. For each new configuration using  all possible next configurations are obtained and so on.
all possible next configurations are obtained and so on.
The nondeterministic pushdown automation  recognizes the word
recognizes the word 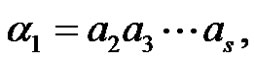 by accepting state, if its work at the beginning of given word
by accepting state, if its work at the beginning of given word , it reaches a configuration of type
, it reaches a configuration of type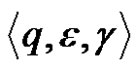 , for each
, for each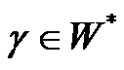 , when
, when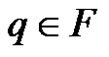 .
.
The nondeterministic pushdown automation M recognizes the word  by empty stack, if its work at the beginning of a given word
by empty stack, if its work at the beginning of a given word  reaches a configuration of type
reaches a configuration of type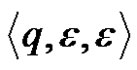 .
.
The pushdown automation 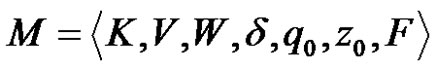 is called deterministic, if for each
is called deterministic, if for each 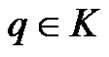 and
and 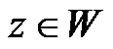 exactly one of the following two conditions is valid:
exactly one of the following two conditions is valid:
1) 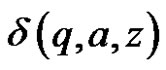 contains no more than one element for each
contains no more than one element for each 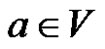 and
and .
.
2)  for each
for each 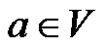 and
and 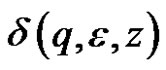 contains no more than one element.
contains no more than one element.
A language which is recognized by some deterministic pushdown automation is called a deterministic language. As it is known the relationship between context-free languages and pushdown automation is given by the following statements:
For each context-free language L a nondeterministic pushdown automation M exists, such that L is recognized by M through an accepting state.
Language L is recognized of a nondeterministic pushdown automation through an empty stack if and only if L is recognized of a nondeterministic pushdown automation through an accepting state.
If L is a language which is recognized by a nondeterministic pushdown automation, then L is a context-free language.
Task 3. For each positive integer 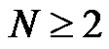 a deterministic pushdown automation MN should be built, which in its work should imitate the work of monks in solving the task of the Hanoi towers (see Task 1).
a deterministic pushdown automation MN should be built, which in its work should imitate the work of monks in solving the task of the Hanoi towers (see Task 1).
Solution. The requested pushdown automation is the following: , where
, where 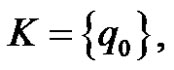
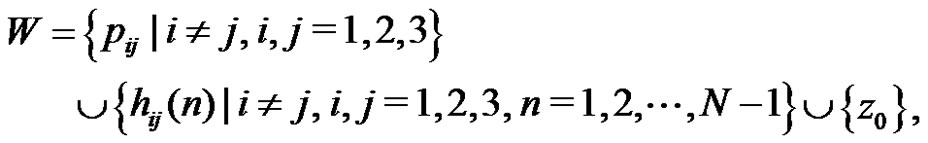
and 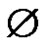 is the empty set. Let
is the empty set. Let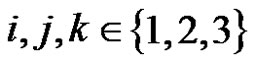 ,
,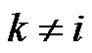
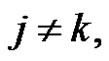
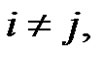 . Then the transition function
. Then the transition function  is defined in following way:
is defined in following way:
 (1)
(1)
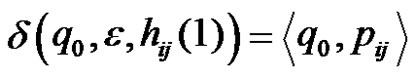 (2)
(2)
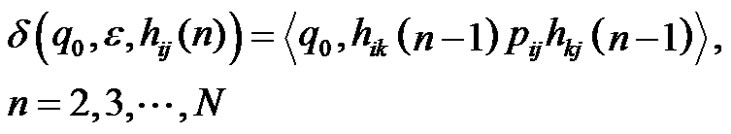 (3)
(3)
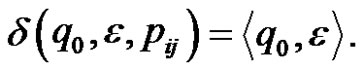 (4)
(4)
Immediately after the inclusion of MN, before being submitted as any input signal, the automation replaces the start stack symbol z0 with word  according to (1) and after a number of actions depending on the current stack symbol (2), (3), or (4). Moreover, we assume that automation MN is designed so that after the reading of the stack symbol of the type
according to (1) and after a number of actions depending on the current stack symbol (2), (3), or (4). Moreover, we assume that automation MN is designed so that after the reading of the stack symbol of the type 
 ,
,  , simultaneously with the action according to (4) another action is carried out, namely the removal of top disk i-th pin on j-th. Transient function is defined so that after a finite number of beats the stack is empty and stops. This occurs because if the current stack symbol of the kind
, simultaneously with the action according to (4) another action is carried out, namely the removal of top disk i-th pin on j-th. Transient function is defined so that after a finite number of beats the stack is empty and stops. This occurs because if the current stack symbol of the kind , then MN deletes it, and if the current stack symbol is of the type
, then MN deletes it, and if the current stack symbol is of the type , then at the next beat of the parameter
, then at the next beat of the parameter  decreases by one unit, if
decreases by one unit, if , or
, or  passes into the symbol
passes into the symbol 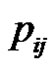 at
at , then that symbol is deleted.
, then that symbol is deleted.
We will prove that  the stack MN of configuration
the stack MN of configuration 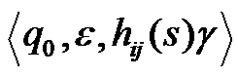 where
where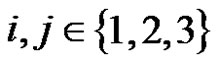 ,
, 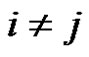 ,
,  as a result of their work reaches a configuration
as a result of their work reaches a configuration 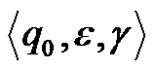 and in the process it transfers, according to the restrictions of Task 1, s discs from pin i to pin j. When s = 1 we have
and in the process it transfers, according to the restrictions of Task 1, s discs from pin i to pin j. When s = 1 we have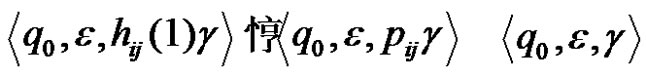 , i.e. the assertion is met. Let’s assume that the assertion is fulfilled for any t, such that
, i.e. the assertion is met. Let’s assume that the assertion is fulfilled for any t, such that  and let
and let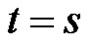 . Then in
. Then in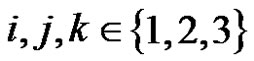 ,
, 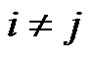 ,
,  ,
,  we have
we have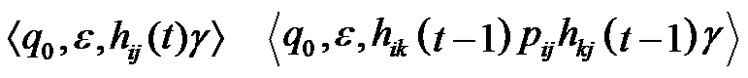 . According to the induction assumption, MN reaches the configuration
. According to the induction assumption, MN reaches the configuration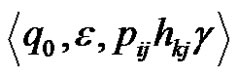 moving t – 1 discs from i-th pin of k-th pin after which it passes in a configuration
moving t – 1 discs from i-th pin of k-th pin after which it passes in a configuration 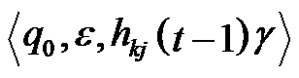 moving the next disc from pin
moving the next disc from pin 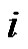 to pin
to pin 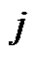 and again according to the induction, it moves
and again according to the induction, it moves 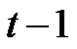 discs (as all are obviously smaller size) on this disk on pin
discs (as all are obviously smaller size) on this disk on pin 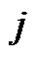 which are taken from pin
which are taken from pin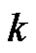 . Therefore the assertion is true for any
. Therefore the assertion is true for any .
.
According to the assertion that has just been just proved, we have:
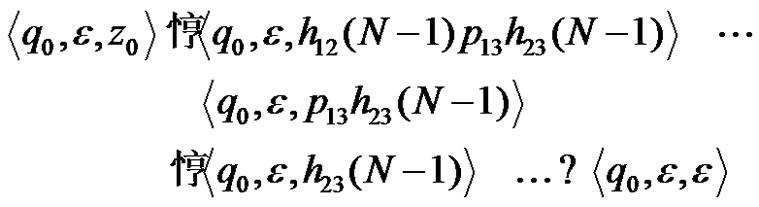 while the stack moves to the upper
while the stack moves to the upper 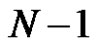 discs from the first to the second pin, then it moves the biggest at the bottom from the first to the third pin and finally it moves discs (
discs from the first to the second pin, then it moves the biggest at the bottom from the first to the third pin and finally it moves discs ( numbers from the second to the third pin observing the restrictions described in Task 1). Therefore the pushdown automation MN solves the task of the Hanoi towers.
numbers from the second to the third pin observing the restrictions described in Task 1). Therefore the pushdown automation MN solves the task of the Hanoi towers.
REFERENCES
- J. Arsac, “Jeux et Casse—Tête a Programmer,” BORDAS, Paris, 1985.
- A. V. Anisimov, “Recursive Information Transducers,” Vishcha Shkola, Kiev, 1987.
- A. V. Anisimov, “Informatics, Creativity, Recursion,” Naukova Dumka, Kiev, 1988.
- N. Wirth, “Algorithms + Data Structures = Programs,” Prentice Hall, Boston, 1976.
- I. Chiswell, “A Course in Formal Languages, Automata and Groups,” Springer-Verlag, London, 2009. doi:10.1007/978-1-84800-940-0
- J. Denev, R. Pavlov and I. Demetrovich, “Discrete Mathematics,” Science and Art, Soa, 1984.
- J. Denev and S. Shtrakov, “Discrete Mathematics,” SouthWest University “N. Rilski”, Blagoevgrad, 1995.
- J. E. Hopcroft, R. Motwani and J. D. Ullman, “Introduction to Automata Theory, Languages, and Computation,” Addison-Wesley, Boston, 2001.
- K. Manev, “Introduction in Discrete Mathematics,” KLMN, Soa, 2003.
- J.-P. Allouche and F. Dress, “Tours de Hanoï et Automates,” Informatique Théorique et Applications, Vol. 24, No. 1, 1990, p. 1.
- J.-P. Allouche and J. Shallit, “Automatic Sequences: Theory, Applications, Generalizations,” University Press, Cambridge, 2003. doi:10.1017/CBO9780511546563
- S. Shtrakov, K. Yordzhev and M. Todorova, “Guide for Solving of Tasks in Discrete Mathematics,” South-West University “N. Rilski”, Blagoevgrad, 2004.
- S. Ginsburg, “The Mathematical Theory of Context-Free Languages,” McGraw-Hill, Boston, 1966.
- G. Lallemant, “Semigroups and Combinatorial Applications,” John Wiley & Sons, Hoboken, 1979.
- A. V. Aho and J. D. Ullman, “The Theory of Parsing, Translation and Computing,” Prentice-Hall, Upper Saddle River, 1972.
NOTES
1It is not necessary L(ΓN) to describe all solutions of Task 1. Some of them may be ineffective, for instance if they involve the useless relocation of disk as soon as moving the same disk to another pin.
2As usual with P(A) is denoted the set of all subsets of the set A, including the empty.

