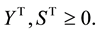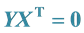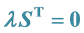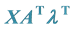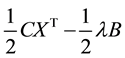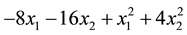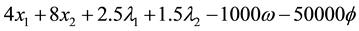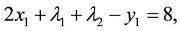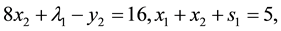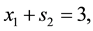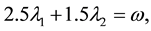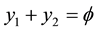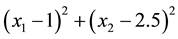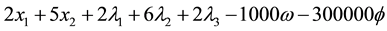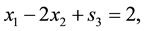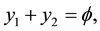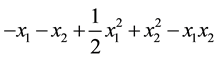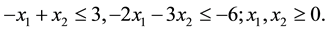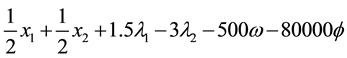American Journal of Operations Research
Vol.05 No.05(2015), Article ID:59358,10 pages
10.4236/ajor.2015.55031
A New Heuristic for the Convex Quadratic Programming Problem
Elias Munapo1, Santosh Kumar2*
1Graduate School of Business and Leadership, University of KwaZulu-Natal, Westville Campus, Durban, South Africa
2Department of Mathematics and Statistics, University of Melbourne, Parkville, Australia
Email: emunapo@gmail.com, *skumar@ms.unimelb.edu.au
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 July 2015; accepted 30 August 2015; published 2 September 2015
ABSTRACT
This paper presents a new heuristic to linearise the convex quadratic programming problem. The usual Karush-Kuhn-Tucker conditions are used but in this case a linear objective function is also formulated from the set of linear equations and complementarity slackness conditions. An unboundedness challenge arises in the proposed formulation and this challenge is alleviated by construction of an additional constraint. The formulated linear programming problem can be solved efficiently by the available simplex or interior point algorithms. There is no restricted base entry in this new formulation. Some computational experiments were carried out and results are provided.
Keywords:
Convex Quadratic Programming, Linear Programming, Karush-Kuhn-Tucker Conditions, Simplex Method, Interior Point Method

1. Introduction
There are so many real life applications for the convex quadratic programming (QP) problem. The applications include portfolio analysis, structural analysis, discrete-time stabilisation, optimal control, economic dispatch and finite impulse design; see [1] -[3] . Some of the methods for solving the convex quadratic problem are active set, interior point, branch and bound, gradient projection, and Lagrangian methods, see [4] -[9] for more information on these methods.
In this paper we present a new heuristic to linearise the convex quadratic programming problem. The usual Karush-Kuhn-Tucker conditions are still used but in this case a linear objective function is also formulated from the set of linear objective function equations and the complementary slackness conditions. There is an unboundedness challenge that is associated with the proposed linear formulation. To alleviate this challenge, an additional constraint is constructed and added to the linear formulation. The new linear formulation can be solved efficiently by the available simplex and interior point algorithms. There is no restricted base entry in the proposed approach. The time consuming complementarity pivoting is no longer necessary. Some computational experiments have been carried out and the objective of the computational experiments was to determine CPU times of the:
1) Proposed heuristic;
2) Regularised Active Set Method Mae and Saunders [10] ;
3) Primal-Dual Interior Point Algorithm.
It may be noted that the proposed method is suitable only if the quadratic programming problem satisfies conditions (1) to (5) mentioned in Section 2.1.
2 Mathematical Background
2.1 The Quadratic Programming Problem
Let a quadratic programming (QP) problem be represented by (1).
Minimize 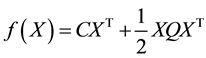
Subject to:
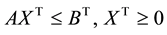 (1)
(1)
where
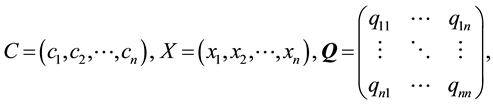
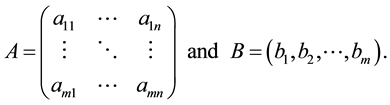
It is assumed that:
1) Matrix 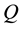 is a
is a 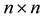 symmetric and positive definite,
symmetric and positive definite,
2) Function 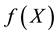 is strictly convex,
is strictly convex,
3) The conditions 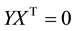 and
and 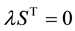 hold. Here
hold. Here 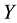 and
and 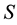 are dual and primal slack variables, respectively.
are dual and primal slack variables, respectively.
4) Since constraints are linear then the solution space is convex, and
5) Any maximization quadratic problem can be changed into a minimization and vice versa.
When the function 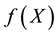 is strictly convex for all points in the convex region then the quadratic problem has a unique local minimum which is also the global minimum [11] .
is strictly convex for all points in the convex region then the quadratic problem has a unique local minimum which is also the global minimum [11] .
2.2. Karush-Kuhn-Tucker Conditions
The convex quadratic programming problem has special features that we can capitalize on when solving. All constraints are linear and the only nonlinear expression is the objective function. Let the Lagrangian function for the QP problem be 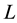 and in this case
and in this case
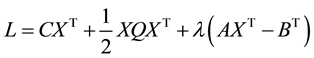 (2)
(2)
where 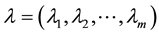 and
and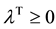 . In this case we exclude the non-negativity conditions
. In this case we exclude the non-negativity conditions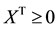
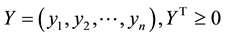
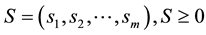
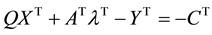
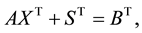
Complementary slackness conditions are given in (5) and are only satisfied at the optimal point. These conditions are:
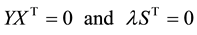
Note 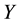
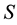
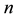
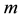
2.3. Some Matrix Operations
Suppose 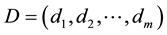
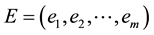
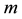
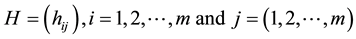
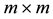
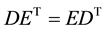
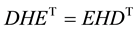
Equations (6) and (7) can be easily verified. These simple results are used to eliminate the complementary slackness conditions.
3. Elimination of Complementary Slackness Conditions
3.1. Elimination of
Pre-multiply (3) by X, we have:
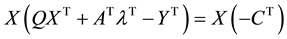
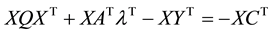
From (6) 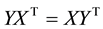
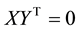
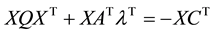
By rearranging, we have
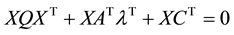
3.2. Elimination of
Pre-multiply (4) by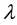
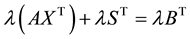
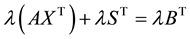
Since from (4)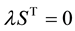
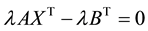
3.3. Elimination of 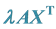
From (7), we have: 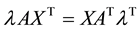
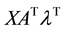
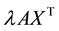

Subtracting (14) from (15), we obtain (16):
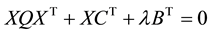
3.4. Linear Objective Function for the Quadratic Programming Problem
Note that the expression in relation (13) is nonlinear but it can be rearranged so that the original quadratic programming objective function becomes a linear quantity. This can be achieved as follows:
Divide relation (16) by two, one obtains:
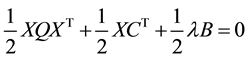
Rearranging (17), we obtain (18):
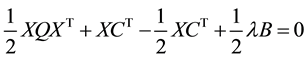
From (1)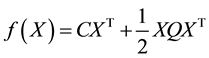
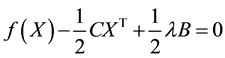
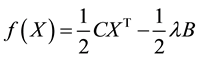
Thus the nonlinear objective function of the QP problem is now linearised but it creates a new challenge. We will discuss this in the next section.
3.5. LP Equivalent to the Given QP
From (1), (3) and (20), we have the following LP problem:
Minimize
Subject to:
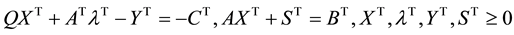
The minimisation problem (21) will have an unbounded solution due to negative coefficient of 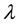
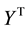
of unboundedness in the LP (21). Here, we let: 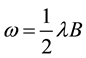
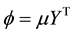
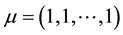
tor of dimension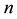
Minimize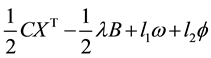
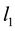
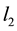
coefficients. Both of these constants do not have to assume the same large values. A large number of experiments were done on a large number of quadratic programming problems and and it was observed that 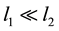
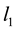
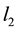
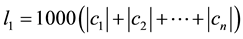
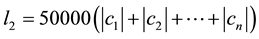
3.6. Existence of a Linear Objective Function and Verification of Optimality
The optimal solution of a convex quadratic programming model is unique and it satisfies the complementary conditions 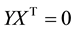
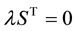
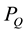
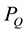
4. Numerical Illustrations
4.1. Example 1
Minimize
Subject to:
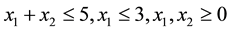
This example was taken from Jensen and Bard (2012) without any modifications.
Linear formulation of the above QP
In this case we took 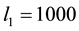
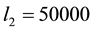
Maximize
Subject to
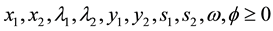
The solution of (23) by the simplex method is given by:
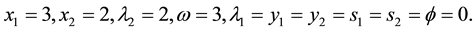
From the original QP objective function, we have the objective value given in (25).
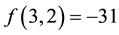
Verification of optimality
The solution is optimal because complementary slackness conditions are satisfied as given in (26).
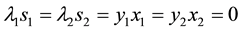
4.2. Two More Examples
Two more examples are solved to illustrate how the large constants are selected. Example 2 is taken from [12] and example 3 is from [13] .
Example 2 from [12]
Minimize
Subject to:
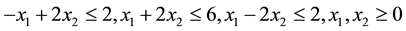
The linear formulation of (27) becomes as given in (28).
Maximize
Such that:
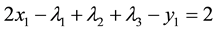
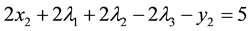
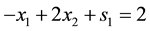
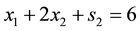
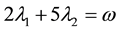
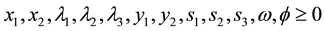
The solution of (28) is as given in (29) and once again it is optimal as all complementary slackness conditions are satisfied.
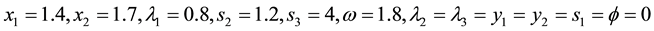
Example 3 from [13]
Minimize
Subject to:
The linear formulation of the above example is given by (30).
Maximize
Subject to:
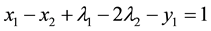
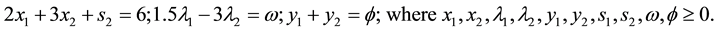
The solution is given by: 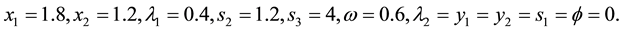
5. Computational Experiments
A set of convex quadratic programming test problems are given in [14] . All these test problems were used in testing the proposed approach. The objective of the computational experiments was:
1) To determine that the LP optimal solution is also optimal to the given QP.
2) Compare CPU times of the proposed heuristics with Regularized Active Set Method and Primal-Dual Interior Point Method
The results are tabulated in Table 1. MATLAB R2013 (version 8.2) running on an Intel Pentium Dual desktop
Table 1. Computational experiments on the set of QP test problems.
(Dual core G2020 2.9 GHz CPU, 2GB DDR3 1333 RAM) was used in these experiments. There were no advanced processing techniques embedded within the three methods. The set up time was excluded from the CPU times in all three methods. The zero (~0.00) means CPU time is less than 0.01 second. In all the test problems, it was found that the LP optimal solution was optimal to the QP problem. However, in the CPU time challenges were observed with the BODYD2 for the proposed heuristic and as a result we could not accurately obtain the necessary CPU time for these two cases. There was no challenge with the other two methods on the same BODYD2 problem. This experiment was conducted twice, but the same observation. We have no reason to support this behaviour but we believe it may be due to some local computational environment.
6. Conclusion
The convex QP problem can be solved like a linear programming problem efficiently either by the simplex method or the interior point algorithm. The restricted base entry is not necessary by the proposed approach. Complementary slackness can retard the simplex method, which is roughly eight times slower than the full speed simplex method. Taking complementary slackness conditions away itself is a big reduction in the number of constraints in the proposed linear formulation of the quadratic programming problem. More experiments are likely to give more insight and advantages of the proposed approach. The proposed method is in fact the usual simplex method applied to solving an ordinary LP that was obtained from the given convex QP. Also note that a large number of Maros-Maszaros test problems are giving rise to small to medium size LPs and therefore the proposed method dominates solving a large number of QPs, as is reflected in Table 1. From these results, it may be noted that, for example in the case of medium sized problems at serial 118 to 124 and large sized problems at serial number 125 to 132, the proposed heuristic outperformed the other two with respect to the cpu time.
Acknowledgements
The authors are thankful to the referees for their helpful and constructive comments.
Cite this paper
EliasMunapo,SantoshKumar, (2015) A New Heuristic for the Convex Quadratic Programming Problem. American Journal of Operations Research,05,373-383. doi: 10.4236/ajor.2015.55031
References
- 1. Gupta, O.K. (1995) Applications of Quadratic Programming. Journal of Information and Optimization Sciences, 16, 177-194.
http://dx.doi.org/10.1080/02522667.1995.10699213 - 2. Horst, R., Pardalos, P.M. and Thoai, N.V. (2000) Introduction to Global Optimization: Non-Convex Optimization and Its Applications. Kluwer Academic Publishers, Dordrecht.
http://dx.doi.org/10.1007/978-1-4615-0015-5 - 3. McCarl, B.A., Moskowitz, H. and Furtan, H. (1977) Quadratic Programming Applications. Omega, 5, 43-55.
http://dx.doi.org/10.1016/0305-0483(77)90020-2 - 4. Burer, S.D. and Vandenbussche, D. (2008) A Finite Branch and Bound Algorithm for Non-Convex Quadratic Programs with Semidefinite Relaxations. Mathematical Programming Series A, 113, 259-282.
http://dx.doi.org/10.1007/s10107-006-0080-6 - 5. Burer, S.D. and Vandenbussche, D. (2009) Globally Solving Box-Constrained Non Convex Quadratic Programs with Semidefinite-Based Finite Branch-and-Bound. Computational Optimisation and Applications, 43, 181-195.
- 6. Freund, R.M. (2002) Solution Methods for Quadratic Optimization. Lecture Notes, Massachusetts Institute of Technology, Cambridge, MA.
- 7. Gondzio, J. (2012) Interior Point Methods 25 Years Later. European Journal of Operational Research, 218, 587-601.
http://dx.doi.org/10.1016/j.ejor.2011.09.017 - 8. More, J.J. and Toraldo, G. (1989) Algorithms for Bound Constrained Quadratic Programming Problems. Numerische Mathematik, 55, 377-400.
http://dx.doi.org/10.1007/BF01396045 - 9. Liu, S.T. and Wang, R.T. (2007) A Numerical Solution Method to Interval Quadratic Programming. Applied Mathematics and Computations, 189, 1274-1281.
http://dx.doi.org/10.1016/j.amc.2006.12.007 - 10. Maes, C. and Saunders, M. (2012) A Regularized Active-Set Method for Sparse Convex Quadratic Programming. 21st International Symposium on Mathematical Programming, Berlin, 19-24 August 2012.
- 11. Jensen, P.A. and Bard, J.F. (2012) Operations Research Models and Methods. John Wiley & Sons Inc., Hoboken.
- 12. Lee, C.R. (2011) Unit 8: Quadratic Programming Active set Method and Sequential Quadratic Programming.
http://www.cs.nthu.edu.tw/~cherung/teaching/2011cs5321/handout8.pdf - 13. Winston, W.L. (2004) Operations Research Applications and Algorithms. 4th Edition, Duxbury Press, Pacific Grove, CA.
- 14. Maros, I. and Meszaros, C. (1999) A Repository of Convex Quadratic Programming Problems. Optimization Methods and Software, 11-12, 671-681.
NOTES
*Corresponding author.