Journal of Applied Mathematics and Physics
Vol.03 No.04(2015), Article ID:55821,11 pages
10.4236/jamp.2015.34053
QED-Lie Algebra and Their 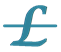 -Modules in Superconductivity
-Modules in Superconductivity
Francisco Bulnes
Research Department in Mathematics and Engineering, TESCHA, Chalco, Mexico
Email: francisco.bulnes@tesch.edu.mx


Received December 2014

ABSTRACT
It’s created a canonical Lie algebra in electrodynamics with all the “nice” algebraic and geometri- cal properties of an universal enveloping algebra with the goal of can to obtain generalizations in quantum electrodynamics theory of the TQFT, and the Universe based in lines and twistor bundles to the obtaining of irreducible unitary representations of the Lie groups 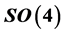 and
and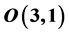 , based in admissible representations of
, based in admissible representations of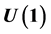 , and
, and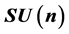 . The obtained object haves the advan- tages to be an algebraic or geometrical space at the same time. This same space of £-modules can explain and model different electromagnetic phenomena in superconductor and quantum pro- cesses where is necessary an organized transformation of the electromagnetic nature of the space- time and obtain nanotechnologies of the space-time and their elements.
. The obtained object haves the advan- tages to be an algebraic or geometrical space at the same time. This same space of £-modules can explain and model different electromagnetic phenomena in superconductor and quantum pro- cesses where is necessary an organized transformation of the electromagnetic nature of the space- time and obtain nanotechnologies of the space-time and their elements.
Keywords:
Electromagnetic Representation, Electro-Physics Theory, Lie Algebra, 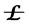 -Modules
-Modules

1. Introduction: Construction of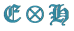 , with
, with , and
, and ,
, 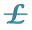 -Modules
-Modules
Let , be the space-time whose causal structure [1] (Segal, 1974), is defined by the space
, be the space-time whose causal structure [1] (Segal, 1974), is defined by the space
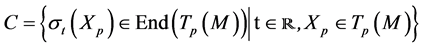
Let the Lorentz group
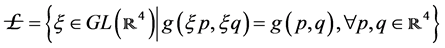
where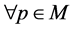 , and to a local coordinates system
, and to a local coordinates system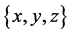 ,1
,1
Is the pseudo Riemannian metric of the manifold

Induced for the orientation of



Consider the electromagnetic field or Maxwell field defined as the differential 2-form of the forms space
Which can be described in the endomorphism space of



where 

We want to obtain a useful form to define the actions of the group







Likewise, the electromagnetic field is the 2-form given by (6) with the property of the transformation
In



In the context of the gauge theories (that is to say, in the context of bundles with connection as the principal 




Consider the 






And let the spaces



And
where











where



In the absence of sources, the Maxwell equations are symmetric under a duality transformation, which interchanges electric and magnetic fields.
Proposition 2.1. (F. Bulnes) [2]. Said 


Proof. Using the definition of


With rule of correspondence
where the images of

Then to a new coordinate system 
where









Let






And such that the 


which is completely equivalent to (8). But is enunciated in this moment because it legitimizes the Maxwell tensor from the scalar and vector potentials and we have (12).
We consider the space of electromagnetic power where we will define the domain of electromagnetic space transformation,6 that is to say, the cross product of 

where




which is universal in the following sense:
For every Abelian group

there is a unique group homomorphism

such that
for all 




We want describe energy flux in liquid and elastic media in a completely generalized diffusion of electromagnetic energy from the source view (particles of the space-time), which must be much seemed as a multi-ra- diative tensor insights space or a electromagnetic insights tensor space. This will permits us to express and model the flux of electromagnetic energy and any their characteristics.
The rate of energy transfer (per unit volume) from a region of space equals the rate of work done on a charge distribution plus the energy flux leaving that region.
Of fact these are elements


Then a source inside the electromagnetic multi-radiative space is obtained with the divergence, to know:
where

2. Lie Algebra Properties
Proposition (F. Bulnes) 3.1. The electrodynamical space


Proof. [2] [6].
Due to that we are using a torsion-free connection (e.g. the Levi Civita connection), then the partial derivative



Proposition (F. Bulnes) 3.2. The closed algebra
Proof.
Then the other properties of Lie algebra are trivially satisfied. Thus

Proposition (F. Bulnes) 3.3. The closed algebra
Proof. Since as Lie algebra, the space


Thus

vectors





3. Applications
Related 
Theorem (F. Bulnes) 3.1. The electro-anti-gravitational effects produced from superconductivity have that to be governed by the actions of the superconducting Lie-QED-algebra
Proof. [6].
3.1. The Algebra 
We want establish the electromagnetic principle that produce levitation or anti-gravity from the electro-anti- gravitational source that include the proper movements in the space-time that are connected with the actions of the group
These proper movements are determined through elements of

action of their Maxwell fields

calibrate the gravitational elements through electromagnetic elements such that these last can change the gravitational effects changing the spin characteristic of the affected region by these superconductor electromagnetic fields.
The initial ideas to this respect are replace the Abelian group








We want these identifications because our superconductivity theory establish the principles to risk the electro- anti-gravitational flight of an object as a sidereal object in the space-time, such that a galaxy or a star. In these sidereal objects, there are electromagnetic transformations explained MHD9, where the superconducting phenomena go given form the accretion rings, and their rotation (see the Figure 1).
3.2. 
Use through the model that consists of a complex scalar field

where





If the potential is such that their minimum occurs at non-zero value of



of 

Figure 1. (a) The cloud energy is created by the superconducting fields in the formatting iso-rotations in a galaxy, this forms, in condensed matter the sidereal objects with autonomous energy; (b) Artificial anti-gravitational wrapping created by superconducting and magnetic rotations. The “spirit of the anti-gravitational effect is in
Figure 2. Circulation around a close circuit in a superconductor under a magnetic field. This brings a discrete magnetic flow which means that the magnetic flow has been quantized.
Developing these topological electromagnetic elements using the tensor
precisely is our tensor algebra given in proposition 3.1., with their conserved Lie structure.
The essential difference between both versions consists in the coupling to a charged

Considering the supercurrent 
where

Considering to an electron field, a representation

And let



Proposition 2.2.1. There is a natural one-to-one correspondence between the set of all representations of









Proof. [6].
Def. 2.2.1. [11]. A 
Before of this, we pass to the fundamental lemma to characterize the algebra
Lemma (F. Bulnes) [11] 2.2.1. All electromagnetic actions and their effects (microscopic and macroscopic) on the superconductor object

Proof. [9] [11].
3.3. Organized Transformations and Nanotechnology by
Theorem (F. Bulnes) 5.1. [6]. The electro-anti-gravitational effects produced from superconductivity have that to be governed by the actions of the superconducting Lie-QED-algebra
The demonstrations was realized in [6] using some results on iso-rotations which also co-help in the electro- anti-gravitational effect. Likewise, considering two elements of the group

And the field is transformed as
where explicitly the image
Which belongs to the charge-conjugated particle. The anti-particle is obtained of accord to the contragradient
There are not charge-conjugated in gravity, since if the gauge group is Lorentz group



But we need affect the immediate space-time at least locally through of these 
We define the field

Under a general diffeomorphism





Then the principal equivalence requires that the fields on our manifold locally transform be as in special relativity, that is to say, if, is an element of the Lorentz group



However, the generalization to a general diffeomorphism is not unique. We could have chosen the field

But as






It will be useful to clarify the emerging picture of space-time properties by having a close look at a contravariant vector field





Then for completeness, let us also define the combined mappings through the relations:
Newly introducing the fields 

where





which is a new connection. Then the Maxwell-anti-gravity Lagrangian (that is to say, for anti-gravitational pendants
Staying a Lagrangian of the type 


4. Conclusion
Different microscopic aspects of electromagnetic nature are analyzed through the construction of an anti-com- mutative algebra of 
Table 1. QED-Lie algebra contexts [15]-[23].
In this table are resumed all the applications mentioned in the sections of this work.
Acknowledgements
I am grateful for the invitation realized by the SCET-2015, organizers to participate with a talk in applied mathematics and physics.
Cite this paper
Francisco Bulnes, (2015) QED-Lie Algebra and Their £ -Modules in Superconductivity. Journal of Applied Mathematics and Physics,03,417-427. doi: 10.4236/jamp.2015.34053
References
- 1. Segal, I.E. (1976) Mathematical Cosmology and Extragalactic Astronomy. Pure and Applied Mathematics, 68, Academic Press, New York.
- 2. Bulnes, F. (2006) Doctoral Course of Mathematical Electrodynamics. SEPI-IPN, Mexico, 9, 398-447.
- 3. Dummit, D.S. and Foote, R.M. (2004) Abstract Algebra. Wiley, Hoboken.
- 4. Marsden, J.E. and Abraham, R. (1982) Manifolds, Tensor Analysis and Applications. Addison Wesley, Massachusetts.
- 5. Wilczek, F (2009) Majorana Returns. Nature Physics, 5, 614.
- 6. Bulnes, F. (2014) A Lie-QED-Algebra and Their Fermionic Fock Space in the Superconducting Phenomena. Quantum Mechanics, Rijeka.
- 7. Bulnes, F., Hernandez, E. and Maya, J. (2010) Design and Development of an Impeller Synergic System of Electromagnetic Type for Levitation, Suspension and Movement of Symmetrical Bodies, IMECE/ASME, British Columbia, Canada.
- 8. Nielsen, H.B. and Olesen, P. (1973) Vortex-Line Models for Dual Strings. Nuclear Physics B, 61, 45-61.
- 9. Alario, M.A. and Vicent, J.L. (1991) Superconductivity. Eudema Fortuny, Madrid, Spain.
- 10. Ginzburg, V.L. and Landau, L.D. (1950) Zh. Eksp. Teor. Fiz. 20, 1064.
- 11. Bulnes, F., Martínez, I. and Maya, J. (2012) Design and Development of Impeller Synergic Systems of Electromagnetic Type to Levitation/Suspension Flight of Symmetrical Bodies. Journal of Electromagnetic Analysis and Applications, 4, 42-52.
- 12. Bulnes, F. (2013) Orbital Integrals on Reductive Lie Groups and Their Algebras. Intech, Rijeka. http://www.intechopen.com/books/orbital-integrals-on-reductive-lie-groups-and-their-algebras/orbital-integrals-on-reductive-lie-groups-and-their-algebrasB
- 13. Strutinsky, V.M. (1967) Shell Effects in Nuclear Physics and Deformation Energies. Nuclear Physics A, 95, 420-442.
- 14. Hossenfelder, S. (2006) Anti-Gravitation. Elsevier Science.
- 15. Dixmier, J. (1969) Les C*-algèbres et leurs representations. Gauthier-Villars, France.
- 16. Cooper, L. (1956) Bound Electron Pairs in a Degenerate Fermi Gas. Physical Review, 104, 1189-1190.
- 17. Verkelov, I., Goborov, R. and Bulnes, F. (2013) Fermionic Fock Space in Superconducting Phenomena and Their Applications. Journal on Photonics and Spintronics, 2, 19-29.
- 18. Bardeen, J., Cooper, L.N. and Schrieffer, J.R. (1957) Microscopic Theory of Superconductivity. Physical Review, 106, 162-164.
- 19. Bulnes, F. (2013) Mathematical Nanotechnology: Quantum Field Intentionality. Journal of Applied Mathematics and Physics, 1, 25-44.
- 20. Llano, M. (2003) Unificación de la Condensación de Bose-Einstein con la Teoría BSC de Superconductores. Rev. Ciencias Exactas y Naturais, 5, 9-21.
- 21. Bulnes, F. (2013) Quantum Intentionality and Determination of Realities in the Space-Time through Path Integrals and Their Integral Transforms, Advances in Quantum Mechanics, Prof. Paul Bracken (Ed.), InTech. http://www.intechopen.com/books/advances-in-quantum-mechanics/quantum-intentionality-and-determination-of-realities-in-the-space-time-through-path-integrals-and-t
- 22. Landau, L.D. and Lifshitz, E.M. (1960) Electrodynamics of Continuous Media. Volume 8 of Course of Theorical Physics, Pergamon Press, London.
- 23. Bulnes, F. (1998) The Super Canonical Algebra . International Conferences of Electrodynamics in Veracruz, IM/UNAM, Mex-ico.
NOTES
1Consider (light speed constant)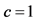 .
.
2The anti-symmetric nature of this form results obvious:
3This is valid since tensor product of free 


4The Levi-Civita tensor can be used to construct the dual electromagnetic tensor in which the electric and magnetic components exchange roles (conserving the symmetry, characteristic that can be seen in the matrices of the electromagnetic tensor

where is the rank-4 Levi-Civita tensor density in Minkowski space.
5The map is automorphism on
6This defines the hyperbolic paraboloid of the space-time region in a region of electromagnetic power.
7Let 







8
9Magneto-Hydrodynamics.
10In a complex scalar field theory, the scalar field takes values in the complex numbers, rather than the real numbers. The action considered normally takes the form
This has a



11If

But
For the Stokes theorem is had that
To it is necessary remember that the superconducting current


For the circulation around a close circuit
we have that on the close circuit
that in our case is
12Remember that
13
14The underlined indices on these quantities do not refer to the coordinates of the manifols, but to the local basis in the tangential. All of these fields still are functions of the space-time coordinates



15A electromagnetic case is given by the algebra:





































































