Journal of Applied Mathematics and Physics
Vol.03 No.04(2015), Article ID:55792,8 pages
10.4236/jamp.2015.34049
Homotopy Analysis Method for Equations of the Type 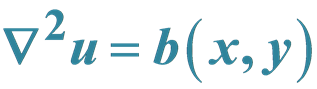 and
and 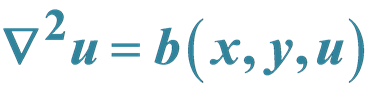
Selcuk Yildirim
Department of Electrical and Electronics Engineering, Siirt University, Siirt, Turkey
Email: syildirim@siirt.edu.tr


Received January 2015

ABSTRACT
In this paper, the homoto pyanalysis method (HAM) is presented to solve some of engineering problems. The homotopy analysis method is applied in obtaining exact solutions for equations of the type 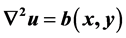 and
and 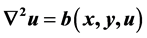 on an elliptical domain. Exact solutions are presented for several examples involving to demon strate the applic ability and efficiency of HAM.
on an elliptical domain. Exact solutions are presented for several examples involving to demon strate the applic ability and efficiency of HAM.
Keywords:
Homotopy Analysis Method, Engineering Problems, Exact Solutions

1. Introduction
The homotopy analysis method is developed in 1992 by Liao [1]-[8]. It is an analytical approach to get the series solution of linear and nonline arpartial differential equations. The difference with the other perturbation methods is that this method is independent of small/large physical parameters. It also provides a simple way to ensure the convergence of series solution [9]. This method has been successfully applied to solve many linear and non linear partial differential equationsin various fields of science and engineering by many authors [1]-[16]. The homotopy analysis method is useful and efficient for obtaining both analytical and numerical approximations of linear or nonlinear differential equations. In this study, we will concentrate on exact solutions for equations type of 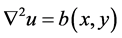 and
and 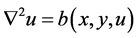 frequently used in applied and engineering mathematics.
frequently used in applied and engineering mathematics.
2. The Engineering Equations on an Elliptical Domain
We refer to the problem given by Partridge and Brebbia [17]. Consider the following engineering equations
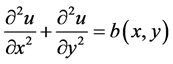 (1)
(1)
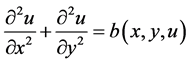 (2)
(2)
where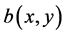 , that is, considered to be a known function of position and
, that is, considered to be a known function of position and 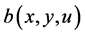 will be considered as a known function of the potential.
will be considered as a known function of the potential.
In all applications, the domain bounded by the ellipse given in Figure 1 will be used. The boundary condition is the Dirichlet condition with 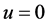 on the boundary.
on the boundary.
The equation of the ellipse is
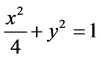 (3)
(3)
3. Homotopy Analysis Method
We apply the HAM to equations of the type 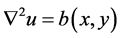 and
and 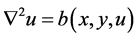 with Dirichlet boundary con- dition. We consider the following differential equation
with Dirichlet boundary con- dition. We consider the following differential equation
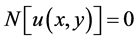 (4)
(4)
where 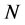 is a linear operator,
is a linear operator, 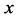 and
and 


where






To both sides of Equation (5), we get the following mth-order deformation equation

where

And
Figure 1. Elliptical domain with Dirichlet boundary condition.

Note that 




4. Applications
We apply Homotopy Analysis Method to equations of the type 

Equation (1) suggests that we define an equation of linear operator as

And Equation (2) suggests that we define an equation of linear operator as

Using the above definitions, the zeroth-orderde formation equation is constructed as
Applying the homotopy-derivative to the zeroth-orderde formation equation, we obtain the following mth- orderde formation equations
Since


where


Example 1. Consider the equation of the type

With initial guess

using HAM, were cursively obtain







When


Example 2. Consider the equation of the type

with initial guess

using HAM, were cursively obtain







When


Example 3. Consider the equation of the type

with initial guess

using HAM, were cursively obtain







For


which is the exact solution.
Example 4. Consider the equation of the type

with initial guess

using HAM, were cursively obtain







For


which is the exact solution.
Example 5. Consider the equation of the type

with initial guess

using HAM, were cursively obtain







For


which is the exact solution.
5. Conclusion
In this paper, the homotopy analysis method has been applied to solve some of engineering problems defined on an elliptical domain. Exact solutions for equations of the type 




Cite this paper
Selcuk Yildirim, (2015) Homotopy Analysis Method for Equations of the Type ∇2=b(x,y) and ∇2u=b(x,y,u). Journal of Applied Mathematics and Physics,03,391-398. doi: 10.4236/jamp.2015.34049
References
- 1. Liao, S.J. (2005) Comparison between the Homotopy Analysis Method and Homotopy Perturbation Method. Applied Mathematics and Computation, 169, 1186-1194.
- 2. Liao, S.J. (2004) On the Homotopy Analysis Method for Nonlinear Problems. Applied Mathematics and Computation, 147, 499-513.
- 3. Liao, S.J. (2010) An Optimal Homotopy-Analysis Approach for Strongly Nonlinear Differential Equations. Communications in Nonlinear Science and Numerical Simulation, 15, 2003-2016.
- 4. Liao, S.J. (2009) Notes on the Homotopy Analysis Method: Some Definitions and Theorems. Communications in Non-linear Science and Numerical Simulation, 14, 983-997. http://dx.doi.org/10.1016/j.cnsns.2008.04.013
- 5. Liao, S.J. (2005) An Analytic Approach to Solve Multiple Solutions of a Strongly Nonlinear Problem. Applied Mathe- matics and Computation, 169, 854-865.
- 6. Liao, S.J. (2003) Beyond Perturbation: Introduction to the Homotopy Analysis Method. Chapman and Hall/CRC Press, Boca Raton.
- 7. Liao, S.J. (2012) Homotopy Analysis Method in Nonlinear Differential Equations. Springer, New York.
- 8. Liao, S.J. (1992) Proposed Homotopy Analysis Techniques for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai.
- 9. Das, S., Vishal, K., Gupt, P.K. and Ray, S.S. (2011) Homotopy Analysis Method for Solving Fractional Diffusion Equation. International Journal of Applied Mathematics and Mechanics, 7, 28-37.
- 10. Song, L. and Zhang, H. (2007) Application of Homotopy Analysis Method to Fractional Kdv-Burgers-Kuramoto Equation. Physics Letters A, 367, 88-94.
- 11. Abdulaziz, O., Hashim, I. and Saif, A. Solutions of Time-Fractional PDEs by Homotopy Analysis Method. Differential Equations and Nonlinear Mechanics, 2008, Article ID: 686512.
- 12. Ganjiani, M. (2010) Solution of Nonlinear Fractional Differential Equations Using Homotopy Analysis Method. Applied Mathematical Modelling, 34, 1634-1641. http://dx.doi.org/10.1016/j.apm.2009.09.011
- 13. Abidi, F. and Omrani, K. (2010) The Homotopy Analysis Method for Solving the Fornberg-Whitham Equation and Comparison with Adomian’s Decomposition Method. Computers & Mathematics with Applications, 59, 2743-2750.
- 14. Molabahrami, A. and Khani, F. (2009) The Homotopy Analysis Method to Solve the Burgers-Huxley Equation. Nonlinear Analysis: Real World Applications, 10, 589-600. http://dx.doi.org/10.1016/j.nonrwa.2007.10.014
- 15. Ghanbari, B. (2104) An Analytical Study for (2+1)-Dimensional Schr?dinger Equation. The Scientific World Journal, 2014, Article ID: 438345.
- 16. Inc, M. (2007) On Exact Solution of Laplace Equation with Dirichlet and Neumann Boundary Conditions by Homotopy Analysis Method. Physics Letters A, 365, 412-415.
- 17. Patridge, P.W., Brebbia, C.A. and Wrobel, L.C. (1992) The Dual Reciprocity Boundary Element Method. CMP, Elsevier Applied Scince, New York.














