 Journal of Applied Mathematics and Physics, 2014, 2, 1079-1084 Published Online November 2014 in SciRes. http://www.scirp.org/journal/jamp http://dx.doi.org/10.4236/jamp.2014.212124 How to cite this paper: Goik, D., Sieniek, M., Gurgul, P. and Paszyński, M. (2014) Modeling of the Absorption of the Elec- tromagnetic Wave Energy in the Human Head Induced by Cell Phone. Journal of Applied Mathematics and Physics, 2, 1079-1084. http://dx.doi.org/10.4236/jamp.2014.212124 Modeling of the Absorption of the Electromagnetic Wave Energy in the Human Head Induced by Cell Phone Damian Goik, Marcin Sieniek, Piotr Gurgul, Maciej Paszyński Department of Computer Science, AGH University of Science and Technology, Kraków, Poland Email: maciej.paszynski@agh.edu.pl Received Oc tob er 2014 Abstract In this paper, we present the Projection Based Interpolation (PBI) technique for construction of continuous approximation of MRI scan data of the human head. We utilize the result of the PBI al- gorithm to perform three-dimensional (3D) Finite Element Method (FEM) simulations of the heat- ing of the human head induced by cell phone. In particular, we utilize the Pennes equation to de- scribe the bioheat transfer with the right hand side representing the heat generated by cell phone. We utilize our own non-stationary time dependent multi-thread parallel direct solver for the solu- tion of this computational problem. From our numerical results it follows that 15 minutes (1000 seconds) exposure to the cell phone radiation implies up to 2 degrees Celsius increase of the tem- perature of the brain in the range close to the cell phone. Keywords Finite Element Meth od , Projection Based Inte rp ola ti on, Pennes Equation , Heating of the Human Head 1. Introduction In this paper we present design and implementation of three dimensional finite element method h adaptive code for efficient and accurate solution of the challenging engineering problem of heating of the human head induced by the propagation of electromagnetic waves generated by cell phone. We use the Pennes bioheat transfer equa- tion for the modeling of the heating of the human head. The heat source in the equation is based on the numeri- cal solution for the Maxwell equations modeling the propagation of the electromagnetic waves over the human head generated by cell phone. This project will allow for the first time find reliable answer to the question of the influence of the cellular phones on the brain tissue, compare Figure 1. This is the project with collaboration with the group of Professor Leszek Demkowicz from ICES (Institute for Computational and Engineering Science, The University of Texas in Austin), in the frame of the Polish National Science Center grant HARMONIA. The collaborating group of prof. Leszek Demkowicz provides the solution of the Maxwell equations, namely the heat source for the right hand side of the Pennes equation. The geometry of the human head is obtained by using my own implementation of the projection based interpolation algorithm 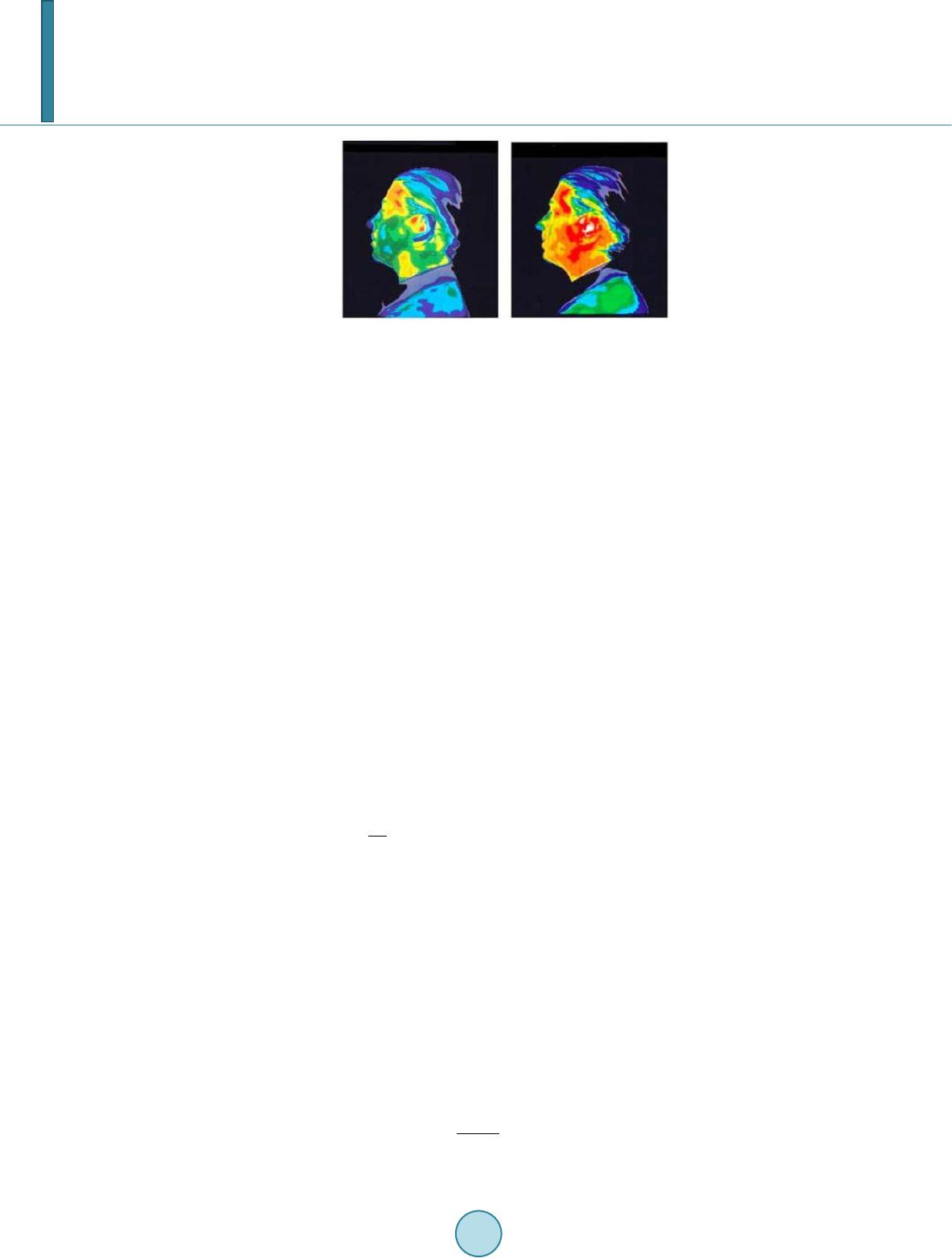 D. Goik et al. Figure 1. Left panel: Thermographic image of the head with no expose to harmful cell phone radiation, Right panel: Thermographic image of the head after a 15-minute phone call. Yellow and red areas indicate thermal (heating) effects that can cause negative health problems (images obtained from Prof. Leszek Demkowicz, The University of Texas at Austin). [1] generating the three dimensional h refined mesh based on the MRI scan of the human head of prof. Maciej Paszyński. This is the challenging problem due to the fact that of the complexity of the human head geometry and the numerical equations involved, which results in huge size of the system of linear equations. 2. Simulation of the Heating of the Human Head The simulation of the absorption of the electromagnetic wave energy over the human head, in particular human brain, induced by cell phone usage, and possible adverse health effects of EM waves are of the great importance. The simulations available so far concerned the simplified geometrical model of the human head [2]. In this pa- per we present a three dimensional finite element method simulations of the heating of the human head induced by electromagnetic waves generated by cell phone for the case of the real human head. In particular we perform the following steps in our simulation. First, we perform a MRI scan of the head of one of the authors of this pa- per (M. Paszyński), compare Figure 1. We create a three dimensional bitmap from the 29 cross-sections of the head with resolution 532 - 565 pixels obtained from MRI scan data. The range of the values at different pixels varies from [0,255]. These values correspond to different material data. Next, we utilize a projection based in- terpolation technique [3] [4] to generate a continuous approximation of the material data, compare Figure 2. We utilize three dimensional h adaptation algorithm [5] with hexahedral finite elements, with the error estimator based on the L2 norm difference between the local element approximation and the MRI scan data. Having the approximation a globally C0 and locally C1 function, we may distinguish different material data. In particular we assume air (approximation < 1), brain (1 <= approximation < 240) and skull (approximation >= 240). Having the PBI approximation, we can formulate the bioheat Pennes equation, taking into account thermal conductivity k as well as metabolism , perfusion , and heat source from the cellphone : () ( ) 0 sar in bb am u ck uWcuuqq t ρ ∂=∇⋅ ∇+−++Ω ∂ (1) The unknown is the temperature distribution in space and time. The values of the parameters are summarized in Figure 1. They are selected according to the kind of the tissue, as suggested by the results of the PBI approximation. 3. Projection Based Interpolation The location of material data inside the human head model has been obtained by using the projection based in- terpolation algorithm that consists the following sub-steps, related to hexahedral finite element vertices, edges, faces and interiors. For each finite element, we are looking for coefficients in a particular order. The com- putational mesh can be generated by using a linear computational cost projection based interpolation routine, first proposed in [1] [5]. We start with vertices, since their coefficients are the most straightforward to compute. There is only one function per each of eight vertexes with a support on it and the interpolating function is re- quired to be equal to the interpolant, which yields: ( ) ( ) 1,,8 i i vii Uv ai v ϕ =∀= , (2) 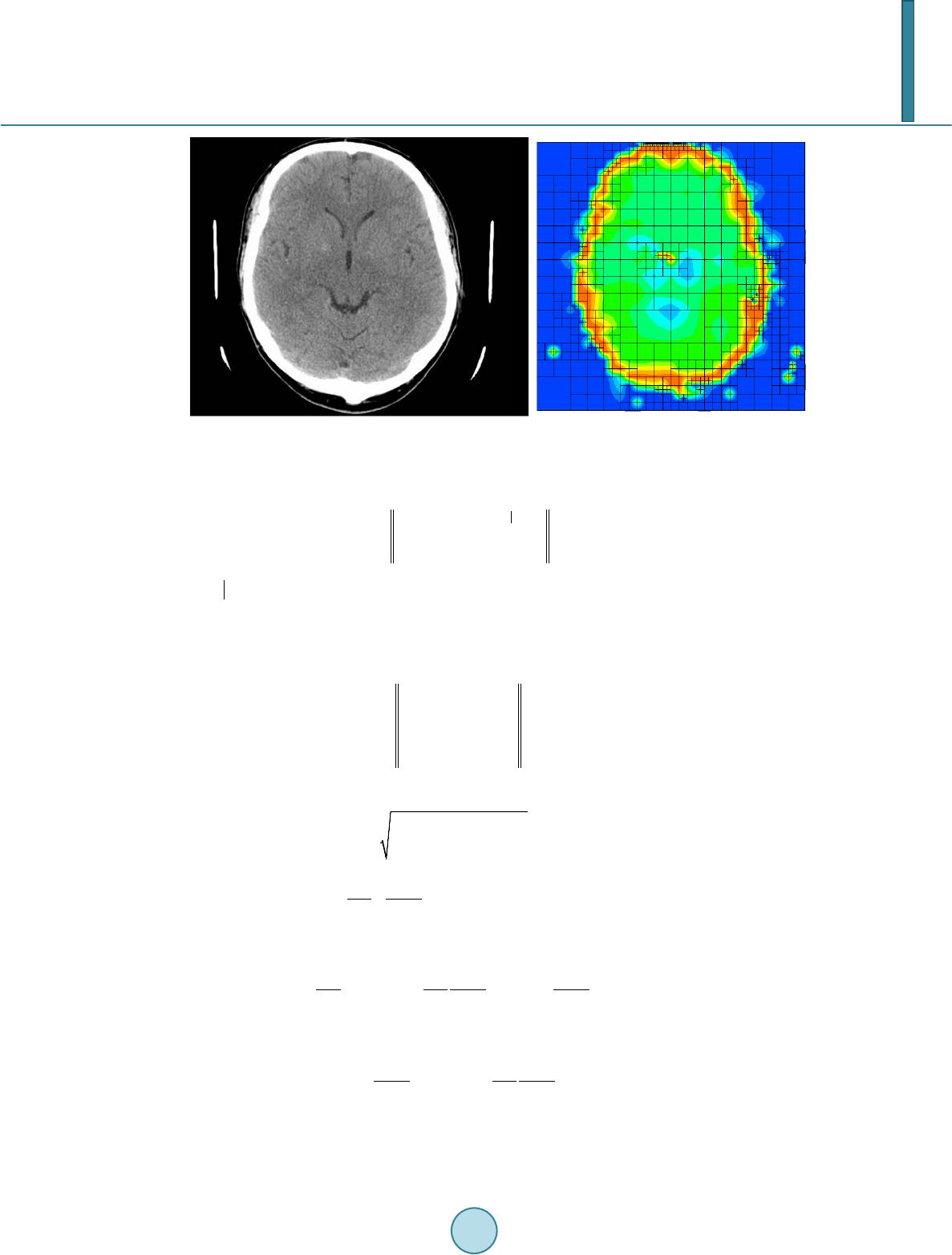 D. Goik et al. Figure 2. Single slice of the MRI scan of the human head and its PBI representation. On nodes other than vertices, the input function cannot be represented exactly, so instead we are trying to mi- nimize the representation error. First, on each one of the 12 edges of tetrahedral element: ( ) 1 0 dim 8 , 11 min1, ,12 ei ii i V v le jl He Uu ui = = −−→ ∀= ∑∑ (3) where signifies the number of edge shape functions in space with supports on edge . Such a problem can be reduced to a linear system and solved with a linear solver, but if we assume the adaptation order on each node, for each edge there exists only one shape function with a support on it. Not only is this re- striction justified performance-wise (one local equation instead of a system), but it also suffices in most cases, according to our experiments. Thus equation (3) reduces to: ( ) 1 0 8 0, 1 min1, ,12 ii i U ve j He Uuu i = −−→ ∀= ∑ , (4) where vanishes on the element’s vertices. After rewriting the norm: ( ) 32 0, 1 dmin1, ,12 i i e k e Uu xi = ∇⋅−→∀ = ∑ ∫ , (5) 2 3, , 1 d ddmin1,,12 and dd i ii i oe oee i kkk e u Ux iua xx ϕ = −→ ∀== ∑ ∫ (6) we have 2 2 33 3 ,, 11 1 dd dd d2ddmin1, ,12 ddd d ii ii i oe oe kk k kkk k ee e uu UU xx xi xxx x = == −+→ ∀= ∑∑ ∑ ∫∫ ∫ (7) which leads to 2 33 ,, 11 dd d d2dmin1, ,12 d dd ii ii oe oe kk k kk ee uu U x xi x xx = = −→ ∀= ∑∑ ∫∫ (8) since the other term is constant and can be omit in minimization. Let be is a bilinear, symmetric form and is a linear form defined as:  D. Goik et al. ()( ) 2 33 ,, 11 dd d ,2d , d dd d ii ii oe oe kk kk k ee uu U buvx lvx xx x = = == ∑∑ ∫∫ (9) It is proven that minimizing is reducible to solving for all test functions v. By applying this lemma we obtain 33 ,, 11 dd dd d2dmin1, ,12 dd dd ii ii oe oe kk kk kk ee uu vU x xi xx xx = = =→ ∀= ∑∑ ∫∫ (10) which leads to 33 11 d dd ddd 1,,12 ddd d i ii i ii e ee ekk kkk k ee U ax xi xxx x ϕ ϕϕ = = = ∀= ∑∑ ∫∫ (11) The next step consists in an optimization on six faces of hexahedral element: () 1 0 8 12 0, 0, 11 min1,, 6 j ji i U v ef jj Hf Uuu ui = = −−−→∀= ∑∑ , (12) where vanishes on vertices and edges. This leads to: 33 11 d dd ddd 1,...,6 ddd d i ii i ii f ff fkk kkk k ff U ax xi xxx x ϕ ϕϕ = = = ∀= ∑∑ ∫∫ (13) Finally, an analogical optimization in the interior of the finite element: ( ) 1 0 8 126 0,0, 0, 11 1 min jjj U v efI jj j HI Uuuu u = == −− −−→ ∑∑ ∑ , (14) (where vanishes everywhere except from the interior) yields: 33 11 d dd ddd dd dd ii I II Ikk kk kk ff U a xx xx xx ϕ ϕϕ = = = ∑∑ ∫∫ (15) It is worth noting that using this method the global matrix is not constructed at all. Thanks to the re- striction, we have a single equation over each vertex, edge, face and interior. This algorithm requires a computa- tional cost linear with respect to the mesh size, because it involves constant number of operations for each vertex, edge, face and interior and the number of respective nodes is proportional to —the number of finite elements. 4. Potential for Multi-Thread Implementation The projection-based interpolation is a fully local operation. The PBI involves four global loops, and all the computations are performed over element vertices, edges, faces and interiors. These operations may be fully pa- rallelizable using Open MP architecture. #pragam omp parallel for for vertex in (vertices of elements of the mesh) compute values of coefficient given by (2) for PBI for vertex store at vertex #pragam omp parallel for for edge in (edges of elements of the mesh) compute values of coefficient given by (11) for PBI for edge store at edge  D. Goik et al. #pragam omp parallel for for face in (faces of elements of the mesh) compute values of coefficient given by (13) for PBI for face store at face #pragam omp parallel for for interior in (interiors of elements of the mesh) compute values of coefficient given by (15) for PBI for vertex store at interior 5. Numerical results In this section we present the numerical results for the heating of the human head induced by cell phone with the material data selected according to the kind of the tissue, as suggested by the results of the PBI approximation, using values from Table 1. The PBI algorithm has been executed on the 3D MRI scan data, compare Figure 2. For the numerical solution of (1) we utilize the finite element method with Crank-Nicolson scheme, proved to be unconditionally stable. In our work we solve the Pennes equations over the real human head model, but the heat source from the cell-phone is based on the solution obtained by [1] (picture 6.14, the dipol located at 2 cm distance from the human head). From our numerical results it follows that 15 minutes (1000 seconds) exposure to the cell phone radiation implies up to 2 Celsius increase of the temperature of the brain in the range close to the cell phone, compare Figure 3. Table 1. Material data used in the simulation. Material Param et ers Air B ra in Skull 1.16 1039 1645 1006 3700 1300 0.02 0.57 0.4 0 7100 590 0 40000 3 300 Figure 3. Left panel: The solution to Pennes equation after 1000 seconds without a cell phone exposure. Uniform temperature Right panel: The solution to the Pennes equation at two cross- sections close to the ear (where the cell-phone is located), with and without the cell phone usage, after 1000 seconds (16 minutes of a cell phone exposure). Maximum temperature (red areas) reaches 38.4 Celsius.  D. Goik et al. 6. Conclusion In this paper we presented a three dimensional simulations on the heating of the human head tissues induced by the cell phone usage. We showed that 16 minutes of the exposure to the cell phone radiation results in a local increase of temperature up to 38.4 Celsius. Our solver can be applied for such the simulations for arbitrary input data, namely the results of the MRI scan of a human head. The heat source induced by cell phone was obtained from the work of [2] for the dipole antenna. In our future work we plan to develop software solving the Maxwell equations over the PBI data, in order to be able to experiment with different cell phone antennas. Acknowledgements The work presented in this paper has been supported by Polish National Science Center grants No. DEC- 2011/03/N/ST6/01397 (Marcin Sieniek, PBI algorithm; Piotr Gurgul, analysis of the concurrency), 2012/ 07/B/ST6/01229 (Damian Goik, non-stationary solver) and 2012/06/M/ST1/00363 (Maciej Paszyński, human head modeling) as well as the Dean’s grant no. 15.11.230.128 (Piotr Gurgul, multi-threa di ng) . References [1] Demkowicz, L. (2013) Projection Based Interpolation. The University of Texas, Austin. [2] Kim, K. (2013) Finite Element Modeling of the Radiation and Induced Hear Transfer in the Human Bodz. Ph.D. Dis- sertation, The University of Texas, Austin [3] Sien iek, M., P aszyński, M., Made j , Ł. and Go i k , D. (2014) Adaptive Projection Based Interpolation as a Pre-Pro ces- sing Tool in the Finite Element Method Workflow for Elasticity Simulations of the Dual Phase Microstructures. Steel Research International, 85, 1109-1119. http://dx.doi.org/10.1002/srin.201300168 [4] Sien iek, M. and Paszyński, M. (2014) Subtree Reuse in Mu lt i -Frontal Solvers for Regular Grids in Step-an d-Flash Im- print Nanolithography Modeling. Adva nced Engineering Materials, 16, 231-240. http://dx.doi.org/10.1002/adem.201300267 [5] Demkowicz, L., Kurtz, J., P ar do, D., Pas zyński, M., Rachowicz, W. and Zdunek, A. (2007) Computing with hp-Ada- ptive Finite Elements, Vol. II. Three Dimensional Elliptic and Maxwell Problems with Applications. Chapmann & Hall, CRC Press.
|