Journal of Electromagnetic Analysis and Applications
Vol. 3 No. 8 (2011) , Article ID: 6556 , 5 pages DOI:10.4236/jemaa.2011.38052
Power Density and SAR in Multi-Layered Life Tissue at Global System Mobile (GSM) Frequencies
![]()
Deptartment of Physics, College of Science, Islamic University, Gaza, Palestinian Territory.
Email: kelwasife@iugaza.edu.ps
Received June 12th, 2011; revised July 13th, 2011; accepted July 23rd, 2011.
Keywords: Electromagnetic Waves, Life Tissues, Specific Absorption Rate, Power Density, Finite Difference Time Domain Method (FDTD)
ABSTRACT
In this paper, the power density and specific absorption rate (SAR) distribution in multi-layered life tissues and exposed to electromagnetic field emitted from handheld cellular phone operating in the 900 MHz and 1800 MHz is studied. A One dimensional Finite-Difference Time-Domain (FDTD) method has been used, and numerical assessment of electromagnetic fields coupled to four biological body tissue. Values of interest in these assessments include induced electric field and specific absorption rate (SAR), which has been a measured of absorbed power density in the body have been evaluated. A comparison of the effect of two frequencies on human body tissue has shown graphically. The results noticed that the effect of frequency 900 MHz by mobile phone Global System Mobile (GSM) is more than the frequency of 1800 MHz.
1. Introduction
The use of mobile phone by people has grown substantially in the last years. In parallel with this, an increased concern by the scientific community, the authorities and the population regarding the safety of these phones has raised. It is currently the most appropriate choice when highly non-homogeneous structures are involved for which boundary techniques have fundamental limitations [1].
The Finite-Difference Time-Domain (FDTD) is the most often used method for evaluating of electromagnetic fields in human tissue.
The heating effects resulted from using a mobile phone operating near a metal wall has been studied [2]. The finite-difference time-domain (FDTD) simulation scheme was used in the simulation. The simulated physical domain consists of a dipole antenna, a high-resolution human head model.
The temperature rise in a human head caused by absorbed power in the form of SAR from a cellular telephone has been computed using a bio-heat equation approach. The SAR is computed using an FDTD solver for a reasonable cellular telephone model that radiates at both 900 and 1800 MHz [3]. The issue of temperature rise in the eye caused by electromagnetic fields has generated some interest due to the low blood flow through the eye tissue has been evaluated [4].
Computation of electromagnetic field inside a tissue at mobile communication has been studied, which presents a new approach to calculate the electromagnetic field inside a tissue, composed of electrically excitable cell by means of the FDTD (finite difference time domain method) [5,6].
A simple planar multi-layered head model irradiated by plane wave in the frequency range of 100 MHz - 300 Ghz is investigated by Akram and Andrew in [7], and it consists of skin, fat, bone, Dura, CSF and brain. Modeling the effect of electromagnetic waves produced by mobile phone base station on human body tissue has been studied [8].
The electromagnetic waves of different power levels and different frequencies penetrate into the human body causing health risks; this is of great public concern.
In this paper, a simple planar multi-layered life tissue model will be used to calculate the electric field, magnetic field, power density and Specific Absorption Rate (SAR) distributions inside the model when exposed to an electromagnetic waves with different frequencies produced from mobile phone using the Finite Difference Time Domain (FDTD) Method. A comparison between the two frequencies on human body tissue will be evaluated.
2. Numerical Method and Modelling
A schematic diagram of the multi-layer structure under consideration is shown in Figure 1. It is exposed vertically to electromagnetic waves with frequency equals 900 MHz and 1800 MHz upon the interface distance between the air and the first life tissue is 30 cm respectively. The electric field is assumed to propagate in the z direction with polarization at the x direction.
The structure has layered media consists of the skin of thickness d1 = 0.00073164 m, the fat of thickness d2 = 0.02441, the Muscle of thickness d3 = 0.04236, and the organs (kidney) layer of infinite thickness tissue [8].
The dielectric properties of the layers are donated with the complex permittivity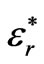 ,
,
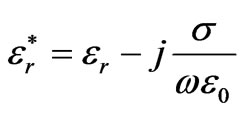 (1)
(1)
where 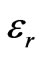 is the real relative part of the permittivity, σ is the conductivity and ω is the radial frequency of the signal. The quantity σ/ωε0 is called the loss tangent. It describes the looseness of the medium. Since the human tissues are nonmagnetic, it has been assumed that µi = µ0, where i stands for 1, 2, 3, and 4 which represents the four layers. The free space is assumed for the exterior of the model with wave number
is the real relative part of the permittivity, σ is the conductivity and ω is the radial frequency of the signal. The quantity σ/ωε0 is called the loss tangent. It describes the looseness of the medium. Since the human tissues are nonmagnetic, it has been assumed that µi = µ0, where i stands for 1, 2, 3, and 4 which represents the four layers. The free space is assumed for the exterior of the model with wave number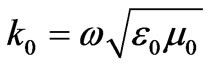 . And the dielectric properties for each two frequencies are illustrated in Table 1.
. And the dielectric properties for each two frequencies are illustrated in Table 1.
3. Finite Difference Time Domain (FDTD) Method
The FDTD method solves the curl Maxwell’s equations supposing divergence free initial conditions for the field strengths. The method starts with the definition of a generally rectangular mesh (with the choice of the step-sizes ∆x, ∆y and ∆z for the electric field and another staggered (by ∆x = 2, ∆y = 2 and ∆z = 2) grid for the magnetic field in the computational domain. The building blocks of this mesh are the so-called Yee-cells [10].
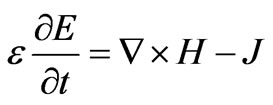 (2)
(2)
 (3)
(3)
where  is the current density.
is the current density.
In 1-D, we consider only Ex and Hy are not equal to zero and traveling in the z-direction. In addition, we assume that the fields do not vary in the x-y plane, i.e.
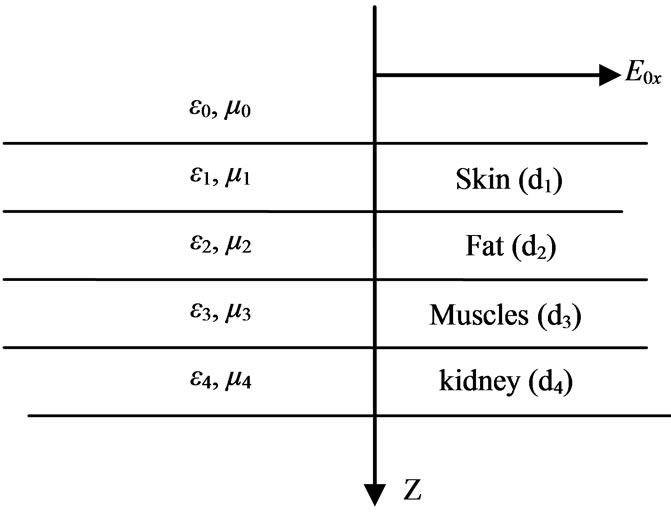
Figure 1. A Electromagnetic handheld cellular phone incident upon the interface between the air and the life tissue.
 and
and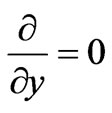 . Then Equations (2) and (3) can be reduced to
. Then Equations (2) and (3) can be reduced to
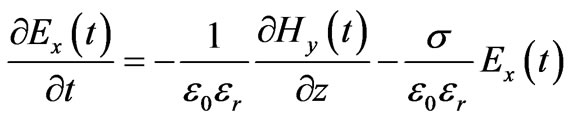 (4)
(4)
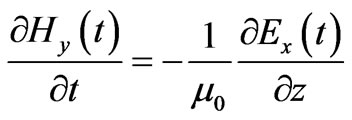 (5)
(5)
In the FDTD formulation, the central difference approximations for both the temporal and spatial derivatives are obtained at 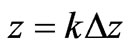 and
and 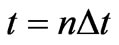 [9]
[9]
With the above notations the FDTD method computes the numerical solution as follows:
For the first equation [9]:
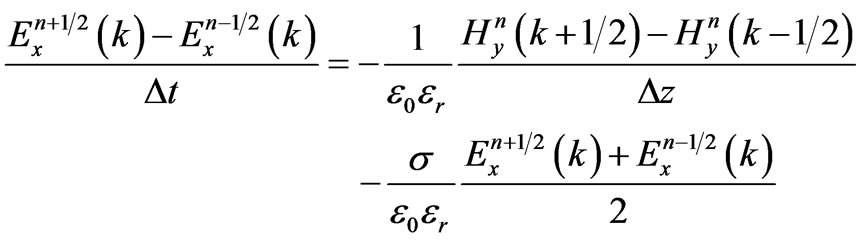 (6)
(6)
And for the second equation:
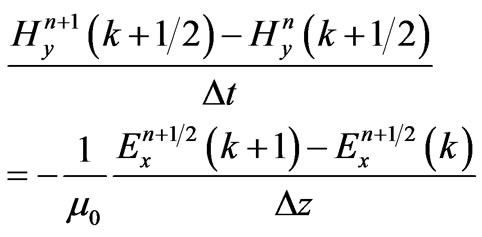 (7)
(7)
In the Equations (6)-(7), n is the time index and k is the spatial index, which indexes times  and positions
and positions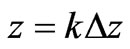 , or times
, or times 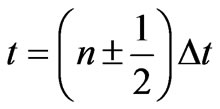 and positions
and positions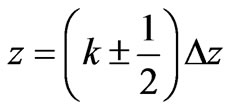 . The time index is written as a superscriptand the spatial index is within brackets. Equations (6) and (7) can be rearranged as a pair of “computer update
. The time index is written as a superscriptand the spatial index is within brackets. Equations (6) and (7) can be rearranged as a pair of “computer update
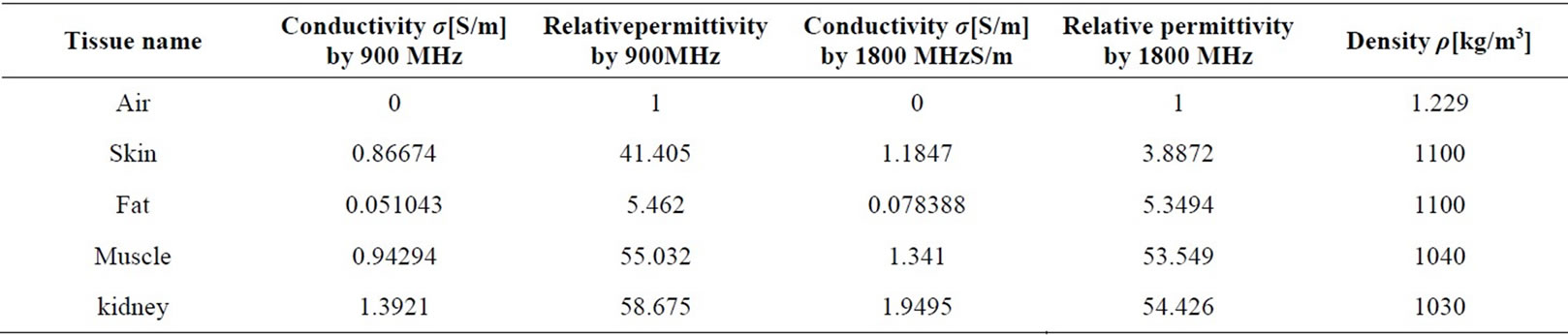
Table 1. Dielectric properties for human body at frequency 900 MHz and 1800 MHz.
equations”, which can be repeatedly updated in loop, to obtain the next time values of 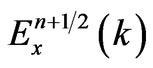 and
and 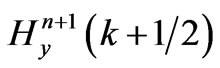 [9] corresponding the Ex (t + ∆t/2, z) and Hy (t + ∆t, z + ∆z/2). In Equations (4) and (5), ε0 and µ0 differ by several orders of magnitude.
[9] corresponding the Ex (t + ∆t/2, z) and Hy (t + ∆t, z + ∆z/2). In Equations (4) and (5), ε0 and µ0 differ by several orders of magnitude.
Equations (6) and (7) become
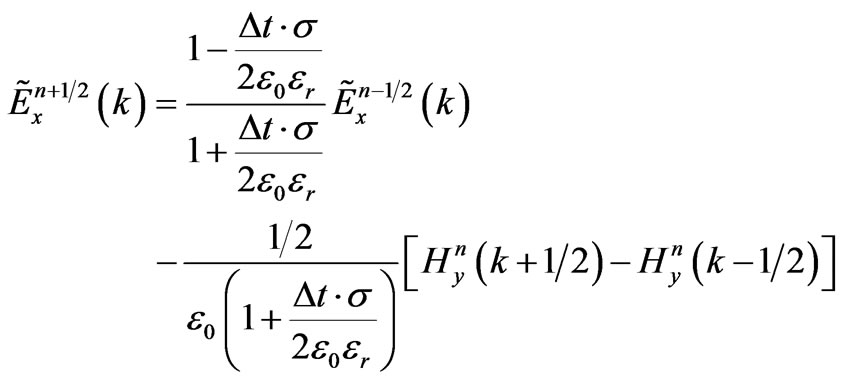 (8)
(8)
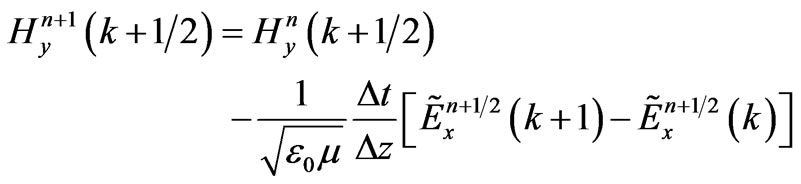 (9)
(9)
Stability and the FDTD method: For stability purposes, we need to choose the cell size 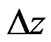 to allow 10 to 15 points per wave length. We used in all our simulations a time step
to allow 10 to 15 points per wave length. We used in all our simulations a time step 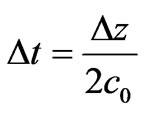 where c0 is the speed of light in free space. The most important points in FDTD calculations are the stability and numerical dispersion [12].
where c0 is the speed of light in free space. The most important points in FDTD calculations are the stability and numerical dispersion [12].
4. Results and Discussion
Simulation of a sinusoidal wave hits a life tissue that has different a dielectric constant according to different frequencies as shown in Table 1. The pulse is generated at the far left side with distance 30 cm and originates at cell number 2 and propagates to the right. This is illustrated graphically. Notice that the waveform in the medium is maximum absorbed at skin as the first layer, power density and specific absorption rate have been evaluated in life tissue where the power density (W/m3) absorbed in the conductivity σ along the layer from the sinusoidal field of the amplitude E is given [8].
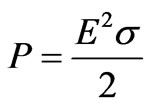 (10)
(10)
And specific absorption rate (SAR) in units of (W/kg) is the most important dosimetric parameter for the evaluation of the exposure hazard at radio and microwaves frequencies [13,14]. It is the biological electromagnetic estimation. It is defined as the power dissipation rate normalized by material density [15].
It can be shown that:
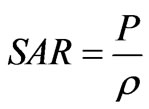 (11)
(11)
where ρi (Kg/m3) is the density of each tissue.
The numerical algorithm for Maxwell’s curl equations requires that the time increment must have a specific bound relative to the spatial discretization Dt , Dx, Dy and this condition is known as the Courant-Friedrichs-Lewy (CFL) Stability Criterion by
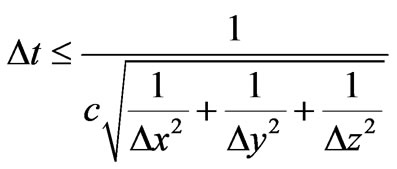 (12)
(12)
where, c is the speed of light in free space. Simulations were run for mobile phone radiation of the human life tissues at distance 30 cm which frequency was 0.9 GHz and 1.8 GHz respectively are continuous wave form source.
Figure 2 illustrates the Simulation of the propagation of the electric field of 900 MHz at (a) [8], and 1800 MHz at (b) into life tissue. It can be seen that the maximum peak of incident electromagnetic waves is at cell 32 which represent a skin layer, and it is decrease as the waves penetrate the other tissue. It mean that the tissues are effected and absorption the electromagnetic fields.
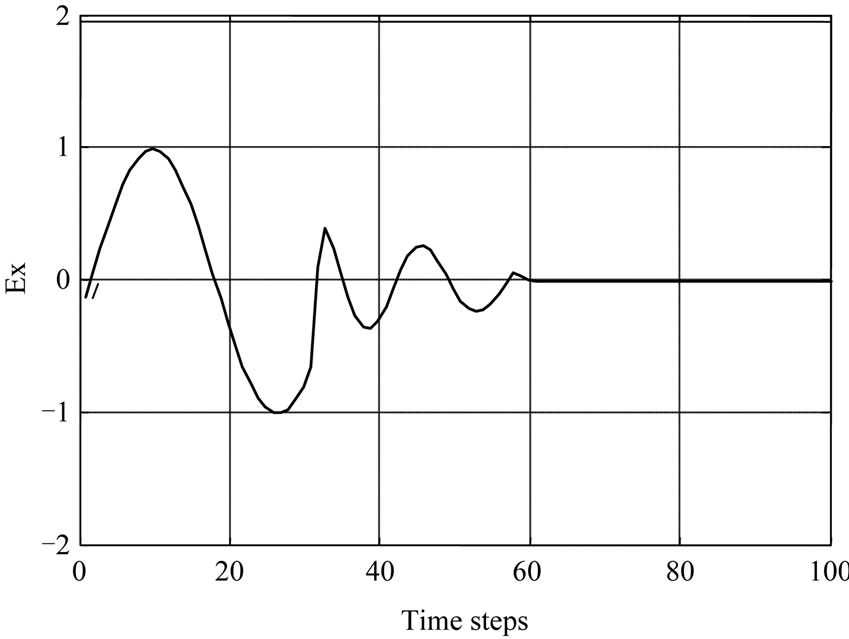
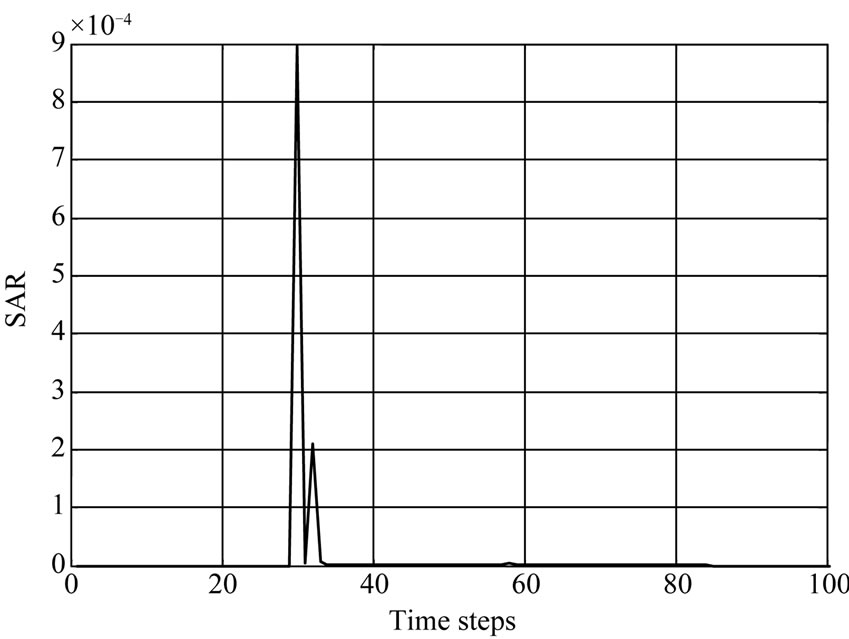
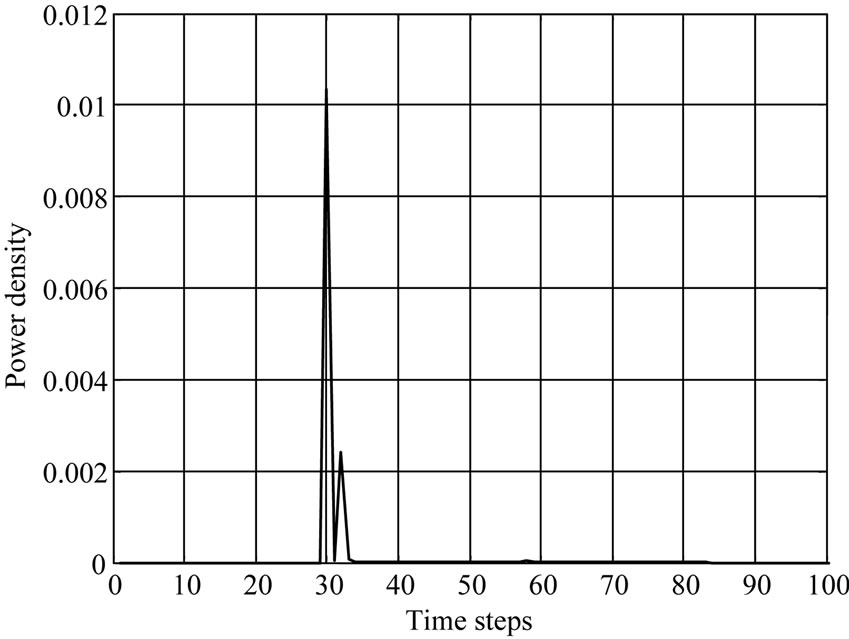
The penetration and absorption by 900 MHz is more than 1800 MHz of Power density and Specific absorption rate (SAR) distribution is shown in Figures 3 and 4.
The second peak value in the case of SAR and power is at 30 and 34 time steps respectively. It represents a fat tissue. In Figure 4, the power density was plotting with respect to time steps and the results show a maximum peak is more amplitude than SAR curve peaks. Also the power density at frequency 1.8 GHz is low comparing with the effect of 0.9 GHz frequency. In each curve the muscles tissue start at 58 time steps and kidney at 62.
 (a)
(a)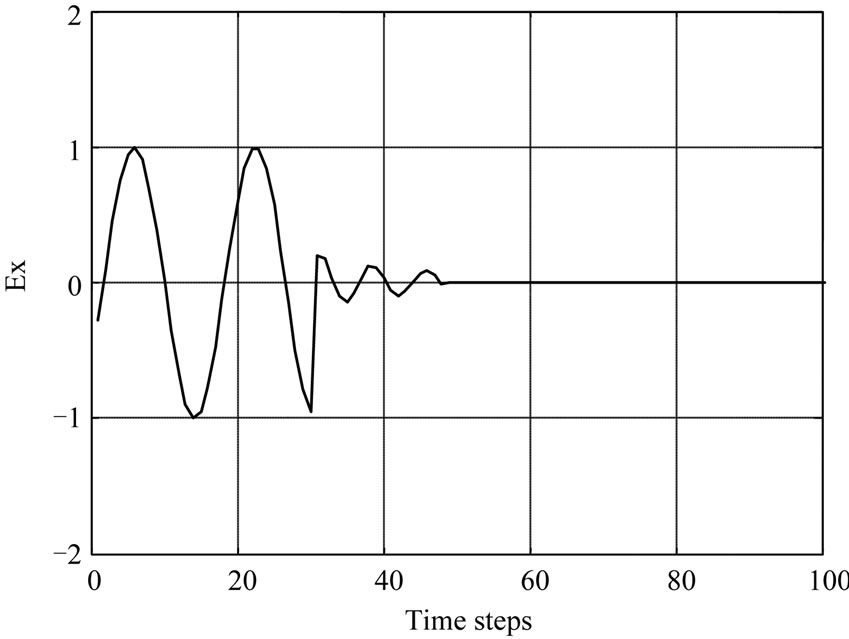 (b)
(b)
Figure 2. Comparison the effect of electric field penetration in human body tissue with different frequencies 900 MHz at (a) and 1800 MHz at (b).
 (a)
(a)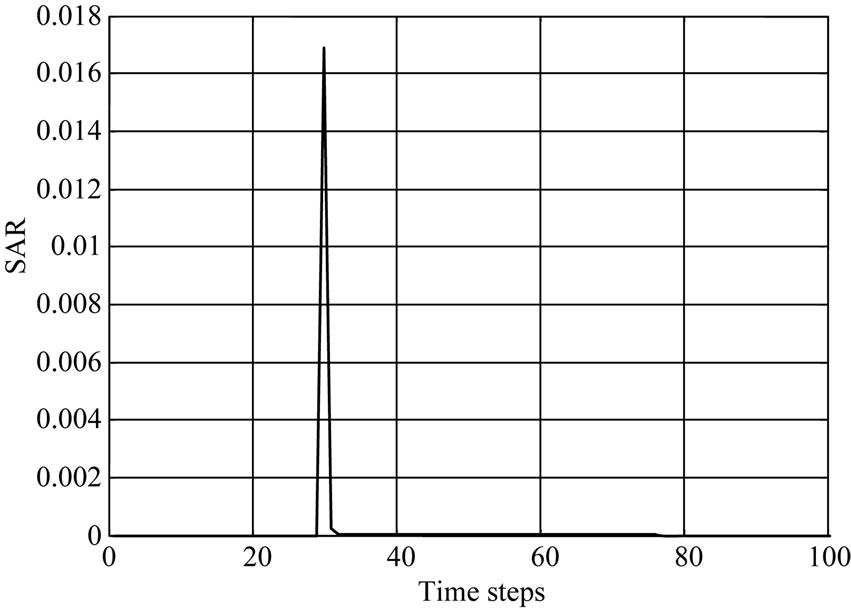 (b)
(b)
Figure 3. SAR in life tissues with different frequencies (900 MHz at (a) and 1800 MHz at (b)).
 (a)
(a)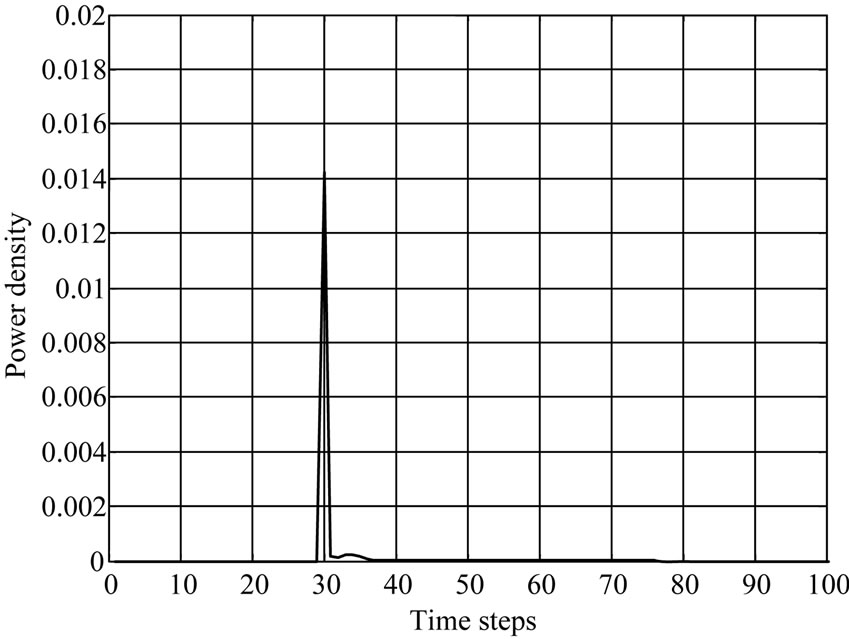 (b)
(b)
Figure 4. Tow different frequencies to evaluate Power density in life tissues (900 MHz at (a) and 1800 MHz at (b)).
This means that there is not any absorption in the later layer instead the electric field at frequency 0.9 MHz in muscles tissue.
5. Conclusions
Geometric of human body tissue with four layers has been supposed. The computer equations depend on FDTD method and simulation a sinusoidal wave hitting a lossy medium that has a dielectric constant and conductivity according the frequency which considered has been studied. It is found that the electromagnetic fields penetrates the considered layer and attenuates rapidly till they reach zero at the kidney layer. A comparison of the effect of two frequencies on human body tissue has shown graphically. The results noticed that the effect of frequency 900 MHz by mobile phone Global System Mobile (GSM) is more than the frequency of 1800 MHz in each case as electric field , SAR and power density versus time steps.
Absorbent power and SAR have maximum values at the skin and fat layers. According to the result from the graphs, notice that the effect of frequency 900 MHz by mobile phone Global System Mobile (GSM) is more than the frequency 1800 MHz. The dielectric properties for tissue are different according the change in frequency. This model enabled us to make simulations with many different tissues in human body.
REFERENCES
- C. R. Fernández, G. Bulla, A. C. Pedra and A. A. A. de Salles, “Comparison of Electromagnetic Absorption Characteristics in the Head of Adult and a Children for 1800 MHz Mobile Phones,” IEEE Transactions on Microwave Theory and Techniques, Vol. 49, No. 12, 2001, pp. 2539- 2546.
- N. Homsup and T. Jariyanorawiss, “FDTD Simulation of a Mobile Phone Operating near a Metal Wall,” Journal of Computers, Vol. 4, No. 2, 2009, pp. 168-175. doi.:10.4304/jcp.4.2.168-175
- R. Luebbers, C. W. Penney and Remcom Inc, “FDTD Comparison of SAR and Temperature Rise in Human Tissue,” IEEE Electromagnetic Compatibility, Vol. 3, No. 1, 2004, pp. 1036-1038.
- P. Bernardi, M. Cavagnaro, S. Pisa and E. Piuzzi, “SAR Distribution and Temperature Increase in an Anatomical Model of the Human Eye Exposed to the Field Radiated by the User Antenna in a Wireless LAN,” IEEE Transactions on Microwave Theory and Techniques, Vol. 46, No. 6, 1998, pp. 2074-2082. doi:10.1109/22.739285
- G. Emili and A. Schiavoni, “Computation of Electromagnetic Field Inside a Tissue at Mobile Communications Frequencies,” IEEE Transactions on Microwave Theory and Techniques, Vol. 51, No. 1, 2003, pp. 178-186. doi:10.1109/TMTT.2002.806899
- A. Talflove, “Computational Electrodynamics,” Artech House, Norwood, 1995.
- A. Abdalla and A. Teoh, “A Multi-Layered Model of Human Head Irradiated by Electromagnetic Plane Wave of 100 MHZ - 300 GHZ,” International Journal of Scientific Research, Vol. 15. No. 2, 2005, pp. 1-7.
- H. Elkhozonar, M. Shabat and K. Elwasife, “Modeling the Effect of Electromagnetic Waves Produced by Mobile Phone,” AlAzhar Journal of Natural Science, Vol. 12, No. 1, 2010, pp. 81-87.
- D. M. Sullivan, “Electromagnetic Simulation Using the FDTD Method,” IEEE Microwave Theory and Society, 1999.
- M. Witting, S. Burkhardt and SICAN Research & Development GmbH, “Automatic Generation of Finite Difference Meshes by an Evolutionary Algorithm,” IEEE Transactions on Magnetics, Vol. 32, No. 36, 1996, pp. 1338-1340. doi:10.1109/20.497493
- IEEE C95.1-1991, “IEEE Standards for Safety Levels Respects to Human Exposure to Radio Frequency Electromagnetic Fields, 3 KHz to 300 GHz,” Institute of Electrical and Electronics Engineers, Inc., New York, 1992.
- U. A. Fill, M. Zankl, N. Petoussi-Henss, M. Siebert and D. Regulla, “Adult Female Voxel Models of Different Stature and Photon Conversion Coefficients for Radiation Protection,” Health Physics, Vol. 86, No. 3, 2004, pp 253-272.
- J. X. Li. and Z. Q. Niu, “Theory of Biological Electromagnetic,” Xidin University Press, Xi’an, 1990.

