Intelligent Control and Automation
Vol.4 No.1(2013), Article ID:27703,4 pages DOI:10.4236/ica.2013.41005
Optimal Control for Time-Delay Bilinear Systems with Sinusoidal Disturbances*
College of Automation and Electronic Engineer, Qingdao University of Science & Technology, Qingdao, China
Email: qdgaodexin@126.com
Received October 18, 2012; revised November 18, 2012; accepted November 25, 2012
Keywords: Time-Delay Bilinear System; Feedback Linearization; Sinusoidal Disturbances; Optimal Control
ABSTRACT
This paper considers the optimal control problem for time-delay bilinear systems affected by sinusoidal disturbances with known frequency and measurable amplitude and phase. Firstly, using the differential homeomorphism, a timedelay bilinear system affected by sinusoidal disturbances is changed to a time-delay pseudo linear system through the coordinate transformation. Then the system with time-delay in control variable is transformed to a linear controllable system without delay using model transformation. At last based on the theory of linear quadratic optimal control, an optimal control law which is used to eliminate the influence of the disturbances is derived from a Riccati equation and Matrix equations. The simulation results show the effectiveness of the method.
1. Introduction
Bilinear system is a class of systems that is derived by introducing the interactive product term of the state variable and the control variable in the linear state equations. It is a rather special nonlinear system, which exists widely in the engineering community of electric, mechanical, biological, chemical and other fields. The study of the bilinear system starts in the 50’s, then becomes an important branch of nonlinear system and made a series of research results. Fang proposed a method of research the stability of MIMO bilinear system [1]; the output-feedback control for bilinear system was studied by Sasaki [2]; a global feedback stability analysis method of bilinear system was presented by Jerbi [3]. In the real Industrial process control, time-delay is ubiquity and the mathematical models put forward from engineering technology, physical, chemical and biomedical had obvious delay amount, which can not be neglected in some accurate control systems. Tang had studied optimal disturbance rejection problem for time-delay system in recent years [4]. Meanwhile, various forms of external disturbances exist on the control system, such as sinusoidal disturbance, periodic perturbation, step disturbance, etc. So it has important actual meanings to study time-delay bilinear system affected by external disturbance [5].
This paper proposed an optimal control design method for time-delay bilinear systems affected by sinusoidal disturbances based on state-feedback linearization [6,7]. Based on the differential homeomorphism, the model of the system that is researched is changed to a time-delay pseudo linear system through the coordinate transition, then through delay-free transform, the time-delay pseudo linear system is converted to an easy pseudo linear system. At last, an optimal control law which is used to eliminate the influence of the disturbances is derived from a Riccati equation and Matrix equations [8,9]. It is shown that the method is easy to realize and has a good convergence.
2. Problem Statement
Consider time-delay bilinear system affected by sinusoidal disturbances
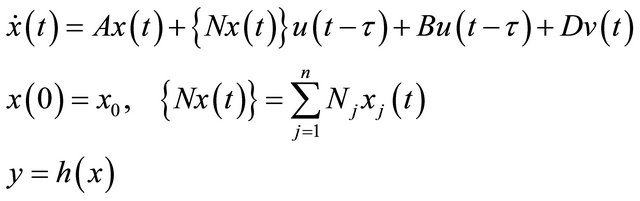 (1)
(1)
where, 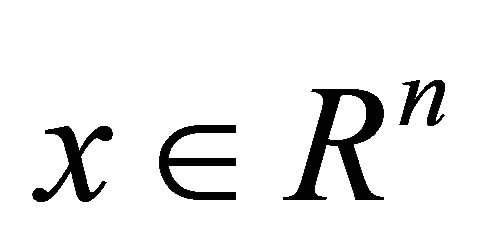 is the state vector;
is the state vector; 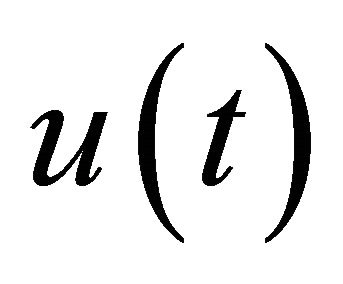 is the control vector;
is the control vector; 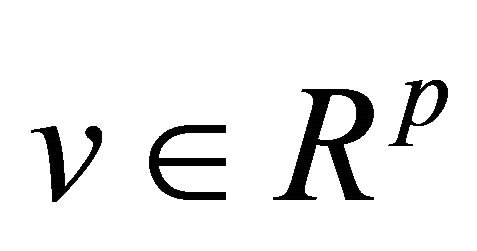 is the external disturbances vector;
is the external disturbances vector; 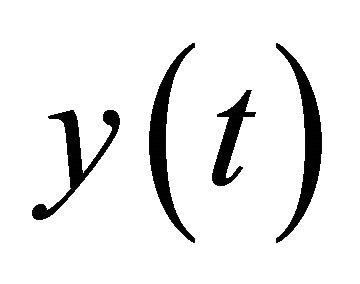 is the output vector; A, B, D, Nj are scalar matrixes of appropriate dimensions; xj is the j-th component of state vector;
is the output vector; A, B, D, Nj are scalar matrixes of appropriate dimensions; xj is the j-th component of state vector; 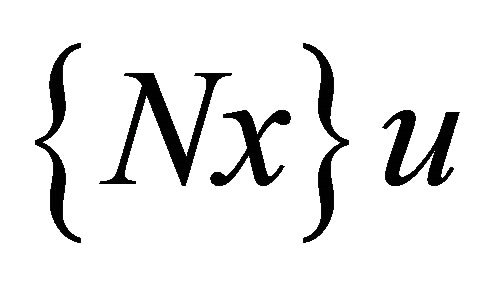 is the bilinear term;
is the bilinear term; 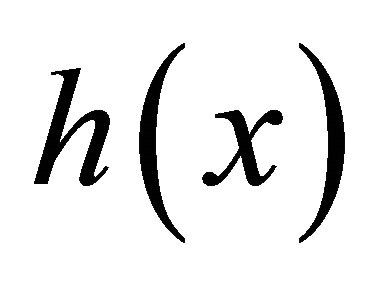 is the scalar function of x.
is the scalar function of x.
Assumption 1 The external disturbances can be expressed as
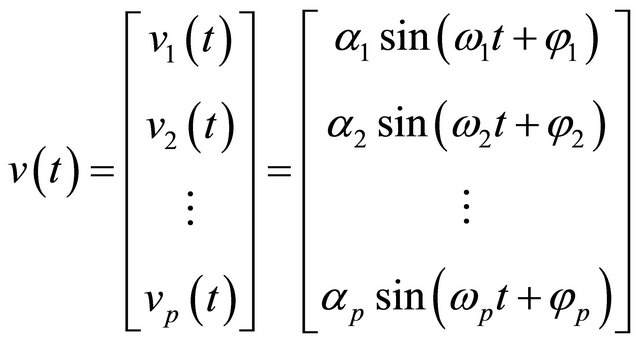 (2)
(2)
which is an m-dimensional sinusoidal vector with known frequencies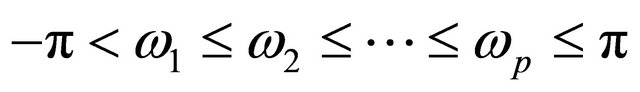 , amplitudes
, amplitudes 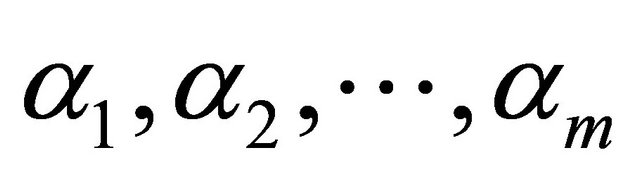 and phases
and phases 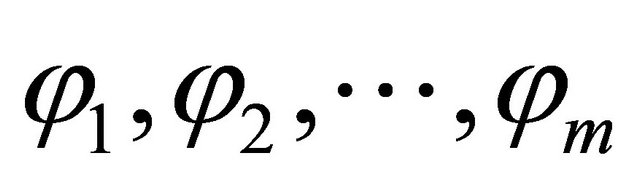 are measurable. By transformation, time-delay bilinear system could be changed as
are measurable. By transformation, time-delay bilinear system could be changed as
 (3)
(3)
Change the bilinear system to the general expression of nonlinear system
 (4)
(4)
where, 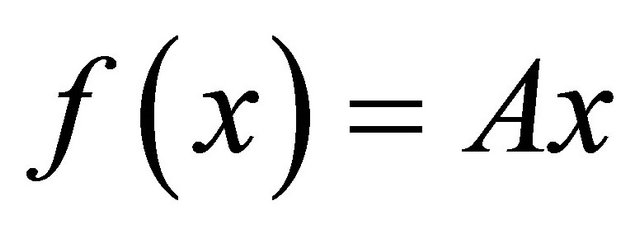 ,
,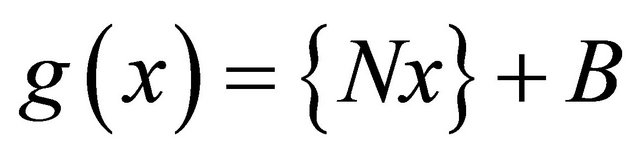 and j, g are continuously differentiable functions.
and j, g are continuously differentiable functions.
Assumption 2 The relation degree of the nonlinear system is r, that is
 (5)
(5)
Through exact delay-free transformation, the nonlinear system (4) can be converted to an easy pseudo linear system (6)
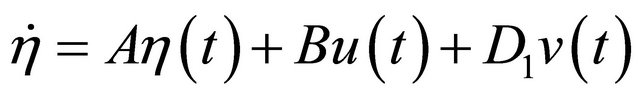 (6)
(6)
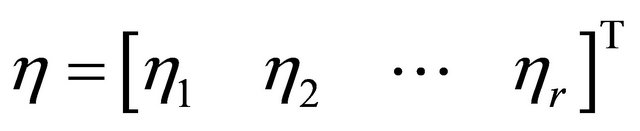 is the new state vector.
is the new state vector.
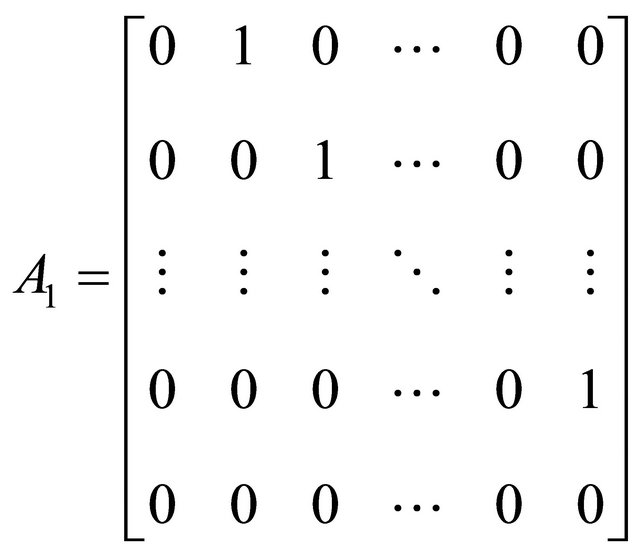
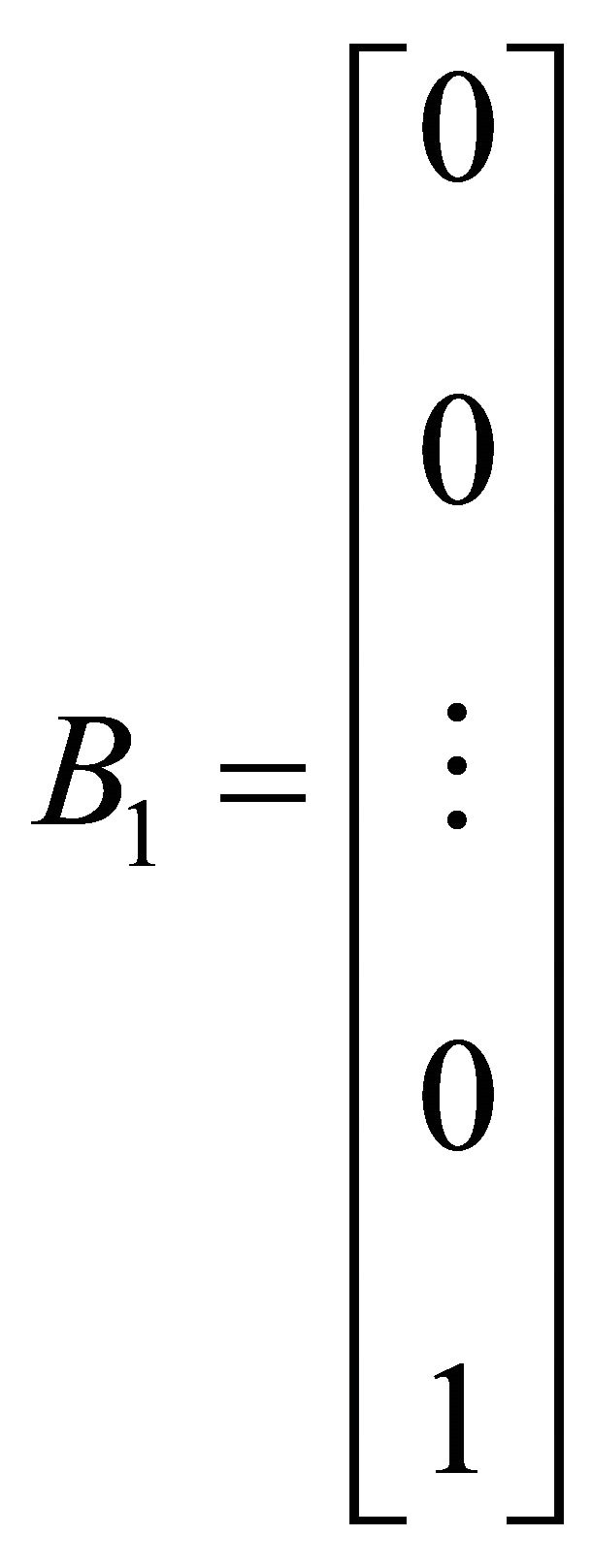
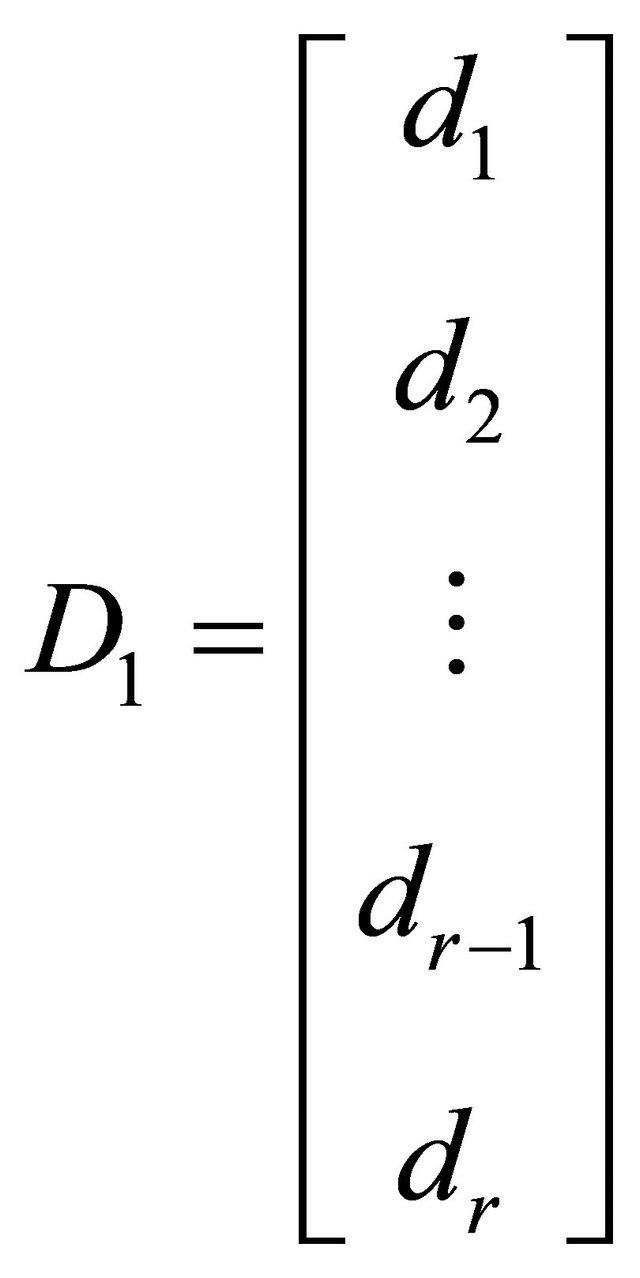
Then based on the theory of linear quadratic optimal control, an optimal control law which is used to eliminate the influence of the disturbances is derived.
3. Exact Delay-Free Linearization
3.1. State Feedback Linearization
State Feedback Linearization is a method of nonlinear controlling design, the design idea of which is to select a coordinate transformation 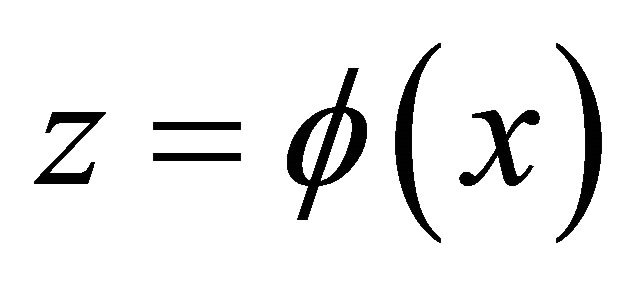 and made a mapping from x coordinate space to z coordinate space, thus the nonlinear system is changed to a linear time-invariant system as
and made a mapping from x coordinate space to z coordinate space, thus the nonlinear system is changed to a linear time-invariant system as . Let
. Let
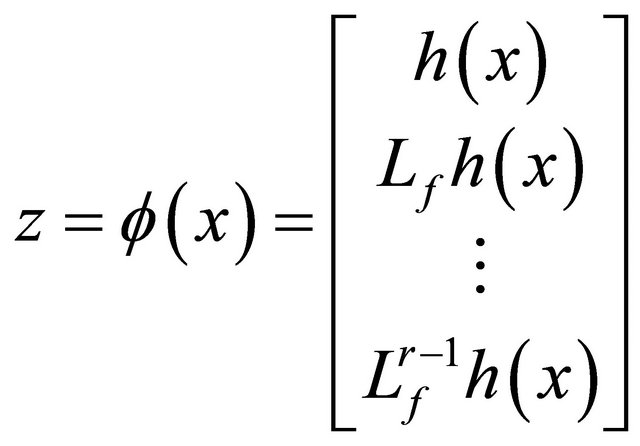 (7)
(7)
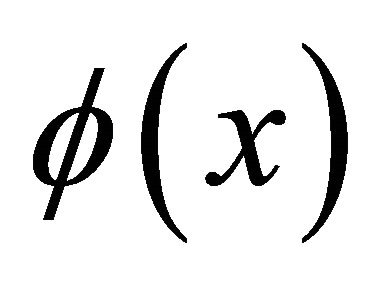 is the partial differential homeomorphism, according to assumption 2, then get
is the partial differential homeomorphism, according to assumption 2, then get
 (8)
(8)
by operation, the system is changed to a new standard form
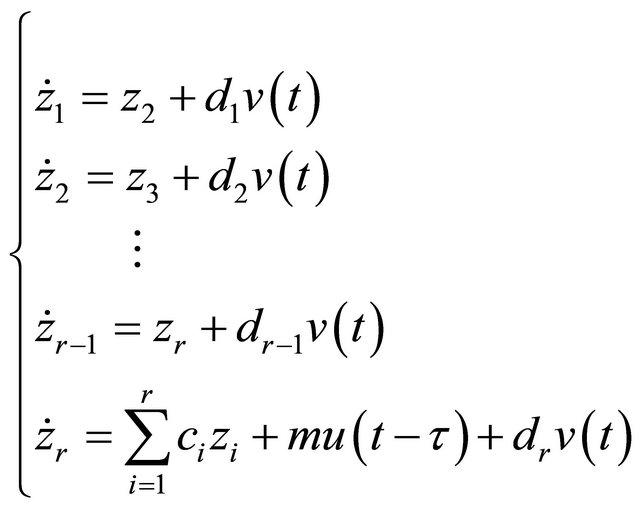 (9)
(9)
r-step time-delay linear system with disturbances can be obtained as follow
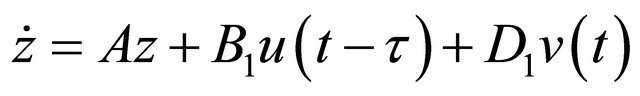 (10)
(10)
where


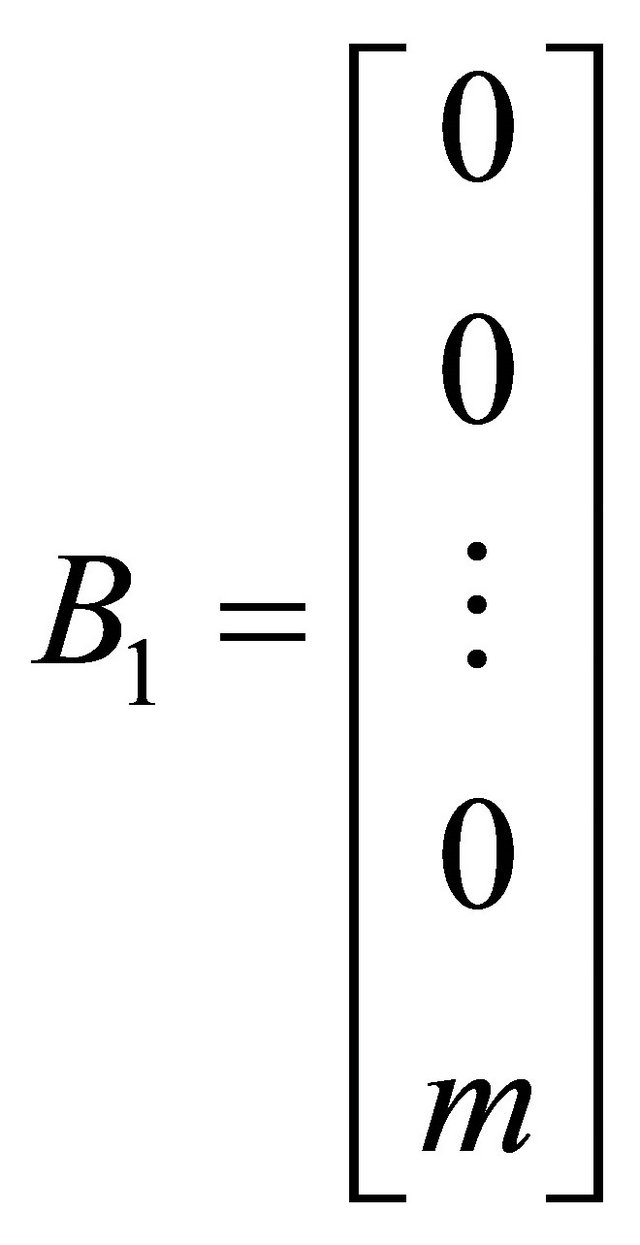
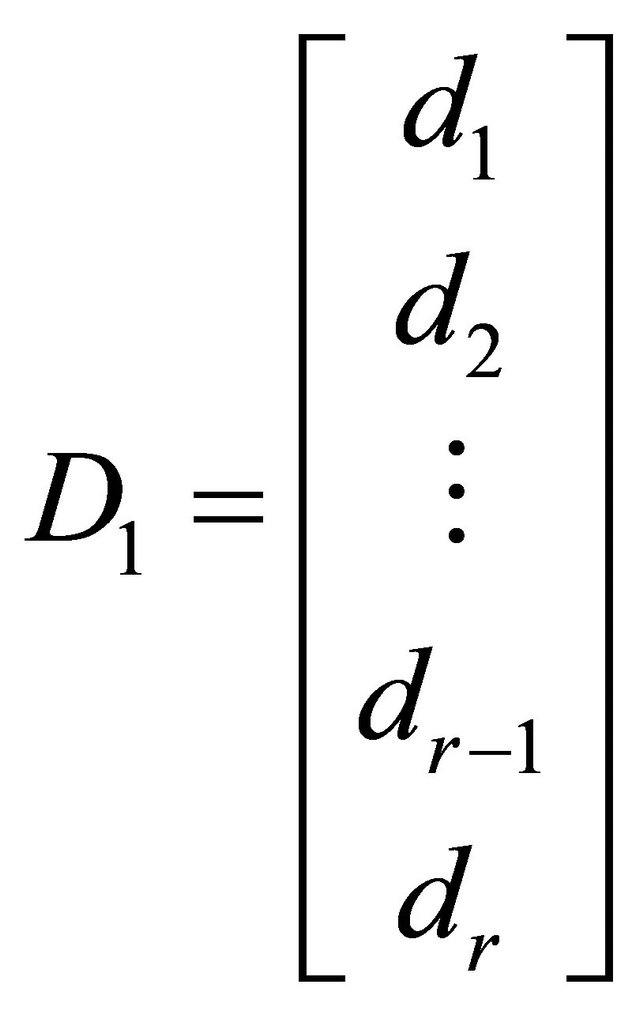
3.2. Exact Delay-Free Transformation
Definite transformation for the time-delay linear system, let
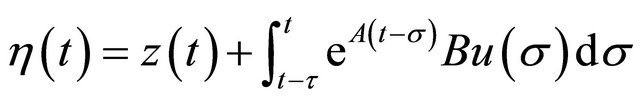 (11)
(11)
The expression (10) is converted to delay-free system
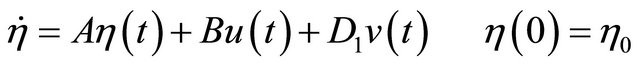 (12)
(12)
where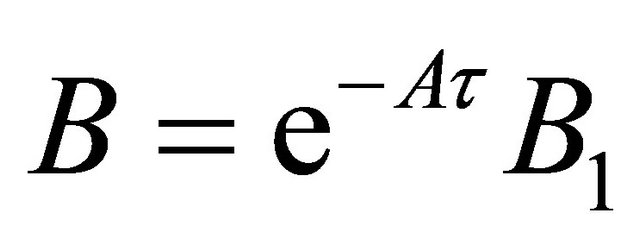 .
.
4. Design of Optimal Control
The time-delay bilinear system (1) is changed to the equivalent delay-free linear system affected by disturbances
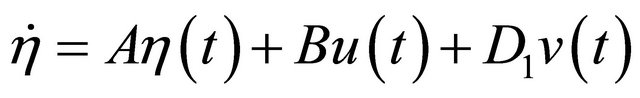 (13)
(13)
where,  is the new state vector;
is the new state vector; 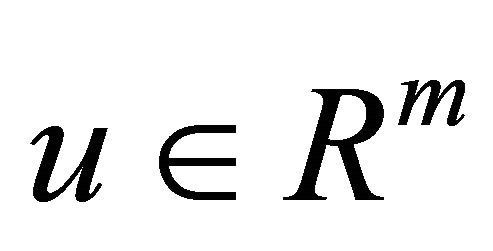 is the new control vector; A is state coefficient matrix; B is control coefficient matrix; the system (6) is completely controllable.
is the new control vector; A is state coefficient matrix; B is control coefficient matrix; the system (6) is completely controllable.
When  select the quadratic performance index of system (6) as
select the quadratic performance index of system (6) as
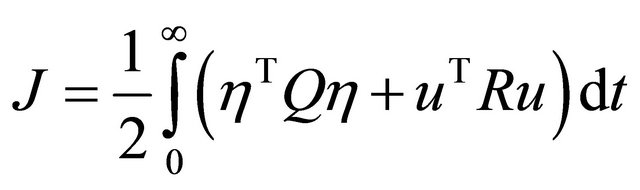 (14)
(14)
where Q is a ![]() positive semi-definite matrix, R is a
positive semi-definite matrix, R is a ![]() positive definite symmetric matrix.
positive definite symmetric matrix.
Theorem: Consider the optimal control problem of system (6) with the quadratic performance index (14). Suppose the system is completely controllable and observable, the optimal disturbance rejection control law is unique existence and can be expressed as
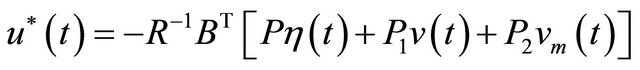 (15)
(15)
P is the unique positive definite solution of the matrix Equation (16)
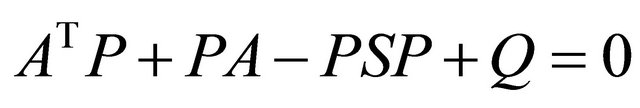 (16)
(16)
P1 is the unique solution of the matrix Equation (17)
 (17)
(17)
P2 is the unique solution of the matrix Equation (18)
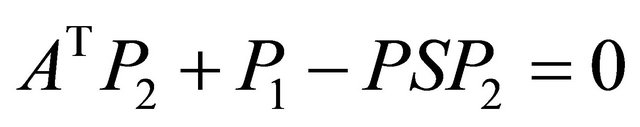 (18)
(18)
where

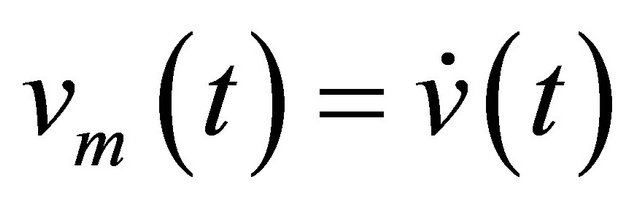
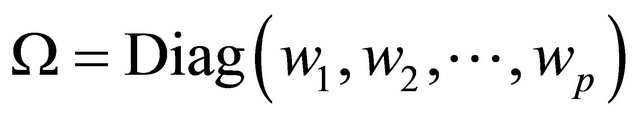
Proof: According to the necessary conditions of the optimal control problem based on maximum principle, the optimal control law of system (6) with the quadratic performance index (14) can be expressed as
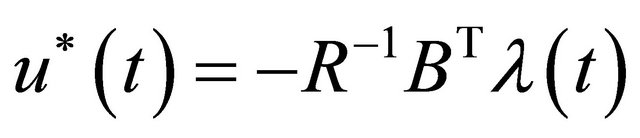 (19)
(19)
where 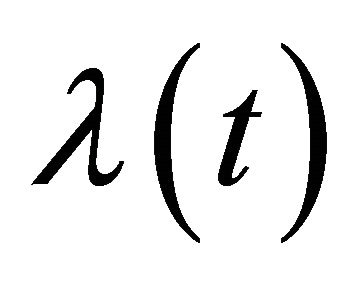 is the solution of the following two-point boundary value problem
is the solution of the following two-point boundary value problem
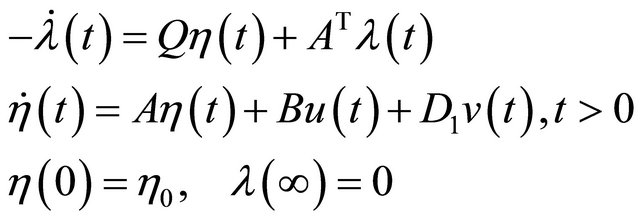 (20)
(20)
In order to obtain the solution to the problem in (14), let
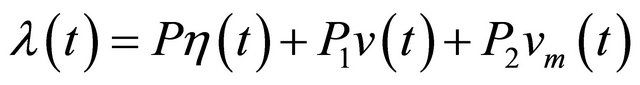 (21)
(21)
where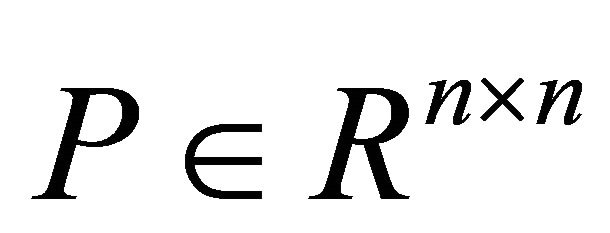 ,
, 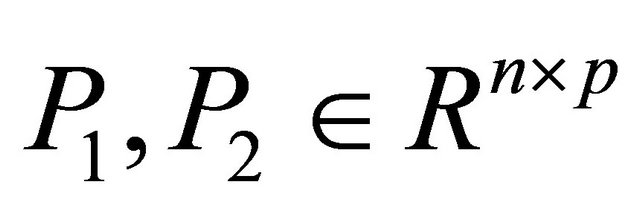 are both undetermined matrix.
are both undetermined matrix.
From expression (2), the vector function ![]() satisfies the following vector differential equation
satisfies the following vector differential equation
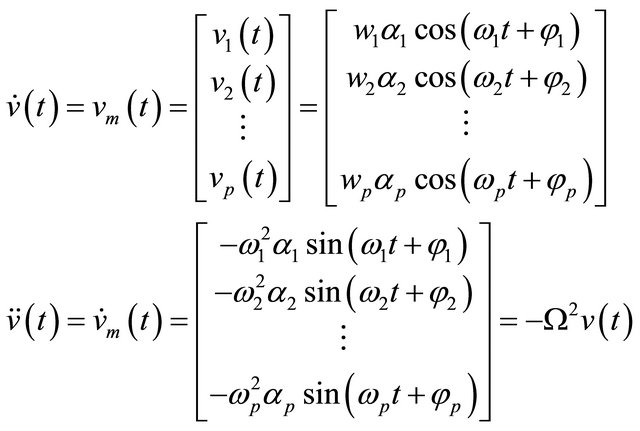 (22)
(22)
Taking the derivatives to the sides in (21) and substituting (22) into it get (23)
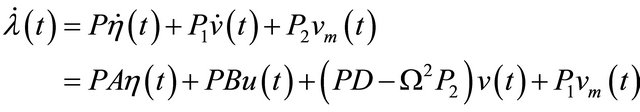 (23)
(23)
Add (23) into the first expression of (20), obtain (24)
 (24)
(24)
Considering for any 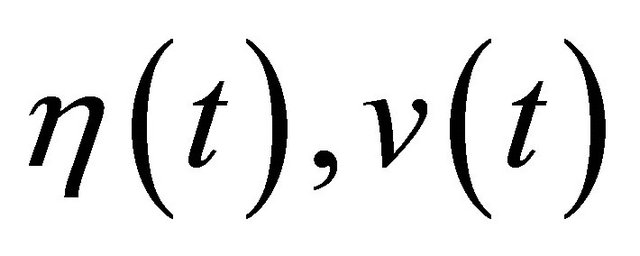 and
and , Equation (24) is all hold, so we can get matrix Equations (16)-(18). The optimal control law of the bilinear systems affected by sinusoidal disturbances is as follow
, Equation (24) is all hold, so we can get matrix Equations (16)-(18). The optimal control law of the bilinear systems affected by sinusoidal disturbances is as follow
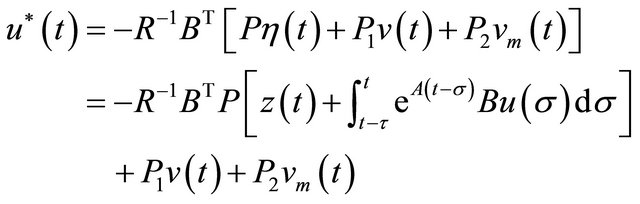 (25)
(25)
5. Simulation Example
Consider a time-delay bilinear system with sinusoidal disturbances, system parameters as follows
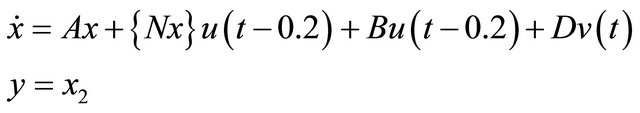 (26)
(26)
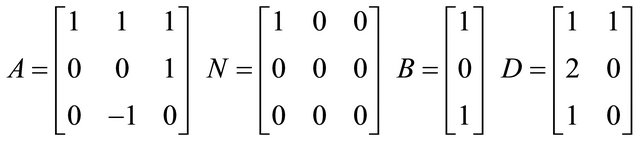
According to calculation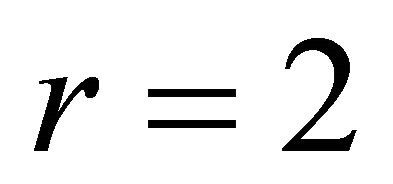 , through local linearization, we can get a two-step linear system affected by sinusoidal disturbances
, through local linearization, we can get a two-step linear system affected by sinusoidal disturbances
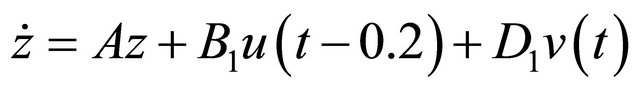 (27)
(27)
where
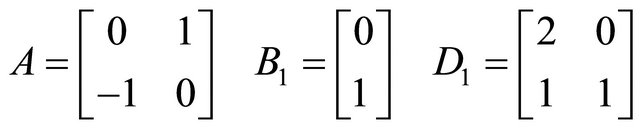
The form of the disturbances described as follows
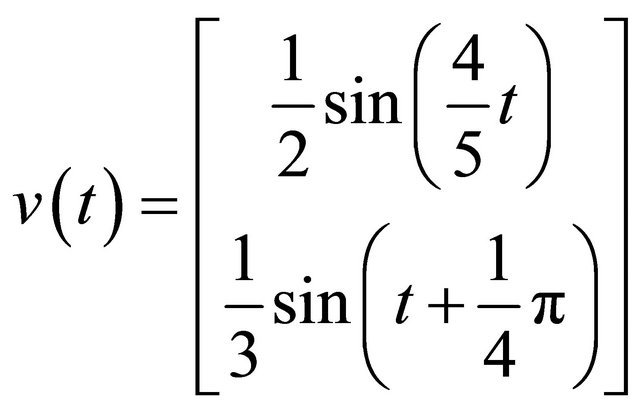 (28)
(28)
Using model transformation, change the system with time-delay to a linear controllable system without delay
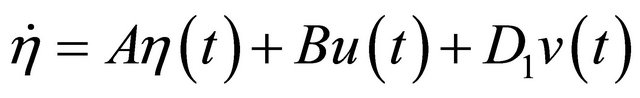 (29)
(29)
where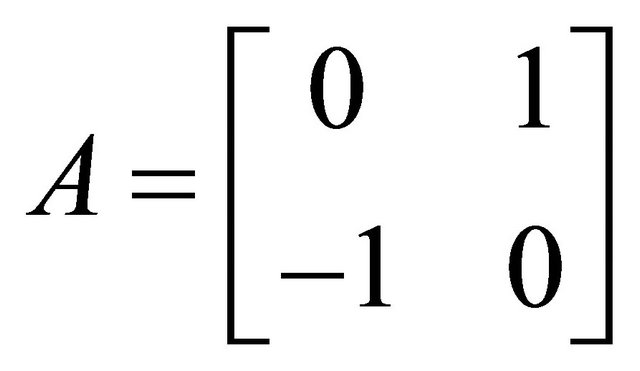 ,
,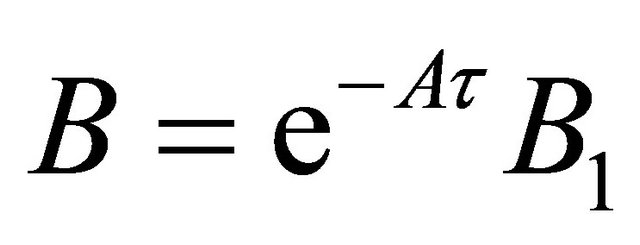 .
.
Select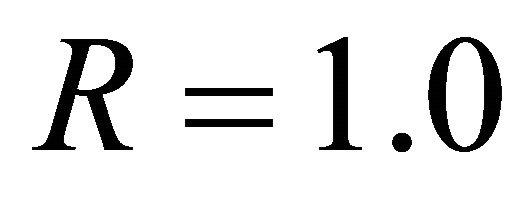 ,
, 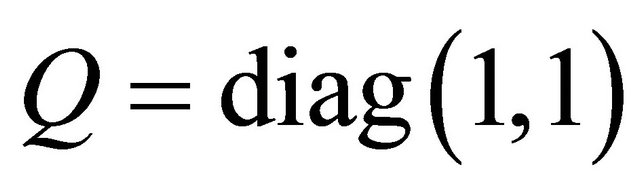 , we get
, we get

The simulation results of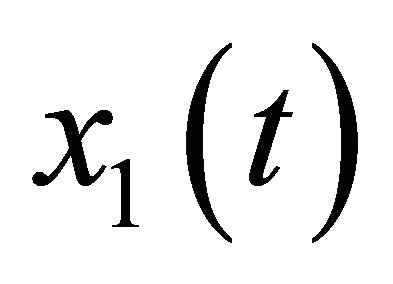 ,
, 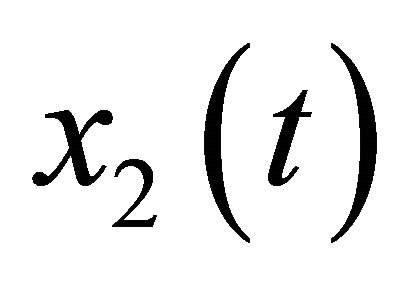 and
and 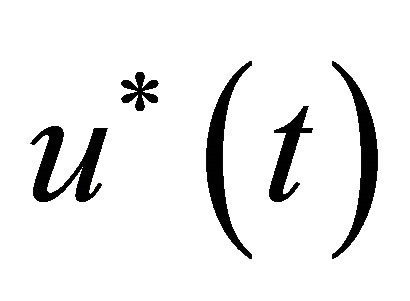 are presented in Figures 1 and 2.
are presented in Figures 1 and 2.
It is shown that the optimal control design method for the system affected by sinusoidal disturbances based on state-feedback linearization is easily realized, and has a good convergence through the simulation results.
6. Conclusion
This paper concentrates on the solution of the optimal control problem for time-delay bilinear system affected by sinusoidal disturbances with known frequency and measurable amplitude and phase based on state feedback, a method of optimal control law is given. Simulation re-
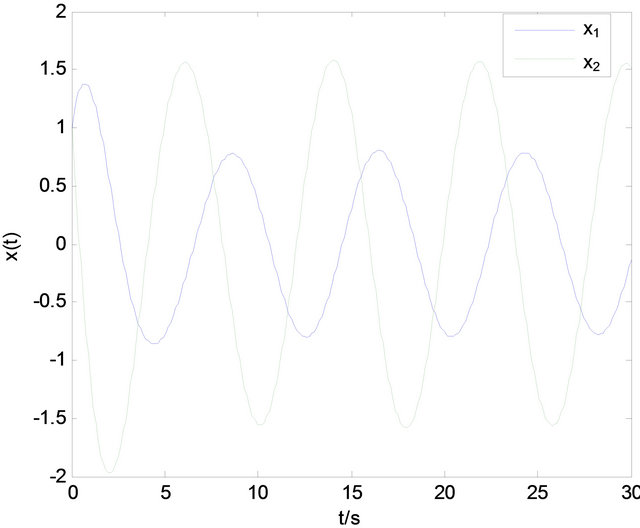
Figure 1. The diagram of state variables x1(t), x2(t).
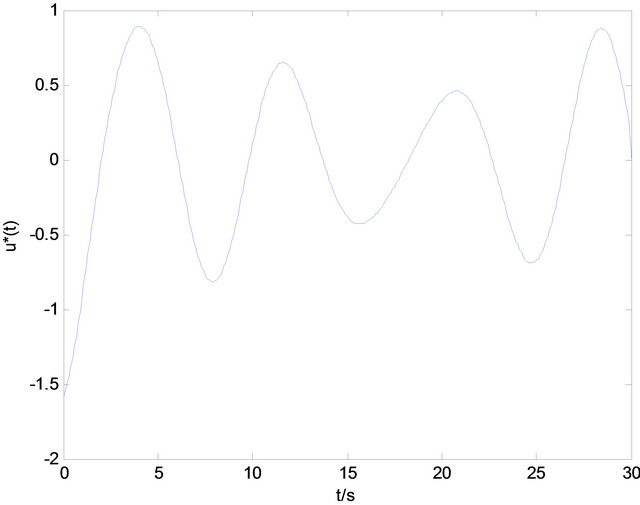
Figure 2. The diagram of the optimal control u*(t).
sults show that the designed control law is accurate and easy to implement.
REFERENCES
- Y. W. Fang, L. C. Jiao and Z. Z. Han, “The New Method of Stability of MIMO Bilinear System,” Journal of Automation, Vol. 27, No. 6, 2001, pp. 845-849.
- S. Sasaki and K. Uchida, “Quadratic Cost Output Feedback Control for Bilinear Systems,” International Journal of Systems Science, Vol. 34, No. 5, 2003, pp. 345-355. doi:10.1080/00207720310001600984
- H. Jerbi, “Global Feedback Stabilization of New Class of Bilinear Systems,” Systems and Control Letters, Vol. 42, No. 4, 2001, pp. 313-320. doi:10.1016/S0167-6911(00)00101-8
- G. Y. Tang and Y. D. Zhao, “Optimal Control for Nonlinear Time-Delay Systems with Persistent Disturbances,” Journal of Optimization Theory and Applications, Vol. 1, No. 131, 2006.
- D. X. Gao, G. Y. Tang and Q. Yang, “Approximate Optimal Disturbance Rejection for Bilinear Systems with Persistent Disturbances,” Control and Instruments in Chemical Industry, Vol. 34, No. 2, 2007, pp. 20-24.
- G. Y. Tang and D. X. Gao, “Feedforward and Feedback Optimal Control for Linear Systems with Persistent Disturbances,” Acta Simulata Systematica Sinica, Vol. 17, No. 6, 2005, pp. 1519-1521.
- D. X. Gao and P. P. Yang, “An Optimal Tracking Control Method for Bilinear Systems Subjected to Sinusoidal Disturbances,” IEEE International Conference on Intelligent Computing and Intelligent Systems, Vol. 2, No. 4, 2009, pp. 251-255.
- G. Y. Tang, “Feedforward and Feedback Optimal Control for Linear Systems with Sinusoidal Disturbances,” High Technology Letters, Vol. 7, No. 4, 2001, pp. 16-19.
- D. X. Gao, X. Y. Yang and B. T. Cui, “Feedback Linearization Optimal Disturbances Rejection Approach of Bilinear Systems,” The 30-th Chinese Control Conference, Vol. 7, 2011, pp. 359-363. doi:10.1109/68.903206
NOTES
*This work was supported in part by the National Natural Science Foundation of China (60804005), and by the Natural Science Foundation of Shandong Province (ZR2011FQ006), by the Natural Science Foundation of Qingdao City (12-1-4-3-(17)-jch).

