Journal of Information Security
Vol.07 No.02(2016), Article ID:65271,22 pages
10.4236/jis.2016.72006
The “Iterated Weakest Link” Model of Adaptive Security Investment
Rainer Böhme1, Tyler Moore2
1Department of Computer Science, Universität Innsbruck, Innsbruck, Austria
2Tandy School of Computer Science, University of Tulsa, Oklahoma, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC).
http://creativecommons.org/licenses/by-nc/4.0/



Received 24 February 2016; accepted 28 March 2016; published 31 March 2016
ABSTRACT
We devise a model for security investment that reflects dynamic interaction between a defender, who faces uncertainty, and an attacker, who repeatedly targets the weakest link. Using the model, we derive and compare optimal security investment over multiple periods, exploring the delicate balance between proactive and reactive security investment. We show how the best strategy depends on the defender’s knowledge about prospective attacks and the recoverability of costs when upgrading defenses reactively. Our model explains why security under-investment is sometimes rational even when effective defenses are available and can be deployed independently of other parties’ choices. Finally, we connect the model to real-world security problems by examining two case studies where empirical data are available: computers compromised for use in online crime and payment card security.
Keywords:
Optimal Security Investment under Uncertainty, Return on Security Investment

1. Security Investment in an Uncertain World
We hear about security breaches in the news almost daily, each bigger and more costly than the last. Does this reflect flawed technology, policy, or simply ineptitude? What if, instead, allowing some attacks to succeed is entirely rational for businesses? Rather than over-invest proactively, firms could wait to observe which attacks work and use this knowledge to better allocate security spending. In this article, we describe a model that weighs the merits of such an approach.
One key insight from the economics of information security literature is that attackers bent on undermining a system’s security operate strategically [1] . Moreover, information systems are often structured so that a system’s overall security depends on its weakest link [2] . A careless programmer in a software firm can intro- duce a critical vulnerability. The Internet’s global, distributed architecture leads to security being dominated by the weakest link―attackers compromise machines hosted at Internet service providers (ISPs) with lax enforce- ment policies or located in uncooperative countries. Attackers have repeatedly exhibited a knack for identifying the easiest way to bypass a system’s security, even when the system’s designer remains unaware of the parti- cular weakness.
However, systems do not exist in a vacuum; rather, defenders respond to attacks by plugging known holes. And yet, as soon as one weakest link is fixed, another weak point is often identified and exploited. Therefore, a strong dynamic component is at play: attackers find the weakest link; defenders fix the problem; attackers find new holes which are then plugged, and so on. We see that this pattern emerges repeatedly. For instance, attackers construct networks of compromised machines (so-called botnets) to pester legitimate users by emitting spam, distributing malware and hosting phishing websites. Attackers concentrate their efforts at the most irresponsible ISPs, moving on to others only after the ISP cleans up its act or is shut down. Likewise, technical countermeasures to payment card fraud have evolved over time, causing fraudsters to adopt new strategies as old weaknesses are fixed. For example, when UK banks migrated to PIN verification of transactions rather than signatures, in-person retail fraud declined while overseas ATM fraud and card-not-present fraud skyrocketed.
In this article, we devise a model that reflects this dynamic interaction between attackers and defenders. Our model captures the iterative aspect of attack and defense; we exclusively study the case where security depends on the weakest link; consequently, we model the iterated weakest link.
Plugging known holes come at a cost for the defender. And as often experienced in real systems, this cost is not always proportional to the number of controls in place. For example, organization science suggests that complexity adds super-linear administrative costs, for instance to pay a manager who directs several employees where each is an expert for a particular control. Conflicting defenses also emerge from incompatible systems, e.g., running two virus scanners on the same machine to increase coverage slows down the machine and causes errors. Lastly, human behavior fundamentally limits the composability of defenses: a password policy that re- quires both special characters (defense 1) and frequent password changes (defense 2) encourages people to stick their password on their monitor. Our model can account for interdependent defensive countermeasures.
Practical security engineers will note that it is already difficult to obtain detailed information on cost struc- tures, but what is even more unrealistic is attempts to determine the attackers’ cost and plug them into decision tables. In the real world, defenders almost always operate with incomplete information, and oftentimes a rough gauge on the relative magnitude of known threats is all the information available to a decision maker.
So another key characteristic of our model is to reflect uncertainty about which components are weakest, and therefore, which components are most susceptible to attack. All chief information security officers (CISOs) know that the security of their computer systems is imperfect at best; the better ones have catalogued the many ways an attacker might penetrate their systems, mitigating risks where possible and accepting the rest. What they remain uncertain about is which, if any, of the vulnerable components an attacker will choose to exploit. We capture this uncertainty into our model and use it to analyze how defense strategies change as knowledge about the attacker varies.
We reach several interesting conclusions upon examining the model. By comparing the static case (a single round of attack and defense) to the dynamic one (multiple rounds), we find that different defender strategies may prevail. When the defender only gets one chance to protect a system, increasing uncertainty about which link is weakest causes the defender to protect more assets, but only up to a point. When uncertainty is too high, the defender does not know which asset to protect and so chooses to protect none. If instead we allow for repeated defensive investments, an uncertain defender will initially protect fewer assets and wait for the attacker to “identify” the weakest links to be fixed in later rounds. Hence, it can be quite rational to under-invest in security until threats are realized. Unlike in other theories, this type of under-investment is not driven by the interrelation with other market participants and resulting incentive systems. Of course, security countermeasures may require significant capital investment from the outset. When we consider unrecoverable costs in our model, we find that for moderate levels of uncertainty, high unrecoverable update costs can raise the proactive protec- tion investment.
We then translate these findings about optimal defensive strategies into accepted security indicators such as annual loss expectancy (ALE) and return on security investment (ROSI). Return on investment drops as uncer- tainty about known attacks rises, even as the defender grows increasingly reactive when countering realized threats.
We do not deal with the problem of distributing costs if the defender is in fact a coalition of multiple parties (such as in the case of protecting global infrastructure) and the resulting incentive systems, which we regard as a separate problem to be studied independently. We refer the reader to the literature on externalities, such as [2] - [4] .
The remainder of this article is organized as follows: Section 2 specifies the model, which is solved later on in Section 3. We apply the model to real problems in two case studies on current topics of information security, namely online crime (Section 5.1) and payment card security (Section 5.2). Section 6 puts our contribution into perspective with prior art, and Section 7 concludes the article.
Readers who want to glance over the article without getting into the formal details may find the model summary in Section 2.6 along with the interpretation of example results in Section 4 most useful. Also the case studies (Section 5) and the general conclusion (Section 7) do not require deep understanding of the model. A non-technical summary of the model’s key ideas has also appeared in a magazine format [5] .
2. Model
Imagine a simplistic world, in which a defender protects an asset of value a against a dispersed set of possibly heterogeneous attackers. There exist n possible threats, which can be regarded as distinct attack vectors against a single system.1 Each threat can be warded off by investing in its corresponding defense (or control). In other words, we assume a one-to-one mapping between threats and defenses, and defenses are always effective.
2.1. Defender’s Options
The model is “run” in an iterated player-versus-nature game with discrete time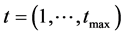 . In each round, the defender makes a security investment decision to define his configuration of defenses
. In each round, the defender makes a security investment decision to define his configuration of defenses 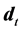 and extracts a net return
and extracts a net return 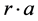 from his asset before the attacker penetrates the system and, if successful, loots a fraction z of the asset. Gross returns are consumed or distributed so that the asset value does not accumulate over time. The defender seeks to maximize his expected return per round, where expectations are taken over the realizations of random variables and averages calculated over time.
from his asset before the attacker penetrates the system and, if successful, loots a fraction z of the asset. Gross returns are consumed or distributed so that the asset value does not accumulate over time. The defender seeks to maximize his expected return per round, where expectations are taken over the realizations of random variables and averages calculated over time.
Let elements 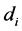 of the binary column vector
of the binary column vector 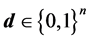 indicate whether a defense against the i-th threat is
indicate whether a defense against the i-th threat is
implemented (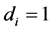 ) or not
) or not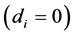 , and let
, and let 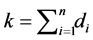 be the number of defenses in place.
be the number of defenses in place.
The cost of defense 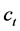 in round t can be calculated from an
in round t can be calculated from an  upper triangular cost matrix
upper triangular cost matrix 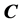 to reflect possible interdependent defenses,
to reflect possible interdependent defenses,
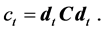 (1)
(1)
Diagonal elements  hold the cost to implement a defense against the i-th threat, and off-diagonal elements
hold the cost to implement a defense against the i-th threat, and off-diagonal elements 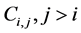 indicate the extra costs if the i-th defense is implemented together with the j-th defense. If all off- diagonal elements are zero, then the defenses are independent:2
indicate the extra costs if the i-th defense is implemented together with the j-th defense. If all off- diagonal elements are zero, then the defenses are independent:2
A nice property of the cost matrix is that for positive off-diagonal elements, decreasing marginal utility of defenses has become endogenous to our model. This compares favorably to, say, the Gordon-Loeb framework, in which this property appears as an assumption (A3 of [6] , p. 443).
2.2. Defender’s Knowledge
While the defender may possess some intuition about the relative difficulty of carrying out the n threats, such knowledge may very well be blurred. To model this uncertainty, we order the threats 
We define a simple functional form for the expected attack costs 

The unknown true cost




The realizations 

The defender’s knowledge about the attack profile will naturally increase over time once attacks occur, and so her uncertainty decreases as the observed attacks reveal which threat is in fact the weakest link with respect to a given configuration
2.3. Unrecoverable Costs
So far we have assumed that the defender can upgrade his configuration 
As is argued in [6] , security disinvestment is often possible to a certain degree, since personnel can be fired or equipment sold (though sometimes at high transaction costs). However, for many businesses, updating 

Figure 1. Attack profile. The defender forms expectations about the rank order of attack costs, but does not know the true costs until attacks are actually observed. (a) [certainty:


Hence, parameter 
2.4. Attacker’s Options and Knowledge
Our attacker model is very simple: the attacker identifies and exploits the weakest link, i.e., the threat least costly to the attacker. We do not require the attacker to make a trade-off between cost and potential gains by assuming the same utility is received for exploiting all threats. If the attacker succeeds, regardless of how, he profits


These attacker assumptions are quite strong and probably unrealistic in some cases. For targeted attackers in particular, searching for the weakest link could be very expensive. So a more appropriate conception is the presence of many opportunistic attackers [7] who operate independently. Like in swarm intelligence, the chance that one of them finds the hole is quite high.
Moreover, the attacker’s gain from successful attacks may only represent a small fraction of the defender’s losses. But this is not crucial here since we do not consider attackers’ profits; we simply need an asset-dependent quantity to relate to the cost

2.5. Simplifying Assumptions
To make the analysis more tractable, we restrict the space of possible cost matrices 





Observe that 




We further assume a risk neutral defender, that is, one who maximizes inter-temporal utility as a linear function of (expected) revenues and costs. We defer consideration of other attitudes towards risk or different time preferences to future work in order to keep the core model lean.
2.6. Model Summary and Example Parameters
Our model can be applied to many scenarios. For now, we demonstrate its parameters in action by considering an imaginary online music store to demonstrate its parameters in action (we describe other scenarios in Section 5). The music store’s asset is the library of audio files and the associated property rights. Let the total value of the asset be one million dollars. To avoid large numbers, we count in thousands of dollars, so asset value a = 1 000. Every year, indexed by t, the net return from online sales amounts to 
Surrounded by malicious competitors, professional cybercriminals and “curious customers”, the store is ex- posed to various threats (say,







The store owner is not entirely helpless: he may spend on security measures to defend against each of the 




Table 1 summarizes the parameters of our model and their values used in the subsequent examples. The following section will show how defenders can optimize their security spending in this model. We are primarily interested in exploring how the optimal strategy changes based on the level of uncertainty

3. Analysis
We distinguish between static analysis, where the defender chooses the configuration in the first round (

Table 1. Overview of model parameters.
3.1. Static Solution
We consider a defender with defense vector 







where q is an indicator variable that takes value one if the attacker is successful and zero otherwise. In the case of certainty, q is fixed for all rounds, so that two outcomes are possible:


The cost term disappears in Equation (8) because if we accept attacks anyway, then there is no need to spend money to make it more difficult for the attacker (i.e., k = 0). Otherwise, the minimal number of defenses 


Typically, the best strategy for the defender is to follow whatever is higher, Equation (8) or (9), with
In the case of uncertainty (




where 


Figure 2 depicts expected returns of the static solution as a function of k for parameters as specified in Table 1. Each curve corresponds to different levels of uncertainty; the utility-maximizing selection of 





3.2. Dynamic (Iterated) Solution
When 
Figure 2. Static solutions for the parameters asset value a = 1000, return r = 5%, loss given attack





information about the true cost of attack. This information could be used to reconfigure the defenses adaptively. In the dynamic case, uncertainty is repeatedly eliminated for targets revealed to be the weakest link. Con- sequently, this reduction in uncertainty for later rounds can lead to a better outcome for the defender than in the static case. In general, the inter-temporal outcome is the sum of all returns over a period of time

and can be maximized by adjusting 







3.2.1. Special Case: All Costs Recoverable
The defender has to choose a proactive defense 










Let 





after inserting Equation (5) we obtain:

Equation (15) holds because 






To calculate


Hence, 


choices for the proactive defense 


Figure 3 shows expected returns per round of the dynamic solution for the same parameters as in Figure 2, now as a function of the proactive defense




Moreover, observe that an indefensible state is already reached for 

3.2.2. General Case
To consider unrecoverable costs in the analysis, Equation (13) is rearranged to the form of Equation (14) as
Figure 3. Dynamic solutions for the same parameters as in Figure 2 (






follows:

The second sum does not include st because dt remains constant for t > tatt. Rearranging and inserting Equation (4) yields

We proceed as with Equation (16) in the special case with all costs recoverable. It is possible to keep the same strategy of iterated investment because the elements of the random vector 





Figure 4 illustrates the structure of the general decision problem and Table 2 displays the corresponding expressions for calculating the costs at the different types of terminal nodes T1, T4. With unrecoverable costs, ignore becomes a valid choice as it may be cheaper than disinvest.
In Figure 5, we fix two settings for the level uncertainty, low (

Figure 4. Decision tree of iterated weakest link model with unrecoverable costs. S is the start node, T1, T4 refer to terminal nodes, P denotes player (i.e., defender) and N denotes nature (i.e., attackers).
Table 2. Cost at terminal nodes as function of k1 and t (if applicable).

Figure 5. Dynamic solutions with unrecoverable costs for low (left) and high (right) uncertainty. All other parameters as in Figure 2 (








returns per period as a function of the proactive defense 



4. Security Investment Based on the Iterated Weakest Link Model
As we have analyzed the optimal strategies of the defender in the previous sections, we can now use the model to calculate some key indicators that relate to practical experience. Table 3 compares typical security indicators derived from the model for different degrees of uncertainty (in columns) and different defense strategies (row sections―static/dynamic/dynamic with unrecoverable costs). The list of indicators includes:
・ Optimal defense is a memo item that describes the optimal defense strategy
・ Attack intensity measures the probability of a successful attack per round, averaged over all 
・ Average gross return is the objective function of the optimization problem, scaled to a percentage of the asset value a. The average is computed over all 

・ Average security spending is the average effort spent on defenses, comprising direct, indirect and un- recoverable costs (if applicable). Averages and expectations are computed as for gross returns. Lower values are not necessarily better; what matters is the efficiency of the security spending, i.e., how security spending compares against prevented losses. This depends on how targeted the defense configuration is to the reali- zation of the attack profile.
・ Annual loss expectation (ALE) measures expected foregone profits per period [10] .4 ALE can be computed for two scenarios: 


・ Return on information security investment (ROSI) is a summary measure to quantify the effectiveness of security investment. We follow the approach in [11] and normalize the indicators by the security spending, i.e.,
Table 3. Key security investment indicators derived from the model.
Parameters: asset value









Higher values denote more efficient security investment. The indicator is not defined for cases where no defenses are optimal.
Unsurprisingly, the three modes of adaptivity concur in the case of certainty (leftmost column in Table 3). However, uncertainty creates some remarkable results, which we now discuss.
For low levels of uncertainty (
Regarding attack intensity, a converse effect is observable when uncertainty is higher (
Unrecoverable costs muddy this picture somewhat. They raise incentives towards more proactive security investment. This leads to higher proactive defenses and thereby lower attack intensity. However, unrecoverable costs also eat up margins, so gross returns tend to decline. Even more importantly, the overall efficiency of the security investment drops, and the differential grows as uncertainty rises. So, some uncertainty combined with expensive infrastructure upgrades can stimulate over-investment―but only to a certain point. Eventually, high uncertainty can demotivate any security investment, similar to what happens in the static case. In the real world, we would expect to see relatively more weight on proactive security when updates case high unrecoverable costs (e.g., payment cards) and the uncertainty is low or moderate, compared to businesses where almost all costs are recoverable (e.g., websites). This prediction could be tested against cross-sectional empirical data in future work. In any case, the above-mentioned excuse of breaches as smart defense strategy does not apply to defenders with high unrecoverable costs. The related policy dimension here is to reduce the uncertainty when it is so high that it discourages security investment. This can be done, for instance, by encouraging information sharing so that the cost of reducing the uncertainty can be borne between several defenders [12] [13] .
Note that all these conclusions remain fairly robust for other parameters than the example set in Table 1. For brevity, we refrain from discussing the influence of all other parameters. Instead, we demonstrate the validity of our model by applying it to two case studies where real data is available.
5. Empirical Evidence for Iterated Weakest Links
In the following, we will point the reader to past “iterated arms races” in the realm of information security. We argue that such dynamics, against the backdrop of our model, may in fact be rational and should not simply be framed as “failures”. We have selected two cases, one where almost all costs are recoverable (Section 5.1) and another one where unrecoverable costs should not be ignored (Section 5.2).
5.1. Case 1: Phishing and Online Crime
Our first argument focuses on the security of computers comprising the Internet follow an iterated weakest link model. Fundamental to the Internet’s design is the notion that any connected computer can communicate with every other computer. Attackers have relentlessly exploited this structure, constructing networks of compromised machines (so-called botnets) to pester legitimate users by emitting spam, distributing malware and hosting phishing websites. Internet service providers (ISPs) are usually well-placed to detect infection, because evidence of a user’s infection flows over an ISP’s communication systems. Moreover, large companies that act as Internet service providers have technical staff who can detect and clean up infected machines, while domestic users and small businesses are mostly helpless to even recognize when they are compromised; let alone to take appropriate remedial action. However, for every responsible ISP that keeps a clean network, there are countless others who find it more cost-effective to ignore the problem and let infections flourish.
There is substantial evidence that attackers concentrate their efforts at the most irresponsible ISPs, moving on to others once the ISP cleans up its act or is shut down. For instance, until 2007, a lot of the world’s malware was hosted by the Russian Business Network (RBN), which refused to comply with requests from international law enforcement [14] . After Russian Business Network suddenly went offline in late 2007, malware distribution shifted to other ISPs. In November 2008, a journalist from the Washington Post persuaded upstream bandwidth providers to shut off their connection to San Francisco-based McColo, which led to a temporary fall of almost 70% in the volume of spam worldwide [15] . Apparently, many botnet herders had been using McColo to host their control machines. Spam volume has since recovered as the spammers found new safe havens. In 2008 EstDomains, which served as the primary domain name registrar for malicious websites hosted by Russian Business Network [16] , became the first domain registrar to have its accreditation terminated by the Internet Corporation for Assigned Names and Numbers [17] . Unfortunately, other irresponsible registrars remain.
Attackers can often move on to exploit the next weakest link in the Internet far faster than defenders can knock them out. Moore and Clayton [18] showed how one leading group of online fraudsters, the rock-phish gang, operated. It registered many malicious web domain names to carry out attacks. Periodically, the gang picked a firm for registering Internet domain names that it had never used before and registered hundreds of web domains, using false names and stolen credit cards. These domains did not resemble normal bank names, so a registrar may not identify foul play, and the first domains to be used for false purposes were not removed quickly.
Figure 6 presents scatter plots of phishing site lifetime based on the date reported from data of [18] . Both .hk (Hong Kong) domains (left) and .cn (China) domains (right) lasted much longer in their first month of use than in later months. The gang targeted Hong Kong domains first in March 2007, followed by Chinese domains in May 2007 after the Hong Kong authorities wised up.
Such iteration over previously untargeted infrastructure operators is prevalent among many forms of cybercrime. Other researchers have found that websites hosting most malware move from one registrar to the next [19] . Liu et al. studied patterns in the registration and take-down of spam-advertised domains [20] , finding that miscreants register many domains at previously untargeted registrars, repeatedly moving on to new ones following crack-downs. McCoy et al. examined the use of payment processors by unlicensed online pharmacies [21] . They showed that the operators of unlicensed pharmacies initially relied on a small number of payment processors. Once banks were made aware of the criminal behavior, many severed ties with the pharmacies, who quickly made arrangements with new processors.
5.2. Case 2: Payment Card Security
Financial transactions have long been subject to fraud, and banks and payment processors have recognized that fraud has to be managed rather than eliminated. In 2000, the UK banks decided to adopt the EMV card payment system designed by Europay, Mastercard and Visa, popularly known as “Chip and PIN” EMV. The EMV roll-out provides a compelling example of taking security decisions to tackle the weakest link, only to find that the attackers react by exploiting new holes previously ignored. A May 2007 internal report prepared by APACS (since rebranded as the UK Cards Association) compared the expected benefits from EMV adoption to fraud incidence over time. While the report was intended to be kept confidential, it was accidentally leaked and is now hosted on the Cryptome website [22] . We use the data gleaned from this report, as well as more recent public statistics [23] [24] , to demonstrate how the banks’ fight against card fraud has essentially been a sequence of patches to plug weak links.
Figure 7 plots the annual percentage of transaction turnover found to be fraudulent from 1972 to 2014.
Figure 6. Take-down latency for phishing attacks targeting different registrars in spring 2007; lines are five-day moving averages broken down by top-level domain (Source: own aggregation based on data of [18] ).
Figure 7. Long-term fraud rates as a fraction of overall turnover (Source: [22] [23] ).
Notably, there are significant swings in the rate. According to the report [22] , “the industry has responded to crises in card fraud by making significant investment in new preventative measures,” including “terminalisation in the early 80s and, later, a major increase in levels of authorisation during the mid 90s.” Such behavior is consistent with our model of iterating through successive weakest links.
Around 2000, a fear arose that another uptick in the fraud rate was imminent. The dashed line with triangle markers in Figure 8 plots the forecast losses due to fraud based on maintaining the status quo as of 2000. To stem this expected rise in fraud, UK banks decided to adopt the EMV standard (Chip and PIN) over the course of the next few years. The estimated cost of implementing EMV across the UK was just over £1 billion, shared between the banks and retailers. We can interpret this investment to roll out EMV as unrecoverable costs. The dashed line with diamond markers in Figure 8 plots the forecast losses following EMV adoption. The uptick to 2003 is due to the phased roll-out of the technology.
In fact, the actual losses look rather different (solid line in Figure 8). The anticipated explosion of fraud in the early 2000s did not materialize; strikingly, the full adoption of EMV (completed in 2005) did not significantly alter the fraud totals. Instead, a slow but steady increase was observed, both before and after EMV adoption.
Digging a little deeper, we can see that the switch to EMV did significantly alter attacker strategy, even if it did not significantly shift the aggregate fraud rates. Instead, as some types of fraud diminished, other techniques quickly filled the gap. For instance, EMV has caused a dramatic drop in face-to-face retail fraud, since forging a signature is easier than guessing the right PIN. In 2004, face-to-face fraud totaled £219 million; in 2006, after EMV became mandatory, it fell to £72 million (see Figure 9). However, card-not-present (CNP) fraud (where only the card number is used, as in online transactions) has sharply risen since the introduction of EMV, from £150 million in 2004 to £328 million in 2008, before falling modestly and reaching a new high of £332 million in 2014. This is not surprising, since PINs are not verified for CNP transactions.
Another example of attackers moving to weaker links can be found by looking at where ATM fraud takes place. With the adoption of EMV, ATMs in the UK stopped verifying PINs using magnetic stripes, requiring the PIN be verified using the more secure chip. However, many ATMs outside the UK continued to allow the less secure verification via magnetic stripe. As UK ATMs switched over during 2006, fraudsters immediately adapted to cashing out via less secure international ATMs. Figure 10 shows how this transformation happened. In December 2005, when most UK ATMs still allowed magnetic stripe PIN verification, £6 million out of the total £6.5 million stolen from ATMs took place within the UK. By the end of the year, after the switch to more secure verification, the total monthly fraud increased to over £9 million, with nearly 75% of the losses occurring overseas. The shift to overseas fraud that is easier to carry out has continued since the EMV rollout. In Figure 11, we see that the share of the total fraud occurring overseas rose from £93M (18% of the total) in 2004 to a peak of £230M (37% of the total) in 2008. In fact, the share of overseas-originated fraud on UK cards in 2008 exceeded the total UK-originated fraud in 2004, just prior to the EMV deployment. This is compelling evidence of how quickly attackers can shift to find the next-weakest link once the biggest hole has been plugged.
The EMV standard actually provides several options for implementation that vary in the cost and security achieved. While the UK EMV implementation was certainly not inexpensive, its designers did opt for many of the lower-cost implementations offered by the standard. For instance, PIN verification is normally done offline, be- tween the card’s chip and the PIN entry device (PED). This enables a relay attack whereby a small, legitimate transaction authorized by a compromised terminal can be used to approve a simultaneous, much larger fraudulent
Figure 8. Ten-year fraud projections made in 2000 comparing whether EMV is adopted (marked dashed lines), plus actual fraud rates (solid line) (Source: [22] ).
Figure 9. Fraud losses for UK face-to-face (F2F) retail transactions protected by EMV and for card-not-present (CNP) transactions not protected by EMV (Source: [23] ).
Figure 10. Shifting attacker strategy following EMV adoption. The bar graph shows how ATM fraud has moved overseas to ATMs which have not made the switch to chip verification, but still rely on less secure magnetic stripes (Source: [22] , trend lines fitted with ordinary least squares).
transaction elsewhere [25] . Furthermore, the communications within the PED between the card’s chip and the PED’s processor are not encrypted. Combined with some shoddy tamper-proofed devices, this enables PINs to be read using a paper clip tapped inside the PED [26] . The same team later discovered an attack on the protocol that could enable a criminal to use a genuine card without knowing the PIN [24] [27] . While entirely practical, there is no evidence that these attacks are being used by attackers at present. Instead, they seem to be focusing on the more obvious weak links of card-not-present transactions and magnetic stripe verification at foreign
Figure 11. Total fraud losses split according to whether the fraud took place in the UK or not (Source: [23] ).
ATMs. If (and when) these holes are plugged5, one might expect these attacks to be deployed, which would trigger defensive countermeasures by the banks.
5.3. Attack Profiles for the Case Studies
Figure 12 plots the expected and realized costs of different attacks for the case studies just presented. Figure 12(a) plots a sequence of top-level domains that potentially targeted by the rock-phish gang. First, many Chinese domains were registered by the gang, followed by domains from Hong Kong (as shown in Figure 6). The next top-level domain targeted―Austria―came as a surprise. Austria has an extensive Internet security community, and its law enforcement has long cooperated with cyber investigations from other countries. None- theless, the rock-phish gang registered many .at domains, and they were not removed for a very long time. It turns out that the Austrian domain registrar nic.at balked at removing the illicit domains without more extensive evidence documenting their illegality. The domains were only removed following a public row between the e-mail-blacklist operator Spamhaus and nic.at [29] . Finally, after .at domains began getting removed promptly, the Turkish top-level domain .tk was targeted.
Meanwhile, many top-level domains have not been targeted by the gang. This includes domains such as Paraguay (.py), which we might have expected to be an easy target for attackers6, as well as domains such as .se, .edu, and .gov that are harder to register.
The many threats to payment card security, along with their expected and actual costs, are shown in Figure 12(b). Face-to-face retail fraud might reasonably be seen as the weakest link in the payment card environment; the reduction in face-to-face retail fraud following the adoption of EMV supports this view. Similarly, the banks correctly anticipated that losses due to credit cards lost or stolen inside the UK (L&S in the figure) would drop once PINs were required for use. By contrast, fraud rates due to cards stolen outside the UK were lower than the banks expected. Card fraud at UK ATMs is a bit harder than retail fraud since a PIN is required. One area where the banks’ expectations were not met is with ATM fraud on UK cards outside the UK. It turns out that fraudsters can easily clone stolen UK cards and use them in foreign ATMs; hence the true cost of attack is lower than expected.
The banks’ losses due to card-not-present fraud were much higher than forecast; unsurprisingly, many banks have now decided to deploy readers that verify PINs in order to carry out online banking. Meanwhile, uncer- tainty remains regarding the attacks on PIN entry devices uncovered in [25] and [26] , though it is apparent that the costs are higher than for card-not-present fraud and foreign ATM fraud.
6. Related Work
The relevance of developing quantitative models of information security has been widely recognized in account- ing [6] [30] , information security [10] [31] , and dependable computing [32] - [35] . Of this and subsequent

Figure 12. Hypothetical attack profiles (derived ex post from predictions and actual attacks). (a) Rock-phish domain costs; (b) EMV attack costs.
literature, we briefly describe several works with similarities to our model.7
Gordon et al.’s “wait-and-see approach” comes closest to our mode l [30] [39] . The authors explain deferred security spending in the framework of real option theory and conclude that “it is economically rational to ini- tially invest a portion of the information security budget and defer remaining investments until security breaches actually occur”. Similar to our argument, Gordon et al. [30] name uncertainty about the attack surface as main reason why one should “expect organizations to use security breaches as a critical determinant of their actual […] expenditures on information security.” In this sense, our model can be regarded as a substantial extension of the two-period case study they discuss. Gordon et al.’s work differs from our approach in that they treat security spending as an allocation problem of a fixed security budget rather than seeing it as capital investment to be put into relation to the assets at risk. Also, the weakest link attacker model is unique to our work. We and Gordon et al. back our claims with empirical evidence. While they draw on cross-sectional survey data collected from senior information officers, we cite time series of actual attacks in Section 5 to emphasize the iterated dimen- sion.
Herath and Herath [40] have transferred Gordon et al.’s [30] real option approach (ROA) to a case study of e-mail spam filtering. They compare net present values (NPV), which imply now-or-never investments, to ROA. Their results concur with our comparison between the static and dynamic solution: for their selected parameters, NPV suggests no security spending whereas ROA indicates positive returns for deferred partial security investment. Franqueira et al. [41] discuss a conceptual framework and tool support for implementing ROA in corporate security decision making.
Real options are in fact another tool to model uncertainty, learning, and sequential investment, so it is both plausible(and reassuring that models based on them come to similar conclusions. Both ROA and our iterated weakest link (IWL) have specific merits. While ROA is more general and builds on mainstream financial mathematics, IWL is more specific to information security and avoids the complexity of nested option contracts and abstract parameters, such as project volatility, which are difficult to interpret and even harder to estimate in practice. Both approaches are compatible, which allows a CISO to use IWL to make his decisions and express it in terms of ROA to convince his CFO.
Besides real options, the optimal timing of security investments has also been analyzed with other tools. [42] propose a graphical model for scenarios where defenders can learn from observed attacker behavior. The model shows the superiority of reactive defenses with concepts from online learning algorithms. Ogut et al. [43] use stochastic dynamic programming for the special case of reacting to signals from intrusion detection systems, which are notorious for false alarms. They compare a myopic strategy, which prescribes a fixed dynamic reac- tion, to the optimal adaptive response. In this setting, the difficulty of finding the optimal adaptive response does not outweigh the security benefit of a fixed dynamic response. One step closer to practice, Zhu et al. [44] simu- late reactive defense strategies based on reinforced learning algorithms for scenarios inspired by the discovery of the Heartbleed vulnerability in 2014. Kwon and Johnson [45] present the only empirical study we are aware of that specifically investigates proactive versus reactive security investment. Notably, their result contrasts the tenor of most analytical models! Proactive security investment was found to be more cost effective that reactive investment, and this effect is further amplified if indirect costs from breach disclosure are taken into account. It remains for future work to verify if these findings are due to the specific characteristics of the US healthcare sector, the subject of this study, or if they apply more broadly. In any case, it would be interesting to identify the driving factor behind this effect and tie it to the IWL model.
Recall that our model is technically not a “game”, but a decision or optimization problem. Over the past couple of years, information security has become a rich application area for game theory [46] . Bier et al. [47] use a non-cooperative game-theoretic setting to study strategic interaction between a single attacker and a defender who optimizes the allocation of defenses to multiple targets (two in their formal model). Unlike in our model, only a single period is modeled; the model is designed to capture terrorism threats. Uncertainty of the defender is a common element in both models, in which the defender has to cope with uncertainty about an assumed hidden preference of the attacker to target a particular target. If our notion of asset is interpreted as a distributed system in which each target potentially gives the attacker access to the entire system (similar to our case study in Section 5.1), then targets can be interpreted as threats and (hidden) attack costs as preferences. A topic that has no counterpart to our work is Bier et al.’s reference to signaling theory to study whether the defense configuration should be kept secret or made public. The model by Cremonini and Nizovtsev [48] ex- plains security investment decisions with uncertainty of the attacker. They too draw on signaling theory and conclude that a defense is good enough if, and only if, it looks strong enough to divert the attackers’ attention towards other, seemingly weaker targets. In this sense, their work can be regarded as a kind of mirror image to our work, which deals with the uncertainty on the defender’s side. Finally, Dijk et al. [49] have devised a con- tinuous-time dynamic game of attacker-defender interaction, which increasingly attracts the attention of security researchers interested in game theory. Unlike in our setup, the game does not capture security investment in a narrow sense, but models the timing of cleanup operations. As it is formulated as a strategic game rather than an inter-temporal optimization problem against a probabilistic attacker, it becomes very hard to find stable equi- libria for realistic strategy spaces. So far, we are only aware of partial solutions that are difficult to interpret in practice.
This article is an extended and updated version of our workshop version [50] . As a follow-up, [51] have studied a variant of this model which allows the defender to commission penetration tests that might reveal the next weakest link without risking the consequences of a successful attack.
7. Summary and Possible Extensions
We have presented an economic model that explains why and under which conditions under-investment in security can be rational, even against known threats for which defenses exist. Under-investment might reasonably occur when a) reactive investment is possible, b) uncertainty exists about the attacker’s relative capability to exploit different threats, c) successful attacks are not catastrophic, and d) the costs to upgrade the defense configuration are largely recoverable.
Unlike in other work explaining security under-investment with market failures, the ingredients to our model solely draw on the relation between defender and attacker, and do not involve actions of other market participants. Our results do not contradict or invalidate the well-known explanations of market failure. It rather complements the picture and highlights that market failure is a sufficient, but not always necessary, cause for security under-investment.
We believe that an iterated weakest link model accurately captures the challenges facing many information security threats today. We discussed two timely examples in the article. First, miscreants committing high- volume online crime exploit the Internet’s global, distributed architecture by compromising insecure machines and defrauding uninformed registrars, wherever they are located. Second, the security of payment cards has evolved over time by reacting to fraudster’s actions. Empirical data on losses show how the introduction of EMV in the UK has simply diverted attacker strategy to other methods, notably card-not-present and foreign ATM fraud.
As with any stylized model, ideas for extensions are abundant and implementation should be guided by the principle of parsimony, especially in the absence of reliable data to validate model assumptions. Nevertheless, a handful of extensions appear reasonable to make the model more applicable. One is to let the cost of attacks decrease over time to reflect learning and the creation of automated tools. Another direction could be to allow more ways for reducing uncertainty. This can be done either by including information gathering as an option for security investment (e.g., penetration testing or information sharing), or by relaxing the independence assumption between the stochastic realizations of the attack profile. The latter would allow the defender to infer knowledge about the probability of other threats from observed attacks, a phenomenon exploited by some technical early warning systems. If updates cause substantial unrecoverable costs, this opens new strategies of bundled investment in new defenses to better amortize the cost. Lastly, it may be of―at least academic―interest to consider other attack strategies. For example, attackers might not choose the weakest link to confuse the defender and trigger misallocations of security spending. Anecdotal evidence for such behavior can be found in the actions of some spammers, who send waves of messages with no other apparent purpose than to wear out self- learning spam filters.
One key future challenge is to find a case study where enough information is available to calibrate the model to empirical data. More generally, it may be worthwhile to explore further the question of when to deal with a problem. When is it better to move first and take proactive measures, and when is it better to defer and respond to other’s actions?
Acknowledgements
We thank Chad Heitzenrater, the anonymous reviewers and participants of the 2009 Workshop on the Economics of Information Security (WEIS), and the anonymous reviewers of this special issue on Cybersecurity Investment for valuable comments and suggestions on earlier versions of this paper. All errors and omissions are the authors’.
Cite this paper
Rainer Böhme,Tyler Moore, (2016) The “Iterated Weakest Link” Model of Adaptive Security Investment. Journal of Information Security,07,81-102. doi: 10.4236/jis.2016.72006
References
- 1. Anderson, R. and Moore, T. (2006) The Economics of Information Security. Science, 314, 610-613.
http://dx.doi.org/10.1126/science.1130992 - 2. Varian, H.R. (2004) System Reliability and Free Riding. In: Camp, L.J. and Lewis, S., Eds., Economics of Information Security, Springer Verlag, New York, 1-15.
http://dx.doi.org/10.1007/1-4020-8090-5_1 - 3. Kunreuther, H. and Heal, G. (2003) Interdependent Security. Journal of Risk and Uncertainty, 26, 231-249.
http://dx.doi.org/10.1023/A:1024119208153 - 4. Bauer, J.M. and van Eeten, M. (2009) Cybersecurity: Stakeholder Incentives, Externalities, and Policy Options. Telecommunications Policy, 33, 706-719.
http://dx.doi.org/10.1016/j.telpol.2009.09.001 - 5. Bohme, R. and Moore, T. (2010) The Iterated Weakest Link. IEEE Security & Privacy, 8, 53-55.
http://dx.doi.org/10.1109/MSP.2010.51 - 6. Gordon, L.A. and Loeb, M.P. (2002) The Economics of Information Security Investment. ACM Transactions on Information and System Security, 5, 438-457.
http://dx.doi.org/10.1145/581271.581274 - 7. Collins, M., Gates, C. and Kataria, G. (2006) A Model for Opportunistic Network Exploits: The Case of P2P Worms. Proc. of Workshop on the Economics of Information Security (WEIS), Cambridge, 26-28 June 2006.
http://weis2006.econinfosec.org/docs/30.pdf - 8. Major, J.A. (2002) Advanced Techniques for Modelling Terrorism Risk. Journal of Risk Finance, 4, 15-24.
http://dx.doi.org/10.1108/eb022950 - 9. Thomas, K., Huang, D.Y., Wang, D., Bursztein, E., Grier, C., Holt, T.J., et al. (2015) Framing Dependencies Introduced by Underground Commoditization. Workshop on the Economics of Information Security (WEIS), Delft, 22-23 June 2015.
- 10. Hoo, K.J.S. (2002) How Much Is Enough? A Risk-Management Approach to Computer Security. Workshop on Economics and Information Security (WEIS), Berkeley, 16-17 May 2002.
http://www.sims.berkeley.edu/resources/affiliates/workshops/econsecurity/ - 11. Purser, S.A. (2004) Improving the ROI of the Security Management Process. Computers & Security, 23, 542-546.
http://dx.doi.org/10.1016/j.cose.2004.09.004 - 12. Gal-Or, E. and Ghose, A. (2005) The Economic Incentives for Sharing Security Information. Information Systems Research, 16, 186-208.
http://dx.doi.org/10.1287/isre.1050.0053 - 13. Laube, S. and Bohme, R. (2015) Mandatory Security Information Sharing with Authorities: Implications on Investments in Internal Controls. 2nd ACM Workshop on Information Sharing and Collaborative Security, Denver, 12-16 October 2015, 31-42.
http://dx.doi.org/10.1145/2808128.2808132 - 14. The Economist (2007) A Walk on the Dark Side.
http://www.economist.com/displayStory.cfm?story_id=9723768 - 15. Krebs, B. (2008) Major Source of Online Scams and Spams Knocked Offline. Washington Post, 11 November 2008.
http://voices.washingtonpost.com/securityfix/2008/11/major_source_of_online_scams_a.html - 16. Krebs, B. (2008) EstDomains: A Sordid History and a Storied CEO. Washington Post, 8 September 2008.
http://voices.washingtonpost.com/securityfix/2008/09/estdomains_a_sordid_history_an.html - 17. ICANN (2008) Termination of Registrar EstDomains to Go Ahead.
http://www.icann.org/en/announcementsannouncement-12nov08-en.htm - 18. Moore, T. and Clayton, R. (2007) Examining the Impact of Website Take-Down on Phishing. Proceedings of the Anti-Phishing Working Groups 2nd Annual eCrime Researchers Summit, Pittsburgh, 4-5 October 2007, 1-13.
http://www.cl.cam.ac.uk/~rnc1/ecrime07.pdf
http://dx.doi.org/10.1145/1299015.1299016 - 19. Day, O., Palmen, B. and Greenstadt, R. (2008) Reinterpreting the Disclosure Debate for Web Infections. In: Johnson, M.E., Ed., Managing Information Risk and the Economics of Security, Springer, New York, 179-197.
- 20. Liu, H., Levchenko, K., Felegyházi, M., Kreibich, C., Maier, G., Voelker, G.M. and Savage, S. (2011) On the Effects of Registrar-Level Intervention. Proceedings of the 4th USENIX Conference on Large-Scale Exploits and Emergent Threats, LEET’11, Berkeley, 5.
- 21. McCoy, D., Dharmdasani, H., Kreibich, C., Voelker, G.M. and Savage, S. (2012) Priceless: The Role of Payments in Abuse-Advertised Goods. Proceedings of the 2012 ACM Conference on Computer and Communications Security, CCS’12, Raleigh, 16-18 October 2012, 845-856.
http://dx.doi.org/10.1145/2382196.2382285 - 22. APACS (2007) 2007 UK Chip and PIN Report.
http://cryptome.org/UK-Chip-PIN-07.pdf - 23. The UK Cards Association. Card Fraud Figures. Retrieved on 29 December 2015.
http://www.theukcardsassociation.org.uk/plastic_fraud_figures/ - 24. LLC EMVCo. EMV 4.1, June 2004.
http://www.emvco.com - 25. Drimer, S. and Murdoch, S.J. (2007) Keep Your Enemies Close: Distance Bounding against Smartcard Relay Attacks. Proceedings of 16th USENIX Security Symposium, Boston, 6-10 August 2007, Article No. 7.
- 26. Drimer, S., Murdoch, S.J. and Anderson, R. (2008) Thinking Inside the Box: System-Level Failures of Tamper Proofing. IEEE Symposium on Security & Privacy, Oakland, 18-22 May 2008, 281-295.
http://dx.doi.org/10.1109/sp.2008.16 - 27. Murdoch, S.J., Drimer, S., Anderson, R. and Bond, M. (2010) Chip and PIN Is Broken. 2010 IEEE Symposium on Security and Privacy (SP), Oakland, 16-19 May 2010, 433-446.
http://dx.doi.org/10.1109/sp.2010.33 - 28. Drimer, S., Murdoch, S.J. and Anderson, R. (2009) Optimised to Fail: Card Readers for Online Banking. In: Dingledine, R. and Golle, P., Eds., Financial Cryptography and Data Security, Lecture Notes in Computer Science, Vol. 5628, Springer, Berlin, 184-200.
http://dx.doi.org/10.1007/978-3-642-03549-4_11 - 29. Spamhaus (2007) Report on the Criminal “Rock Phish” Domains Registered at Nic.at (Press Release).
http://www.spamhaus.org/organization/statement.lasso?ref=7 - 30. Gordon, L.A., Loeb, M.P. and Lucyshyn, W. (2003) Information Security Expenditures and Real Options: A Wait-and-See Approach. Computer Security Journal, 14, 1-7.
- 31. Schechter, S.E. (2005) Toward Econometric Models of the Security Risk from Remote Attacks. IEEE Security and Privacy, 3, 40-44.
http://dx.doi.org/10.1109/MSP.2005.30 - 32. Littlewood, B., Brocklehurst, S., Fenton, N., Mellor, P., Page, S., Wright, D., et al. (1994) Towards Operational Measures of Computer Security. Journal of Computer Security, 2, 211-229.
- 33. Jonsson, E. and Andersson, M. (1996) On the Quantitative Assessment of Behavioural Security. In: Pieprzyk, J. and Seberry, J., Eds., Information Security and Privacy, Lecture Notes in Computer Science, Vol. 1172, Springer-Verlag, Berlin, 228-241.
http://dx.doi.org/10.1007/bfb0023302 - 34. Jonsson, E. and Olovsson, T. (1997) A Quantitative Model of the Security Intrusion Process Based on Attacker Behaviour. IEEE Transactions on Software Engineering, 23, 235-245.
http://dx.doi.org/10.1109/32.588541 - 35. Avizienis, A., Laprie, J.-C., Randell, B. and Landwehr, C. (2004) Basic Concepts and Taxonomy of Dependable and Secure Computing. IEEE Transactions on Dependable and Secure Computing, 1, 11-33.
http://dx.doi.org/10.1109/TDSC.2004.2 - 36. Anderson, R. (2001) Why Information Security Is Hard—An Economic Perspective. Annual Computer Security Applications Conference (ACSAC), New Orleans, 10-14 December 2001, 358-365.
http://www.cl.cam.ac.uk/~rja14/econsec.html
http://dx.doi.org/10.1109/acsac.2001.991552 - 37. Bohme, R. and Schwartz, G. (2010) Modeling Cyber-Insurance: Towards a Unifying Framework. Workshop on the Economics of Information Security (WEIS), Harvard University, Cambridge, 7-8 June 2010.
- 38. Yue, W.T. and Cakanyildirim, M. (2007) Intrusion Prevention in Information Systems: Reactive and Proactive Responses. Journal of Management Information Systems, 24, 329-353.
http://dx.doi.org/10.2753/MIS0742-1222240110 - 39. Gordon, L.A., Loeb, M.P., Lucyshyn, W. and Zhou, L. (2015) The Impact of Information Sharing on Cybersecurity Underinvestment: A Real Options Perspective. Journal of Accounting and Public Policy, 34, 509-519.
http://dx.doi.org/10.1016/j.jaccpubpol.2015.05.001 - 40. Herath, H.S.B. and Herath, T.C. (2008) Investments in Information Security: A Real Options Perspective with Bayesian Postaudit. Journal of Management Information Systems, 25, 337-375.
http://dx.doi.org/10.2753/MIS0742-1222250310 - 41. Franqueira, V.N.L., Houmb, S.H. and Daneva, M. (2010) Using Real Option Thinking to Improve Decision Making in Security Investment. In: Meersman, R., Dillon, T.S. and Herrero, P., Eds., On the Move to Meaningful Internet Systems: OTM, Lecture Notes in Computer Science, Vol. 6426, Springer, Berlin, 619-638.
http://dx.doi.org/10.1007/978-3-642-16934-2_46 - 42. Barth, A., Rubinstein, B.I.P., Sundararajan, M., Mitchell, J.C., Song, D. and Bartlettm, P.L. (2010) A Learning-Based Approach to Reactive Security. In: Radu, S., Ed., Financial Cryptography and Data Security, Lecture Notes in Computer Science, Vol. 6052, Springer, Berlin, 192-206.
http://dx.doi.org/10.1007/978-3-642-14577-3_16 - 43. Ogut, H., Cavusoglu, H. and Raghunathan, S. (2008) Intrusion Detection Policies for It Security Breaches. INFORMS Journal on Computing, 20, 112-123.
http://dx.doi.org/10.1287/ijoc.1070.0222 - 44. Zhu, M., Hu, Z. and Liu, P. (2014) Reinforcement Learning Algorithms for Adaptive Cyber Defense against Heartbleed. Proceedings of the 1st ACM Workshop on Moving Target Defense, Scottsdale, 3-7 November 2014, 51-58.
http://dx.doi.org/10.1145/2663474.2663481 - 45. Kwon, J. and Johnson, M.E. (2014) Proactive versus Reactive Security Investments in the Healthcare Sector. MIS Quarterly, 38, 451-471.
- 46. Manshaei, M.H., Zhu, Q., Alpcan, T., Basar, T. and Hubeaux, J.-P. (2013) Game Theory Meets Network Security and Privacy. ACM Computing Surveys, 45, Article No. 25.
http://dx.doi.org/10.1145/2480741.2480742 - 47. Bier, V., Oliveros, S. and Samuelson, L. (2007) Choosing What to Protect: Strategic Defensive Allocation against an Unknown Attacker. Journal of Public Economic Theory, 9, 563-587.
http://dx.doi.org/10.1111/j.1467-9779.2007.00320.x - 48. Cremonini, M. and Nizovtsev, D. (2006) Understanding and Influencing Attackers’ Decisions: Implications for Security Investment Strategies. Workshop on the Economics of Information Security (WEIS), Robinson College, University of Cambridge, 26-28 June 2006.
http://weis2006.econinfosec.org/docs/3.pdf - 49. van Dijk, M., Juels, A., Oprea, A. and Rivest, R.L. (2013) FlipIt: The Game of “Stealthy Takeover”. Journal of Cryptology, 26, 655-713.
http://dx.doi.org/10.1007/s00145-012-9134-5 - 50. Bohme, R. and Moore, T. (2009) The Iterated Weakest Link: A Model of Adaptive Security Investment. Workshop on the Economics of Information Security (WEIS), University College London, 24-25 June 2009.
http://weis09.infosecon.net/files/152/paper152.pdf - 51. Bohme, R. and Felegyházi, M. (2010) Optimal Information Security Investment with Penetration Testing. In: Alpcan, T., Buttyán, L. and Baras, J.S., Eds., Decision and Game Theory for Security, Lecture Notes in Computer Science, Vol. 6442, Springer, Berlin, 21-37.
http://dx.doi.org/10.1007/978-3-642-17197-0_2
NOTES
1An alternative interpretation is that threats represent distinct targets in a distributed system that together form asset a.
2We do not consider higher-order interdependence such as extra costs if three or more defenses are involved.
3All other parameters are as specified in Table 1.
4We stick to the term “annual” to be consistent with the literature and assume that time periods in the model correspond to financial years.
5Unfortunately, card readers used to secure online banking (and potentially all card-not-present e-commerce) have also been demonstrated to be insecure CAPFC [28] .
6We do not intend to single out Paraguay; many smaller countries have not been targeted by the rock-phish gang.
7For the sake of brevity, we do not review in detail the extensive literature explaining security underinvestment by interactions with other market players (e.g., by undersupply in a lemon market Anderson 2001 [36] , moral hazard in risk sharing contracts Kunreuther 2003, market failure in residual risk transfer BS2010-WEIS [37] , defense effectiveness conditional to other players’ actions Varian 2004, or general externalities Bauer 2009). A trade-off between proactive and reactive measures is also studied in the literature on optimal configuration of response in intrusion detection and prevention systems Yue 2007 [38] . We deem this related, but not very relevant, due to the narrow scope of adjusting a technical decision threshold.
















