Journal of Modern Physics
Vol.06 No.03(2015), Article ID:54201,14 pages
10.4236/jmp.2015.63028
The Nature of Dark Matter and of Dark Energy
Jacob Schaf
Instituto de Física, Universidade Federal do Rio Grande do Sul (UFRGS), Porto Alegre, Brazil
Email: schaf@if.ufrgs.br
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2015; accepted 16 February 2015; published 25 February 2015
ABSTRACT
The aim of the present work is showing that the observed non-Keplerian rotation of the galaxies is predicted by the space dynamic gravitational mechanism without dark matter and that the current explanation of the galactic gravitational dynamics in terms of dark matter is hypothetical. Visibly, the need of dark matter is an emergency created by a mistaken view about the nature of space and gravitation. Furthermore, in the view of the present work, the accelerated expansion of the universe is expansion of the Higgs quantum space itself, driven by minimization of its total energy. Spontaneous breaking of the U(1) gauge symmetry and Bose-Einstein condensation of the Higgs bosons creates a potential energy well in the form of the Mexican sombrero. If the density  of the condensate is larger than the equilibrium density, then the Higgs quantum space can minimize its energy by volumetric expansion. The idea that the accelerated expansion of the universe is driven by a positive potential energy, dubbed dark energy, needs to be unveiled.
of the condensate is larger than the equilibrium density, then the Higgs quantum space can minimize its energy by volumetric expansion. The idea that the accelerated expansion of the universe is driven by a positive potential energy, dubbed dark energy, needs to be unveiled.
Keywords:
Dark Matter, Dark Energy, Gravity, Gravitational Physics, Gravitational Fields

1. Introduction
It is well known since decades that the orbital velocity of the stars round the galactic nucleus falls not off with distance as predicted by the current theories of gravity. Many published papers [1] -[3] display observed velocity profiles of the orbital velocity of the stars in the Andromeda galaxy, of our Milky Way galaxy as well as for other galaxies as a function of the distance from the galactic center, determined by spectroscopic methods. Figure 1 displays the observed velocity profile of our Milky Way Galaxy together with a typical Keplerian rotation. From the viewpoint of the current theories, the rotation rate of galaxies is much too fast to be accounted for by the gravitational force generated by their content and distribution of visible matter.
Instead of mistrusting the current theoretical view about space and gravitation, people preferred to mistrust the actual instruments of observation. Accordingly, these observations are alleged to see only a small part of the matter content of the galaxy and that a huge amount of invisible gravitating dark matter must be acting there. The nature of dark matter is really very exotic. It acts by gravity, but does not scatter, absorb or emit electromagnetic radiation. Actually a variety of very massive hypothetical non-hadronic particles (MACHOS, WIMPS etc.) are being proposed as possible candidates for dark matter. Challengingly, the amount of dark matter, necessary to account for the observed galactic rotation rate, must be about 5 times larger than that of the whole visible matter. To present date nobody has idea where such a huge amount of dark matter could be hided and what its nature is. Some authors assert that an external halo of dark matter round the galaxies may explain the observed galactic rotation. However, if dark matter interacts by gravity, why then is it not concentrated within stars and the center of galaxies? Besides its very exotic nature, its conduct is even much more exotic. The abnormal galactic rotation rate is actually the most challenging impasse in the current theories of space and gravitation.
The distribution of mass within galaxies is neither homogeneous nor spherically symmetric. Galaxies have a central bulge, formed by elliptically orbiting stars that normally harbors within it a super-massive black hole. Beyond the bulge, up from about 104 light years, galaxies are formed by a swarm of stars that orbit round the galactic center along nearly equatorial circular orbits within a thin disk that extends up to about 5 × 104 light years. Almost the whole mass of a galaxy is in the form of stars that are orbiting round the galactic nucleus under the collective self-consistent gravitational field created by them. The stars are separated from each other by large distances, in the order of light years, so that most of the space within a galaxy is empty. The density of the galactic matter undergoes weak variation with distance from the galactic center, due to their spiraled structure. Our Milky Way Galaxy is an old barred spiral galaxy having a central bulge of about 104 light years across, that is surrounded by a disk-shaped swarm of hundreds of billions of stars orbiting along closely circular orbits that extend out to about 4.5 × 104 light years. The bulge contains a central region of lower mass density having a diameter of some thousand light years wherein it exhibits a bar shaped halo of hot and dense flowing gases and within the bar it harbors a super-massive black hole. Almost the whole mass of the galaxy is orbiting round the galactic center within the bulge and the disk in the form of dense stars under their self-consistent gravitational field.
The challenging point in the galactic gravitational dynamics is that within the galactic disk the orbital velocity of the stars round the galactic center does not fall off with distance from the galactic center, as predicted by the current theories of gravitation. In some galaxies the velocity even increases with distance. However, at the outer
Figure 1. The figure displays the profile of the observed rotation rate of the Milky Way galaxy as a function of distance from the galactic center and the Keplerian rotation rate.
border of the galaxy the galactic rotation rate falls off rather steeply. None of the current theories of gravity can explain this galactic gravitational dynamics. Explanations have been attempted introducing a preposterous amount of dark matter. In order to be able to explain the galactic gravitational dynamics the dark matter must form an external halo of matter round the galaxy. However if this dark matter interacts by gravity, why then is it not concentrated within the stars and in the galactic center like usual matter? In the view of the present work, the idea of dark matter is an emergency idea enforced by wrong concepts about the nature of space and the gravitational physics. In contrast, the physical mechanism of gravity, proposed by the theory of space dynamics, predicts the observed galactic gravitational dynamics without the need of dark matter.
2. Brief Outline of the Space Dynamic Gravitational Mechanism
According to the new theory of space and gravitation, named space dynamics, [4] -[9] the real space, ruling the inertial motion of matter and the propagation of light, is moving in the ordinary three dimensions round each astronomical body throughout the universe according to a Keplerian velocity field, consistent with the local main astronomical motions (please see Equation (1) and Figure 2). With respect to this real space earth, the other planets and satellites of the solar system as well as all the astronomical bodies in general throughout the universe very nearly are stationary. This directly explains the null results of the Michelson light anisotropy experiments. Such real space, ruling the inertial motion of matter and the propagation of light, needs not to be invented. The
Figure 2. The velocity of the Keplerian velocity field 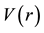 of the QS, due to a spherically symmetric body of radius R, with a homogeneous density of mass. The figure displays the velocity as a functions of r, from the origin up to
of the QS, due to a spherically symmetric body of radius R, with a homogeneous density of mass. The figure displays the velocity as a functions of r, from the origin up to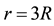 . This profile of the velocities is exactly the same along any direction, for all
. This profile of the velocities is exactly the same along any direction, for all 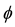 and all
and all 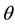 from the equator to the poles.
from the equator to the poles.
Quantum Field Theory (QFT) underlying the Standard Elementary Particle Model (SEPM), that now is fairly well established, entails the idea that ordinary 3D-space is filled up with the Higgs condensate (HC). This HC is a very powerful quantum space (QS) stable up to 1015 degrees Kelvin, that is formed by Bose-Einstein condensation of the zero spin Higgs bosons by spontaneously breaking the universal U(1) gauge symmetry. This HC is a quantum fluid, totally analogous to the superconducting condensate (SCC). The HC is to the weak and strong nuclear fields (elementary particle fields) what the SCC is to photons. Quantum fluids are well known to intrinsically quantize all their cyclic excitations. Likewise superconductors develop screening currents (velocity fields of the SCC) and a Lorentz force field in the presence of magnetic fields, confining and compressing these fields by the Meissner effect and making them short-range, thereby giving inertial mass to the photons within the superconductor, the HC develops velocity fields of the HC round matter fields, confining them by the Higgs mechanism, giving inertial mass to the elementary particles, that is, giving them mechanical properties. This lets clear that the HC is the QS that rules the inertial motion of matter and the propagation of light and hence is the locally ultimate but moving reference for rest and for motions of matter and light. As the HC rules the inertial motion of matter, its motion according to a non-uniform velocity field, generates a field of inertial (gravitational) forces compressing matter into dense matter bodies.
Recent experimental observations, achieved with the help of the tightly synchronized clocks of the Global Positioning System (GPS) [10] -[12] show that this QS-dynamics is not simply a guess. They show very clearly that the QS, ruling the propagation of light and the rate of clocks, is moving round earth according to a Keplerian velocity field consistently with the Moon’s orbital motion and round the Sun consistently with the earth’s orbital motion. [4] -[6] In order to describe this velocity field let us define non-rotating systems of orthogonal coordinate axes (XYZ), with origins fixed respectively to the center of earth, to the center of the sun and to the galactic center, the direction of these axes being fixed with respect to very distant astronomical objects and the Z axis along to rotation axis of earth, of the solar system and of the galaxy. Let 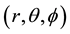 be the usual sperical coordinates and
be the usual sperical coordinates and  unit vectors pointing along the positive direction of these sperical coordinates.
unit vectors pointing along the positive direction of these sperical coordinates.
In terms of these usual spherical coordinates the Keplerian velocity field associated with a body of radius R and mass M for 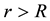 is:
is:
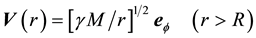 (1)
(1)
where 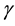 is the gravitational constant (please see Figure 2). Within the homogeneous and spherically symmetric matter body
is the gravitational constant (please see Figure 2). Within the homogeneous and spherically symmetric matter body 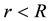 the velocity field of the QS is given by:
the velocity field of the QS is given by:
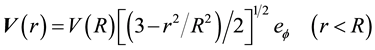 (2)
(2)
where 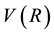 is the velocity of the QS at the surface of the body. It is important to observe that within the gravitational source the velocity still increases toward the gravitational center, but becomes completely flat near to the center (see Figure 2).
is the velocity of the QS at the surface of the body. It is important to observe that within the gravitational source the velocity still increases toward the gravitational center, but becomes completely flat near to the center (see Figure 2).
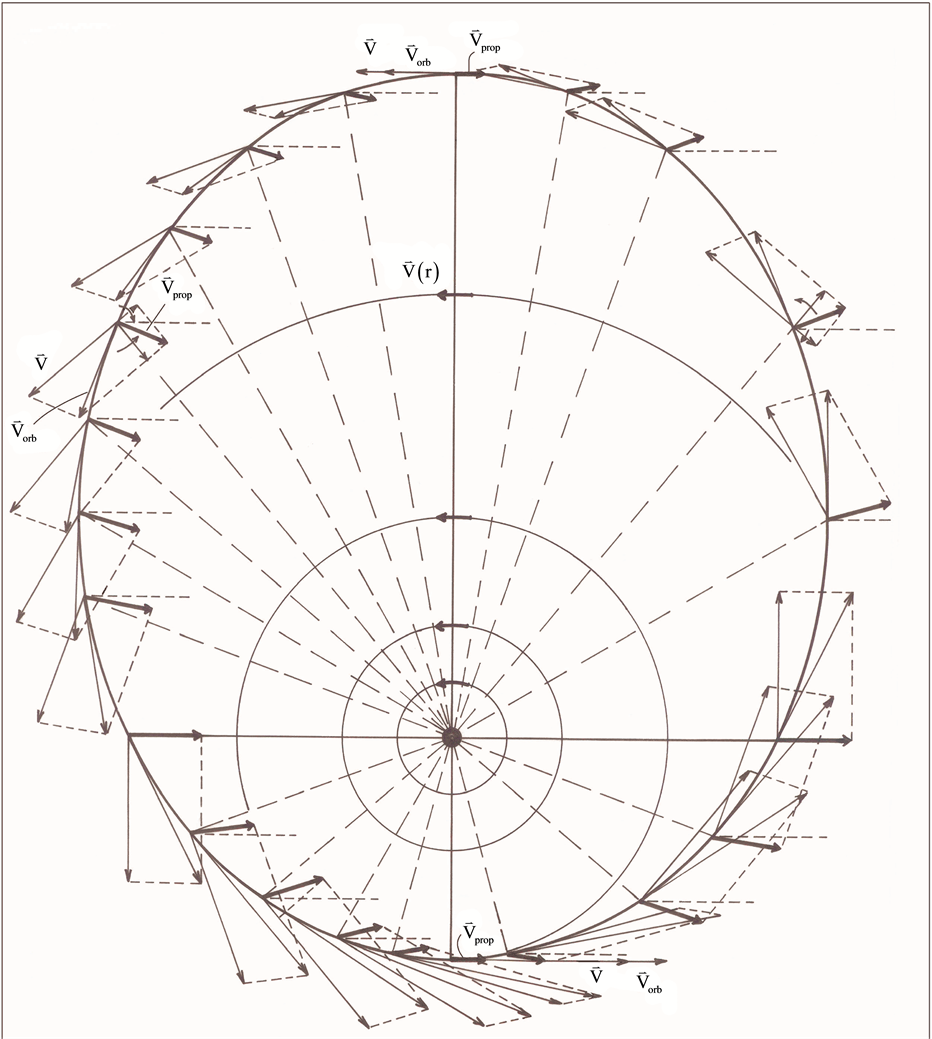
In Refs. [6] [7] it is shown that this Keplerian velocity field of the QS Equation (1) straightforwardly creates the observed gravitational dynamics on earth and within the solar system. It also is shown to correctly generate all the observed effects of the gravitational fields on the propagation of light and the rate of clocks, there including all the new effects recently discovered with the help of the GPS. Within this Keplerian velocity field the circular orbital motions of the planets round the Sun and of the natural satellites round the planets trace out very closely the circulation field of the QS and hence closely rest with respect to this QS. These bodies are essentially carried around by the moving QS. In fact the planets have only very low velocities with respect to the local moving QS. In particular, the small orbital eccentricity of the planet Earth shows that it moves with only about 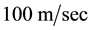 with respect to the QS in the solar Keplerian velocity field. The effects of such low velocities are much too small to be detected even by the actual most sensitive instruments. Within an astronomical scale of velocities, the planets do very nearly rest with respect to the QS. This explains the null results of the Michelson experiments, searching for light anisotropy due to the orbital and cosmic motion of earth. The very slow motion of the planets with respect to the QS is ruled by the usual principle of inertia. Due to the differential velocity of the QS in the Keplerian velocity field, the velocity vector of the free bodies with respect to the QS continuously changes direction and size. These variations involve effects of refraction and wavelength stratching-compression. Figure 3 is a highly precise graphical display, showing how the direction and length of the velocity vector of a
with respect to the QS in the solar Keplerian velocity field. The effects of such low velocities are much too small to be detected even by the actual most sensitive instruments. Within an astronomical scale of velocities, the planets do very nearly rest with respect to the QS. This explains the null results of the Michelson experiments, searching for light anisotropy due to the orbital and cosmic motion of earth. The very slow motion of the planets with respect to the QS is ruled by the usual principle of inertia. Due to the differential velocity of the QS in the Keplerian velocity field, the velocity vector of the free bodies with respect to the QS continuously changes direction and size. These variations involve effects of refraction and wavelength stratching-compression. Figure 3 is a highly precise graphical display, showing how the direction and length of the velocity vector of a
Figure 3. The figure is a very precise graphical representation of the orbital velocity
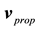
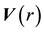
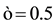
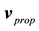
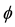
free body with respect to the local QS changes along an equatorial excentric orbit. From this variation of the velocity vector the effective time rate of the opposite refraction of the 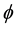

Equations (3) show the result of this lecture:


Using Equations (3a) and (3b) the hyperbolic rotation matrix can be defined:
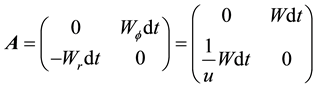
The collumn matrix of the r and 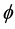
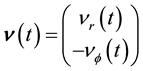
In terms of the matrices Equations (4) and (5) the equation ruling the vertical free-fall can be written as:
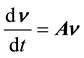
This equation develops into:
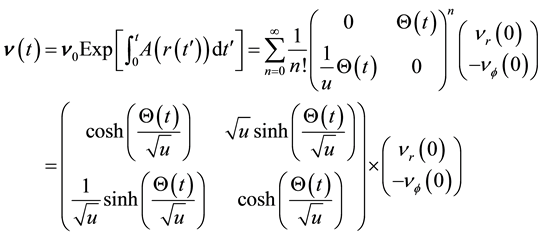
The solution of this equation (please see Section 5 of Refs. [6] [7] for details) leads to the usual expression for velocity of vertical free-fall and the implicit velocity as a function of position. For bodies in orbit, it is necessary to add in Equation (3) and in the matrix Equation (4) the effect of the trigonometric angular velocity, due to the orbital motion round the gravitational center. In Refs. [6] [7] it is shown that the spacedynamic gravity field is spherically symmetric with orbital motions.
The weak ellipticity of the planetary orbits is consequence of the hyperbolic refraction rate (Equation (3) of the very slow r and 
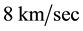
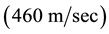
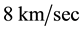
3. The Observed Galactic Gravitational Dynamics without the Need of Dark Matter
From the viewpoint of the present theory of space dynamics, in the galactic gravitational dynamics it is fundamental to take into account the fact that almost the whole matter, creating and ruling the galactic gravitational dynamics, is moving round the galactic nucleus. While in the solar system 99.9% of the mass in concentrated in the sun, in the galaxy more than 99.9% is orbiting round the galactic center. This obviously makes a difference. Each orbiting star carries with it its velocity (gravitational) field given by Equation (1). Likewise in the solar system, these velocity fields are fairly well polarized and rotate all in the same sense. Adequate addition of these velocity fields generates the galactic velocity (gravitational) field that rules the galactic gravitational dynamics. The stable spiraled structure of the galaxies must be seen as a perturbation of this ordered composition.
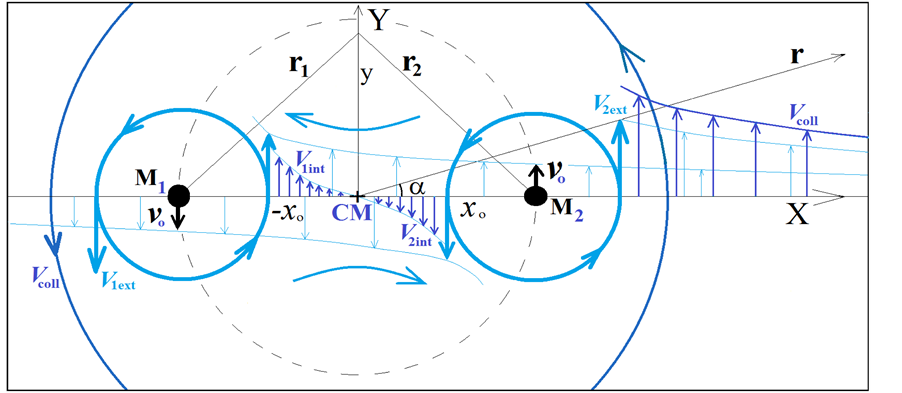
In order to highlight the relevance of the effect of motion of the individual gravitational sources on the collective velocity field of the Higgs quantum space QS of a system of bodies gravitating in their self-consistent field, let us begin with the simple case of a binary system of two equal stars of mass M moving in the same circular orbit round the center of mass in the equatorial plane of the collective velocity field as shown in Figure 4. The ordinary dynamics of such a system can fairly well be described by Newtonian mechanics. Balance of the mutual Newtonian gravitational forces 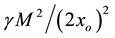
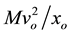
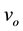
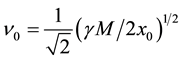
On the other hand, the velocity of a small test particle, orbiting round an equal isolated (static) mass M at the same distance 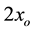
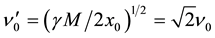
Obviously, from the viewpoint of the current gravitational theories there is nothing wrong with Equation (8) and Equation (9). However, although these equations express exactly what is observed, it must be remembered that the Newtonian gravitational forces are not physically real and moreover that after four decades of efforts, Quantum Gravity has not succeeded in providing physical reality to them. Hence, the explanation in terms of gravitational forces must be abandoned. GR is a much more realistic theory of gravitation, in which no gravitational forces are acting. However, GR too cannot explain the galactic gravitational dynamics. Moreover, now GR is in serious troubles with several recent experimental facts, because it cannot explain the absence of the gravitational time dilation on the GPS clocks, due to the solar gravitational potential as well as other clear-cut experimental observations (please see Section 3 in Refs. [4] [5] ). These facts frontally contradict predictions of GR. On the other hand, the theory of space dynamics provides the simple physical origin of the inertial dynamics
Figure 4. Two equal masses 
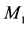
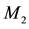
observed within the gravitational fields. It also accounts in terms of simple and genuine physical effects for all the other effects caused by gravitational fields on the velocity of light and on the rate of clocks, including all the new effects recently discovered with the help of the GPS. Here it moreover will be shown that this space dynamic gravitational mechanism predicts the observed gravitational dynamics of galaxies, without the need of dark matter, thereby providing a simple solution to this impasse.
From the viewpoint of space dynamics, Equations (8) and (9) unveil a key feature that discloses the effect of motion of the gravitational sources on their velocity fields of the QS. This is a fundamental ingredient in the gravitational dynamics of a system of bodies gravitating in their self-sustained gravitational field. Equation (9) gives the local velocity of the QS in the Keplerian velocity field round a static mass M. However, this is certainly true also in the case of the binary system. Equation (8) too gives the velocity of the QS, due to each one of the stars at the site of the companion star in the combined velocity field of the binary system. Hence, both Equations (8) and (9) describe the velocity of the QS in the respective velocity fields. However, why are these velocities so different? The only possible reason for the reduced velocity of the QS of 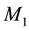
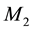
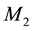
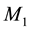
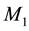
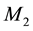
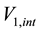
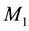
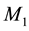
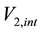
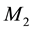
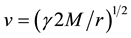
For large r this expression too represents the velocity of the QS in the collective velocity field round the binary system:

In order to reconcile the addition of the velocity fields of 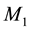
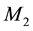
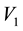


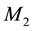
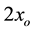
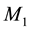
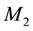
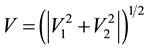
This rule arises because in the expression for the velocity field Equation (1) only the square root of the source mass appears. Accordingly, addition of the velocity fields as a function of x along the X axis outside of the binary in Figure 4 conforms to the equation:
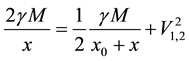
Solving for 
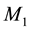
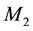

so that for large x, large r
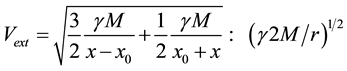
This shows that effectively the same orbital velocity that reduces the velocity fields of 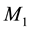
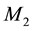
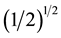
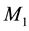


In-between the orbiting bodies of the binary system the velocity fields of 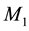
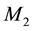



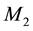
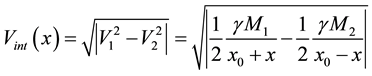
For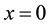
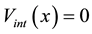
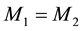
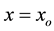
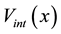


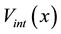
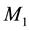
For other directions, adequate vector addition in conformity with Equation (12) must be performed. Along the Y axis the collective velocity field may be expressed by:
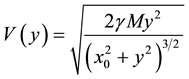
However, this equation is certainly not correct close to the binary because the collective velocity field is considerably affected by the flow continuity and conservation of volume. However, for large y Equation (17) too approximates Equation (10).
Note that within the binary orbit the circulation field of the QS round the CM is opposite to the orbital motion of the binary as well as opposite to the external velocity field as indicated in Figure 4. It is clear that within the orbit of the binary the velocity field is strongly reduced and that a stagnation point exists at the CM where the velocity of the QS falls to zero.
With the increase of the number of masses moving in the same sense in the same orbit, the opposite internal and external velocity fields of the QS become more and more symmetric. However, while the opposite internal velocity field remains reduced, the collective velocity field outside the loop is enhanced by more and more sources. Figure 5 displays a sketch for a system of four masses M orbiting round the center of mass under their collective velocity (gravitational) field.
In order to advance closer toward the realistic situation of a galactic system, consider now multiple concentric circular orbit loops with larger and larger radii and each loop containing a large number of bodies. Each loop acts in the sense of reducing the velocity field toward the inner side while enhancing it outward. The velocity field of the QS increases at each loop from 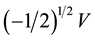
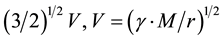
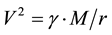
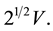
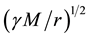

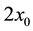
The model is of course an idealization. It however shows that, if the density of matter in the galaxy increases with distance, the orbital velocity of the stars may strongly increase. If the matter density becomes constant with distance from the galactic center, the orbital velocity must increase moderately. If the density decreases moderately with distance, the orbital velocity may become constant. However, if the density falls to zero at the
Figure 5. The figure is a qualitative sketch of the collective velocity field generated by four polarized equal masses moving in the same sense in the same circular orbit round the center of mass. Note that with- in the orbit the velocity field of the QS is weak and circulates in the opposite sense with respect to the much stronger external velocity field.
galactic border, the velocity field recovers the Keplerian dependence with distance on from this border.
The inner part of the galaxies is a region of hot flowing gases and has low mass density. However, outward the mass density and hence the orbital velocity increases very steeply as observed. Moreover, depending on the rate of the mass density increase, a retrograde rotation with respect to the outer galactic disk may form. In some galaxies such retrograde rotation is effectively observed. NGC 7331 is an example of a galaxy in which the inner bulge rotates in the opposite sense to that of the disk. [13] However, many other known examples exist. Moderate decrease of the mass density with distance, like observed in our Milky Way galaxy is expected to lead to nearly constant velocity as a function of distance from the galactic center. However, beyond the border of the rotating galaxy the velocity field may retake the decrease according to the Keplerian rotation.
The above analysis evidences that the space dynamic gravitational mechanism provides the base to account for the observed non-Keplerian galactic rotation as a function of the distance from the galactic center and can appropriately settle the galactic gravitational dynamics without the need of dark matter. The velocity field of the QS (gravitational field) that rules the galactic gravitational dynamics of a system of orbiting bodies certainly is much different from the Keplerian velocity field of the QS created by a single, compact, homogeneous, spherically symmetric and nearly static system of matter. The galactic rotation takes place within the self-consistent velocity field of the QS (gravitational field) generated by the whole ensemble of orbiting stars. Hence, from the viewpoint of the above analysis, it is not at all strange that the rotation of galaxies be a non-Keplerian one. Also in the central part of the galaxy the velocity field of the QS may be much reduced, analogously as shown by Equation (16) for the binary and becomes even more evident in the case of loops of four or more bodies [Figure 5]. Even the possibility of retrograde rotation of the inner part of a galaxy, as observed in some galaxies, is predicted. Hence, from the viewpoint of space dynamics, the observed non-Keplerian rotation of the galaxies is in no way a surprise.
It may be interesting to note that within the solar system the planets too are expected to induce a very weak but non-vanishing attenuation in the 
Beyond the bulge, up from about 7 × 103 light years, the stars are well known to move round the galactic center within the galactic disk in orbits that are closely circular. From the viewpoint of space dynamics, this is evidence that these stars are commoving with the QS in the galactic velocity field of the QS. Otherwise their orbits could not be so circular. Moreover, the null results of the Michelson experiments searching for light anisotropy due to the orbital and cosmic motion of Earth demonstrate that the velocity of our solar system with respect to the QS, despite its orbital velocity of about 230 km/sec round the galactic center, is closely zero and by consonance the velocity of all the stars of the galaxy within the galactic disk may be closely zero too. This will say that the equator of the galactic velocity field of the QS creating the galactic gravitational field coincides with the galactic disk and that the motion of stars along the circular orbits round the galactic center are in fact commoving with the QS in the galactic velocity field. They simply trace out the motion of the QS in the galactic velocity field. Hence, the function that describes well the observed circular orbital velocities of the stars as a function of distance within the galactic disk round the galactic center also describes well the galactic velocity field of the QS. These stars are resting with respect to the QS and therefore the velocity of light is isotropic with respect to them.
Moreover, clocks locally commoving with these stars, rest with respect to the QS. They run naturally synchronous and show all the same universal proper time. The circular orbital motions of the stars are of course not constrained to these circular orbits by gravitational forces. According to space dynamics, these stars are locally stationary with respect to the moving QS. They are essentially carried around by the moving QS in the galactic velocity field of the QS, analogously as the planets are carried around the sun by the solar Keplerian velocity field of the QS. Therefore, these orbital motions need not to be explained anymore, because it is space itself that so moves.
Within the bulge of the galaxy the orbits of stars are much elliptic and the orbital planes are much inclined with respect to the galactic plane. This will say that the velocity of these stars with respect to the QS is relatively large and this is what gives rise to the bulge.
Another important parameter in the gravitational dynamics is the gravitational potential

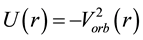
Hence, knowing the orbital velocity, the gravitational potential can be directly calculated from Equation (18) and vice-versa.
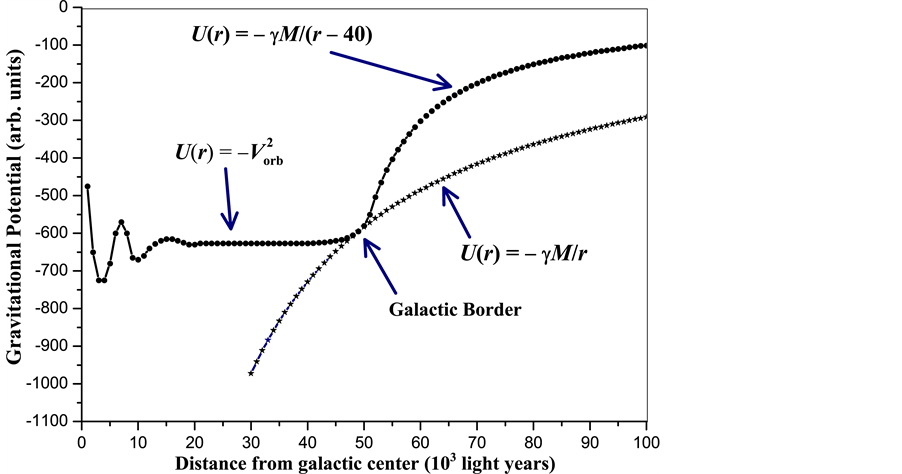
Several authors have computed the gravitational potential 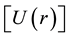
As predicted by space dynamics, the gravitational potential determined within the galactic disk, with base in Equation (18) (please see Figure 6), is considerably more leveled than the potentials computed with base in the current gravitational theories. The velocity gradient in the galactic velocity field and hence the gravitational acceleration of a body resting within the galactic disk, predicted by space dynamics, is very low and notwithstanding the stars move along circular orbits round the galactic center (no need of a central force field). They are carried around the galactic nucleus by the moving QS; likewise the planets are carried round the sun by the solar Keplerian velocity field of the QS and need no centripetal force to move so. The impasse of the current theories with these observations arises because, in order to account for the circular motion of the stars round the galactic center they absolutely need a gradient of the gravitational potential (centripetal force), pointing to the gravitational center. The absence of such a gradient gives rise to an unsolvable paradox. Instead of amending the theories, people preferred to believe in the presence of invisible halo of dark matter crating such a gradient.
On from the galactic border, the density of stars falls much more steeply. Beyond the galactic border, the velocity field of the QS may fall according to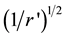
Although an exact determination of the galactic velocity field with base in the space dynamic gravitational mechanism has not been worked out, the above analysis gives convincing evidence that space dynamics can predict qualitatively, even with details the observed galactic gravitational dynamics without the need of dark matter. Even the possibility of the unbelievable retrograde rotation of the inner part of galaxies, observed in many galaxies, is a natural outcome of space dynamics.
Figure 6. The figure depicts the usual gravitational potential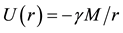
4. Dark Energy a Global Higgs Quantum Space Phenomenon
The observed accelerated expansion of the universe [17] [18] has no physical explanation to present date.
Usually it is imputed to a hypothetical new kind of positive potential energy, simply dubbed dark energy. The consensus is that dark energy distributes it homogeneously throughout space and is estimated to be 68% of the total mass-energy content of the universe (fourteen times the whole visible matter). The accelerated expansion also has been explained in terms of the cosmological constant in Einstein’s equation for the spacetime curvature. This however is not a physical explanation, but only a mathematical account. The present work proposes a suitable physical mechanism, that may be responsible for the accelerated expansion of the universe.
The null results of the Michelson light anisotropy experiments show that earth is resting with respect to Higgs quantum space (QS), ruling the inertial motion of matter and the propagation of light. However, obviously earth cannot be kinematically privileged in detriment to all the other astronomical bodies throughout the universe. From the viewpoint of the present work, the gravitational dynamics is created by motion of the real QS round each astronomical body, according to a Keplerian velocity field, consistent with the local main astronomical motions. Within the galaxy this velocity field is consistent with the galactic gravitational dynamics (see the previous Section 3). However, while this accounts for the null results of the Michelson light anisotropy experiments concerning the motion within the solar system and within the galaxy, it does not explain why the velocity of light is isotropic with respect to earth, viewed the recession between the galaxies. In fact the close isotropy of light with respect to earth and certainly with respect to all the main astronomical bodies, demonstrates that the recession of the galaxies does not make the velocity of light anisotropic with respect to earth. This can be reasonable only if the quantum space (QS), ruling the inertial motion of matter and the propagation of light, is itself expanding consistently with the recession of the galaxies and with the expansion of the matter universe. In this case the red-shift of the radiation, emitted by the distant astronomical objects, is not a usual Doppler shift but is due to stretching of the wavelength, caused by the expansion of the QS, its medium of propagation, as a function of time. The wavelength of radiation from more distant objects stretches during a longer time and so becomes more red-shifted.
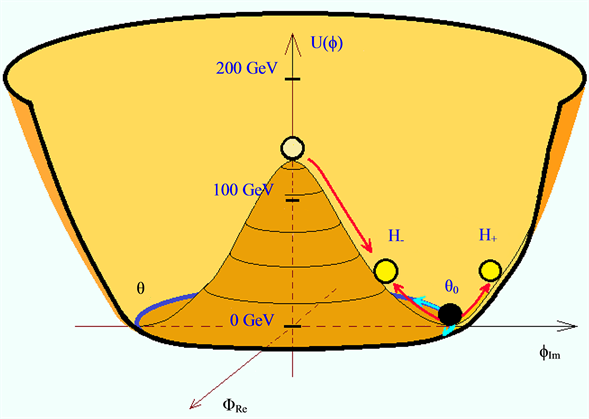
Expansion of the QS is a phenomenon that necessarily is related with the physics involved in the creation of the Higgs condensate. In Section 2 it has been asserted that the Higgs condensate is created by Bose-Einstein (BE) condensation of the zero spin Higgs bosons. BE condensation occurs because of the phase correlation between the wavefunctions of the zero spin Higgs bosons, leading to spontaneous breaking of the U(1) gauge symmetry of the system of particles. Phase coherence allows the system of bosons to lower their energy. During BE condensation the bosons undergo a transition to a long-range phase coherent state, the particles all assuming a well defined phase, becoming indistinguishable and tunneling throughout the volume of the condensate. The Higgs condensate (HC) is a quantum fluid analogous to the superconducting condensate. The HC plays in space an analogous role as the superconducting condensate plays is superconductivity. It is described by a complex order parameter


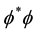
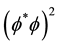

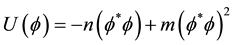
However, the negative coefficient of the first (bonding) term is significantly larger than the positive one of the anti-bonding term. Therefore, the effective potential energy forms a negative potential energy well, analogously as the covalent chemical bond, the form of which is a characteristic of the boson system and the deepness depends on the strength of the BE correlation. The minimum of potential energy occurs not for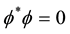


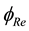

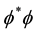

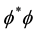

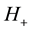
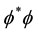
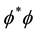
Figure 7. The figure depicts the form of the Mexican sombrero potential, indicating the transition to the lower energy phase coherent Higgs condensate (HC) with the well-defined phase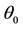


lerated shrinking (after which the density becomes maximum). In the language of the QFT the fluctuations of the density 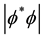
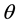
The Higgs condensate is a BE condensate to which such cyclic expansion and contraction may apply. Volumetric expansion of the Higgs condensate (HC) is volumetric expansion of the Higgs quantum space (QS), which entails expansion of the universe. Observations show that actually the universe is in a stage of accelerated expansion. This means that the density 
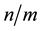
Finally, what is the role of gravity in the life of the universe? Observations show that the direction of the rotation axes of the galaxies is almost random. From the viewpoint of the present work, because of this randomness, the gravitational interaction may be attractive or repulsive. It is attractive between galaxies rotating in the same sense (round rotation axes making an angle lower than 90 degrees), but is repulsive between oppositely rotating galaxies (round axes making angles larger than 90 degrees). In this way attractive gravitation may on the overall be neutralized by anti-gravitation. In order to explain what is here meant by anti-gravitation, consider two well separated astronomical bodies of equally large masses and the Keplerian velocity fields of the QS, creating their gravitational fields (see Section 2), spinning round parallel axes. The important question to be answered is: What will happen if the two bodies approximate each-other? The point here is not giving an exact quantitative answer. A qualitative answer suffices. According to the space dynamic gravitational mechanism, if their velocity fields are spinning in the same sense, they will add up their velocity fields according to Equation (12), thereby increasing the total negative gravitational potential of the system. However, in case the velocity fields are spinning in opposite senses, their velocity fields will gradually add up to zero according to Equation (12) and their total effective negative gravitational potential may gradually cancel. While in the first case approximation of the bodies creates an additional negative (attractive) gravitational potential term, in the second case the approximation adds a positive (repulsive) gravitational potential term that gradually cancels the total negative potentials of the individual bodies. While the behavior in the first case fits into the view of the current gravitational theories, the second case is a novelty predicted by space dynamics. According to conservation of energy, while in the first case kinetic energy can be created by letting the two bodies approximate each-other, because this increases the negative gravitational potential energy of the system, in the second case, kinetic energy can be created by letting the bodies move away from each-other, because this too increases the gravitational potential energy of the system. This behavior evidences that while in the first case the bodies interact attractively, in the second case they repel each other, they antigravitate.
Within the solar system the rotation axes of the velocity fields of the sun, of the planets and of the planetary satellites are fairly well polarized (aligned), their velocity fields spinning in the same sense as can be verified from the motions of the satellites round the planets and of the planets round the Sun. The only anomalous case is with the satellites of Uranus. This however may be due because the satellites of Uranus are captured satellites. An analogous polarization seems to be well present between the stars of each galaxy. Therefore, within the solar system, within the Milky-Way galaxy and within galaxies in general only attractive gravitational interaction is observed. However, astronomical observations show that the direction of the rotation axes of the different galaxies throughout the universe is almost random. Hence, in the large scale dynamics of the universe the gravitational interaction does not play a dominant role. This dominant role belongs to the cyclic expansion-contraction of the Higgs-QS. The gravitational interaction is responsible for the filamentary large scale structure of the universe.
5. Conclusion
This work shows that the space dynamic gravitational mechanism, which straightforwardly explains the gravitational dynamics on earth and in the solar system, [5] -[7] can predict correctly the observed gravitational dynamics of the galaxies, without the need of dark matter. This work also appoints expansion of the Higgs quantum space itself, driven by energy minimization, as the physical origin of the accelerated expansion of the universe. This mechanism has the virtue of being intrinsically homogeneous throughout the universe and does not put the astronomical bodies into motion with respect to the Higgs quantum space, which would run into conflict with the null results of the Michelson light anisotropy experiments.
References
- Rubin, V. and Ford Jr., W.K. (1970) Astrophysical Journal, 159, 379. http://dx.doi.org/10.1086/150317
- Rubin, V., Thonnard, N. and Ford Jr., W.K. (1980) Astrophysical Journal, 238, 471. http://dx.doi.org/10.1086/158003
- Remmen, G. (2010) Journal of Undergraduate Research in Physics, 1.
- Schaf, J. (2014) Recent Progress in Space Technology, 4, 44-66.
- Schaf, J. (2014) Journal of Modern Physics, 5, 407-448. http://dx.doi.org/10.4236/jmp.2014.56053
- Schaf, J. (2013) Journal of Modern Physics, 4, 676-685. http://dx.doi.org/10.4236/jmp.2013.45095
- Schaf, J. (2012) Journal of Modern Physics, 3, 714-749. http://dx.doi.org/10.4236/jmp.2012.38097
- Schaf, J. (2009) Physics Essays, 22, 435. http://dx.doi.org/10.4006/1.3211086
- Schaf, J. (2003) Physics Essays, 16, 213. http://dx.doi.org/10.4006/1.3025578
- Hatch, R.R. (2007) Physics Essays, 20, 83. http://dx.doi.org/10.4006/1.3073811
- Hatch, R.R. (2004) GPS Solutions, 8, 67. http://dx.doi.org/10.1007/s10291-004-0092-8
- Hatch, R.R. (2004) Foundations of Physics, 34, 1725. http://dx.doi.org/10.1007/s10701-004-1313-2
- Prada, F., Gutierrez, C., Peletier, R.F. and McKeith, C.D. (1996) A Counter-Rotating Bulge in the Sb Galaxy NGC 7331.
- Turyshev, S.G. and Toth, V.T. (2010) The Pioneer Anomaly.
- Anderson, J.D., Laing, P.A., Lau, E.L., Liu, A.S., Nieto, M.M. and Turyshev, S.G. (2002) Physical Review D, 65.
- Barbanis, B. and Prendergast, K.H. (1966) The Astronomical Journal, 72, 215. http://dx.doi.org/10.1086/110220
- Riess, A., et al. (1998) Astronomical Journal, 116, 1009.
- Perlmutter, S., et al. (1999) Astrophysical Journal, 517, 565. http://dx.doi.org/10.1086/307221