Journal of Modern Physics
Vol.5 No.9(2014), Article
ID:47110,8
pages
DOI:10.4236/jmp.2014.59087
Energy Levels of Spin-1/2 Particles with Yukawa Interaction
Mohammad Reza Shojaei, Ali Akbar Rajabi, Maryam Farrokh, Niloufar Zoghi-Foumani
Department of Physics, Shahrood University of Technology, Shahrood, Iran
Email: niloofar.zoghi@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 March 2014; revised 1 April 2014; accepted 27 April 2014
ABSTRACT
In this article, Yukawa interaction is used to study the relativistic spin-1/2 particles and obtain their energy levels. The role of Yukawa potential on the spin and pseudospin symmetry solution is investigated systematically by solving the Dirac equation with attractive scalar S(r) and repulsive vector V(r) potentials. Bound state spectrum and wave functions of Yukawa potential are obtained. It is found that the energy eigenvalues strongly depend on the potential parameters.
Keywords:Yukawa Interaction, Dirac Equation, Spin and Pseudospin Symmetry, Spin-1/2 Particles

1. Introduction
The nature of interactions between nucleons is one of the fundamental and essential concepts of nuclear physics. It is required to clarify the nuclear structure of nucleus which comprises of relativistic spin-1/2 particles. The Dirac equation is the most perfect example of a relativistic equation which is able to describe the relativistic effects in a simple manner. In recent years, considerable attention has been paid to exactly solvable Dirac equation [1] . To the best of our knowledge, this equation is exactly solvable for only a few simple interactions and the solutions usually come with a strong constraint on the potentials [2] . For example, some authors assumed that the scalar potential is equal to the vector potential and obtained the exact solution of Dirac equation with some typical simple potentials by using different methods. These investigations include the harmonic oscillator potential [3] , the triaxial and axially deformed harmonicoscillator potential [4] , Eckart potential [5] [6] , Woods-Saxon potential [7] , Hulth´en potential [8] , pseudo harmonic oscillator [9] and ring-shaped Kratzer-type potential [10] , ring-shaped non-spherical oscillator [11] and double ring-shaped oscillator potential [12] , Hartmann potential [13] [14] , Rosen-Morse type Potential [15] , generalized symmetrical double-well potential [16] , Scarf-type potential [17] , etc. [18] . The methods include the standard method, super symmetry quantum mechanics [5] [19] and [20] , and the Nikiforov-Uvarov (NU) method [21] and so on. Formerly, Yukawa potential has been used in nonrelativistic quantum mechanics to study the interactions between nonrelativistic particles. Recently there has been much interest in solutions of Dirac equation for spin-1/2 particles with high energies [22] . In addition, thespin and pseudospin symmetry [23] [24] has been originally observed almost about 40 years ago as a mechanism to explain different aspects of the nuclear structure with relativistic spin-1/2 particles. Ginocchio has shown that the pseudospin symmetry arises from the near equality of the magnitude of the attractive scalar potential S(r) and the repulsive vector potential V(r), i.e., S(r)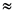 ‒V(r) in nuclei. The pseudospin symmetry refers to a quasi-degeneracy of the single-particle doublets and can be characterized with the quantum numbers (n, l, j = l + 1/2) and (n ‒ 1, l + 2, j = l + 3/2), where n, l and j are the radial, orbital and total angular momentum quantum numbers for a single particle, respectively. The spin symmetry and the pseudospin symmetry occur for
‒V(r) in nuclei. The pseudospin symmetry refers to a quasi-degeneracy of the single-particle doublets and can be characterized with the quantum numbers (n, l, j = l + 1/2) and (n ‒ 1, l + 2, j = l + 3/2), where n, l and j are the radial, orbital and total angular momentum quantum numbers for a single particle, respectively. The spin symmetry and the pseudospin symmetry occur for 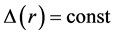 and
and  in Dirac equation [25] -[27] . The screened Coulomb potential is used in various areas of physics to model singular but short-range interactions [28] [29] . In high energy physics, for example, it is used to model the interaction of hadrons in short range gauge theories where coupling is mediated by the exchange of a massive scalar meson [28] [30] . In atomic and molecular physics, it represents a screened Coulomb potential due to the cloud of electronic charges around the nucleus. It has also been used to describe the interaction between charged particles in plasma, solid and colloidal suspensions [31] .
in Dirac equation [25] -[27] . The screened Coulomb potential is used in various areas of physics to model singular but short-range interactions [28] [29] . In high energy physics, for example, it is used to model the interaction of hadrons in short range gauge theories where coupling is mediated by the exchange of a massive scalar meson [28] [30] . In atomic and molecular physics, it represents a screened Coulomb potential due to the cloud of electronic charges around the nucleus. It has also been used to describe the interaction between charged particles in plasma, solid and colloidal suspensions [31] .
In this work, we have obtained the energy equation of relativistic spin-1/2 particles with the consideration of spin symmetry and pseudospin symmetry case. Solution of Dirac equation with standard Yukawa potential is presented by using the Nikiforov-Uvarov (NU) method and the eigen functions related to these cases of Dirac equation are obtained. Standard Yukawa-potential is given by
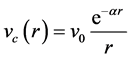 , (1)
, (1)
where 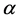 and
and  are range of nuclear force and strength of potential, respectively [28] .
are range of nuclear force and strength of potential, respectively [28] .
2. Dirac Basic Equation for Spin-1/2 Particles
In the relativistic description, the Dirac equation for a single-nucleon with the mass of M moving in an attractive scalar potential S(r) and a repulsive potential V(r) in natural units  can be written as [32] :
can be written as [32] :
 , (2)
, (2)
where E is the relativistic energy, P is the momentum operator, and  are the 4 ´ 4 Dirac matrices as follows:
are the 4 ´ 4 Dirac matrices as follows:
 , (3)
, (3)
I is the unit matrix and ![]() represents Pauli matrices. For a particle in a central field, the total angular momentum J and
represents Pauli matrices. For a particle in a central field, the total angular momentum J and 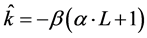 commute with the Dirac Hamiltonian, where L is the orbital angular momentum. For a given total angular momentum j, the eigenvalues of
commute with the Dirac Hamiltonian, where L is the orbital angular momentum. For a given total angular momentum j, the eigenvalues of 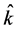 are
are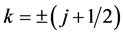 , where the negative sign is related to aligned spin and the positive sign represents the unaligned spin. The wave functions can be classified according to their angular momentum j and spin-orbit quantum number k as follows:
, where the negative sign is related to aligned spin and the positive sign represents the unaligned spin. The wave functions can be classified according to their angular momentum j and spin-orbit quantum number k as follows:
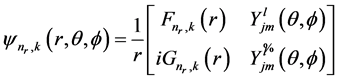 , (4)
, (4)
where  and
and 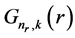 are the upper and lower components,
are the upper and lower components,  and
and  are the spherical harmonic functions.
are the spherical harmonic functions. ![]() is the radial quantum number and m is the projection of the angular momentum on the z-axis. The orbital angular momentum quantum numbers
is the radial quantum number and m is the projection of the angular momentum on the z-axis. The orbital angular momentum quantum numbers  and
and  are related to the spin and pseudospin quantum numbers. Substituting equation (4) into equation (2), we obtain a couple of equations for the radial part of the Dirac equation as follows:
are related to the spin and pseudospin quantum numbers. Substituting equation (4) into equation (2), we obtain a couple of equations for the radial part of the Dirac equation as follows:
 , (5)
, (5)
 . (6)
. (6)
By eliminating 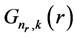 in Equation (5) and
in Equation (5) and 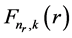 in equation (6), we obtain the following two secondorder differential equations for the upper and lower components:
in equation (6), we obtain the following two secondorder differential equations for the upper and lower components:
 , (7)
, (7)
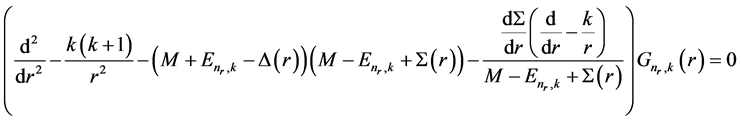 . (8)
. (8)
where 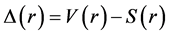 and
and 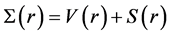 are the difference and the sum of the potentials V(r) and S(r), respectively [26] [27] . We consider the bound state solution that demands the radial components satisfying
are the difference and the sum of the potentials V(r) and S(r), respectively [26] [27] . We consider the bound state solution that demands the radial components satisfying 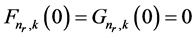 and
and .
.
3. Spin Symmetry Solution
This symmetry arises from the near equality in magnitudes of an attractive scalar, S(r), and repulsive vector, V(r), relativistic mean field, 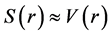 in which the nucleon moves [29] . In this case
in which the nucleon moves [29] . In this case , and equation (7) reduces to
, and equation (7) reduces to
 , (9)
, (9)
where  for
for 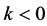 and
and 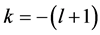 for
for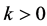 . The energy eigenvalues depend on
. The energy eigenvalues depend on ![]() and
and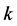 . By inserting the standard Yukawa potential instead of
. By inserting the standard Yukawa potential instead of  in Equation (9) we get
in Equation (9) we get
 . (10)
. (10)
This equation is a combination of the exponential and inverse square potentials, which cannot be solved analytically by using the standard methods such as SUSY or NU. Therefore, we must find an approximation to Yukawa potential term to solve the equation analytically. Considering the Taylor expansion, we adopt the approximation bellow [33] :
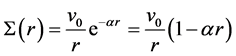 .(11)
.(11)
Rewriting Equation (10) with above term yields
 , (12)
, (12)
 . (13)
. (13)
If we introduce the notations
 , (14)
, (14)
and
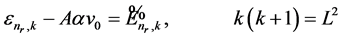 . (15)
. (15)
We obtain
 . (16)
. (16)
To solve this equation, we consider
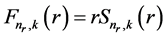 , (17)
, (17)
So we can rewrite Equation (16) as
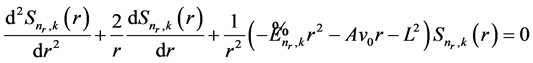 . (18)
. (18)
It is known that the solution of the second order differential equations plays an essential role in studying many important problems of theoretical physics. At this point, the NU method can be used to solve these types of equations.
4. Basic Concepts of NU Method
The NU method has been used to solve Schrodinger, Dirac, Klein-Gordon wave equations for certain kinds of potentials [34] . In this method the differential equations can be written in the following form:
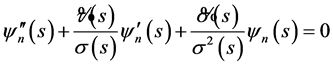 , (19)
, (19)
where  and
and  are polynomials that can be at most second degree, and
are polynomials that can be at most second degree, and  is a first-degree polynomial. To find a particular solution for Equation (19) by separation of variables, we have the following transformation:
is a first-degree polynomial. To find a particular solution for Equation (19) by separation of variables, we have the following transformation:
 . (20)
. (20)
It reduces Equation (19) to a hyper-geometric type function:
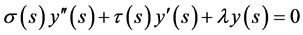 . (21)
. (21)
The function φ(s) is defined as a logarithmic derivative
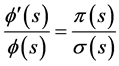 , (22)
, (22)
y(s) is the hypergeometric type function whose polynomial solutions are given by Rodrigues relation:
 , (23)
, (23)
Bn is the normalizing constant and the weight function ρ must satisfy the following condition:
 . (24)
. (24)
The function π and the parameter λ required for this method are defined as:
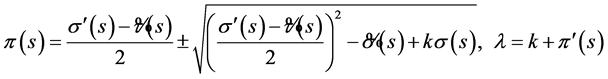 , (25)
, (25)
π(s) is a polynomial with the parameter s and the determination of k is the essential point in the calculation of π(s). In order to find the value of k, the expression under the square root must be square of a polynomial, so we have a new eigenvalue equation:
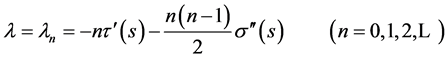 , (26)
, (26)
where
 , (27)
, (27)
and it will have a negative derivative. By comparing (25) and (26), we obtain the energy eigenvalues [34] .
If we apply the NU method, by comparing (18) and (19), the following expressions are obtained:
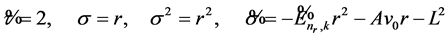 . (28)
. (28)
Substituting the above expression into (25), we have:
 . (29)
. (29)
The constant parameter  can be determined from the condition that the expression under the square root must be the square of a polynomial of first degree. So, it has a double zero. Therefore, possible forms of π(r) are as follows:
can be determined from the condition that the expression under the square root must be the square of a polynomial of first degree. So, it has a double zero. Therefore, possible forms of π(r) are as follows:
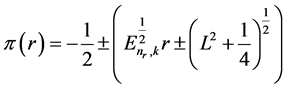 . (30)
. (30)
Since we have the polynomial 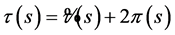 and it has a negative derivative, the suitable form is established. Therefore,
and it has a negative derivative, the suitable form is established. Therefore,
 . (31)
. (31)
According to (22) and (24) these values can be obtained:
 (32)
(32)
 . (33)
. (33)
Substituting (33) into (23), yn can be found:
 . (34)
. (34)
By using , the solution of (16) can be written as the wave function of the Dirac equation as follow:
, the solution of (16) can be written as the wave function of the Dirac equation as follow:
 . (35)
. (35)
Considering the notations of (14), (15) and Equation (26) the eigenvalues of energy can be obtained:
 . (36)
. (36)
This equation can be used to determine the difference in energy between energy levels of spin-1/2 particles with spin symmetry.
5. Pseudospin Symmetry Solution
Now we return to Equation (8) under pseudospin symmetry, i.e. . with the consideration of Equation (11), Equation (8) reduces to:
. with the consideration of Equation (11), Equation (8) reduces to:
 . (37)
. (37)
If we introduce the notations:
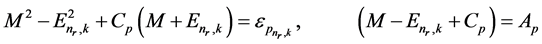 , (38)
, (38)
and
 . (39)
. (39)
We will obtain:
 . (40)
. (40)
In order to solve the above equation, as we did in Equation (17), we consider:
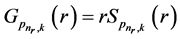 . (41)
. (41)
So we can rewrite Equation (41) as:
 . (42)
. (42)
Applying the NU method and comparing (42) and (19), the following expressions are obtained:
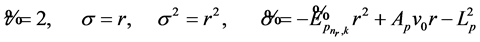 . (43)
. (43)
Using (25), π(r) can be found as follow:
 . (44)
. (44)
The constant parameter 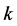 can be determined from the condition that the expression under square root must be the square of a polynomial of first degree. So, it has a double zero, therefore possible forms of π(r) are:
can be determined from the condition that the expression under square root must be the square of a polynomial of first degree. So, it has a double zero, therefore possible forms of π(r) are:
 . (45)
. (45)
Since the polynomial 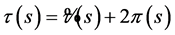 has a negative derivative, we have:
has a negative derivative, we have:
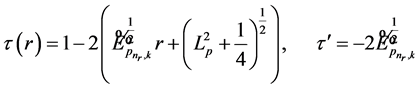 . (46)
. (46)
According to (22) and (24) these values can be obtained:
 , (47)
, (47)
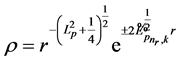 . (48)
. (48)
Substituting (48) into (23), yn can be written as:
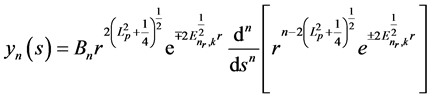 . (49)
. (49)
Using , the solution of (37) can be written as the wave function of Dirac equation under the pseudospin symmetry as follow:
, the solution of (37) can be written as the wave function of Dirac equation under the pseudospin symmetry as follow:
 . (50)
. (50)
Finally, considering the notations (38), (39) and Equation (26), the eigenvalues of energy can be obtained:
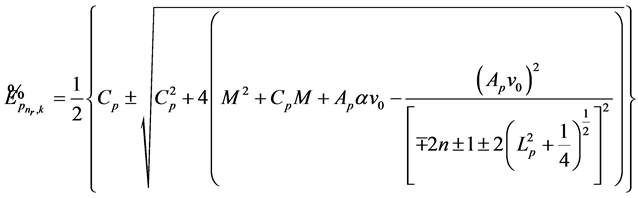 . (51)
. (51)
This energy equation yields the energy levels of spin-1/2 particles with pseudospin symmetry.
6. Conclusion
In this study, the energy equations of relativistic spin-1/2 particles are calculated with the consideration of spin symmetry and pseudospin symmetry case. The analytical NU method is applied to obtain the energy spectrum and eigen functions related to these cases of Dirac equation with standard Yukawa interaction.
References
- Alhaidari, A.D., Bahlouli, H. and Al-Hasan, A. (2006) Physics Letters A, 349, 87-97. http://dx.doi.org/10.1016/j.physleta.2005.09.008
- Schulze-Halberg, A. (2006) Chinese Physics Letters, 23, 1365. http://dx.doi.org/10.1088/0256-307X/23/6/003
- Su, R.K. and Ma, Z.Q. (1986) Journal of Physics A: Mathematical and General, 19, 1739.http://dx.doi.org/10.1088/0305-4470/19/9/045
- Ginocchio, J.N. (2004) Physical Review C, 69, Article ID: 034318. http://dx.doi.org/10.1103/PhysRevC.69.034318
- Jia, C.S., Guo, P. and Peng, X.L. (2006) Journal of Physics A: Mathematical and General, 39, 7737.http://dx.doi.org/10.1088/0305-4470/39/24/010
- Zou, X., Yi, L.Z. and Jia, C.S. (2005) Physics Letters A, 346, 54-64. http://dx.doi.org/10.1016/j.physleta.2005.07.075
- Guo, J.Y. and Sheng, Z.Q. (2005) Physics Letters A, 338, 90-96. http://dx.doi.org/10.1016/j.physleta.2005.02.026
- Hu, S.Z. and Su, R.K. (1991) Acta Physics Sinica, 40, 1201. (in Chinese)
- Chen, G., Chen, Z.D. and Lou, Z.M. (2004) Chinese Physics, 13, 279. http://dx.doi.org/10.1088/1009-1963/13/3/002
- Qiang, W.C. (2004) Chinese Physics, 13, 575. http://dx.doi.org/10.1088/1009-1963/13/5/002
- Zhang, X.A., Chen, K. and Duan, Z.L. (2005) Chinese Physics, 14, 42. http://dx.doi.org/10.1088/1009-1963/14/1/009
- Lu, F.L., Chen, C.Y. and Sun, D.S. (2005) Chinese Physics, 14, 463. http://dx.doi.org/10.1088/1009-1963/14/3/005
- Chen, C.Y. (2005) Physics Letters A, 339, 283-287. http://dx.doi.org/10.1016/j.physleta.2005.03.031
- de Souza Dutra, A. and Hott, M. (2006) Physics Letters A, 356, 215-219. http://dx.doi.org/10.1016/j.physleta.2006.03.042
- Yi, L.Z., Diao, Y.F., Liu, J.Y. and Jia, C.S. (2004) Physics Letters A, 333, 212-217. http://dx.doi.org/10.1016/j.physleta.2004.10.054
- Zhao, X.Q., Jia, C.S. and Yang, Q.B. (2005) Physics Letters A, 337, 189-196. http://dx.doi.org/10.1016/j.physleta.2005.01.062
- Zhang, X.C., Liu, Q.W., Jia, C.S. and Wang, L.Z. (2005) Physics Letters A, 340, 59-65. http://dx.doi.org/10.1016/j.physleta.2005.04.011
- Shojaei, M.R. and Rajabi, A.A. (2008) Modern Physics Letters A, 23, 3411. http://dx.doi.org/10.1142/S0217732308027291
- Shojaei, M.R., Rajabi, A.A. and Momen, Y. (2011) AIP Conference Proceedings, 1400, 135.
- Feizi, H., Rajabi, A.A. and Shojaei, M.R. (2011) Acta Physica Polonica B, 42, 2143. http://dx.doi.org/10.5506/APhysPolB.42.2143
- Nikiforov, A.F. and Uvarov, V.B. (1988) Special Function of Mathematical Physics. Birkhauser, Boston. http://dx.doi.org/10.1007/978-1-4757-1595-8
- Ginocchio, J.N. (2004) Physical Review C, 69, Article ID: 034318. http://dx.doi.org/10.1103/PhysRevC.69.034318
- Arima, A., Harvey, M. and Shimizu, K. (1969) Physics Letters B, 30, 517-522. http://dx.doi.org/10.1016/0370-2693(69)90443-2
- Hecht, K.T. and Adler, A. (1969) Nuclear Physics A, 137, 129-143. http://dx.doi.org/10.1016/0375-9474(69)90077-3
- Ginocchio, J.N. (2005) Physics Reports, 414, 165-261. http://dx.doi.org/10.1016/j.physrep.2005.04.003
- Guo, J.Y. (2012) Physical Review C, 85, Article ID: 021302(R). http://dx.doi.org/10.1103/PhysRevC.85.021302
- Chen, S.W. and Guo, J.Y. (2012) Physical Review C, 85, Article ID: 054312. http://dx.doi.org/10.1103/PhysRevC.85.054312
- Yukawa, H. and Sakata, S. (1935) Proceedings of the Physico-Mathematical Society of Japan, 17, 48.
- Feizi, H., Shojaei, M.R. and Rajabi, A.A. (2012) The European Physical Journal Plus, 127, 41. http://dx.doi.org/10.1140/epjp/i2012-12041-y
- Wilczek, F. (2007) Nature, 445, 156-157. http://dx.doi.org/10.1038/445156a
- Messina, R. and Lowen, H. (2003) Physical Review Letters, 91, Article ID: 146101. http://dx.doi.org/10.1103/PhysRevLett.91.146101
- Greiner, W. (2000) Relativistic Quantum Mechanics: Wave Equations. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-04275-5
- Shenk, A. (2000) Calculus and Analytic Geometry. Scott Foresman & Co., Glenview.
- Farrokh, M., Shojaei, M.R. and Rajabi, A.A. (2013) Klein-Gordon Equation with Hulth’en Potential and Position-Dependent Mass. The Europeanphysical Journal Plus, 128, 14.

