ABSTRACT

Following an inspiring idea due to D. Gross, we arrive at a topological Planck energy E_p and a corresponding topological Planck length 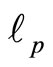effectively scaling the Planck scale from esoterically large 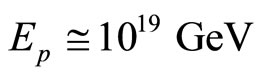and equally esoterically small numbers to a manageably 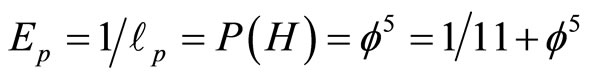where P(H) is the famous Hardy’s probability for quantum entanglement which amounts to almost 9 percent and 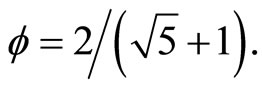Based on these results, we conclude the equivalence of Einstein-Rosen “wormhole” bridges and Einstein’s Podolsky-Rosen’s spooky action at a distance. In turn these results are shown to be consistent with distinguishing two energy components which results in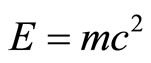, namely the quantum zero set particle component 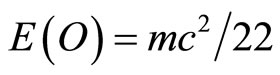which we can measure and the quantum empty set wave component which we cannot measure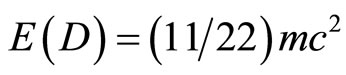, i.e. the missing dark energy. Together the two components add to where E is the total energy, m is the mass and c is the speed of light. In other words, the present new derivation of the world’s most celebrated formula explains in one stroke the two most puzzling problems of quantum physics and relativistic cosmology, namely the physicomathematical meaning of the wave function and the nature of dark energy. In essence they are one and the same when looked upon from the view point of quantum-fractal geometry.

1. Introduction

In a remarkable essay [1] the founding father of Heterotic superstring theory and Nobel Laureate in physics D. Gross gave without any mathematical elaboration in a novel general direction for the unification of all fundamental forces and arriving at quantum gravity via an imaginative, unconventional and in fact revolutionary idea of scaling the almost esoteric Planck scale [1,2]. In the present work which tackles one of the currently most researched and hotly debated problems in quantum physics and cosmology [1-72], we take this idea literally and seriously to mean a mathematical topological formulation of physics starting from a unit interval spacetime with non-classical and non-smooth transfinite discrete geometry and topology [2-5]. Proceeding in this way, we arrive at a quintessential, i.e. five dimensional Kaluza-Klein space-time [26,30] and a general formula for quantum entanglement 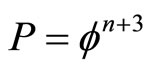which reduces in the case of two particles n = 2 to Hardy’s famous probability [16-21] of quantum entanglement where 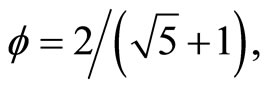i.e. a quantum probability of almost 9%. This result was repeatedly verified experimentally with a very high degree of accuracy [3,4].

In the present work we show how 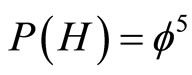is related to Gross’ proposal [1,2] and discusses its various ramifications for dark energy [2,3] and the connection between general relativity’s Einstein-Rosen bridges [24, 25] and the quantum mechanics of Einstein-PodolskyRosen non-locality [3,4,6]. This insight leads to an effective quantum gravity theory [69,70] and an explanation for the true meaning of the quantum wave function and the missing dark energy of the cosmos by fusing Einstein’s relativity and quantum mechanics entanglement together [3,4]. Our basic philosophy and technical strategy may be summed up succinctly as follows: By facing infinity and zero head on and endorsing them, we eliminate the drawback of both and suddenly everything in physics looks right [44-54]. Although the present work is reasonably self contained, for a deep understanding of the transfinite nonlinear techniques used to develop our theory, it is helpful to read carefully at least Refs. [1,3] and [5] as well as Ref. [58-72] for a bird’s eye view of the general theory [5,16]. We may also note that the theory of quantum sets was extensively developed by D. Finkelstein who also introduced the notion of quantum relativity [69].

2. Analysis

The present analysis consists of several interconnected vital steps which need to be explained consecutively with a reasonable degree of logical order as follows:

2.1. Space-Time Topology in the Unit Interval

Let us start by constructing a random Cantor set from the unit interval [7-10]. Proceeding in the usual way well known from the theory of fractals for the classical triadic Cantor set but adding uniform randomness to the construction procedure. That way we end up with a zero measure “thin” Cantor set of a topological dimension D_T = 0 and a Hausdorff dimension very close to the classical deterministic set, namely 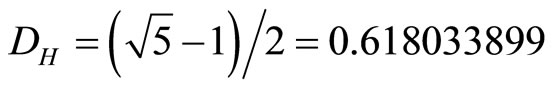[7-10]. Notice now that the gaps left from the iterative deletion of parts of the unit interval forms a second Cantor set. By contrast to the first “thin” Cantor set this one is a “fat” Cantor set with a positive measure equal to the length of the original unit interval because L = 1 – 0 = 1. 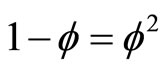However, in this case this Hausdorff dimension is not but obviously because for the original unit interval both the topological dimension and the Hausdorff dimension coincide and are equal to unity so that 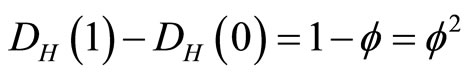as should be [7-10]. Noticing on the other hand that the thick Cantor set is made of totally empty gaps, it is clear that it is the epitome of the empty set which due to deductive dimensional and consistency reasons is assigned a topological dimension equal minus one, i.e. D_T (empty) = −1 [22]. All the preceding result follows smoothly from Grothendieck Ktheoretical (i.e. the general theory of classes) conception of Penrose’s fractal tiling universe [11-25] and Connesvon Neumann dimensional function [11-14] as well as E-infinity Cantorian space-time bijection formula developed by the present author [5,16]. We showed previously how quantum physics could be formulated using a quantum set theory based on the preceding thin and thick Cantor sets. These particles and waves arise naturally from a KAM-like fractal-Cantorian space-time which is the ultimate source of matter and fields [18,22,61]. In this picture the origin of the quantum particle-like state is modelled by the zero set while the quantum wave-like state is modelled by the empty set [10,14] as will be made more precise in the next subsections.

2.2. The Zero Set Quantum Particle and the Empty Set Quantum Wave from a Generic Non-Commutative Space and the Speed of Light as an Expectation Value

As hinted at in the previous section Penrose fractal tiling universe [5,11,24] is the prototype par excellence of a noncommutative geometry reflecting the essence of Ktheory as well as E-infinity theory and its bijection formula which gives the Hausdorff dimension as a function of the zero set topological dimension and the topological dimension n [5,11]. The corresponding dimension function is given by A. Connes in [11] as

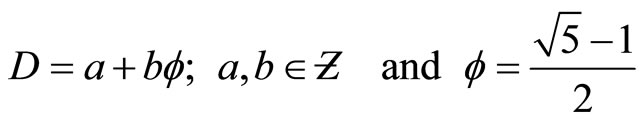(1)

For a = 0 and b = 1 one finds the bi-dimensions of the zero set, i.e.

(2)

where

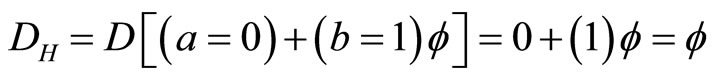. (3)

Similarly for the unit set we find [11-27]

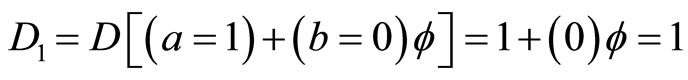. (4)

Subsequent dimensions are found using the Fibonacci prescription. For instance D₂ is found as

(5)

and so on. For the empty set D₋₁ the same procedure holds true but we need to mind the correct negative sign. That way one finds the Hausdorff dimension of the empty set to be [11-27]

. (6)

The bijection formula on the other hand leads to the same result as mentioned at the beginning of this section however in a far simpler way because of the far more compact and economical notation. Thus from the bijection [5, 11,2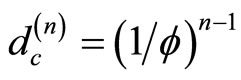7]

(7)

we find the zero set by simply setting n = 0

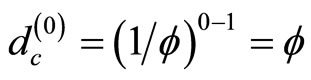(8)

while the empty set is found by setting n = −1

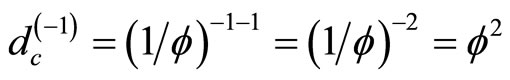(9)

Finally we mention on passing that the same result may be found using the gap labelling DIS method [12]. It is also obvious from the above that the empty set is the cobordism i.e. the surface of the zero set. In addition both the union and the intersection of the inverse dimensions of the zero and the empty set give rise to Hilbert-He’s 4D fractal cube which is the core of our E-infinity space [5, 17]. That means [16]

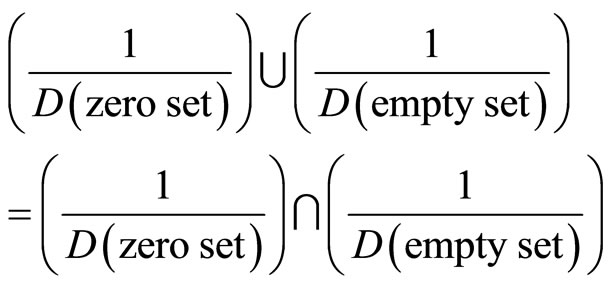. (10)

Thus

(11)

which is probably the most recognizable formula of E-infinity theory [5]. Another immensely important result of the von Neumann-Connes K-formula [11,18] and E-infinity bijection is that for we have 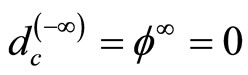[55]. That means we have an infinity of empty sets with an increasing degree of emptiness. This has physical consequences regarding the speed of light. For the speed of light must be infinite. Consequently the observed constancy of the speed of light is nothing but the average speed of light in a fractal spacetime harbouring infinitely many empty sets [57]. Some experimental evidence for the reality of Cantorian spacetime is discussed by E. Goldfain in [62,67].

2.3. The Topological Invariants of E-Infinity Space and Suslin Operation

Consider a space given by an infinite number of unions and intersections of elementary Cantor sets resembling a Suslin operation [29] of the form

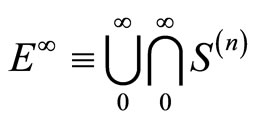(12)

so that

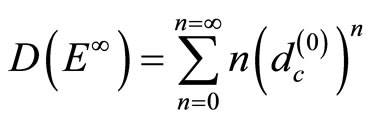(13)

where and 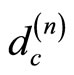is the Hausdorff of the Cantor sets S⁽ⁿ⁾. Since, the infinite series can be summed and one finds the topological dimension to be determined by the expectation value or a center of gravity given by [5,15-24]

. (14)

Noting that the average Hausdorff dimension is [5, 15-24]

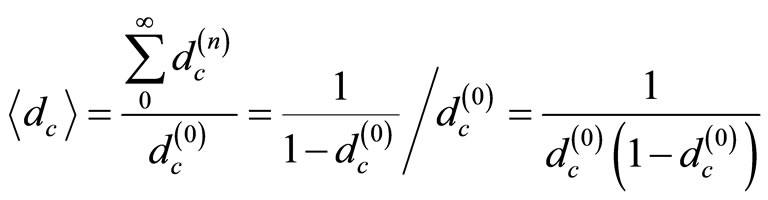(15)

then by requiring space filling we see that we must have 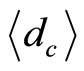equal 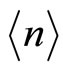and one finds the following condition [5,15-24]

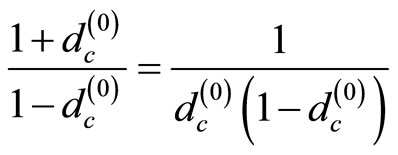. (16)

This leads to a quadratic equation in with two solutions of which the only positive one is.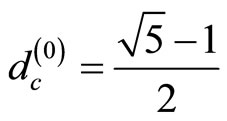

Inserting in one finds that [5]

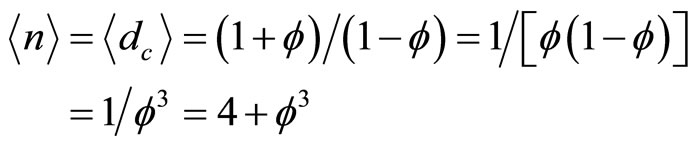. (17)

In other words our E-infinity space is essentially the same space which we gained by considering the two Cantor sets constructed from the unit interval discussed earlier on [27]. We mention here without derivation that detailed analysis of E-infinity established a remarkable result, namely the equality of the curvature of the E-infinity manifold and its Euler characteristic which amounts to 26 + k = 26.18033989 [55].

2.4. The Space E-Infinity (E^∞) as a Probability Space and Quantum Entanglement—The Immirzi Parameter and Unruh Temperature

Let us derive a general expression for the probability that two different points in co-exist at the same location, i.e. being geometrically entangled. To do this we consider the probability of finding a single Cantor point in an isolated elementary Cantor set. The probability for that is obviously 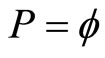and for n points this is therefore given by the multiplication theorem to be [3,16,27]

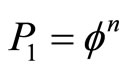. (18)

On the other hand the global probability and sometimes the contrafactual probability effect of finding a Cantor point in E-infinity is clearly the inverse of 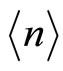namely [3,16,27]

(19)

Consequently to find n points in a Cantor set in E-infinity is the multiplication of the local probability 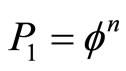with the global “contrafactual” probability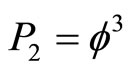. This means the total probability is given by [3, 17-19]

. (20)

Now we can distinguish various cases of P with definite physical meaning corresponding to different numbers of particles n. The first is for n = 2 which means the quantum entanglement of Hardy

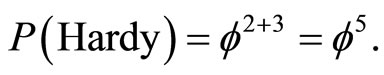(21)

This result was verified experimentally to a very high accuracy in various recognized laboratories [3,30-33]. The second value is for n = 3 which gives us the famous Immirzi parameter of loop quantum gravity [28,70]

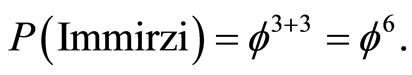(22)

The third result is that of the celebrated Unruh temperature for which we must set n = 1 and consequently [30,34]

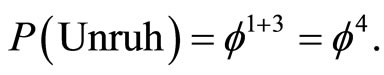(23)

In addition for 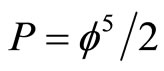one finds the measurable ordinary energy density of the cosmos, i.e. the energy of the quantum particle [2,34,35]

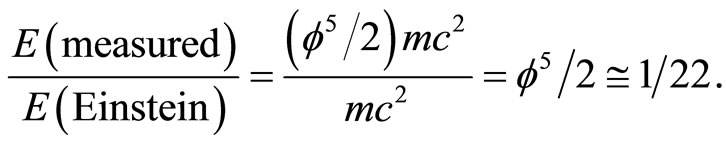(24)

Finally the microwave background radiation of the cosmos is found for n = 0 to be related to geometrical self entanglement [36-38,67]

(25)

as discussed in more detail elsewhere [40-51]. Now we are actually in a position to answer Nobel Laureate G. ‘tHooft’s deep question “What are the building blocks of Nature?” The building blocks of nature and the building blocks of spacetime are the elementary random Cantor sets [64].

2.5. The Dark Energy of Quantu Kaluza-Klein Space-Time

By raising the zero set modelling the quantum particle characterized by the bi-dimension to literally the quintessence, i.e. the 5 dimensional Kaluza-Klein core of E-infinity, one easily arrives at an expression of energy density of the universe in complete agreement with cosmic measurement of COBE, WAMP and supernova burst analysis [34,35]. To show that we calculate the pseudo Hausdorff volume of D_o which is a straight forward naive generalization of classical volume to [26, 27]

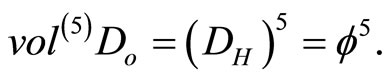(26)

Using Newton’s kinetic energy as a template or simplistically speaking as a “Newtonian” rather than Hamiltonian operator one finds [26,27,61]

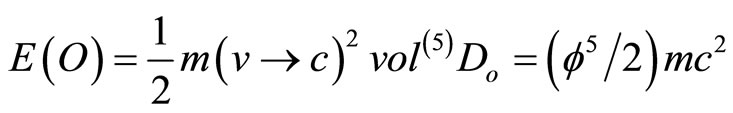(27)

where m is the mass and c is the speed of light. Several vital points should be stressed at this stage. First while it is useful to distinguish sometime between mass, rest mass and relativistic mass the previous formula stresses that physical real mass does not change and that such concepts are only mathematical. The only “rest” quantity is the rest energy namely E(O) itself. Second the speed of light c is quantitatively the same one we always used however its meaning here is different. The speed of light in E-infinity is variable and c is an expectation i.e. average value [10] as much as 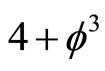is the expectation for the formal topological dimension 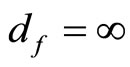of E-infinity [5]. In this sense E(O) represents a potential energy of the momentarily at resting measured quantum particle and we are entitled to ask now where is the kinetic energy? The answer of this question is as simple as it is surprisingly because it is the energy of the EinsteinBohm “ghost” quantum wave responsible for the propagation of the quantum particle [30,61]. To find the magnitude of this energy we calculate again a corresponding volume which turned out to be the dual value for namely an additive volume of the empty set in D = 5 [27,61]

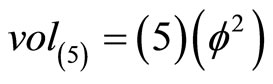(28)

where is the Hausdorff component of the empty set bi-dimension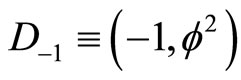. The kinetic energy of the quantum wave in D = 5 is thus [27,61]

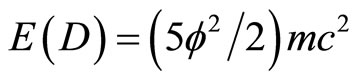. (29)

The incredible fact which we should have noticed long ago but we did not is not only that E(D) is the missing energy density of the cosmos (95% of the total) but that E(O) + E(D) = mc² which is the classical expression found by Einstein using not solely mathematical deduction but also a quantum “leap” of “faith”. In other words Einstein included quantum mechanical features in his famous formula although at the time of E = mc² quantum mechanics was not yet invented and that later on when quantum mechanics was around Einstein did not believe in it because of the spooky action at a distance of quantum entanglement. Ironically the energy expression E(O) consists of two parts, namely mc² multiplied with 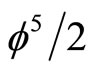where is the Hardy probability of quantum entanglement of two quantum particles so that 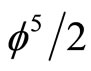accounts for the effect of quantum entanglement of the one particle energy expression. There is an even simpler interpretation of E(O) and consequently E(D) = 1 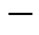E(O) when involving the mathematics and physics of NambuVeneziano’s old bosonic string theory of strong interaction. According to this theory the space-time dimensions needed are not 4 but 26. Consequently if we understand E = mc² as a theory for D = 4 then according to the D = 26 theory we have ignored the effect of the 26 4 = 22 “compactified” dimensions of space-time [27,57]. Since E is an eigenvalue, then by Rayleigh theorem we should reduce by division E = mc² which means Weyl-Nottale scale [14] it using a scaling exponent so that we find

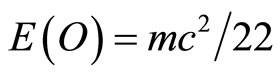. (30)

Noting that the exact value is

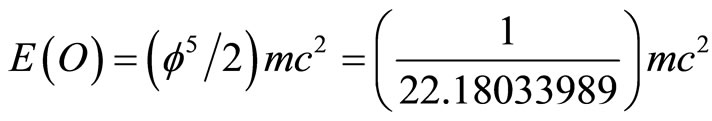(31)

We see that 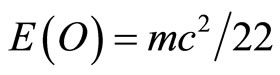is an excellent integer approximation [27,28,34,35]. Similarly the dark energy density of the quantum wave

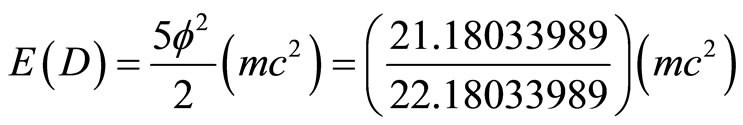(32)

could be approximated to [27]

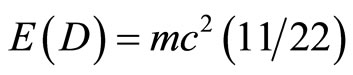. (33)

The preceding two results are probably the most important achievements of many research efforts of many scientists [1-51] rather than a single person and could be truly said to stand on the shoulders of giants [53]. From this privileged position we can now answer a second deep question by G. Ord [63], namely “What is the wave function?” From the above it is clear that it is the empty set or the surface of the zero set quantum particle. In addition the wave function is the source of dark energy [61, 63]. In other words the surface of the zero set quantum particle is the source of dark energy.

2.6. Accelerated Cosmic Expansion, Anticlastic Curvature and Hawking’s Negative Vacuum Energy Fluctuation

To make a long story short, the surprising discovery of the accelerating rather than decelerating expansion of the universe is argued here to be due to the well known geometrical effect of anticlastic, i.e. negative curvature of the spacetime manifolds of the cosmos. In turns this anticlastic curvature accumulates at the edge of the world to a maximum as can be seen from the analogy with a long elastic thin walled cylinder squeezed at the middle as shown in Figure 14 of Ref [2]. The situation is thus analogous to that of the negative energy of vacuum fluctuation found by S. Hawking to exist at the horizon of a black hole. In other words when we look at the two dimensional projection of a ramified i.e. compactified Klein modular curve or a fractal Penrose universe [65], then at the edges being in the hyperbolic plane at infinity surrounded by a Cantorian circle we have anticlastic curvature, i.e. negative curvature producing negative dark energy causing negative gravity pushing the universe apart rather than pulling it together. The preceding geometrical picture could be translated to a topological picture by reasoning that in simplistic terms, while the visible 4 dimensions of our space produce positive curvature and ordinary gravity, the 26 − 4 = 22 compactified bosonic string dimensions are responsible for dark energy, i.e. negative curvature and consequently negative gravity which is the force behind the measured increased acceleration of cosmic expansion at the edge of the holographic Klein-Penrose universe [65]. The situation can be explained quantitatively by taking the ratio between Heterotic string theory 504 states and the 528 states of maximally symmetric spaces such as Witten’s M-theory [2-4,10,27,28].

2.7. Scaling the Planck Scale—The Connection between Wormholes (Einstein-Rosen Bridges) and Quantum Entanglement (Einstein-Podolsky-Rosen Spooky Action at a Distance)

The Planck energy 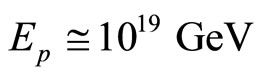and not dissimilarly the Planck length 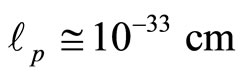are quite esoteric scales difficult to visualize and totally outside present or near future experimental capacities if at all [30]. Never the less by going back to our initial unit interval universe and noting the unexpected result arising from Hardy’s entanglement 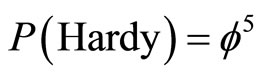and related conclusions regarding Sigalotti’s critical “topological” velocity of light c = f and the isomorphic length of a super symmetric compactified hyperbolic Penrose universe [65] with a Hawking black hole circular horizon given by [10,61]:

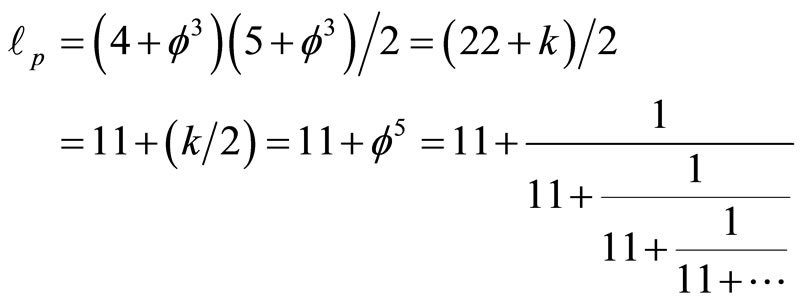(34)

we realize the following vital topological facts which amount to a realization of D. Gross’ idea of scaling the Planck scale [10]:

a) The topological Planck energy is nothing but Hardy’s quantum entanglement

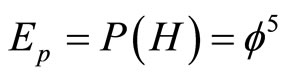. (35)

b) The topological expectation value of the speed of light is

. (36)

c) The topological Planck length is equal to the dimension of a fractal M-theory

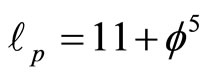(37)

since 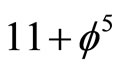is equal to 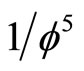where is the E_p we see that E-infinity space is infinitely multi-connected and that all these fractal gaps and voids in their space are essentially wormholes with length equal to which constitutes Einstein-Rosen bridges [30]. It is ironic as well as surreal to see that the ultimate resolution of the Einstein-Podolsky-Rosen spooky action at a distance existed always in the Einstein-Rosen bridges and consequently in quantum entanglement which Einstein as well as Schrödinger rejected so vehemently [5].

3. Conclusion

At the beginning there was topology, or was it the golden mean number system in which the topological properties of elementary Cantor sets are expressed so that we can do calculations with them and draw general conclusions [4,17,45]? The authors hope that the present work makes it clear that we can deal with infinity without processing an infinite number of information [17,54,56]. In fact written in decimal expansion 0.618033989… is infinite.

However written as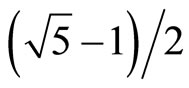, we can easily work out that 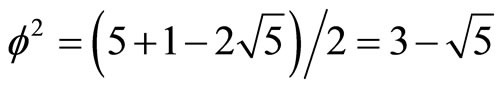and that [45]. In any event we showed here beyond any reasonable doubt that E = mc² consists of two parts, E(O) = mc²/22 which is the position or potential energy of a quantum particle or equivalently a five dimensional “quintic” zero set at rest and 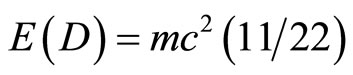which is the absolute value of the negative kinetic energy of the quantum wave or equivalently the moving “quintic” empty set [2,61]. Together E(O) + E(D) = mc² give Einstein’s iconic formula for the maximal total energy of a classical particle [4,26,61]. It is important to note the E(O) density is only 4.5% of the total expected energy density of the universe in agreement with the most recent sophisticated accurate cosmological measurements [34, 35,61]. On the other hand present measurement technologies do not permit measurement of E(D) which constitutes 95.5% of the total expected energy because of the well documented but ill understood quantum wave collapse at measurement [10,20,33]. For this reason E(D) is dubbed dark energy and baring new developments in wave collapse free non-demolition measurement instruments [2,4,10,20], dark it will remain [30,34,35]. Negative dark energy is linked here to the anticlastic curvature at the edge of the universe and is therefore a cousin of Hawking’s negative energy fluctuation of the vacuum at the horizon of a black hole which constitutes a circular edge of the hyperbolic compactified edge lying at infinity of a Klein-Penrose holographic universe [2,61,65]. It is negative gravity force which is responsible for the unexpected measured and accelerated expansion of the cosmos [10,34,35]. Technically speaking we could not have obtained accurate quantitative results for the preceding effect if it would not have been for L. Hardy’s magnificent quantum entanglement exact solutions for two particles [31-33] as well as the work of Sigalotti [10] leading to the topological speed of light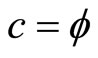. In addition, the general theory of noncommutative space of A. Connes and the realization that Penrose universe is a K-theoretical explicit realization of a generic noncommutative space which played a pivotal role in reaching our conclusion. Finally the inspiring idea of D. Gross to scale the Planck scale [1] gave an overall intuitive justification for and 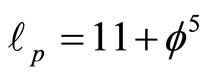to realize that E-infinity fractal geometry is the geometry of quantum entanglement linking EinsteinRosen bridges with quantum entanglement, zero measure geometry and Magueijo-Smolin theory of varying speed of light [44]. The entire analysis and result obtained has testified once more to Einstein’s dictum “Raffiniert is der Herr Gott aber boshaft ist er nicht”. Einstein added later that “Die Natur verbirgt ihr Geheimnis durch die Erhabenheit ihres wesen, aber nicht durch List” [52]. In fact nature is simple to a degree that at least initially defies human expectation, in order not to say human comprehension. However, as H.R.H. the Prince of Wales, T. Juniper and I. Shelly emphasized in their book [53], harmony is the way to comprehension and nothing could be more harmonious than a golden ratio based number system which we used in E-infinity theory [2,17,53]. In E-infinity the most irrational number 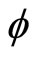with infinite decimal expansion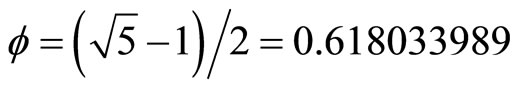... is taken as basic and integers as constructed from 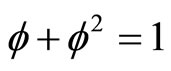and so on. Similarly rationed as given by 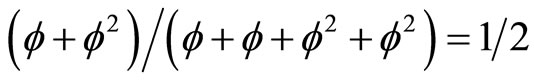. That way we tame infinity and extend what D. Hilbert called Cantor’s paradise to physics [17,54]. The authors firmly believe in the preceding concept of the role of infinity in physics and the work of Hugh Wooden.

REFERENCES