Journal of Modern Physics
Vol.3 No.4(2012), Article ID:18904,5 pages DOI:10.4236/jmp.2012.34046
On the Relativistic Stars
1Instituto de Física Rosario (CONICET-UNR) Bv. de Febrero 210 bis, Rosario, Argentina
2Observatorio Astronómico, Planetario y Museo Experimental de Ciencias Municipal de Rosario, Parque Urquiza, Rosario, Argentina
3Facultad de Ciencias Exactas, Ingeniería y Agrimensura (UNR) Av. Pellegrini 250, Rosario, Argentina
Email: aquilano@ifir-conicet.gov.ar
Received January 13, 2012; revised March 1, 2012; accepted March 19, 2012
Keywords: Compact Stars; Oscillations; General Relativity; Strange Matter
ABSTRACT
At the present knowledge, neutron and strange pulsar models agree reasonably well with pulsar observations, mainly because the comparison of theory and observation is not accurate enough to discriminate between neutron and strange stars. In this paper we analyze the neutron stars and the strange matter stars with the formalism of general relativity, in order to study radial oscillations. The nature and correlation with observational data are analyzed.
1. Introduction
The X-ray bursters are binaries stars with a neutron star and a normal companion star of mass approximately to a solar mass. Due to their weak magnetic fields and high accretion rates, the neutron star equilibrium spin periods are expected to be of order of milliseconds. Detection of coherent millisecond X-ray pulsations would constitute a strong evidence for the evolution of millisecond radio pulsars [1-3]. It would support the currently favored beat frequency model of horizontal-branch QPO formation [4, 5], in which quasi-periodic oscillations occur at different frequencies between the neutron star rotation frequency and the Kepler frequency of the accreting matter, as it falls onto the neutron star. It would provide a precise means to measure orbital periods and masses and to study accretion torques and neutron star dynamics on very short time scales.
Instead of ordinary matter, the possibility that strange matter was the true ground state of strong interactions has attracted considerable attention [6]. Thus, normal matter would then be in a metastable state and would decay to strange matter yielding a finite amount of energy. Besides the possibility of its detection in experiments, strange matter may occur in certain astrophysical objects like neutron stars and supernovae cores.
In this work a simple model of non-rotating stars is studied and modelled by a spherically symmetric distribution, to neutron and strange matter stars.
2. Equations of Stellar Equilibrium and Its Perturbation
The hydrostatic equilibrium equation for relativistic stars in the Tolmann-Oppenheimer-Volkoff equation is
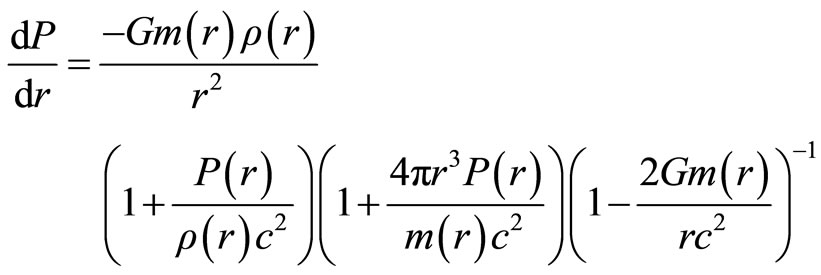 (2.1)
(2.1)
where m(r) is the mass enclosed in a sphere with radius r and local density G is the gravitational constant and P(r) the pressure with radious r, and this equation in the Newtonian limit is as follows
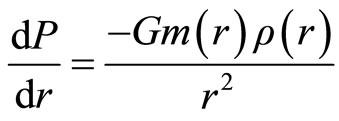 (2.2)
(2.2)
and
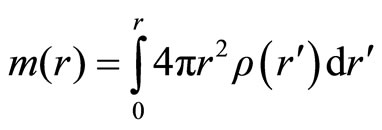 (2.3)
(2.3)
The differential form of this equation is
 (2.4)
(2.4)
with constant density 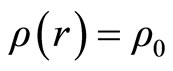
 (2.5)
(2.5)
if 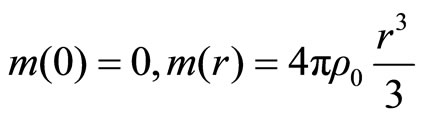
also, the total mass of star is
 (2.6)
(2.6)
The Equation (2.5) in function of the total mass will be
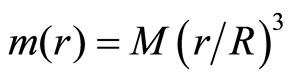 (2.7)
(2.7)
Then, with (2.7) in (2.2), we have  and putting (2.5) in (2.2) we have
and putting (2.5) in (2.2) we have 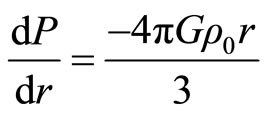
where, with radial integrating, we obtain

But,  , and
, and 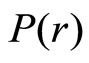 in the equilibrium is
in the equilibrium is
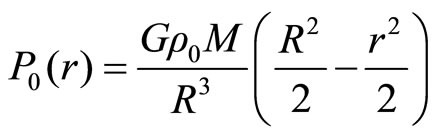 (2.8)
(2.8)
or in function of other constant
 (2.9)
(2.9)
We define the new constant 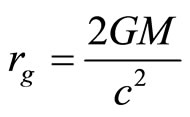 also, we can write the Equation (2.8) in this form
also, we can write the Equation (2.8) in this form
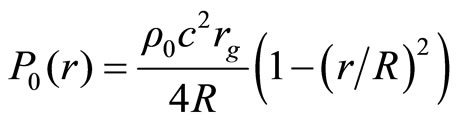 (2.10)
(2.10)
Considering small perturbations around the equilibrium, we will obtain the frequency. For a non relativistic fluid, no viscous and without dissipative effects, the moment equation is
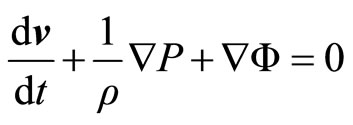 (2.11)
(2.11)
where P is the pressure, 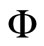 is the gravitational potential and v is the velocity of fluid. The oscillation dynamic will be governed for the Lagrangian perturbations of this equation
is the gravitational potential and v is the velocity of fluid. The oscillation dynamic will be governed for the Lagrangian perturbations of this equation
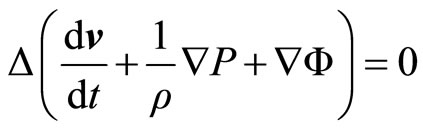
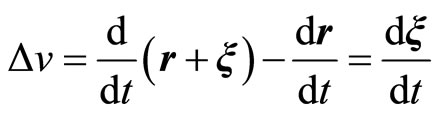
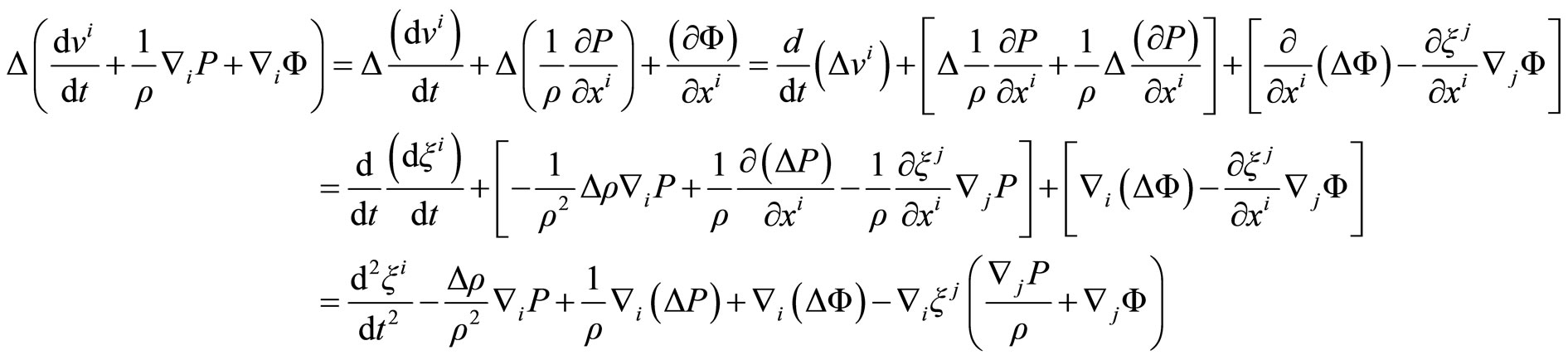
If in the moment Equation (2.11), we consider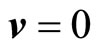 , we obtain the hydrostatic equilibrium equation
, we obtain the hydrostatic equilibrium equation
 (2.12)
(2.12)
The non perturbative configuration is static, thus we write
 (2.13)
(2.13)
And we have
1) 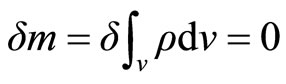
By the application of the perturbative properties, we can write the integrals in this form
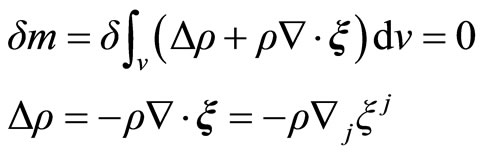 (2.14)
(2.14)
2) For the state equation 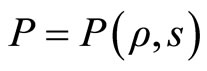 (
( : density, s: entropy)
: density, s: entropy)
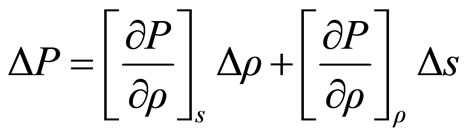
For adiabatic perturbations 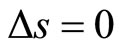
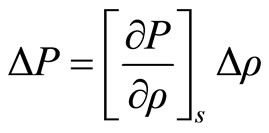 (2.15)
(2.15)
 where
where 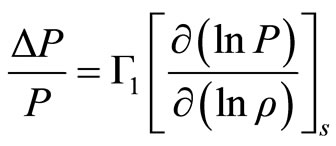 is the adiabatic index that governs the perturbations (2.16).
is the adiabatic index that governs the perturbations (2.16).
With the Equations (2.14) and (2.15), and replacing in the Equation (2.13), and for the adiabatic equation we will utilize 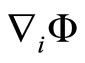 for
for 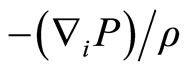 and we obtain this
and we obtain this
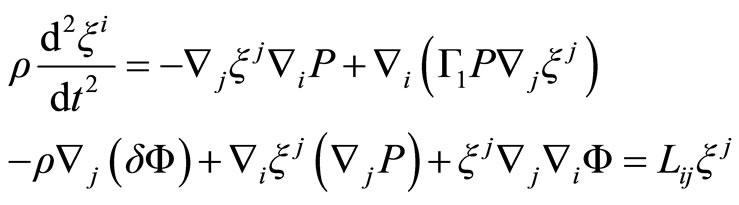 (2.17)
(2.17)
Here, the quantities are expressed in terms of 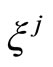 and non perturbative variables. The perturbation in the gravitational potential is deduced of the Poissón equations,
and non perturbative variables. The perturbation in the gravitational potential is deduced of the Poissón equations,

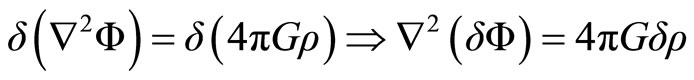 (2.18)
(2.18)
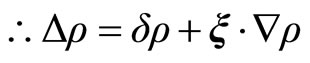 (2.19)
(2.19)
or
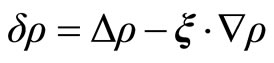
For the Equations (2.14) and (2.19)
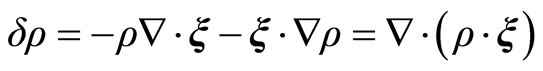 (2.20)
(2.20)
The Equation (2.18) has this solution
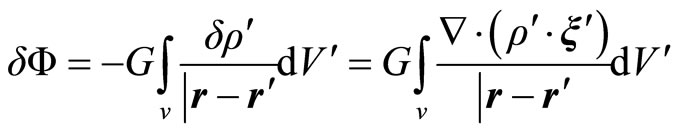
To radial perturbations of the spherical star
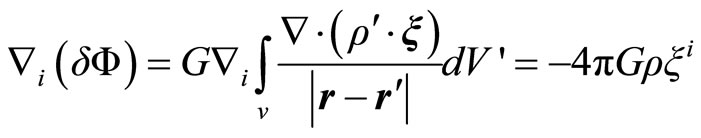 (2.21)
(2.21)
Replacing the Equation (2.21) in (2.17)
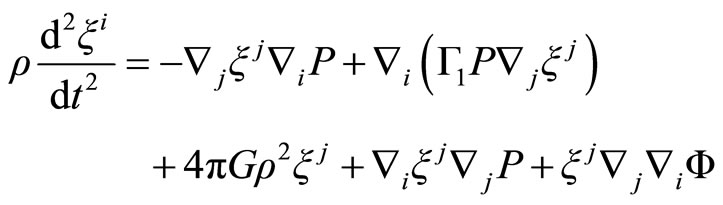 (2.22)
(2.22)
and considering radial oscillations of this form
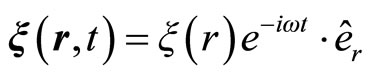 (2.23)
(2.23)
the Equation (2.22) is reduced to
 (2.24)
(2.24)
United with appropriate outline conditions it is a lineal self-value problem. The outline conditions are
•
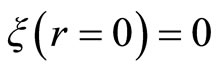 (2.25)
(2.25)
•
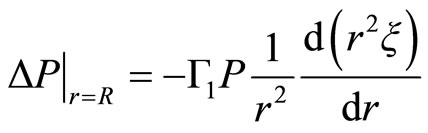 (2.26)
(2.26)
As  we say that
we say that  is finite in
is finite in .
.
The Equation (2.25) is obvious because of its spherical symmetry. The Equation (2.26) informs us that an element of fluid in the non perturbative surface is moving toward the perturbative surface. In the equilibrium configuration (Equation (2.9)) this equation is valid

To make simpler the calculus, it has been defined a constant “a” ((7)), then  and we can write the Equation (2.24) in this form
and we can write the Equation (2.24) in this form
In order to simplify, we will omit the sub-index 0 (equilibrium values) (7) and propose a potential with solution in series

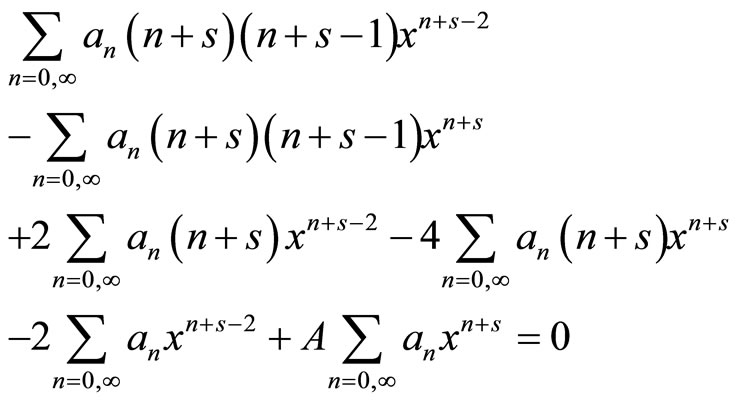
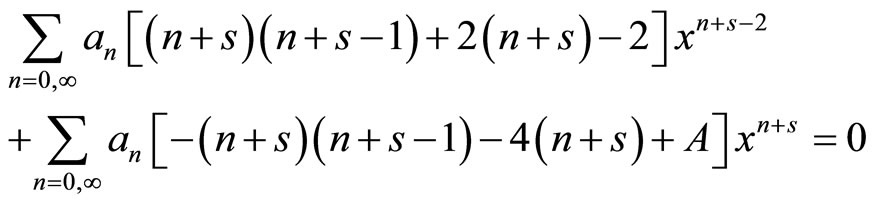
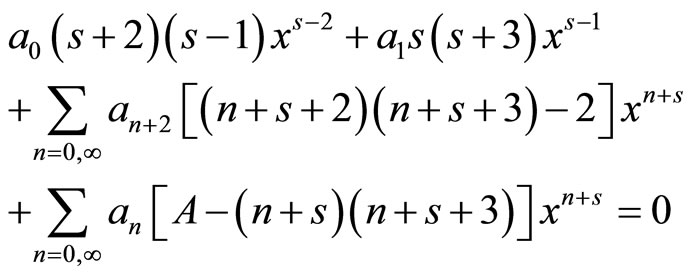
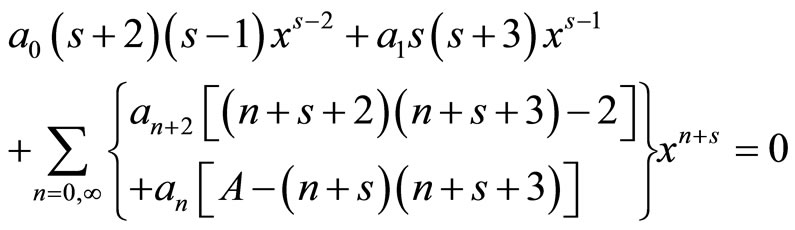 (2.27)
(2.27)
The coefficient of 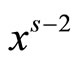 is the initial equation
is the initial equation 
Also,  or
or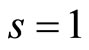 . We choose
. We choose 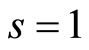 to carry out the outline condition (2.25), the Equation (2.27) results
to carry out the outline condition (2.25), the Equation (2.27) results
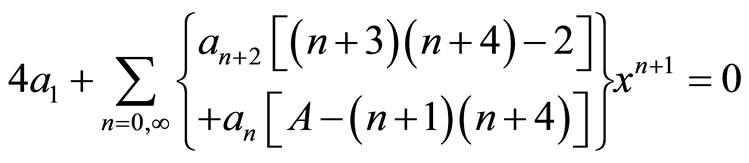
with 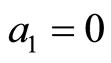

We obtain that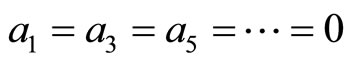 , then
, then

 constant
constant
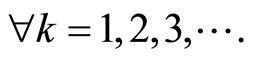
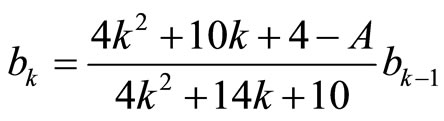
These series diverge, and 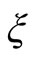 can not satisfy the outline condition (2.26), safe that the series finish. For this
can not satisfy the outline condition (2.26), safe that the series finish. For this
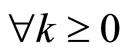

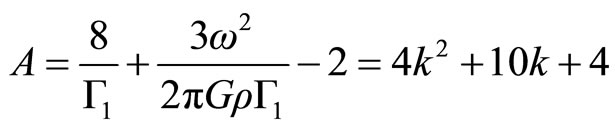
Then
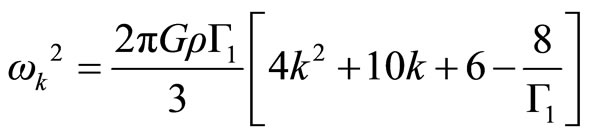
The solution in the minor mode with k = 0 is
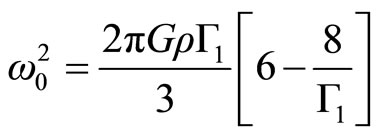 (2.28)
(2.28)
• Si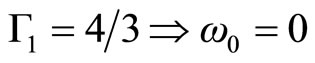 .
.
• Si 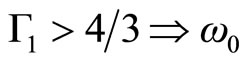 is real.
is real.
• Si 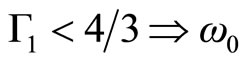 is imaginary and the star is unstable.
is imaginary and the star is unstable.
These conclusions are equivalent to the Chandrasekhar limit, which should be correct only for stars with  (e.g. normal neutron stars and white dwarfs), but not for stars with non-zero surface density.
(e.g. normal neutron stars and white dwarfs), but not for stars with non-zero surface density.
3. Strange Stars and Their Oscillations
A method to solve the self-valued Equation (2.24) for strange matter stars is the variational principle

where 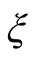 satisfies the outline conditions in (2.25) and (2.26). The absolute minimum of this expression is the square of the angular frequency of fundamental mode pulsation. In the Newtonian limit an approximate expression is
satisfies the outline conditions in (2.25) and (2.26). The absolute minimum of this expression is the square of the angular frequency of fundamental mode pulsation. In the Newtonian limit an approximate expression is
 (3.1)
(3.1)
where 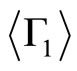 is the adiabatic index to average according to the pressure
is the adiabatic index to average according to the pressure
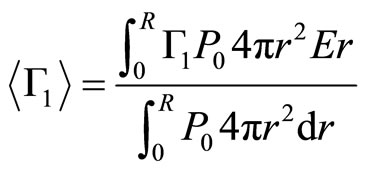 (3.2)
(3.2)
Then, the Equation (3.1) will be
 (3.3)
(3.3)
where 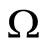 is the self-gravity energy of the star,
is the self-gravity energy of the star,
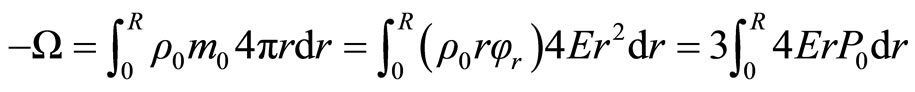
and
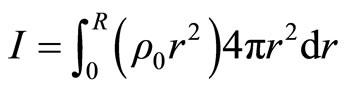
Then, the equation of state to strange matter is
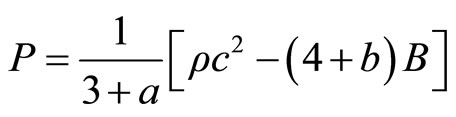 (3.4)
(3.4)
where B = 60 MeV/fm3
If  and
and :
: 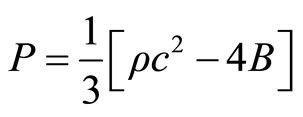
If the density is constant, with the outline conditions 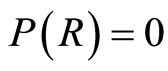 only for quark stars not very massive, but not suitable for normal neutron stars,
only for quark stars not very massive, but not suitable for normal neutron stars,
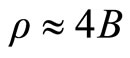 (3.5)
(3.5)
with the Equations (3.4) and (3.5) the expressions ,
, and
and  are
are
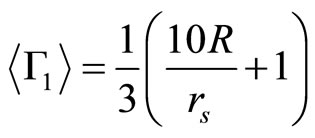 (3.6)
(3.6)
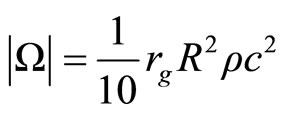 (3.7)
(3.7)
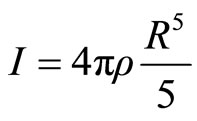 (3.8)
(3.8)
Replacing these results in the Equation (3.1), we obtain the expression to angular frequency of fundamental mode as
 (3.9)
(3.9)
4. Conclusions
In this work we used a strange matter star not very massive with a general relativistic formalism in order to

Figure 1. It is showed the relation between the period (in seconds units) and the radius (in kilometers units) to different values of neutron stars. It can be seen that the values obtained are very close to the data obtained from observations.

Figure 2. It is showed the relation between the period (in seconds units) and the mass (in solar mass units) to different values of neutron stars. It can be seen that the values obtained are very close to the data obtained from observations.
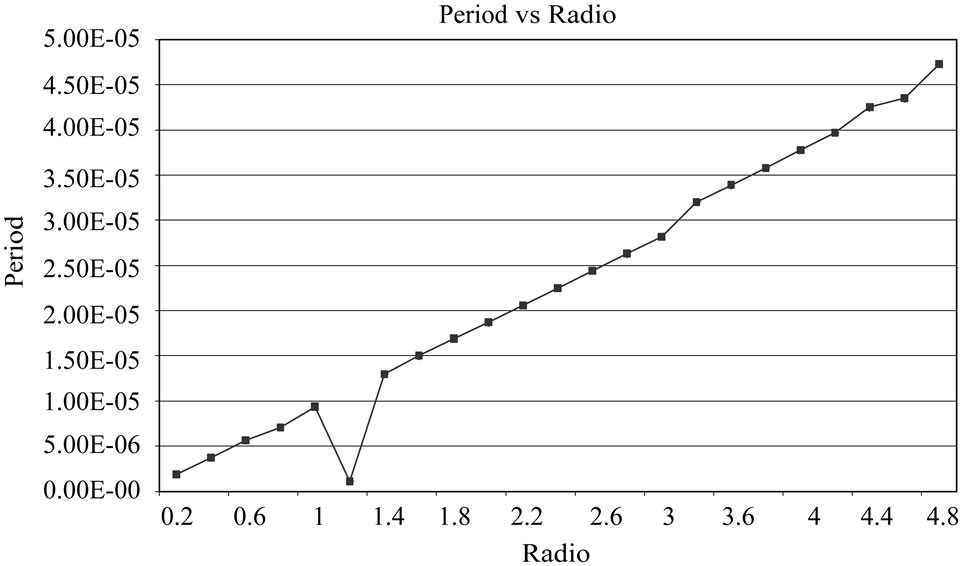
Figure 3. It is showed the relation between the period (in seconds units) and the radius (in kilometers units) to different values of strange stars. The values obtained are slightly different from those calculated for neutron stars.

Figure 4. It is showed the relation between the period (in seconds units) and the mass (in solar mass units) to different values of strange stars. The values obtained are slightly different from those calculated for neutron stars.
study radial oscillations and to compare with normal neutron stars. In this case, we use different values to 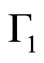 and confirm the previous results obtained [7], where the strange matter adjust better that neutron stars in short periods. In more realistic stellar models (i.e. in case of the density not to be constant), we are not sure if the oscillation behaviors of neutron and quark stars could still be distinguishable, but our contribution is a new element to be considered. In Figures 1-4 we can see the comparative values in several cases.
and confirm the previous results obtained [7], where the strange matter adjust better that neutron stars in short periods. In more realistic stellar models (i.e. in case of the density not to be constant), we are not sure if the oscillation behaviors of neutron and quark stars could still be distinguishable, but our contribution is a new element to be considered. In Figures 1-4 we can see the comparative values in several cases.
REFERENCES
- M. D. Valle, G. Chincarini, N. Panaglia, G. Tagliaferri, D. Malesani, V. Testa, D. Fugazza, S. Capana, S. Covino, V. Mangano, L. A. Antonelli, P. D. Avanzo, K. Hurley, I. F. Mirabel, L. J. Pellizza, S. Piranomonte and L. Stella, “An Enigmatic Long-Lasting γ-Ray Burst Not Accompanied by a Bright Supernova,” Nature, Vol. 444, No. 7122, 2006, pp. 1050-1052. doi:10.1038/nature05374
- P. Ghosh and F. K. Lamb, “Acreetion by Rotating Magnetic Neutron Stars,” Astrophysical Journal, Vol. 234, 1979, pp. 259-276. doi:10.1086/157285
- A. Ray and B. Datta, “Rotating Neutron Star Structure. Implications of Milliseconds Pulsar PSR193772142,” Astrophysical Journal, Vol. 282, 1984, pp. 542-549.
- M. A. Alpar and J. Shaham, “Is GX5-1 a Millisecond Pulsar?” Nature, Vol. 316, 1985, pp. 239-241. doi:10.1038/316239a0
- O. Benvenuto, J. Horvath and H. Vucetich, “Nucleation of Strange Matter in Dense Stellar Cores,” Physics Review D, Vol. 45, No. 10, 1992, pp. 3865-3868.
- E. Witten, “Cosmic Separation of Phases,” Physics Review D, Vol. 30, No. 2, 1984, pp. 272-285.
- E. Losada and R. Aquilano, “Oscillations of Short Periods in Neutron and Strange Stars,” General Relativity and Gravitation, Vol. 35, No. 8, 2003, pp. 1385-1398. doi:10.1023/A:1024578417187

