Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5826 , 6 pages DOI:10.4236/jmp.2011.27078
The Use of the Special Theory of Relativity for the Meissner Effect in a Superconductor
Delft University of Technology, Delft, The Netherlands
E-mail: mirwaisrashid@hotmail.com
Received January 20, 2011; revised March 7, 2011; accepted April 3, 2011
Keywords: Superconductor, Meissner Effect, Special Theory of Relativity, Electromagnetic Waves
ABSTRACT
The electromagnetic waves are considered in this article as the mediators of interaction in the Meissner Effect or the diamagnetic property of the superconductors. During the cooling of a superconductor electromagnetic waves may be released when the electrons occupy lower states of the energy. These electromagnetic waves may combine in circularly, elliptically and spherically rotating ways, being called in this article the rounded electromagnetic fields. The application of the Lorentz transformation of the Special Theory of Relativity to the magnetic vectors of the mediating electromagnetic fields implies the magnetic orthogoniopedic effect inside the bulk of a superconductor in the Meissner Effect.
1. The Electromagnetic Waves as Mediators in the Interaction inside a Superconductor
The existing models which have tried to explain the phenomenon of superconductivity, amongst which belongs the B.C.S. theory [1,2], consider mainly the phonons or the quanta of the elastic vibrations for the interaction of the superconducting particles known as the Cooper pairs. The present article considers a contribution of the electromagnetic waves [3,4] as the interaction mediators in the Meissner Effect [2,3]. For the scientists who are specialized in the theory of electromagnetic waves this may seem evident, since electric and magnetic interactions between charged particles are, according to the standard models of interactions, mediated by electromagnetic fields. However, this electromagnetic wave mediation may not have already been much considered by the scientists of superconductivity in the solid state physics. When the superconductor is cooled below its critical temperature, the orbital electrons may release electromagnetic fields, when the orbital electrons are going to occupy lower states of energy [5]. However, the released electromagnetic fields are confined to the space in and close to the bulk of the superconductor if their magnetic fields are combined, for instance, (in the 3 dimensional Euclidean space) in an arbitrary Cartesian coordinate system 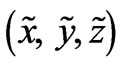 as
as
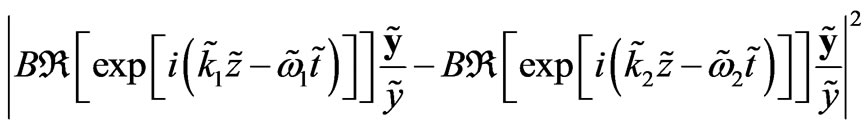 +
+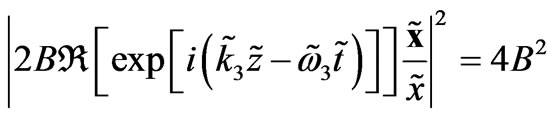
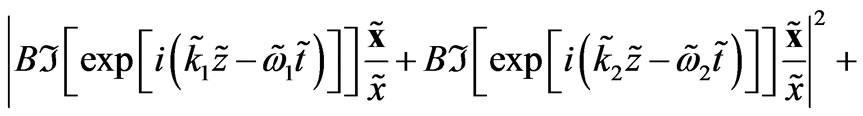 (1)
(1)
with the following conditions
 and
and  (2)
(2)
Analogous to Equation (1) one can write an equation for the electric field in which the roles of the directions x and y are interchanged. Equation (1) is the three dimensional analogous to the two dimensional case where one sees a circle on the screen of the oscilloscope when on the x-axis the signal of “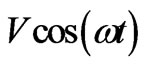 ” and on the y-axis the signal of “
” and on the y-axis the signal of “ ” are brought.
” are brought.
One may recall that the parametric representation of a circle [6] is
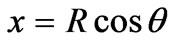 and
and 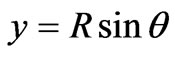 (3)
(3)
which is equivalent to
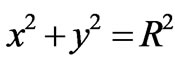 (4)
(4)
And the parametric representation of an ellipse [6] is
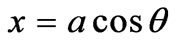 and
and  (5)
(5)
which is equivalent to
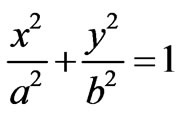 (6)
(6)
And the parametric representation of a sphere [7] is

and 
and 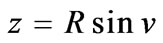 (7)
(7)
which is equivalent to
 (8)
(8)
The result of Equation (1) shows a field, which if it is time-averaged, it obeys an equation analogous to an equation of a sphere. Let us call this combination of the electromagnetic fields in Equation (1) and its analogous counterpart for the electric field the rounded electromagnetic fields. The Equation (1) uses the expressions for harmonic functions of plane waves [4], since according to the Fourier [8] analysis, a wave or a periodic oscillation can be decomposed into harmonic functions. In the case of the combination of the electromagnetic waves described by Equation (1), these combined electromagnetic waves are becoming confined in space instead of propagating.
If 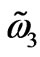 and
and 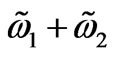 are commensurable, that is if [
are commensurable, that is if [ ] is a rational fraction, still a space contained as a box with the side-lengths as long as the amplitude of the magnetic field 2B is effective and extended will be filled with a Lissajous surface (which is an extension of the notion of Lissajous curve [9] to three dimensions) confining the magnetic field.
] is a rational fraction, still a space contained as a box with the side-lengths as long as the amplitude of the magnetic field 2B is effective and extended will be filled with a Lissajous surface (which is an extension of the notion of Lissajous curve [9] to three dimensions) confining the magnetic field.
Also while a magnet levitates above a superconductor when the magnet is tapped the magnet starts to rotate. This rotary motion of the levitating magnet can be explained by the electromagnetic waves and by the Fourier [8] theorem again which says that every periodic function can be described as a sum of the sine and cosine functions. Let us consider the following Fourier series for the magnetic parts of two electromagnetic waves
 (9)
(9)
 (10)
(10)

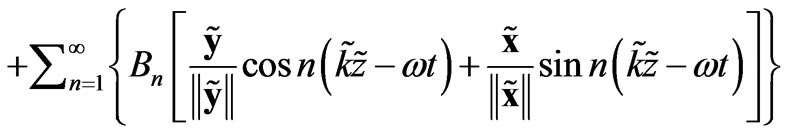 (11)
(11)
The coefficients 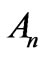 and
and 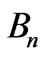 are proportionally related to the radii of the rotary circles. Further the following relations [8] would hold
are proportionally related to the radii of the rotary circles. Further the following relations [8] would hold
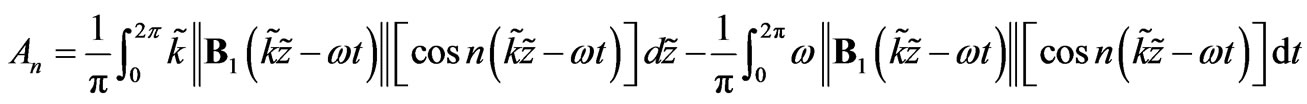 (12)
(12)
 (13)
(13)
 (14)
(14)
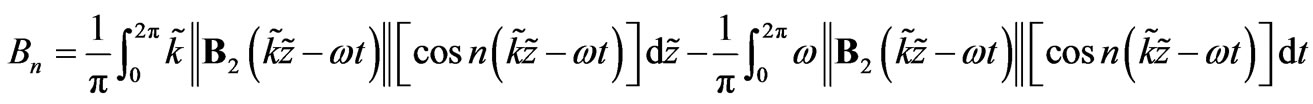 (15)
(15)
If one had two electromagnetic waves the magnetic parts of which are as follows:
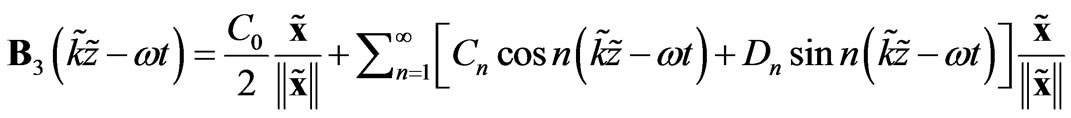 (16)
(16)
 (17)
(17)
then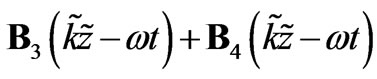 involves a summation of magnetic vectors performing elliptical rotations.
involves a summation of magnetic vectors performing elliptical rotations.
The application of an external magnetic field, let us assume, in the z-direction of a Cartesian coordinate system (x, y, z), in the 3 dimensional Euclidean space, to the superconducting material bulk works as a magnetomotive force on the rounded electromagnetic fields. In the Equation (1) one does not observe in the  direction a vector component of the magnetic field belonging to the released and mediating electromagnetic field.However, letting the direction of
direction a vector component of the magnetic field belonging to the released and mediating electromagnetic field.However, letting the direction of  to be arbitrarily chosen by the combined electromagnetic waves described by Equation (1), but related to the z-direction of an applied external magnetic field, then by a linear transformation, such as Equation (18) (see the bottom of the page.)
to be arbitrarily chosen by the combined electromagnetic waves described by Equation (1), but related to the z-direction of an applied external magnetic field, then by a linear transformation, such as Equation (18) (see the bottom of the page.)
 (18)
(18)
where the angles 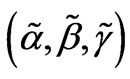 are the Euler angles [8], one may allow a z-component of the magnetic field belonging to the released and mediating electromagnetic field to exist in the Cartesian coordinate system (x, y, z).
are the Euler angles [8], one may allow a z-component of the magnetic field belonging to the released and mediating electromagnetic field to exist in the Cartesian coordinate system (x, y, z).
2. The Use of the Special Theory of Relativity for the Meissner Effect in a Superconductor
For the Meissner effect the existing theory is the proportionality of the electric current density j to the vector potential A of the externally applied magnetic field which leads to the London equation [1,2], however, the direction of the magnetization for a superconductor is not yet specified.
Inside a superconductor on a scale of the elementary particles there are some parts of space not occupied by material particles which can be considered as vacuum, though a bulk of a superconductor is by itself not considered as vacuum. In a bulk of a superconducting material, the rounded electromagnetic fields may have interactions with the spin magnetic dipole moments of charged particles, amongst them the electrons, and the rounded electromagnetic fields may not move with the same speed as in vacuum. Let us consider the following situation:
At time t = 0, an external magnetic field is applied above the superconducting bulk. The direction of this applied external magnetic field is taken here as the direction of the z-axis of the Cartesian coordinate system. The rounded electromagnetic fields are under the exertion of this magnetomotive force. The vectors of the rounded electromagnetic fields comply with the Lorentz transformation of the Special Theory of Relativity [9,10], while they are under the exertion of the magnetomotive force of the external magnetic field, and while the rounded electromagnetic fields are moving with the speed v close to the speed c of light in vacuum, because the restriction of inertia is not applicable to the rounded electromagnetic fields here, since they are massless. Decomposing the vector radii of the rounded electromagnetic fields into three components in the Cartesian coordinate system and taking a general function f(r) for the amplitude of the magnetic vector, instead of restricting ourselves to the Coulomb law of the inverse of the square of the vector radius or the distance, one can write the expressions of the components of the magnetic vector of the rounded electromagnetic fields in their own rest frame or in the moving reference frame (with respect to an observer who is at rest and observes the motion of the rounded electromagnetic fields) in the z-direction with a speed v, using polar and Cartesian coordinates as follows

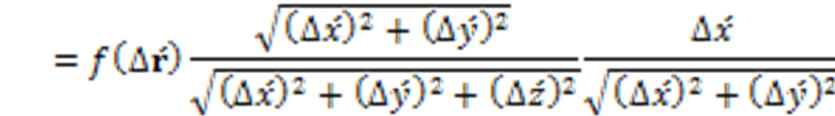
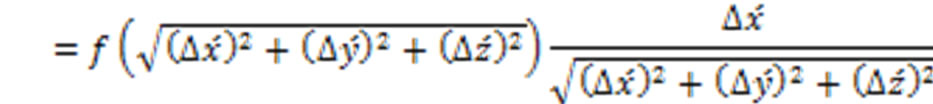 (19)
(19)
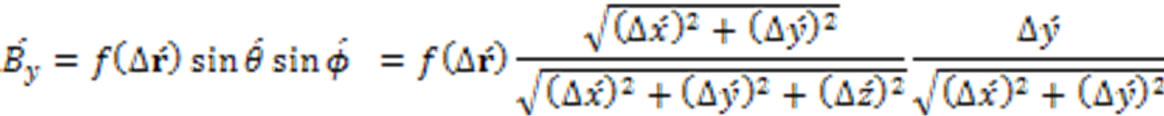
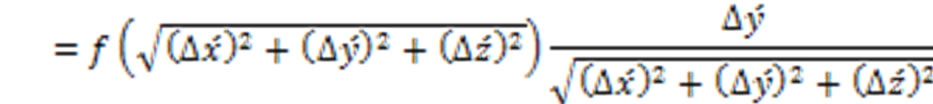 (20)
(20)
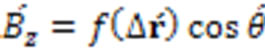
 (21)
(21)
In the Expressions (19)-(21) the “ ” is the difference between the final and the initial Cartesian coordinates
” is the difference between the final and the initial Cartesian coordinates
(the Cartesian coordinates of two points which are denoted by the subscripts f and i which stand for the words final and initial, respectively, are used to indicate a direction of a vector in the three dimensional spatial part of the Minkowski space [10]). For instance
 (22)
(22)
Using the following Lorentz transformation to the observer’s reference frame at rest by considering the direction of motion of the moving reference frame in the z-direction of the Cartesian coordinate system [9,10]

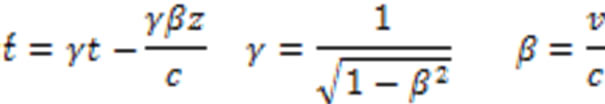
or
 (23)
(23)
The angle that the magnetic vector is having with the z-axis (or with the z-axis in the moving reference frame) can be found from its tangent function (using Equations (19), (20) and (21)) as follows

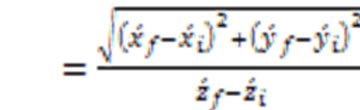 (24)
(24)
One can see here that the function 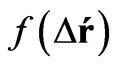 cancels out. Therefore, the result (24) holds in general for magnetic fields which might not even satisfy the Coulomb law. Using the Lorentz transformation (23), one can write the tangent of the angle between the magnetic vector and the z-axis, found to the observer’s reference frame at rest, as follows
cancels out. Therefore, the result (24) holds in general for magnetic fields which might not even satisfy the Coulomb law. Using the Lorentz transformation (23), one can write the tangent of the angle between the magnetic vector and the z-axis, found to the observer’s reference frame at rest, as follows
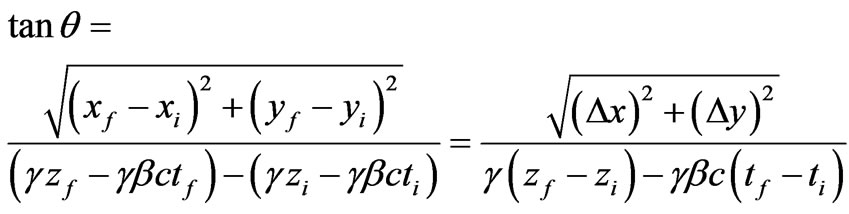 (25)
(25)
In Equation (24) all primed coordinates are measured at the same instant of the primed time, therefore
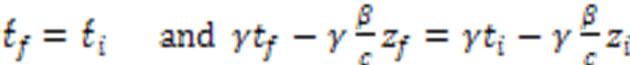 (26)
(26)
From Equation (26) we find the following
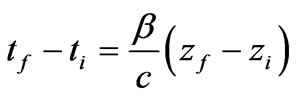 (27)
(27)
Substituting the result of Equation (27) into Equation (25) one gets
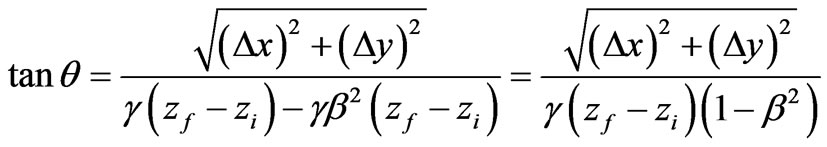
 (28)
(28)
Thus we have
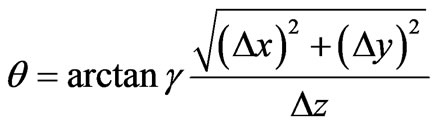 (29)
(29)
In the limit when the speed of motion of the rounded electromagnetic fields reaches a value close to the value of the speed of light in vacuum, one obtains the following
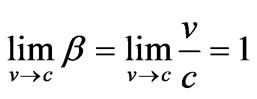 (30)
(30)
and the limit of Equation (29) is obtained as
 (31)
(31)
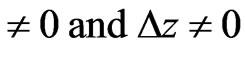
3. Detecting the Magnetic Orthogoniopedic Effect
Equation (31), as a result of the property of the Minkowski relativistic space shows that the magnetic field vectors of the rounded electromagnetic fields approach an angle of 90 degrees with respect to the direction of motion when the rounded electromagnetic fields move with a speed approaching the speed of light in vacuum (Figure 1).
The concentration of the magnetic field vectors of the rounded electromagnetic fields inside the superconducting bulk perpendicular to their direction of motion and also perpendicular to the direction of the applied external magnetic field results in the alignment of the spin magnetic moments of the orbital electrons of the atoms or molecules or ions of the superconductor (therefore, not the resultant spins of the Cooper pairs [1] which are according to the B.C.S. theory equal to zero [1]) in perpendicular directions with respect to the external magnetic field and enforcing the expulsion of the external magnetic field.
When the external applied magnetic field is expelled,

Figure 1. (a) Two opposite vectors which are equal in magnitude cancel each other. (b) Each of the dashed vertical vectors added respectively with each of the square-dotted vectors result in respectively each of the solid-line resultant vectors.
the rounded electromagnetic fields are not undergoing the exertion of the magnetomotive force. At that instant, the magnetic field vectors of the rounded electromagnetic fields have a state of comparatively diminished constraint due to the expulsion of the external applied magnetic field and the rounded electromagnetic fields try to restore the state when the constraint by the external applied magnetic field was absent. They do it by exerting forces, causing a motion opposite to the original direction of the applied external magnetic field again with a speed close to the speed of light in vacuum. For this opposite motion again Equation (31) holds and the external applied magnetic field is still expelled. When the original state is reached, at that short instant the rounded electromagnetic fields are not moving and the effect of Equation (31) is not present for a very short instant of time, until the external applied magnetic field assumes its role again as the magnetomotive force, and the steps mentioned above repeat themselves, causing an oscillatory (motion in the z direction) of the magnetic field the vectors of which are perpendicular to the direction of the applied external magnetic field. For the time dependence of the velocity of motion of the rounded electromagnetic fields, one may write in this way the following function
 (32)
(32)
where “Intgr” indicates that only the integer part of the argument should be taken, H(t) is the Heaviside step function [8] and ξ is a fraction number taken as the length, traveled by a bunch of the rounded electromagnetic fields in a bulk of a superconductor of length L along the direction of the applied external magnetic field, divided by L. If the equations written above theoretically (using among others the Lorentz transformation of the Special Theory of Relativity [9,10]), hold indeed in reality, then the oscillatory motion of the magnetic field the vectors of which are perpendicular to the externally applied magnetic field should be detectable by equipments which are sensitive enough. Figure 2 shows a simplified version of such an experimental set-up. If the period of oscillation, which is given from Equation (32) as
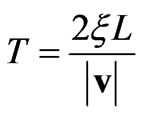 (33)
(33)
is too short or equivalently the frequency of the oscillation is too high then the oscillatory effect of the motion of the magnetic field the vectors of which are perpendicular to the externally applied magnetic field may not easily be detectable. However, by another experimental set-up, presumably one might be able to observe that there is indeed a perpendicular magnetic field with respect to the direction of the external applied magnetic field by moving a planar conducting loop (Figure 2) in an oscillatory way (as a rotation), causing a change of the magnetic flux in time, which in its turn would induce an electric current in the planar loop, according to the well-known relation [11]
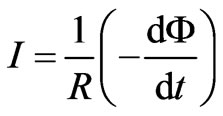 (34)
(34)
where I is the current which might be measurable by an ammeter or an electric current meter, R the resistance of the conducting loop and Φ the magnetic flux enclosed by the conducting loop. The external magnetic field would have, in this configuration of the conducting loop (as in
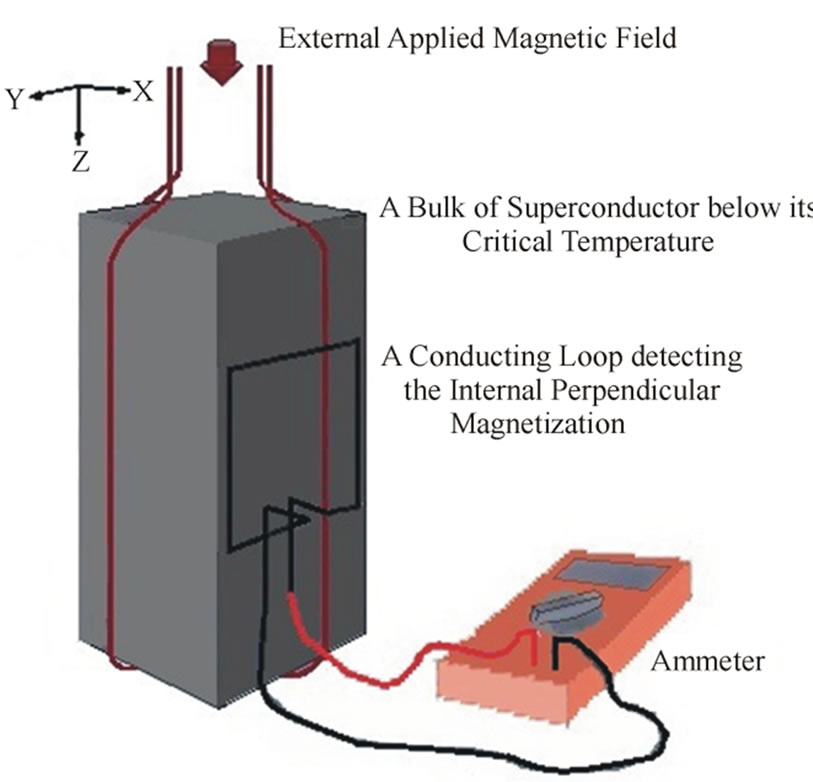
Figure 2. The Meissner Effect in which an applied external magnetic is expelled by a superconductor. The lines of the external magnetic vector field suggest a magnetization inside the superconductor with the directions perpendicular to the applied external magnetic field (comparing Figure 1(b)).
Figure 2), no or negligible flux contribution to the electric current in the conducting loop, since the conducting loop would be parallel to the external magnetic field, and a current signal in the ammeter may indicate the existence of the internal (presumably oscillatory) magnetic field inside the bulk of the superconductor due and perpendicular to the externally applied magnetic field. Etymologically the word “orthogoniopedic” is chosen for this theoretical effect, which is an abbreviated combination of three words “orthogonio” or perpendicular, referring to the result of the limit as  radians from Equation (31) or the right angle of 90 degrees, and “pedio” being the Greek word for “field” and the adjective suffix “-ic”.
radians from Equation (31) or the right angle of 90 degrees, and “pedio” being the Greek word for “field” and the adjective suffix “-ic”.
4. Conclusions
The article brought the electromagnetic waves as the plausible interaction mediators in the Meissner Effect or the diamagnetic property of the superconductors, based on the existing standard model of the interaction between charged particles [12]. During the cooling process of a superconductor below its critical temperature, the electrons are occupying lower states of the energy possibly releasing the excess of energy in comparison with the original state as electromagnetic waves which can, by a combination of the harmonic functions (which are according to Fourier’s analysis, the components of any periodic oscillation or any wave), remain inside the superconductor. These electromagnetic fields may mediate the interaction of an externally applied magnetic field and the internal magnetization field [2] of a superconductor in the Meissner Effect. The Lorentz transformation of the Special Theory of Relativity applied to the mediating electromagnetic fields can explain the direction of the internal magnetization field [2] inside a superconductor in a manner compatible with the published phenomenon in the scientific communities of the expulsion of the externally applied magnetic field by a superconductor which is already well known as the Meissner Effect. An experiment is proposed with the title of the Magnetic Orthogoniopedic Effect to detect more exactly the probable directions of the internal magnetization field inside a superconductor in the Meissner Effect.
REFERENCES
- P. L. Taylor and O. Heinonen, “A Quantum Approach to Condensed Matter Physics,” Cambridge University Press, Cambridge, 2002.
- N. W. Ashcroft and N. D. Mermin, “Solid State Physics,” Thomson Learning Inc., Glendale, 1976.
- H. D. Young and R. A. Freedman, “University Physics,” 9th Edition, Addison-Wesley Publishing Company, Inc., Boston, 1996.
- G. R. Fowles, “Introduction to Modern Optics,” 2nd Edition, Dover Publications, Inc., New York, 1989.
- S. Gasiorowicz, “Quantum Physics,” 2nd Edition, John Wiley & Sons, Inc., New York, 1996.
- T. M. Apostol, “Calculus; Volume I,” 2nd Edition, John Wiley & Sons, Singapore City, 1967.
- T. M. Apostol, “Calculus; Volume II,” 2nd Edition, John Wiley & Sons, Singapore City, 1969.
- J. Mathews and R. L. Walker, “Mathematical Methods of Physics,” 2nd Edition, Addison-Wesley Publishing Company, Inc., Boston, 1970.
- J. B. Marion and S. T. Thornton, “Classical Dynamics of Particles and Systems,” 4th Edition, Harcourt Brace & Company, San Diego, 1995.
- R. d’Inverno, “Introducing Einstein’s Relativity,” Clarendon Press, Oxford, 1995.
- E. M. Purcell, “Electricity and Magnetism,” 2nd Edition, McGraw-Hill Inc., Boston, 1985.
- W. E. Burcham and M. Jobes, “Nuclear and Particle Physics,” Addison Wesley Longman Limited, Singapore City, 1997.

