Applied Mathematics
Vol.4 No.9A(2013), Article ID:36702,5 pages DOI:10.4236/am.2013.49A005
Common New Fixed Point Theorem in Modified Intuitionistic Fuzzy Metric Spaces Using Implicit Relation
1School of Mathematics and Computer Applications, Thapar University, Patiala, India
2Department of Mathematics, Faculty of Science, Jazan University, Jazan, KSA
Email: sauravmanro@yahoo.com, sauravmanro@hotmail.com, mathsqueen_d@yahoo.com
Copyright © 2013 Saurabh Manro, Sumitra. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 5, 2013; revised June 5, 2013; accepted June 13, 2013
Keywords: Modified Intuitionistic Fuzzy Metric Space; Compatible Mappings; Subcompatible Mappings; Subsequential Continuous Mappings; Reciprocal Continuity; Implicit Relation
ABSTRACT
In this paper, we prove some common fixed point theorems for two pair of compatible and subsequentially continuous mappings satisfying an implicit relation in Modified Intuitionistic fuzzy metric spaces. Consequently, our results improve and sharpen many known common fixed point theorems available in the existing literature of metric fixed point theory.
1. Introduction
The concept of fuzzy set was introduced in 1965 by Zadeh [1]. In 1986, with similar endeavour, Atanasov [2] introduced and studied the concept of Intuitionistic fuzzy sets (IFS). Using the idea of IFS, a generalization of fuzzy metric space was introduced by Park [3] which is known as Intuitionistic fuzzy metric space. Since the Intuitionistic fuzzy metric space has extra conditions (see [2]), Saadati et al. [4] reframed the idea of Intuitionistic fuzzy metric space and proposed a new notion under the name of Modified Intuitionistic fuzzy metric space by introducing idea of continuous t-representable.
In 1986, Jungck [5] introduced the notion of compatible maps for a pair of self mappings. Jungck et al. [6] initiated the study of weakly compatible maps in metric space. With a view to improve commutativity conditions in common fixed point theorems, Sessa [7] introduced the notion of weakly commuting pair. Most recently, Bouhadjera et al. [8] (see also [9]) introduced two new notions namely: subsequential continuity and subcompatibility.
In this paper, we prove some common fixed point theorems for two pair of compatible and subsequentially continuous mappings satisfying an implicit relation in modified Intuitionistic fuzzy metric spaces. Consequently, our results improve and sharpen many known common fixed point theorems available in the existing literature of metric fixed point theory and generalize the results of D. Gopal et al. [10, Theorem 3.1 and Theorem 3.2].
2. Preliminaries
Lemma 2.1. [11] Consider the set L* and the operation ≤L* defined by
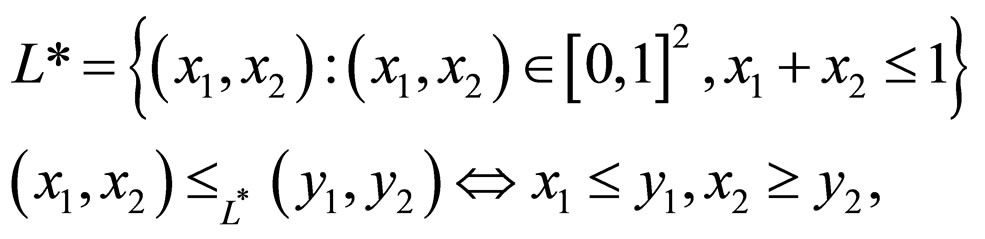
for every (x1, x2), (y1,y2) 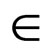 L*. Then (L*, ≤L*) is a complete lattice.
L*. Then (L*, ≤L*) is a complete lattice.
We denote its units by 0L* = (0,1) and 1L* = (1,0).
Definition 2.1. [12] A triangular norm (t-norm) on L* is a mapping 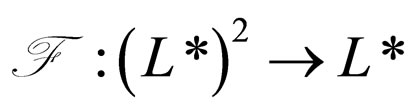 satisfying the following conditions:
satisfying the following conditions:
(1) 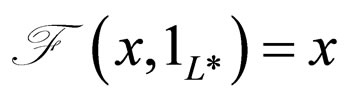 for all x
for all x 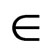 L*(2)
L*(2) 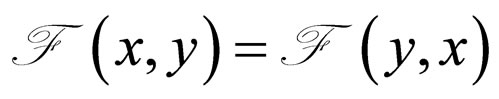 for all x, y
for all x, y 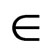 L*(3)
L*(3) 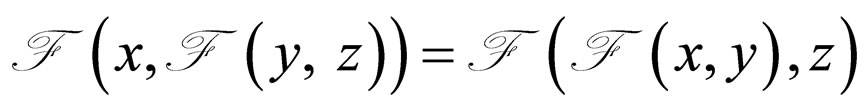 for all x, y, z
for all x, y, z 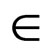 L*(4) If for all x,
L*(4) If for all x, 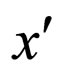 , y,
, y, 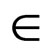
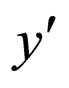 L*,
L*, 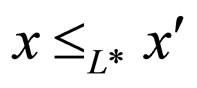 and
and 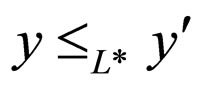 implies
implies
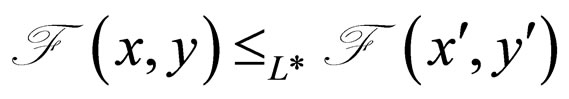 .
.
Definition 2.2. [11,12] A continuous t-norm F on L* is called continuous t-representable iff there exist a continuous t-norm * and a continuous t-conorm  on [0, 1] such that for all
on [0, 1] such that for all 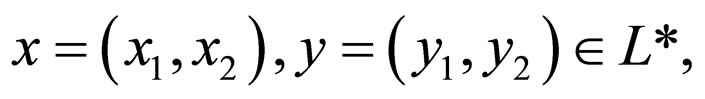
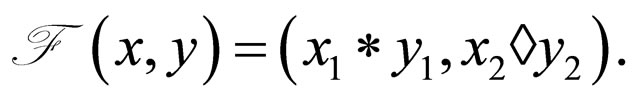
Definition 2.3. [4] Let M, N are fuzzy sets from 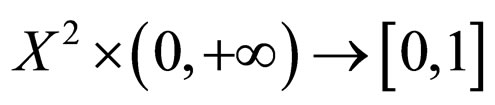 such that
such that
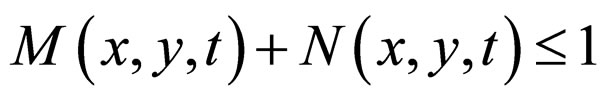 for all x, y
for all x, y  X and t > 0. The 3-tuple
X and t > 0. The 3-tuple 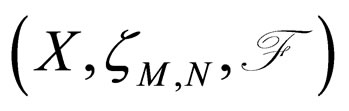 is said to be a Modified Intuitionistic fuzzy metric space if X is an arbitrary non empty set,
is said to be a Modified Intuitionistic fuzzy metric space if X is an arbitrary non empty set,  is a continuous t-representable and
is a continuous t-representable and 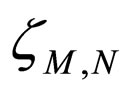 is a mapping
is a mapping 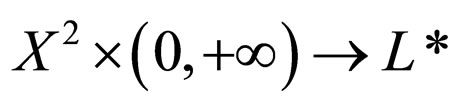 satisfying the following conditions for every x, y
satisfying the following conditions for every x, y  X and t, s > 0:
X and t, s > 0:
(a)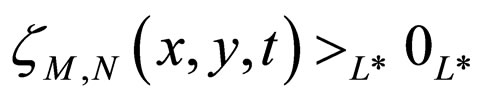 ;
;
(b)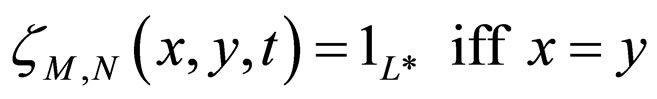 ;
;
(c)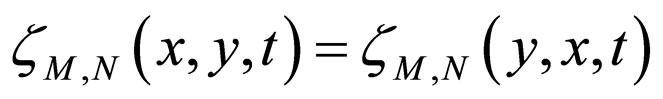 ;
;
(d) 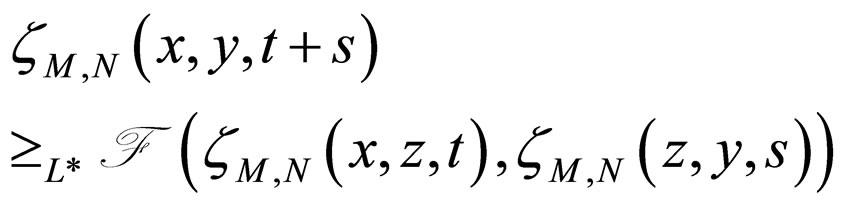 ;
;
(e) 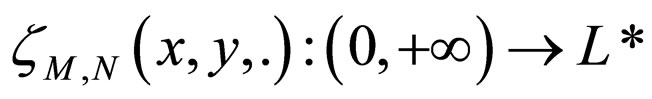 is continuous.
is continuous.
In this case, 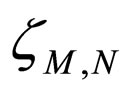 is called an Intuitionistic fuzzy metric. Here,
is called an Intuitionistic fuzzy metric. Here,
 .
.
In the sequel, we will call 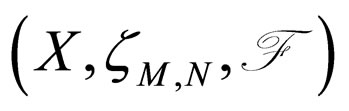 to be just a Modified Intuitionistic fuzzy metric space.
to be just a Modified Intuitionistic fuzzy metric space.
Remark 2.1. [13] In Modified Intuitionistic fuzzy metric space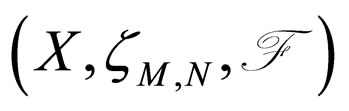 ,
, 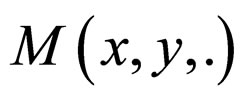 is non decreasing and
is non decreasing and 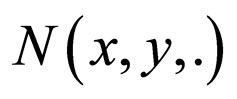 is non-increasing for all x, y
is non-increasing for all x, y 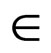 X. Hence
X. Hence 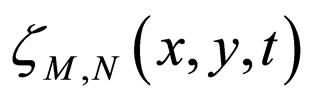 is non-decreasing with respect to t for all x, y
is non-decreasing with respect to t for all x, y 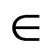 X.
X.
Definition 2.4. [4] A sequence {xn} in a Modified Intuitionistic fuzzy metric space 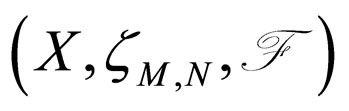 is called a Cauchy sequence if for each
is called a Cauchy sequence if for each 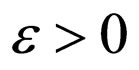 and t > 0, there exists
and t > 0, there exists 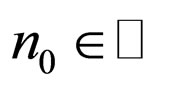 such that
such that 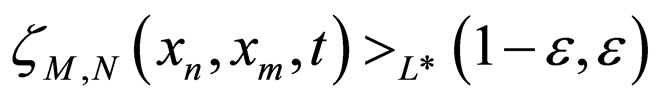 for each
for each 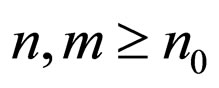 and for all t.
and for all t.
Definition 2.5. [4] A sequence {xn} in a Modified Intuitionistic fuzzy metric spac 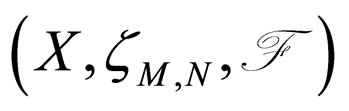 is said to be convergent to x
is said to be convergent to x 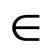 X, denoted by
X, denoted by 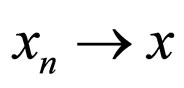 if
if
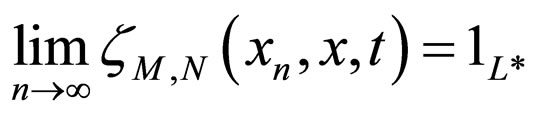 for all t.
for all t.
A Modified Intuitionistic fuzzy metric space
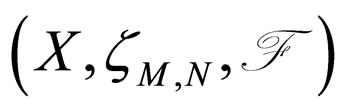 is said to be complete iff every Cauchy sequence is converges to a point of it.
is said to be complete iff every Cauchy sequence is converges to a point of it.
Definition 2.6. [14] Let f and g be maps from a Modified Intuitionistic fuzzy metric space 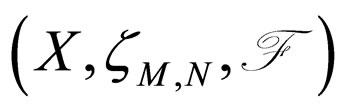 into itself. The maps f and g are said to be weakly commuting if
into itself. The maps f and g are said to be weakly commuting if 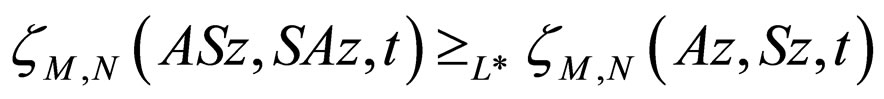 for all
for all 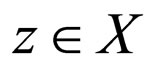 and
and 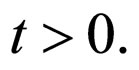
Definition 2.7. [4] A pair of self mappings (f, g) of Modified Intuitionistic fuzzy metric space
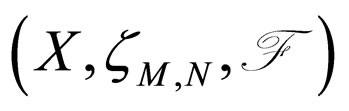 is said to be compatible if
is said to be compatible if
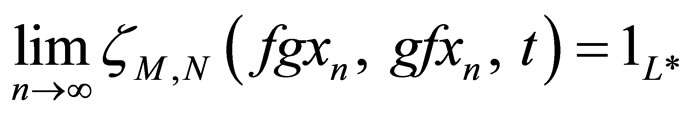 whenever
whenever 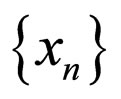 is a sequence in X such that
is a sequence in X such that 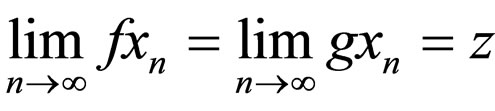 for some z
for some z 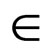 X.
X.
Definition 2.8. [13] Two self-mappings f and g are called non-compatible if there exists at least one sequence  such that
such that 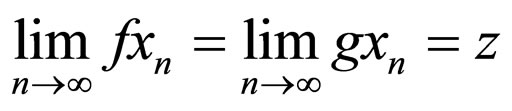 for some z
for some z 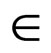 X but either
X but either 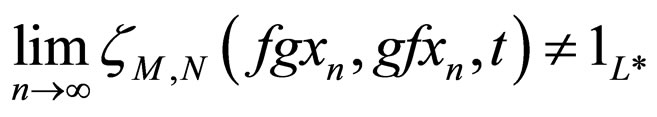 or the limit does not exist for all z
or the limit does not exist for all z 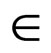 X.
X.
Definition 2.9. [15] A pair of self mappings (f, g) of Modified Intuitionistic fuzzy metric space
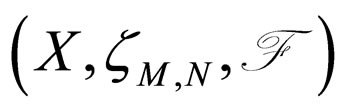 is said to be weakly compatible if they commute at coincidence points i.e. if fu = gu for some u
is said to be weakly compatible if they commute at coincidence points i.e. if fu = gu for some u  X, then fgu = gfu.
X, then fgu = gfu.
Definition 2.10. [16] A pair of self mappings (f, g) of Modified Intuitionistic fuzzy metric space
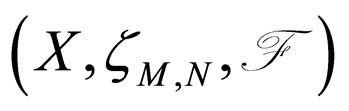 is said to be occasionally weakly compatible (owc) if the pair (f, g) commutes at least one coincidence point i.e. there exists at least one point x
is said to be occasionally weakly compatible (owc) if the pair (f, g) commutes at least one coincidence point i.e. there exists at least one point x  X such that fx = gx and fgx = gfx.
X such that fx = gx and fgx = gfx.
Definition 2.11. [9] Let f and g be maps from a Modified Intuitionistic fuzzy metric space 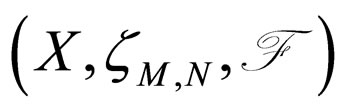 into itself. The maps f and g are said to be subcompatible if there exist a sequence
into itself. The maps f and g are said to be subcompatible if there exist a sequence 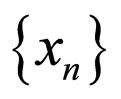 in X with
in X with
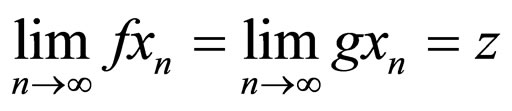 for
for 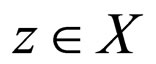 and for all t > 0,
and for all t > 0,
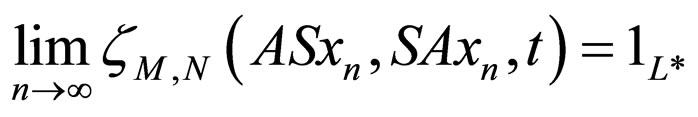 .
.
Definition 2.12. [10] Let f and g be maps from a Modified Intuitionistic fuzzy metric space
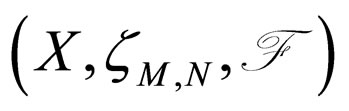 into itself. The maps f and g are said to be reciprocally continuous if for a sequence
into itself. The maps f and g are said to be reciprocally continuous if for a sequence 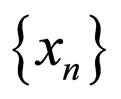 in X
in X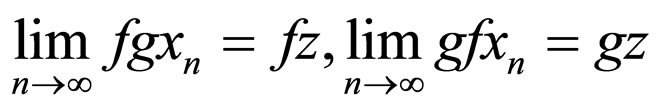 , whenever
, whenever 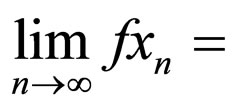
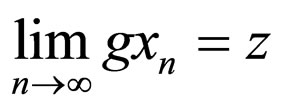 for some
for some 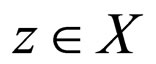 and for all
and for all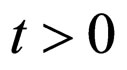 .
.
Definition 2.13. [17] Let f and g be two maps from modified intuitionistic fuzzy metric space
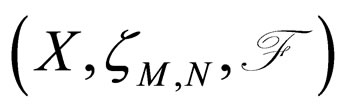 into itself. The maps f and g are said to be subsequentially continuous if there exist a sequence
into itself. The maps f and g are said to be subsequentially continuous if there exist a sequence 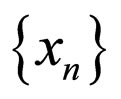 in X such that
in X such that
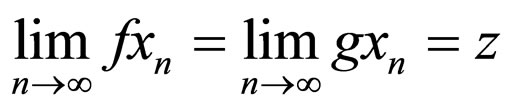 for some
for some 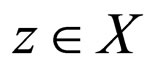
and 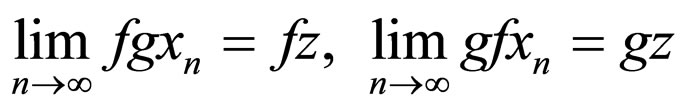 for all
for all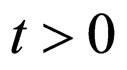 .
.
3. Main Results
Implicit relations play important role in establishing of common fixed point results.
Let M6 be the set of all continuous functions
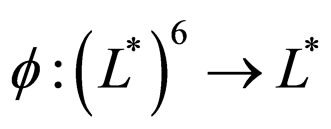 satisfying the following conditions (for all
satisfying the following conditions (for all
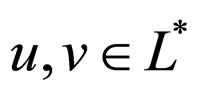 ,
, 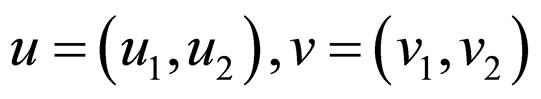 and
and
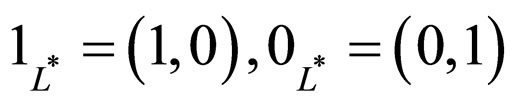 ):
):
(A) 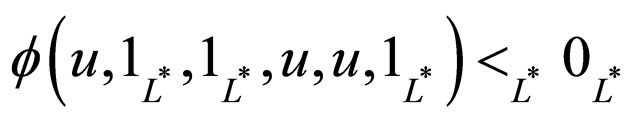
and
(B) 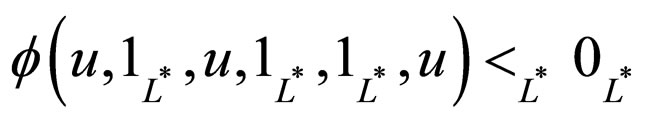
for all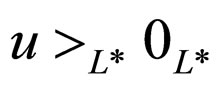 .
.
Example 3.1. Define 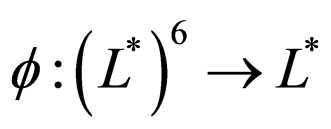 as
as
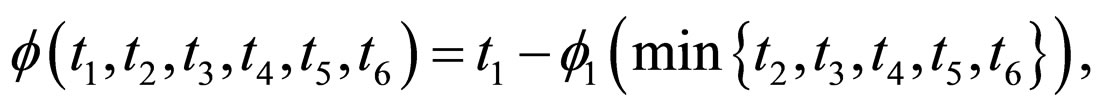 where
where
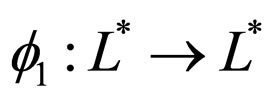 is increasing and continuous function such that
is increasing and continuous function such that 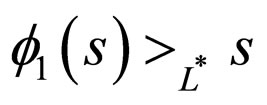 for all
for all 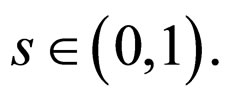 Clearly,
Clearly,  in M6.
in M6.
We begin with following observation:
Theorem 3.1. Let A, B, S and T be four self mappings of a Modified Intuitionistic fuzzy metric space
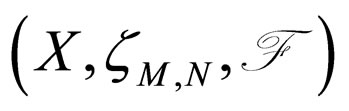 . If the pairs (A, S) and (B, T) are compatible and subsequentially continuous mappings, then
. If the pairs (A, S) and (B, T) are compatible and subsequentially continuous mappings, then
(3.1) the pair (A, S) has a coincidence point
(3.2) the pair (B, T) has a coincidence point.
Further, A, B, S and T have a unique common fixed point provided A, B, S and T satisfy the following:
(3.3) for any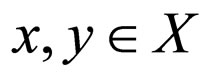 ,
, 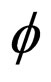 in M6 and for all t > 0,
in M6 and for all t > 0,
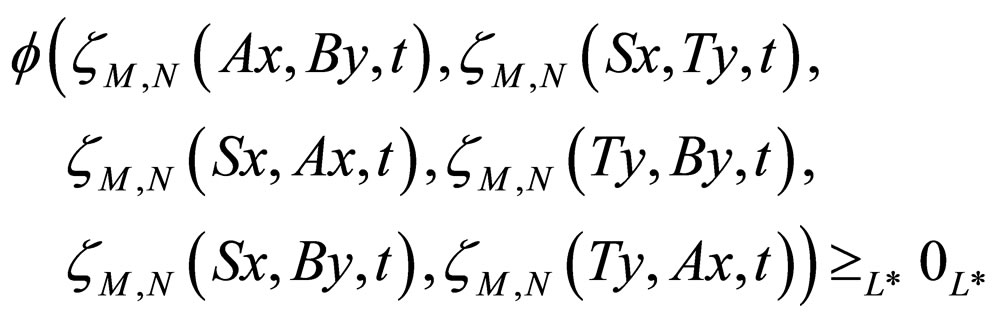
Proof. Since the pairs (A, S) and (B, T) are compatible and subsequentially continuous mappings, therefore there exist sequences {xn} and {yn} in X such that
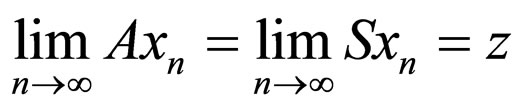 ,
,
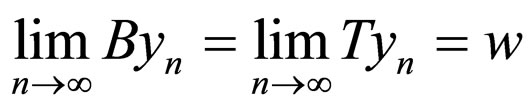 for some
for some  and
and
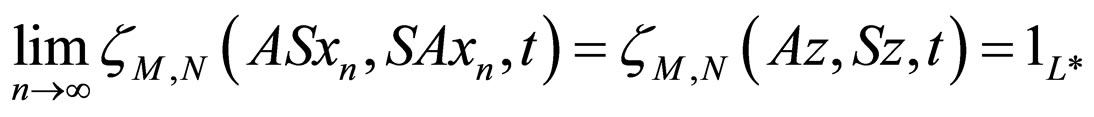
and 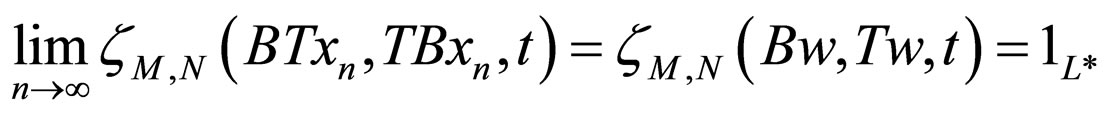
so that Az = Sz and Bw = Tw i.e. z is a coincidence point of A and S where as w is a coincidence point of B and T, which proves (3.1) and (3.2).
Now, we prove that z = w, if not, then by using (3.3), we have
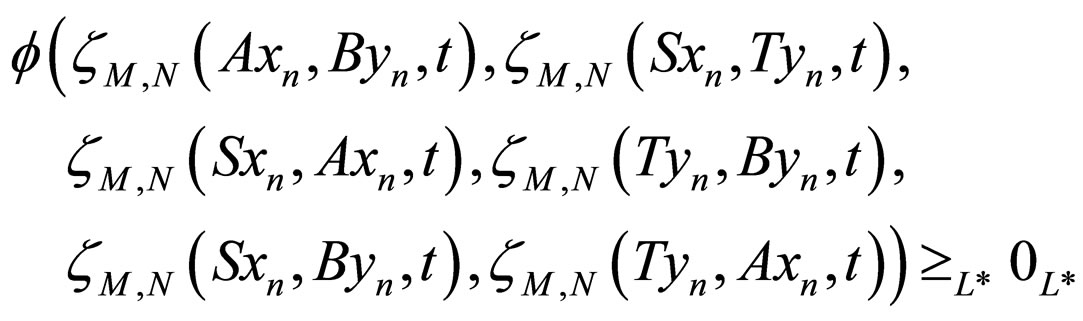
which on making  reduces to
reduces to
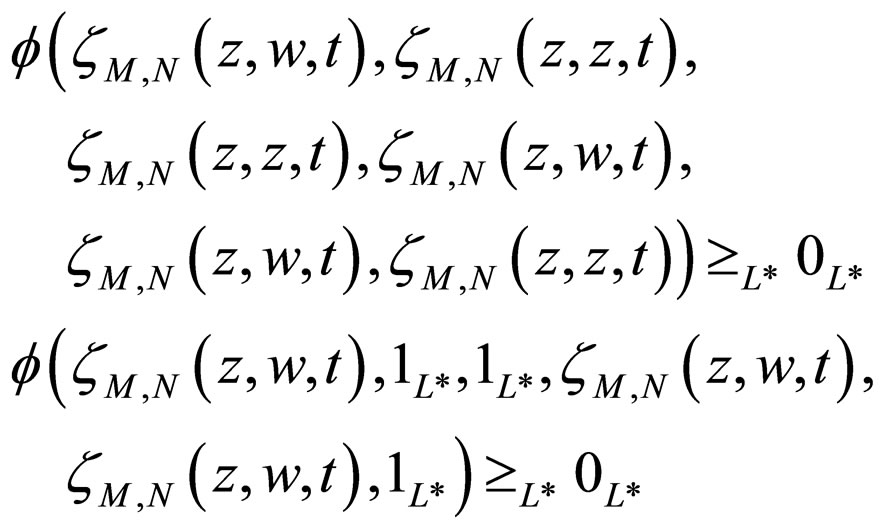
a contradiction to (A) so that z = w.
Now, we assert that Az = z, if not, then by (3.3), we get
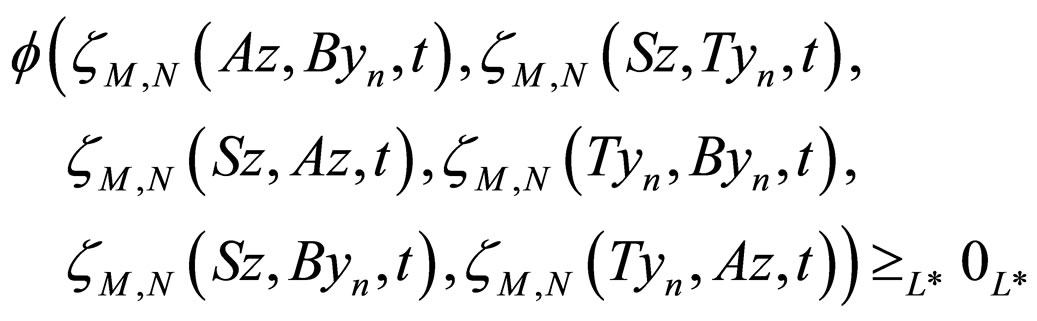
taking the limit as , we get
, we get
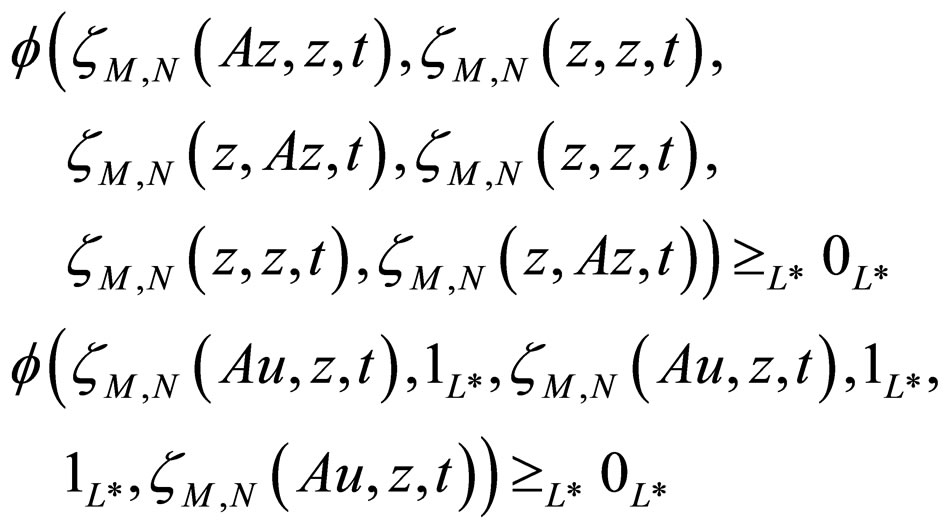
which is a contradiction to (B). Therefore, Az = z = Sz.
Similarly, we prove that Bz = z = Tz by using (3.3). Therefore, in all, z = Az = Bz = Sz = Tz. i.e. z is common fixed point of A, B, S and T. The uniqueness of common fixed point is an easy consequence of the inequality (3.3). This completes the proof of the theorem. □
Theorem 3.2. Let A, B, S and T be four self mappings of a Modified Intuitionistic fuzzy metric space
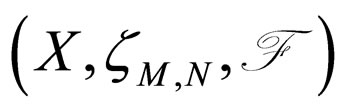 . If the pairs (A,S) and (B,T) are subcompatible and reciprocally continuous mappings, then
. If the pairs (A,S) and (B,T) are subcompatible and reciprocally continuous mappings, then
(3.4) the pair (A, S) has a coincidence point
(3.5) the pair (B, T) has a coincidence point.
Further, A, B, S and T have a unique common fixed point provided A, B, S and T satisfy the condition (3.3).
Proof. Proof easily follows on same lines of Theorem 3.1 and using definition of reciprocally continuous and subcompatible mappings. □
Corollary 3.1. The conclusions of Theorem 3.1 and Theorem 3.2 remain true if we replace the inequality (3.3) by any one of the following:
(3.6) 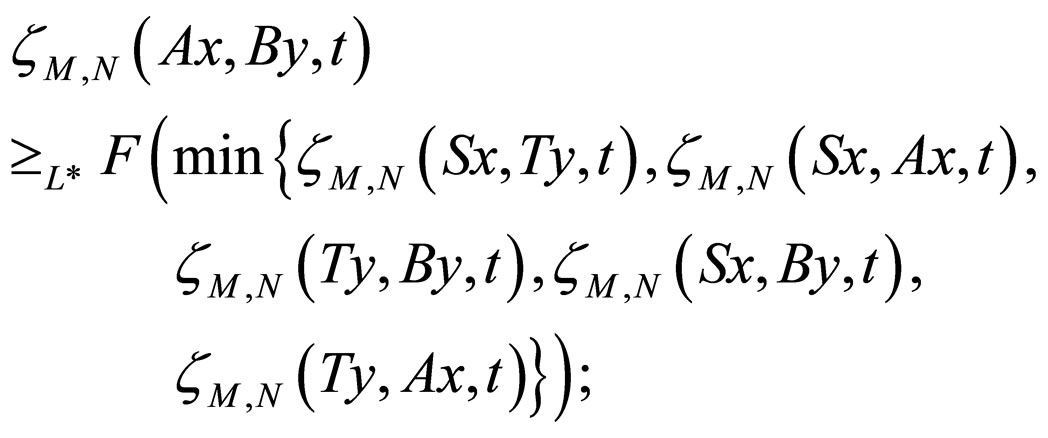
where 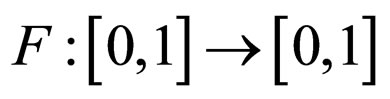 is increasing and continuous function such that
is increasing and continuous function such that 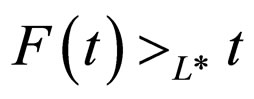 for all
for all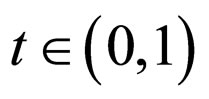 .
.
(3.7) 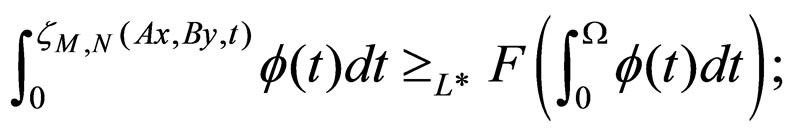
where

where 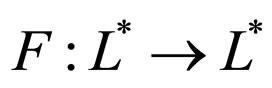 is increasing and continuous function such that
is increasing and continuous function such that 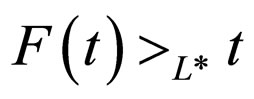 for all
for all 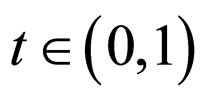 and
and
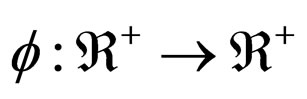 is a Lebesgue integrable function which is summable and satisfies
is a Lebesgue integrable function which is summable and satisfies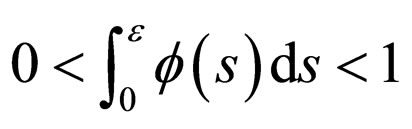 , for all
, for all
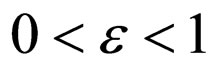 .
.
By setting A = B in Theorems 3.1, 3.2, we derive the following corollaries for three mappings.
Corollary 3.2. Let A, S and T be three self mappings of a Modified Intuitionistic fuzzy metric space
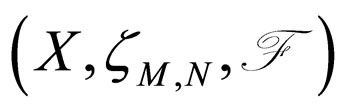 . If the pairs (A,S) and (A,T) are compatible and subsequentially continuous mappings, then
. If the pairs (A,S) and (A,T) are compatible and subsequentially continuous mappings, then
(3.8) the pair (A, S) has a coincidence point
(3.9) the pair (A, T) has a coincidence point.
Further, A, B, S and T have a unique common fixed point provided A, B, S and T satisfy the following:
(3.10) for any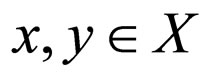 ,
,  in M6 and for all t > 0,
in M6 and for all t > 0,
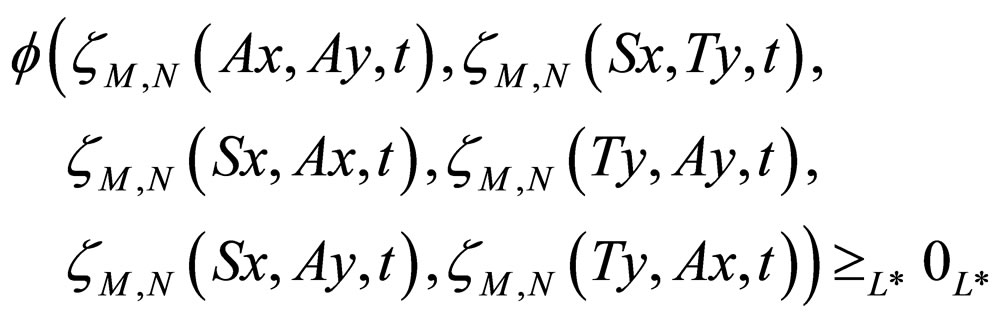
Corollary 3.3. Let A, S and T be three self mappings of a Modified Intuitionistic fuzzy metric space
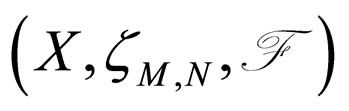 . If the pairs (A,S) and (A,T) are subcompatible and reciprocally continuous mappings, then (3.8) and (3.9) satisfied. Further, A, S and T have a unique common fixed point provided A, S and T satisfy the condition (3.10).
. If the pairs (A,S) and (A,T) are subcompatible and reciprocally continuous mappings, then (3.8) and (3.9) satisfied. Further, A, S and T have a unique common fixed point provided A, S and T satisfy the condition (3.10).
Alternatively, by setting S = T in Theorems 3.1, 3.2, we derive the following corollaries for three mappings.
Corollary 3.4. Let A, B and S be three self mappings of a Modified Intuitionistic fuzzy metric space
 . If the pairs (A,S) and (B,S) are compatible and subsequentially continuous mappings, then
. If the pairs (A,S) and (B,S) are compatible and subsequentially continuous mappings, then
(3.11) the pair (A, S) has a coincidence point
(3.12) the pair (B, S) has a coincidence point.
Further, A, B and S have a unique common fixed point provided A, B and S satisfy the following:
(3.13) for any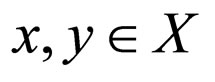 ,
,  in M6 and for all t > 0,
in M6 and for all t > 0,
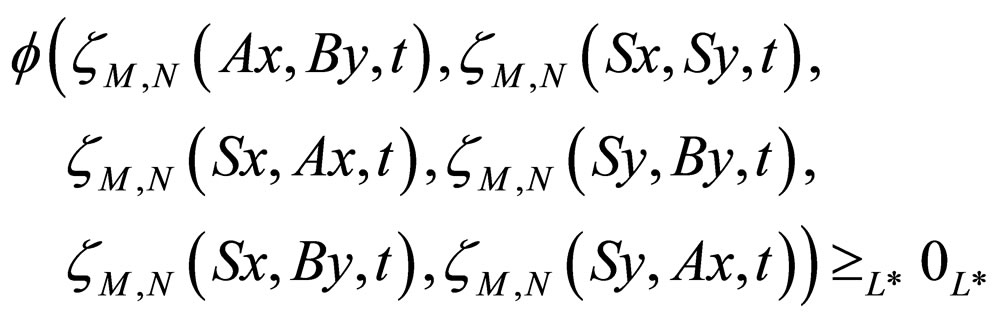
Corollary 3.5. Let A, B and S be three self mappings of a Modified Intuitionistic fuzzy metric space
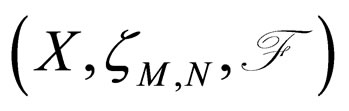 . If the pairs (A,S) and (B,S) are subcompatible and reciprocally continuous mappings, then (3.11) and (3.12) satisfied. Further, A, B and S have a unique common fixed point provided A, B and S satisfy the condition (3.13).
. If the pairs (A,S) and (B,S) are subcompatible and reciprocally continuous mappings, then (3.11) and (3.12) satisfied. Further, A, B and S have a unique common fixed point provided A, B and S satisfy the condition (3.13).
Finally, by setting A = B and S = T in Theorems 3.1 and 3.2, we derive the following corollaries:
Corollary 3.6. Let A and S be four self mappings of a modified intuitionistic fuzzy metric space
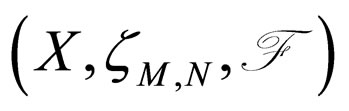 . If the pair (A,S) is compatible and subsequentially continuous mappings, then
. If the pair (A,S) is compatible and subsequentially continuous mappings, then
(3.14) the pair (A, S) has a coincidence point.
Further, A and S have a unique common fixed point provided A and S satisfy the following:
(3.15) for any ,
,  and
and 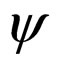 in M6 and for all t > 0,
in M6 and for all t > 0,
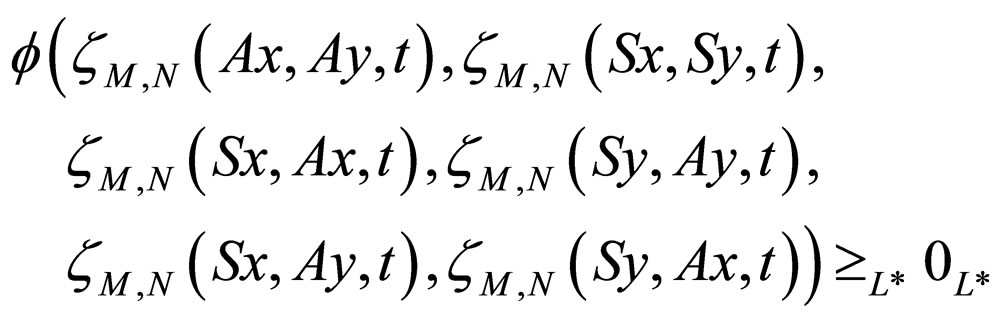
Corollary 3.7. Let A and S be pair of self mappings of a modified intuitionistic fuzzy metric space
 . If the pair (A,S) is subcompatible and reciprocally continuous mappings, then (3.14) is satisfied. Further, A and S have a unique common fixed point provided A and S satisfy the condition (3.15).
. If the pair (A,S) is subcompatible and reciprocally continuous mappings, then (3.14) is satisfied. Further, A and S have a unique common fixed point provided A and S satisfy the condition (3.15).
Example 3.1. [10]
Let 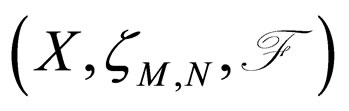 be a Modified Intuitionistic fuzzy metric space where
be a Modified Intuitionistic fuzzy metric space where 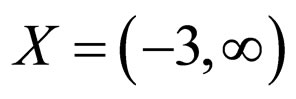
and define 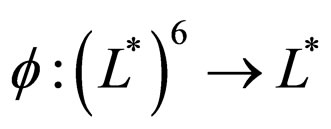 as
as
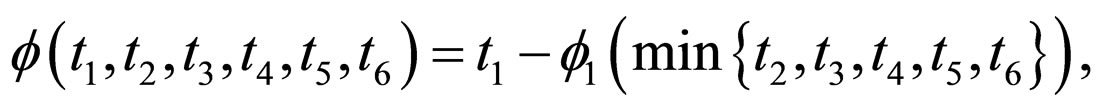 where
where
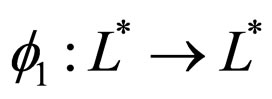 is increasing and continuous function such that
is increasing and continuous function such that 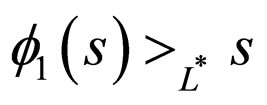 for all
for all 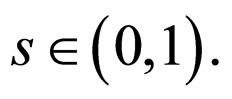 Clearly,
Clearly, 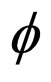 satisfies all conditions (A) and (B). Define A, B, S and T by
satisfies all conditions (A) and (B). Define A, B, S and T by
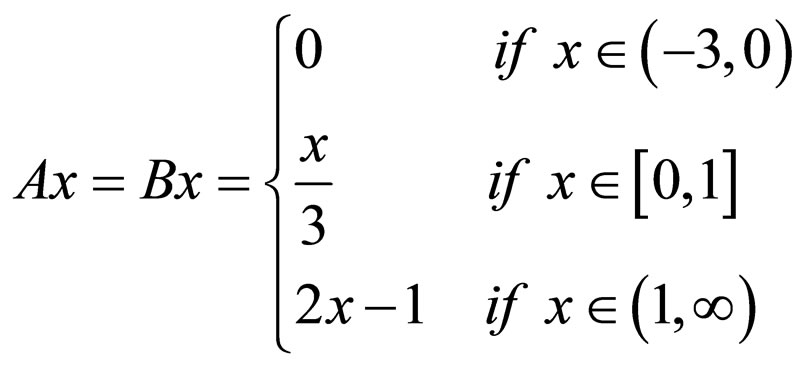
and 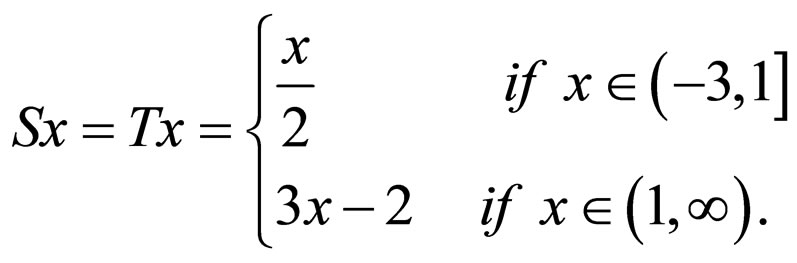
where
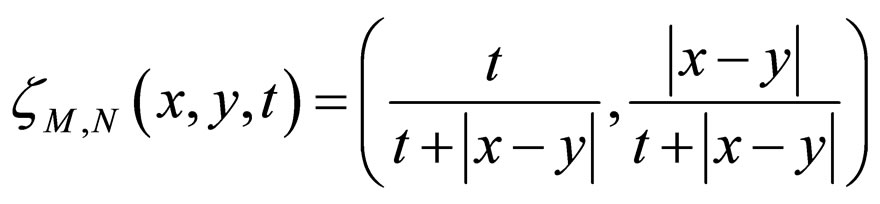 for all
for all
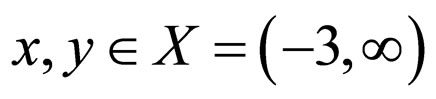 , t > 0. Clearly, for the sequence
, t > 0. Clearly, for the sequence
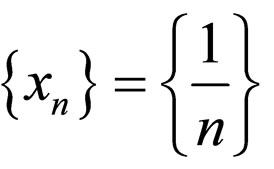 , (A,S) and (B,T) are compatible as well as subsequentially continuous. Therefore, all the conditions of Theorem 3.1 are satisfied. Evidently, z = 0 is a coincidence as well as unique common fixed point of A, B, S and T.
, (A,S) and (B,T) are compatible as well as subsequentially continuous. Therefore, all the conditions of Theorem 3.1 are satisfied. Evidently, z = 0 is a coincidence as well as unique common fixed point of A, B, S and T.
Example 3.2. [10]
Let 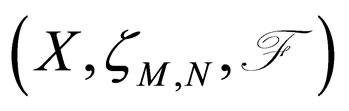 be a Modified Intuitionistic fuzzy metric space where
be a Modified Intuitionistic fuzzy metric space where 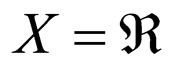 and define
and define 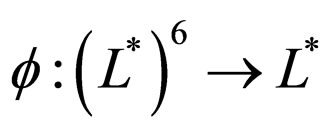
as 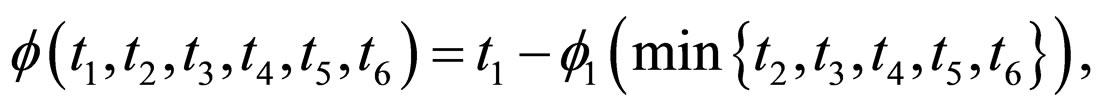
where 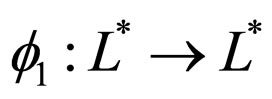 is increasing and continuous function
is increasing and continuous function
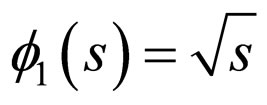 such that
such that 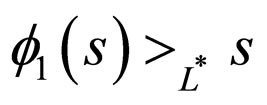 for all
for all 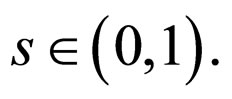
Clearly, 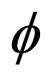 satisfies all conditions (A) and (B). Define A, B, S and T by
satisfies all conditions (A) and (B). Define A, B, S and T by

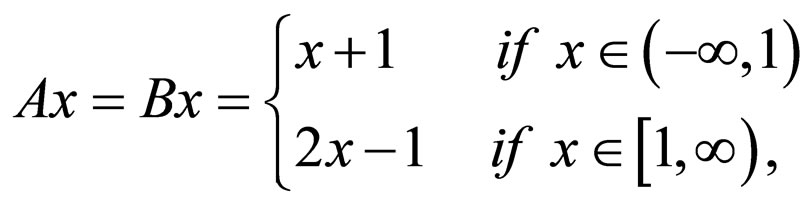
and
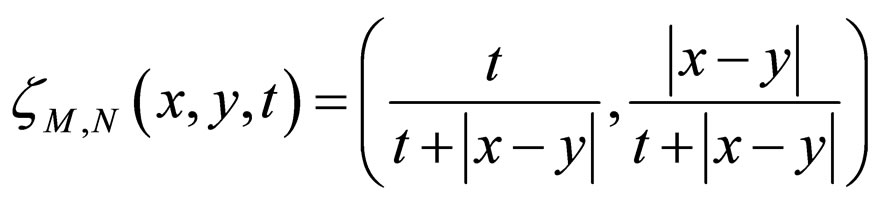 for all
for all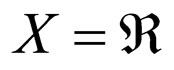 , t > 0. Clearly, for the sequence
, t > 0. Clearly, for the sequence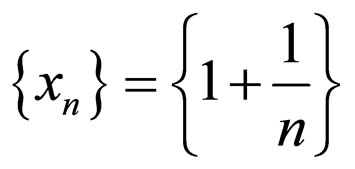 , (A,S) and(B,T) are subcompatible as well as reciprocally continuous. Therefore, all the conditions of Theorem 3.2 are satisfied. Evidently, z = 0 is a coincidence as well as unique common fixed point of A, B, S and T.
, (A,S) and(B,T) are subcompatible as well as reciprocally continuous. Therefore, all the conditions of Theorem 3.2 are satisfied. Evidently, z = 0 is a coincidence as well as unique common fixed point of A, B, S and T.
4. Acknowledgements
The authors thank the referee for his/her careful reading and useful suggestions of the manuscript.
REFERENCES
- L. A. Zadeh, “Fuzzy Sets,” Information and Control, Vol. 8, No. 3, 1965, pp. 338-353. doi:10.1016/S0019-9958(65)90241-X
- A. T. Atanassov, “Intuitionistic Fuzzy Sets,” Fuzzy Sets and Systems, Vol. 20, No. 1, 1986, pp. 87-96. doi:10.1016/S0165-0114(86)80034-3
- J. H. Park, “Intuitionistic Fuzzy Metric Spaces,” Chaos, Solitons & Fractals, Vol. 22, No. 5, 2004, pp. 1039-1046. doi:10.1016/j.chaos.2004.02.051
- R. Saadati, S. Sedghi and N. Shobhe, “Modified Intuitionistic Fuzzy Metric Spaces and Some Fixed Point Theorems,” Chaos, Solitons & Fractals, Vol. 38, No. 1, 2008, pp. 36-47. doi:10.1016/j.chaos.2006.11.008
- G. Jungck, “Compatible Mappings and Common Fixed Points,” International Journal of Mathematics and Mathematical Sciences, Vol. 9, No. 4, 1986, pp. 771-779. doi:10.1155/S0161171286000935
- G. Jungck and B. E. Rhoades, “Fixed Points for Set Valued Functions without Continuity,” Indian Journal of Pure and Applied Mathematics, Vol. 29, No. 3, 1998, pp. 227-238.
- S. Sessa, “On a Weak Commutativity Condition in Fixed Point Considerations,” Publications de l’Institut Mathé- matique (Beograd), Vol. 34, No. 46, 1982, pp. 149-153.
- H. Bouhadjera and C. Godet-Thobie, “Common Fixed Theorems for Pairs of Subcompatible Maps,” 2009.
- D. Gopal and M. Imdad, “Some New Common Fixed Point Theorems in Fuzzy Metric Spaces,” Annali dell’ Università di Ferrara, Vol. 57, No. 2, 2011, pp. 303-316. doi:10.1007/s11565-011-0126-4
- S. Manro, H. Bouharjera and S. Singh, “A Common Fixed Point Theorem in Intuitionistic Fuzzy Metric Space by Using Sub-Compatible Maps,” International Journal of Contemporary Mathematical Sciences, Vol. 55, No. 55, 2010, pp. 2699-2707.
- G. Deschrijver and E. E. Kerre, “On the Relationship between Some Extensions of Fuzzy Set Theory,” Fuzzy Sets and Systems, Vol. 133, No. 2, 2003, pp. 227-235. doi:10.1016/S0165-0114(02)00127-6
- G. Deschrijver, C. Cornelis and E. E. Kerre, “On the Representation of Intuitionistic Fuzzy T-Norm and T-Conorm,” The IEEE Transactions on Fuzzy Systems, Vol. 12, No. 2, 2004, pp. 45-61. doi:10.1109/TFUZZ.2003.822678
- M. Tanveer, M. Imdad, D. Gopal and D. Kumar, “Common Fixed Point Theorem in Modified Intuitionistic Fuzzy Metric Spaces with Common Property (E.A.),” Fixed Point Theory and Applications, Vol. 36, 2012. doi:10.1186/1687-1812-2012-36
- D. Turkoglu, C. Alaca, Y. J. Cho and C. Yildiz, “Common Fixed Point Theorems in Intuitionistic Fuzzy Metric Spaces,” Journal of Applied Mathematics and Computing, Vol. 22, No. 1-2, 2006, pp. 411-424. doi:10.1007/BF02896489
- C. Alaca, “A Common Fixed Point Theorem for Weak Compatible Mappings in Intuitionistic Fuzzy Metric Spaces,” International Journal of Pure and Applied Mathematics, Vol. 32, No. 4, 2006, pp. 25-36.
- S. Manro, S. Kumar and S. S. Bhatia, “Common Fixed Point Theorems in Intuitionistic Fuzzy Metric Spaces Using Occasionally Weakly Compatible Maps,” The Journal of Mathematics and Computer Science, Vol. 2, No. 2, 2012, pp. 73-81.
- R. P. Pant, “Common Fixed Foints of Four Mappings,” Bulletin of Calcutta Mathematical Society, Vol. 90, No. 4, 1998, pp. 281-286.

