Received 23 May 2016; accepted 28 May 2016; published 31 May 2016

ABSTRACT

The paper presents a very simple and straight forward yet pure mathematical derivation of the structure of actual spacetime from quantum set theory. This is achieved by utilizing elements of the topological theory of cobordism and the Menger-Urysohn dimensional theory in conjunction with von Neumann-Connes dimensional function of Klein-Penrose modular holographic boundary of the E8E8 exceptional Lie group bulk of our universe. The final result is a lucid sharp mental picture, namely that the quantum wave is an empty set representing the surface, i.e. boundary of the zero set quantum particle and in turn quantum spacetime is simply the boundary or the surface of the quantum wave empty set. The essential difference of the quantum wave and quantum spacetime is that the wave is a simple empty set while spacetime is a multi-fractal type of infinitely many empty sets with increasing degrees of emptiness.

Keywords:

Quantum Spacetime, Transfiite Theory, Noncommutative Geometry, ‘tHooft-Susskind Holography, Cantorian Spacetime, Penrose-Connes Fractal Universe, E-Infinity Theory, E8 Exceptional Lie Group

1. Introduction

Renown Austrian writer Ferdinand Kürnberger [1] once wrote “…and whatever a man knows, whatever is not mere rambling and roaring that he has heard, can be said in three words”. It seems that these words made such a strong impression on his fellow compatriot and Cambridge Professor, Ludwig Wittgenstein [2] that he made it to the motto of his most famous book “Tractatus Logico-Philosophicus” [2] .

In the present short paper the author goes even further than Wittgenstein by taking the three words to literally mean three steps leading to the emergence of spacetime from the quantum [3] - [24] . It is the main aim of the present analysis to give these three steps in an irreducibly simple way. To keep this simplicity as well as a short presentation we had to include a large selection of references [1] - [84] . In particular refs. [44] - [89] may be regarded as supplementary literature which may be skipped over at first reading and considered in depth only later at a second reading of the present paper.

2. The Emergence of Spacetime from the Quantum

The following derivation consists of exactly three steps as alluded to in our short introduction:

Step 1

We start with the quantum pre-particle as modelled by the zero set [3] . Consequently following the dimensional recursive function of von Neumann-Connes (see Appendix 1 for details), we have for the quantum particle [3] [5] [20]

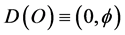
where the zero is the Menger-Urysohn topological dimension and 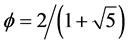is the Hausdorff dimension of the zero set.

Step 2

From step one it follows naturally that the surface of D(O) is given by the empty set [3] - [6] [36] [37] . Consequently the quantum wave as the cobordism of the quantum particle can be modelled by the empty set. This is given by the same dimensional function of von Neumann-Connes as [3] [20] [26]

.

A short explanation for the negative minus one topological dimension of the empty set is given in Appendix 2.

Step 3

Now it may come as a slight surprise that continuing in the same manner as above, the surface of the quantum wave turns out to be nothing else but our quantum spacetime [3] [25] [26]

.

In other words, quantum spacetime is an emptier set than the empty set. Not only that but the average empty set from 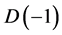to 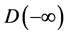turns out to have on average a Hausdorff dimension equal [3] [25] [26] . This follows neatly from the fact that the expectation value of quantum spacetime is given by the Hausdorff dimension of Cantorian spacetime 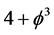[43] [57] . Therefore the average empty set dimension must be the reciprocal value of 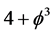which is. This proves the correctness of what we stated above [3] - [6] [36] [37] .

The preceding three steps give the quintessence of our theory and explain both the quantum wave and quantum spacetime in one stroke in terms of each other [3] . Quantum spacetime is simply the surface of the quantum wave in exactly the same manner as the quantum wave is the surface of the quantum particle. Thus quantum wave and quantum spacetime are basically more or less the very same substance or said more subtly, the very same “non-substance” [27] [42] . Implications for ‘tHooft-Susskind holographic theory and the black hole information paradox will not be discussed here [18] [19] .

3. The Hausdorff Dimension of Space, Time and Spacetime

Let us consider the dimensions corresponding to the unfolding of our three basic steps or basic sets.

Set 1

Unfolding the zero set with which we mean moving from the negative topological dimensions domain to the positive one by inversion [3] - [10] one finds

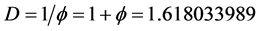
This we interpret as a one dimensional classical string plus an irrational tail (f). In other words 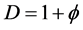represents what we may call a fractal string.

Set 2

In analogy to the preceding zero set, our empty set leads to [3] - [10]

This may be interpreted as a classical world sheet plus an irrational tail. Again this may be seen as a fractal world sheet [3] - [10] . It is remarkable how the intersection as well as the union of the fractal strings and the fractal world sheet span the E-infinity Cantorian space modelling quantum spacetime because [43] [57]

as well as

.

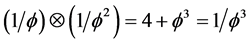Consequently we conclude from the above that there is an intrinsic indistinguishability latent in our Cantorian manifold modelling quantum spacetime with regard to the operations of union and intersection, which explains the superficially paradoxical outcome of the two-slit experiment with quantum particles [71] . In fact we can reason that time is a fractal phenomena of our “space-time” manifold. The simplest way to show this is to consider the average zero-like set and empty set with Hausdorff dimension ranging from zero to f. This is easily found to be which is a sort of coarse graining zero set [39] . Inserting into the expectation formula for the topological dimension and the Hausdorff dimension we find for the topological case [39] [40]

and for the Hausdorff counterpart

respectively. The time dimension is consequently the difference between the two:

The preceding remarkable result could be used to elucidate the strong link between number theory and physics. We could for instance argue that our classical 3D space is simply an “integer” approximation of the basic two dimensions

and

leading to

On the other hand Einstein’s 4D could be seen as a rational approximation

and

leading to

An even more striking feature of the deep relation between number theory as well as transfinite set theory and physics as seen through the mathematics of our present analysis is the following result which follows from the inversion of the zero set and empty set at the averaging level [39]

and

This leads clearly to

and

In other words the empty set quantum wave gives us directly the topological dimension of spacetime while the zero set particle gives us the topological dimension of the spacetime world sheet [3] - [10] [43] [48] . Clearly two world sheets corresponding to two quantum particles will give rise to spacetime dimensions when interacting whether by union, i.e. addition rule or intersection, i.e. multiplication rule because of the unique although trivial equation

There are no other two integers which could stimulate the basic interaction of our two irrational numbers and except 2 and 2 as we pointed out on earlier occasions in more detail [38] [43] . However we feel that the present discussion which started with von Neumann-Connes recursive Fibonacci-like dimensional function (see Appendix 1) is mathematically much deeper and testifies for what we call post modernistic physics with which we anticipate a new era in physics were pure mathematics and real physics are one and the same thing [3] .

4. Conclusion

“God made the bulk ‘but’ the surface was invented by the devil”. This is a well known quotation ascribed to Wolfgang Pauli which may be viewed as the theme for the present work. On the other hand the present work showed how the word bulk could be replaced by the quantum particle and then concluded that the quantum wave is simply the “surface” of this particle. Going one step further it was shown here in unheard of simplicity that spacetime is the multilayer (multi-fractal) surface of the quantum wave. This demonstrates how in three simple steps spacetime emerges from the quantum. Seen that way the surface as well as ‘tHooft-Susskind holography is definitely not an invention by the devil but a great idea of deep, subtle beauty worthy of the great pure mathematician who created existence.

Cite this paper

Mohamed S. El Naschie, (2016) The Emergence of Spacetime from the Quantum in Three Steps. Advances in Pure Mathematics,06,446-454. doi: 10.4236/apm.2016.66032

References

Appendix 1

The present analysis and derivation depends fundamentally upon the von Neumann-Connes recursive dimensional function [25] [32]

and

This function was used to describe superficially pathological x spaces such as that of Penrose tiling in noncommutative geometry [33] [34] . Subsequently the present author demonstrated that the Penrose fractal tiling may be viewed as a compactified Klein modular curve with degrees of freedom and that as such it is generic and represents the surface or the holographic boundary of a universe described in bulk by E8E8 exceptional Lie groups of super strings [57] . The dimensionality conservation equation connecting E8E8 with the Klein-Penrose boundary may be given in various forms of which the following is the simplest [19] [43] [49]

where is the inverse electromagnetic fine structure constant and G = 20 is the degrees of freedom of pure gravity in D = 8 super space or alternatively, the number of the independent components of the Riemannian curvature tensor in D = 4 Einstein space [43] [49] .

Appendix 2

The following illustrates and derives the basic results of cobordism as applied to our theory in an elementary fashion. We start from a three dimensional cube. The surfaces of the cube are evidently square, i.e. two dimensional. This means we have an equation stating that [3] - [16]

where n = 3 for a cube and it follows then that its “borders” or surface have. It is trivial to see that the same will go on for the square where the “borders” are one dimensional lines

.

For a line the “borders” are the end points so that our elementary equation still holds

.

The next step is on the other hand not trivial. We ask our self what is the border” or the surface of a point? The point is a zero dimensional object, which in theory is the best model of a pre-quantum particle and now we are de facto asking what is the dimension of the neighbourhood of a zero point? Our equation says then that it is

.

This is exactly how K. Menger and P. Urysohn defined the empty set [36] [37] . The present author, following various ideas partially connected to Mandelbrot’s notion of the degrees of emptiness of an empty set, then reasoned that the total insubstantial nothingness is neither the zero set nor the empty set but the completely empty set [20] [26] [39] [40] .