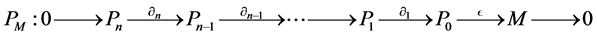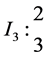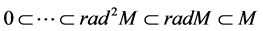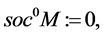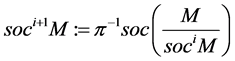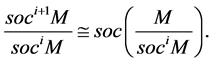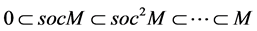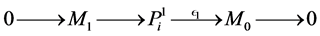Received 27 October 2015; accepted 21 December 2015; published 24 December 2015

ABSTRACT

Our purpose in these notes is to present a result for a specific Nakayama Algebra. In essence, it affirms that for any order of simple modules, the cyclic Nakayama Algebras with relations 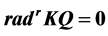(i.e.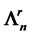) are not standardly stratified or costandardly stratified.

Keywords:

Standardly Stratified, Cyclical Nakayama Algebras, Infinite Projective Dimension

1. Introduction

The aim of this paper is to present a series of results obtained in relation to a particular class of Nakayama algebras. We will begin by recalling the fundamental notions and results of standarly stratified and almost hereditary algebras theory, which will be our main tool.

The concept of standardly stratified algebras emerged as a natural generalization of quasi-hereditary algebras. The class of quasi-hereditary algebras was introduced by Cline, Parshall and Scott in connection with their study of highest weight categories arising in the representation theory of semisimple complex Lie algebras and alge- braic groups.

We present our first result, which allows to obtain the main theorem of the article as an immediate con- sequence.

Theorem 1. Let L be an algebra, such that all non trivial quotient of indecomposable projective has infinite projective dimension, then L is not a standardly stratified algebra for any order of simple modules, unless 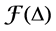is the subcategory.

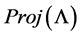Later, we introduce some notions of uniserial algebras and uniserial modules. In section 4, we introduce Nakayama algebras, also known as uniserial generalised Algebras that are studied by Tadasi Nakayama in [1] . In his short notes, as Nakayama called his publication, it was proposed to make some observations to his previous publication about Frobeniusians Algebras, whose first part was published in 1939 at Annals of Mathematics.

We conclude by presenting a special class of Nakayama algebras, for which is the main result of this paper that we quote below:

Theorem 2. There is no simple order of simple modules for which the cyclical Nakayama Algebras with rela- tions 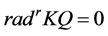(i.e.) are standardly stratified or costandardly stratified.

2. Projective Dimension, Injective Dimension and Global Dimension

The following concepts will allow us to define the notions of projective dimension, injective dimension and global dimension; which we will be very useful in demonstrating the fundamental result of this paper.

Definition 1. Let M be an L-module. A projective resolution of M is a complex P whit 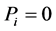for in

where 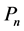is a projective module for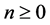. It should also satisfy that the map 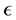is an epimorphism and.

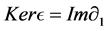It is possible show that being L a K-algebra, it follows that every 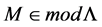has a projective resolution in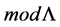. More generally , if an abelian category A has enough projectives, then every object M in A has a pro- jective resolution.

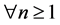
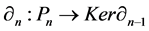
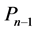
Definition 2. Let M be an L-module. A minimal projective resolution of M is a projective resolution of M such that, the homomorphism is a projective cover and is a pro- jective cover of M.

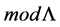
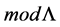
Dually we define concepts injective resolution and minimal injective resolution. Is possible also prove that if L is a finite dimensional algebra then all module in has a minimal projective resolution and minimal injective resolution in. The concepts of projective dimension, injective dimension and global dimension for a L-module M are as follows.

Definition 3. Projective dimension of L-module M is the number 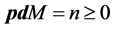such that there is a pro- jective resolution,

M of length n and M does not have projective resolution of length. If M does not admit a finite projective resolution, then by convention the projective dimension is said to be infinite.

Dually it has the injective dimension of a L-module M.

Definition 4. Let L be an finite dimensional K-algebra. The global dimension is the supremum of the set of projective dimensions of all L modules, i.e.

.

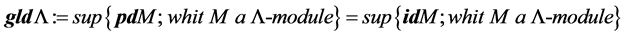
3. Standarly Stratified Algebras and Quasi-Hereditary Algebras

Let R be a commutative Artin ring and L a basic Artin algebra over R. As further we assume full subcategories of, unless otherwise stated. We consider K-algebras of finite dimension basic and indecomposable, where K is an algebraically closed field and by the Gabriel theorem, , where Q is a finite quiver and I is an admissible ideal.

The principal results of this section can be find in [2] - [8] .

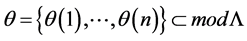
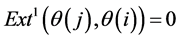
Definition 5. Let L be a Artin algebra and such that,. We denote:

1. the class of for wich there is a chain of submodules with.

2. the subcategory on of modules are direct summands of modules in.

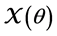
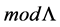
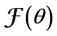
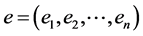
In the following we consider that L denote an -algebra to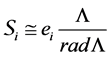gether with a fixed ordering on a complete set of primitive orthogonal idempotents (given by the natural ordering of indices). Note that con- sider the system e is equivalent to consider an order established of set of all simple L-modules not isomorphic

to (we know to be L an Artin algebra has a finite number of L-modules).

Definition 6. Let M be a L-module. A normal series in M is a sequence of submodules

.

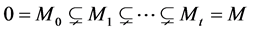
The number t is called the length of the series. The quotients 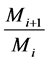are called factors of the series. A series

of composition is a normal series whose factors are simple modules, i.e., a normal serie which can not be refined to another longest.

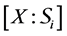
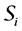
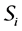
If X is a L-module, we denote by the number of factors isomorphic to in composition series X, ie, the multiplicity of as composition factor of X.

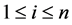
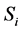
For, let be the simple L-module, which is the simple top of the indecomposable projective.

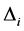
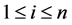
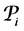
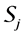
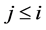
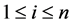
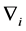
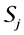
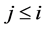
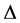
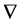
Definition 7. Standard module, for, is the maximal factor module of without composition factors, for. Dually for, module coestndar is the maximum submodule without composition factors, for. Let be the full subcategory consisting of all. In similar way, we introduce, and so on.

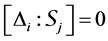
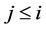
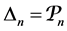
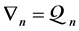
Note that the above definition implies that to and module. Dually, it has that to and module.

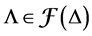
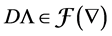
Definition 8. An algebra L is said standardly stratified if. If in addition to that, the endomorphism ring of each standard module is simple then we say that algebra is quasi-hereditary (i.e. standardly stratified algebras generalize the concept of quasi-hereditary algebras where we require the additional condition that the standard modules are Schur modules). Dually, if we say that L is costandarly stratified.

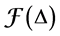
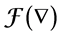
Note that if L is standardly stratified the projective modules are in. In addition, if L is quasi- hereditary the injective modules are and.

The following example will allow us to understand the theory discussed above.

Example 3.1. Let L be the algebra given by the following quiver whit relations;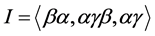

We have to:

and

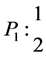
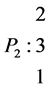
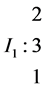
It is not difficult to check that this algebra is standardly stratified and costandardly stratified only at orders for respective simple modules given below:

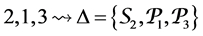
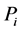
1. To order all are filtered.

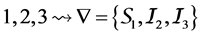
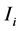
2. To order all are filtered.

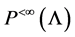
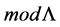
We denote by the full subcategory of defined by modules of finite projective dimension. The following result is in [8] which will be of great utility.

Proposition 3. Let L be an standardly stratified algebra, then.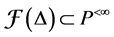

The following theorem is the first result that present us in this paper. It will allow us to obtain, as an immediate consequence, our main result.

Theorem 4. Let L be an algebra, such that all non trivial quotient of indecomposable projective has infinite projective dimension, then L is not standardly stratified algebra for any order of simple modules, unless is the subcategory.

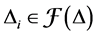
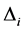
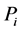
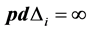
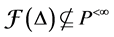
Proof. It’s clear that. Furthermore is quotient of projective. As we assume that all in- decomposable projective quotient has infinite projective dimension then therefore so L is standardly stratified in any order of simple modules.

4. Nakayama Algebras

Throughout, L is assumed to be a finite dimensional K-algebra, defined over an algebraically closed field K.

The principal results of this section can be find in [1] [9] [10] .

Definition 9. Let M be a L-module. Radical series M is defined as follows:

We agree to denote by 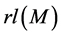the radical series length of M.

We can define inductively soclo series for module M as:

where 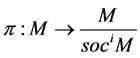is the quotient application, i.e.

We denote 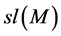the soclo series lenght of M.

Note that if, and furthermore it has to. This clearly implies that the radical

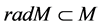
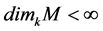
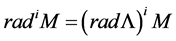
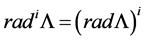
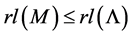
series M is finite. How, then and.

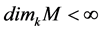
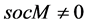
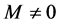
We can observe that, then if and the soclo series

is finit.

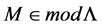
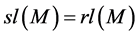
Proposition 5. Let, then.

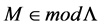
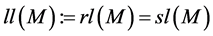
Definition 10. Let, the Loewy lenght of M is defined by.

Is necessary introduce new notion for define the Nakayama Algebras.

Definition 11. Let M be an L-module. We say that M is uniserial if M possesses exactly one composition series.

Lemma 4.1 Let M be an L-module. Next conditions are equivalents.

1. M is uniserial;

2. Radical series of M is a composition serie;

3. Soclo series of M is a composition serie;

4..

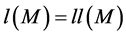
Definition 12. Let L be an K = - algebra. L is right serial if all right indecomposable projective is a uniserial L-module. Dually define us the left indecomposable projective notion.

If denote the underlying quiver of L then,

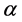
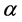
Theorem 6. A basic K-algebra L is left serial izquierda if and only if for each vertex in there is at most one arrow that starts in.

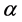
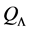
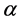
Corollary 1. A basic K-algebra L is right serial if and only if for each vertex in there is at most one arrow that ends in.

Definition 13. The algebra L is a Nakayama Algebra if every projective indecomposable and every injective indecomposable L-module is uniserial.

It is possible to characterize Nakayama Algebras through its underlying quiver.

Theorem 7. A basic and connected algebra L is a Nakayama Algebra if and only if 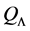it has one of the forms:

or (cyclical)

Proof. Immediately of Theorem 6 and Corollary 1.

5. Main Result

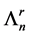
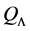
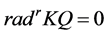
Let L be a Nakayama algebra. We denote the Nakayama algebra with cyclical underlying quiver with relations.

In [11] , it shows that both 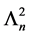and are not standarly stratified or costandarly stratified to any order of the simple modules, which motivates us to prove the following generalization of these results.

Theorem 8. There is no simple order of simple modules for which the cyclical Nakayama Algebras with rela- tions (i.e.) are standardly stratified or costandardly stratified.

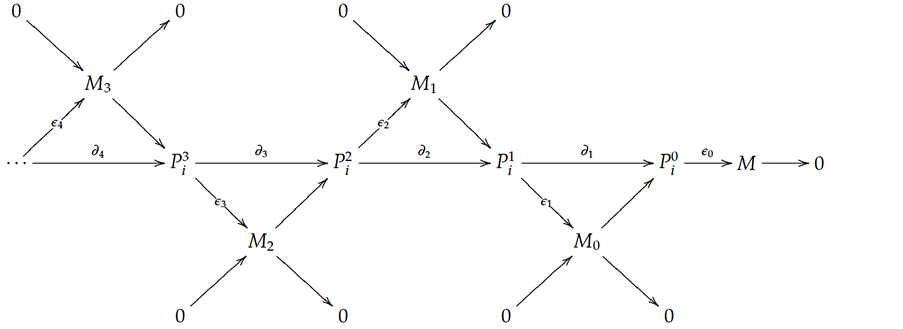
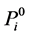
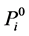
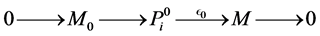
Proof. It is easy to see that every projective module has the same length and we also know that has an only one composition series. Let M be a quotient of projective module and consider the following short exact sequence,

.

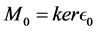
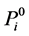
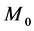
Note that the length of L-module is strict less than, therefore is not projective. Now the following short exact sequence is considered,

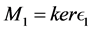
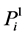
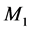
in which, again, we note us that the length of L-module is strict less than, therefore is not projective.

Inductively, given a module we choose a projective and a surjection. Let, and let be the composite. Since, this chain complex is a projective resolution of M,. Then, through Theorem 12, the result is concluded.

□

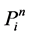
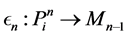
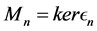
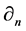
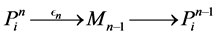
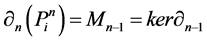
Commentary 5.1. Generally Nakayama algebras that are not 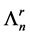may be standarly stratified or not to be, as we saw in Example 3.1.

Acknowledgements

We thank the Editor and the referee for their comments.

Cite this paper

José Fidel Hernández Advíncula,Rafael Francisco Ochoa de la Cruz, (2015) Stratification Analysis of Certain Nakayama Algebras. Advances in Pure Mathematics,05,850-855. doi: 10.4236/apm.2015.514079

References