Received 19 February 2015; accepted 12 March 2015; published 23 March 2015

ABSTRACT

In the paper N˚II, we describe some isomorphism classes and we apply their properties to the study of five crystal families of space E⁵. The names of these families are the following ones (monoclinic di iso squares)-al, decadic-al, (monoclinic di iso hexagons)-al, (rhombotopic)-al and rhombotopic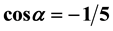. The meaning of these names will be given in Paragraphs 5 and 6 with some geometric properties of their cell.

Keywords:

Crystal Families of Space E⁵, Names, Point Groups of the Families, Rhombotopic Crystal Families

1. Introduction

Besides the study of the isomorphism classes and in order to complete the study of the crystal families of space E⁵, five families are studied in this paper:

1) The crystal families N˚XXIII (monoclinic di iso squares)-al, N˚XXIV decadic-al and N˚XXV (monoclinic di iso hexagons)-al. The suffix “al” means that the family cell in space E⁵ is a right hyper prism based on a cell of space E⁴. The WPV holohedry symbols are ([8] 2 2)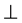 m, group of order 32 for the family N˚XXIII, ([10] 2 2) m, group of order 40 for the family N˚XXIV and ([12] 2 2)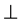 m, and group of order 48 for the family N˚XXV. These families have 7, 12, and 7 crystallographic (cr) point groups respectively. We remark that the WPV symbol of the holohedry of these families contains double rotations of order 8, 10 and 12 (Paragraphs 2, 3 and 4).

2) The crystal families N˚XXX (rhombotopic)-al and N˚XXXII rhombotopic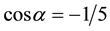. The meaning of these names will be given in Paragraphs 5 and 6. The family N˚XXX splits in two sub-families:

the centred family N˚XXXa with group 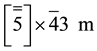of order 240 for holohedry and 8 cr point groups; the

primitive family N˚XXX with group 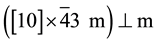of order 480 for holohedry and 15 cr point groups.

The WPV holohedry symbol of family N˚XXXII is 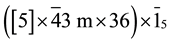of order 1440 and this family has 10

cr point groups. Some cr point groups of the family N˚XXX are obtained from those of the rhombotopic 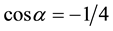family of space E⁴ while all the 10 cr point groups of the family N˚XXXII belong to space E⁵. Moreover, this family is one of the irreducible families of space E⁵ [1] .

The mark “×” means direct product.

To end the study of the crystal families of space E⁵, the crystal families (hypercube 4 dim.)-al (N˚XXVIII), (di iso hexagons)-al (N˚XXIX) and hypercube 5 dim. N˚XXXI will be described in the next paper.

The results about the cr point groups are obtained from our Scientific Software SS E5 (explanations are given paper N˚1).

2. (Monoclinic di iso Squares)-al Crystal Family. Point Groups. Isomorphism Classes

2.1. Recall

Let be denoted 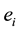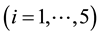, the 5 vectors of a basis of space E⁵. The metric tensor of the quadratic form defining a cell is a symmetric tensor with the scalar products. as elements.

2.2. Cell of the (Monoclinic di iso Squares)-al Crystal Family (N˚ XXIII)

The cell of the “(monoclinic di iso squares)-al” family is a right hyper prism, generalization of the right prism of space E³. The word “al” is the abbreviation of the adjective orthogonal”.

The metric tensor of the quadratic form defining the cell of this family is as follows (matrix N˚1):

Matrix N˚1 associated with the cell of the (monoclinic di iso squares)-al family

Caption

As the name suggests, this cell is a right hyper prism which basis is built from two equal squares in space E⁴. These two squares are built in the planes defined by the axes for the first one and by the axes for the second one; these two planes are not orthogonal but the angles between them depend on one angular parameter b. It is the reason why the word “monoclinic” appears in the family name. One of the two length parameters is the length of the two square sides, the other one is the length of the edge of the hyper prism (see the caption of the matrix N˚1).

The angles between the axes and on one hand, between the axes and on the other hand have equal values while the axis is orthogonal to the space defined by the axes, , ,.

2.3. Crystallographic Point Groups of the (Monoclinic di iso Squares)-al Family

The WPV symbols of all cr (cr for crystallographic) point groups of the family (monoclinic di iso squares)-al

contain groups or either alone or as product with one or two binary groups such as m, 2,. It is a

characteristic property of the cr point groups of this family. We recall that [8] is the WPV symbol of the cyclic group generated by the double rotation through angles and denoted 8¹8³, these two rotations 8¹ and 8³ take place into the planes and. The elements of the cyclic group [8], isomorphic to group C₈, are 8¹8³, 4¹4³, 8³8¹, , 8⁵8⁷, 4³4¹, 8⁷8⁵, 1.

In the same way, is the WPV symbol of a cyclic group of order 8 generated by the symmetry operation, being the total homothetie of space E⁵. The group has for elements 8¹8³m_u, 4¹4³, 8³8¹m_u, ,

8⁵8⁷m_u, 4³4¹, 8⁷8⁵m_u, 1, where u is the unit vector of the axis e₅ orthogonal to space E⁴.

Group cannot be confused with the following two groups of order 16, and, the last

one acts into a space of dimension 9 = 4 + 5 and belongs to the crystal family “(monoclinic di iso squares) decaclinic”.

Table 1 lists the seven cr point groups of family XXIII which belong to four isomorphism classes, C₈, D₈, C₈ × C₂, D₈ × C₂, D₈ is the dihedral group of order 16 (see Annex, paper N˚I).

Remark

WPV symbols, , and of the groups of the isomorphism class D₈ are very similar

to Hermann-Mauguin symbols 4 mm, 422, (groups of the isomorphism class D₄).

3. (Monoclinic di iso Hexagons)-al Crystal Family. Point Groups. Isomorphism Classes

3.1. Cell of the (Monoclinic di iso Hexagons)-al Crystal Family (N˚XXV)

Family N˚XXV, (monoclinic di iso hexagons)-al, presents great similarities with family N˚XXIII (monoclinic di iso squares)-al. The metric tensor of the quadratic form defining the cell of this family is as follows (matrix N˚2):

Matrix N˚2 associated with the cell of the (monoclinic di iso hexagons)-al family in space E⁵

Caption:

The cell of this family is a righthyper prism which basis in space E⁴ is built from two equal hexagons into the planes defined by the axes for the first one and by the axes for the second one; these planes are not orthogonal and the angles between these two planes depend on one angular parameter b. It is the reason

Table caption: First column: Symbols of the isomorphism classes. Second column: Order classes. Third column: WPV symbol of the point groups of the (monoclinic di iso squares)-al family in space E⁴. Fourth column: WPV symbol of the point groups of the (monoclinic di iso squares)-al family in space E⁵. Fifth column: Lists of the elements of the isomorphism classes denoted arrangement. SS E5 gives this information.

why the word “monoclinic” appears in the family name. One of the two length parameters is the length of the two hexagon sides, the other one is the length of the edge of the hyper prism, b is the angular parameter (see caption of matrix N˚2).

3.2. Crystallographic Point Groups of the (Monoclinic di iso Hexagons)-al Crystal Family

All WPV point group symbols of this family contain the group [12] or either alone or as product with

one or two binary groups such as m, 2,. It is a characteristic property of the cr point groups of this family.

We recall that [12] is the WPV symbol of the cyclic group of order 12, isomorphic to group C₁₂. It is generated by the double rotation 12¹12⁵ through angles 2π/12 and 5 × 2π/12, each of these rotations 12¹ and 12⁵ takes place into the planes and. The group [12] elements are the following ones 12¹12⁵, 6¹6⁵, 4¹4¹,

3¹3², 12⁵12¹, , 12⁷12¹¹, 3²3¹, 4³4³, 6⁵6¹, 12¹¹12⁷, 1. In the same way, the group denoted is the WPV

symbol of the cyclic group of order 12 generated by the symmetry operation or 12⁷12¹¹m_u. The ele-

ments of the group are 12⁷12¹¹m_u, 6¹6⁵, 4³4³m_u, 3¹3², 12¹¹12⁷m_u, , 12¹12⁵m_u, 3²3¹, 4¹4¹m_u, 6⁵6¹,

12⁵12¹m_u, 1.

Group cannot be confused with the following two groups of order 24, and, the last group acting into a space of dimension 9 = 4 + 5.

Table 2 lists the seven cr point groups of family N˚XXV, these groups belong to four isomorphism classes C₁₂, D₁₂, C₁₂ × C₂, D₁₂ × C₂ (D₁₂ is the dihedral group of order 24).

Remark

WPV symbols, and of the groups of the isomorphism class D₁₂ are very

similar to Hermann-Mauguin symbols 4 mm, 422, (groups of the isomorphism class D₄).

4. Decadic-al Crystal Family. Point Groups. Isomorphism Classes 6

4.1. Cell of the Decadic-al Crystal Family (N˚ XXIV)

The word “decadic” means that double rotations of order 10 belong to several cr point groups of this family.

The cell of the decadic-al family is a right hyper prism, the basis of which is a particular parallelotope of space E⁴. The faces of this cell are equal lozenges in planes and, so are the faces in planes and but these lozenges are different from the previous ones. The metric tensor of the quadratic form of the decadic-al family is as follows:

Table caption: First column: Symbols of the isomorphism classes. Second column: Order of these classes. Third column: WPV symbol of the point groups of the (monoclinic di iso hexagons)-al family in space E⁴. Fourth column: WPV symbol of the point groups of the (monoclinic di iso hexagons)-al family in space E⁵. Fifth column: Lists of the elements of the isomorphism classes. SS E5 gives this information.

Matrix N˚3 associated with the cell of the (monoclinic di iso hexagons)-al family

Caption:

This metric tensor depends on three parameters of length a, b and c; the parameter is the length of the side of the first lozenge, the one of the second lozenge and the hyperprism side. The angles between the axes depend on the two parameters a and b.

Family N˚XXIV splits in two sub-families, the centred sub-family N˚XXIVa and the primitive sub-family N˚XXIV.

4.2. Crystallographic Point Groups of the Two Decadic-al Crystal Sub-Families

All the WPV point group symbols of these two families contain groups or (family N˚XXIVa) and

group [10] (family N˚XXIV) either alone or as product with a binary group such as 2, , m, ・・・ It is a charac-

teristic property of the cr point groups of these families. Symbols, , have the same meaning as

[8] and or and (see Paragraphs 2-3 and 3-2).

The five cr point groups of the sub-family N˚XXIVa belong to four isomorphism classes C₅, D₅, C₁₀ = C₅ × C₂, D₁₀ = D₅ × C₂ and the seven cr point groups of the sub-family N˚XXIV belong to four isomorphism classes C₁₀, D₁₀, C₁₀ × C₂, D₁₀ × C₂. Groups D₅ and D₁₀ are dihedral groups of orders 10 and 20. Table 3 gives the list of the point groups of the decadic-al sub-families. Only groups of centred sub-family XXIVa are pointed out.

Remarks

・ One group of class C₁₀ belongs to the centred sub-family and two to the primitive sub-family.

・ . This group is a cyclic group of order 10, generated by the symmetry 10¹10³m_u operation. Its

elements are 10¹10³m_u, 5¹5³, 10³10⁹m_u, 5²5¹, , 5³5 ⁴, 10⁷10¹m_u, 5⁴5², 10⁹10⁷m_u, 1. We explain how the planes of the double rotation 10¹10³ can be defined. Indeed,thanks to the symmetry operation list, it is easy to find the generators of the different cr point groups. With respect to the general basis, e₂, e₃, e₄, e₅ or x, y, z, t, u, the double rotation [10] is generated by the symmetry operation described by the following matrix A:

Table caption: First column: Symbol of the isomorphism classes. Second column: Order of these classes. Third column: WPV symbols of the point groups of the decadic-al family in space E⁴. Fourth column: WPV symbols of the point groups of the decadic-al family in space E⁵. Fifth column: Lists of the symmetry elements with their number of every isomorphism class.

Matrix N˚4 associated with the double rotation 10¹10³

It is possible to calculate the roots of the characteristic polynomial of the matrix and the eigen subspaces associated to the different eigen values. As the double rotation [10] takes place in a four-dimensional space, the eigenvalue 1 appears. The other eigen values of the matrix are and. This double rotation 10¹10³ takes place in the two planes defined by the axes:

and for the rotation 10¹

, for the rotation 10³.

The coefficients which define the planes are

For all the symmetry operations of the group, we repeat the same process. For instance, the double rotation [5] is generated by the element 5¹5³ which is described by the matrix:

Matrix N˚5 associated with the double rotation 5¹5³

The eigenvalues are numbers and and 1. The same process leads to the same eigen subspaces for double rotation [5] as for double rotation [10].

5. (Rhombotopic)-al Crystal Family. Point Groups. Isomorphism Classes

The crystal family N˚XXX splits into two sub-families, one primitive sub-family N˚XXX, one centred sub-family N˚XXXa. This family is a particular case of the (rhombotopic)-al family. The cell of this family is a right hyper prism which basis is a regular rhombotope. We remind some properties of these types of cells.

5.1. Generalities about the (Rhombotopic)-al Family

The cell of the (rhombotopic)-al family is a right hyperprism of the -dimensional space. The base of this cell is a regular rhombotope of the n-dimensional space. The metric tensor associated to the basis in space E^{n + 1} is the matrix N˚6. The n vectors of the lattice basis of the space Eⁿ have the same norm and the cosine of the angle between two of them is. The norm of the vector is and this vector is orthogonal to space Eⁿ.

Matrix N˚6 associated with the cell of the (rhombotopic)-al crystal family

Caption:

5.1.1. Description of Some Simplexes

A simplex is the generalization of a triangle. Any set of points which do not lie in one -di- mensional space are the vertices of an n-dimensional simplex. A regular simplex has all edges equal, all faces equal and so on. For instance, regular simplexes are the equilateral triangle (space E²), the regular tetrahedron (space E³), the regular pentatope (space E⁴) in [2] [3] .

A regular simplex is not a crystal cell in (E³). To obtain a crystal cell, we must add a second regular simplex symmetrical to the previous one at the centre of the initial cell and so the lattice of the crystal (rhombotopic) family is obtained.

Some additional properties are given in the Annex.

5.1.2. Point Groups of the Simplexes and of the (Rhombotopic) Family

Now, it is easy to find the WPV point groups of some regular simplexes and the holohedries of the associated crystallographic family together with its order. Table 4 gives point groups of some simplexes and of some rhombotopic crystal families.

[7] is the abridged WPV symbol of a cyclic group of order 7 generated by the triple rotation of space E⁶,.

5.2. Primitive (Rhombotopic)-al Sub-Family

The cell of the primitive (rhombotopic)-al sub-family is a right hyper prism which basis is the regular rhombotope of space E⁴. Hence, the previous results are applicable. This family can be considered as a particular case of the decadic-al family if the parameter b is equal to.

The metric tensor of the quadratic form of the primitive family N˚XXX is as follows (matrix N˚7):

Matrix N˚7 associated with the cell of the (rhombotopic)-al family

Caption:

This metric tensor depends on two parameters of length a and c.

Table caption: First column: WPV point group symbols of simplexes. Second column: Order of these point groups. Third column: Space of these simplexes. Fourth column: WPV symbol holohedries of the (rhombotopic) families. Fifth column: Order of these point groups.

5.3. Isomorphism Classes of the Two Sub-Families (Rhombotopic)-al of Space E⁵

The isomorphism classes have point groups belonging to the two sub-families N˚XXXa and N˚XXX so that it is useful to gather them, only groups of sub-family N˚XXXa are pointed out. To sum up, the eight cr point groupsof sub-family N˚XXXa and the five teen cr point groups of sub-family N˚XXX belong to nine isomorphism classes. Table 5 gives all this results.

Remarks

・ In the isomorphism class S₅ × C₂, only one group, [10] × (42 3 2), is a positive point group, two groups are of the type g₄m with group g₄ acting in space E⁴.

・ The list of symmetry operations of all cr point groups of space E⁵ established by Veysseyre [4] gives ten mirrors to the group. The symmetry group of the regular tetrahedron has six mirrors. The(rhombotopic)-al cell is bounded by five regular tetrahedrons, therefore, we can expect to find 6 × 5 = 30 mirrors, but each mirror of this cell belongs to three adjacent tetrahedrons, then, it remains 30/3 = 10 different mirrors. In the same way, the list of the symmetry operations gives ten symmetry operations to the group. To each mirror m, we can associate a total homothetie of space E⁴ orthogonal to the mirror. It is the reason why we find the same number of mirrors and of total homotheties.

・ Groups (42 3 2) and are two iso cubic groups isomorphic to cr cubic point group. Iso cubic point groups have been defined and studied in [5] .

Table caption: First column: Symbols of the isomorphism classes and these orders. Second column: Lists of the symmetry elements with their number of every isomorphism class. Third column WPV symbols of the point groups of the (rhombotopic)-al family in space E⁴. Fourth column: WPV symbols of the point groups of the (rhombotopic)-al family in space E⁵.

6. Rhombotopic Crystal Family. Point Groups. Isomorphism Classes

This family (N˚XXXII) is a particular case of the families studied Paragraph 5-1. The metric tensor of the quadratic form of family XXXII is as follows (Matrix N˚8):

Matrix N˚8 associated with the cell of the rhombotopic family

Caption:

The ten point groups of the irreductible family N˚XXXII are listed Table 6, they act in five-dimensional space and they belong to eight isomorphism classes.

7. Conclusions

Thanks to the geometric approach, thanks to the study of the isomorphism classes of cr point groups in spaces E², E³, E4 and E⁵ and thanks to the Hermann-Mauguin or WPV symbols, we prove that substitutions groups, cr point groups, molecular or polytope symmetry groups are strongly correlated. Cayley’s theorem anticipates this property. Let us verify these properties through Table 7 and Table 8.

Table 7 lists some cr point groups isomorphic to mathematic groups C_n and D_n, from to. The numbers of the families 60 and 61 are given in [6] .

・ [7] is the symbol of a cyclic group of order 7, in space E⁶. It is generated by the triple rotation 7¹7²7³ through angles 2π/7, 2 × 2π/7 and 3 × 2π/7; each of these rotations 7¹, 7² and 7³ takes place into the planes, and. The elements of group [7] are the following ones: 7¹7²7³, 7²7⁴7⁶, 7³7⁶7², 7⁴7¹7⁵, 7⁵7³7¹, 7⁶7⁵7⁴, and 1. All these elements, except for 1, are of order 7.

・ [9] is the symbol of a cyclic group of order 9, in space E⁶. It is generated by the triple rotation 9¹9²9⁴ through angles 2π/9, 2 × 2π/9 and 4 × 2π/9; each of these rotations 9¹, 9² and 9⁴ takes place into the planes, and of space E⁶. The elements of group [9] are the following ones: 9¹9²9⁴, 9²9⁴9⁸, 3¹3²3¹, 9⁴9⁸9⁷, 9⁵9¹9², 3²3¹3², 9⁷9⁵9¹, 9⁸9⁷9⁵, and 1; two elements of this group are of order 3, and the other ones are of order 9, except for 1.

Table caption: First column: Symbols of the isomorphism classes. Second column: Orders of these classes. Third column: WPV symbols of the cr point groups of the rhombotopic family in space E⁵. Fourth column: Lists of the symmetry elements with their number of every isomorphism class.

Table caption: First column and fourth column: Symbols of the isomorphism classes. Second column and fifth column: WPV symbols of the point groups. Third column: Generators of the point groups. Sixth column: Family names.

Table caption: First column: Symbols of the isomorphism classes. Second column: Lists of the symmetry elements with their number of every isomorphism class. Third column: WPV symbols of the dihedralpoint groups in space E⁴. Fourth column: WPV symbols of the dihedral cr point groups in space E⁵. Fifth column: Names of the crystal families.

・ [11] is the symbol of a cyclic group of order 11, in space E⁸. It is generated by a «quadruple» rotation 11¹11²11³11⁴ through angles 2π/11, 2 × 2π/11, 3 × 2π/11 and 4 × 2π/11; each of these rotations 11¹, 11², 11³ and 11⁴ takes place into the planes, , and of space E⁸. The elements of group [11] are the following ones: 11¹11²11³11⁴, 11²11⁴11⁶11⁸, 11³11⁶11⁹11¹², 11⁴11⁸11¹11⁵, 11⁵11¹⁰11⁴11⁹, 11⁶11¹11⁷11², 11⁷11³11¹⁰11⁶, 11⁸11⁵11²11¹⁰, 11⁹11⁷11¹⁰11⁵, 11¹⁰11⁹11⁸11⁷, and 1; all the elements of this group are of order 11, except for 1.

In the same way, [13] is the symbol of a cyclic group of order 13, in space E⁸. It is generated by a «quadruple» rotation 13¹13²13³13⁴ through angles 2π/13, 2 × 2π/13, 3 × 2π/13 and 4 × 2π/13. The elements of this group are obtained as previously.

Table 8 gives the list of the cr point groups of the isomorphism classes D₈, D₁₂, D₅ and D₁₀ of the spaces E⁴ and E⁵.

If you like mathematic crystallography, it is easy to prove and to generalize these results to space Eⁿ whatever the dimension of space is.

References

Annex

Some Additional Results about the Symmetry of the Polyhedrons, Molecules, Holohedries of the Crystal Families in Spaces E², E³, E⁴, E⁵, ・・・

The definition of the simplexes with their properties has been given Paragraph 5-1.

Crystal family segment in space E¹: the holohedry m is a realization of mathematic group S₂ or D₂ with the list of element 1(2), in the set of the two cr point groups in E¹ (1, m). This symbol means that the segment is bounded by two points. The mirror, a point, is the middle of the segment.

Crystal family hexagon in space E²: the hemihedry 3 m is a realization of the mathematic group D₃ of order 6 with the list of elements 2(3) 3(2), in the set of the ten cr point groups of space E². This symbol means that the equilateral triangle is bounded by three equal segments. As an example, we can cite the chemisorbed (in a mono molecular layer) molecule BF₃.

The holohedry 3 m × 2 = 6 mm of order 12 is a realization of the mathematic group D₃ × C₂, with the list of elements 2(6) 2(3) 7(2). This symbol means that the regular hexagon in space E² is bounded by six equal segments. As example, we can cite the chemisorbed benzene molecule C₆H₆.

Crystal family cubic in space E³: the hemihedry is a realization of the mathematic group S₄ of order 24, with the list of elements 6(4) 8(3) 9(2), in the set of the thirty-two cr point groups of space E³. This symbol means that the regular tetrahedron in space E³ is bounded by four equilateral triangles. Group is the symbol of the cr point group of the molecule SiH₄ (or Td Schöenflies symbol) and the one of the crystal ZnO (blende) which has F as space group (International Tables of Crystallography) or Schöenflies symbol).

The holohedry is a realization of the mathematic group S₄ × C₂ of order 48 with the list of elements 8(6) 12(4) 8(3) 19(2), in same set of the point groups of space E³. This symbol means that the cube in space E³ is bounded by six equal squares. This symbol is the symmetry group of the regular octahedron, O_h or of the molecule Co(OH)₆.

Crystal family rhombotopic in space E⁴: the hemihedry is a realization of the mathematic group S5 of order 120 with the list of elements 24(5) 20(6) 30(4) 20(3) 25(2) in the set of the 227 cr

point groups of space E⁴. The holohedry WPV symbol is a realization of the

mathematic group S₅ × C₂ of order 240, with the list of elements 24(10) 24(5) 60(6) 60(4) 20(3) 51(2) in the set of the 227 cr point groups of space E⁴. This symbol means that the cell of this family, in space E⁴, is bounded by ten regular tetrahedrons.

Crystal family rhombotopic in space E⁵: the hemihedry is a realization of the mathematic group S₆ of order 720 with the list of elements 144(5) 240(6) 180(4) 80(3) 75(2) in the set of the

955 cr point groups of space E⁵. The holohedry is a realization of the

mathematic group S₆ × C₂ of order 1440, with the list of elements 144(10) 144(5) 560(6) 360(4) 80(3) 151(2) among the set of the point groups of space E⁵. The holohedry symbol means that the cell of this family is bounded by twelve regular rhombotopes of space E⁴.

NOTES

^*Corresponding author.