World Journal of Condensed Matter Physics
Vol.3 No.4(2013), Article ID:38332,4 pages DOI:10.4236/wjcmp.2013.34029
Anisotropic Magnetocaloric Effect and Magnetic Order in Antiferromagnetic Gd2InGe2
![]()
1Sandia National Laboratories, Albuquerque, USA; 2Instituto de Física, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil.
Email: lima.sharma@gmail.com
Copyright © 2013 A. L. Lima Sharma et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 7th, 2013; revised August 27th, 2013; accepted September 11th, 2013
Keywords: Intermetallic Compounds; Flux Growth; Magnetocaloric Effect; Anisotropy
ABSTRACT
We investigated the transport, thermal and magnetic properties of antiferromagnetic (TN = 45 K) Gd2InGe2. Magnetization measurements under applied magnetic field, oriented along different crystallographic directions, were used to extract the anisotropic magnetocaloric effect. We also measured magnetization under pulsed field up to 45 T. From the analysis of the electrical transport and magnetization, conduction band electrons were weakly coupled to Gd f-electron local moments. Differential scanning calorimeter data confirmed a second order phase of the antiferromagnetic to paramagnetic transition. The anisotropic magnetocaloric effect points to a model of magnetic ordering whereby Gd local moments couple ferromagnetically and antiferromagnetically perpendicular and parallel, respectively, to the c-axis.
1. Introduction
Magnetic refrigeration is based on the magnetocaloric effect, which is the ability of a solid to change its temperature with a change in magnetic field. The physical quantities that characterize the magnetocaloric effect (MCE) are DS, the isothermal entropy change, and DTad, the adiabatic temperature change. The presence of a structural transition concomitant with magnetic ordering increases the MCE. Gd-based compounds, such as Gd5Si2Ge2 [1,2], Gd5Ge4 [3,4], GdAl2 [5], have remarkable magnetocaloric properties and are considered for magnetic refrigeration application. Such compounds tend to have a large MCE due to a magnetostructural transition combined with the large Gd magnetic moment and reduced crystalline electrical field effects (zero orbital angular momentum), which reduces anisotropy in the magnetic properties.
Preliminary results on the intermetallic series RE2T2X (R = rare earth or actinide metal; T = late transition element; X = Mg, In, Sn, Cd) indicate unusual magnetic and electrical properties [6] and therefore, open the possibility of an unusual magnetocaloric effect. The crystal structure of the RE2InGe2 phases can be viewed as flat InGe2 layers stacked along the direction of the c-axiswith rare earth layers between them. In the present compound RE = Gd is 10 fold coordinated and a projection of the Gd sub-network also comprises planar layers stacked along the c-axis [6]. The effective magnetic moment was found to be 7.72 mb, similar to the effective moment for pure metallic Gd (7.0 mb). This fact suggests that the magnetism in Gd2InGe2 originates from the Gd local moments. Based on the magnetic susceptibility, the Gd2InGe2 system orders antiferromagnetically at TN = 45 K and is thought to have a ferromagnetic coupling of the f-electrons within the layers—shorter Gd-Gd distances, while the layers are anti-ferromagnetically coupled between layers-longer Gd-Gd distances, mediated by Ge orbitals. The anisotropic magnetic interactions could give rise to interesting magnetic phenomena at low Ts such as multiple ordering energy scales [7] and/or quantum effects such as entanglement [8]. The anisotropic MCE can be, in this case, an interesting probe of magnetic phenomena.
In the present work, we evaluated the magnetization, MCE and the transport properties of the Gd2InGe2. Our measurements indicate ordering of Gd local moments that are not coupled to conduction electrons but with a pronounced anisotropy in the magnetization. The MCE for magnetic field oriented perpendicular to the c-axis is much larger than that for fields applied along the c-axis. This anisotropy in the MCE points to the proposed model for magnetic ordering [9], where magnetic moments are ferromagnetically coupled within the Gd layers (perpendicular to the c-axis) and antiferromagnetically among layers (parallel to the c-axis). Extensive neutron scattering measurements will be published elsewhere to confirm details of the magnetic structure of Gd2InGe2; however, the anisotropic MCE provides information beyond than temperature dependent magnetization measurements alone.
2. Experimental Details
Starting materials were rare-earth metals (with purity >99.9%, Ames Laboratory or Alfa-Aesar), Ge (lump, 99.999%, Acros), and In (shot, 99.99%, Alfa-Aesar). The elements with the stoichiometric ratios were loaded in 2 cm3 alumina crucibles enclosed in evacuated sealed silica tubes. Temperature treatments were performed with a fast heating to 1100˚C at a rate of 300˚C/h, homogenization for 48 h, and cooling at a rate of 30˚C/h. Details can be found elsewhere [6]. The sample grows needle-shaped preferentially following c-axis direction. The dc-magnetization data was taken for direction parallel and perpendicular to c-axis in a Quantum Design MPMS for fixed T, varying applied field. The pulse field data was taken at NHMFL at Los Alamos National Lab up to 45 T at 0.5 K. The four-probe resistivity was measured in a Quantum Design PPMS from 2 - 300 K. A single crystal was selected from the same batch used to measure the magnetization and electric resistivity. Indium flux was mechanically removed before etching the specimen for 10 minutes in 5 parts water, 1 part Nitric acid by volume. After etching, the sample was rinsed in deionized water then washed in ethanol and dried. Electrical contacts were made with silver epoxy and resistivity was measured with current directed along the long direction, corresponding to the c-axis direction, of the needle-shaped crystals.
3. Results and Discussion
The heat capacity of Gd2InGe2 as a function of the T in 0 T (Figure 1) shows a peak near the ordering T (42 K). Measurements using a differential scanning calorimeter indicate a very small latent heat, consistent with a second order magnetic phase transition. The resistivity of Gd2InGe2 changes little upon magnetic ordering at TN (Figure 2). Similar to other members of RE2InGe2 [6], only a slight decrease in r is seen for T < TN. At low T, r(T) ~T2, while at the higher T, the data are consistent with electron-phonon scattering [10]. A small ~H2 magnetoresistance was observed below TN, characteristic of conventional metals with a simple Fermi surface.
The very weak change of r at TN usually indicates that itinerant electrons are only weakly coupled to the localized Gd spins. The decrease of r at T < TN is consistent with the presence of spin scattering of carriers. Upon magnetic ordering, spin fluctuations of localized spins are sharply reduced, eliminating a source of electron scattering. If the Fermi surface enclosed all or only a portion of the localized Gd electrons, which contribute to the local moments observed in the magnetization data, r(T) would be expected to sharply change at TN. The lack of a prominent anomaly at r(TN) mainly shows that spin ordering occurs independently of itinerant electrons. Structural transitions are also observed at magnetic transition, especially in materials relevant for MCE applications. The r(T) then changes markedly at TN due to changes in electron-phonon scattering. The weak change of r(T) at TN, the lack of thermal hysteresis, and small latent heat point against the presence of a structural transition upon magnetic ordering. The resistivity and thermal data support local moment ordering without an accompanying structural transition or coupling to a conduction band. These conclusions are consistent with the full Gd effective (local) magnetic moment observed in magnetization data [6].

Figure 1. Heat capacity as a function of temperature for 0 T. Inset: DSC trace as a function of temperature across the magnetic transition.
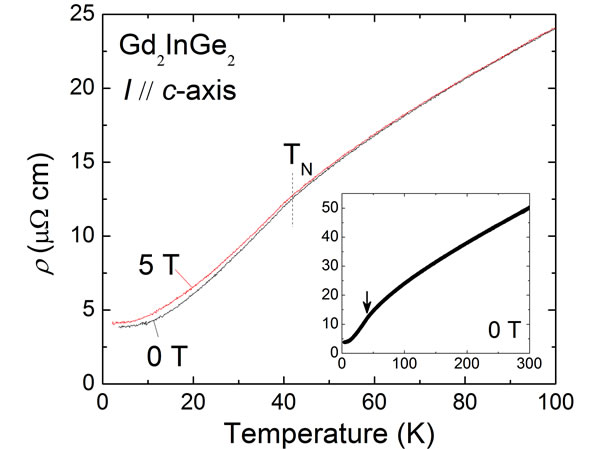
Figure 2. Resistivity as a function of the temperature from 0 to 100 K at 0 and 5 T; the inset shows metallic behavior from 0 to 300 K.
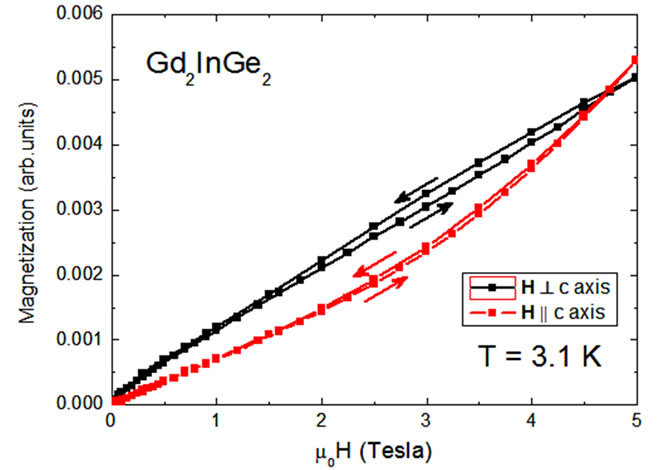
Having established the basic nature of the magnetic ordering, we now present the magnetization as a function of magnetic field applied parallel and perpendicular to the c-axis (Figure 3(a), recorded at 3.1 K). The magnetization perpendicular to the c-axis is nearly linear, while that along the c-axis shows an upward curvature near ~5 T, suggesting a field induced transition. Magnetization with H along the c-axis measured up to 45 T in pulsed magnetic fields (Figure 3(b), recorded at 0.5 K) confirms that this upward curvature in Figure 3(a) is due to a field-induced transition at around 5 Tesla. Since Gd has L = 0 and thus no crystal electric field effects are present, the two non-equivalent Gd sites may play a role in the observed anisotropy and field-induced transition. If the observed field induced transition originates from spinflop, this would mean that local moment spins point parallel or antiparallel to the c-axis at low fields, then “flop” perpendicular to the c-axis above ~5 T. In order to give further insight into the magnetic structure of Gd2InGe2, we extract the anisotropic MCE using magnetization measurements and the Maxwell equations.
 (a)
(a)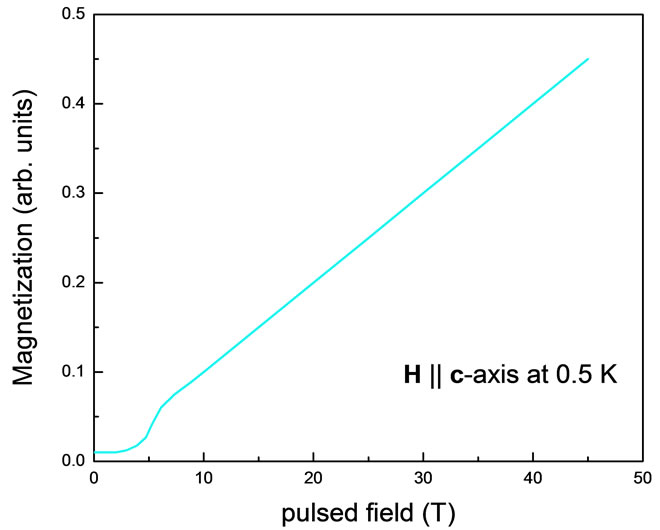 (b)
(b)
Figure 3. Anisotropic magnetization of Gd2InGe2 (a) Magnetization as a function of applied field at 3.1 K taken perpendicular and parallel to the crystallographic c-axis; (b) Magnetization along the c-axis at 0.5 K for pulsed magnetic fields up to 45 T.
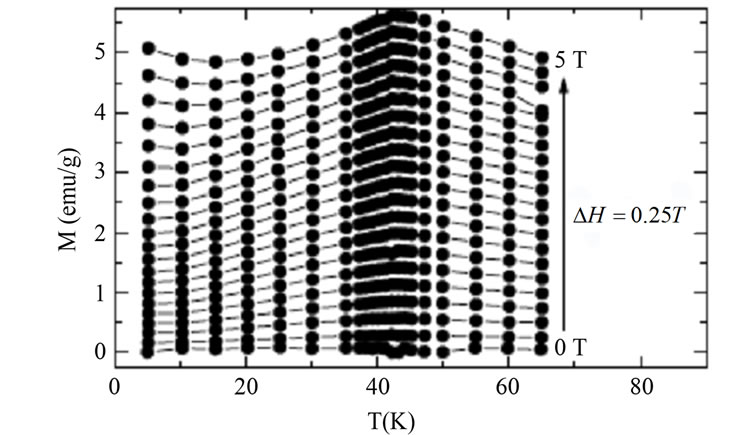
While field dependent heat capacity measurements can also be used, it is often difficult to accurately orient high aspect ratio specimens inside a calorimeter, while also achieving good thermal contact. In the present case, the long needle-like samples are easier to measure using magnetometry. The magnetization parallel to the c-axis as a function of temperature for several fields and as a function of applied H for several temperature is shown in Figures 4(a) and (b), respectively. This data set was used to calculate the MCE along the c-axis. An identical data set (not shown for clarity) was collected to calculate the MCE with the field applied perpendicular to the c-axis. Due to the small value of magnetization, demagnetizing shape effects are negligible.
The anisotropic MCE is shown in Figure 5 for field applied along and perpendicular to the c-axis. The MCE perpendicular to the c-axis is positive for T > TN and changes to negative values for T < TN. Along the c-axis, the MCE is T independent and nearly zero absolute value except very near TN.
This overall behavior is consistent with that expected from a two-sublattice, uniaxially anisotropic antiferromagnet, with, in this case, the anisotropy axis perpendicular to the c-axis [11]. Within a local moment picture, the MCE perpendicular to the anisotropy axis (parallel to
 (a)
(a)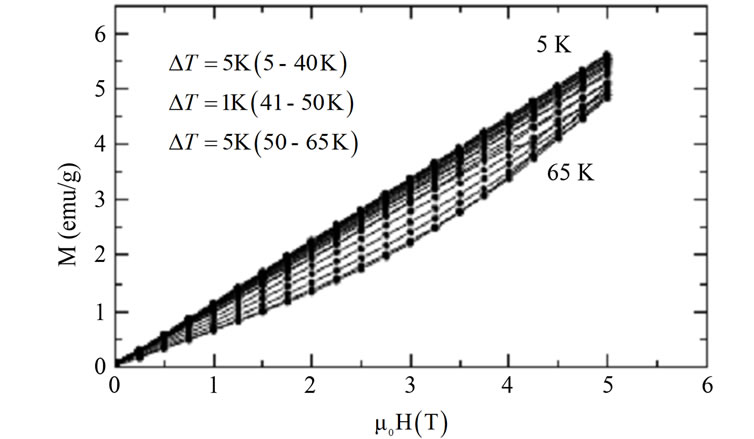 (b)
(b)
Figure 4. (a) Magnetization as a function of the temperature for several applied fields; (b) Magnetization data as a function of the applied field for several temperatures. The applied field was oriented along the c-axis.
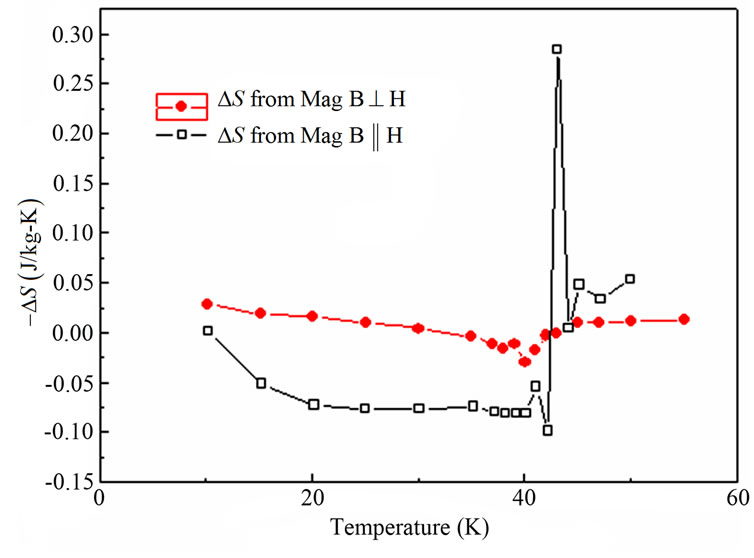
Figure 5. Anisotropic magnetocaloric effect for Gd2InGe2. The MCE perpendicular to the c-axis is nearly zero and temperature independent, while that parallel to the c-axis is positive for T > TN and negative for T < TN.
the c-axis) is negative for T < TN and shows a positive, paramagnetic contribution for T > TN. The MCE parallel to the anisotropy axis is zero since any gain in Zeeman energy is balanced by an increase in exchange energy [11,12]. The anisotropic MCE is thus broadly consistent with magnetization measurements [6], which indicates that local moments couple ferromagnetically within Gd layers and antiferromagnetically along the c-axis. However, small deviations in the anisotropic MCE near TN might indicate subtle changes to this simple picture of magnetic ordering that can be studied further with neutron scattering. The anisotropic MCE is thus an important tool to evaluate magnetic ordering since it can be directly calculated from mean field theory, and can help constrain neutron scattering measurements.
4. Acknowledgements
We would like to thank N. Harrison and the NHMFL at Los Alamos National Laboratories for the assistance with the pulse field measurements. AMG would like to acknowledge the financial support from the Brazilian Agencies: CNPq and FAPERJ. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Co., for the U.S. DoE.
REFERENCES
- V. K. Pecharsky and K. A. Gschneidner Jr., “Tunable Magnetic Regenerator Alloys with a Giant Magnetocaloric Effect for Magnetic Refrigeration from ~20 to ~290 K,” Applied Physics Letters, Vol. 70, No. 24, 1997, pp. 3299. http://dx.doi.org/10.1063/1.119206
- V. K. Pecharsky, A. P. Holm, K. A. Gschneidner Jr. and R. Rink, “Massive Magnetic-Field-Induced Structural Transformation in Gd5Ge4 and the Nature of the Giant Magnetocaloric Effect,” Physical Review Letters, Vol. 91 No. 19, 2003, Article ID: 197204. http://dx.doi.org/10.1103/PhysRevLett.91.197204
- E. M. Levin, V. K. Pecharsky, K. A. Gschneidner Jr. and G. J. Miller, “Spontaneous Generation of Voltage in Gd5(SixGe4-x) during a First-Order Phase Transition Induced by Temperature or Magnetic Field,” Physical Review B, Vol. 64, 2001, Article ID: 144406.
- E. M. Levin, K. A. Gschneidner Jr. and V. K. Pecharsky, “Magnetic-Field and Temperature Dependencies of the Electrical Resistance near the Magnetic and Crystallographic First-Order Phase Transition of Gd5(Si2Ge2),” Physical Review B, Vol. 60, No. 11, 1999, pp. 7993-7997. http://dx.doi.org/10.1103/PhysRevB.60.7993
- Z. W. Ouyang, V. K. Pecharsky, K. A. Gschneidner Jr., D. L. Schlagel and T. A. Lagrasso, “Magnetic Anisotropy and Magnetic Phase Diagram of Gd5Ge4,” Physical Review B, Vol. 74, No. 2, 2006, Article ID: 024401. http://dx.doi.org/10.1103/PhysRevB.74.024401
- P. H. Tobash, D. Lins, S. Bobev, A. L. Lima, M. F. Hundley, J. D. Thompson and J. L. Sarrao, “Crystal Growth, Structural and Magnetic Property Studies on a Family of Ternary Rare Earth Phases RE2InGe2 (RE = Sm, Gd, Dy, Ho, Yb),” Chemistry of Materials, Vol. 17, No. 22, 2005, pp. 5567-5573. http://dx.doi.org/10.1021/cm051618g
- P. A. Goddard, J. Singleton, A. L. Lima Sharma, E. Morosan, S. J. Blundell, S. L. Bud’ko and P. C. Canfield, “Separation of Energy Scales in the Kagome Antiferromagnet TmAgGe: A Magnetic-Field Orientation Study up to 55 T,” Physical Review B, Vol. 75, No. 9, 2007, Article ID: 094426. http://dx.doi.org/10.1103/PhysRevB.75.094426
- A. L. Lima Sharma and A. M. Gomes, “Experimental Investigations of the Entanglement in the Magnetization of Layered CaMn2Sb2 Compound,” Europhysics Letters, Vol. 84, No. 6, 2008, Article ID: 60003. http://dx.doi.org/10.1209/0295-5075/84/60003
- A. L. Lima Sharma, S. Bobev and J. L. Sarrao, “Oscillatory Behavior of Magnetocaloric Effect of RE2Al3Si2 and CeAlSi,” Journal of Magnetism and Magnetic Materials, Vol. 312, No. 2, 2007, pp. 400-404. http://dx.doi.org/10.1016/j.jmmm.2006.11.125
- J. M. Ziman, “Principles of the Theory of the Solids,” Cambridge University Press, London, 1964.
- E. Z. Valiev, “Entropy and Magnetocaloric Effect in Ferromagnets and Antiferromagnets,” Physics of Metals and Metallography, Vol. 104, No. 1, 2007, pp. 8-12. http://dx.doi.org/10.1134/S0031918X07070022
- C. G. Garrett, “The Critical Field Curve in an Antiferromagnetic Crystal,” Journal of Chemical Physics, Vol. 19, No. 9, 1951, p. 1154. http://dx.doi.org/10.1063/1.1748495

