International Journal of Modern Nonlinear Theory and Application
Vol.04 No.02(2015), Article ID:57666,7 pages
10.4236/ijmnta.2015.42011
Induction Motor Modeling Based on a Fuzzy Clustering Multi-Model―A Real-Time Validation
Abid Aicha, Bnhamed Mouna, Sbita Lassaad
National Engineering School of Gabes, Photovoltaic, Wind and Geothermal Systems Research, Gabes, Tunisia
Email: aicha.abid@gmail.com, benhamed2209@yahoo.fr, Lassaad.sbita@enig.rnu.tn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC).
http://creativecommons.org/licenses/by-nc/4.0/



Received 19 April 2015; accepted 23 June 2015; published 30 June 2015
ABSTRACT
This paper discusses a comparative study of two modeling methods based on multimodel approach. The first is based on C-means clustering algorithm and the second is based on K-means clustering algorithm. The two methods are experimentally applied to an induction motor. The multimodel modeling consists in representing the IM through a finite number of local models. This number of models has to be initially fixed, for which a subtractive clustering is necessary. Then both C-means and K-means clustering are exploited to determine the clusters. These clusters will be then exploited on the basis of structural and parametric identification to determine the local models that are combined, finally, to form the multimodel. The experimental study is based on MATLAB/SIMULINK environment and a DSpace scheme with DS1104 controller board. Experimental results approve that the multimodel based on K-means clustering algorithm is the most efficient.
Keywords:
Multi-Model Modeling, C-means Clustering Algorithm, K-Means Clustering Algorithm, Induction Motor (IM), Experimental Validation

1. Introduction
Induction motors are the basis elements in industrial applications thanks to their economic cost, judicious size, and easy maintenance [1] [2] . However, these motors are complex and have a strongly nonlinear system. It is often hard to determine an adequate model that represents all the dynamic behavior of this machine.
Modeling is an essential initial step in the industrial process control. This fundamental step is necessary either for a control law development or for the development of a diagnosis procedure. Modeling a process consists in establishing relationships between its characteristics variables and in representing the dynamic behavior of this process in a particular field of operation.
Based on a priori knowledge of the studied process, many modeling types are used. The increasing complexity of industrial process pushes many researchers to develop modeling techniques that exploit linear systems tools. Hence, in this paper we will consider the modeling based on multimodel approach that recently, has been implemented in various science and engineering domains, concerning application to modeling, control and fault diagnosis [3] -[10] .
The multimodel approach consists in replacing the unique nonlinear model by a set of simpler linear models to create a model-base. Generally, each model of this base contributes to the whole description of the considered system through weighed functions or validities functions.
The modeling via this approach needs to follow up a scheme of four steps that are database acquisition, clustering, structural and parametric identification and fusion.
For clustering, many algorithms are adopted in literature [11] -[14] , in this paper we will focus on three fuzzy clustering algorithms that are subtractive, C-means and K-means clustering algorithms. The subtractive algorithm is used to determine the cluster number, whereas the C-means and the K-means will be exploited to generate the cluster centers then to construct the clusters. Thus, we will compare two modeling methods, the first is based on the association of subtractive-C-means algorithm and the second is based on the association of subtractive-K-means algorithm.
The two proposed modeling method are experimentally implemented to an induction motor.
The organization of this paper is as follows. The second part consists in describing the modeling with multi- model approach, the third part develops the application of the two modeling methods based on the two clustering algorithm to the induction motor. The part four is a comparative study of the two modeling method and finally the conclusion is in the fifth part.
2. Multi-Model Modeling
To obtain a multimodel, we have to follow a strategy of four stages that are database acquisition, data clustering, structural and parametric identification and local models fusion.
The system is considered as a black box. Thus, it is exited via a rich frequency input. The collected data is consisting of a set of input/output measurements. Then the collected data will be divided into N clusters through clustering algorithms. Later, three clustering algorithms will be developed: the subtractive, C-means and K-means algorithm. Next, structural and parametric identification follow the clustering to obtain the local models. The structural identification is achieved using the general procedure of order estimation and the Instrumental determinant ratio (IDR). For the parametric identification, the generalized recursive least square is implemented.
The obtained local models are combined through weighted functions that are calculated based on residue approach [5] -[8] .
Two strategies are adopted. The first is based on the C-means clustering algorithm and the second is based on K-means clustering method as shown in Figure 1 and Figure 2.
3. The Clustering Algorithms
Clustering data consists of organizing and collecting similar data points into group or cluster. The similarity is estimated by a function that computes the distance between the data points, usually, the Euclidean distance.
In literature, various clustering algorithm was proposed to deal with clustering problem [11] -[14] . Subtractive, C-means and K-means are among the most commonly-used clustering algorithm
3.1. Subtractive Clustering
The subtractive clustering algorithm was suggested by Chiu as an extension of the mountain function. It is able to determine the number and the value of cluster centers.
The process is provided with the following steps.
Figure 1. Modeling strategy based on C-means clustering algorithm.
Figure 2. Modeling strategy based on K-means clustering algorithm.
1) Each data point is considered as a cluster center that has the calculated potential pi given in (1).
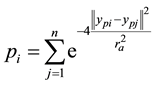 (1)
(1)
where ra defines the neighborhood radius.
The data with the high potential is the first cluster center.
2) The data potentials are recalculated by (2).
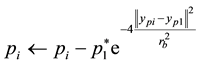 (2)
(2)
where rb > 0 is the new neighborhood radius that must be rather greater then ra to not having cluster centers that are closely spaced. Usually rb = 1.5ra.
3) The process is repeated until the obtaining of the k-th center and the potentials are recalculated by (3).
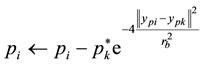 (3)
(3)
4) The process is repeated until the following condition (4).
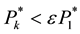 (4)
(4)
3.2. C-Means Clustering
The C-means known as FCM is a data clustering algorithm that considers that each data point belongs to a cluster through a membership function. It consists in producing an optimal partition by minimizing the objective function J on the basis of the following process.
1) Initialize arbitrarily the Fuzzy membership matrix µik
2) Calculate the cost function J by (5).
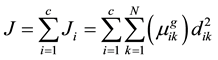 (5)
(5)
3) Estimate the clusters centers ci by the Equation (6).
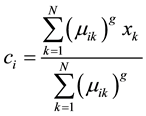 (6)
(6)
4) Updates the membership functions as the relation (7).
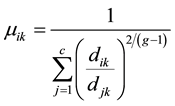 (7)
(7)
5) Recalculate the cost function J. If J is less than a threshold, the process will be ended. If not, return to step 3.
3.3. K-Means Clustering
The K-means clustering algorithm is known as an efficient and rapid one. It is able to construct a fixed finite number of clusters by minimizing the Euclidean distance between the data and the equivalent cluster center.
The K-means clustering algorithm is detailed by the following process.
1) Select arbitrarily cluster centers ci from the training data set.
2) Calculate the membership matrix uij using the Equation (8).
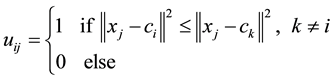 (8)
(8)
3) Calculate the cost function J by the Equation (9). Stop the process if it is less than a certain threshold.
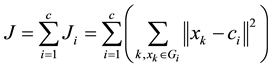 (9)
(9)
4) Update the cluster center ci according to the relation (10).
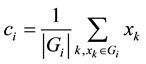 (10)
(10)
Next, return to step 2.
4. Application of the Two Modeling Strategy on the IM
We propose in this section to modeling the IM by the two multimodel modeling strategies previously described.
Firstly, we have to collect a rich data base from the measurement of input/output of the IM. The electric motor is 1 kw squirrel cage Induction motor.
The training data set is generated through an experimental set-up that is described by Figure 3. It is used with the help of Matlab/Simulink and DSpace system with DS1104 controller board to collect the database.
The data collection requires the use of speed and current sensors. For that, Hall type sensors are exploited to measure stator currents and an incremental encoder position sensor delivering 1024 pulses per revolution is mounted on the shaft to measure the IM speed.
To test the robustness of the modeling approach we propose to vary the IM parameter and to apply a wide range of loads.
The load is a resistive bank fed by a DC generator that is connected to the IM.
To vary the stator resistances, three variable resistors are linked in series to the motor phases.
A large data set is selected out after input/output measurements at an operating point of 600 rpm.
4.1. Modeling of IM via the Method Based on C-Means Clustering Algorithm
The subtractive clustering algorithm helps to determine the clusters number that is N = 8. So, the objective of the C-means clustering is to generate these eight clusters.
The obtained clusters will be identified to obtain the local models that are defined by these recurrent equations.
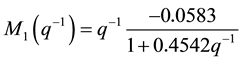 (11)
(11)
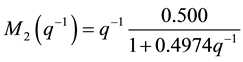 (12)
(12)
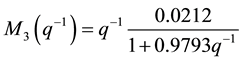 (13)
(13)
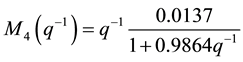 (14)
(14)


Figure 3. Experimental set up.


The combination of the local models through the validities shown in Figure 4 helps to construct the final multimodel as shown in Figure 5.
4.2. Modeling of IM via the Method Based on K-Means Clustering Algorithm
The same modeling process is respected. In fact, the K-means clustering is applied in order to generate the eight clusters that will be identified and combined to create the multimodel.
The local models are described by the following discrete transfer functions (19)-(26).



Figure 4. The validities evolutions.
Figure 5. Multimodel modeling of IM based on C-means.





The obtained results are illustrated by Figure 6 that illustrates the evolution of the real speed and the modeled speed.
The different validities functions are illustrated by Figure 7.
Figure 6. Multimodel modeling of IM based on K-means.
Figure 7. Validities evolutions.
Table 1. Comparative study of the two modeling strategies.
We propose to compare the two modeling strategies. Therefore, we calculate for each strategy the normalized roots mean square modeling error NRMSE. Then, a comparative table (Table 1) is dressed.
We can notice that the method based on K-means clustering algorithm is the most convergent as the NRMSE calculated is the lowest.
5. Conclusion
In this paper, the multimodel modeling strategy is described. Two strategies are developed. The first is on the basis of C-means clustering algorithm and the second is based on K-means clustering algorithm. The two methods are applied in real time to an induction motor at an operating point of 600 rpm submissive to load insertion and parameter variation. A comparative study helps to confirm that the method based on K-means is the most convergent. In future work, to improve the modeling performance the modeling should take into account the total behavior of the induction motor.
References
- Salahat, M., Barbarawe, O., Abu Zalata, M. and Asad, S. (2011) Modular Approach for Investigation of the Dynamic Behavior of Three-Phase Induction Machine at Load Variation. Engineering, 3, 525-531. http://dx.doi.org/10.4236/eng.2011.35061
- Vodovozov, V., Gevorkov, L. and Raud, Z. (2014) Modeling and Analysis of Pumping Motor Drives in Hardware-in- the-Loop Environment. Journal of Power and Energy Engineering, 2, 19-27. http://dx.doi.org/10.4236/jpee.2014.210003
- Men, Z.X., Yee, E., Lien, F.-S., Ji, H. and Liu, Y.Q. (2014) Bootstrapped Multi-Model Neural-Network Super-En- sembles for Wind Speed and Power Forecasting. Energy and Power Engineering, 6, 340-348. http://dx.doi.org/10.4236/epe.2014.611029
- Shankar, H., Raju P.L.N. and Rao, K.R.M. (2012) Multi Model Criteria for the Estimation of Road Traffic Congestion from Traffic Flow Information Based on Fuzzy Logic. Journal of Transportation Technologies, 2, 50-62. http://dx.doi.org/10.4236/jtts.2012.21006
- Abid, A., Ben Hamed, M. and Sbita, L. (2011) Induction Motor Real Time Application of Multimodel Modeling Approach. International Review of Electrical Engineering (IREE), 6, 655-660.
- Abid, A., Adouni, A., Ben Hamed, M. and Sbita, L. (2012) A New PV Cell Model Based On Multi Model Approach. The 4th International Renewable Energy Congress, Sousse, 20-22 December 2012, 1447-1452.
- Abid A., Ben Mabrouk Z., Ben Hamed M., Sbita L., (2013) Multiple Lunberger Observer for an Induction Motor Represented by Decoupled Multiple Model. 10th International Multi-Conference on Systems, Signals & Devices (SSD) Hammamet, March 18-21 2013, 1-6. http://dx.doi.org/10.1109/ssd.2013.6564050
- Elfelly, N., Dieulot, J.-Y., Benrejeb, M. and Borne, P. (2012) A Multimodel Approach for Complex Systems Modeling Based on Classification Algorithms. International Journal of Computers Communications Control, 7, 644-659.
- Orjuela, R., Marx, B., Ragot, J. and Maquin, D. (2013) Nonlinear System Identification Using Heterogeneous Multiple Models. International Journal of Applied Mathematics and Computer Science, 23, 103-115. http://dx.doi.org/10.2478/amcs-2013-0009
- Hamdi, H., Rodrigues, M., Mechmeche, C., Theilliol, D. and BenHadj Braiek, N., (2012) Fault Detection and Isolation in Linear Parameter-Varying Descriptor Systems via Proportional Integral Observer. International Journal of Adaptive Control and Signal Processing, 26, 224-240. http://dx.doi.org/10.1002/acs.1260
- Guldemır, H. and Sengur, A. (2006) Comparison of Clustering Algorithms for Analog Modulation Classification. Expert Systems with Applications, 30, 642-649. http://dx.doi.org/10.1016/j.eswa.2005.07.014
- Velmurugan, T. (2014) Performance Based Analysis between K-Means and Fuzzy C-Means Clustering Algorithms for Connection Oriented Telecommunication Data. Applied Soft Computing, 19, 134-146. http://dx.doi.org/10.1016/j.asoc.2014.02.011
- Chiu, S.L. (1994) Fuzzy Model Identification Based on Cluster Estimation. Journal of Intelligent and Fuzzy Systems, 2, 267-278.
- Fan, J.L. and Li, J. (2014) A Fixed Suppressed Rate Selection Method for Suppressed Fuzzy C-Means Clustering Algorithm. Applied Mathematics, 5, 1275-1283. http://dx.doi.org/10.4236/am.2014.58119









