ABSTRACT

The public key of the integer homomorphic encryption scheme which was proposed by Van Dijk et al. is long, so the scheme is almost impossible to use in practice. By studying the scheme and Coron’s public key compression technique, a scheme which is able to encrypt n bits plaintext once was obtained. The scheme improved the efficiency of the decrypting party and increased the number of encrypting parties, so it meets the needs of cloud computing better. The security of the scheme is based on the approximate GCD problem and the sparse-subset sum problem.

Keywords:

Fully Homomorphic Encryption, Multipart to One Fully Homomorphism Encryption, Approximate GCD Problem, Sparse-Subset Sum Problem

1. Introduction

Full homomorphic encryption (FHE) was proposed by Rivest, Adleman, and Dertouzos in 1978 [1]. This encryption method can perform operations on ciphertext. After decryption, the same operation is performed on the corresponding plaintext. The results are consistent. With such characteristics, the data can be encrypted and handed over to the cloud for processing, which not only utilizes the computing power of the cloud, but also reduces the amount of local computing and ensures the security of the data [2][3].

To this end, many scholars have studied how to construct a homomorphic encryption scheme, and proposed a variety of encryption schemes that satisfy partial homomorphism [4]- [9]. In 2009, Gentry et al. [10]proposed the first true homomorphic encryption scheme based on the ideal lattice on a polynomial ring, but because it is too complicated and inefficient, it has larger difficulty in practical applications. In 2010, Dijk et al. [11]improved the above ideal lattice scheme and proposed an integer homomorphic encryption scheme, namely the DGHV scheme. The public key size of this scheme is $\tilde{O}\left({\lambda }^{10}\right)$. In 2011, Coron et al. [12]optimized the DGHV scheme. For the problem of the large number of public keys in the DGHV scheme, a scheme for generating public key integers in quadratic form was proposed, which shortened the public key length to $\tilde{O}\left({\lambda }^7\right)$. The following year, Coron et al. [13]proposed a “public key compression technique” for the problem of excessive public key elements in the DGHV scheme, shortening the public key length to $\tilde{O}\left({\lambda }^5\right)$.

Through comparison and research, it is found that the above schemes are composed of one encryption party and also a single decryption party, which is difficult to meet the problem of multi-party interaction in the cloud computing environment. In view of the above problems, this paper studies Coron’s public key compression technology, shortens the size of the public key, expands the plaintext space in the scheme to n bits, and expands the number of encryption parties to achieve multiple encryption methods. A solution composed of a decryption party is more in line with the application needs of actual scenarios such as cloud computing. The public key size of this scheme is $\tilde{O}\left({\lambda }^5\right)$.

2. Basic Symbols and Concepts

2.1. Fully Homomorphic Encryption

A compact encryption scheme E encrypts the plaintext according to the encryption method in scheme E. After the obtained ciphertext is arbitrarily operated, the result is decrypted and the result is the same as the plaintext, and the scheme E is fully homomorphic Encryption scheme. Expressed as a mathematical formula as:

$Dec\left[f\left(Enc\left(m_1\right),Enc\left(m_2\right),\cdots ,Enc\left(m_n\right)\right)\right]=f\left(m_1,m_2,\cdots ,m_n\right)$

Enc is an encryption algorithm, Dec is a decryption algorithm, f is an arbitrary function, c_n is ciphertext, and m_n is plaintext.

In general, a fully homomorphic encryption algorithm consists of four parts:

Key generation algorithm KeyGen (λ): Generate public key pk, private key sk.

Encryption algorithm Encrypt (pk, m): encrypts the plaintext m with the public key pk to obtain the ciphertext c.

Decryption algorithm Decrypt (sk, c): Decrypt the ciphertext c with the private key sk to obtain the plaintext m.

The ciphertext calculation algorithm Evaluates $\left(pk,f,c_1,c_2,\cdots ,c_n\right)$ : the operation of the ciphertext should satisfy:

$Dec\left[f\left(Enc\left(m_1\right),Enc\left(m_2\right),\cdots ,Enc\left(m_n\right)\right)\right]=f\left(m_1,m_2,\cdots ,m_n\right)$

2.2. DGHV Program

In 2010, Dijk, Gentry et al. proposed an integer homomorphic encryption scheme, namely the DGHV scheme, which is no longer based on ideal lattices but on modular operations on integers.

The encryption algorithm of the DGHV scheme is

$c\leftarrow m+2r+pq$

where c is ciphertext, m is plaintext, r is random noise interference, p is a private key, and q is a large positive integer generated during the key generation phase.

The decryption algorithm is

$\left(c\mathrm{mod}p\right)\mathrm{mod}2=\left(c-p\ast \frac{c}{p}\right)\mathrm{mod}2=Lsb\left(c\right)xorLsb(cp)$

The public key size of this scheme is $\tilde{O}\left({\lambda }^{10}\right)$.

In order to ensure security, the approximate maximum common divisor problem is introduced. In the encryption process, some ciphertext $x_i$ encrypted by 0, $\left\{x_i:x_i=r_i+pq\right\}$ is added, then reorder $x_i$ so that $x_0$ is the largest and $x_0$ is odd. $\left(x_0\mathrm{mod}p\right)$ is an even number, then the public key $pk=\left(x_0,x_1,\cdots ,x_{\tau }\right)$. When encrypting, a subset of the set is randomly added to the ciphertext, and the encryption algorithm is

$c\leftarrow \left(m+2r+{\displaystyle {\sum }_{1\le i\le \tau }{x}_i}\right)\mathrm{mod}{x}_0$.

The addition of the approximate greatest common divisor problem means that the attack on the program is due to an attack on the approximate greatest common divisor problem, so the scheme is safe [14].

2.3. Many-to-One Homomorphic Encryption

The many-to-one fully homomorphic encryption scheme [15]contains a plurality of encryption parties $P_i\left(i=1,2,\cdots ,n\right)$ and a decryption party P. The plaintext space is M, the public-private key pair $\left(p{k}_i,s{k}_i\right)$ of the encrypting party, and the public-private key pair $\left(pk,sk\right)$ of the decrypting party. And the encryption algorithm E(⋅) and the corresponding decryption algorithm D(⋅). In this model, the plaintext $m_i\in M$ of the encryption side, the generated ciphertext $c_i$ is $m_i$ encrypted by $p{k}_i$, and needs to satisfy the following properties, where $\oplus$ denotes the operator, $i\ne j$ :

1) Both the encrypting party and the decrypting party can use their own private key to decrypt the message encrypted by their own public key, i.e.

$D_{s{k}_i}\left(E_{p{k}_i}\left(m_i\right)\right)=m_i$, $D_{sk}\left(E_{pk}\left(m\right)\right)=m$.

2) The encrypting party i cannot use its own private key $s{k}_i$ to decrypt the message encrypted by the encrypting party j with its own public key $p{k}_j$, that is,

$D_{s{k}_i}\left(E_{p{k}_j}\left(m_j\right)\right)\ne m_j$.

3) The message encrypted by the encrypting party i with its own public key $p{k}_i$ can be decrypted by the decrypting party P with its own private key sk, that is,

$D_{sk}\left(E_{p{k}_i}\left(m_i\right)\right)=m_i$.

4) Different messages encrypted by the encrypting party i with its own public key $p{k}_i$ have homomorphism under the operation of the decrypting party P, that is,

$D_{sk}\left(E_{p{k}_i}\left(m_1\oplus m_2\right)\right)=D_{sk}\left(E_{p{k}_i}\left(m_1\right)\oplus E_{p{k}_i}\left(m_2\right)\right)$.

5) Different messages encrypted by different encrypting party i and encrypting party j have homomorphism under the operation of decrypting party P, that is,

$D_{sk}\left(E_{p{k}_i}\left(m_1\right)\oplus E_{p{k}_j}\left(m_2\right)\right)=D_{sk}\left(E_{pk}\left(m_1\oplus m_2\right)\right)$.

3. Improved N-Bit “One-to-One” Homomorphic Encryption Scheme

The DGHV scheme can only encrypt 1 bit of plaintext at a time, and the size of the public key element is too large. This section extends the plaintext space to n bits, and uses the public key compression technique to improve the key generation algorithm, using pseudo-random number generation. The f and the seed se generate a set of integers ${\chi }_i$ having the same number of bits as $x_i$, so that it is not necessary to store the large integer $x_i$, and it is only necessary to store the difference between ${\chi }_i$ and $x_i$ as a public key element.

3.1. Program Establishment

KeyGen: randomly generate a large prime number $p\in \left[2^{\eta -1},2^{\eta }\right)$ of length $\eta$ bits, and calculate $x_0=q_0\cdot p$, where $q_0\in \left[0,2^{\gamma }/p\right)$ is a random odd number. Initialize the pseudo-random number generator f and the seed se, and generate $\tau$ integers by using $f\left(se\right)$, that is, ${\chi }_1,{\chi }_2,\cdots ,{\chi }_{\tau }$, and calculate

${\delta }_i=\left({\chi }_i\mathrm{mod}p\right)+{\xi }_i\cdot p-r_i$, $1\le i\le \tau$,

where $r_i\in Z\cap \left(-2^{\rho },2^{\rho }\right)$, ${\xi }_i\in Z\cap \left[0,2^{\lambda +\eta }/p\right)$. Then $x_i={\chi }_i-{\delta }_i$. The public key $pk=\left(se,x_0,{\delta }_1,{\delta }_2,\cdots ,{\delta }_{\tau }\right)$, private key $sk=p$.

Encrypt: Randomly select the integer vector $b={\left(b_i\right)}_{1\le i\le \tau }\in {\left[0,2^{\alpha }\right)}^{\tau }$, randomly select the integer $r\in Z\cap \left(-2^{{\rho }^{\prime }},2^{{\rho }^{\prime }}\right)$, ciphertext

$c\leftarrow \left(m+2^n\cdot r+2^n\cdot {\displaystyle {\sum }_{1\le i\le \tau }{b}_i\cdot x_i}\right)\mathrm{mod}{x}_0$.

Decrypt: $m\leftarrow \left(c\mathrm{mod}p\right)\mathrm{mod}{2}^n$.

In order to ensure the security of the scheme, the parameters in the above method need to meet the following restrictions: to resist violent attacks, select $\rho =\omega \left(\log \lambda \right)$; in order to make the compressed decryption circuit belong to the permissible circuit, select $\eta \ge \rho \cdot \Theta \left(\lambda {\log }^2\lambda \right)$; to resist the lattice-based attack, choose $\gamma =\omega \left({\eta }^2\cdot \log \lambda \right)$; apply the residual hash theorem to the approximation of the approximate GCD problem, choose $\alpha \cdot \tau \ge \gamma +\omega \left(\log \lambda \right)$; To ensure correct decryption of ciphertext, select $\eta \ge \rho +\alpha +2+{\log }_2\tau$; second noise parameter ${\rho }^{\prime }=\rho +\alpha +\omega \left(\log \lambda \right)$. In this scheme, the parameters take $\rho =\lambda$, $\eta =\tilde{O}\left({\lambda }^2\right)$, $\gamma =\tilde{O}\left({\lambda }^5\right)$, $\tau =\tilde{O}\left({\lambda }^3\right)$, $\alpha =\tilde{O}\left({\lambda }^2\right)$, ${\rho }^{\prime }=\tilde{O}\left({\lambda }^2\right)$.

3.2. Proof of Correctness

$\begin{array}{l}\left(c\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left[\left(m+2^n\cdot r+2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot x_i\right)\mathrm{mod}p\right]\mathrm{mod}{2}^n\\ =\left[\left(m+2^n\cdot r+2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot \left({\chi }_i-{\delta }_i\right)\right)\mathrm{mod}p\right]\mathrm{mod}{2}^n\end{array}$

In which

$\begin{array}{l}\left({\chi }_i-{\delta }_i\right)\mathrm{mod}p=\left({\chi }_i-\left({\chi }_i\mathrm{mod}p\right)-{\xi }_i\cdot p+r_i\right)\mathrm{mod}p\\ =\left\{\left[{\chi }_i-\left({\chi }_i\mathrm{mod}p\right)\right]\mathrm{mod}p-\left[{\xi }_i\cdot p\right]\mathrm{mod}p+r_i\right\}\mathrm{mod}p\\ =\left(0-0+r_i\right)\mathrm{mod}p\\ =r_i\end{array}$

So the original

$\left(c\mathrm{mod}p\right)\mathrm{mod}{2}^n=\left(m+2^n\cdot r+2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot r_i\right)\mathrm{mod}{2}^n=m$

3.3. Test of Homomorphism

There are ciphertext $c_1=m_1+2^n\cdot r_1+2^n\cdot {\displaystyle {\sum }_{1\le i\le \tau }{b}_i\cdot x_i}$ and ciphertext $c_2=m_2+2^n\cdot r_2+2^n\cdot {\displaystyle {\sum }_{1\le i\le \tau }{b}_j\cdot x_j}$, then

$\begin{array}{l}\left[\left(c_1+c_2\right)\mathrm{mod}p\right]\mathrm{mod}{2}^n\\ =\left(\left(\left(m_1+m_2\right)+2^n\cdot \left(r_1+r_2\right)+2^n\cdot \left(\underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot x_i+\underset{1\le j\le \tau }{{\displaystyle \sum }}{b}_j\cdot x_j\right)\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_1+m_2\right)+2^n\cdot \left(r_1+r_2\right)+2^n\cdot \left(\underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot r_i+\underset{1\le j\le \tau }{{\displaystyle \sum }}{b}_j\cdot r_j\right)\right)\mathrm{mod}{2}^n\\ =m_1+m_2\end{array}$

$\begin{array}{l}\left[\left(c_1{c}_2\right)\mathrm{mod}p\right]\mathrm{mod}{2}^n\\ =((\left(m_1+2^n\cdot r_1\right)\left(m_2+2^n\cdot r_2\right)+\left(m_1+2^n\cdot r_1\right)\left(2^n\cdot \underset{1\le j\le \tau }{{\displaystyle \sum }}{b}_j\cdot x_j\right)\\ +\left(2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot x_i\right)\left(m_2+2^n\cdot r_2\right)+\left(2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot x_i\right)\left(2^n\cdot \underset{1\le j\le \tau }{{\displaystyle \sum }}{b}_j\cdot x_j\right))\mathrm{mod}p)\mathrm{mod}{2}^n\end{array}$

$\begin{array}{l}=(\left(m_1+2^n\cdot r_1\right)\left(m_2+2^n\cdot r_2\right)+\left(m_1+2^n\cdot r_1\right)\left(2^n\cdot \underset{1\le j\le \tau }{{\displaystyle \sum }}{b}_j\cdot r_j\right)\\ +\left(2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot r_i\right)\left(m_2+2^n\cdot r_2\right)+\left(2^n\cdot \underset{1\le i\le \tau }{{\displaystyle \sum }}{b}_i\cdot r_i\right)\left(2^n\cdot \underset{1\le j\le \tau }{{\displaystyle \sum }}{b}_j\cdot r_j\right))\mathrm{mod}{2}^n\\ =\left(\left(m_1+2^n\cdot r_1\right)\left(m_2+2^n\cdot r_2\right)\right)\mathrm{mod}{2}^n\\ =m_1{m}_2\end{array}$

4. Improved N-Bit “Many-to-One” Fully Homomorphic Encryption Scheme

Based on the scheme given in Section 3.1, this section changes the key generation algorithm, expands the number of encryption parties, and gives a “many-to-one” fully homomorphic encryption scheme for processing n-bit plaintext, and corrects it. Sex and homomorphism have been proved.

4.1. Program Establishment

KeyGen: There are multiple encryption parties $P_i\left(i=1,2,\cdots ,n\right)$ and one decryption party P in this scheme. The decryption party P generates the public key $pk=\left(se,x_0,{\delta }_1,{\delta }_2,\cdots ,{\delta }_{\tau }\right)$ from the 3.1 scheme, the encryption side $P_i\left(i=1,2,\cdots ,n\right)$ selects the integer $p_i\in \left[2^{{\eta }_i-1},2^{{\eta }_i}\right)\cap \left(2Z+1\right)$ as its own key $s{k}_i$, then change the order of $\left({\delta }_1,{\delta }_2,\cdots ,{\delta }_{\tau }\right)$ in the public key randomly to obtain $\overline{pk}=\left(se,x_0,\overline{{\delta }_1},\overline{{\delta }_2},\cdots ,\overline{{\delta }_{\tau }}\right)$, and then randomly selected integer

$q_{i,0},\cdots ,q_{i,\tau }\in Z\cap \left[0,\frac{2^{{\gamma }_i}}{p_i}\right)$,

randomly select integer $r_{i,0},\cdots ,r_{i,\tau }\in Z\cap \left[-2^{{\rho }_i},2^{{\rho }_i}\right]$, such that

$x_{i,j}={\chi }_{i,j}-{\delta }_{i,j}=p_i{q}_{i,j}\left({\chi }_j-\overline{{\delta }_j}\right)+2^n{r}_{i,j}$, $1\le j\le {\tau }_i$, $x_{i,0}=p_i{q}_{i,0}{x}_0+2^n{r}_{i,0}$,

and $x_{i,0}$ is the largest. Then the public key of $P_i$ is

$p{k}_i=\left(se,x_0,x_{i,0},{\delta }_{i,1},{\delta }_{i,2},\cdots ,{\delta }_{i,{\tau }_i}\right)$.

Encrypt: Encryption party $P_i$ randomly selects the integer vector

$b_i={\left(b_{i,j}\right)}_{1\le j\le {\tau }_i}\in {\left[0,2^{\alpha }\right)}^{{\tau }_i}$,

randomly selects integer $s_i\in Z\cap \left(-2^{{\rho }_i},2^{{\rho }_i}\right)$, ciphertext

$c_i\leftarrow \left(m+2^n\cdot s_i+2^n\cdot {\displaystyle {\sum }_{1\le j\le {\tau }_i}{b}_{i,j}\cdot x_{i,j}}\right)\mathrm{mod}{x}_{i,0}$.

Decrypt: The encryption party $P_i$ can decrypt $s{k}_i=p_i$ according to $s{k}_i=p_i$; the decryption party P can decrypt $m_i\leftarrow \left(c_i\mathrm{mod}p\right)\mathrm{mod}{2}^n$ according to $sk=p$.

4.2. Proof of Correctness

1) $\left(pk,sk\right)$ is the public-private key pair generated by P. It can be seen from 3.2 that P can perform correct encryption and decryption.

2) $P_i$ can correctly decrypt $c_i$ using the key $s{k}_i=p_i$ prove:

$c_i=\left(m_i+2^n\cdot s_i+2^n\cdot \underset{1\le j\le {\tau }_i}{{\displaystyle \sum }}{b}_{i,j}\cdot x_{i,j}\right)\mathrm{mod}{x}_{i,0}$

Since $x_{i,0}$ is the largest, it can be written as

$\begin{array}{c}{c}_i=m_i+2^n\cdot s_i+2^n\cdot \underset{1\le j\le {\tau }_i}{{\displaystyle \sum }}{b}_{i,j}\cdot x_{i,j}+k_i\cdot x_{i,0}\\ =m_i+2^n\cdot s_i+2^n\cdot \underset{1\le j\le {\tau }_i}{{\displaystyle \sum }}{b}_{i,j}\cdot \left(p_i{q}_{i,j}\left({\chi }_j-\overline{{\delta }_j}\right)+2^n{r}_{i,j}\right)+k_i\cdot \left(p_i{q}_{i,0}{x}_0+2^n{r}_{i,0}\right)\end{array}$

Finishing can get $c_i=m_i+2^{n}A+p_{i}B$, where

$A=s_i+{\displaystyle {\sum }_{1\le j\le {\tau }_i}{b}_{i,j}\cdot 2^n{r}_{i,j}}+k_i{r}_{i,0}$, $B=2^n\cdot {\displaystyle {\sum }_{1\le j\le {\tau }_i}{b}_{i,j}\cdot q_{i,j}\left({\chi }_j-\overline{{\delta }_j}\right)}+k_i{q}_{i,0}{x}_0$.

According to the defined parameters, $m_i+2^{n}A<p_i$, then

$\left(c_i\mathrm{mod}{p}_i\right)\mathrm{mod}{2}^n=m_i$.

So $P_i$ can correctly decrypt $c_i$ using the key $s{k}_i=p_i$.

3) P can correctly decrypt $c_i$ using the key $sk=p$ prove:

As can be seen from 2),

$c_i=m_i+2^n\left(s_i+\underset{1\le j\le {\tau }_i}{{\displaystyle \sum }}{b}_{i,j}\cdot 2^n{r}_{i,j}+k_i{r}_{i,0}\right)+p_i\left(2^n\cdot \underset{1\le j\le {\tau }_i}{{\displaystyle \sum }}{b}_{i,j}\cdot q_{i,j}\left({\chi }_j-\overline{{\delta }_j}\right)+k_i{q}_{i,0}{x}_0\right)$

According to 3.2, $\left({\chi }_j-\overline{{\delta }_j}\right)\mathrm{mod}p=r_j$, ${\chi }_j-\overline{{\delta }_j}$ can be written as $r_j+l_j\cdot p$, $l_j\in Z$, and $x_0=q_0\cdot p$, so it is sorted into: $c_i=m_i+2^{n}A+pB$, where

$A=s_i+{\displaystyle {\sum }_{1\le j\le {\tau }_i}{b}_{i,j}\cdot \left(2^n{r}_{i,j}+p_i\cdot q_{i,j}\cdot r_j\right)}+k_i{r}_{i,0}$,

$B=p_i\cdot 2^n{\displaystyle {\sum }_{1\le j\le {\tau }_i}{b}_{i,j}\cdot q_{i,j}\cdot l_j}+k_i{q}_{i,0}{q}_0$.

According to the defined parameters, $m_i+2^{n}A<p$, then $\left(c_i\mathrm{mod}p\right)\mathrm{mod}{2}^n=m_i$. So P can correctly decrypt $c_i$ using the key $sk=p$.

4.3. Test of Homomorphism

1) P has the homomorphism of the decrypted ciphertext. Proof from 3.3 is known.

2) The encrypting party $P_i$ has homomorphism to the encrypted ciphertext. Proof: From 4.2 (2), $c_i=m_i+2^{n}A+p_{i}B$, with ciphertext $c_{i,1}=m_{i,1}+2^n{A}_1+p_i{B}_1$ and ciphertext $c_{i,2}=m_{i,2}+2^n{A}_2+p_i{B}_2$, then

$\begin{array}{l}\left(\left(c_{i,1}+c_{i,2}\right)\mathrm{mod}{p}_i\right)\mathrm{mod}{2}^n\\ =\left(\left(m_{i,1}+2^n{A}_1+p_i{B}_1+m_{i,2}+2^n{A}_2+p_i{B}_2\right)\mathrm{mod}{p}_i\right)\mathrm{mod}{2}^n\\ =\left(\left(m_{i,1}+m_{i,2}+2^n\left(A_1+A_2\right)+p_i\left(B_1+B_2\right)\right)\mathrm{mod}{p}_i\right)\mathrm{mod}{2}^n\\ =m_{i,1}+m_{i,2}\end{array}$

$\begin{array}{l}\left(\left(c_{i,1}{c}_{i,2}\right)\mathrm{mod}{p}_i\right)\mathrm{mod}{2}^n\\ =\left(\left(m_{i,1}+2^n{A}_1+p_i{B}_1\right)\left(m_{i,2}+2^n{A}_2+p_i{B}_2\right)\mathrm{mod}{p}_i\right)\mathrm{mod}{2}^n\\ =((m_{i,1}{m}_{i,2}+2^n\left(m_{i,1}{A}_2+A_1{m}_{i,2}+A_1{2}^n{A}_2\right)\\ +p_i\left(m_{i,1}{B}_2+2^n{A}_1{B}_2+B_1\left(m_{i,2}+2^n{A}_2+p_i{B}_2\right)\right))\mathrm{mod}{p}_i)\mathrm{mod}{2}^n\\ =m_{i,1}{m}_{i,2}\end{array}$

Therefore, $P_i$ has homomorphism to the encrypted ciphertext.

3) The decryption party P has homomorphism to the encrypted ciphertext. Proof: From 4.2 (3), $c_i=m_i+2^{n}A+pB$, with ciphertext $c_{i,1}=m_{i,1}+2^n{A}_1+p{B}_1$ and ciphertext $c_{i,2}=m_{i,2}+2^n{A}_2+p{B}_2$, the

$\begin{array}{l}\left(\left(c_{i,1}+c_{i,2}\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_{i,1}+2^n{A}_1+p{B}_1+m_{i,2}+2^n{A}_2+p{B}_2\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_{i,1}+m_{i,2}+2^n\left(A_1+A_2\right)+p\left(B_1+B_2\right)\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =m_{i,1}+m_{i,2}\end{array}$

$\begin{array}{l}\left(\left(c_{i,1}{c}_{i,2}\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_{i,1}+2^n{A}_1+p{B}_1\right)\left(m_{i,2}+2^n{A}_2+p{B}_2\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =((m_{i,1}{m}_{i,2}+2^n\left(m_{i,1}{A}_2+A_1{m}_{i,2}+A_1{2}^n{A}_2\right)\\ +p\left(m_{i,1}{B}_2+2^n{A}_1{B}_2+B_1\left(m_{i,2}+2^n{A}_2+p{B}_2\right)\right))\mathrm{mod}p)\mathrm{mod}{2}^n\\ =m_{i,1}{m}_{i,2}\end{array}$

Therefore, the decryption party P has homomorphism to the encrypted ciphertext.

4) The decryption party P has homomorphism for different encryption parties $P_i$ and the ciphertext of the encryption party $P_j$. Proof: From 4.2 (3), $c_i=m_i+2^{n}A+pB$, with ciphertext $c_i=m_i+2^n{A}_i+p{B}_j$ and ciphertext $c_j=m_j+2^n{A}_j+p{B}_j$, then

$\begin{array}{l}\left(\left(c_i+c_j\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_i+2^n{A}_i+p{B}_i+m_j+2^n{A}_j+p{B}_j\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_i+m_j+2^n\left(A_i+A_j\right)+p\left(B_i+B_j\right)\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =m_i+m_j\end{array}$

$\begin{array}{l}\left(\left(c_i{c}_j\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =\left(\left(m_i+2^n{A}_i+p{B}_j\right)\left(m_j+2^n{A}_j+p{B}_j\right)\mathrm{mod}p\right)\mathrm{mod}{2}^n\\ =((m_i{m}_j+2^n\left(m_i{A}_j+A_i{m}_j+A_i{2}^n{A}_j\right)\\ +p\left(m_i{B}_j+2^n{A}_i{B}_j+B_i\left(m_j+2^n{A}_j+p{B}_j\right)\right))\mathrm{mod}p)\mathrm{mod}{2}^n\\ =m_i{m}_j\end{array}$

Therefore, the decryption party P has homomorphism to different encryption parties $P_i$ and the ciphertext of the encryption party $P_j$.

4.4. Compression and Decryption Circuit

In order to avoid excessive noise generated during the encryption process and affect the correctness of the homomorphic operation, the ciphertext needs to be re-encrypted, and the condition of re-encryption is that the decryption circuit can be operated in the Evaluate algorithm. This requires that the depth of the decryption circuit is less than the maximum depth allowed by the Evaluate algorithm. Therefore, the decryption circuit needs to be compressed to preprocess some of the calculations in the decryption circuit.

KeyGen: With the KeyGen algorithm in Section 4.1, generate

$p{k}_i^{*}=\left(se,x_0,x_{i,0},{\delta }_{i,1},{\delta }_{i,2},\cdots ,{\delta }_{i,{\tau }_i}\right)$.

On the basis of this, add three parameters $\kappa ,\theta ,\Theta$, and randomly generate a bit vector $s=\left(s_{i,1},s_{i,2},\cdots ,s_{i,\Theta }\right)$ with length $\Theta$.Its Hamming weight is $\theta$.

The pseudo random number generator $f_2$ and the seed $s{e}_2$ are initialized, and an integer $u_{i,j}\in \left[0,2^{\kappa +1}\right)$, $2\le j\le \text{Θ}$ is generated by using $f_2\left(s{e}_2\right)$.

${\displaystyle {\sum }_{1\le j\le \Theta }{s}_{i,j}\cdot u_{i,j}}=x_{p_i}\mathrm{mod}{2}^{\kappa +1}$,

where $x_{p_i}$ = ⌈2^κ/p_i⌋. Let $y_{i,j}=u_{i,j}/2^{\kappa }$.

Initialize pseudo-random number generator $f_3$ and seed $s{e}_3$, use $f_3\left(s{e}_3\right)$ to generate integer ${{\chi }^{\prime }}_{i,j}\in \left[0,2^{{\gamma }_i}\right)$, and randomly generate integer ${r^{\prime }}_{i,j}\in \left(-2^{{\rho }_i},2^{{\rho }_i}\right)$, , calculate

,

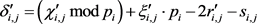then the result of the vector s is encrypted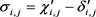. The public key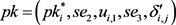, and the private key.

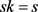Encrypt: Encrypt the plaintext with an encryption algorithm to obtain the ciphertext, and find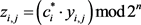. The ciphertext 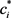and the extended ciphertext are the output.

Decrypt: Decrypt, output secret civilization

.

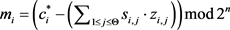This results in a fully homomorphic encryption scheme.

5. Conclusion

Based on the DGHV scheme and the public key compression technology of Coron et al., this paper improves the encryption process, expands the number of encryption parties, and builds a multi-party encryption with a smaller public key size. The integer-homomorphic encryption scheme can encrypt the n-bit plaintext at a time, which is more in line with the needs of practical applications such as cloud computing. Whether it can further reduce the amount of calculation, whether it can achieve “multi-party encryption, multi-party decryption” will be the direction that will be improved in the future.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Hu, C.J. and Zhao, J.W. (2018) An Improved Multiple to One Fully Homomorphic Encryption on the Integers. Journal of Computer and Communications, 6, 50-59. https://doi.org/10.4236/jcc.2018.69005

References