Received 12 June 2016; accepted 19 August 2016; published 22 August 2016

ABSTRACT

This paper presents a new approach to identify and estimate the dispersion parameters for bivariate, trivariate and multivariate correlated binary data, not only with scalar value but also with matrix values. For this direction, we present some recent studies indicating the impact of over- dispersion on the univariate data analysis and comparing a new approach with these studies. Following the property of McCullagh and Nelder [1] for identifying dispersion parameter in univariate case, we extended this property to analyze the correlated binary data in higher cases. Finally, we used these estimates to modify the correlated binary data, to decrease its over-dispersion, using the Hunua Ranges data as an ecology problem.

Keywords:

Measures of Association, Correlated Binary Data, Dispersion Parameters, Scaled Deviance, Scalar Value, Scalar Matrix

1. Introduction

The dispersion parameter should be the unity in case of the univariate Bernoulli data, but there may be deviation if there is a sequence of the Bernoulli outcomes included in a study that may lead to a binomial variable. The over-dispersion is happened if the variance of actual response is more than the nominal variance, 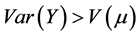, as a function of the mean,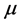. The estimation of dispersion parameter in the univariate case can be obtained easily using the Pearson’s Chi-square or the deviance function. Many studies have devoted the over-dispersion criteria in the univariate case, namely, when the binomial data are used. It is difficult to extend these methods to estimate the dispersion parameters in the bivariate case, because in the bivariate case, the association between correlated response variables may be happened. So, we must take this association into account when estimate the dispersion parameter. But in the independence case, the estimate of dispersion parameter is performed as in the univariate case. The estimate of dispersion parameters for the bivariate correlated binary data can be obtained using different methods. The first one when the dispersion parameter is scalar. The second one when we have a matrix values of dispersion parameters. These estimates can be extended to the trivariate and multivariate correlated binary data. So, we present a new approach to identify and estimate the dispersion parameters, in scalar and matrix values, for the bivariate, trivariate and multivariate correlated binary data. Also, after obtaining these estimates we can modify the correlated binary data, this happens to obtain a dispersion parameter equal or near to the unity.

This paper can be organized as follows: Some of the previous studies are presented in the Section 2.

A proposed approach for identifying and estimating the dispersion parameters in a scalar and matrix values, and the impact of over-dispersion in the case of bivariate, trivariate and multivariate binary outcomes associated with covariates, are demonstrated in the Sections 3, 4 and 5, respectively.

Finally, the numerical examples for the vectorized generalized additive model, VGAM, or vectorized generalized linear model, VGLM, Yee and Wild [2] , and the alternative quadratic exponential form, AQEF, measure, El-Sayed et al. [3] , are demonstrated in Section 6.

2. Previous Studies

In this section, we present some studies on the over-dispersion problem as shown below:

(1) Smith and Heitjan [4] provided an appropriate statistical tool to detect extra binomial variation (over-disp- ersion). To test the nominal dispersion in the i-th (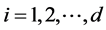) margin, it is important to give the relation, for 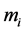trials,

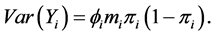(1)

The hypothesis testing problem is formulated as

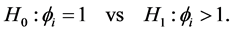
An appropriate procedure to test 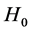is the score statistic suggested by Smith and Heitjan

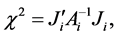(2)

where is a random vector that registers the difference between actual information and nominal information, in the i-th margin with respect to every j-th (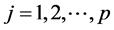) parameter, for 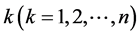observations, namely

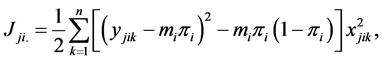(3)

And is the covariance matrix of 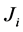corrected for estimation of linear predictors, 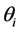, where

. Under the null hypothesis, , the asymptotic distribution of statistic (2) is the distribution

with p degrees of freedom. The eventual rejection of will be a clear evidence that.

(2) Cook and Ng [5] described a bivariate logistic-normal mixture model for over-dispersed two state Markov processes. The use of these mixed models cause increase in the standard error of marginal probability estimates. They did not specify the explicit form for the over-dispersion estimate, but display the log-likelihood function for the full sample of m subjects, as

(4)

where, the expectation, , is taken with respect to the bivariate normal distribution, hence , , are regression parameters.

(3) Saefuddin et al. [6] showed the effect of over-dispersion on the hypothesis test of logistic regression.

A simple method proposed by William, [7] , was used to correct the effect of over-dispersion by taking inflation factor into consideration. This method takes account of adjusting the estimate of the standard error of the parameter resulting from the over-dispersion. Modeling of the over-dispersion is often expressed in the equation of the variance of response variable, , for binomial case for trials, as follows

(5)

where is the over-dispersion scale and denote inflation factor. When the over-dispersion does not occur or very small over-dispersion occurs, will be approximately equal to zero, so exactly follows binomial distribution, , and, Collett [8] . However, when over-dis- persion exists, exceeds zero and leads to be greater than. The parameter estimate of, is obtained by equating statistic of the model to its approximate expected value, written as

(6)

where, is the weight and is the diagonal element of the variance-covariance matrix of the linear predictor, say. The value of statistic depends on, so iteration process is needed to find the optimum value. This procedure was the first introduced by William, [7] , and is known as William method.

The algorithm of the William method is described as follows:

1. Assume, calculate parameter estimate of logistic regression parameter, , using maximum likelihood method. Calculate the statistics of fitted model.

2. Compare statistics to distribution. If statistic is too large, conclude that and calculate the initial estimates of using following formula

(7)

3. Using the initial weights

(8)

we can recalculate the value of and statistic.

4. If statistic close to its degrees of freedom, , then the estimated value of is sufficient. If not, re-estimate using following expression:

(9)

If statistic remains large, return to step (3) until optimum value of estimated is obtained. Once has been estimated by, could be used as weights in fitting the new model, Collett [8] , and William [7] . We conclude that the over-dispersion problem causes lower standard errors of the estimates of parameters.

(4) Davila et al. [9] introduced a new approach for modeling the multivariate marginals over-dispersed binomial data. They illustrate this approach by analyzing the data using the Gaussian copula with Beta-binomial margins. In order to model the over-dispersion, they used the Beta-binomial model, a generalization of binomial distribution, Casella and Berger [10] . In this model, it is supposed that, whereas. Then, they make the assumption that each margin, , follows a Beta-binomial distribution. Therefore, unconditionally the compound density, with respect to the counting measure of, is given by

(10)

where,. Conditional to, the expectation is given by

(11)

The conditional variance is

(12)

From the relation (12), we see that the marginal dispersion parameter is

(13)

Comparing the relation (1) with the relation (12), it is noted that the later has a greater variance. In their study, as compared with the multivariate normal (MVN), the marginal GLM, and the marginal over-dispersion model (ODM), they have shown that the model based on the Beta-binomial model (BBM) displayed the higher standard errors associated to estimated parameters.

(5)-The vectorized generalized additive model (VGAM) introduced by Yee and Wild [2] and implemented by Yee [11] [12] . The conditional distribution of VGAM function for bivariate correlated binary responses, given that some covariates, x, is:

(14)

where, is the normalizing constant,

And the, , are additive predictors. If all the functions are constrained to be linear, then the resulting model is a vector generalized linear model (VGLM).

The conditional distribution of VGAM family function for trivariate binary responses, given that some covariates, x, is

(15)

Note that a third order association parameter, , for the product, , is assumed to be zero for this family, Yee and Wild [2] .

The conditional distribution of VGAM (VGLM) function for multivariate correlated binary responses, , given that some covariates, x, is

(16)

where is the normalizing constant.

In the next section, we suggest a new approach to estimate the dispersion parameter, , using a scalar and a matrix values of the dispersion parameters and indicate how the dispersion parameter may influence on the analysis of correlated binary data, specially on the standard errors, the Wald statistics and the LRTs for the bivariate, trivariate and multivariate binary outcomes variables associated with covariates. For fitting the correlated binary data, we use the log-likelihood function for the alternative quadratic exponetial form (AQEF) measure, [3] , in the bivariate, trivariate and multivariate case, respectively.

Using the following notations which imply to the link functions which enable us to use the regression model:

(17)

we have the log-likelihood function for the bivariate AQEF measure as

(18)

The log-likelihood function for the trivariate AQEF measure is

(19)

where,

Finally, the log-likelihood function for the multivariate AQEF measure is

(20)

where,

(21)

3. Dispersion Parameters in Bivariate Case

In this section, we determine the identification and estimation of a fixed value for dispersion parameter, , and also a matrix of dispersion parameters to extend the effect of over-dispersion on the analysis of bivariate correlated binary data.

3.1. Scalar Dispersion Parameter

We can use the variance-covariance matrix of and to estimate a scalar dispersion parameter, , in the bivariate binary outcomes. So, we can define the response vector

and its mean vector.

Following the GLM property, the variance-covariance matrix of Y is

where,

And,

Then, the estimator of, for n observations, is

(22)

Hence, we can show that

(23)

Then,

Follows the non-central. Under independence, this quantity follows, approximately,. An estimator of in this case is

(24)

3.2. Matrix of Dispersion Parameters

Now, we use different values for dispersion parameter, such that and, here,. The variance-covariance matrix of Y is

(25)

The estimator of dispersion parameters matrix is

Then,

(26)

From the equation (26), we have

Follows the non-central. Under independence, this quantity follows, approximately,. If, and, then the estimator of is same as (24).

We can correct the data using the estimates of dispersion parameters, , and Equation (25), for the i-th observation, in the bivariate case as

(27)

4. Dispersion Parameters in Trivariate Case

We can define the response vector

and its mean vector.

4.1. Scalar Dispersion Parameter

The variance-covariance matrix of Y can be written as

(28)

where,

The estimator of, for n observations, is

(29)

Since,

Follows the non-central. Then, under independence, this quantity follows, approximately,. Under independence, the estimator of is

(30)

4.2. Matrix of Dispersion Parameters

The variance-covariance matrix of Y can be displayed as

(31)

The estimator of dispersion parameters, , are

(32)

Since,

Follows the non-central. Under independence, this quantity follows, approximately,. If and, then the estimator of is same as (30).

Similarly, we can correct the data using the estimates of dispersion parameters, and, and the equation (31), for the i-th observation, in the trivariate case as

(33)

5. Dispersion Parameters in Multivariate Case

We can define the response vector

and its mean vector.

5.1. Scalar Dispersion Parameter

The variance-covariance matrix of Y can be written as

(34)

where,

The estimator of, for observations, is

(35)

Since,

Follows non-central. Then, under independence, this quantity follows, approximately,. Under independence, the estimator of is

(36)

5.2. Matrix of Dispersion Parameters

The variance-covariance matrix of Y can be displayed as

(37)

The estimator of dispersion parameters, , are

(38)

Since,

Follows non-central. Under independence, this quantity follows, approximately,. If and, then the estimator of is same as (36). Similarly, we can correct the data using the estimates of dispersion parameters, , and the equation (37), for the -th observation, in the multivariate case as

(39)

6. Numerical Examples

In this section, we present two examples. The first one applies to the bivariate correlated binary data. This example presents the results obtained by using AQEF measure and the VGLM measure which are similar in the bivariate case. The second one applies on the trivariate binary data. However, the third association is absent in the VGAM (VGLM) measure. In both examples, we will use the Hunua Ranges data, Yee [11] [12] . These data were collected from the Hunua Ranges, a small forest in the Southern Auckland, New Zealand.

At 392 sites in the forest, the presence/absence of 17 plant species was recorded along with the altitude. Each site was of area size 200 m². The Hunua Ranges data frame has 392 rows and 18 columns. Altitude is a continuous variable, and there are binary responses (presence = 1, absence = 0) for 17 plant species. These data frame contains the following columns: agaaus, beitaw, corlae, cyadea, cyamed, daccup, dacdac, eladen, hedarb, hohpop, kniexc, kuneri, lepsco, metrob, neslan, rhosap, vitluc and altitude (meters above the sea level).

6.1. Application to Bivariate Case

Hence, we will use the first two columns, agaaus and beitaw, as correlated binary outcome variables, and, respectively. A third column, corlae, is used as the explanatory binary variable, X.

We will use the estimates, and, to modify the correlated data according to the relationship (27).

From Table 1 and Table 2, we demonstrate the conclusions after modifying the correlated data by the estimates of dispersion parameters, as follows:

1. The estimates of the regression parameters are changed.

2. The standard errors are decreased for the estimates of association parameters. This leads to a significant association between the two outcomes binary variables, , associated with covariate, x.

3. The Wald statistic test shows lower values, this confirms a significant association between the two outcomes binary variables, , associated with covariate, x.

4. The LRT is increased, this also confirms the conclusion observed from the Wald statistic.

5. The estimate of a scalar dispersion parameter, , is increased.

6. The estimates of the matrix of dispersion parameters, and, increased and close to the unity.

7. The scaled deviance value is increased.

6.2. Application to Trivariate Case

We will use the columns, cyadea, beitaw and kniexc, as the dependent correlated binary variables, and, respectively. On the other hand, we will use the column “altitude”, meters above sea level, as the continuous explanatory variable, X. The estimates of the regression parameters and their tests for the association parameters can be determined for the AQEF and VGLM measures, before and after modifying the correlated data by the estimates of dispersion parameters, and, as shown in Table 3.

Hence, the LRT’s will be compared with. Log-likelihood = −454.1039.

Hence, the LRTs will be compared with. Log-likelihood = −461.6315.

Hence, the LRT’s will be compared with.

From Table 3, we demonstrate the conclusions after modifying the data by the estimates of dispersion parameters, as follows:

1. The estimates of regression parameters in the two measures are changed.

2. The scaled deviance is increased for the two measures.

3. The estimate of a scalar dispersion parameter, , is decreased for the two measures.

4. The estimates of values of dispersion parameters, , and, are decreased for the two measures, but close to the unity for the AQEF measure. On the other hand, the estimates of dispersion parameters, , and, are decreased for the two measures, but close to the unity for the VGLM measure.

5. For the VGLM measure, the LRTs reflect significant association between the pairwise outcome variables, , and, associated with covariates, x.

For the AQEF measure, the LRTs also reflect significant association between the pairwise outcome variables, and, associated with covariates, x.

However, no significant association is observed between the correlated binary outcome variables, , associated with covariates, x.

6. The LRT for the third association, which is observed from the AQEF measure, reflects no significant association between the correlated binary outcome variables, , associated with covariates, x.

So, when modifying the correlated data, the estimates of dispersion parameters, , and, tend to the unity. This leads to no significant association between the outcome variables, and, associated with covariates, x.

Acknowledgements

For all my professors.

Cite this paper

Ahmed Mohamed Mohamed El-Sayed, (2016) A New Approach for Dispersion Parameters. Journal of Applied Mathematics and Physics,04,1554-1566. doi: 10.4236/jamp.2016.48165

References