Journal of Applied Mathematics and Physics
Vol.2 No.2(2014), Article ID:42205,4 pages DOI:10.4236/jamp.2014.22005
Method of Lines for Third Order Partial Differential Equations
1Department of Mathematics, Faculty of Art and Science, Erzincan University, Erzincan, Turkey
2Department of Mathematics, Faculty of Art and Science, Sinop University, Sinop, Turkey
Email: muskud28@yahoo.com, ailhame@gmail.com
Received December 5, 2013; revised January 5, 2014; accepted January 10, 2014
ABSTRACT
The method of lines is applied to the boundary-value problem for third order partial differential equation. Explicit expression and order of convergence for the approximate solution are obtained.
Keywords:Method of Lines; Partial Differential Equation; Convergence; Error Estimates
1. Introduction
We consider the boundary value problem for the third order differential equation in the domain
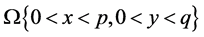 :
:
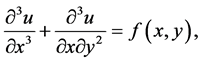 (1)
(1)
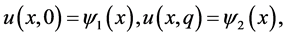 (2)
(2)
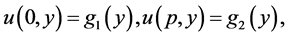 (3)
(3)
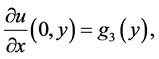 (4)
(4)
where 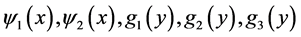 are sufficiently smooth functions.
are sufficiently smooth functions.
The problems of type (1)-(4) arise in many mathematical and scientific applications [1-3]. In this study, we construct first order accurate differential difference scheme for this problem and give error estimate for its solutions. The approach to the construction of the discrete problem and the error analysis for the approximate solution are similar to those in [4].
Let the solution of the problem (1)-(4) have a bounded derivative  in the domain
in the domain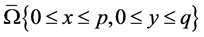 .
.
2. Differential-Difference Algorithm and Convergence
We divide the domain 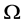 into
into 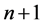 stripe by lines
stripe by lines  On this lines the problem (1)-(4) we approximate by the following differential difference problem:
On this lines the problem (1)-(4) we approximate by the following differential difference problem:
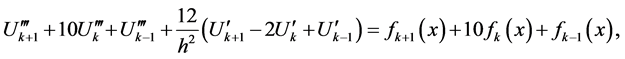 (5)
(5)
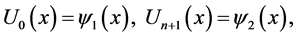 (6)
(6)
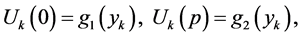 (7)
(7)
 (8)
(8)
Let we rewrite the problem (5)-(8) in the form
 (9)
(9)
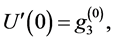
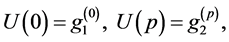
where
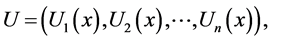
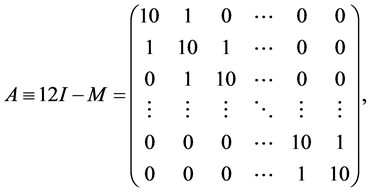
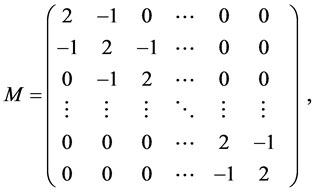
I-unit matrix,
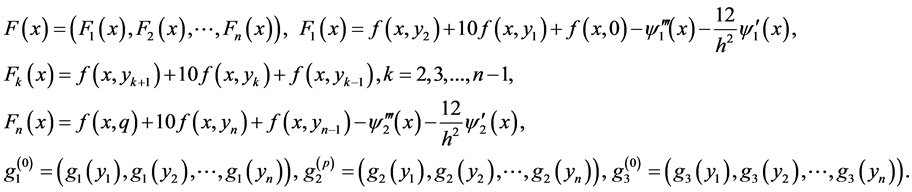
The matrix 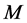 can be diagonalized as [5,6]
can be diagonalized as [5,6]

with
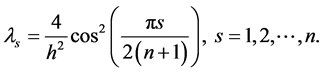
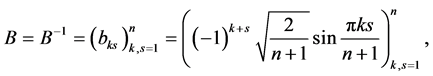
Multiplying equation (9) on the left by 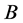 we have
we have
 (10)
(10)
 (11)
(11)
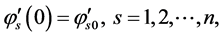 (12)
(12)
where

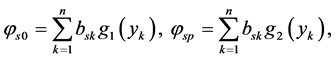
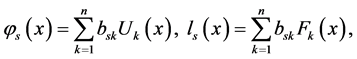
The solution of (10)-(12) containing the third order ordinary differential equation with constant coefficients can be explicitly found
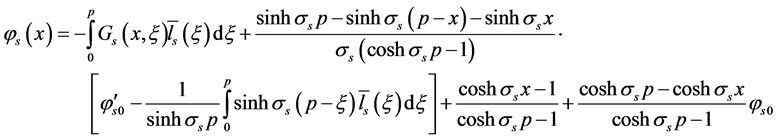
where

Therefore the solution of (5)-(8) can be expressed as

where
 .
.
Now we investigate the error of the approximate solution. For the error  we have the following boundary value problem:
we have the following boundary value problem:

where
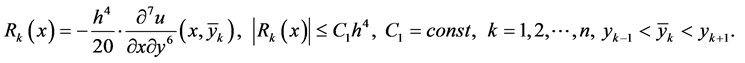

or
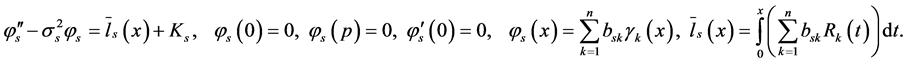
Next for

By the mean value theorem we have
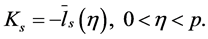
Then
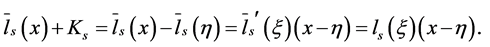
Since  then it follows that
then it follows that

Further, we note that  and
and

Hence

Using here the inequality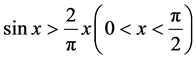 , and taking into account
, and taking into account 
it follows that
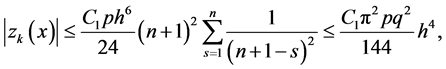
i.e., fourth order convergence for the approximate solution is established.
REFERENCES
- A. I. Kozhanov, “Mixed Boundary Value Problem for Some Classes of Third Order Differential Equations,” Matematicheskii Sbornik, Vol. 118 (160), No. 4 (8), 1982, pp. 504-522. (in Russian)
- A. I. Kozhanov, “Mixed Problem for One Class of Quasilinear Equation of Third Order,” In: Boundary Value Problems for Nonlinear Equations, Novosibirsk, 1982, pp. 118-128. (in Russian)
- S. A. Gabov and A. G. Sveshnikov, “Problems of the Dynamics of Stratified Fluids,” Nauka, Moscow, 1986, p. 288. (in Russian)
- G. M. Amiraliyev and P. Okcu, “Error Estimates for Differential Difference Schemes to Pseudo-Parabolic Initial-Boundary Value Problem with Delay,” Computers & Mathematics with Applications, Vol. 18, No. 3, 2013, pp. 283-292.
- S. B. Nemchinov, “On the Finite Difference Method to the Elliptic Boundary Value Problems,” Journal of Computational and Applied Mathematics, Vol. 2, 1962, pp. 418-436. (in Russian)
- A. A. Samarskii, “The Theory of Difference Schemes,” Marcel Dekker, New York, 2001.

