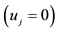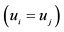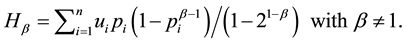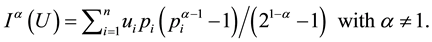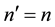Theoretical Economics Letters Vol.05 No.02(2015), Article ID:55171,10
pages
10.4236/tel.2015.52023
Combining Expected Utility and Weighted Gini-Simpson Index into a Non-Expected Utility Device
José Pinto Casquilho
Postgraduate and Research Program, Universidade Nacional Timor Lorosa’e, Díli, Timor-Leste
Email: josecasquilho@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 February 2015; accepted 22 March 2015; published 30 March 2015
ABSTRACT
We present and discuss a conceptual decision-making procedure supported by a mathematical device combining expected utility and a generalized information measure: the weighted Gini- Simpson index, linked to the scientific fields of information theory and ecological diversity analysis. After a synthetic review of the theoretical background relative to those themes, such a device― an EU-WGS framework denoting a real function defined with positive utility values and domain in the simplex of probabilities―is analytically studied, identifying its range with focus on the maximum point, using a Lagrange multiplier method associated with algorithms, exemplified numerically. Yet, this EU-WGS device is showed to be a proper analog of an expected utility and weighted entropy (EU-WE) framework recently published, both being cases of mathematical tools that can be referred to as non-expected utility methods using decision weights, framed within the field of decision theory linked to information theory. This kind of decision modeling procedure can also be interpreted to be anchored in Kurt Lewin utility’s concept and may be used to generate scenarios of optimal compositional mixtures applied to generic lotteries associated with prospect theory, financial risk assessment, security quantification and natural resources management. The epistemological method followed in the reasoned choice procedure that is presented in this paper is neither normative nor descriptive in an empirical sense, but instead it is heuristic and herme- neutical in its conception.
Keywords:
Non-Expected Utility, Weighted Entropies, Weighted Gini-Simpson Index, Decision Theory, Mean Contributive Value

1. Introduction
Expected utility theory may be considered to be born in 1738, relative to the general problem that choosing among alternatives imply a consistent set of preferences that can be described by attaching a numerical value to each―designated its utility; also, choosing among alternatives involving risk entails that it is selected that one for which the expected utility is highest (e.g. [1] ). As Weirich [2] points out, such an utterance inherits from the theory of rationality a collection of problems concerning evaluation of acts with respect to information. It is useful to distinguish among decisions under risk, meaning circumstances or outcomes with known probabilities, as opposed to situations on uncertainty where probabilities are not known (e.g. [3] ). Shannon entropy [4] measures the uncertainty of a random variable, and, for example, an entropy-based risk measure concerning financial asset pricing is claimed to be more precise than other models [5] . A recent review of applications of entropy in finance, mainly focused in portfolio selection and asset pricing, but also in decision theory, can be acknowl- edged in [6] .
This work is an analogous development of another paper recently published, where it was discussed an expected utility and weighted entropy framework, with acronym EU-WE [7] . We shall prove that the claimed analogy has here a proper sense, as either weighted Shannon entropy or weighted Gini-Simpson index may be considered two cases of generalized useful information measures. Hence, the conceptual framework to be discussed and elucidated in this paper is referred to with the acronym EU-WGS, and, as it will be justified later, consists of another form of mean contributive value of a finite lottery in the context of decision theory.
Combining the concepts of expected utility and some measure of variability of the probability score―generat- ing utility functions that are nonlinear in the probabilities―is not an innovative method and we can identify an example concerning meteorology forecasts dating back to 1970 [8] . Those approaches were later merged under the name of “non-expected utility” methods in the 1980s and consist of different conceptual types, the one we shall be dealing with framing into the category of decision models with decision weights or non-additive probabilities, also named capacities. A decision-making model based on expected utility and entropy (EU-E) introducing a risk tradeoff factor was discussed by Yang and Qiu [9] , where Shannon entropy measures the objective uncertainty of the corresponding set of states, or its variability; recently, the authors reframed their model into a normalized expected utility-entropy measure of risk [10] , allowing for comparing acts or choices where the num- ber of states are quite apart.
First, we shall present a synthetic review of the theoretical background anchored in two scientific fields: expected or non-expected utility methods and generalized weighted entropies or useful information measures. Then, we shall proceed merging the two conceptual fields into a mathematical device that combines tools from each and follow studying it analytically and discussing the main issues that are entailed for such a procedure. The spirit in which this paper is written is neither normative nor descriptive―instead it is conceived as a heuristic approach to a decision procedure tool whose final judge will be the decision maker.
2. Theoretical Background
2.1. Expected and Non-Expected Utility Approaches
The concept of “expected utility” is one of the main pillars in Decision Theory and Game Theory, going back at least to 1738, when Daniel Bernoulli proposed a solution to the St. Petersburg paradox using logarithms of the values at stake, thereby making the numerical series associated with the calculation of the mean value convergent (there referred to as “moral hope”). Bernoulli [11] explicitly stated that the determination of the value of an item should not be based on its price but rather on the utility that it produces, being the marginal utility of money inversely proportional to the amount one already has. Bernoulli approach―considered the first statement on Expected Utility Theory (EUT)―presupposes the existence of a cardinal utility scale, and that remained an obstacle until the theme was revived by the remarkable work of John von Neumann and Oskar Morgenstern in 1944, showing that the expected utility hypothesis could be derived from a set of axioms on preference [12] , considering the utilities experienced by one person and a correspondence between utilities and numbers, involving complete ordering and the algebra of combining. Nevertheless, based on their theorem one is restricted to situations in which probabilities are given (e.g. [13] ).
Since that time there were innumerable contributions on the theme. For instance, Alchian [14] outlines the issue stating that if, in a given context, it is possible to assign numerical values for different entities competing, then a selection process of rational choices is made to maximize the utility and one can say that the normal form of expected utility reduces to the calculation of the average value of a pattern of preferences expressed by li- mited numerical functions. But soon also appeared the objections relative to the adherence of EUT to empirical evidence, namely the Allais paradox which was first published in 1953, showing that individual’s choices in many cases collided with what was predicted by the theory, one reason being because expected utility devices associated with lotteries do not take into account the dispersion of the utilities around their mean values and also because, in general, people overweight positive outcomes that are considered certain compared to outcomes which are merely probable (e.g. [15] for a review).
Subjective expected utility, having a first cornerstone in the works of de Finetti and Ramsey [16] both published in 1931, followed by a further substantial development with Savage in 1954, was regarded by most decision analysts to be the preferred normative model for how individuals should make decisions under uncertainty, eliciting vectors of probabilities given the preferences in outcomes; but that approach was also revealed to be violated in empirical situations, what was illustrated for example by the Ellsberg paradox published in 1961. Other paradoxes were mentioned later such as those referred to by Kahneman and Tversky concerning prospect theory [17] where the carriers of value are changes in wealth or welfare rather than final states. Machina [18] highlighted that the independence axiom of EUT tends to be systematically violated in practice and concluded that the main concepts, results and tools of expected utility analysis may be derived from the much weaker assumption of smoothness of preferences over alternative probability distributions; this remarkable work outlined the scope of generalized expected utility analysis or non-expected utility frameworks. Other methods were pro- posed and used such as mean-variance analysis (e.g. [19] [20] ); based on this type of method and using mean absolute deviation instead of standard deviation, Frosini [21] presented recently a discussion revisiting Borch paradox linked to a general criterion of choice between prospects.
Here we will be focused in lotteries, a concept we shall retain (e.g. [22] ): a
lottery is defined as a list or finite collection of simple consequences or outcomes
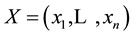 with associated, usually unknown, probabilities stated as
with associated, usually unknown, probabilities stated as
 for
for
 completed with the standard normalization conditions
completed with the standard normalization conditions
 and
and
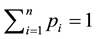 defining a
defining a
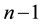 simplex
simplex
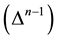 and denoting a vector
and denoting a vector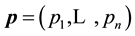 .
The axioms of EUT with the most usual version―ordering, continuity and independence―allow
for preferences over lotteries to be represented by the maximand functional
.
The axioms of EUT with the most usual version―ordering, continuity and independence―allow
for preferences over lotteries to be represented by the maximand functional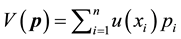 , where
, where
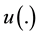 is a utility function mapping the set of consequences with image conceived as a
set of real numbers
is a utility function mapping the set of consequences with image conceived as a
set of real numbers
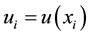 with
with
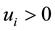 for
for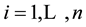 . For simplicity
of notation we shall write a discrete random variable representing a finite lottery
denoted as
. For simplicity
of notation we shall write a discrete random variable representing a finite lottery
denoted as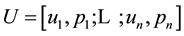 ,
from what follows that expected utility is therefore evaluated like
,
from what follows that expected utility is therefore evaluated like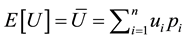 .
.
The geometry of ,
supposed monotonous, has a simple behavioral interpretation under EUTaxioms, whereby
being concave implies risk aversion―such as the logarithm function used by Bernoulli―and
convexity entails risk prone behavior by an individual agent. The Arrow-Pratt measure
(e.g. [23] ) is commonly used to assess the issues of risk-avert or risk-prone behavior.
Recently, Baillon et al. [24] presented a general and simple technique for comparing
the concavity of different utility functions isolating its empirical meaning in
EUT, and an example of a concave utility function used to assess optimal expected
utility of wealth under the scope of insurance business can be acknowledged in [25]
.
,
supposed monotonous, has a simple behavioral interpretation under EUTaxioms, whereby
being concave implies risk aversion―such as the logarithm function used by Bernoulli―and
convexity entails risk prone behavior by an individual agent. The Arrow-Pratt measure
(e.g. [23] ) is commonly used to assess the issues of risk-avert or risk-prone behavior.
Recently, Baillon et al. [24] presented a general and simple technique for comparing
the concavity of different utility functions isolating its empirical meaning in
EUT, and an example of a concave utility function used to assess optimal expected
utility of wealth under the scope of insurance business can be acknowledged in [25]
.
As Shaw and Woodward [26] say, focusing on the issue of natural resources management, the problem in classical utility theory is that the optimization of the models may have to accommodate preferences that are nonlinear in the probabilities. There are many approaches with this perspective, known at least since Edwards in 1955 and 1962 [27] discussed in parallel the theory of Kurt Lewin utility and the theory of subjective probability of Francis Irwin, introducing the concept of decision weights instead of probabilities; the Lewin utility theory was referred to as anchored in the concept that an outcome which has a low probability will, by virtue of its rarity, have a higher utility value than the same outcome would have if it had a high probability.
A substantial review was made by Starmer [28] under the name of non-expected utility
theory, the case of subjective probabilities being framed within the conventional
strategy approach focused on theories with decision weights, in particular the simple
decision weight utility model where individuals concerned with lotteries are assumed
to maximize the functional
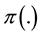

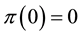

There are many other approaches to surpass the limitations of independence axiom, and, for example, Hey and Orme [31] compared traditional expected utility and non-expected utility methods with a total of 11 types of preference functionals, evaluating the trade-off of explaining observed differences of the data relative to the models versus loosing predictive power. Recently, a reasoning of decision-making with catastrophic risks motivated the incorporation of a new axiom named sensitivity to rare events [32] . But simple decision weight utility modeling is the conceptual type of non-expected utility methods that is relevant in this paper.
2.2. Generalized Useful Information Measures and Weighted Gini-Simpson Index
The quantitative-qualitative measure of information generalizing Shannon entropy
characterized by Belis and Guiasu [33] is additive and may be associated with a
utility information scheme, anchored in a finite sample space, establishing that
an elementary event
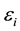
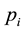
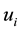
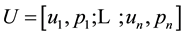
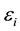
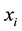
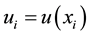
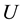
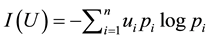
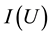
In 1976, Emptoz―quoted in Aggarwal and Picard [42] ―introduced the entropy of degree
Using l’Hôpital’s rule it is easy to prove the result of the limit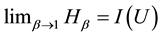
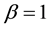
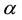
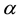
The formula above means exactly the same entity as entropy of degree
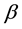
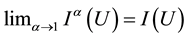
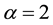
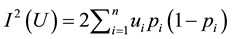
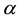
Weighted Gini-Simpson (WGS) index was outlined by Guiasu and Guiasu [45] in the
scope of conditional and weighted measures of ecological diversity denoted as
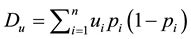
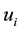
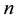

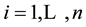
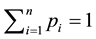
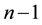

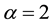
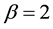
The formulation and analytical study of weighted Gini-Simpson index was first introduced by Casquilho [49] within a set of indices built as mathematical devices applied to discuss compositional scenarios of landscape mosaics (or ecomosaics), using either ecological or economic weights―there referred to as positive characteristic values of the habitats―in order to assess the relevance of the actual extent of the components, as compared with the optimal solutions of the different indices.
One main feature of WGS index we must keep in mind is that we have
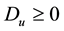
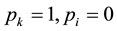
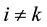
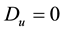
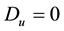
Weighted Gini-Simpson index is used in several domains, besides ecological and phylogenetic assessments― focusing in economic applications we have examples such as: estimating optimal diversification in allocation problems [50] and other developments concerning ecomosaics composition assessment with forest habitats [51] [52] . In [49] [51] it is shown that weighted Gini-Simpson index can be interpreted as a sum of variances of interdependent Bernoulli variables thus becoming a measure of the variability of the system and enabling a criterion for its characterization.
3. Combining Expected Utility and Weighted Gini-Simpson Index
3.1. Definition and Range
In what follows, the simple lottery
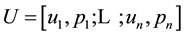
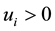
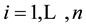

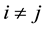
simplex:
In this setting used to characterize the discrete random variable

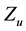
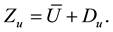
Equation (1) therefore has the full expression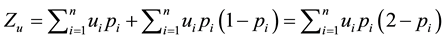
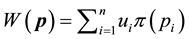
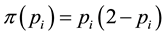

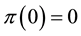

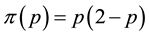
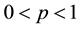
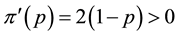
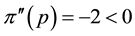
Still, we can proceed with the subsequent interpretation: denoting

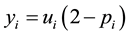

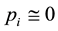
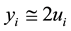

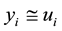
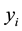
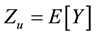
The function
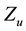

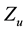
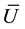
Concerning the evaluation of the minimum point we see that denoting
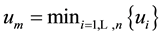
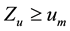
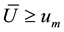
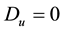
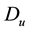
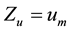
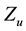
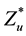
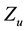
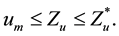
3.2. Searching the Maximum Point
Searching for the maximum point correspondent to the maximum value
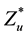
build the auxiliary Lagrange function
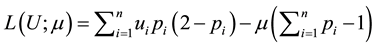
partial derivative(s) as follows: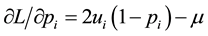
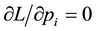
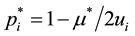

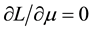
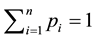
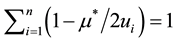
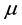
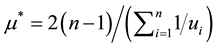
Using Equation (3) combined with the equation
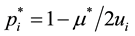
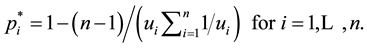
As it is known, the critical value of the Lagrange multiplier reflects the importance
of the constraint in the problem and we can check directly from Equation (3) that
we have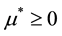
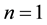
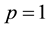

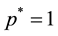
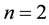
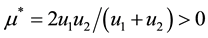
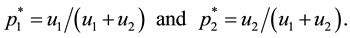
We can also check that the result




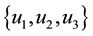
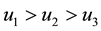
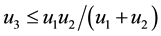
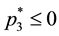
Thus, combining
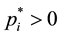

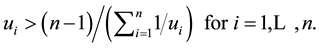
Otherwise, we have to proceed using an algorithm, as it will be shown next. But
we can already notice, from direct inspection of Equation (4) to Inequality (6)
that the candidates to optimal coordinates would be the same if we use a positive
linear transformation of the utilities such as
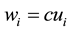
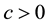
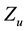
3.3. Algorithms for Obtaining the Maximum Point
It must be noted that we are certain that the maximum point exists as it is implied
by Weierstrass theorem. The problem we are dealing has an old root, as Jaynes [53]
in 1957 had already noticed, saying that the negative term
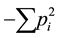
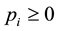
Here, first we shall choose a forward selection procedure since we know that when
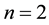
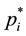
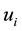


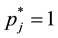
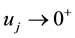
get the result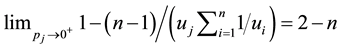
So, given the set of utilities defined in
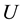
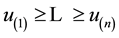

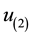
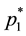
the problem begins with the evaluation of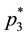
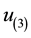
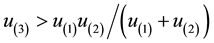
Whether not, stop and state
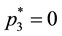
now with the condition (6) restated as

tion until you verify that there is an order
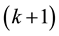
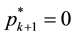
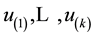

It must be noted that we could have chosen a backward elimination procedure instead with a faster algorithm, begin-
ning with the lowest utility
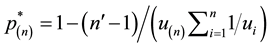
and if observing

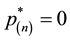

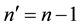

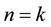
3.4. Numerical Example
Assume that we have the following lottery with n = 5 and ordered utilities: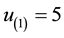
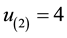

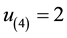
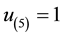
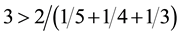
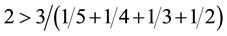
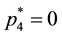
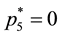
luate the optimal point with Equations (4) relative to the set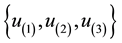
reset to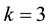
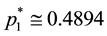
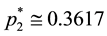
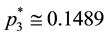
Now, exemplifying the backward elimination procedure with the same utility values: first we evaluate
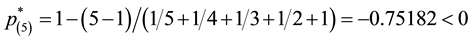
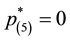
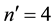
late
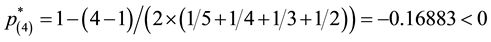
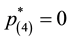
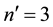
we get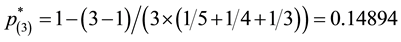
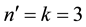
3.5. The Maximum Value
The maximum value of
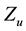
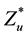
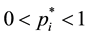
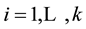

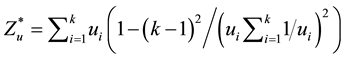
In the case of the numerical example described above we get the number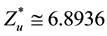
4. Discussion
Going back to the beginning, we can state that the reasoned choice modeling we introduced
was a sequential decision-making procedure that began with a lottery
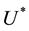
First, we shall focus the discussion comparing optimal proportions of function
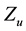
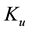
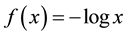
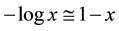
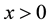

Nevertheless, there are differences, perhaps the most noticeable ones being qualitative,
as the fact that the optimal point of
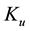

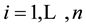
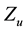
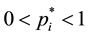
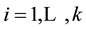

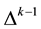
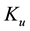

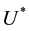

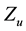
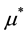

Yet there is another point that deserves an explanation: it was claimed in [7] that
index
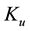
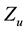
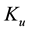

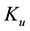
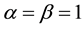
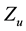
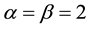
There is also another issue that demands an explanation, or, the least, to be posed
straightforwardly: consider the lottery

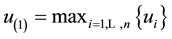
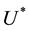
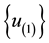
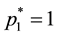
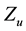
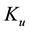
Weirich [2] points out, concerning the discussion of generalized expected utility methods, that comprehensive rationality requires adopting the right option for the right reason. Whether these models are appropriate for rooting such an utterance is a question that remains open, as we were not concerned with the moral issues that could be raised related to the criteria embodied in the formulas.
Discussing the limitations of this modeling approach we have to highlight that the
weighting function

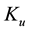
Gilboa [13] says that a decision is objectively rational if the decision maker can
convince others that she is right in making it, whether it is subjectively rational
for her if others cannot convince her that she is wrong in making it―the ultimate
judge of the choices remaining the decision maker. Hence, with this reference on
mind, taking the decision of adopting the optimal result
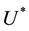
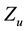
5. Conclusions
In this work we outlined a reasoned decision-making tool combining traditional expected utility with a generalized useful information measure (a type of weighted entropy) referred to as the weighted Gini-Simpson index― thus becoming a conceptual framework with acronym EU-WGS. This device is original and applies to simple lotteries defined with positive utilities and unknown probabilities, denoted as a real function with domain in the standard simplex.
It was shown that this mathematical device frames into the class of non-expected utility methods relative to the type concerning the use of decision weights verifying standard conditions; also, it was shown that function could be interpreted as a mean value of a finite lottery with utilities conceived in the sense of Kurt Lewin, where the rarity of a component enhances the correspondent utility value by a maximum of a two-fold factor. For each set of fixed positive utilities, the real function is differentiable in the open simplex and concave, having an identifiable range with a unique and global maximum point; we settled the procedure to identify the optimal point coordinates, highlighting the sequence of stages with a numeric example; also, we conclude that the maximum point doesn’t change if utilities are affected by a positive linear transformation.
Such a framework can be used to generate scenarios of optimal compositional mixtures
relative to finite lotteries associated with prospect theory, financial risk assessment,
security quantification or natural resources management. Nowadays, different entropy
measures are proposed to be used to form and rebalance portfolios concerning optimal
criteria, and some state that the portfolio values of the models incorporating entropies
are higher than their correspondent benchmarks [56] . Also, we discussed the similarity
between this EU-WGS device and an EU-WE framework recently published denoted index
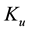
References
- Friedman, M. and Savage, L.J. (1948) The Utility Analysis of Choices Involving Risk. The Journal of Political Economy, 56, 279-304. http://dx.doi.org/10.1086/256692
- Weirich, P. (2008) Utility Maximization Generalized. Journal of Moral Philosophy, 5, 282-299. http://dx.doi.org/10.1163/174552408X329019
- Ananda, J. and Herath, G. (2005) Evaluating Public Risk Preferences in Forest Land-Use Choices Using Multi-Attri- bute Utility Theory. Ecological Economics, 55, 408-419. http://dx.doi.org/10.1016/j.ecolecon.2004.12.015
- Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-423. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
- Ormos, M. and Zibriczky, D. (2014) Entropy-Based Financial Asset Pricing. PLoS ONE, 9, e115742.
- Zhou, R., Cai, R. and Tong, G. (2013) Applications of Entropy in Finance: A Review. Entropy, 2013, 4909-4931. http://dx.doi.org/10.3390/e15114909
- Casquilho, J.P. (2014) Discussion of an Expected Utility and Weighted Entropy Framework. Natural Science, 6, 545- 551. http://dx.doi.org/10.4236/ns.2014.67054
- Winkler, R.L. and Murphy, A.H. (1970) Nonlinear Utility and the Probability Score. Journal of Applied Meteorology, 9, 143-148. http://dx.doi.org/10.1175/1520-0450(1970)009<0143:NUATPS>2.0.CO;2
- Yang, J. and Qiu, W. (2005) A Measure of Risk and a Decision-Making Model Based on Expected Utility and Entropy. European Journal of Operational Research, 164, 792-799. http://dx.doi.org/10.1016/j.ejor.2004.01.031
- Yang, J. and Qiu, W. (2014) Normalized Expected Utility-Entropy Measure of Risk. Entropy, 2014, 3590-3604. http://dx.doi.org/10.3390/e16073590
- Bernoulli, D. (1738/1954) Exposition of a New Theory on the Measurement of Risk. Econometrica, 22, 23-36. http://dx.doi.org/10.2307/1909829
- Von Neumann, J. and Morgenstern, O. (1953) Theory of Games and Economic Behavior. 3rd Edition, Princeton University Press, Princeton.
- Gilboa, I. (2009) Theory of Decision under Uncertainty. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511840203
- Alchian, A.A. (1953) The Meaning of Utility Measurement. American Economic Review, 43, 26-50. http://www.jstor.org/stable/1810289
- Machina, M.J. (1987) Choice under Uncertainty: Problems Solved and Unsolved. The Journal of Economic Perspectives, 1, 121-154. http://dx.doi.org/10.1257/jep.1.1.121
- Ramsey, F.P. (1931) Truth and Probability. In: Braithwaite, R.B., Ed., The Foundations of Mathematics and other Logical Essays, Harcourt, Brace and Company, New York, 156-198.
- Kahneman, D. and Tversky, A. (1979) Prospect Theory: An Analysis of Decision under Risk. Econometrica, 47, 263- 291. http://dx.doi.org/10.2307/1914185
- Machina, M.J. (1982) “Expected Utility” Analysis without the Independence Axiom. Econometrica, 50, 277-323. http://dx.doi.org/10.2307/1912631
- Baron, D.P. (1977) On the Utility Theoretic Foundations of Mean-Variance Analysis. The Journal of Finance, 32, 1683-1697. http://dx.doi.org/10.1111/j.1540-6261.1977.tb03363.x
- Kroll, Y., Levy, H. and Markowitz, H.M. (1884) Mean-Variance versus Direct Utility Maximization. The Journal of Finance, 39, 47-61. http://dx.doi.org/10.1111/j.1540-6261.1984.tb03859.x
- Frosini, B.V. (2014) A General Criterion of Choice, with Discussion of Borch Paradox. Theoretical Economics Letters, 4, 691-696. http://dx.doi.org/10.4236/tel.2014.48087
- Machina, M.J. (1989) Dynamic Consistency and Non-Expected Utility Models of Choice under Uncertainty. Journal of Economic Literature, 26, 1622-1668. http://www.jstor.org/stable/2727025
- Pratt, J.W. (1964) Risk Aversion in the Small and in the Large. Econometrica, 32, 122-136. http://dx.doi.org/10.2307/1913738
- Baillon, A., Driesen, B. and Wakker, P.P. (2012) Relative Concave Utility for Risk and Ambiguity. Games and Economic Behavior, 75, 481-489. http://dx.doi.org/10.1016/j.geb.2012.01.006
- Gosio, C., Lari, E.C. and Ravera, M. (2014) Optimal Expected Utility of Wealth for Two Dependent Classes of Insurance Business. Theoretical Economics Letters, 3, 90-95. http://dx.doi.org/10.4236/tel.2013.32015
- Shaw, W.D. and Woodward, R.T. (2008) Why Environmental and Resource Economists Should Care about Non-Ex- pected Utility Models. Resource and Energy Economics, 30, 66-89. http://dx.doi.org/10.1016/j.reseneeco.2007.05.001
- Edwards, W. (1962) Utility, Subjective Probability, Their Interaction and Variance Preferences. Journal of Conflict Resolution, 6, 42-51. http://dx.doi.org/10.1177/002200276200600106
- Starmer, C. (2000) Developments in Non-Expected Utility Theory: The Hunt for a Descriptive Theory of Choice under Risk. Journal of Economic Literature, 38, 332-382. http://dx.doi.org/10.1257/jel.38.2.332
- Wu, G. and Gonzalez, R. (1999) Nonlinear Decision Weights in Choice under Uncertainty. Management Science, 45, 74-85. http://dx.doi.org/10.1287/mnsc.45.1.74
- Roberts, D.C., Boyer, T.A. and Lusk, J.L (2008) Preferences for Environmental Quality under Uncertainty. Ecological Economics, 66, 584-593. http://dx.doi.org/10.1016/j.ecolecon.2008.05.010
- Hey, J.D. and Orme, C. (1994) Investigating Generalizations of Expected Utility Theory Using Experimental Data. Econometrica, 62, 1291-1326. http://dx.doi.org/10.2307/2951750
- Chanel, O. and Chichilnisky, G. (2013) Valuing Life: Experimental Evidence Using Sensitivity to Rare Events. Ecological Economics, 85, 198-205. http://dx.doi.org/10.1016/j.ecolecon.2012.03.004
- Belis, M. and Guiasu, S. (1968) A Quantitative-Qualitative Measure of Information in Cybernetic Systems (Corresp.). IEEE Transactions on Information Theory, 14, 593-594. http://dx.doi.org/10.1109/TIT.1968.1054185
- Guiasu, S. (1971) Weighted Entropy. Reports on Mathematical Physics, 2, 165-179. http://dx.doi.org/10.1016/0034-4877(71)90002-4
- Bouchon, B. (1976) Useful Information and Questionnaires. Information and Control, 32, 368-378. http://dx.doi.org/10.1016/S0019-9958(76)90279-5
- Nawrocki, D.N. and Harding, W.H. (1986) State-Value Weighted Entropy as a Measure of Investment Risk. Applied Economics, 18, 411-419. http://dx.doi.org/10.1080/00036848600000038
- Bhattacharyya, R., Chatterjee, A. and Kar, S. (2013) Uncertainty Theory-Based Multiple Objective Mean-Entropy- Skewness Stock Portfolio Selection Model with Transaction Costs. Uncertainty Analysis and Applications, 1, 16. http://dx.doi.org/10.1186/2195-5468-1-16
- Ormos, M. and Zibriczky, D. (2013) Asset Pricing and Entropy. Proceedings of the 10th International Scientific Conference in European Financial Systems, Masaryk University, Brno, 241-248. http://is.muni.cz/do/econ/soubory/konference/efs/Sbornik_2013.pdf#page=241
- Patsakis, C., Mermigas, D., Pirounias, S. and Chondrokoukis, G. (2013) The Role of Weighted Entropy in Security Quantification. International Journal of Information and Electronics Engineering, 3, 156-159. http://dx.doi.org/10.7763/IJIEE.2013.V3.288
- Nager, R. and Singh, R.P. (2013) Application of Information Theoretic Divergence Measures―Forecasting Profit Maximization in Share Market. Journal of Mathematics, Statistics and Operations Research, 2, 45-54. http://dl6.globalstf.org/index.php/jmsor/article/viewFile/338/341
- Suhov, Y. and Sekeh, S.Y. (2014) Simple Inequalities for Weighted Entropies. http://arxiv.org/pdf/1409.4102.pdf
- Aggarwal, N.L. and Picard, C.-F. (1978) Functional Equations and Information Measures with Preference. Kybernetika, 14, 174-181. http://dml.cz/dmlcz/125412
- Sharma, B.D., Mitter, J. and Mohan, M (1978) On Measures of “Useful” Information. Information and Control, 39, 323-336. http://dx.doi.org/10.1016/S0019-9958(78)90671-X
- Havrda, J. and Charvát, F. (1967) Quantification Method of Classification Processes. Concept of Structural -Entropy. Kybernetika, 3, 30-35. http://dml.cz/dmlcz/125526
- Guiasu, R.C. and Guiasu, S. (2003) Conditional and Weighted Measures of Ecological Diversity. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 11, 283-300. http://dx.doi.org/10.1142/S0218488503002089
- Anscombe, F.J. and Aumann, R.J. (1963) A Definition of Subjective Probability. The Annals of Mathematical Statistics, 34, 199-205. http://dx.doi.org/10.1214/aoms/1177704255
- Guiasu, R.C. and Guiasu, S. (2012) The Weighted Gini-Simpson Index: Revitalizing an Old Index of Biodiversity. International Journal of Ecology, 2012, Article ID: 478728. http://dx.doi.org/10.1155/2012/478728
- Guiasu, R.C. and Guiasu, S. (2014) Weighted Gini-Simpson Quadratic Index of Biodiversity for Interdependent Species. Natural Science, 6, 455-466. http://dx.doi.org/10.4236/ns.2014.67044
- Casquilho, J.A.P. (1999) Ecomosaico: Índices para o Diagnóstico de Proporções de Composição. Ph.D. Thesis, Ins- tituto Superior de Agronomia, Universidade Técnica de Lisboa. http://hdl.handle.net/10400.5/6932
- Purcaru, I. (2009) Optimal Diversification in Allocation Problems. Anfiteatru Economic, 26, 494-502. http://core.ac.uk/download/pdf/6283822.pdf
- Casquilho, J.P. (2009) Complex Number Valuation of Habitats and Information Index of Landscape Mosaic. Silva Lusitana, 17, 171-180. http://www.scielo.oces.mctes.pt/pdf/slu/v17n2/v17n2a03.pdf
- Casquilho, J.P. (2011) Ecomosaic Composition and Expected Utility Indices. Silva Lusitana, 19, 55-65. http://www.scielo.gpeari.mctes.pt/pdf/slu/v19n1/v19n1a05.pdf
- Jaynes, E.T. (1957) Information Theory and Statistical Mechanics. The Physical Review, 106, 620-630. http://dx.doi.org/10.1103/PhysRev.106.620
- Schmeidler, D. (1989) Subjective Probability and Expected Utility without Additivity. Econometrica, 57, 571-587. http://dx.doi.org/10.2307/1911053
- Casquilho, J.P. (2010) Landscape Mosaic Composition and Mean Contributive Value Index. Silva Lusitana, 18, 197- 203. http://www.scielo.gpeari.mctes.pt/pdf/slu/v18n2/v18n2a06.pdf
- Yu, J.-R, Lee, W.-Y. and Chiou, W.-J.P. (2014) Diversified Portfolios with Different Entropy Measures. Applied Mathematics and Computation, 241, 47-63. http://dx.doi.org/10.1016/j.amc.2014.04.006
- Casquilho, J.A.P. (2012) Ecomosaico Florestal: Composição, Índices de Informação e Abdução. Revista Árvore, 36, 321-329. http://dx.doi.org/10.1590/S0100-67622012000200013
Notes
1We discard the cases with null utilities