Open Journal of Statistics
Vol.04 No.07(2014), Article ID:49309,26 pages
10.4236/ojs.2014.47051
Comparison of Outlier Techniques Based on Simulated Data
Adaku C. Obikee1*, Godday U. Ebuh2, Happiness O. Obiora-Ilouno1
1Department of Statistics, Faculty of Physical Sciences, Nnamdi Azikiwe University, Awka, Nigeria
2Monetary & Policy Department, Central Bank of Nigeria, Abuja, Nigeria
Email: *pobikeeadaku@yahoo.com, ablegod007@yahoo.com, obiorailounoho@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2014; revised 8 July 2014; accepted 18 July 2014
ABSTRACT
This research work employed a simulation study to evaluate six outlier techniques: t-Statistic, Modified Z-Statistic, Cancer Outlier Profile Analysis (COPA), Outlier Sum-Statistic (OS), Outlier Robust t-Statistic (ORT), and the Truncated Outlier Robust t-Statistic (TORT) with the aim of determining the technique that has a higher power of detecting and handling outliers in terms of their P-values, true positives, false positives, False Discovery Rate (FDR) and their corresponding Receiver Operating Characteristic (ROC) curves. From the result of the analysis, it was revealed that OS was the best technique followed by COPA, t, ORT, TORT and Z respectively in terms of their P-values. The result of the False Discovery Rate (FDR) shows that OS is the best technique followed by COPA, t, ORT, TORT and Z. In terms of their ROC curves, t-Statistic and OS have the largest Area under the ROC Curve (AUC) which indicates better sensitivity and specificity and is more significant followed by COPA and ORT with the equal significant AUC while Z and TORT have the least AUC which is not significant.
Keywords:
Area under the ROC Curve, Reference Line, Sensitivity, Specificity, P-Value, False Discovery Rate (FDR), Simulation

1. Introduction
In statistics, an outlier is an observation that is numerically distant from the rest of the data. [1] Grubbs (1969) defined an outlier as an observation that appears to deviate markedly from other members of the sample in which it occurs. [2] Hawkins (1980) formally defined the concept of an outlier as “an observation which deviates so much from the other observations so as to arouse suspicions that it was generated by a different mechanism”. Outliers are also referred to as abnormalities, discordants, deviants, or anomalies in data mining and statistics literature [3] (Aggarwal, 2005). Outliers can also be defined in a closed bound: For example, if
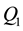 and
and
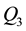 are the lower and upper quartiles of a sample, then one can define an outlier to be any observation outside the range:
are the lower and upper quartiles of a sample, then one can define an outlier to be any observation outside the range:
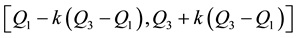 for some constant
for some constant
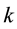 [4] (Barnett and Lewis, 1994). Outliers can occur by chance in any distribution, but they are often indicative either of measurement error or that the population has a heavy-tailed distribution. Outliers provide interesting case studies. They should always be identified and discussed. They should never be ignored, or “swept under the rug”. In any scientific research, full disclosure is the ethical approach, including a disclosure and discussion of the outliers.
[4] (Barnett and Lewis, 1994). Outliers can occur by chance in any distribution, but they are often indicative either of measurement error or that the population has a heavy-tailed distribution. Outliers provide interesting case studies. They should always be identified and discussed. They should never be ignored, or “swept under the rug”. In any scientific research, full disclosure is the ethical approach, including a disclosure and discussion of the outliers.
In many analyses, outliers are the most interesting things. Outliers often provide valuable insight into particular observations. Knowing why an observation is an outlier is very important. For example, outlier identification is a key part of quality control. The box plot and the histogram can also be useful graphical tools in checking the normality assumption and in identifying potential outliers. While statistical methods are used to identify outliers, non-statistical theory (subject matter) is needed to explain why outliers are the way that they are.
In sampling of data, some data points will be farther away from the sample mean than what is deemed reasonable. This can be due to incidental errors or flaws in the theory that generated an assumed family of probability distributions or it may be that some observations are far from the center of the data. Outlier points can therefore indicate faulty data, erroneous procedures, or areas where a certain theory might not be valid. Outliers can occur by chance in any distribution, but they are often indicative either of measurement error or that the population has a heavy-tailed distribution. In the former case one wishes to discard them or use statistics that are robust to outliers, while in the latter case they indicate that the distribution has high kurtosis.
Hence, this study is set out to evaluate six different outlier techniques using their P-values, true positives, false positives, FDRs and their corresponding Receiver Operating Characteristics ROC Curves using a simulated data.
Researchers that have similar work in this regards include [5] Dudoit et al. (2002), [6] Troyanskaya et al. (2002), [7] Tomlins et al. (2005), [8] Efron et al. (2001), [9] Iglewicz and Hoaglin (2010), [10] Lyons et al. (2004), [11] Tibshirani and Hastie (2006), [12] Benjamini and Hochberg(1995), [13] Wu (2007), [14] June (2012), [15] Fonseca (2004), [16] MacDonald and Ghosh (2006), [17] Jianhua (2008), [18] Heng(2008), [19] Ghosh (2009), [20] Lin-An et al. (2010), [21] Ghosh (2010), [22] Filmoser et al. (2008) and [23] Keita et al. (2013)
2. Method of Analysis
The six outlier methods include: The Modified Z-statistic, t-Statistic, OS, COPA, ORT and TORT.
This paper considers a 2-class data for detecting outliers. Let xij be the expression values for the normal group for
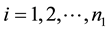 and
and
 the number of sample groups and let yij be the expression values for the disease group and
the number of sample groups and let yij be the expression values for the disease group and
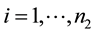 and
and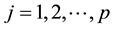 . Where n1 + n2 = n.
. Where n1 + n2 = n.
The standard Z-statistic for 1 sample test is
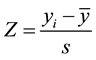 (1)
(1)
Iglewicz and Hoaglin (2010) recommend using the modified Z-score
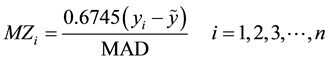 (2)
(2)
With MAD denoting the median absolute deviation, yi are the observed values and
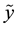 denoting the median
denoting the median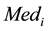 .
.
These authors recommended that modified Z-scores with an absolute value of greater than 3.5 be labeled as potential outliers. i.e.
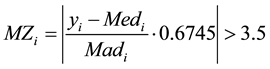 (3)
(3)
The t-Statistic for a two sample test by Dudoit et al. (2002) and Troyanskaya et al. (2002) is given as:
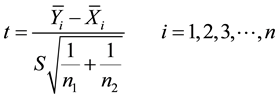 (4)
(4)
Here,
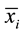 and
and
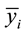 are the sample means for i in the normal group and the disease group respectively. The denominator is the pooled standard deviation for the variable i.
are the sample means for i in the normal group and the disease group respectively. The denominator is the pooled standard deviation for the variable i.
Tomlins (2005) defined the COPA statistic, which is the


where






According to Tibshirirani and Hastie (2006),

where





Accordingly, Wu (2007) defined Outlier Robust t-Statistic ORT as:

where

The statistic ORT concentrates on the outlier set

According to June (2012), TORT is given as:

where

The false discovery rate can be calculated using the modified formula:

where FP and TP are the False Positive (Specificity) and the True Positive (Sensitivity).
Quartiles: The 1st quartiles Q1, 2nd quartiles, the 3rd quartiles Q3 and the Interquartile Range IQR of each of the sample the simulated data were calculated for analysis. The quartiles can be calculated using the modified formula:

where Ly is the required quartile, y is the percentile of the require quartile and n is the number of observation.
・ First quartile (designated Q1) = lower quartile = splits lowest 25% of data = 25th percentile.
・ Second quartile (designated Q2) = median = cuts data set in half = 50th percentile.
・ Third quartile (designated Q3) = upper quartile = splits highest 25% of data, or lowest 75% = 75th percentile. The difference between the upper and lower quartiles is called the interquartile range IQR.
Area under the ROC Curve (AUC): The area under the ROC curve AUC can be estimated using the modified formula:

where




a) The smallest cutoff value is the minimum observed test value minus 1, and the largest cutoff value is the maximum observed test value plus 1. All the other cutoff values are the averages of two consecutive ordered observed test values.
b) Null Hypothesis: Significant/True Area under the ROC Curve (AUC) = 0.5.
3. Data Simulation and Application
Table 1 is random numbers generated from a normal distribution with parameters-sample size n = 27, the mean = 30.96 and the standard deviation = 10.58 given that k = 10. Where k is the number of simulations for each sample.
Table 1. Simulated data for the disease group.
Table 2 is computed parameters from the 10 simulated data. Here the mean, standard deviation, 1st quartile (Q1), median, 3rd quartile (Q3) and the interquartile range (IQR) of each of the 10 simulated data were computed and the mean is the average of the data. StDev is the standard deviation. Q1 is the 1st quarter or the 25th percentile of the data. Median is the middle value or the 2nd quartile or the 50th percentile of the data. Q3 is the 3rd quartile or the 75th percentile of the data. IQR is the difference between the Q3 and Q1 i.e., IQR = Q3 − Q1.
Table 3 is random numbers generated from a normal distribution with parameters-sample size n = 27, the mean = 30 and the standard deviation = 5.46 with k = 10.
Table 2. Computed parameters from the disease group.
Table 3. Simulated data for the normal group.
Table 4 is computed parameters from the normal group samples.
Table 5 contains calculated Modified Z-Statistic, COPA and OS from the first sample of the disease group. From the table, Y1 are the values of the first simulated data from the sample. Q1 of Y1 = 22.3 is the first quartile of Y1, Med1 = 31.5 is the median and 2nd quarter of Y1. Q3 of Y1 = 43.45 is the third quartile of Y1 and IQR of Y1 = 21.14 is the interquartile range of Y1.
Table 4. Computed parameters from the normal group samples.
Table 5. Calculated Modified Z, COPA and OS.





same scale which facilitates comparison across the values i.e.

parison. The choice of COPA is based on the M' corresponding to any value in Y1 that is less than n1 = 27 the total number of values in Y1. Here, COPA value is −1.7603 corresponding to 15.32 in Y1 which is less than 27. The use of the constant (75) the rth percentile to multiply M' was ignored since it will not affect the order of the values.
The Z-Value = 0 is calculated by multiplying M' by a constant 0.6745 and the choice of Z is based on any of 0.6745 × M' that is greater than 3.5 in absolute value. i.e.

OS = 1.4 is calculated by summing up all the M' corresponding to the outlier set in Y1.
3.1. Two Sample t-test and Confidence Interval
Here, a two sample t-test was conducted to obtain the t-values, confidence interval and its corresponding P-values using the sample means and standard deviations from both the disease and normal group samples of the simulated data assuming equal variances.
Table 6 is the parameters from both the normal group and the disease group data used for the two-sample t-Test.
The Test Difference = mu (1) − mu (2).
Estimate for difference: 4.00000.
95% CI for difference: (−0.31762; 8.31762).
t-test of difference = 0 (vs not = 0): t-value = 1.86, P-value = 0.069 df = 52.
Both use Pooled StDev = 7.9057.
From the t-test above, sample 1 is the first sample from the disease group with parameters: n = 27, mean = 32, standard deviation = 10 and squared error = 1.9. Sample 2 also is the first sample from the normal group with parameters: n = 27, mean =28, standard deviation = 5 and squared error = 0.96, mu (1) − mu (2) is the difference between the mean of sample 1 and the mean of sample 2 and this is equal to 4. From the test also, we are 95% confident that the mean will lie between the interval (−0.31762; 8.31762).
The test hypothesis is:
Ho: mu(1) = mu(2).
vs
H1: mu(1) ≠ mu(2).
t-value = 1.86, P-value = 0.069. The degree of freedom df is calculated by adding the two sample sizes and subtracting 2 from it. i.e. (n1 + n2) − 2.
Therefore df = ((27 +27) − 2) = 52 with a pooled standard deviation of 7.9057 which is the square root of the pooled sample variances of the two samples assuming equal variances i.e. homogeneity of variances and since the P-value = 0.069 is greater than the significant level α = 0.05, hence Ho is rejected which implies that the mean ≠ 0.
Table 7 shows calculated ORT and TORT. ORT and TORT utilizes information from both the normal and the disease group sample.
From Table 16, Y1 represents the values of the first simulated data from the first sample regarded as the disease group. Q1 = 22.3 is the first quartile of Y1,

Table 6. Two-sample t-test and confidence interval for sample 1.
Table 7. Calculated ORT and TORT.
the third quartile of the disease group and IQR = 21.14 is the interquartile range of the disease group Y1 and


In order to standardize and put the outliers on the same scale for comparison across the outliers,



X1 are the values of the first simulated data from the second sample regarded as the normal or control group.





These values were calculated to facilitate comparison across the two samples.
The value for ORT= 2.303 is obtained by dividing



Table 8 shows the summary of the computed values of all the simulated data by the six outlier methods. From the table, we have 80 samples of the simulated data from the disease group. The value for each of the outlier method Z, t-distribution, COPA, OS, ORT and TORT was calculated for each sample for comparison among the outlier methods.
Table 9 shows the computed P-values. Here, P-values were computed for all the values computed by the outlier methods. The P-values were generated from the standard normal Z-distribution and t-distribution. This is based on the assumption that the Modified Z-Statistic, COPA and OS are assumed to follow a normal distribution while the t-Statistic, ORT and TORT are assumed to follow a t-distribution.
Table 8. Summary of computed values for the various outlier techniques.
Table 9. Summary of computed P-values for the various outlier techniques.
From Table 18, we observed that all the outlier methods have equal maximum P-value of 1 (one). Modified Z has a minimum P-value of 1 (one), t and COPA have a minimum P-value of 0 (Zero) while OS, ORT and TORT have the least minimum P-value of 0.0001. Modified Z has 80 true positives and 0 false positives, t-Statistic has 61 true positives and 19 False Positives, COPA has 39 true positives and 41 false positives, OS has 16 true positives and 64 false positives, ORT has 62 true positives and 18 false positives while TORT has 42 true positives and 38 false positives. The Mean of the P-values of the different outlier methods were computed giving the following results: Z = 1, t = 0.360188, COPA = 0.144847, OS = 0.134311, ORT = 0.388911 and TORT = 0.472614. From these values, we can see that OS has the least minimum P-value, least number of true positives and the least average P-value followed by COPA, followed by t, followed by ORT, followed by TORT while Z has the highest maximum P-value, highest true positive rate and the highest average P-Value. Since OS has the least average P-value, it implies that OS performs better than the other methods. Based on this, OS has a higher detection power than the rest of the other methods followed by COPA, t, ORT, TORT and Z.
Table 10 shows the ranking of the P-values computed by the various outlier techniques in an ascending order. The P-values and the Ranks were used in computing the False Discovery Rate FDR for the various outlier techniques
From Table 11, the true positives are the false null hypothesis (Type II error). These are the probabilities of accepting the null hypothesis given that the null hypothesis is false and should be rejected. These true positives are P-values that are greater than the given significant level of α = 0.05. The blank cells in the table are the False Positives.
From Table 12, the false positives are the true null hypothesis (Type I error). These are the probabilities of rejecting the null hypothesis given that the null hypothesis is true and should be accepted. These False Positives are P-values that are less than the given significant level α = 0.05. The blank spaces in the table are the false null hypothesis.
Table 13 shows the FDR computed by the various outlier techniques. The P-values and the rank of the P-values were used in computing the False Discovery Rate (FDR). We can observed that all the outlier methods have equal minimum FDR of 0 (zero) except Z-Statistic with minimum FDR of 160.506. Modified Z has the highest maximum FDR of 160.506 followed by TORT = 114.838, OS = 84.819, ORT = 83.962, t-Statistic = 81.806 while COPA has the least maximum FDR of 79.25.
The Mean of the FDRs of the different outlier techniques were computed giving the following results: Z = 160.506, t = 42.6748813, COPA = 13.8631125, OS = 11.4017125, ORT = 45.64245 and TORT = 48.4732125. From results obtained, we observed that OS has the least average FDR and minimum FDR. Since OS has the least error rate, it implies that OS performs better than the other methods. Based on this, OS has a highest detection power with a smaller FDR followed by COPA, t, ORT, TORT and Z.
From Figure 1, we can see the performance of the FDRs of the various outlier methods. From the plot, we can see that the FDR of Z has the highest point at 160 constantly at the peak of the plot folllowed by the FDR of TORT, t and ORT. COPA has its highest point at the middle of the plot while OS has its points clustered at the floor of the plot. Based on these observations, we can see that OS performs better than the other methods in terms of having a smaller error rate (FDR) and therefore has the highest detection power follwed by COPA, ORT, t, TORT and Z.
3.2. Comparison Based on ROC Curves
The sensitivities were plotted against the specificities at different thresholds to compare the behaviour of the outlier methods. The ROC Curves were plotted for n = 27 and k = 6, n = 27 and k = 10, n = 27 and k = 16, n = 27 and k = 25. Where k is the numbers simulations. Larger area under the ROC curves indicates better sensitivity and specificity. An ROC curve along the diagonal line indicates a random-guess. The test result variable(s): Z, t, COPA, OS, ORT, TORT has at least one tie between the positive actual state group and the negative actual state group.
a) The smallest cutoff value is the minimum observed test value minus 1, and the largest cutoff value is the maximum observed test value plus 1. All the other cutoff values are the averages of two consecutive ordered observed test values.
Table 10. Summary of ranks of the P-values for various outlier techniques.
Table 11. Summary of calculated True Positives (TP) for various outlier techniques.
Table 12. Summary of calculated False Positives (FP) for various outlier techniques.
Table 13. Summary of computed False Discovery Rate (FDR) for various outlier techniques.
Figure 1. Plot of the FDRs.
b) Null hypothesis: Significant/True Area under the ROC Curve (AUC) = 0.5.
From the Figure 2, we can observe that for a smaller k = 6, T and OS have a larger Area Under the ROC Curve AUC with values 0.813 and 0.750 which indicate better sensitivity and specificity and are significant. COPA and ORT have equal AUC with point 0.563 followed by Z with point 0.500 while TORT has the least AUC of 0.375 which is not significant.
Table 14 shows the ROC curves analysis for n = 27 and k = 6, the area under the ROC curve (AUC) and the confidence interval for all the test variables.
From Figure 3, we can observe that for a smaller k = 10, T and OS have a larger Area Under the ROC Curve AUC with values 0.781 and 0.719 which indicate better sensitivity and specificity and are significant. COPA and ORT have equal significant AUC with point 0.594 followed by Z with point 0.500 which is on the refference line while TORT has the least AUC of 0.438 which is not significant.
Table 15 shows the ROC curves analysis for n = 27 and k = 10, the area under the ROC curve (AUC) and the confidence interval for all the test variables.
From Figure 4, we can observe that for bigger k = 16, T and OS have a larger Area Under the ROC Curve AUC with values 0.804 and 0.732 which indicate better sensitivity and specificity and are more significant. COPA and ORT have better significant AUC with points 0.536 and .0518 followed by Z with point 0.500 which is on the refference line while TORT has the least AUC of 0.429 which is not significant.
Table 16 shows the ROC curves analysis for n = 27 and k = 16, the area under the ROC curve (AUC) and the confidence interval for all the test variables.
From Figure 5, we can observe that for a bigger k = 25, t and OS have a larger Area Under the ROC Curve AUC with values 0.828 and 0.734 which indicate better sensitivity and specificity and are more significant. COPA has a better significant AUC with points 0.563 followed by Z and ORT which have equal AUC with point 0.500 while TORT has the least AUC of 0.438 which is not significant.
Table 17 shows the ROC curves analysis for n = 27 and k = 20, the area under the ROC curve (AUC) and the confidence interval for all the test variables.
Table 18 is a summary of all the findings in the analysis for all the outlier techniques on the bases of their P-values, false positives, true positives, false discovery rates and their corresponding ROC curves.
Figure 2. ROC curve when n = 27 and k = 6.
Figure 3. ROC curve when n = 27 and k = 10.
Figure 4. ROC curve when n = 27 and k = 16.
Figure 5. ROC curve when n = 27 and k = 25.
Table 14. ROC curve when n = 27 and k = 6 area under the curve.
Table 15. ROC curve when n = 27 and k = 10 area under the curve.
Table 16. ROC curve when n = 27 and k = 16 area under the curve.
Table 17. ROC curve when n = 27 and k = 25 area under the curve.
Table 18. Summary of findings for the various outlier techniques.
4. Conclusion
The performance of the various outlier methods―Z, T, COPA, OS, ORT and TORT has been statistically studied using simulated data to evaluate which of these methods has the highest power of detecting and handling outliers in terms of their P-Values, true positives, false positives, false discovery rate FDR and their corresponding ROC curves.
The result of their P-values showed that all the outlier methods have equal maximum P-value. Modified Z has the highest minimum P-Value followed by T and COPA while OS, ORT and TORT have the least minimum P-Value. Modified Z has the highest true positives rate followed by ORT, t-Statistic, TORT, COPA, while OS has the least true positives rate. Z has the highest average P-Value followed by TORT, ORT, T, COPA while OS has the least average P-Value. Based on these results, OS performed better than the methods followed by COPA, T, ORT, TORT and Z in terms of their P-Values. When comparison was made on the FDRs, OS also performs the best by having the smallest FDR followed by COPA, T, ORT, TORT and Z.
In terms of their ROC curves, for a smaller k = 6 and 10, T and OS have the largest Area Under the ROC Curve AUC which indicate a better sensitivity and specificity and are significant. COPA and ORT have equal significant AUC followed by Z with insignificant AUC while TORT has the least AUC which is not significant. Also for larger k = 16 and 25, T and OS still have the largest Area Under the ROC Curve AUC which indicate better sensitivity and specificity and are more significant. COPA and ORT have better significant AUC followed by Z with insignificant AUC while TORT has the least AUC which is still not significant. Based on the above results so far obtained from this analysis, it is obvious that the Outlier Sum Statistic OS has more power of detecting and handling outliers with a smaller False Discovery Rate (FDR) followed by COPA, T, ORT, TORT and Z.
Cite this paper
Adaku C.Obikee,Godday U.Ebuh,Happiness O.Obiora-Ilouno, (2014) Comparison of Outlier Techniques Based on Simulated Data. Open Journal of Statistics,04,536-561. doi: 10.4236/ojs.2014.47051
References
- 1. Grubbs, F.E. (1969) Procedures for Detecting Outlying Observations in Samples. Technometrics, 11, 1-21.
http://dx.doi.org/10.1080/00401706.1969.10490657 - 2. Hawkins, D. (1980) Identification of Outliers. Chapman and Hall, Kluwer Academic Publishers, Boston/Dordrecht/ London.
- 3. Aggarwal, C.C. (2005) On Abnormality Detection in Spuriously Populated Data Streams. SIAM Conference on Data Mining. Kluwer Academic Publishers Boston/Dordrech/London.
- 4. Barnett, V. and Lewis, T. (1994) Outliers in Statistical Data. 3rd Edition, John Wiley & Sons, Kluwer Academic Publishers, Boston/Dordrecht/London.
- 5. Dudoit, S., Yang, Y., Callow, M. and Speed, T. (2002) Statistical Methods for Identifying Differentially Expressed Genes in Replicated DNA Microarray Experiments. Statistica Sinica, 12, 111-139.
- 6. Troyanskaya, O.G., Garber, M.E., Brown, P.O., Botstein, D. and Altman, R.B. (2002) Nonparametric Methods for Identifying Differentially Expressed Genes in Microarray Data. Bioinformatics, 18, 1454-1461.
http://dx.doi.org/10.1093/bioinformatics/18.11.1454 - 7. Tomlins, S., Rhodes, D., Perner, S., Dhanasekaran, S., Mehra, R., Sun, X., Varambally, S., Cao, X., Tchinda, J., Kuefer, R., et al. (2005) Recurrent Fusion of TMPRSS2 and ETS Transcription Factor Genes in Prostate Cancer. Science, 310, 644-648.
http://dx.doi.org/10.1126/science.1117679 - 8. Efron, B., Tibshirani, R., Storey, J. and Tusher, V. (2001) Empirical Bayes Analysis of a Microarray Experiment. Journal of the American Statistical Association, 96, 1151-1160.
http://dx.doi.org/10.1198/016214501753382129 - 9. Iglewicz, B. and Hoaglin, D.C. (2010) Detection of Outliers. Engineering Statistical Handbook, 1.3.5.17. Database Systems Group.
- 10. Lyons-Weiler, J., Patel, S., Becich, M. and Godfrey, T. (2004) Tests for Finding Complex Patterns of Differential Expression in Cancers: Towards Individualized Medicine. Bioinformatics, 5, 1-9.
- 11. Tibshirani, R. and Hastie, R. (2006) Outlier Sums Statistic for Differential Gene Expression Analysis. Biostatistics, 8, 2-8.
http://dx.doi.org/10.1093/biostatistics/kxl005 - 12. Benjamini, Y. and Hochberg, Y. (1995) Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society Series B, 57, 289-300.
- 13. Wu, B. (2007) Cancer Outlier Differential Gene Expression Detection. Biostatistics, 8, 566-575.
http://dx.doi.org/10.1093/biostatistics/kxl029 - 14. Luo, J. (2012) Truncated Outlier Robust T-Statistic for Outlier Detection. Open Journal of Statistics, 2, 120-123.
http://dx.doi.org/10.4236/ojs.2012.21013 - 15. Fonseca, R., Barlogie, B., Bataille, R., Bastard, C., Bergsagel, P.L., Chesi, M., et al. (2004) Genetics and Cytogenetics of Multiple Myelom: A Workshop Report. Cancer Research, 64, 1546-1558.
http://dx.doi.org/10.1158/0008-5472.CAN-03-2876 - 16. MacDonald, J.W. and Ghosh, D. (2006) Copa—Cancer Outlier Profile Analysis. Bioinformatics, 22, 2950-2951.
http://dx.doi.org/10.1093/bioinformatics/btl433 - 17. Hu, J. (2008) Cancer Outlier Detection Based on Likelihood Ratio Test. Bioinformatics, 24, 2193-2199.
http://dx.doi.org/10.1093/bioinformatics/btn372 - 18. Lian, H. (2008) MOST: Detecting Cancer Differential Gene Expression. Biostatistics, 9, 411-418.
http://dx.doi.org/10.1093/biostatistics/kxm042 - 19. Ghosh, D. (2009) Genomic Outlier Profile Analysis: Mixture Models, Null Hypotheses, and Nonparametric Estimation. Biostatistics, 10, 60-69.
http://dx.doi.org/10.1093/biostatistics/kxn015 - 20. Chen, L.A., Chen, D.T. and Chan, W. (2010) The Distribution-Based P-value for the Outlier Sum in Differential Gene Expression Analysis. Biometrika, 97, 246-253.
http://dx.doi.org/10.1093/biomet/asp075 - 21. Ghosh, D. (2010) Discrete Nonparametric Algorithms for Outlier Detection with Genomic Data. Journal of Biopharmaceutical Statistics, 20, 193-208.
http://dx.doi.org/10.1080/10543400903572704 - 22. Filmoser, P., Maronna, R. and Werner, M. (2008) Outlier Identification in High Dimensions. Computational Statistics and Data Analysis, 52, 1694-1711.
- 23. Mori, K., Oura, T., Noma, H. and Matsui, S. (2013) Cancer Outlier Analysis Based on Mixture Modeling of Gene Expression Data. Computational and Mathematical Methods in Medicine, 2013, Article ID: 693901.
http://dx.doi.org/10.1155/2013/693901
NOTES
*Corresponding author.












