Applied Mathematics, 2011, 2, 653-660
doi:10.4236/am.2011.25086 Published Online May 2011 (http :/ /www.SciRP.org/journal/am)
Evolution of Weak Shock Waves in Perf ectly
Conducting Gases
Lal Pratap Singh, Dheerendra Ba hadur Singh, Subedar Ram
Department of Applied Mathematics, Institute of Technology, Ban aras Hindu Universit y, Varanasi, India
Received February 22, 2011; revised March 31, 2011; accepted April 5, 2011
Abstract
This article aims at studying one dimensional unsteady planar and cylindrically symmetric flow involving
shocks under the influence of magnetic field. The method of generalized wavefront expansion (GWE) is em-
ployed to derive a coupled system of nonlinear transport equations for the jump of field variables and of its
spatial derivatives across the shock, which, in turn determine the evolution of wave amplitude and admit a
solution th at agrees with the classical decay laws of weak shocks. A clo sed form solution exhibiting the fea-
tures of non linear steepening of the wave front. A general criterion for a compression wave to steepen i nto a
shock is derived. An analytic expression elucidating how the shock formation distance is influenced by the
magnetic field strength is obtained. Also, the effects of geometrical spreading and nonlinear convection on
the distorti on of the waveform are investigated in the presence of magnetic field.
Keywords: Magnetogasdynamic Flow, Weak Shock, Induced Discontinuity, Generalized Wavefrontexpansion (GWE)
1. Introducti o n
To study the propagation of nonlinear waves, such as
shock waves and acceleration waves, which belong to the
singular surface theory, have been, and remain, the topic
of considerable interest in continuum mechanics [1-6].
This is primarily due to the fact that when the nonlineari-
ties are present in the governing equations, these waves
can manifest a wide range of behaviors, the most striking
one is finite time blow up. Thomas [7] appears to have
been one of the first investigator describing the evolutio-
nary behavior of acceleration waves in flows of inviscid
ideal gases. Later, Coleman and Gurtin [8] studied the
problem of acceleration waves and higher order waves
(or ‘mild discontinuities’ as they are named by the au-
thors) in fluids that exhibit mechanical d issipation v ia the
relaxation of internal state variables. However, these au-
thors went on to conjecture that blow-up of acceleration
wave implies that a shock wave, which is a propagating
jump in at least one of the acoustic field variables the m-
selves, had in fact formed. Since then extensive investi-
gations on singular surfaces and the phenomena of finite
time blowup o f acceleration wav es have been d ocumented
in the literature of continuum mechanics (see [9-13] and
those cited therein). Recently, Christov et al. [14] have
considered the nonlinear acoustic propagation in homen-
tropic prefect gas flow and provided numerical support
for the shock-conjecture of Coleman and Gurtin [8]. Still
more recently, Shekhar and Sharma [15] have studied the
propagation of weak discontinuities in shallow water and
their subsequent culmination into shock waves.
In contrast to acceleration wave, which is defined as
the propagating jump discontinuity in at least one of the
first derivative of the field variables, with the field va-
riables themselves being continuous, the shock waves are
very difficult to analyze because their evolutionary beha-
vior is always coupled with that of the higher order dis-
continuities that accompany them. Whereby, the evolu-
tionary behavior of shock amplitude is governed by an
equation that also involves the amplitude of the accom-
panying second order discontinuity. One can derive ano-
ther evolution equation for the amplitude of the accom-
panying second order discontinuity, but this equation
involves the amplitude of the accompanying third order
discontinuity. This procedure could be carried out to high-
er order derivatives and thus one obtains infinite number
of transport equations. It was Maslov [16] who proposed
for the first time the idea of an inf inite system of compa-
tibility conditions and provided a rigorous mathematical
approach to describe the kinematics of a weak shock
wave propagating through an inviscid, isentropic gas;
using the theory of generalized functions. He derived an

L. P. SINGH ET AL.
654
infinite set of identities for the shock amplitude and
higher order derivatives of field variables which hold
along the rays. Maslov’s work presents a clear under stand-
ing of the problem mathematically and can be regarded as
a major breakthrough in approximate determination, at
least in theory, of the shock position. Similar method has
been developed by Grinfeld [17] to study weak shocks in
elastic materials.
Another approximate analytical method for studying
the kinematics of weak shock, called generalized wave-
front expansion, has been proposed by Anile [18] and is
based on an asymptotic expansion in a neighborhood of
the wavefront. Russo [19] applied this method to a rather
simple case of single wave equation in one space dimen-
sion and made a comparison with the shock fitting me-
thod given by Whitham [1]. Furthe r, Anile and Russo [20]
extended this method to higher order corrections and
derived an infinite hierarchy of coupled transport equa-
tions along the wavefront (rays) for the shock amplitude
and the jumps of the field gradients. In this context Mad-
humita and Sharma [21] employed a different approach to
describe the kinematics of a shock wave of arbitrary
strength by considering an infinite sequence of transport
equations for the variation of jump in the field variable
and their space derivative across the shock, and used a
truncation pro cedure similar to that proposed by Maslov.
The present work, which deals with the unsteady pla-
nar and cylindrically symmetric flow of an inviscid gas
under the influence of magn etic field, derives motivation
from the study relating to the propagation of weak shock
proposed by Anile [18]. The method of generalized wa-
vefront expansion is used to analyze the main features of
weakly nonlinear waves propagating in an electrically
conducting gas permeated by a transverse magnetic field.
It is assumed that the fluid ahead of the shock is at rest
and the dissipative effects, except due to the magnetic
field, are negligible.
A system of two transport equations, coupled through
the amplitude of accompanying discontinuity, is derived
along the rays of governing equations; these equations
effecttively describe the evolutionary behavior of shock
front. The loc ati on of s hoc k formation, i.e. the point where
the characteristics begin to coalesce, is determined. Also,
the influence of the magnetic field on the nonlinear dis-
tortion of the wave form and the shock formation distance
is assessed.
2. Formulation of the Problem
In carrying out the analytical part of our study, it is con-
venient to treat the wave phenomena as being kinematic
Whitham [1], rather than dynamic. Mathematically, this
means recasting the equations, governing a physical phe-
nomenon, as a system consisting of a ‘conservation/ba-
lance law’ and a ‘flux’ relation. Omitting the details, it is
not difficult to establish that the fundamental equations,
describing the nonlinear wave process, for one dimen-
sional planar or cylindrically symmetric motion of an
ideal gas in the pres ence o f magnetic field can be modeled
as Sharma et al. [22]
( )( )( )
0,
FG
f
tx
∂∂
+ +=
∂∂
UU
U
(1)
where
i
≡UU
,
14i≤≤
, is the column vector repre-
senting dependent field variables,
( )
T
,,,uph ρ =U
( )
T
212
,, ,
12
pu
F uhh
ρ
ρρ γ

= ++

−

U
,
( )
T
3
2 12
, ,2,
12
pu u
Guuphhu hu
γρ
ρρ γ

=+++ +

−

U,
( )
( )
T
23 12
U
2
,, ,
12
f
m um umpum umhumuh
xxxxx x
ρργρ
γ
=

++


−

.
Here, it is assumed that the electrical conductivity of
the medium is infinite and the direction of the magnetic
field is orthogonal to the trajectories of the fluid par ticles.
The field variables
ρ
,
u
and
p
denote, respectively,
the fluid density, velocity and pressure;
h
is the mag-
netic pressure defined as
2
2hH
µ =
with
µ
as the
magnetic permeability and
H
the transverse magnetic
field. The variables
x
and
t
, respectively, are the
space and time coordinates and
γ
is the adiabatic index.
We consider that initially the wave propagation takes
place into a uniform state characterized by a flow field at
rest with constant density and pressure fields, namely
( )
T
0 00
,0, ,ph ρ
+
=U
. Hereafter the subscript “
0
” refers
to evaluation at the uniform state unless stated otherwise.
It is well known that a system of equations written in
the form (1) admits a shock wave that may be initiated in
the flow region, and once it is formed, it will propagate
by separating the portions of continuous regions. Let
( )
xt χ =
represents the location of the moving shock
front at any time
t
across which the flow variables and
their derivatives suffer finite jump discontinuities, th en a
shock wave solution of (1) may exist if across the surface
of discontinuity
( )
t χ
, following Rankine-Hugoniot con-
ditions are satisfied,
( )( )
0VF G    − +=
  
UU
(2)
where
ddVt χ =
is the speed of propagation of the
wavefront into the medium characterized by U+. The
square brackets enclosing an entity denote the amplitude
of the jump in that entity across the shock front
( )
t χ
,

L. P. SINGH ET AL.
655
defined as
[ ]
+
= −U UU
. In this context we usually call
U
+ the unperturbed field and
U
the perturbed field,
which correspond, respectively, the states just ahead and
behind the shock front
( )
t χ
. If it is assumed that the
discontinuity
[ ]
U
across
( )
t χ
is a ‘
k shock−
’ (see
Jeffrey [4]), then there exist an eigenvalue of (1), say
()k
λ
, such that,
( )
kV
λ <
and
()
lim
k
V λ
+
→
=UU
.
Assume that, over some finite time interval
0
,tt


, the
following asymptotic expansion hol d (s e e Anile [18])
[ ] ( )
1
ll
l
Yt ε
∞
=
=
∑
U
,
( )
()
0
mjm
j
mj
Yt
x
ε
∞
=

∂=

∂

∑
U
, (3)
where
1, 2, 3m=
.
Then, because of the analyticity of
( )
FU
and
( )
GU
they can be expanded, behind the shock, in terms of
small parameter
ε
; therefore for any quantity
( )
qU
(either of
( )
FU
or
( )
GU
), we have
( )( )
( ) ( )
2
12
23
11
()
()
2
UU
UU
qU qqYqY
q YY
εε
εε
+++
+
= +∇+∇
+∇∇+Ο
(4)
3. Evolution Law for Weak Sh o cks
In this section, we employ the elegant theory of Genera-
lized Wavefront Expansion (GWE) Anile [18], to deter-
mine how an initial jump discontinuity in flow variables
propagate and evolves over time. Equation (1) can be
recast into a quasilinear hyperbolic system of first order
PDEs a s
( )( )
0
tx
∂∂
+ +=
∂∂
UU
AU BU
, (5)
where,
1
ij −
≡=A AMN
is a
44×
matrix having the
non zero components
1122 33 44
AAAAu= == =
,
12
A ρ =
,
1
23 24
AA ρ
−
= =
,
2
32
Aa ρ =
,
42
2Ah=
,
and
( )
T
1
2
,0, ,
m umpumuh
fx xx
ργ
−

≡=


BM U
,
where,
M
and
N
are the Jacobian Matrices defined
as,
U
F= ∇M
and
UG= ∇N
.
Clearly, eigenvalues of the coefficient matrix
( )
AU
are
(1,2)
uc λ = ±
and
( 3,4)
u λ =
. Among them two (i.e.
(1,2)
λ
) represent the waves propagating in
x±
direction
with the speed
uc±
, where
( )
12
22
cab= +
repre-
sents the magneto-acoustic speed with
( )
12
2bh ρ =
as
the Alfvén velocity. The re maining two character istics re-
present entropy waves or particle paths propag a ting with
fluid velocity.
As stated earlier, let a ‘
k shock−
’ corresponds to ei-
genvalue
(1)
λ
, then it is possible to write
(1)
Vv λε = +
(6)
With the foregoing assumptions, we set ourselves for
the task of determining the evolution law of weak shocks
and assessing the magnetic field effects on the process of
shock formation. The first step is to use Equations (3)
and (4) in (2) and equating to zero the coefficients of like
orders of
ε
, we obtain the following equation governing
the variables of first order
( )
(1) 1
0 λ −=A IY
,
which implies that
1
Y
is an eigenvector of
( )
AU
co-
rresponding to the eigenvalue
(1)
λ
. If the left and right
eigenvectors of
A
corresponding to the eigenvalue
(1)
λ
are
( )
0,2,1 2,12c ρρ =L
( )
T
2 22
,1/,,ccac bc ρ ρρ =R
.
Then it is possible to write
( )
1
t= πYR
, (7)
with
( )
tπ
as the amplitude of a right running shock front
impinging on the state + U with the speed
(1)
λ
0
c=
and to be determined later.
Also, from the jump conditions, to the second order of
ε
, we get,
( )
( )()
{ }
1 (1)
2
UU
t
v λ
−
π
=∇ −∇LMN RRM RR
. (8)
From the kinematics of singular surfaces, it is known
that the following compatibility relation must hold at the
wavefront Achenbach [2], Thomas [6]
[ ]
tx
ffV f
t
δ=∂ +∂


δ
(9)
where,
tδδ
is the Thomas displacement derivative and
provides the time rate of change measured by an observ-
er travelling with
( )
t χ
. Taking the jump in the field Eq-
uation (5), which is permissible since it is assumed that
the equations holds on both sides of
( )
t χ
, and using the
compatibility relation (9) we get
[ ]
( )
{ }
[ ] ( ) ( )
() 0
xx
V
t
+
δ

+− ∂+∂+= 


δ
UAUIUAUUB U
(10)
Introducing expansions (3-4) into (10) and equating to
zero, the coefficients of the various powers of
ε
one
obtains,
0
ε
:
( )
( )
(1) (1)
0
0 λ
+
−=AU IY
,

L. P. SINGH ET AL.
656
which implies,
( )
(1)
0
t ψ =YR
(11)
1
ε
:
( )
( )
( )
( )
( )()( )
(1) (1)(1) 11 10
11
d
d
0
U
UxU
v
t
λ
++
++ +
+−+∇ −
+∇∂ +∇=
YAUIYAYIY
AY UBY
.
Here,
(1)
dd
tx
t λ =∂+ ∂
is the derivative taken along
the rays, which implies that,
dd
x
t tv ε δδ =+∂
.
The above equation, after lef t multiplication b y
L
and
using Equations (7), (8) and (11), yields the following
ordinary differential equation
0
d0
d2tc
ψ
πΓ
+ Φπ+π=
(12)
where,
0
2mc xΦ=
and
( )
( )
2
322 2 γα Γ=+−
, with
00
ca α =
as the Alfvén number.
In deriving Equation (12), we have made use of the re-
lation,
( )
( )
(1)
.
UU
L AR λ
+
∇=∇
It evidently follows from
Equation (12) that the temporal evolution of shock am-
plitude at any time
t
depends not only on the shock
strength, its curvature and the dissipation on account of
applied magnetic field but also on the function
ψ
. Since
the quantity
ψ
is still unknown, this equation is, how-
ever, unable to give an analytical description of the com-
plete evolutionary behavior of the wave front. We, there-
fore, need to work out certain aspects in more detail.
4. Evolution of Accompanying Discontinuity
In order to proceed further, it is necessary to obtain a
transport equation for
ψ
, which may be think of as the
amplitude of jump in the slope of unsteady disturbance at
the wave front. To achieve this goal, we proceed as fol-
lows:
We differentiate Equation (5) with respect to
x
ahead
and behind the shock and subtract these equations writ-
ten ahead and behind the shock. The resulting equation,
after using equations the compatibility relatio n (9) g ives
( ) ( )
( )( )()
() () ( )
( )
( )( )()
( )
2
2
0.
xx
Ux xU x x
Ux xx
U xxUx
Ux
VI
t
+
++
++
+
δ∂

 
+ −∂

δ
+∇∂∂ +∇∂∂ 

 +∇∂∂ +∂



+∇∂∂+∇ ∂
 
 
+∇ ∂=


UAU U
AUUAU U
A UUAUU
AU UBU
BU
The above equation after using expansions (3-4) and
left multiplying by
L
, while zeroth order terms only are
retained, yields the following compatibility equation
2
0
d0
dtc
ψψψ Γ
+Φ +=
(13)
It follows immediately tha t Equation (13) does not con-
tain any unknown term and thus the system of compati-
bility equations for weak shocks is closed at the second
compatibility equation. Also, it may be noticed that the
evolution Equation (16) contains only the zeroth order
terms therefore the derivation is valid only if the ampli-
tude of accompanyi n g discont i nuities are of
( )
1O
.
It is interesting to notice that Equatio n (13) is in the
form of Bernoulli type equation which governs the evo-
lutionary behavior of acceleration waves in nonlinear
material media and elsewhere. In (13) the linear term
ψ Φ
depends upon the unperturbed conditions of the me-
dium and it takes into account the gradient in the flow
variables as well as the geometry of the problem. The ne-
gative value of
ψ
corresponds for compression waves
and positive for expansion waves. The coefficient of non-
linear term,
Γ
, which is positive for most of the fluids,
is responsible for the nonlinear steepening of the wave
front. However, in past years, fluids with negative non-
linearity have been found Murlidharan and Sujith [23].
The present paper deals with positive values of
Γ
. Thus,
the nonlinear term makes a negative value of
ψ
more
negative and a positive value of
ψ
less positive, that is,
the nonlinearity alone causes a compression wave to
steepen and an expansion wave to relax.
5. Results and Discussion
As Equation (13) is of the form which describes the evo-
lutionary behavior of wave amplitude in various gasdy-
namic regimes [9-13] and therefore the analysis of this
equation concerning the local behavior of wave ampli-
tude follows on parallel lines. However, to investigate
the magnetic field effects on the process of nonlinear
steepening of wave front we rewrite Equations (12) and
(13) in non -dimensiona l fo rm as
( )
d20
dx
ψ
π+π Φ+Γ=




(14)
2
d0
dx
ψψψ
+Φ+Γ=



(15)
where,
π

,
ψ

,
Φ

,
Γ

and
x

are dimensionless
quantities defined as
0
π=π π

,
0
ψ ψψ =

,
0
x xx=

Φ

2mx=
and
( )
( )
22
322 2 γ αα
−
Γ=+−Θ

with
α
00
ca=
as the Alfvén number and
2
000
xa ψ Θ=
as
the dimensionless measure of the strength of the initial
jump discontinuity in the field gradients. Indeed, these
two transport equations govern the evolutionary behavior
of the shock amplitude as well as the jump in the first
order gradient of the field variables. In deriving Equa-
tions (14) and (15) we have made use of the characteris-
tic relation
(1)
0
d
d
x
t
λ =
(16)

L. P. SINGH ET AL.
657
Performing required integration subject to the initial
conditions for
ψ

and
π

at
1x=

, say
1 ψ =

and
1π=

,
the Equations (14) and (15) along with the characteristic
relation (16) yield the following so lutions .
Plane case
( )
0m=
: Integrating Equations (14) and
(15) subject to the above initial conditions yield
( )
( )
1
2
11x ψα
−
−
=+ ΓΘ−

, (17)
( )
( )
1/2
2
11x α
−
−
π=+ΓΘ−

. (18)
Cylindrical case
( )
1m=
: In this case the solution of
Equations (14) and (15) takes the following form
( ) { }
1
1/221/2
12 1xx ψα
−
−−
=+ΓΘ−

(19)
( )
( )
{}
1/2
2 1/2
12 1xx α
−
−
π =+ΓΘ−
 
(20)
5.1. Nonlinear Steepening of the Wave Front
Since
Γ
and
α
are positive quantities and
( )
1/2
1x−

is
an increasing function of
x

, therefore it follows from
(17)-(20) that the behavior of
π

and
ψ

will depend
on sign of
0
ψ
and hence that of
Θ
. It is evident from
Equations (17)-(20) that if
0
ψ
is positive (i.e. an expan-
sion wave front with
0Θ>
),
π

as well as
ψ

decreas-
es as the expansion wav e advan ces in
x
direction. While
for negative values of
0
ψ
(i.e. a compression wave with
0Θ<
),
π

and
ψ

increases monotonically and the solu-
tion provided by (17)-(20) no longer remains valid and
steepens into a shock wave after a finite running length
s
x

. In fact, the weak shock assumption breaks down be-
fore
π

and
ψ

approach to infinitely large values and
existence of the distance
s
x

may be regarded as an in-
dication of this. A simple physical explanation of the ap-
pearance of shock wave may be that it is formed owing
to the inertial overtaking of flow particles, that is when
the first characteristic could intersect the successive one.
Thus a shock can form only when initial disturbance is
compressive and the corresponding shock formation dis-
tance
s
x

in the above two cases (for
0Θ<
) are given
by
Plane case:
2
1
s
x α = −ΓΘ

,
Cylindrical case:
1/2 2
12
s
x α = −ΓΘ

.
5.2. Comparison with Exact Results for Decay of
Weak Shocks
For large values of
x

the asymptotic behavior of plane
and cylindrical shock waves is shown in the flollowing
table.
From Table 1 it is clear that for plane waves
1
x ψ
−
∝

and
12
x
−
π∝

therefore, width of the plane shock, i.e.
Table 1. Decay behavior of weak shock waves and first or-
der discont inuities.
Shock
strength First order discontinuity
Shock width
varies as
Plane case
12
x
−
π∝

1
x ψ
−
∝

12
x

Cylindrical
case
34
x
−
π∝

1
x ψ
−
∝

14
x

the distance between shock front and tail of the rarefac-
tion wave increases like
12
x

. Also, for cylindrical
waves,
1
x ψ
−
∝

and
34
x
−
π∝

therefore, width of the
cylindrical shock waves increase like
14
x

. These results
are in closed agreement with the earlier results obtained
by Whitham [1, pp. 312-322], Courant and Frie drichs [24,
pp. 164-168] and by Landau [25].
Now our objective is to investigate how the nonlinear
steepening or flattening of the wave form is influenced
by the presence of magnetic field. For the sake of com-
parison, the integral curves for Equations (17)-(20) are
sketched in the Figures 1-9. These curves help to illu-
strate the effect of magnetic field strength, which enters
through an increase in the Alfvén number
α
, and the
geometry of the problem on the nonlinear steepening or
flattening of the wave.
Figures 1-4 illustrate the magnetic field effects on the
flattening of expansion waves for both the cases, that is,
weak shock (
π

) and correspnding accompanying dis-
continuity (
ψ

). It is evidently clear from Figures 1 and
2 that a cylindrical wave attenuate faster than a plane
wave as one would expect and the attenuation rate is
decreased by the dissipative mechanism due to presence
of magnetic field strength (
α
) as compared to what it
would be in non-magnetic case
( )
1 α =
. Also, from Fi-
gures 3 and 4 we infer that the amplitude of the first
order discontinuity
ψ

, which accompany the weak
shock, decays more rapidly as compared to the shock
amplitude
π

itself.
As discussed earlier that only compressive waves can
evolve into a shock and the corresponding situations are
depicted in the Figures 5-8, showing thereby that, for
compression waves, an increase in the magnetic field
strength delays the onset of shock. Also, it is clear from
these figures that amplitude of accompanying disconti-
nuity (
ψ

) steepen more rapidly in comparision to the
shock amplitude
π

itself.
Figure 9 shows the variation of shock formation dis-
tance with changes in the value of the initial jump
0
ψ
. It
may be noticed that an increase in the magnetic field
strength enhances the shock formation distance. How-
ever, higher values of the initial jump
0
ψ
and hence
Θ
lead to sh ort er shock f ormation di s t a nc e .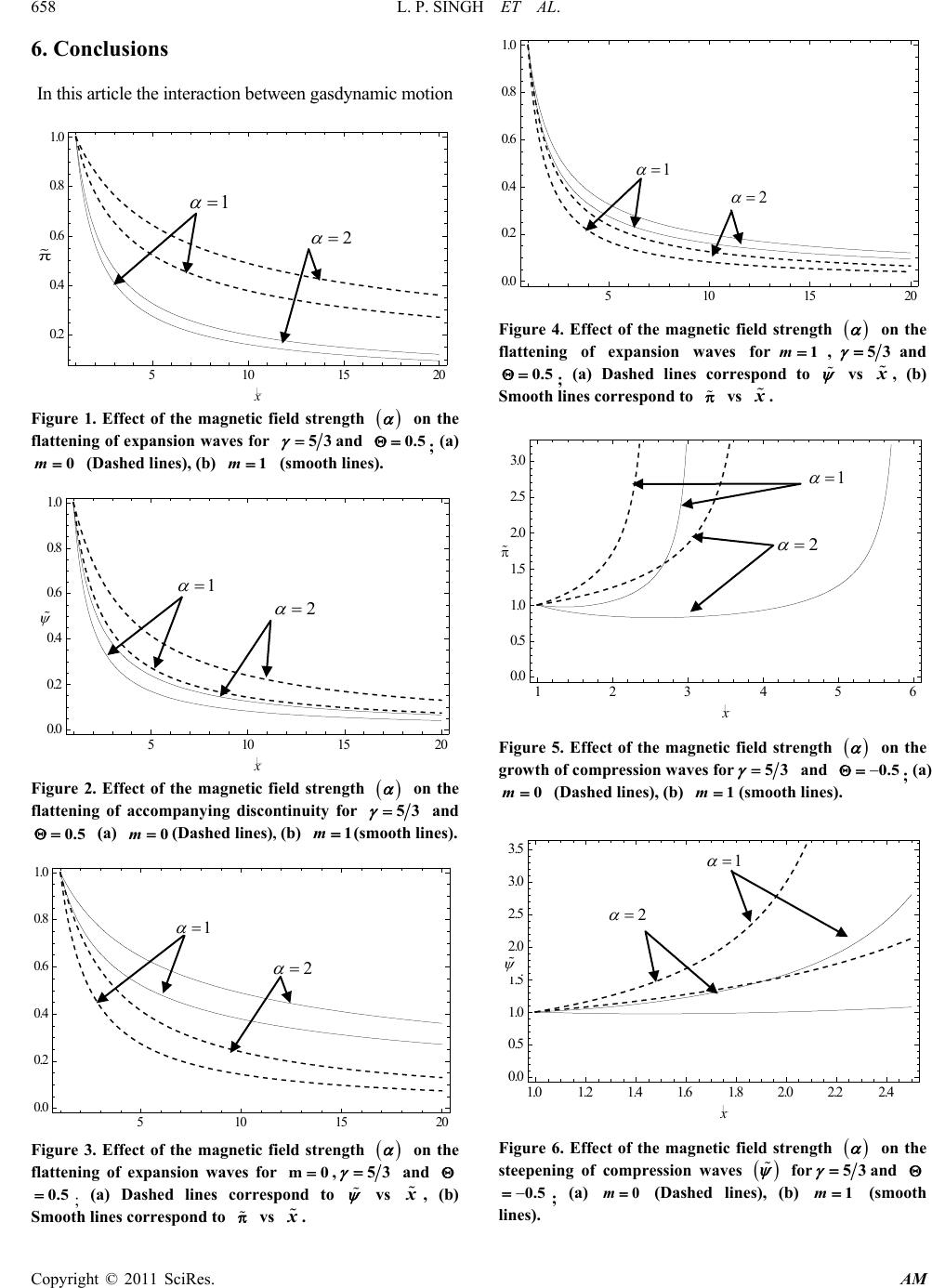

L. P. SINGH ET AL.
658
6. Conclusions
In thi s a rticl e the i ntera cti on betwee n gas dynam ic m otion
Figure 1. Effect of the magnetic field strength
( )
α
on the
flattening of expansion waves for
53 γ =
and
0.5Θ=
; (a)
0m=
(Dashed lines), (b)
1m=
(smooth lines).
Figure 2. Effect of the magnetic field strength
( )
α
on the
flattening of accompanying discontinuity for
53 γ =
and
0.5Θ=
(a)
0m=
(Dashed lines), (b)
1m=
(smooth lines).
Figure 3. Effect of the magnetic field strength
( )
α
on the
flattening of expansion waves for
m0=
,
53 γ =
and
Θ
0.5=
; (a) Dashed lines correspond to

ψ
vs

x
, (b)
Smooth lines correspond to

π
vs

x
.
Figure 4. Effect of the magnetic field strength
( )
α
on the
flattening of expansion waves for
1m=
,
53 γ =
and
0.5Θ=
; (a) Dashed lines correspond to

ψ
vs

x
, (b)
Smooth lines correspond to

π
vs

x
.
Figure 5. Effect of the magnetic field strength
( )
α
on the
growth of compression waves for
53 γ =
and
−0.5Θ=
; (a)
0m=
(Dashed lines), (b)
1m=
(smooth lines).
Figure 6. Effect of the magnetic field strength
( )
α
on the
steepening of compression waves
( )

ψ
for
53 γ =
and
Θ
−0.5=
; (a)
0m=
(Dashed lines), (b)
1m=
(smooth
lines).
5
10
15
20
0.2
0.4
0.6
0.8
1.0
x

5
10
15
20
0.0
0.2
0.4
0.6
0.8
1.0
x

5
10
15
20
0.0
0.2
0.4
0.6
0.8
1.0
5
10
15
20
0.0
0.2
0.4
0.6
0.8
1.0
1
2
3
4
5
6
0.0
0.5
1.0
1.5
2.0
2.5
3.0
x

1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
x

1 α =
2 α =
1 α =
2 α =
1 α =
2 α =
1 α =
2 α =
1 α =
2 α =
1 α =
2 α =
π

π

ψ

ψ


L. P. SINGH ET AL.
659
Figure 7. Effect of the magnetic field strength
( )
α
on the
growth of compression waves for
0m=
,
53 γ =
and
−0.5Θ=
; (a) Dashed lines correspond to

ψ
vs

x
, (b)
Smooth lines correspond to

π
vs

x
...
Figure 8. Effect of the magnetic field strength
( )
α
on the
growth of compression waves for
1m=
,
53 γ =
and
−0.5Θ=
; (a) Dashed lines correspond to

ψ
vs

x
, (b)
Smooth lines correspond to

π
. vs

x
.
Figure 9. Effect of the magnetic field strength
( )
α
and
initial shock strength
( )
Θ
on the shock formation distance
(
s
x
) for
53 γ =
; (a)
0m=
(Dashed lines), (b)
m
1=
(smooth lines).
and magnetic field has been analyzed in detail for the
classic problem of propagation of weak shocks in one-
dimensional unsteady planar and cylindrically symmetric
flows of an inviscid electrically conducting gas. It is as-
sumed that the conductivity of the gas is infinite, and the
direction of magnetic field is orthogonal to the trajecto-
ries of the fluid particles. Though the mathematics of th e
governing system of equations is quite complex, the qua-
litative physical results obtained are r e markably simple.
The method employed in this paper, for investigating
general properties of propagating shock waves, is based
on an expansion in a neighborhood of the wave front and
in a subsequent expansion in terms of the shock ampli-
tude (assumed to be small). To the first order this tech-
nique introduces the concept of rays and yields a coupled
system of transport equations that hold along the rays of
the governing equations. The solutions of this system
efficiently describe shock motion and enable us to de-
termine explicitly the position and time of shock forma-
tion which also serve as an important parameter in stud-
ying the effects of magnetic field strength and the wave
front geometry on convective nonlinear steepening and
dissipative flattening of the wave which is also illu strated
through Figures 1-9. It may be noticed that the effects of
dissipative mechanism due to the presence of magnetic
field is to slow down the decaying process of expansion
waves; whereas, it has stabilizing effect on shock for-
mation in the sense that an increase in the magnetic field
strength enhances the shock formation distance. Also, it
is observed that the decaying of plane and cylindrical
shocks varies according to
1/2
x
−

and
3/4
x
−

, respectively;
whereas the width of the shock for the above two cases
increase like
1/2
x

and
1/4
x

. These results are found to be
in good agreement with earlier results investigated th-
rough various other approaches. We conclude this sec-
tion with a remark regarding the mathematical structure
noticed in Section 3, where the governing system of equ-
ations is used to derive transport equations for the jump
in flow variables. In fact, in this development it is as-
sumed that the flow on both sides of the shock is smooth.
The case in which the flow behind a shock near the triple
point is not smooth, yields many technical difficulties is
postponed to a future work.
7. Acknowledgements
The second and third authors acknowledge the financial
support from the CSIR and UGC, India, under the SRF
scheme.
8. References
[1] G. B. Whitham, “Linear and Nonlinear Waves,” Wiley-
Interscience, New York, 1974.
[2] J. D. Achenbach, “Wave Propagation in Elastic Solids,”
1.0
1.2
1.4
1.6
1.8
2.0
2.2
2.4
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
1.0
1.5
2.0
2.5
3.0
0.0
0.5
1.0
1.5
2.0
1.0
1.5
2.0
2.5
3.0
2
3
4
5
6
7
8
9
Magnetic  fieldstrength   
Shock

formatio ndistance

x 
s

1 α =
2 α =
1 α =
2 α =
0.5Θ=−
0.7Θ=−
Magnetic field strenghth

L. P. SINGH ET AL.
660
North-Holland Am er ican E lsevier, Amsterd am, 1973.
[3] P. J. Chen, “Selected Topics in Wave Propagation,”
Noordhoff, Leyden, 1976.
[4] A. Jeffrey, “Quasilinear Hyperbolic System and Waves,”
Pitman, London, 1976.
[5] M. F. McCarthy, “Singular Surfaces and Waves,” In: A.
C. Eringen, Ed., Continuum Physics, Vol. 2, Academic
Press, London, 1975, pp. 449-521.
[6] C. Truesdell and K. R. Rajagopal, “An Introduction to the
Mechanics of Fluids,” Birkhäuse, Boston, 2000.
doi:10.1007/978-0-8176-4846-6
[7] T. Y. Thomas, “The Growth and Decay of Sonic Discon-
tinuities in Ideal Gases,” Journal of Mathematics and
Mechanics, Vol. 6, No. 3, 1957, pp. 455-469.
[8] B. D. Coleman and M. E. Gurtin, “Growth and Decay of
Discontinuities in Fluids with Internal State Variables,”
Physics of Fluids, Vol. 10, No. 7, 1967, pp. 1454-1458.
doi:10.1063/1.1762305
[9] V. V. Menon, V. D. Sharma and A. Jeffrey, “On the Ge-
neral Behavior of Acceleration Waves,” Applicable Ana-
lysis, Vol. 16, No. 2, 1983, pp. 101-120.
doi:10.1080/00036818308839462
[10] H. Lin and A. J. Szeri, “Shock Formation in the Presence
of Entropy Gradient,” Journal of Fluid Mechanics, Vol.
431, No. 1, 2001, pp. 161-188.
doi:10.1017/S0022112000003104
[11] P. M. Jordan, “Growth and Decay of Shock and Accele-
ration Waves in a Traffic Flow Model with Relaxation,”
Physica D: Nonlinear Phenomena, Vol. 207, No. 3-4,
2005, pp. 220-229. doi:10.1016/j.physd.2005.06.002
[12] D. Bhardwaj, “Formation of Shock Waves in Reactive
Magnetogasdynamic Flow,” International Journal of En-
gineering Science, Vol. 38, No. 11, 2000, pp. 1197-1206.
doi:10.1016/S0020-7225(99)00071-3
[13] M. Tyagi and R. I. Sujith, “The Propagation of Finite
Amplitude Gasdynamic Disturbances in a Stratified At-
mosphere around a Ce le sti al Body : An Analy t ical St udy ,”
Physica D: Nonlinear Phenomena, Vol. 211, No. 1-2,
2005, pp. 139-150. doi:10.1016/j.physd.2005.08.006
[14] I. Christov, P. M. Jordan and C. I. Christov, “Nonlinear
Acoustic Propagation in Homentropic Perfect Gases: A
Numerical Study,” Physics Letters A, Vol. 353, No. 4,
2006, pp. 273-280. doi:10.1016/j.physleta.2005.12.101
[15] T. R. Sekhar and V. D. Sharma, “Evolution of Weak Dis-
continuities in Shallow Water Equations,” Applied Ma-
thematics Letters, Vol. 23, No. 3, 2010, pp. 327-330.
doi:10.1016/j.aml.2009.10.003
[16] V. P. Maslov, “Propagation of Shock Waves in an Isen-
tropic Non-Viscous Gas,” Journal of Mathematical Sci-
ences, Vol. 13, No. 1, 1980, pp. 119-163.
doi:10.1007/BF01084111
[17] M. A. Grinfel’d, “Ray Method for Calculating the Wave-
front Intensity in Non-Linear Elastic Material,” Journal
of Applied Mathematics and Mechanics, Vol. 42, No. 5,
1978, pp. 958-977.
[18] A. M. Anile, “Propagation of Weak Shock Waves,” Wave
Motion, Vol. 6, No. 6, 1984, pp. 571-578.
doi:10.1016/0165-2125(84)90047-7
[19] G. Russo, “Generalized Wavefront Expansion: Properties
and Limitations,” Meccanica, Vol. 21, No. 4, 1986, pp.
191-199. doi:10.1007/BF01556485
[20] A. M. Anile and G. Russo, “Generalized Wavefront Ex-
pansion I: Higher Order Corrections for the Propagation
of Weak Shock Waves,” Wave Motion, Vol. 8, No. 3,
1986, pp. 243-258. doi:10.1016/S0165-2125(86)80047-6
[21] G. Madhumita and V. D. Sharma, “Imploding Cylindrical
and Spherical Shock Waves in a Non-Ideal Medium,”
Journal of Hyperbolic Differential Equations, Vol. 1, No.
3, 2004, pp. 521-530. doi:10.1142/S0219891604000184
[22] V. D. Sharma, L. P. Singh and R. Ram, “The Progressive
Wave Approach Analyzing the Decay of a Sawtooth Pro-
file in Magnetogasdynamics,” Physics of Fluids, Vol. 30,
No. 5, 1987, pp. 1572-1574. doi:10.1063/1.866222
[23] S. Muralidharan and R. I. Sujith, “Shock Formation in the
Presence of Entropy Gradients in Fluids Exhibiting
Mixed Nonlinearity,” Physics of Fluids, Vol. 6, No. 11,
2004, pp. 4121-4128. doi:10.1063/1.1795272
[24] R. Courant and K. O. Friedrichs, “Supersonic Flow and
Shock Waves,” Interscience Inc, New York, 1948.
[25] L. D. Landau, “On Shock Waves at Large Distances from
the Place of Their Origin,” Soviet Physics Journal, Vol. 9,
1945, pp. 496-500.