 Journal of Intelligent Learning Systems and Applications, 2011, 3, 70-81 doi:10.4236/jilsa.2011.32009 Published Online May 2011 (http://www.SciRP.org/journal/jilsa) Copyright © 2011 SciRes. JILSA Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible? Biliana Alexandrova-Kabadjova1, Edward Tsang2, Andreas Krause3 1General Directorate of Payment Systems and Risks, Bank of Mexico, Mexico City, Mexico; 2Centre for Computational Finance and Economic Agents (CCFEA), University of Essex, Colchester, England; 3School of Management, University of Bath, Bath, England. Email: balexandrova@banxico.org.mx Received July 10th, 2010; revised October 1st, 2010; accepted December 1st, 2010. ABSTRACT In this paper, we study the dynamics of competition in the payment card market. This is done through a multi-agent based model, which captures explicitly the commercial transactions at the point of sale between consumers and mer- chants. Through simulation, we attempt to model the demand for payment instruments on both sides of the market. Con- strained by this complex demand, a Generalised Population Based Incremental Learning (GPBIL) algorithm is applied to find a profit-maximizing strategy, which in addition has to achieve an average number of card transactions. In the present study we compare the performance of a profit-maximizing strategies obtained by the GPBIL algorithm versus the performance of randomly selected strategies. We found that under the search criteria used, GPBIL was capable of improving the price structure and price level over randomly selected strategies. Keywords: Competition in Payment Card markets, Multi-Agent Modeling, Evolutionary Computation 1. Introduction The payment cards, known as credit and debit cards, in the last two decades have become an important element of the modern economies. The growing importance of these electronic payment instruments is among the rea- sons why economists and policymakers have put a lot of efforts to understand the way in which the payment card market works [1-4]. This is built over so called two-sided platform [5], in which for a successful transaction with an electronic instrument the consumers have to hold a card and the merchants have to accept it as a payment. Consumers and merchants prefer the use of plastic cards over cash for security reasons or because it could save them time at the counter. These, so called convenience externalities arise among the different retail payment methods used. Further, the higher the number of estab- lishments that accept a particular card, the higher the benefits to the card holders. Similarly, the merchants obtain higher benefits if the number of consumers using a particular card increases. These, known as network ex- ternalities, are crucial element of the competition among payment card purveyors. Platform operators, as Visa and Mastercard, organize their business in a four party scheme: consumers, mer- chants, issuers (banks that provide cards to the consum- ers) and acquirers (financial institutions that provide electronic terminals to merchants). Each network estab- lishes a specific level of interchange fees, which is charged per transaction and usually flows from acquirers to issuers. For a long time, the main focus of the litera- ture has been on the fee structure of payment cards, with the emphasis laid on the interchange fee [6,7]. The re- search in the field can be divided into models studying the problematic of a single card [1,2,8,9] and [10], and models that allow the competition between payment card platforms [11-14]. Nevertheless, given that the possibility to incorporate the complex market dynamics into an analytical model is limited, the results of the theoretical studies strongly de- pend on the assumptions regarding the relationships among the market participants. In addition, these models are unable to incorporate the heterogeneity in the prefer- ences of consumers and merchants, neither the external- ities arising from the complex dynamics of two-sided demand for electronic payment cards. Following a different approach, in order to gain better insight of the market, in [15] the authors have developed an agent-based model, which was motivated from [8]. The model simulates the interactions at the point of sale among consumers and merchants. This artificial market  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible?71 reproduces the demand of payment cards on both sides and opens the possibilities to study the market dynamics, using computational environment. Further, this work was extended in [16], in which evolutionary computational techniques were applied to find a profit-maximizing strategy. In that environment, instead of representing explicitly issuers and acquirers, the model captures the competition among different platform operators, which payment cards are not compatible. More specifically, each competitor decides his own price level and structure as well as the amount to spend in publicity. The price structure consists in variable and fixed fees on both sides of the market1, but each card provider decides which particular fees to apply. The four elements that deter- mined the price, together with the publicity cost form the payment card purveyor’s strategy, which is modelled as a vector. Given the complex domain of this vector, there exist multiple possibilities of sampling it. For instances, the authors applied a Generalised Population Based In- cremental Learning (GPBIL) [17] algorithm in order to obtain profit-maximizing strategies, which in addition have to achieve an average number of card transactions. Under this line of research, here we present a study that tests how efficient the GPBIL-strategies reported in [17] are. At this point the Box’s statement: “all models are wrong, but some are useful” (p.424 in [20]) could not be more appropriate. Motivated by Box, our aim is to find out if this model is purposeful? To this end, we sub- ject the five elements of a card provider’s strategy to training. These are the variable and fixed fees on both sides of the market and the publicity cost. The simplest mechanism of sampling the strategy is to follow a ran- dom selection. Alternatively, an instantiation of the vec- tor could be the result of an extensive search over the strategy space constrained by the complex shape of the modelled demand. The space of possible strategies is enormous, due to combinatorial explosion. To improve search efficiency, this search has to be guided by par- ticular criteria of interest, e.g. to find profit-maximizing strategies. The search method chosen could make sub- stantial difference in finding better strategies, in terms of both the quality of the strategies found and search effi- ciency [21]. In order to find the advantage and disadvan- tage of using the GPBIL, in the present study our aim is to compare the performance of the GPBIL-strategy and the randomly generated strategy. To that end, we have created an artificial market with nine competitors, in which local interactions among consumers and mer- chants are reproduced. We report the performance of five different GPBIL-strategies against ten different random strategies. The test is organized in five exercises, struc- tured in the following way. Each exercise consists of ten independent instantiations of the model, also refereed as cases. In each independent case, eight of the nine com- petitors use the same profit-maximizing strategy, whereas one competitor applies a randomly generated strategy. Therefore, the exercise consists in comparing the per- formance of one GPBIL-strategy against ten different ran- dom strategies. For each exercise we compare the stra- tegies in two aspects: profit and number of card transac- tions. The randomly generated strategy needs to obtain higher number of card transactions and better profit in comparison to the GPBIL-strategies, in order for the for- mer to be considered more efficient. The paper is organized as following: in the next sec- tion we briefly introduce the elements’ definition and the decisions of the agents interacting at the artificial pay- ment card market. Following, in Section 3 we present the insides of the GPBIL algorithm, whereas in Section 4 we explain the structure of the experiment. Next, Section 5 is dedicated to present the results of the experiment with our observations and finally in Section 6 the related con- clusions and suggestions for future work are given. 2. Artificial Payment Card Market The artificial payment card market is a model that simu- lates commercial transactions among consumers and merchants, following as a framework the model pre- sented in [8]. In this section we introduce formally the elements’ definitions and the decisions of the agents. 2.1. Elements’ Definition 2.1.1. Merchants Suppose we have a set of merchants with M=NM M, who are offering a homogeneous good at a common price and face marginal cost of production lower than this price. In other words, we eliminate the price competition among merchants in order to concentrate our analysis on the competition among payment cards. The merchants are located at random intersections of a N × N lattice, where . Let the top and bottom edges as well as the right and left edges of this lattice be connected. 2 NNM 2.1.2. C ons umers Consumers occupy all remaining intersections of the N × N lattice. The set of consumers is denoted C with =NC C, where M and M . Each consumer has a budget constraint that allows him to buy in a single interaction exactly one unit of the good of- fered by the merchants. The utility gained from the con- sumption of this good is bigger than its price. In order to NN C 2 NN C N 1The variable fees are charged for each transactions paid with a card, whereas fixed fees are membership fees, which are charged regularly regardless the use of the card. Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible? 72 obtain the good any consumer has to travel to a merchant . The distance is measured by the Manhattan distance dc,m between the locations on the lattice and it imposes travel costs on consumers. The longitude between two adjacent intersections is normal- ized to unity. Let c denotes the set of merchants a consumer considers to go to, given that we restrict him to the nearest merchants2. cC mM M 2.1.3. Payment Card s There exists a set of payment methods with P =1NPP and M . All payment forms are card payments offered by network operators, with the excep- tion of the first element of the set, which is the bench- mark and can be interpreted as cash payment method. The cash is used by all consumers and is accepted by all merchants. Furthermore, in order for a card payment to occur, the consumer as well as the merchant must have a subscription to the card in question. We assume that consumers prefer card payments over cash payments. N P N A fixed subscription fee of could be charged per each transaction to the consumer, whereas 0 p F 0 p could be charged per each transaction to the merchant. The domains of those fees, and are subsets of real numbers. Cash payments do not attract any fees. For each unit of goods sold using a payment card , a merchant receives net benefits of pm PmM . Such benefits may include reduced costs from cash handling and could differ across payment methods. These are identical for all merchants for a given card. The domain is a subset of real numbers. Note that the benefits could have a negative value, which means that the variable fee paid by the merchant to the card issuer is bigger than the benefits he receives from that particular electronic payment method. Cash pay- ments do not produce any benefits. Consumers also receive net benefits from paying by card, b, but no benefits from cash payments. Here, the benefits may arise from the delayed payment, insurance cover or cash-back options. The benefits are the same for all consumers, but could differ across card purveyors. The b is a subset of real numbers and as in the case of the merchants could also include negative values. Finally, the issuer of the payment method has to de- cide how much it should spend in publicity l l , in order to increase the number of consumers and mer- chants using the electronic card that he is providing. The publicity domain, l, is a subset of real numbers. Thus, the variables controlled by the card purveyors are , , , b and l and those form its strategy. 2.2. Decisions of the Agents 2.2.1. Merchants’ Decisions After certain period of interactions3 at the point of sale the merchants have elements to decide to which new cards to subscribe and which old subscriptions to keep. In order to do so, at the beginning of the simulation, merchants start with certain number of cards assigned to them. Then for each commercial transaction the estab- lishments keep track of the cards presented at the counter. Every time a card p P is presented to the merchant mM and he has a subscription to this card p m P with =m mP he increases the score of the card ,mp NP by one. Here, ,mp is an element of the vector defined as ,1 , ,, m mmN P On the other hand, if the merchant does not have sub- scription to the card, i.e. , the score of the card ,mp 1 m pP is increased by one, given that ,mp is an element of the vector: ,1 , ,, m mmN P The merchant decides to cancel the subscription of a card with probability4 , , π exp m mp mp m m xq xq (1) where m denotes the number of cards presented. Simi- larly he decides to subscribe to a new card with probabil- ity , , , exp π exp mp m mp mp m m xq (2) where m q and m q represent the inertia to add or drop a card; 1m p p qN P , whereas m and m are constants. 2.2.2. Consumers ’ D ec ision In the model the consumers take three decisions: which merchant to visit, which card to use and similar to the merchants’ decision, to which card to subscribe? 3The number of interactions is dissimilar across merchants and it is determined by Poisson distribution specific for each m. 4The probabilities defined in Equations (1) and (2) are affected by the ublicity applied by each payment card provider. 2We have modelled local network connections. Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible?73 Regarding the first decision, we assume that when de- ciding which merchant to visit, the consumer has not yet decided which of the cards he holds will be used. Sup- pose ,cm is the set of cards the consumers and mer- chants have in common. Given that P , ,cm cmP , we assume that the more common payment cards the mer- chant and the consumer have, the more attrac- tive a merchant becomes. This is due to the fact that the consumer always carries all his cards with him and he decides which card to use at the moment of the payment. Additionally, the smaller the distance , between the consumer and the merchant, the higher the possibility for this merchant to be chosen by the consumer. From these deliberations we propose to use a preference function for consumer to visit merchant: NP m c dcm , , , , , N d vN d cm cm c P cm cm P mM cm (3) Each consumer chooses a merchant cC mM with probability , as defined in 3. The consumers will continuously update their beliefs regarding the number of common payment cards for all merchants they may visit. With respect to the second decision, the con- sumer decides which payment card he wants to use at the counter of the chosen merchant. We assume a preferred card choice, given that the consumer chooses the card with the higher benefits vcm b, alternatively if the merchant does not accept any of the consumers’ cards the transac- tion is settled using cash payment. Finally, after certain periods of interactions5 the card- holders decide which new cards to subscribe to and which old subscriptions to keep. This decision has the following structure. Similarly to the merchants, initially consumers have certain number of cards c P with Nc cP . Every consumer P cC keeps track whether the cards he owns are accepted by the merchant or not. If card is accepted by the visited merchant , the consumer increases the score of the card , pc P c mM c by one. Here , c is an element of the vector specified as ,1 , ,, N cc P c Assume that he cancels his subscription with probabil- ity6 defined in 4, given that the number of merchants visited is c. , , π exp p p xk x xk c c c c c (4) Here k c accounts for the inertia of the consumer to change cards; 1p p kFN b c P , whereas ε and c are constants. At the other hand, let with c PN c cP be the set of payment cards, to which the consumer does not have subscription. Suppose consumer c visits a mer- chant and they are faced with the situation, in which they do not have cards in common. The set of cards the merchant accepts is . In that case the consumer increases the score , P m m P cby one p mc PP. Here , c is an element of the vector, which is defined as ,1 , ,, N P c cc . Given that c is a constant, the probability of sub- scribing to these cards is then determined by , , , exp π exp p p p k c c c c c c . (5) 2.2.3. Payment Card s Providers’ Decisions The payment card providers’ decision is to define what strategy they are going to use. For that reason we define the solution space of the payment card’s strategy as pp pp bl rewritten as 15 15 with ,, . pl (6) In addition we assume that the cost of publicity, l mp , spend by the card issuer in each interaction, has a direct impact in the consumers’ and the merchants’ decisions to subscribe/cancel a card. The probabilities, ,, ,, , πmp π π c, , π c, defined in Equations (1), (2), (4) and (5) are then adjusted according to the rule presented in the fol- lowing equation ππ2π . (7) Here substitutes any of the above probabilities, Δ represents the differences between the original value of π and the adjusted , and finally π 5The number of interactions is different across consumers and is de- fined by individual Poisson distribution. 6The probabilities defined in Equations (4) and (5) are affected by the ublicity applied by each payment card provider. π exp p l . The constants and satisfy the constrains Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible? 74 ππ0 and ππ1 . ,, N Let 1 sSP be the vector of sample strate- gies for all payment methods. The decisions of a particu- lar payment card provider are an instantiation of this vector. Sampling from could follow a random selection process. Alternatively, the vector P could be the result of an extensive search over the strat- egy space constrained by the complex shape of the mod- elled demand. In the next section we briefly explain how we have applied the GPBIL algorithm, which incorpo- rates positive and negative learning, and is able to ap- proximate versatile distributions. 1,, N ss 3. Applying GPBIL in Finding Profit Maximizing Strategy The strategy’s domain i is interval of real numbers. Assume a probability distribution functions :0 ,1 5 i for unconditional random variables over the ranges i, we define the joint probability distribution over S by 1 Ss ,p . (8) All electronic cards providers have the same joint probability distribution and we are using it firstly to sample individual strategies from the space, and secondly to modify through learning. We have defined P as the vector of strategies of all payment methods in one execution of the artificial payment card market. Additionally, we define 1,, N s pp , p T N as the measurement of the perform- ance achieved in one execution of the model for one payment method. The three elements that compose it are the profit of the card issuer , the number of transac- tions obtained in the market T and the corresponding index of the card p. The vector P represents the performance of all payment cards in one execution of the artificial market, after certain number of interactions among consumers and merchants. N 1,, N In Figure 1 we present the MARKET-GPBIL process used to find a profit-maximizing strategy. In our applica- tion the strategy should fulfill the following main objec- tive: obtain the highest possible profit under the constraint that the number of transactions obtained T N should be equal or above average. The first step is to initialize the joint probability func- tion. This is performed by the function initialisation, which receives as a parameter the solution space and returns the initialized joint probability function, . The main part of the algorithm consists of a loop over R runs. At the beginning of each run every payment card pro- vider selects a strategy S. This process is carried out by the function sampling (line 5 of the GPBIL algorithm Figure 1), which returns a strategy S for each one of 11 1 1 MARKET-GPBIL 1;; ; 2 3FOR1, ,DO 4FOR1,,DO 5s 6,,MARKET,,, 7,, 8,,,, 9RETURN p NN N N INR initialisation rN pN sampling sI profitDescendingSort learnings s IS N R PP P P PP P P Figure 1. The process MARKET-GPBIL for profit-maxi- mizing strategies. the payment cards, following the probability distribution function . Thereafter, in line 6, we instantiate the process MARKET with the strategy vector 1,, N ssP and the number of interactions I. This process reproduces the transactions at the point of sale among consumers and merchants. At the end it returns a vector of all payment cards performance measures 1,, N P Before the learning function is carried out, the per- formance of the payment cards providers P are sorted (line 7) according to the profit . 1,, N achieved at the MARKET. The new vector is denoted . Fol- lowing this step, the joint probability function FS is modified by a learning process (line 8). This task is ac- complished considering the market share T N obtained in the MARKET. More specifically, the function receives as parameters the current values of the joint probability distribution , the profit ordered according the per- formance and the vector of strategies P. The strategies that have obtained better than or equal to the average number of transactions are considered exam- ples of positive learning, whereas the rest of the strate- gies form the set of negative learning examples. 1,, N ss Finally, in line 9, the GPBIL algorithm returns the re- sulting joint probability distribution. This function is used as a probabilistic model to generate strategies that fulfill the main objective: to achieve the highest possible profit, given the additional restriction of obtaining above or equal average number of card transactions. In the next section we compare the performance of randomly gener- ated strategies over the performance of the strategies resulting from the joint probability distribution found by the MARKET-GPBIL. 4. The Setting of the Experiment In this section we present the setting of the model’s pa- rameters and the structure of the efficiency test. We have Copyright © 2011 SciRes. JILSA 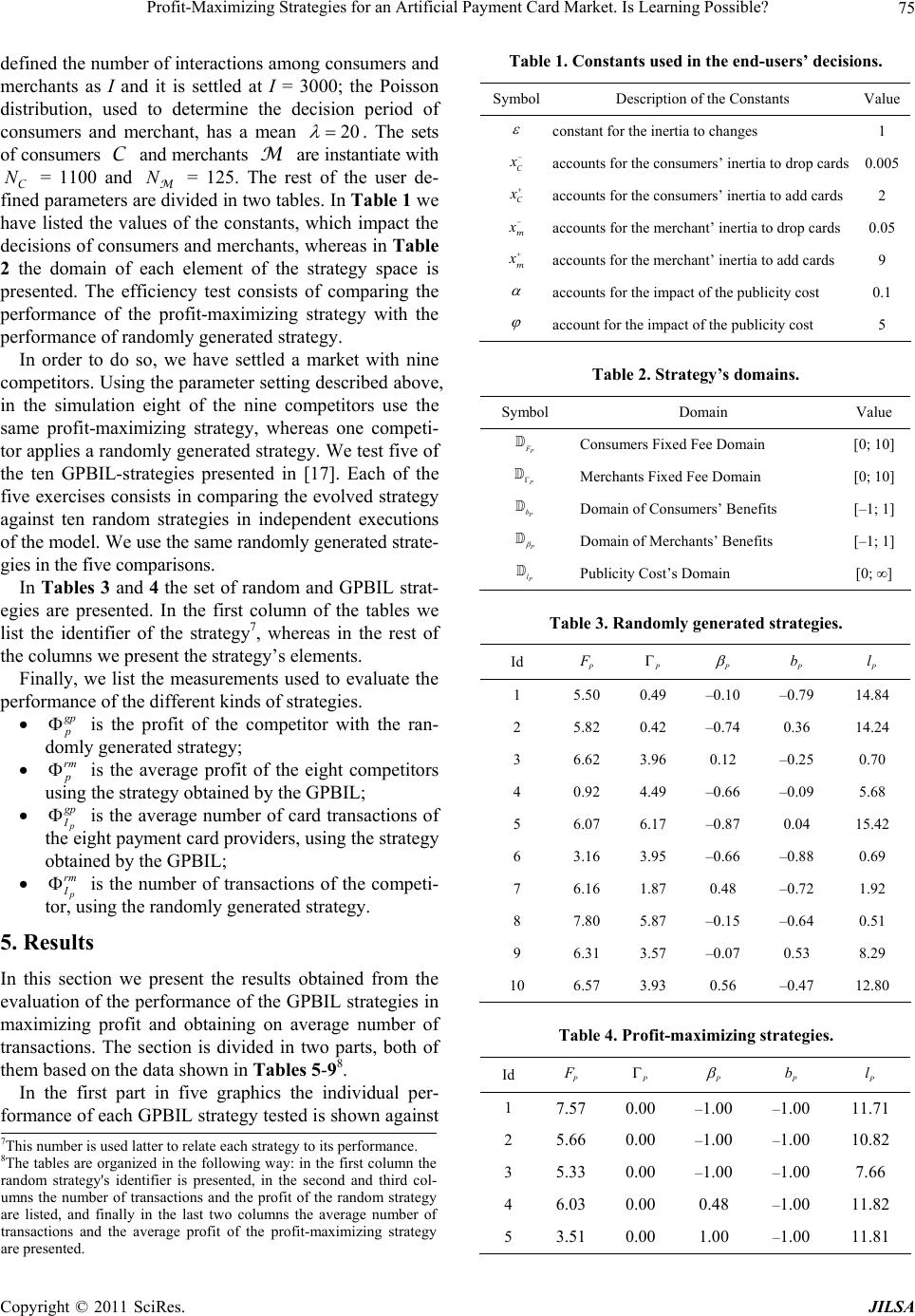 Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible?75 defined the number of interactions among consumers and merchants as I and it is settled at I = 3000; the Poisson distribution, used to determine the decision period of consumers and merchant, has a mean 20 . The sets of consumers and merchants M are instantiate with = 1100 and = 125. The rest of the user de- fined parameters are divided in two tables. In Table 1 we have listed the values of the constants, which impact the decisions of consumers and merchants, whereas in Table 2 the domain of each element of the strategy space is presented. The efficiency test consists of comparing the performance of the profit-maximizing strategy with the performance of randomly generated strategy. C NCNM In order to do so, we have settled a market with nine competitors. Using the parameter setting described above, in the simulation eight of the nine competitors use the same profit-maximizing strategy, whereas one competi- tor applies a randomly generated strategy. We test five of the ten GPBIL-strategies presented in [17]. Each of the five exercises consists in comparing the evolved strategy against ten random strategies in independent executions of the model. We use the same randomly generated strate- gies in the five comparisons. In Ta bles 3 and 4 the set of random and GPBIL strat- egies are presented. In the first column of the tables we list the identifier of the strategy7, whereas in the rest of the columns we present the strategy’s elements. Finally, we list the measurements used to evaluate the performance of the different kinds of strategies. p is the profit of the competitor with the ran- domly generated strategy; rm is the average profit of the eight competitors using the strategy obtained by the GPBIL; p is the average number of card transactions of the eight payment card providers, using the strategy obtained by the GPBIL; rm is the number of transactions of the competi- tor, using the randomly generated strategy. 5. Results In this section we present the results obtained from the evaluation of the performance of the GPBIL strategies in maximizing profit and obtaining on average number of transactions. The section is divided in two parts, both of them based on the data shown in Tables 5-98. In the first part in five graphics the individual per- formance of each GPBIL strategy tested is shown against Table 1. Constants used in the end-users’ dec i sions. SymbolDescription of the Constants Value constant for the inertia to changes 1 C accounts for the consumers’ inertia to drop cards0.005 C accounts for the consumers’ inertia to add cards2 m accounts for the merchant’ inertia to drop cards0.05 m accounts for the merchant’ inertia to add cards 9 accounts for the impact of the publicity cost 0.1 account for the impact of the publicity cost 5 Table 2. Strategy’s domains. Symbol Domain Value P Consumers Fixed Fee Domain [0; 10] P Merchants Fixed Fee Domain [0; 10] P b Domain of Consumers’ Benefits [–1; 1] P Domain of Merchants’ Benefits [–1; 1] P l Publicity Cost’s Domain [0; ∞] Table 3. Randomly generated strategies. Id b l 1 5.50 0.49 –0.10 –0.79 14.84 2 5.82 0.42 –0.74 0.36 14.24 3 6.62 3.96 0.12 –0.25 0.70 4 0.92 4.49 –0.66 –0.09 5.68 5 6.07 6.17 –0.87 0.04 15.42 6 3.16 3.95 –0.66 –0.88 0.69 7 6.16 1.87 0.48 –0.72 1.92 8 7.80 5.87 –0.15 –0.64 0.51 9 6.31 3.57 –0.07 0.53 8.29 10 6.57 3.93 0.56 –0.47 12.80 Table 4. Profit-maximizing strategies. Id b l 1 7.57 0.00 –1.00 –1.00 11.71 2 5.66 0.00 –1.00 –1.00 10.82 3 5.33 0.00 –1.00 –1.00 7.66 4 6.03 0.00 0.48 –1.00 11.82 5 3.51 0.00 1.00 –1.00 11.81 7This number is used latter to relate each strategy to its performance. 8The tables are organized in the following way: in the first column the random strategy's identifier is presented, in the second and third col- umns the number of transactions and the profit of the random strategy are listed, and finally in the last two columns the average number o transactions and the average profit of the profit-maximizing strategy are presented. Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible? 76 Table 5. Efficiency test, strategy 1. Id p rm N rm p p p N gp p 1 293 587 4 183 603 190 045 6 112 638 2 155 146 4 777 710 196 131 6 074 918 3 71 466 3 818 894 205 027 6 127 442 4 109 469 1 267 441 199 041 6 016 778 5 31 243 5 217 924 209 679 6 148 302 6 154 401 3 352 744 197 677 6 045 649 7 190 495 4 020 676 195 060 6 062 770 8 63 695 3 896 739 206 835 6 154 275 9 59 307 3 726 206 205 612 6 053 948 10 56 643 4 061 625 208 539 6 177 387 Table 6. Efficiency test, strategy 2. Id p rm N rm p p p N p p 1 270 086 4 028 220 200 859 5 508 231 2 132 753 4 580 050 206 786 5 467 251 3 65 463 3 638 983 215 090 5 531 546 4 89 048 1 195 634 211 330 5 404 561 5 25 704 4 932 694 220 308 5 537 538 6 138 006 3 235 442 208 256 5 429 815 7 173 742 3 837 502 206 364 5 482 818 8 56 985 3 745 939 217 497 5 532 962 9 53 913 3 525 837 215 560 5 458 349 10 51 820 3 860 624 218 343 5 554 859 Table 7. Efficiency test, strategy 3. Id p rm N rm p p p N gp p 1 264 663 3 990 413 202 948 5 367 858 2 130 425 4 586 414 208 333 5 328 684 3 64 575 3 603 082 216 486 5 394 379 4 87 680 1 187 830 212 724 5 271 941 5 24 624 4 897 958 222 170 5 389 579 6 133 747 3 193 190 210 157 5 291 645 7 173 181 3 793 127 207 436 5 346 346 8 54 461 3 710 916 219 947 5 399 237 9 53 267 3 511 761 217 211 5 342 348 10 50 646 3 832 682 220 048 5 412 604 Table 8. Efficiency test, strategy 4. Id p rm N rm p p p N gp p 1 158 276 4 051 594 242 115 4 379 904 2 120 743 4 864 813 245 621 4 375 830 3 43 607 3 837 620 249 250 4 415 086 4 70 769 1 225 230 240 926 4 291 554 5 27 929 5 252 087 251 869 4 384 489 6 99 064 3 228 579 244 468 4 357 959 7 129 401 4 051 465 241 096 4 375 036 8 32 625 3 875 549 250 768 4 459 407 9 34 440 3 765 368 250 344 4 412 800 1045 266 4 122 748 247 065 4 399 842 Table 9. Efficiency test, strategy 5. Id p rm N rm p p p N p p 1 115 092 3 711 873 276 873 3 235 839 2 78 536 4 502 427 281 802 3 226 917 3 31 653 3 539 388 285 434 3 273 227 4 47 468 1 130 966 277 161 3 172 209 5 17 945 4 842 936 286 763 3 231 322 6 69 554 3 037 368 279 898 3 224 163 7 73 756 3 711 376 280 569 3 242 955 8 23 724 3 669 594 285 970 3 291 332 9 21 821 3 476 859 286 019 3 264 873 1027 007 3 807 948 283 580 3 256 304 the ten random strategies used, whereas in the second part we compare the performance between the set of GPBIL strategies against the set of random strategies. 5.1. Individual Performance In this subsection we make an individual comparison between each of the five profit-maximizing strategy (see Figures 2-6) versus the performances of the ten ran- domly generated strategies9. We present the performance of the strategies in two dimensions: profit and number of card transactions. Observation 1: In the first three exercises the GPBIL- strategies (Figures 2-4) have achieved better profit then the ten randomly generated strategies. Further, the evolved strategies report a higher number of card transactions in night of the ten cases tested, i.e. only one randomly 9Please refer to Table 3. Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible?77 Figure 2. Efficiency test, strategy 1. Figure 3. Efficiency test, strategy 2. Figure 4. Efficiency test, strategy 3. Figure 5. Efficiency test, strategy 4. Figure 6. Efficiency test, strategy 5. generated strategy outrange the three evolved strategies in terms of card transactions, but regarding the profit none of the random strategy could perform better than the GPBIL-strategies 1, 2, and 3. Following, strategy 4 outperforms eight of the ten randomly generated strate- gies in terms of profit and overpasses all of them in terms of number of card transactions. Finally, strategy 5 outranges significantly the random strategies in terms of number of card transactions, but in terms of profit was passed in eight of the ten cases tested. Over all, with respect to the profit achieved, the GPBIL- strategies have performed statistically better than the randomly generated strategies. Even more, regarding the number of card transactions reported, the performance of the evolved strategies are better than the randomly gen- erated strategies. Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible? Copyright © 2011 SciRes. JILSA 78 5.2. The Performance of the Set of GPBIL Strategies vs. the Set of Random Strategies In Figures 7 and 8 we plot the random strategies’ and GPBIL strategies’ areas, resulting from the performance in terms of number of transactions. Next, in Figures 9 and 10 we present the random strategies’ and GPBIL strategies’ areas formed according to the obtained profit. In this subsection we present a second comparison, which is made using the same data presented in Tables 5-9. This time we compare on one hand the performance of each GPBIL-strategy among its own records achieved in the ten cases tested and on the other hand the per- formance of each random generated strategy among its own achievements in the five exercises presented. To that end the performance of each strategy is presented graphically as an area, by plotting together the different performances of the same strategy (either random or GPBIL) resulting from independent instantiations of the model. Observation 2: In the second comparison, we observe that the areas formed by the individual performance of profit-maximizing strategies have regular shape in con- trast to the areas from by the individual performance of the randomly generated strategies, which is irregular. In particular the evolved strategies’ areas in terms of profit and number of card transactions are approaching a rec- tangular shape, whereas the individual areas of the ran- dom strategies are irregular in the both dimensions. Fur- ther, a more detailed observation which compare the de- gree of heterogeneity among the sizes of the areas formed by the individual performance inside the same set, allow us to say that the evolved strategies present similar sizes, whereas the randomly generated strategies have significant differences among the individual perform- ances achieved. This observation is true for the both di- mensions studied: profit and card transactions. More specifically, given that there are five GPBIL strategies tested against ten random strategies, each ran- dom strategy has five different performances, whereas each GPBIL strategy has ten performances. In this pres- entation, if the resulting strategy’s area has similar to a rectangle shape, it means that its achievements are simi- lar among the different scenarios and its performance is consistent. On contrary, if the resulting strategy’s area has an irregular shape, it means that the performance of the strategy varies among scenarios and it is not consis- tent. Observation 3: Regarding the GPBIL-strategies, in Figures 8 and 10 an inverse relation is observed between profit and number of card transactions, i.e. the strategies that have achieved the highest profit are the strategies Figure 7. Random strategies performance in terms of number of transactions.  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible?79 Figure 8. GPBIL strategies performance in terms of number of transactions. Figure 9. Random strategies performance in terms of profit. Copyright © 2011 SciRes. JILSA  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible? Copyright © 2011 SciRes. JILSA 80 Figure 10. GPBIL strategies performance in terms of profit. with the lower number of card transactions and vice versa. On the other hand, with respect to the randomly gener- ated strategies the relation between profit and market share observed in Figures 7 and 9 is different. For in- stance, random strategy 5, which is the strategy with the highest profit, is also the strategies with the lower num- ber of card transactions, nevertheless random strategy 4, which had achieved the lower profit is not among the three best performance in terms of card transactions. Conclusions: from Observations 1, 2 and 3 it follows that the strategies found by the Generalised Population Based Incremental Learning algorithm are efficient strategies in achieving average number of card transac- tions and maximum profit. It also follows that with randomly generated strategies is not possible to archive similar performance, therefore the GPBIL-strategies fulfill the purpose they have been designed for. 6. Conclusions In this section we present general conclusions and we give suggestions for further research. The payment card market is characterized with complex relationships among market participants. The two-sided nature of the market gives rise to network externalities that influences the dynamics of the competition. Therefore in the context of the growing importance of the payment cards, the models of the market aimed to study the competition need to incorporate more realistic features. In this sense we consider that the use of agent-based models will al- low us to gain better understanding of the payment card market dynamics. In the current study, given the complex shape of the aggregated end-users’ demand for electronic payment methods modelled explicitly at the artificial market, the GPBIL algorithm applied has been able to find a price structure and price level that maximize the profit of the card purveyors and has successfully fulfill the objectives of the search. More the all so, we conclude that applying evolutionary techniques, as the GPBIL, in studying relevant aspects of this market opens new re- search opportunities, untractable with the analytical models. A possible extension of the model is to convert it to a four party scheme, as Visa and Mastercard organized their business this way. From our observations of the market, we believe that the issuers’ and acquirers’ deci- sions affect substantially the market competition. There- fore incorporating into the model the sets of issuers and acquirers and their corresponding decisions will allow us to study which rules governing the participants’ behavior, could make the market more efficient. Furthermore, of particular interest could be to understand what conditions are required in order for the competitors to offer better  Profit-Maximizing Strategies for an Artificial Payment Card Market. Is Learning Possible?81 prices to consumers and merchants. 7. Acknowledgements The authors want to express their gratitude to Francisco Solís and Sara Castellanos for the multiple insights on this and other payment systems matters. The views ex- pressed in this paper are those of the authors and do not involve the responsibility of the institutions they belong to. REFERENCES [1] J.-C. Rochet and J. Tirole, “Cooperation among Com- petitors: Some Economics of Payment Card Associa- tions,” The RAND Journal of Economics, Vol. 33, No. 4, Winter 2002, pp. 1-22. [2] R. Schmalensee, “Payment Systems and Interchange Fees,” Journal of Industrial Economics, Vol. 50, No.2, 2002, pp. 103-122. doi:10.1111/1467-6451.00170 [3] D. Cruichshank, “Competition in UK Banking,” Report to the Chancellor of the Exchequer, 2000. Internet Available: http://www.bankreview.org.uk [4] Reserve Bank of Australia, “Reform of Credit Card Schemes in Australia IV: Final Reforms and Regulation Impact Statement,” August 2002. [5] D. Evans and R. Schmalensee, “The Industrial Organiza- tion of Markets with Two-Sided Platforms,” National Bureau of Economic Research, September 2005. Internet Available: http://www.nber.org/papers/W11603 [6] J.-C. Rochet, “The Theory of Interchange Fees: A Syn- thesis of Recent Contributions,” Review of Network Eco- nomics, Vol. 2, No. 2, June 2003, pp. 97-124. doi:10.2202/1446-9022.1021 [7] D. Evans and R. Schmalensee, “The Economics of Inter- change Fees and their Regulation: An Overview,” Work- ing Paper 4548-05, Massachusetts Institute of Technology, Sloan, 2005. [8] J. Wright, “Pricing in Debit and Credit Card Schemes,” Economics Letters, Vol. 80, No. 3, 2003, pp. 305-309. doi:10.1016/S0165-1765(03)00143-5 [9] S. Chakravorti and W. R. Emmons, “Who Pays for Credit Cards?” Journal of Consumer Affairs, Vol. 37, No. 2, 2003, pp. 208-230. doi:10.1111/j.1745-6606.2003.tb00451.x [10] S. M. Markose and Y. J. Loke, “Network Effects on Cash-Card Substitution in Transactions and Low Interest Rate Regimes,” The Economic Journal, Vol. 113, No. 487, April 2003, pp. 456-476. doi:10.1111/1468-0297.00124 [11] J.-C. Rochet and J. Tirole, “Platform Competition in Two-Sided Markets,” Journal of the European Economic Association, Vol. 1, No. 4, 2003, pp. 990-1029. doi:10.1162/154247603322493212 [12] G. Guthrie and J. Wright, “Competing Payment Sche- mes,” National University of Singapore Department of Economics, Working Paper 0311, 2003. [13] S. Chakravorti and R. Roson, “Platform Competition in Two-Sided Markets: The Case of Payment Networks,” Working Paper WP-04-09, Federal Reserve Bank of Chi- cago, Chicago, 2005. [14] W. Bolt and K. Soramaki, “Competition, Bargaining Power and Pricing in Two-Sided Markets,” DNB Work- ing Paper 181, De Nederlandsche Bank, Amsterdam, 2008. [15] B. Alexandrova-Kabadjova, A. Krause and E. Tsang, “An Agent-Based Model of Interactions in the Payment Card Market,” Proceedings of the 8th International Conference on Intelligent Data Engineering and Automated Learning, 2007. [16] B. Alexandrova-Kabadjova, E. Tsang and A. Krause, “Market Structure and Information in the Payment Card Market,” International Journal of Automation and Com- puting, Forthcoming, 2011. [17] B. Alexandrova-Kabadjova, E. Tsang and A. Krause, “Evolutionary Learning of the Optimal Pricing Strategy in an Artificial Payment Card Market,” Natural Comput- ing in Computational Economics and Finance, Series Studies in Computational Intelligence, Vol. 100, 2008, pp. 233-251. [18] B. Alexandrova-Kabadjova, E. Tsang and A. Krause, “Competition is Bad for Consumers: Analysis of an Arti- ficial Payment Card Market,” Journal of Advanced Com- putational Intelligence and Intelligent Informatics, Vol. 2, No. 15, 2011, pp. 188-196. [19] M. Kern, “Parameter Adaptation in Heuristic Search, A Population-Based Approach,” Ph.D. Dissertation, Uni- versity of Essex, Colchester, 2005. [20] G. E. P. Box and N. R. Draper, “Empirical Model- Building and Response Surface,” John Wiley & Sons, Inc., New York, 1986. [21] E. P. K. Tsang, “Computational Intelligence Determines Effective Rationality,” International Journal on Automa- tion and Control, Vol. 5, No. 1, 2008, pp. 63-66. doi:10.1007/s11633-008-0063-6 Copyright © 2011 SciRes. JILSA
|