Applied Mathematics, 2011, 2, 504-507
doi:10.4236/am.2011.24065 Published Online April 2011 (http://www.SciRP.org/journal/am)
A New Bandwidth Interval Based Forecasting Method for
Enrollments Using Fuzzy Time Series
Hemant Kumar Pathak1, Prachi Singh2
1S. O. S. in Mathematics, Pandit Ravishankar Shukla University, Raipur, India
2Government VYT Post Graduate Autonomous College, Durg, India
Received February 25, 2011; revised March 11, 2011; accepted March 14, 2011
Abstract
In this paper, we introduce the concept of (4/3) bandwidth interval based forecasting. The historical en-
rollments of the university of Alabama are used to illustrate the proposed method. In this paper we use the
new simplified technique to find the fuzzy logical relations.
Keywords: Fuzzy Sets, Fuzzy Time Series, Fuzzy Logical Relations
1. Introduction
For planning the future forecasting plays an important
role. During last few decades, various approaches have
been developed for forecasting data of dynamic and non-
linear in nature. Fuzzy theory [1] has been successfully
employed to prediction. Many studies on forecasting
using fuzzy logic time series have been discussed such as
enrollments, the stock index, temperature and fi- nancial
forecasting. Some researchers used time invariant model
and some used time variant model. The traditional statis-
tical approaches can not predict problems in which the
values are in linguistic terms.
After introduction of fuzzy sets by Zadeh [1], Song
and Chissom [2] presented the definition of fuzzy time
series and outlined its model by means of fuzzy relation
equations, and approximate reasoning. They applied the
model for forecasting under fuzzy environment in which
historical data are of linguistic values. In that article, they
showed that a universal forecasting method using fuzzy
sets can be derived from the model of his process. After
then many researchers ([2-7]) used this data to forecast.
Cheng et al. [8] presented the trend-weighed fuzzy time
model for TAIEX forecasting. Song et al. [2] and [9]
used the relationship model, in which they constructed a
relation matrix to relate the fuzzified enrollments of year
(i – 1) and year i. Chen [3] presented a method which has
the advantage of reducing the calculation time and sim-
plifying the calculation process. Chen et al. [10] used the
differences of the enrollments to present a method to
forecast the enrollments of the University of Alabama.
Huang [11] extended Chen’s [3] work and used simpli-
fied calculations with the addition of heu- ristic rules to
forecast the enrollments. Chen [4] presented a forecasting
method based on high-order fuzzy time series for fore-
casting the enrollments of the University of Alabama.
Most of the forecasting methods require fuzzy relation.
All such methods have following drawbacks:
1) Framing of fuzzy relation requires a lot of computa-
tions.
2) Computation cost is very high.
However, obtaining accurate forecast of student enroll-
ment is not an easy task, as many factors determine the
impact of the enrolment numbers. So, in the proposed
method we introduced the interval based forecasting, wh-
ich gives most plausible range of enrollments.
2. Basic Concepts of Fuzzy Time Series
Let U = {u1, u2, u3, u4, ···, un} be the universe of dis-
course and let A = |fA (u1)/u1| + |fA (u2)/u2 + ··· + |fA (un)/un|
be the fuzzy set defined on U. Here fA: U[0,1] is the
membership function of A, fA (ui),  i  [1,n] indicates
the grade of membership of ui in the fuzzy set A.
2.1. Fuzzy Time Series
Let X(t) (t = 0,1,2, ···) be the universe of discourse and
the fuzzy set defined on X(t) be fi(t) (t = 0,1,2, ···). Then
F(t) = fi(t) t = 0,1,2, ···, i = 1,2, ··· the collection of all
fuzzy sets defined on X(t) is called a fuzzy time series of
X(t) (t = 0,1,2, ···).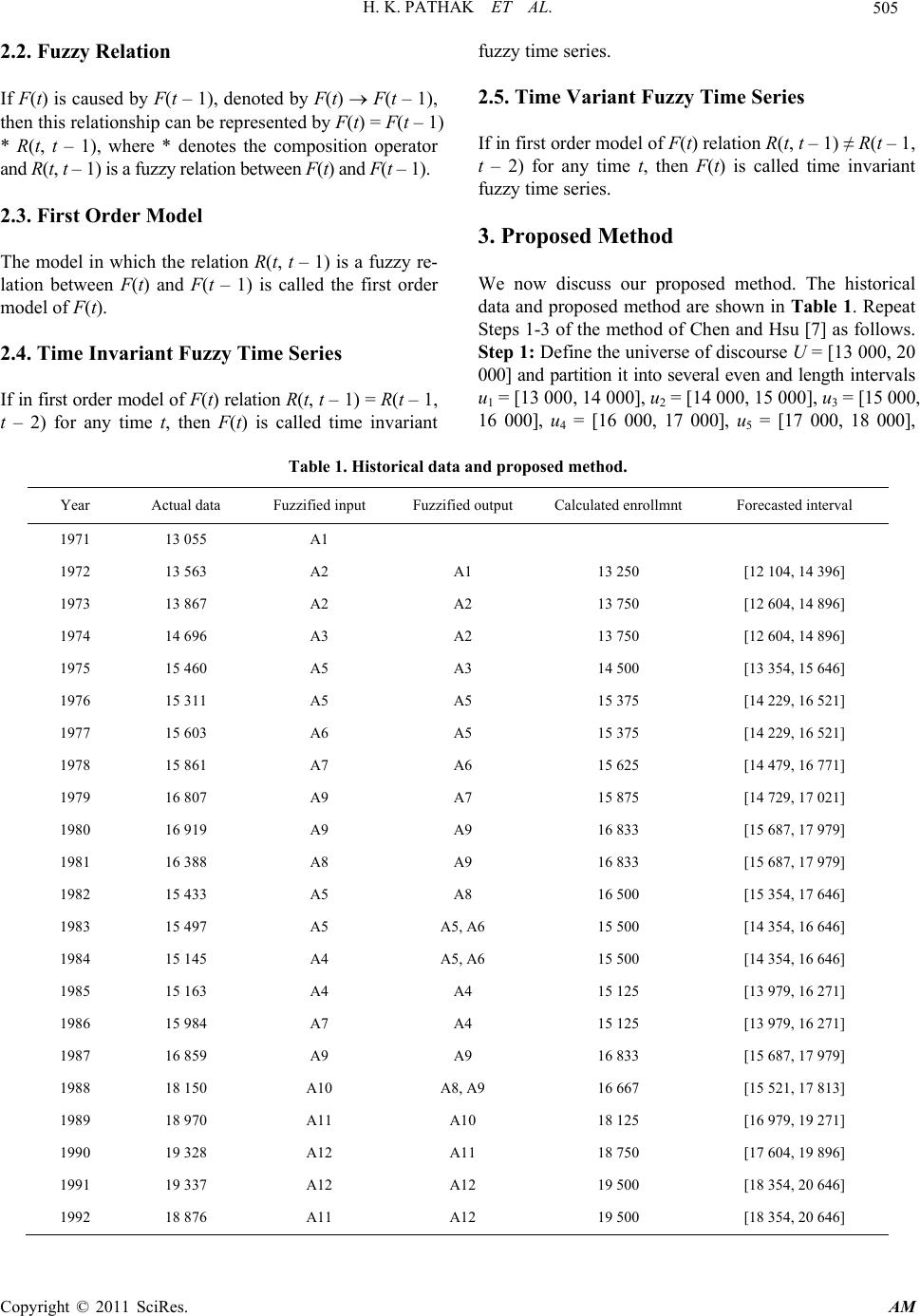

H. K. PATHAK ET AL. 505
2.2. Fuzzy Relation
If F(t) is caused by F(t – 1), denoted by F(t)  F(t – 1),
then this relationship can be represented by F(t) = F(t – 1)
* R(t, t – 1), where * denotes the composition operator
and R(t, t – 1) is a fuzzy relation between F(t) and F(t – 1).
2.3. First Order Model
The model in which the relation R(t, t – 1) is a fuzzy re-
lation between F(t) and F(t – 1) is called the first order
model of F(t).
2.4. Time Invariant Fuzzy Time Series
If in first order model of F(t) relation R(t, t – 1) = R(t – 1,
t – 2) for any time t, then F(t) is called time invariant
fuzzy time series.
2.5. Time Variant Fuzzy Time Series
If in first order model of F(t) relation R(t, t – 1) ≠ R(t – 1,
t – 2) for any time t, then F(t) is called time invariant
fuzzy time series.
3. Proposed Method
We now discuss our proposed method. The historical
data and proposed method are shown in Tabl e 1. Repeat
Steps 1-3 of the method of Chen and Hsu [7] as follows.
Step 1: Define the universe of discourse U = [13 000, 20
000] and partition it into several even and length intervals
u1 = [13 000, 14 000], u2 = [14 000, 15 000], u3 = [15 000,
16 000], u4 = [16 000, 17 000], u5 = [17 000, 18 000],
Table 1. Historical data and proposed method.
Year Actual data Fuzzified input Fuzzified output Calculated enrollmnt Forecasted interval
1971 13 055 A1
1972 13 563 A2 A1 13 250 [12 104, 14 396]
1973 13 867 A2 A2 13 750 [12 604, 14 896]
1974 14 696 A3 A2 13 750 [12 604, 14 896]
1975 15 460 A5 A3 14 500 [13 354, 15 646]
1976 15 311 A5 A5 15 375 [14 229, 16 521]
1977 15 603 A6 A5 15 375 [14 229, 16 521]
1978 15 861 A7 A6 15 625 [14 479, 16 771]
1979 16 807 A9 A7 15 875 [14 729, 17 021]
1980 16 919 A9 A9 16 833 [15 687, 17 979]
1981 16 388 A8 A9 16 833 [15 687, 17 979]
1982 15 433 A5 A8 16 500 [15 354, 17 646]
1983 15 497 A5 A5, A6 15 500 [14 354, 16 646]
1984 15 145 A4 A5, A6 15 500 [14 354, 16 646]
1985 15 163 A4 A4 15 125 [13 979, 16 271]
1986 15 984 A7 A4 15 125 [13 979, 16 271]
1987 16 859 A9 A9 16 833 [15 687, 17 979]
1988 18 150 A10 A8, A9 16 667 [15 521, 17 813]
1989 18 970 A11 A10 18 125 [16 979, 19 271]
1990 19 328 A12 A11 18 750 [17 604, 19 896]
1991 19 337 A12 A12 19 500 [18 354, 20 646]
1992 18 876 A11 A12 19 500 [18 354, 20 646]

H. K. PATHAK ET AL. 506
u6 = [18 000, 19 000], u7 = [19 000, 20 000].
Sort the intervals based on the number of historical en-
rollment data in each interval from the highest to lowest
and find the interval having largest number of data. Re-
divide this interval into four equal parts. Find the interval
having second largest number data and re-divide it in
three equal length sub-intervals find the interval having
third largest number of data and re-divide it in two equal
length sub-intervals. If there are no data in any interval
then discard this interval. In this case the new distribu-
tion is shown in Table 2.
Step 2: Re-divide the intervals and rename them as
follows: u1 = [13 000, 13 500], u2 = [13 500, 14 000], u3
= [14 000, 15 000], u4 = [15 000, 15250, u5 = [15 250,15
500], u6 = [15 500, 15 750], u7 = [15 750, 16 000], u8 =
[16 333, 16 667], u9 = [16 667, 17 000], u10 = [18000, 18
500], u11 = [18 500, 19 000], u12 = [19 000, 20 000].
Step 3: Define each fuzzy set based on the re-divided
intervals and fuzzify the data shown in Table 1, where
fuzzy set Ai denotes a linguistic value of the data re-
presented by a fuzzy set.
A1 = very4 few = 1/u1 + 0.5/u2
A2 = very3 few = 0.5/u1 + 1/u2 + 0.5/u3
A3 = very2 few = 0.5/u2 + 1/u3 + 0.5/u4
A4 = very few = 0.5/u3 + 1/u4+ 0.5/u5
A5 = few = 0.5/u4 + 1/u5+ 0.5/u6
A6 = moderate = 0.5/u5 + 1/u6 + 0.5/u7
A7 = many = 0.5/u6 + 1/u7 + 0.5/u8
A8 = very many = 0.5/u7 + 1/u8 + 0.5/u9
A9 = too many = 0.5/u8 + 1/u9 + 0.5/u10
A10 = too many2 = 0.5/u9 + 1/u10 + 0.5/u11
A11 = toomany3 =0.5/u10 + 1/u11 + 0.5/u12
A12 = too many4 = 0.5/u11 + 1/u12
For simplicity the membership values of fuzzy set Ai
are either 0, 0.5, 1. Notice that we have not displayed the
membership value 0.
Now we give the steps of our proposed method.
Step 4: Fuzzify the data on Table 1. The reason for
fuzzifying is to translate crisp values fuzzy sets to get a
fuzzy time series. Now establish fuzzy logical relation-
ships based on fuzzified data as “Aj Ak” means if the
fuzzified enrollments of year (n – 1) is Aj then the fuzzi-
fied enrollments of year n is Ak.
Step 5: By Table 3 it is clear that the fuzzy logical re-
lationship groups are as follows.
Step 6: The fuzzified output is obtained by fuzzified
input of previous years if 1) fuzzified input of nth year is
Ai then fuzzified output of (n + 1)th year is also Ai (as in
years 1971,1972, ···). 2) If the fuzzified input of nth year
Table 2. Frequency of data.
Intervals No. of data
[13 000,14 000] 3
[14 000,15 000] 1
[15 000,16 000] 9
[16 000,17 000] 4
[17 000,18 000] 0
[18 000,19 000] 3
[19 000,20 000] 2
Table 3. Logical groups.
Serial No. Fuzzy logical relationship groups
1 A1→A2
2 A2→A2, A2→A3
3 A3→A5
4 A4→A4, A4→A7
5 A5→A4, A5→A5, A5→A6
6 A6→A7
7 A7→A9
8 A8→A5
9 A9→A9, A9→A8, A9→A10
10 A10→A11
11 A11→A12
12 A12→A11, A12→A12
is Ai and in previous years we have got more relations as
AiAj, AiAk, ··· then the fuzzified output will be (Aj,
Ak, ···) (as in years 1983, 1984, 1988).
Step 6: The fuzzified output is obtained by fuzzified
input of previous years if 1)fuzzified input of nth year is
Ai then fuzzified output of (n+1)th year is also Ai (as in
years 1971,1972, ···). 2)If the fuzzified input of nth year
is Ai and in previous years we have got more relations as
AiAj, AiAk, ··· then the fuzzified output will be (Aj,
Ak, ···) (as in years 1983, 1984, 1988).
Step 7: Output values are the mid-values of the inter-
vals in which the fuzzified output occurs.
Step 8: Next we calculate the mean, standard devia-
tion(  ) of output and interval by formula [output –2/3  ,
output +2/3  ].
Step 9: Now we can plot graphs of intervals lower
limit of forecasted interval(LL of fore), upper limit of
forecasted interval(UL of fore) and actual data to see that

H. K. PATHAK ET AL. 507
Figure 1. Graph of actual data and interval.
most of the actual data comes in the range of interval.
4. Conclusions
The development of technology and programming of lan-
guages with expert systems has considerably reduced the
burden of decision makers. With regard to classical me-
thods, fuzzy set theory give solutions in a quicker easier
and most sensitive way.
In this proposed method there is no need of relation-
matrix, so it reduces its calculation. It also reduces the
next calculation for output by this relation-matrix.
The most remarkable thing in this method is that we
give the most plausible range of forecasting, which is in
the form of interval rather than a single value. It is also
remarkable that in normal curve this interval is in the
range ±3  but in our method it is in the range of ±2/3  .
5. References
[1] L. A. Zadeh, “Fuzzy Sets,” Information Control, Vol. 8,
No. 3, 1965, pp. 338-353.
[2] Q. Song and B. S. Chissom, “Forecasting Enrollment
with Fuzzy Time Series-Part I,” Fuzzy Sets and Systems,
Vol. 54, No. 1, 1993, pp. 1-9.
doi:10.1016/0165-0114(93)90355-L
[3] S. M. Chen, “Forecasting Enrollments Based on Fuzzy
Time Series,” Fuzzy Sets and Systems, Vol. 81, No. 3,
1996, pp. 311-319. doi:10.1016/0165-0114(95)00220-0
[4] S. M. Chen, “Forecasting Enrollments Based on High
Order Fuzzy Time Series,” Cybernetics and Systems: An
International Journal, Vol. l33, No. 1, 2002, pp. 1-16.
[5] I. H. Kuo, S. J. Horng, T. W. Kao, C. L. Lee, T. L. Lin
and Y. Pan, “An Improved Method for Forecasting En-
rollment Based on Fuzzy Time Series and Particle Swarm
Optimization,” Expert Systems with Applications, Vol. 36,
No. 3, 2009, pp. 311-319.
[6] S. M. Chen and C. C. Hsu, “A New Method to Forecast
Enrollment Using Fuzzy Time Series,” International
Journal of Applied Science and Engineering, Vol. 3, No.
2, 2004, pp. 234-244.
[7] M. H. Lee, R. Efendi and Z. Ismail, “Modified Weighted
for Enrollment Forecasting Based of Fuzzy Time Series,”
Matematika, Vol. 25, No. 1, 2009, pp. 67-78.
[8] C. H. Cheng, T. L. Chen and C. H. Chiang, “Trend-
Weighted Fuzzy Time Series Model for TAIEX Fore-
casting,” Proceedings of the 13th International Con-
ference on Neural Information Processing, Part-III, Lec-
ture Notes in Computer Science, Hong Kong, Vol. 4234,
3-6 October 2006, pp. 469-477.
[9] Q. Song and B. S. Chissom, “Fuzzy Time Series and Its
Models,” Fuzzy Sets and Systems, Vol. 54, No. 3, 1993,
pp. 267-277.doi:10.1016/0165-0114(93)90372-O
[10] S. M. Chen and J. R. Hwang, “Temperature Prediction
Using Fuzzy Time Series,” IEEE Transactions on Sys-
tems, Man and Cybernatics-Part B: Cybrnetics, Vol. 30,
No. 2, 2000, pp. 263-275.
[11] K. Huarng, “Effective Lengths of Intervals to Improve
Forecasting in Fuzzy Time Series,” Fuzzy Sets and Sys-
tems, Vol. 123, No. 3, 2001, pp. 387-394.
doi:10.1016/S0165-0114(00)00057-9