Applied Mathematics, 2011, 2, 482-486
doi:10.4236/am.2011.24062 Published Online April 2011 (http://www.SciRP.org/journal/am)
Improving Middle Square Method RNG Using
Chaotic Map
Hamed Rahimov1, Majid Babaie1, Hassan Hassanabadi2
1Department of Computer Engineering, Shah rood University of Technology, Shahrood, Iran
2Physics Department, Shahrood University of Technology, Shahrood, Iran
Received January 23, 2011; revised March 10, 2011; accepted March 12, 2011
Abstract
One of the classic approaches in PRNGs is the middle square method in which with a simple mathematical
model generating pseudorandom numbers in high speed and minimum correlation between output numbers.
Despite these unique characteristics, the method contains weaknesses that a broader application of this algo-
rithm will face. In this paper is studied middle square method and then a logistic chaotic map is introduced
with its specific features and its improved weaknesses via using these characteristics. Finally the NIST tests
suite s are presented, in order to detect the specific characteristics expected from truly random sequences.
Keywords: Middle Square Method (MSM), Random Number Generator, Logistic Map, NIST Tests Suite
1. Introduction
Nowadays, the world is connected together by networks.
The main problem in the pr esent networks is the security
protocols. This is due to growing interest in the use of
digital chaotic systems offering the possibility to support
the security of cryptog r aphic alg orithms fo r d ata encrypt-
tion, like thos e presented in the networking security pro-
tocols [1,2].
The best ways to increase security in modern commu-
nication methods is using the cryptography algorithms.
Most of these new algorithms use chaotic maps as pseu-
dorandom number generators (PRNGs) [3,4] to obtain a
binary stream including symmetric encryption algorithm
[5]. PRNGs are very important in several fields like sta-
tistical studies, simulations, cryptography and solving spe-
cific mathematical problems [6-8]. They may be based
on unpredictable physical resources such as physical
phenomenon or on mathematical algorithms like “Halton
algorithm” [6]. However, truly random numbers (i.e.
physical phenomenon) are not gained by a specific algo-
rithm [8,9] as they are used in the encryption systems [9].
So we should make use of any real implementation some
simple functions for RNG instead of TRNGs [10,11]. A
PRNG should be checked by certain statistical tests
which it must pass all statistical tests that are restricted to
polynomial time in the size of the seed and frequency of
“0”s and “1”s in the specific sequences [12].
In this paper we have presented a chaotic RNG based
on middle square method to prepare a mathematical mo-
del for generating random numbers. Our model is then
tested by the best known statistical method, i.e. th e NIST
test suite.
One of the fundamental subjects in generating random
numbers is the Uniform distribution [11] in the interval
[0, 1] (e.g. generating real numbers like: 0.0293 or
0.8934). Generating in this interval enables us to inves-
tigate our practical purposes for introducing an efficient
encryption method. The reason is that the samples from
the other distributions are derived using the Uniform
Distribution [11]. So it is important that our proposed
generator has the uniform distrib uti on .
This part introduces a brief history of some PRNG al-
gorithms, The “Van der Corput” [6], “Halton” [6] and
“Sobol” [6] sequences are three basic mathematical algo-
rithms for PRNGs. These are based on low discrepancy
method with which unique properties are used in the ef-
fective areas such as army industry. Nevertheless, they
have some disadvantages in high dimensions, an exam-
ple being the generated numbers in 20 × 21 dimensions
for Halton sequence due to multidimensional clustering
[6] (as shown in Figure 1).
In order to clarify the purpose of the proposed algori-
thm, one can see some of methods i n References [13-27] .
With this background, it is understood that in the re-
cent years the PRNG’s algorithm developed by some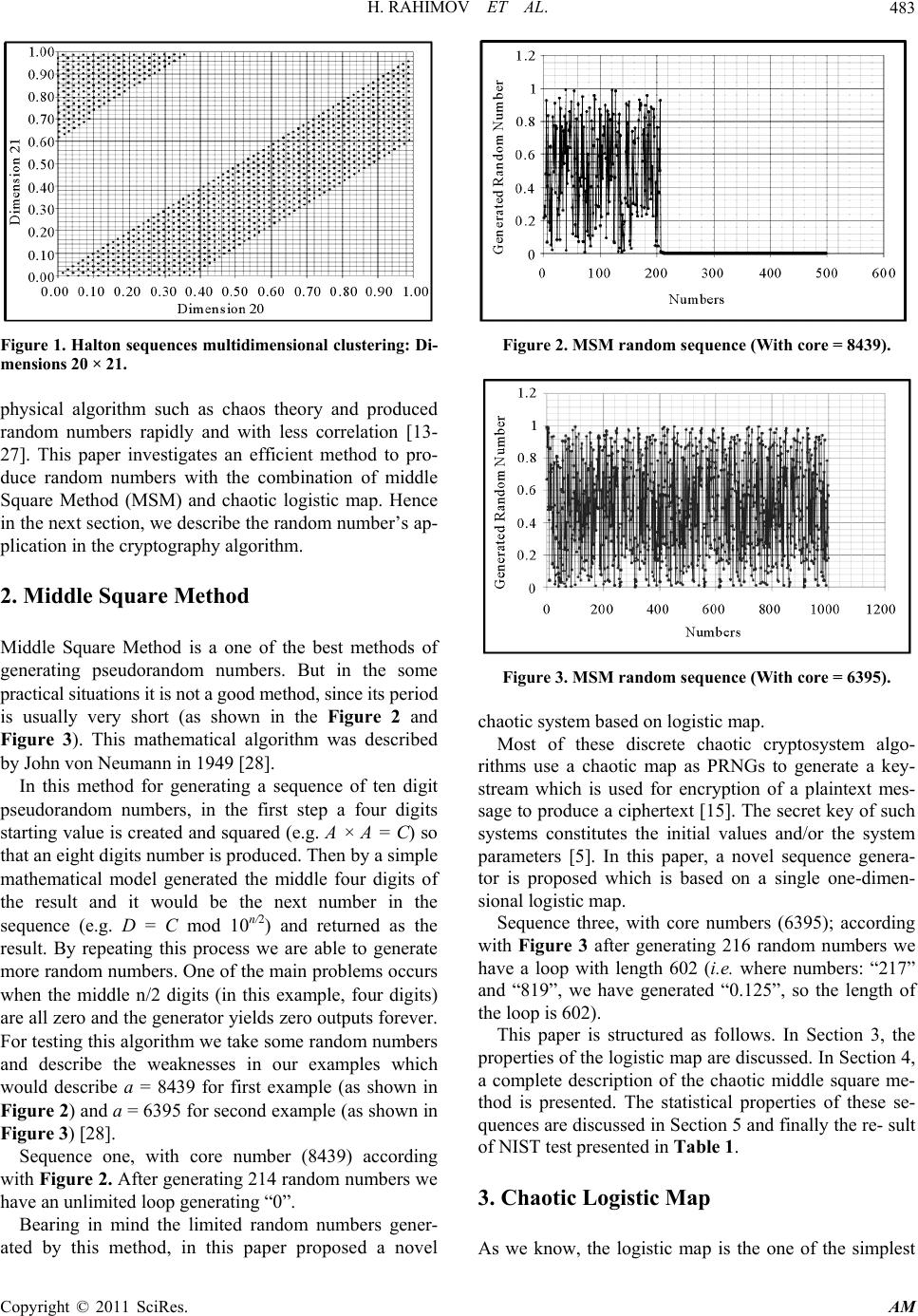

H. RAHIMOV ET AL. 483
Figure 1. Halton sequences multidimensional clustering: Di-
mensions 20 × 21.
physical algorithm such as chaos theory and produced
random numbers rapidly and with less correlation [13-
27]. This paper investigates an efficient method to pro-
duce random numbers with the combination of middle
Square Method (MSM) and chaotic logistic map. Hence
in the next section, we describe the random number’s ap-
plication in the cryptograph y algorith m.
2. Middle Square Method
Middle Square Method is a one of the best methods of
generating pseudorandom numbers. But in the some
practical situations it is not a good method, since its period
is usually very short (as shown in the Figure 2 and
Figure 3). This mathematical algorithm was described
by John von Neumann in 1949 [28].
In this method for generating a sequence of ten digit
pseudorandom numbers, in the first step a four digits
starting value is created and squared (e.g. A × A = C) so
that an eight digits number is produced. Then by a simple
mathematical model generated the middle four digits of
the result and it would be the next number in the
sequence (e.g. D = C mod 10n/2) and returned as the
result. By repeating this process we are able to generate
more random numbers. One of the main problems occurs
when the middle n/2 digits (in this example, four digits)
are all zero and the generator yields zero outputs forever.
For testing this algorithm we take some random numbers
and describe the weaknesses in our examples which
would describe a = 8439 for first example (as shown in
Figure 2) and a = 6395 for second example (as show n in
Figure 3) [28].
Sequence one, with core number (8439) according
with Figure 2. After generating 214 random numbers we
have an unlimited loop generating “0”.
Bearing in mind the limited random numbers gener-
ated by this method, in this paper proposed a novel
Figure 2. MSM random sequence (With core = 8439).
Figure 3. MSM random sequence (With core = 6395).
chaotic system based on logistic map.
Most of these discrete chaotic cryptosystem algo-
rithms use a chaotic map as PRNGs to generate a key-
stream which is used for encryption of a plaintext mes-
sage to produce a ciphertext [15]. The secret key of such
systems constitutes the initial values and/or the system
parameters [5]. In this paper, a novel sequence genera-
tor is proposed which is based on a single one-dimen-
sional logistic map.
Sequence three, with core numbers (6395); according
with Figure 3 after generating 216 random numbers we
have a loop with length 602 (i.e. where numbers: “217”
and “819”, we have generated “0.125”, so the length of
the loop is 602).
This paper is structured as follows. In Section 3, the
properties of the logistic map are discussed. In Section 4,
a complete description of the chaotic middle square me-
thod is presented. The statistical properties of these se-
quences are discussed in Section 5 and finally the re- sult
of NIST test presented in Table 1.
3. Chaotic Logistic Map
As we know, the logistic map is the one of the simplest

H. RAHIMOV ET AL. 484
and most studied nonlinear that was introduced as a de-
mographic model. The logistic map is given by that is
shown in Equation (1):
 
11 nnn n
f
xx rxx

 (1)
Where xn is the state variable, which generates values
in the interval [0, 1] and r is called system parameter
which can have any value between one and four [10,2 9].
There is a non-trivial fixed point where 3.4 4r


which is seen in Figure 4. Finally for 4r, we observe
that chaos values are generated in the complete range of
[0, 1]. In this paper, the logistic map has application of
Table 1. Result of NIST tests suite for proposed RNG.
Test P-value Pass rate
Frequency 0.804645 0.9890
Block-Frequency 0.322901 0.9900
CuSums-forward 0.265567 0.9900
CuSums-backward 0.090388 0.9895
Rans 0.569766 0.9915
Long run 0.066673 0.9940
Rank 0.248649 0.9915
FFT 0.000159 0.9995
Overlapping templates 0.906745 0.9905
Universal 0.971354 0.9885
Approximate entropy 0.558502 0.9925
Serial 1 0.357000 0.9875
Serial 2 0.864494 0.9905
Liner complexity 0.671820 0.9920
Figure 4. Bifurcation plot of the Logistic map in


0,1
n
x


3.4,4r.
the form:
4. Proposed Chaotic PRNG
Middle square method has some big problems [28] that
were mentioned in Section 3 with the notice of these
problems in MSM and consider to unique properties of
chaotic logistic map in this section presented a chaotic
solution for solving these problems.
When efficient values are chosen for numbers in the
core that have no loop with the specific length, next we
can correct the unlimited loop (when PRNG joust “0”
generated in sequence) by exchanging one of the core’s
numbers [ 28].


2
2
1
1
1
%10
10 %10
10
if(0)then {
1
}
n
nn
t
n
t
t
nn n
n
nn
CAA DC
ECD ResultE
Num Result
Num
xxrx
Bx
xx



 
 





(2)
Assume the logistic chaotic map with r = 4 in x0 = 0.6
Generates a random number and replaces it with a num-
ber in A’s place and continues generating random num-
bers without any unlimited loop and the loop with a par-
ticular length. These problems can be solved by imple-
mentation of chaotic iteration that is generated in paral-
lel.
Middle square method algorithm described in Equa-
tion (2) al so seen belo w, having the n umber (i.e. A).
5. NIST Statistical Tests Suite
The NIST tests suite is a statistical package involving 15
tests and is based on hypothesis testing. Also The NIST
tests suite focus on a variety of different types of
non-randomness. In the present case, the tests consist
determining whether or not a specific sequence of zeroes
and ones is random [8]. The theoretical background of its
distribution is based on null hypothesis which is deter-
mined by mathematical methods and corresponding
probability value (P-valu e).
The P-value is the probability that a perfect RNG for
each test would produce a sequence less random than the
sequence that was tested, given the kind of non-random-
ness assessed by the test. If the P-value for a test is de-
termined to be equal zero, that means the sequence ap-

H. RAHIMOV ET AL. 485
pears to be exactly non-random and a P-value to be 1,
then the sequence has perfect randomness [8].
6. Conclusions
In this paper we have proposed a pseudorandom number
generator (PRNG) based on the combination of chaotic
logistic map and Middle Square Method, the chaotic
system iterated independen tly starting from initial condi-
tions could help to generate appropriate values; we have
also tested the generated sequences using the NIST tests
to detect the unique characteristics expected from truly
random bit sequences. The results of statistical testing
are reliable so has been used as a part of encryption sys-
tem to generate secret key and have an efficient algo-
rithm. Finally the result of their statistical tes ts presented
in the Table 1.
7. References
[1] Y. Hu, X. Liao, K. W. Wong and Q. Zhou, “A True
Random Number Generator Based on Mouse Movement
and Chaotic Cryptography,” Chaos, Solitons and Fractals,
Vol. 40, No. 15, 2009, pp. 2286-2293.
doi:10.1016/j.chaos.2007.10.022
[2] P. L. Ecuyer and J. Granger-Piché, “Combined Gene-
rators with Components from Different Families,” Mathe-
matics and Computers in Simulation, Vol. 62, No. 3,
2003, pp. 395-404. doi:10.1016/S0378-4754(02)00234-3
[3] M. Orlov, “Optimized Random Number Generation in an
Interval,” Information Processing Letters, Vol. 109, No.
13, 2009, pp. 722-725. doi:10.1016/j.ipl.2009.03.008
[4] Q. Zhou, X. Liao, K. W. Wong, Y. Hua and D. Xiao,
“True Random Number Generator Based on Mouse
Movement and Chaotic Hash Function,” Information
Sciences, Vol. 179, No. 19, 2009, pp. 3442-3450.
doi:10.1016/j.ins.2009.06.005
[5] K. Nakano, K. Kawakami and K. Shigemoto, “RSA En-
cryption and Decryption Using the Redundant Number
System on the FPGA,” IEEE International Symposium on
Parallel & Distributed Processing, Rome, 23-29 May
2009, pp. 1-8.
[6] I. Krykova, “Evaluating of Path-Dependent Securities
with Low Discrepancy Methods,” Master of Science
Thesis, Worce-Ster Polytechnic Institute, 2003.
[7] T. Stojanovski and L. C. Kocarev, “Chaos-Based Random
Number Generators,” IEEE Transactions on Circuits and
Systems, Vol. 48, No. 3, 2001, pp. 281-288.
[8] K. H. Tsoi, K. H. Leung and P. H. W. Leong, “High Per-
formance Physical Random Number Generator,” IET
Proceeding Computers & Digital Techniques, Vol. 1, No.
4, 2007, pp. 349-352. doi:10.1049/iet-cdt:20050173
[9] M. I. Youssef, M. Zahara, A. E. Emam and M. A. El-
ghany, “Image Encryption Using Pseudo Random Num-
ber and Chaotic Sequence Generators,” Radio Science
Conference, New Cairo, 17-19 March 2009, pp. 1-15.
[10] C. Pellicer-Lostao and R. Lopez-Ruiz, “Pseudo-Random
Bit Generation Based on 2D Chaotic Maps of Logistic
Type and Its Applications in Chaotic Cryptography,”
Journal of Computational Science and Its Applications,
Vol. 5073, 2008, pp. 784-796.
[11] X.-J. Tong, M.-G. Cui and W. Jiang, “The Production
Algorithm of Pseudo-Random Number Generator Based
on Compound Non-Linear Chaos System,” Proceedings
of the International Conference on Intelligent Informa-
tion Hiding and Multimedia Signal Processing, California,
18-20 December 2006, pp. 685-688.
doi:10.1109/IIH-MSP.2006.265094
[12] Q. Wang, C. Guyeux and J. M. Bahi, “A Novel Pseudo-
Random Number Generator Based on Discrete Chaotic
Iterations,” First International Conference on Evolving
Internet, Cannes/La Bocca, 23-29 August 2009, pp. 71-76.
doi:10.1109/INTERNET.2009.18
[13] H. P. Lü, S. H. Wang and G. Hu, “Pseudo-Random
Number Generator Based on Coupled Map Lattices,” In-
ternational Journal of Modern Physics B, Vol. 18, No.
17-19, 2004, pp. 2409-2414.
[14] X. M. Li, H. B. Shen and X. L. Yan, “Characteristic
Analysis of a Chaotic Random Number Generator Using
Piece-Wise-Linear Map,” Journal of Electronics and In-
formation Technology, Vol. 27, No. 6, 2005, pp. 874-878.
[15] J. Liu, “Design of a Chaotic Random Sequence and Its
Application,” Computer Engineering, Vol. 31, No. 18,
2005, pp. 150-152.
[16] Y. Wang, H. Shen and X. Yan, “Design of a Chaotic
Random Number Generator,” Chinese Journal of Semi-
conductors, Vol. 26, No. 12, 2005, pp. 2433-2439.
[17] L. Wang, F. P. Wang and Z. J. Wang, “Novel Chaos-
Based Pseudo-Random Number Generator,” Acta Physica
Sinica, Vol. 55, No. 8, 2006, pp. 3964-3968.
[18] M. Andrecut, “Logistic Map as a Random Number Ge-
nerator,” International Journal of Modern Physics B, Vol.
12, No. 9, 1998, pp. 921-930.
doi:10.1142/S021797929800051X
[19] J. A. Gonzalez and R. Pino, “Random Number Generator
Based on Unpredictable Chaotic Functions,” Computer
Physics Communications, Vol. 120, No. 2-3, 1999, pp.
109-114. doi:10.1016/S0010-4655(99)00233-7
[20] L. Kocarev and G. Jakimoski, “Pseudo-Random Bits
Generated by Chaotic Maps,” IEEE Transactions on
Circuits and Systems, Vol. 50, No. 1, 2003, pp. 123-126.
doi:10.1109/TCSI.2002.804550
[21] S. M. Fu, Z. Y. Chen and Y. A. Zhou, “Chaos Based
Random Number Generators,” Computer Research and
Development, Vol. 41, No. 4, 2004, pp. 749-754.
[22] S. Ergun and S. Ozoguz, “Truly Random Number Gen-
erators Based on a Non-autonomous Chaotic Oscillator,”
AEU-International Journal Electronics & Communica-
tions, Vol. 61, No. 4, 2007, pp. 235-242.
doi:10.1016/j.aeue.2006.05.006
[23] V. V. Kolesov, R. V. Belyaev and G. M. Voronov, “A
Digital Random-Number Generator Based on the Chaotic

H. RAHIMOV ET AL. 486
Signal Algorithm,” Journal of Communications Techno-
logy and Electronics, Vol. 46, No. 11, 2001, pp. 1258-
1263.
[24] T. Stojanovski and L. Kocarev, “Chaos-Based Random
Number Generators,” IEEE Transactions on Circuits and
Systems, Vol. 48, No. 3, 2001, pp. 281-288.
doi:10.1109/81.915385
[25] T. Stojanovski, J. Pihl and L. Kocarev, “Chaos Based
Random Number Generators,” IEEE Transactions on
Circuits and Systems, Vol. 48, No. 3, 2001, pp. 382-385.
doi:10.1109/81.915396
[26] S. Oishi and H. Inoue, “Pseudo-Random Number Gen-
erators and Chaos,” Transactions of the Institute of Elec-
tronics and Communication Engineers of Japan E, Vol.
65, No. 9, 1982, pp. 534-541.
[27] T. Lin and L. O. Chua, “New Class of Pseudo-Random
Number Generator Based on Chaos in Digital Filters,”
International Journal of Circuit Theory and Applications,
Vol. 21, No. 5, 1993, pp. 473-480.
doi:10.1002/cta.4490210506
[28] W. Gao, G. Y. Zhang, Y. M. Li and W. H. Chen, “Re-
search and Realization of Random Encryption Algo-
rithm,” International Conference on Internet Computing
in Science and Engineering, Washington, 24 June 2008,
pp. 23-26.
[29] J. Szczepa´nski and Z. Kotulski, “Pseudo-Random Number
Generators Based on Chaotic Dynamical Systems,”
Journal of Open Systems & Information Dynamics, Vol.
8, No. 2, 2001, pp. 137-146.