Creat ive Educati on
2011. Vol. 2, No. 1, 27 -40
Copyright © 2011 SciRes. DOI:10.4236/ce.2011.21005
How to Introduce the Cyclic G roup and Its Properties
Representation with Matlab? Thanks to Magic Usi ng the Perfect
Faro Shuffle
Pierre Schott
Art et Recherche NUMér ique (ARNUM), Ecole Supérieure d’Informati que, d’Electronique et d’Automatis me ( ESIEA),
Paris, France
Received July 21st, 2010; revised February 21st, 2011; accepted February 23rd, 2011.
Why use Magic for teaching arithmetic and geometric suit, additive groups, and algorithmic notions through
Matlab? Magicians know that, once the surprise has worn off, the audience will seek to understand how the trick
work s. The aim of ev ery teach er is to int erest their students, and a magic trick will lead them to ask how? And
why? And how can I create one myself? In this article we consider a project I presented in 2009. I summarize
the project scope, the students' theoretical studies, their approach to this problem and th eir comput er reali zati o ns.
I conclude using the mathematical complement as well as weak and strong points of this approach. What ever t h e
student's professional ambitions, they will be able to see the impact that originality and creativity have when
combined with an interest in one's work. The stud ent s kn ow how to “per for m” a magi c tri ck for thei r fa mi ly and
friends, a trick that they will be able to explain and so enjoy a certain amount of success. Sharing a mathematical
/ inf ormati cs dem onstra tion is not easy and that they do so means that they will have worked on understood and
are capable of explaining this knowledge. Isn't this the aim of all teaching?
Keywords: Higher Education, E ng ineer, Educa tional Metho d
Introduction
I am fascinat ed by Magic (or rather conjuring!) and for many
years I have used this way of teaching, both in my physics
classes and as higher education teacher trainer.
I present all the notions in this paper, a brief history of Magic
and finally I present the researchers who have used this Art to
teach an d/or to research .
The aim of the magician is to hide the principles he uses (us-
ing Maths, Physics, Psychology, sleight of hand, etc...) by dis-
guising the trick so that the audience has no way of discovering
how it is done thus allowing the Magic to remain.
The Teacher can do exactly the opposite: unraveling a magic
trick to highlight the principles used!
A Brief History of Magic
From the beginning of time people have feared what they
don't understand and sought logical explanations for inexpli-
cable phenomena. To begin with they considered them to be the
work of magic, then the work of the gods, then the work of God
himself. The church discouraged the spread of the conjurer's art
as it preferred not to have rational explanations for what was
considered supernatural.
The first magi c tricks were per formed in th e Middle Ages b y
clowns and/or con-men who would entertain passers-by by
getting them to bet on the position of a ball hidden in one of
three up-turned goblets, the bet being usually lost. This trick is
known nowadays by the name ‘cups and balls’ (Mayol, 2000).
The first book considered to be about modern Magic (or should
we say “conjuring”) was written and printed in the 16th Cen-
tury. It was about Magic with ropes (Ammar, 1998). It wasn't
until the end of the 19th Century that the word Magic took on
its present-day meaning when the famous magician Houdini,
father of modern Magic, made i t the art i t is today.
Since then a good number of principles have been invented
and improved on by magicians and gamblers (Erdnase, 1902),
especially for card t ricks with bets . Since the 1980s the secrets
that were once passed on from master to apprentice are now
universally available through the use of video cassettes and
modern communicatio n techno log y, and Magic h as b ecome Big
Business.
Card Magic as the Vector of Research and Teachi ng
From 1886 till 1896, Poincaré occupied the chair of proba-
bility Calculus” in the Paris university ‘La Sorbonne’. He wrote
a work named 'probability calculus' (Poincare, 1912; Sheynin,
1991) which was printed for the first time in 1896. In the
second edition, he brings very fundamental new reflections on
the groups and the hypercomplex systems and on the ergodic
theory. He is brought to these innovations by the study of the
card shuffling and liquids mixing. The problems of card shuf-
fling and liquid diffusion studied by Poincaré are applica-
tion cases of the ergodic theory which is in the center of the
probability leveling phenomenon: if the deck was shuffled for a
long time, all the possible permutations have the same proba-
bility.
Both principles of Gilbreath (Gilbreath, 1958; Gilbreath,
1966; Gilbreath, 1989) are fascinating principles, allowing to
do extr aordinary card tr icks!
Some Mathematicians – such as M.Gardner (Magid, 2005;

P. SCHOTT
28
Gardner, 1958; Gardner, 2005), P.Diaconis (Diaconis, 1998;
Diaconis, 2003; Assaf, 2009) or C.Mulcahy (Mulcahy, 2003;
Mulcahy, 2004; Mulcahy, 2007)-, some computer specialists -
as G. Huet (Huet, 1991) one of creator of COQ l anguage which
allows to make automatic mathematical proof - studied this
principle (and they are not the only ones !).
We shall not present this principle here but it is necessary to
know that it is based on a commonly used card shuffles on both
sides of the Atlantic Ocean: the American sh uffle.
Summary
The subject was given for the 4th semester students in higher
education school (named in France ‘Grandes écoles d’ingé-
nieurs’). The students had to solve and illustrate a fifty-year -old
prob lem of Elmsley (Elmsley, 1957):
How to bring the original top card to position p by perfect
shuffles.
A theoretical solution is written in (Diaconis, 2006) by
P. Diaconis and R. Graham.
By giving this project, I wo uld like that the students:
 under stand some mathematical notions as the cyclic group,
 learn a new useful programming language as M atlab™,
 discover a fas cinating ar ea and impr ove their creativity.
A deeper description of them is given in the third section.
Having worked 4 months (part-time, that is approximate-
ly 75 hours per student or 300 hours for the whole project), the
students have written Matlab™ functions and finally answered
the su bj ect requir ement s :
 find the number of Faro IN (or OUT) shuffles so that a
card deck find s its initial order,
 find the Faro IN and\or OUT shuffle suit so that a card in
position 'k' in the deck arrives in position 'j'.
Thus I explain the mathematical notions used as well as the
associated equations which are resolved by the students Matlab
functions!
The Multi Disciplinary Project (M.D.P) of
ESIEA in the French Higher Education
We shall see successively the organization of higher educa-
tion in France, the scope and the objectives of the M.D.P
proj ect .
Higher Education in FRANCE
In Fran ce, the secondar y education is sanctioned by the high
school diploma. Ideally the pupils obtain it at the age of 18.
Then, they have a plethora of possibilities following 3 orienta-
tions:
 Some undertake short studies called “professional” in an
I.U.T at the University or in high school with the aim of obtain-
ing a BT S . B oth pr og r ams l e a d to a 2-y ear technical degree,
 Others undertake longer studies. In this case, if they have
obtained their high school diploma they can:
1) Enrol in university,
2) Or enter preparatory courses (classes for entrance into
‘Grandes Ecoles’) for 2 years, which will lead them, via na-
tional entrance examinations, to enter a ‘Grande Ecole’ in
busines s or eng ineering.
The studies take 3 years and once they have their degree in
hand, the students find employment easily.
The school in which I work, named E.S.I.E.A, is an engi-
neering school.
The Scopes of the M.D. P. Project
The M.D.P. is a 4th semester project, taking place between
February and May (75 homework hours are planned for each
student) and students are organized into groups of 4. Their
work is closely followed by a professor. Because the project is
to be developed during the students' free time, they also take
other courses during this semester.
The subjects can be of th ree kinds:
 ‘Professional’ subjects requested directly by the partner
companies of the school,
 ‘Research’ subjects given by research centers,
 ‘Educational’ subjects proposed by the school’s profes-
sors.
The subjects are collected by the school administration,
communicated to the students and finally 3 subjects are chosen
by each 4-student group. Through an internal process, the stu-
dent s are assigned a subject (most frequently their first request).
The M.D.P Educational Objectives
The main objective is to apply to a project the knowledge
acquired during coursework, and if need be, to enrich this
knowledge.
A second objective is to raise students' awareness that a
project is not reduced to a single academic subject but is in fact
a conglomerate of knowledge taught in various courses.
Finally, let us note the importance of project management
among these objectives.
An extract of the program is given in appendix A.
The Assigned M.D.P
The contents of a project I assigned to a group of students,
the motivat ions an d my expectatio ns are descri bed below.
Diaconis has entirely solved this subject in (Diaconis,
1983) … but I think it’s unreadable by the students … and me !
The Proposed Subject in 2009-2010
The magic arts co nsist of several sp ecialties: cl ose - up, cups
and balls, coin tricks, transformists, card tricks, and so on ...
The most mediat ized special ty, enjoyed by all kinds of au dience,
is: the Grand Illusion. But the easiest is self-working card
tricks.
In fact, man y magic t ricks are b as ed on mathe matical n o tio n s.
The art of the magician consists in the fact that the spectators
do not realize it!
The Faro shuffle (which is a particul ar case of the American
shuffle) admits many properties; in particular the one which
consists in making 8 Faro shuffles from a new 52 cards deck
and the deck returns to its initial order!
We propose you:
 To demonstrate this property mathematically and by com-
puter.
 To generalize this principle: to define in advance (Thanks
to mathematical equations) or after (thanks to the computer)

P. SCHOTT
29
how much IN (or OUT) Faro shuffles are necessary so that an
N = 2p card deck returns to its in itial order.
 To determine how many IN and/or OUT Faro shuffle suit
are necessary so that a card in ‘k’ position in the N = 2p card
deck arrives in ‘j’ position.
 To use the previous results to create a magic trick.
 To create a Human-Machine Interface (HMI) which allows
displaying step by step -with cards- the mathematical demon-
strations.
If you want to know the secrets of the greatest magicians,
come!
If you want to learn and apply math ematical and in formatics
theory in a fun way, come!
ATTENTION:
My Expectati o ns
I thus expect from my students:
1) That they perform research on different magic shuffles
(American, Faro, Z arrow …) and their as s ociated properties.
2) That they perform research in mathematics:
a) properties of divisibility and associated equations,
b) cyclic grou ps,
3) That they perform research in informatics:
a) programming with Matlab,
b) representing with 2D-3D Matlab’s figures,
4) That they model well the ‘magic’ problem.
5) That the realization of a card trick based on the Faro proper-
ties is interesting from both angles: magic and mathematics.
once the secret is known, the illusion loses all
its magic … but not its spectacular beauty!
My Motivations to Propose such a Subje c t
I chose the topic o f magic, a su bject which fascin ates me, to
be virtually certain that the topic would be completely new for
the students. So they are in an unfamiliar situation. They will
thu s have to implement al l the necessar y means to co mplete th e
project successfully.
I also try to arouse the students’ curiosity by proposing a
subject that is more playful than usual.
Following these objectives, I propose a project in informatics
and math analysis (in cyclic groups), while the school in which
I work hardly teaches this subject. I go out very slightly of the
project scope because once in a company, the students will
have to study - or to solve - proble ms that they have never seen
durin g t heir academic car eer.
Consequently, the students have to look for, find and unders-
tand a ‘new’ theory of math ematics and new software: Matlab.
After all I gi ve them work that is mo re difficult than that ex-
pected by the school. Indeed there is little chance that I will
have a student, who is the son or daughter of a magician or who
is a magician himself.
Finally, I try to change the traditional way of teaching: a
downward method (the professor teaches the student) usually
used in France, become an ascending method here (it is the
student who will have to explain to the professor).
The ascending method has the merit of showing whether the
problem posed is well understood. As Boileau wrote (Boileau,
1740) “what is well conceived expresses itself clearly, and the
words to say it come easily” (“ce qui se conçoit bien s'énonce
clairement, et les mots p our le dire arri vent aisément”).
Finally its presentation during the viva must be well orga-
nized and as magic as possible.
The Group Composition
Table 1 speci fies the cap acities of a stud ent having foll owed
our engineering school program, at the beginning of the M.D.
Project:
• The group consisted of 3 students. Their initial level is
‘above average’ according to the standards of evaluation used
in Fr ance.
• The first one had been interested, thanks to extra school
activities, to the website design using databases. This student is
rather classified at the top of class (Having A- to B in the An-
glo-S axo n system).
• The second one is a hard-working student. Thanks to it,
he manages to validate all modules with notes included be-
tween (B- to D+).
The third one asks a lot of good questions -which are often
out of the teaching program. But he doesn’t manage to be clear
in his’ mind on a given theme. So his notes are dissimilar.Tous
trois sont
The Theoretical Part of the Student’s
Realization
Before solving the problem, it is clearly necessary to define
Faro and American shuffles for example. It is also necess ary to
know how the cards could be informatics represented.
Card Deck Representation
Some important definitions, shown on Figure 1:
 The card is called face up if everyone can see the value
(from Ace to King) and the color (club – diamond – spade –
heart).
 The card is called face down if no one can see the value
(from Ace to King) and the color (club – diamond – spade –
heart).
A card d eck is the superimposing of several card s. To simpl-
ify, either all the cards are face up, or face down. The current
card value (resp. color) abbreviations included in Table 2 (resp.
3) are used here.
To end, let us use the following example:
1C-4D-QS-KH-10D-3C-JD-4S-10H
Tab l e 1.
Initial students’ leval according to my expectations.
Expected objective s
Students’ initial level
Magic documentation None is magician
Research in
mat hematics
Properties of divis bility They had a course on
this subject and obtained
a C
Cyclic group
Only explained at the
end of the algebra course
Research in
informatics
Programming with
Matlab
Have never written a
Matlab program but had
3 semesters C language
course
Representing with 2D
Matlab figures
Had never use gr aphic
tools library.
Modelisation
Insufficient in mathe-
matics and average for
computing using C.

P. SCHOTT
30
Figure 1.
Face u p cards (lef t an d c enter) an d fa c e down card (r i ght).
The first card is the Ace of clubs and the last one is the 10 of
hearts. Two configurations are evadible:
 The cards ar e face down and , when the deck i s face down
too, the order is the same (thus the first card is th e Ace of clubs
and the last one is the 10 of hearts), as shown on Figure 2.
The cards are face do wn an d, when the d eck is face down too ,
the order is the same (thus the first card is the 10 of hearts and
the last one is the Ace of clubs), as shown on Figure 3.
The American Shuffle
Let’s consider an N card deck cut in two equal parts (or al-
most) as shown on Figure 4.
To shuffle a deck in the American way, each card held in
right hand (for example) must be inserted in the deck held in left
hand. The number of cards inserted as well as the position (for
every insertion) is totally random, as presented on Fig ur e 7.
The Faro Shuffle (or the Pharaoh Shuffle)
Let us consider a deck cut in two subdeck named C and D as
shown before. The Faro shuffle is a particular American shuf-
fle. Each card from one subdeck is inserted in the second sub-
deck between two different suitabl e car ds (and conversely!).
The OUT (resp. IN) Faro shuffle begins with the top card of
the C-deck (resp. D-deck) as presented on Figure 6 (resp. 7).
What is remarkable is that only for the OUT Faro shuffle;
two cards always stay in their initial position (the first and the
last card ) .
Table 2.
Used Abbreviations for the cards values.
Value
Ace
2 3 4 5 6 7 8 9 10
Ja ck
Queen
King
Ab-
bre via-
tion 1 2 3 4 5 6 7 8 9 10 J Q K
Figure 2.
An exa m p le o f a c ards deck (f a ce d own) : [1C-4D-QS-KH-10D-
3C-JD-4S-10H].
Table 3.
Abbr eviations us ed for the c ard colors.
Color Club Diamond Spade Heart
Abbreviation C D S H
Figure 3.
The same example as figure 2 face up:
[1C-4D-QS-KH-10D-3C-JD-4S-10H].
Figure 4.
N car d deck cut in two (almost) equ al part.
Figure 5.
Shuffled dec k by t he American way.
The IN and OUT F aro Shuffl e with a New Card Deck
A new deck is in the order as shown on Figure 8.
The deck is cut exactly in two equal 26 card parts. The first
deck is held in the right hand (for example) and the second in
the left hand, as shown on Figure 9.
In Figure 10 (resp. 11) the result of a new deck OUT (resp.
IN) faro shuffle is presented.
The initial and final positions of each club (resp. diamond –
spade – heart ) card is gi ven in Table 4 (resp. 5 - 6 - 7) for an I N
or OUT Faro shuffle.
Let us remark the following property for an OUT faro shuf-
fle: the final position (pn+1) of a card belonging to the 26 first
(resp. last) cards deck is obtained by multiplying by 2 the initial
position (pn) (modulo 52) less 1 (resp. 0) ; the following equa-
tion is also obtained :
pn+1 = 2pn - 1 [52] or pn+1 = 2pn [52] (1)
Let us remark the following property for an IN faro shuffle:
the final position (pn+1 ) of a card belonging to the 26 first (resp.
last) cards deck is obtained by multiplying by 2 the initial posi-
tion (pn) (modulo 52) less 0 (resp. 1) ; the following equation is
also obt a ined :
pn + 1 = 2pn [52] pn + 1 = 2pn - 1 [52] (2)

P. SCHOTT
31
Figure 6.
The OUT F aro Shuff le of a N ca rds deck.
Figure 7.
The IN Faro Shuffle of a N cards deck.
Figure 8.
A New card deck with the bi cycle
 ord er.
Figure 9.
A New card deck wit h th e bi cyc le
 or der cut in two ha lv e s .
Figure 10.
The OUT faro shuffle from a new card deck with the the bicycle  or-
der.
Table 4.
The initial positions of each club card and their positions after an IN or
OUT Faro shuffle.
Clubs 1 2 3 4 5 6 7 8 9 1
0 J Q K
Initial 1
4 1 5 1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 2 6
Faro
OUT 2 7 2 9 3 1 3 3 3 5 3 7 3 9 4 1 4 3 4 5 4 7 4 9 5 1
Faro
IN 2 8 3 0 3 2 3 4 3 6 3 8 4 0 4 2 4 4 4 6 4 8 5 0 5 2
Table 5.
The ini tial position s of each diamon d card and thei r positions af ter an
IN or OUT Faro shuffle .
Diamond K Q J 1
0 9 8 7 6 5 4 3 2 1
Initial 27 2
8 2 9 3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7 3 8 3 9
Faro
OUT 2 4 6 8 1 0 1 2 1 4 1 6 1 8 2 0 2 2 2 4 2 6
Faro
IN 1 3 5 7 9 1 1 1 3 1 5 1 7 1 9 2 1 2 3 2 5
Table 6.
The initial positions of each club card and their positions after an IN or
OUT Faro shuffle.
Spade K Q J 1
0 9 8 7 6 5 4 3 2 1
Initial 4
0 4 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 5 0 5 1 5 2
Faro
OUT 2 8 3 0 3 2 3 4 3 6 3 8 4 0 4 2 4 4 4 6 4 8 5 0 5 2
Faro
IN 2 7 2 9 3 1 3 3 3 5 3 7 3 9 4 1 4 3 4 5 4 7 4 9 5 1
Table 7.
The initial positions of each heart card and their positions after an IN
or OUT Faro shuffle.
Heart 1 2 3 4 5 6 7 8 9 1
0 J Q K
Initiale 1 2 3 4 5 6 7 8 9 1
0 1 1 1 2 1 3
Faro
OUT 1 3 5 7 9 1 1 1 3 1 5 1 7 1 9 2 1 2 3 2 5
Faro
IN 2 4 6 8 1 0 1 2 1 4 1 6 1 8 2 0 2 2 2 4 2 6
8 OUT Faro Shuffle and Nothing is done!
Armed with these results, the students have been able to ve-
rify the following properly : if a card deck is 8 times In Faro
shuffled, then the deck is in its initial order !
 The demonstration is proposed in appendix B for a d eck.
 The visualization is proposed below –obtained by infor-
matics Matlab™ function given in appendix C)
‘‘Initially, the card deck is in the following order (presented
on Figure 12 ):
By cutting the deck between both Kings and after an OUT
Faro Shuffle, the card deck is in the following order (presented
on Figure 13):
By cutting the deck between both Aces and after an OUT
Faro Shuffle, the card deck is in the following order (presented
on Figure 14):

P. SCHOTT
32
By cutting the deck between both 7s (club and diamond) and
after an OUT Faro Shuffle, the card deck is in the following
order (presented on Figure 15):
By cutting the deck between both 4s (club and diamon d) and
after an OUT Faro Shuffle, the card deck is in the following
order (presented on Figure 16):
By cutting the deck between both 9s (spade and heart and af-
ter an OUT Faro Shu ffle, the car d deck is in the foll owin g order
(presented on Figure 17):
By cutting the deck between both 5s (spade and heart and af-
ter an OUT Faro Shu ffle, the car d deck is in the foll owin g order
(presented on Figure 18):
By cutting the deck between both 3s (spade and heart and af-
ter an OUT Faro Shu ffle, the car d deck is in the foll owin g order
(presented on Figure 19):
By cutting the deck between both 2s (club and diamond) and
after an IN Faro Shuffle, the card deck order is the initial one
(presented on Figure 12).’’(Ch ardiny, 2010).
The demonstration is proposed in appendix B for a deck.
Figure 11.
The IN faro shuffle from a new card deck with the the bicycle
 order.
Figure 12.
A new (b icycle  ) card deck.
Figure 13.
A new (b icycle  ) card deck after one OUT Faro shuf fle.
Figure 14.
A new (b icycle
 ) card deck after two OUT Faro shuffle.
Figure 15.
A new (b icycle  ) card deck after three OUT Faro shuffle.
Figure 16.
A new (b icycle  ) card deck after four OUT Faro shuffle.
Figure 17.
A new (b icycle
 ) card d eck aft er fiv e OUT Faro shuffle.
Figure 18.
A new (b icycle  ) card deck after six OUT Faro shuf fle.
Figure 19.
A new (b icycle
 ) card deck after seven OUT Faro shuff le.
The Informatics Part of the Student’s
Realization
The students had the following aim; to answer both ques-
tions:
 find the number of Faro IN (or OUT) shuffles so that a
card deck find s its initial order,
 find the Faro IN and\or OUT shuffle suit so that a card in
position 'k' in the deck arrives in position 'j'.
The students answered both these questions simply by using
the function 'faro_function' (described in appendix C).
How many Faro shuffles (IN or OUT) are necessary in
order to find the initial order of a deck of N =2p cards?
To answer this question, the students simply made a 'while'
loop with the condition: the vector representing the card deck
after ‘k’ IN (or OUT) shuffles is identical to the initial vector
representing th e initial card d eck.
The res ult s are gi v e n on Figure 20 where we have:
 in the X-axis the number of cards in the initial deck,
 in the Y-axis the number of successive shuffles it is neces-
sary to do so that the deck returns to its initial order.
Two curves are drawn (one for the IN Faro shuffle and the
other one for the OUT). The third represents the first bisector.
We notice that with a series of OUT Faro Shuffles, it is al-
ways possibl e to find a shuffle number lower than the card deck
number to realize the property (contrary to the IN Faro shuf-
fle!).
What succession of IN and OUT shuffles is necessary so that
a card in position j is to be found in position k in a deck of N =
2p cards?
Typically to solve this problem, it is necessary to make a tree
by computer.
In Figure 21 we propose, a tree for:
 an initial 16 card deck ( p = 8 ),
 the initial position for the selected card is the top (the first
card has the position 0).
 To find the successive shuffles needed in order for the se-
lected card to be in the fourth position (equivalence class 3)
will be:
 in position 8 : only one IN shuffle,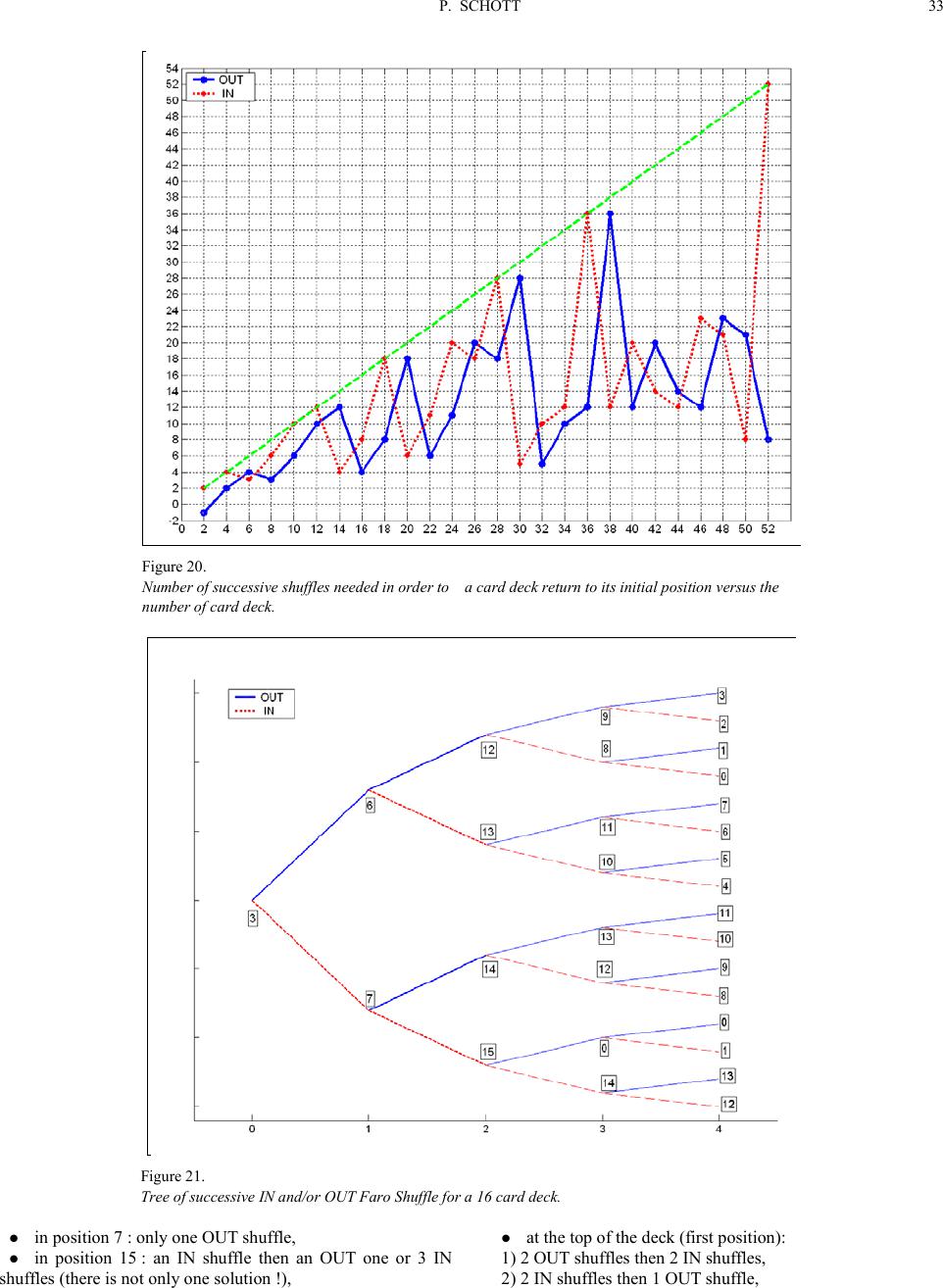

P. SCHOTT 33
Figure 20.
Num ber of s uccessive shuffles ne ed e d in o rder to a c ard deck ret urn to its in it ial position versus the
numb er of card deck.
Figure 21.
Tree of successive IN and/or OUT Faro Shuffle for a 16 card deck.
 in posit i on 7 : only one OUT shuffle,
 in position 15 : an IN shuffle then an OUT one or 3 IN
shuffles (there is not only one solution !),
 at the top of the deck (first position):
1) 2 OUT shuffles then 2 IN shuffles,
2) 2 IN shuffles then 1 OUT shuffle,

P. SCHOTT
34
The Notions —Which I Gave—Can be the
Summary of a Maths Course on the Cyclic
Groups
The students found the laws for the OUT (resp. IN) shuffles
written in the equation 1) (resp. 2). Now these equations must
be written in a unique equation which could allow us to solve
both problems.
It is then necessary to use the equivalence classes (thus to
work in Z/mZ) which represent the possible positions of cards.
They are bet ween 0 and ( m-1) for associated positions between
1 and m.
I thus give the new relations governing IN and OUT shuffles
as well as the equations to be resolved in order to solve the both
proposed questions which were solved by computer by the
students.
The New Equations for t he IN and OU T Faro Shuff le
Let us illustrate the results for the OUT (resp. IN) Faro shuf-
fle given by the equation (1) (resp. 2); let us note the possible
positions of cards for a N = 2p deck. The results are shown in
Table 8.
For the OUT (resp. IN) Faro shuffle, the final position of the
‘p-1’ first cards from the top follows the equation ‘2k’ (resp.
‘2k+1’).
The transition is between the ‘p-1’ term and the ‘p’ term. If
we use the same relation as before, we obtain the value '2p’
(resp. '2p+1’). But we have to obtain the value 1 (resp. 0).
So the modulo to use is for the OUT (resp. IN) Faro shuffle
'2p-1’ (resp. '2p+1’). The new relations are given to the equa-
tion (3) (resp. 4):
pk+1 ≡ 2pk [2p - 1] (3)
pk+1 ≡ 2pk + 1 [2p + 1] (4)
The card d eck return s to its initial o rder if the card in the ini-
tial position k = p0, after m Faro sh uffl es of a N=2p card deck,
returns to its position k = pm , where pi is the position of this
considered card at the ith shuffle.
Table 8.
What happens to the position of each card of a 2p card deck AFTER an
IN or an OUT Faro shuffle ?
Init ia l po sitions After an
OUT-shuffle After an IN-shuffle
0 → 0 1
1 → 2 3
2 → 4 5
∴ ∴ ∴ ∴
p-1 → 2p-2 2p-1
p → 1 0
p+1 → 3 2
∴ ∴ ∴ ∴
2p-2 → 2p-3 2p-4
2p-1 → 2p-1 2p-2
For that purpose, it is necessary to solve, for each of both
cases, the following equation:
pm ≡ p0 [ 2p - 1] (OUT) or pm ≡ p0 [2p + 1] (IN) (5)
For the OUT faro shuffle, it occurs that:
pm ≡ 2mp0 [2p - 1] (6)
For the IN faro shuffle, it occurs that:
pm ≡ 2mp0 + 2m - 1 [2p + 1] (7)
The demonstration can be made by recurrence.
The OUT Faro shuffle
The equation (6) becomes:
2mk ≡ k [2n - 1] ⇔ 2m ≡ 1 [2p - 1] (8)
This equation is solvable for ‘m’ if p is given. When p varies
from 1 to 26, the Figure 20 is also obtained (by calculating only
powers of 2!).
Let us take th e mo st classic case -a 5 2 card deck- Thus 2p =
52, and 2p - 1 = 51 = 17*3. So by the theorem of Euler-Fermat,
we know that there are 16 numbers which divide the class 51.
Let us th en try the values of 2j until we fin d the value of m:
21 ≡ 2[51]; 22 ≡ 4[51]; 23 ≡ 8[51]; 24 ≡ 16[51] (9)
25 ≡ 32[5 1] ; 26 ≡ 13[51] ; 27 ≡ 26[51] ;28 ≡ 1[51] (10)
So, effectiv ely 8 OUT Faro shu ffles are need ed in order for a
shuffled deck to return to its initial order!
By stori ng the success ive valu es of 2j [ 51], we have th e suc-
cessive clas ses tak en b y the i nitial card at the posi tion 1 (class 0)
in the d eck. Figure 22 p resents these values gi ven by the Equa-
tions (9) and (10) as well as their order of appearance.
IN shuffle
The Equation (7) becomes:
2mk + 2m – 1 ≡ k [2p + 1] ⇔ 2m ≡ 1 [2p + 1] (11)
This equation is solvable for ‘m’ if p is given. When p varies
from 1 to 26, figure 20 is also obtained (by calculating only
powers of 2!).
Let us take th e mo st classic case -a 5 2 card deck- Thus 2p =
52, and 2p + 1 = 53 which is a prime number ! So by the theo-
rem of Euler-Fermat, we kn o w that t her e are 52 n umbers whi ch
divide the class 53. Let us try th en the values of 2j until find the
value of m:
21 ≡ 2[53] ; 22 ≡ 4[53] ; 23 ≡ 8[53] ; 24 ≡ 16[53] (12)
25 ≡ 32[5 3] ; 26 ≡ 11[53] ; 27 ≡ 22[53] ;28 ≡ 48[53] (13)
And so on … effectively 53 IN Faro shuffles are needed in
order for a shuffle deck to return to its initial order –as we can
read on Figure 20!
By storing the successive values of 2j [51], we have the suc-
cessive classes taken by the initial card at the position 1 (class 0)
in the deck. Figure 23 presents these values given by the Equa-
tions (12) and (13) as well as t heir order of appearance.
We notice that all the classes are thus affected. We can con-
clude that 2 is generative of the multiplicative group.
What successi on of IN and OUT shuffles is necessar y so that a
card in position j is to be found in position k in a deck of N =
2p
Diacon is gave the following lemma to answer this question
when j=0.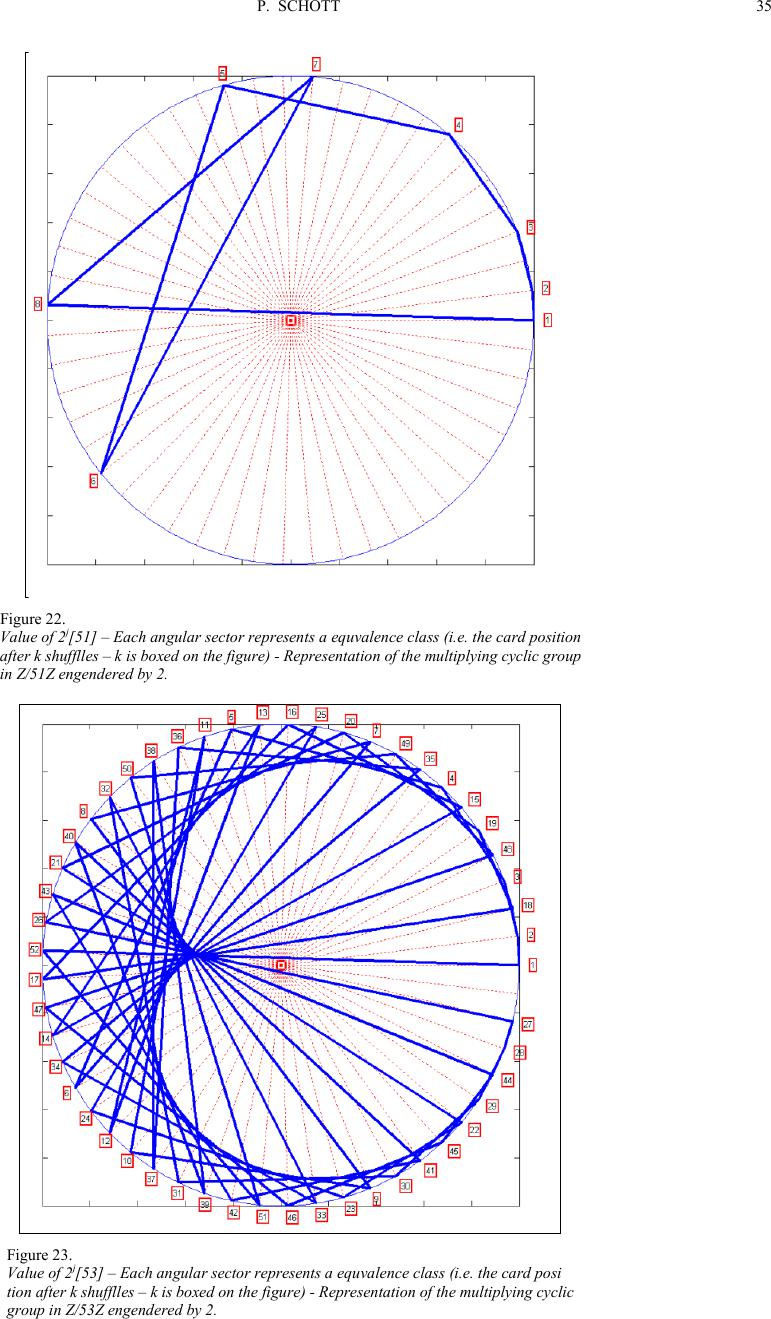

P. SCHOTT 35
Figure 22.
Value of 2j[51] – Each angular sector represents a equvalence class (i.e. the card position
after k shufflles – k is boxed on the figure) - Representation of the m ul t i plying cyclic group
in Z/51Z engendered by 2.
Figure 23.
Value of 2j[53] – Eac h angular se ctor repres ents a equvalence class (i.e . the card posi
tion after k shufflles – k is boxed on the figu re) - Representation of the mul tiplyin g cyclic
group in Z/53Z engendered by 2.

36 P. SCHOTT
‘‘LEMMA 2. Let the positions in a deck of 2n cards be la-
beled 0, 1, . . . ,2n - 1. To bring the top card to position k, ex-
press k in binary, interpret 0 as OUT and 1 as IN, and perform
the indicated sequence of IN and OUT shuffles from left to
right.’’ (Diaconis, 1983).
This lemma is verified on the following figures:
• the figure number 26 is for a 16 = 24 car d deck,
• the figure number 24 is for a 8 = 23 card deck,
• the figure number 25 is for a 12 card deck.
To find the successive shuffles needed in order to bring the
top car d:
 in posi tion 0 = (0)2: one OUT shuffle,
 in posi tion 3 = (11) 2: two IN shuffles,
 in position 5 = (101) 2: one IN shuffle then one OUT then
one IN,
in position 11 = (1011) 2: an OUT shuffle then an IN one and
two OUT .
Synthesis, Conclusion, Going Further and
Prospects
Before asking the following question ‘‘is it opportune to de-
velop this type of teaching?’’, let me make a synthesis of stu-
dents' work and then a conclusion in relation to my expecta-
tions. After that, I can answer the following question ‘‘is it
opportune to develop this type of teaching?’’ by suggesting
ways to go further.
Synthesis and Conclusions
Let us sum up the students’ realization according to my ex
pectations in Table 9. The report would completely reach my
expectations and objectives if the students had searched more
and found theoretical mathematical notions. The student group
was more interested in the informati cs part.
The students have completely achieved the MDP project but
not the uns a id objectiv e s …
It is very interesting to note that th e group did not create the
asked magic trick, while they had chosen this project to learn
the secrets of the magic. Eventually they got involved in the
scientific work and left aside the playful aspect. This is partially
due to my project management: I reminded them repeatedly
that t he project was at first s cientific applicable to the magic.
That is why I can think that this method is efficient and prac-
ticabl e.
Going Further a nd Pro spects
This kind of project could be continued by these ideas:
 Calculating how many American shuffles can be reached
with an N car d deck.
 Find relations for a 2p card deck; for example answer to
this question: “Whose suit of IN and OUT Faro must have done
 to move a card from position ‘j’ to position ‘k’ in the card
deck?”
 The answer is given by (Lachal, 2010), but it must be very
interesting to give a new project in order to the students dis-
cover and prove this property.
 What leads me to think about adapting this to the whole
mathe matics te aching is t o use magic a s a metho d of investiga-
tion to lead students to understand the principles of mathemat-
ics and to come to love this subject.
Figure 24.
Relation between the successive IN and OUT Faro shuffles to bring the top car d a t the p os ition k in a 8=23 card deck.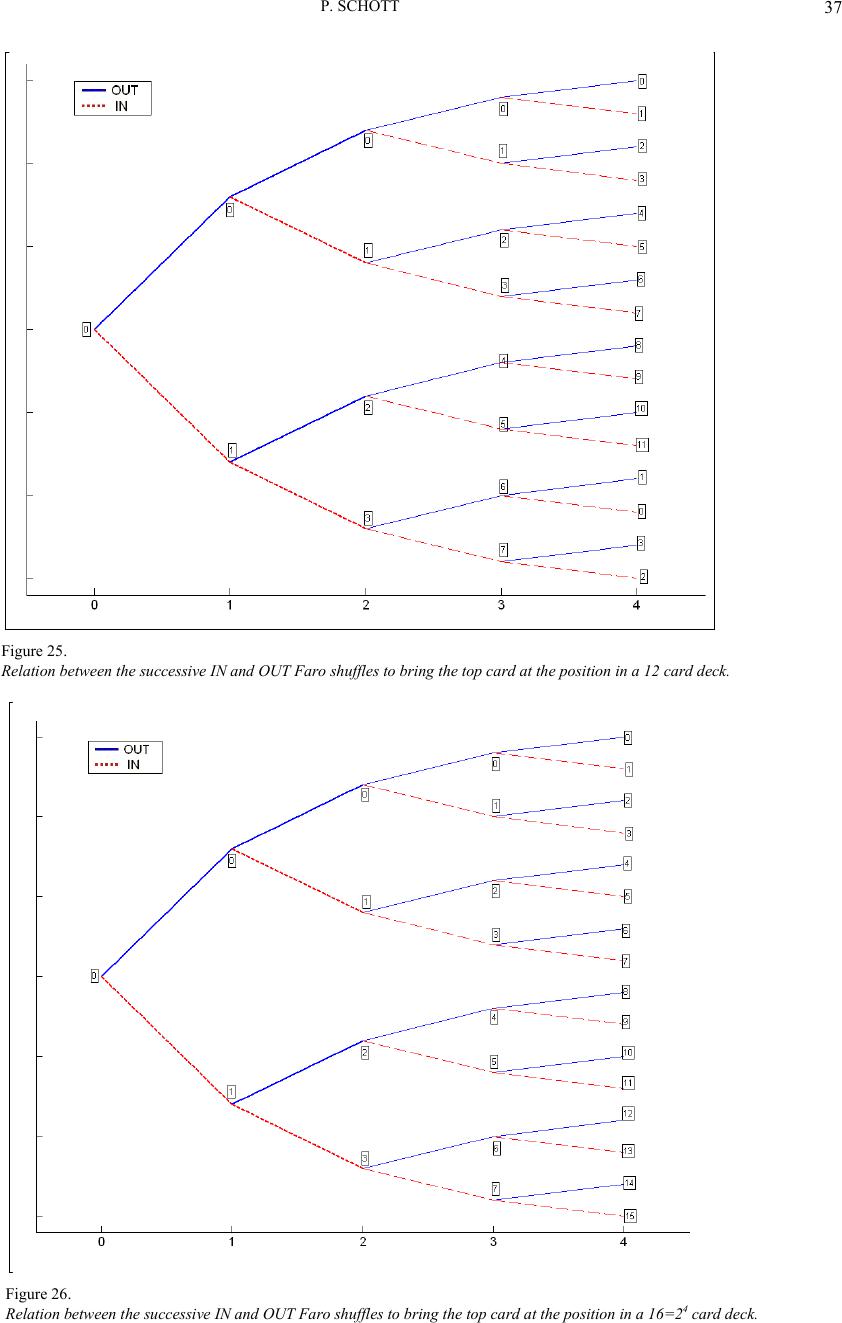

P. SCHOTT
37
Figure 25.
Relation between the successive IN and OUT Faro shuffles to bring the top card at the position in a 12 card deck.
Figure 26.
Relatio n b et wee n th e successive IN and OUT Faro shuffles to bring the top card at the position in a 16=24 card deck.

38 P. SCHOTT
Table 9.
Synt he sis of stu de n t w or k ac cording to my ex pectation s.
Expected objective s Students
Magic d ocumentation G ood
Research in
mat hematics
Properties of divis bility
Average
Cyclic group
Insufficient
Research in
informatics
Programming with
Matlab Very good
Representing with 2D
Matlab figures
Very good
Modelisation
Insufficient in mathe-
matics and very good for
computing
New magic card trick Not done
In past, I had proposed to two groups of students a first pro-
ject using the magic to make discover the optics principles
(Schott, 2010). The results were different: a group having fo-
cused on the realizati on of the magic trick, the ot her one on the
physical principles.
That’s why I continued to propose these kinds of subjects
and by a more formal follow-up, the results improved. One
group even suggested t o me a differ ent (magic) su bject which I
reformatted to fit the P.E.S imp eratives.
What leads me to think about adapting this to the whole ma-
thematics teaching from primary school to high education
(Schott, 2009) is to use magic as an investigation method to
lead students to understand the mathematics principles and to
come to fond of maths. I participate in the “we ek of the sci ence”
with primary and college classes; the results are promising.
However, magic/science parallel must be perfect and is not
felt by the students as a trick. It is for it that I develop at pr esent
approaches which seem to me much more adapted than the
magic:
 an informatics project: using origami for teaching the C
language,
 an electronics project: creation of a robot playing several
musical “home made” instruments in order to allow them dis-
cover the principles of waves p ropagatio n, the pro gramming o f
an embarked syste m …
Acknowledgements
This paper could not have been written without the encou-
ragement s of Bernard SCHOTT, my father, the invaluable help
of Anne SERRIE, my mother, Claire LEROUX, the head of
ARNUM, Peter WILSON and Carol MACLAREN who cor-
rected the English. Thanks to Philippe QUOST who has read
the mathematical demonstrations
References
Ammar, M. (1998). The complete cups & balls. L&L Publishing.
Assaf, S., Soundararajan, K., & Diaconi s, P. (200 9). Riffle sh uffles of a
deck with repeated cards. DMTCS Proceedings, 21st International
Conference on Formal Power Series and Algebraic Combinatorics,
FPSAC 2009, 89-102.
Boileau, N. (1740). La sco lastique. Souchay, Paris.
Chardiny, N., Dupin, B., & Grosgeorge, S. (2010). Utiliser les mat-
héma tiques p our créer u n tour d e Magi e utili sant le méla nge FARO .
Mémoire de P.S.I, ESIEA.
Diaconis, P., Graham, R. L., & Kantor, W.M. (1983). The mathematics
of perfect sh uffles. Advances in Applied Mathematics, 4, 175-196.
doi:10.1016/0196-8858(83)90009-X
Diac onis, P. (1998). From shuffling cards to walking around the build-
ing. An in t roduct i on to markov c hain th eory. Procee ding s of Interna-
tional Congress, Berlin, I, 187-204 .
Diaconis, P. (2003). Mathematical Developments from the Analysis of
Riffle-Shuffling. In A. Fuanou and M. Lieb eck (eds .), Groups Com-
binatorics and Geom etry (pp. 73-97). N.J.: World Scientific.
Diaconis, P., & Graham, R. L. (2005). The solutions to Elmsley’s
Problem. Mathematics magazine. doi:10.1142/9789812564481_0005
Elms ley, A. (19 57). Mat hém atic s of the wea ve sh uffle. The Pentagram,
11, 70-71.
Erdnase, S. W. (1902). The expert at the ca rd table . Chicago.
Gardner, M . (1958). Mathematics, m a g i c a n d mystery. Dover.
Gardner, M. (2005). Martin Gardner's mathematical games : the entire
collection of his scientific American columns. Mathematical Associ-
atio n of America.
Gilbreath, N. L. (1958). Magnetic colors. The Linking Ring, 38, 60.
Gilbreath, N. L. (1966). Second Gilbreath Principle. Linki ng Ring , June
1966.
Gilbreath, N. L. (March, April, May, 1989). Magic for an Audience.
series of 3 ar t icles in Genii, 52 , No. 9-10-11.
Huet, G. (1991). The Gilbreath trick: A case study in axiomatisation
and proof development in the Coq Proof Assistant. Proceedings,
Second Workshop on Logical Frameworks, Edinburgh.
doi :1 0.1017/C BO9780511569807
Lachal, A. (2010). Quelques mélanges parfaits de cartes. Quadrature.
Magid, A. (2005). Notices. American Mathematical Society.
Mayol, H. (2000). La Magie des cordes Maestro, HBM Production.
Mulcahy, C. (2003). Fitch Cheney's Five Card Trick. Mathematics
Horizon, 10.
Mulcahy, C. (2004). Top 5 reasons to like mathematical card tricks. 11.
Mulcahy, C. (2007). An ES per im e n t with cards. 14.
Poincaré, H. (1912). Calcul des probabilités. Rédaction de A. Quiquet.
Deuxième éd it ion, revue et augmentée par l’auteur, Gauthier-Villars,
Paris.
Schott, P. (2010). The use of magic in optics in higher education.
Creative Educat ion, 1, 11-17.
Schott, P. (2009). The use of magic in mathematics: From primary
school to higher education. Proceedings of ICERI2009 Conference,
Madrid, Spain, 58-70.
Sheynin, O. B. (1991). H. Poincaré’s work on probability. Archive for
History of Exact Sciences, 42, Berlin: Springer.

P. SCHOTT
39
Appendix A
The Objectives
The Multi Disciplinary Project (M.D.P), works hops pr o pos e d
to the 4th semester students group activities of project type
which take place throughout the winter semester (from
01/30/ 2010 till 05/3 1/ 2 01 0)
Their main objective is the study of concrete applications in
companies, technical-scientific matters leading to a realization
or an experi ment. The as pects o f person al develop ment train ing
and of project management will have to be approached there.
They also allow developing work in a group, communication
techn iques as well as coll aborative wor k.
The Activit ies
The students, 3 to 5 students per group, are accompanied by
a teacher:
 They develop their project.
 They make an intermediat e r eport.
 They draft a final report.
 They speak during an oral presentation.
The Subjects
The subjects are proposed by teachers of various subjects :
mathematics, electronic systems, physics, scientific calculation,
personal development, communication...
The proposed subjects list will be available at the office of th e
educational assistant and posted at the latest on December 14th,
2009.
Every domain has a limited number of subjects.
A student group can propose a subject: they have to find a
teacher who wants to follow this group with their subject. Then
the group must contact the educational assistant who takes care
of registering the project.
The Teacher
He accompanies the student groups in their work and is in
charge of the evaluatio n.
He assures t hree major meet ings:
 At the beginning of activity, he advises and directs the
student groups.
 During the intermediate balance report, he possibly reo-
rientates the group and estimates t he presented work.
 At the end of activity, during the oral presentation.
Appendix B : 8 OUT Faro Shuffle and Nothing is
done Presen t ed with a Numbered 52 Card Deck
Initially, the card deck is in the following order (presented on
Figure 27). Each card is numbered from 1 to 52:
By cutting the deck between t he cards 26 an d 27 and after an
OUT Faro Shuffle, the cards deck is in the following order
(presented on Figure 28):
By cutti ng the deck b etween the cards 39 and 14 and after an
OUT Faro Shuffle, the cards deck is in the following order
(presented on Figure 29):
By cutti ng the deck b etween the cards 20 and 33 and after an
OUT Faro Shuffle, the cards deck is in the following order
(presented on Figure 30):
Figure 27.
A numb er ed card dec k fr o m 1 to 52.
Figure 28.
A numb e r e d c ard deck fr om 1 t o 52 deck after on e OU T F aro sh u ffle.
Figure 29.
A numbered card deck from 1 to 52 deck after two OUT Faro shuffle.
Figure 30.
A numbere d car d d eck from 1 to 52 deck after three OUT Faro shuff le .
By cutti ng the deck b etween the cards 37 and 17 and after an
OUT Faro Shuffle, the cards deck is in the following order
(presented on Figure 31):
By cutti ng the deck b etween the cards 44 and 09 and after an
OUT Faro Shuffle, the cards deck is in the following order
(presented on Figure 32):
By cutti ng the deck b etween the cards 48 and 05 and after an
OUT Faro Shuffle, the card deck is in the following order (pre-
sented on Figure 33):
By cutti ng the deck b etween the cards 50 and 03 and after an
OUT Faro Shuffle, the card deck is in the following order (pre-
sented on Figure 34):
By cutti ng the deck between th e card 51 and 02 and after an
OUT Faro Shuffle, the card deck order is the initial one (pre-
sented on Figure 27).
Appendix C: Informa ti cs Mat lab Program ‘Faro
IN’ and ‘Faro OUT’
function [X] = faro_function(P,Q,faro_menu)
X = [];
p = length(P);
q = length(Q);
n = p+q;
faro_menu = faro_men u-1;
for i = 1:(faro_menu-1);
X(i) = P(i);
end
j = faro_menu+1;
t1 = 1;
t2 = faro_menu+1;
while j<=n
x = 1;
while x<=1 & t1< = q

P. SCHOTT
40
X(j) = Q(t1);
t1 = t1+1;
j = j+1;
x = x+1;
end
x=1;
while x<=1 & t2< = p
X(j) = P(t2);
t2 = t2+1;
j = j+1;
x = x+1;
end
end
if faro_menu==1
X(1) =P(1);
End
Figure 31.
A numbered card deck from 1 to 52 deck after four OUT Faro shuffle.
Figure 32.
A numbered card deck from 1 to 52 deck after five OUT Faro shuffle.
Figure 33.
A numbered card deck from 1 to 52 deck after six OUT Faro shuffle.
Figure 34.
A numbered card deck from 1 to 52 deck after seven OUT Faro shuffle.
Table 10.
Position of each heart card during the 8 Out Faro shuffle.
Heart 1 2 3 4 5 6 7 8 9
1
0 J Q K
Initial 1 2 3 4 5 6 7 8 9
1
0
1
1
1
2
1
3
Faro
IN 1
1 3 5 7 9
1
1
1
3
1
5
1
7
1
9
2
1
2
3
2
5
Faro
IN 2 1 5 9
1
3
1
7
2
1
2
5
2
9
3
3
3
7
4
1
4
5
4
9
Faro
IN 3 1 9
1
7
2
5
3
3
4
1
4
9 6
1
4
2
2
3
0
3
8
4
6
Faro
IN 4
1
1
7
3
3
4
9
1
4
3
0
4
6
1
1
2
7
4
3
8
2
4
4
0
Faro
IN 5
1
3
3
1
4
4
6
2
7
8
4
0
2
1
2
3
4
1
5
4
7
2
8
Faro
IN 6 1
1
4
2
7
4
0 2
1
5
2
8
4
1 3
1
6
2
9
4
2 4
Faro
IN 7 1
2
7 2
2
8 3
2
9 4
3
0 5
3
1 6
3
2 7
Faro
IN 8
1 2 3 4 5 6 7 8 9
1
0
1
1
1
2
1
3
Table 11.
Different calculated position of the 4 of heart thanks to equation (1)
and (8).
Posi-
tions
Equation (1) :
pk+1=2*pk-1 ou
p
k+1=
2*p
k
Equation (8) :
up≡ 2m k [2p-1]
Initial 4 p0=4 p0=4 => u0=3=k
Faro IN 1 7 p1=4*2-1=7 u1 = 21*3=6 => p1=7
Faro IN 2 13 p2=7*2-1=13 u2 = 22*3=12 => p2=13
Faro IN 3 25 p3=13*2-1=25 u3 = 23*3=24 => p3=25
Faro IN 4 49 p4=25*2-1=49 u4 = 24*3=48 => p4=49
Faro IN 5 46 p5=49*2[52]=46
u
5
= 25*3=96
[51]=45 => p5=46
Faro IN 6 40 p6=46*2[52]=40
u
6
= 26*3=192
[51]=39 => p
6
=40
Faro IN 7 28 p7=40*2[52]=28
u
7
= 27*3=384
[51]=27 => p7=28
Faro IN 8 4
p
8
=28*2[52]=4=p
0
u
8
= 28*3=768
[51]=3 => p8=4
Appendix D: 8 OUT Faro Shuffle and Nothing is
Done Presented with the Different Positions of
the Hearts
The Table 10 presents the position of each heart card during
the 8 OUT Faro shuffle.
For the 4 of hearts, thanks to the equations (1) and (8), their
different positions are calculated:
We notice that when j is higher than 53, the computer can no
lon ger calculate 2 j … and we have to mix the both equations !