Journal of Environmental Protection, 2011, 2, 154-161
doi:10.4236/jep.2011.22017 Published Online April 2011 (http://www.SciRP.org/journal/jep)
Puff Models for Simulation of Fugitive Hazardous
Emissions in Atmosphere
Ledina Lentz Pereira1, Camila Pinto da Costa2, Marco Tullio Vilhena3, Tiziano Tirabassi4
1University of the South End of Santa Catarina ( UNESC), Criciúma, Brasil; 2Federal University of Pelotas (UFPel), Pelotas, Brazil;
3Federal University of Rio Grande do Sul (UFRGS), Porto Alegre, Brazil; 4Institute of Atmospheric Sciences and Climate (ISAC),
National Research Council (CNR), Bologna, Italy.
Received November 10th, 2010; revised December 20th, 2010; accepted February 6th, 2011.
ABSTRACT
A puff model for the dispersion of material from fugitive hazardous emissions is presented. For vertical diffusion the
model is based on general techniques for solving time dependent advection-diffusion equation: the ADMM (Advection
Diffusion Multilayer Method) and GILTT (Generalized Integral Laplace Transform Technique) techniques. Both ap-
proaches accept wind and eddy diffusion coefficients with any restriction in their height functions. Comparisons be-
tween values predicted by the models against experimental ground-level concentrations (from Copenhagen data set)
are shown. The preliminary results confirm the applicability of the approaches proposed and are promising for future
work.
Keywords: Hazardous Emissions, Advection-Diffusion Equation, Analytical Solutions, Air Pollution Modeling, Puff
Models
1. Introduction
The study on hazardous material dispersion shows that
the diffusion in the atmosphere depends strongly on the
meteorological scenario and boundary layer evolution.
Traditionally, the advection-diffusion equation has been
largely applied in operational atmospheric dispersion
models to predict the mean concentration of contami-
nants in the Atmospheric Boundary Layer (ABL). In
principle, from this equation it is possible to obtain a
theoretical model of dispersion from a point source given
appropriate boundary and initial conditions plus knowl-
edge of the mean wind velocity and turbulent fluxes.
Much of the turbulent researches are related to the
specification of turbulent fluxes in order to allow the
solution of the averaged advection-diffusion equation:
this procedure, sometimes, is called as the closure of the
turbulent diffusion problem. The main scheme for clos-
ing the equation has to take into account the relationship
between concentration turbulent fluxes and the gradients
of the mean concentration by exchange coefficients.
A broad class of numerical solutions to the advec-
tion-diffusion equation can be encountered in the litera-
ture. Nevertheless, the search of analytical solutions for
this equation has several advantages. Indeed, in the ana-
lytical solution all the influencing parameters are explic-
itly expressed in a mathematical closed form and cones-
quently sensitivity analysis over model parameters may
be easily performed and, more important in order to
manage alarms for fugitive hazardous emissions, air pol-
lution model based on analytical formula run fast.
In fact, in order to model fugitive emissions, fast
evaluation and relative decisions are necessary. So, fast
codes are preferred and is better if they run in personal
computer and can evaluate air pollution concentrations
although some meteorological measures are present.
Moreover, in the case of fugitive hazardous emissions,
time dependent models are necessary.
Puff models are a practical approach to describe the
dispersion from a time-dependent emission point source
in an inhomogeneous and non-stationary ABL. Most of
the operative puff models are based on the Gaussian ap-
proach (the shape of the puffs is Gaussian). Gaussian
models are theoretically based upon an exact, but not
realistic solution of the equation of transport and diffu-
sion in the atmosphere, in cases where both wind and
turbulent diffusion coefficients are constant with height.
The solution is forced to represent real situations by
means of empirical parameters, referred to as “sigma”.
The input parameters of the Gaussian plume model are

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere155
often related to simple turbulence typing schemes or sta-
bility classes. The problem with such stability classes is
that each covers a broad range of stability conditions;
they are also very site specific and based towards neutral
stability when unstable or convective conditions actually
exist. Moreover, the shapes of puffs are not symmetric in
vertical, while the Gaussian distribution is symmetric.
In fact, a distorting effect of the variation with height
of the mean wind, both in speed and direction, is often
evident in the development of puffs or plumes smoke.
The effect is most evident in stably stratified conditions.
In fact wind shear creates variance in the direction of the
wind, vertical diffusion destroys this variance and tries to
re-establish a non skewed distribution. The interaction
between vertical mixing and velocity shear is continu-
ously effective.
Conversely, Gaussian models are fast, simple, do not
require complex meteorological input. For these reasons
they are still widely employed for regulatory applications
by environmental agencies all over the world. Nonethe-
less, because of their well known intrinsic limits, the re-
liability of a Gaussian model strongly depends on the
way the dispersion parameters are determined on the
basis of the turbulence structure of the ABL and the
model’s ability to reproduce experimental diffusion data.
However, non-Gaussian puffs have been proposed in the
literature [1-4].
In this paper we present two puff models where hori-
zontal dispersion is Gaussian, but the vertical puff shape
is non-Gaussian and it is evaluated by two different tech-
niques that allow to obtain an analytical solution of the
one-dimensional advection-diffusion equation: the GILTT
(Generalized Integral Laplace Transform Technique) [5,6]
and ADMM (Advection Diffusion Multilayer Method)
[7,8] techniques.
The first one is a well-known hybrid method that had
solved a wide class of direct and inverse problems main-
ly in the area of Heat Transfer and Fluid Mechanics and
the solution is given in series form.
The second one is an analytical solution based on a
discretization of the Atmospheric Boundary Layer (ABL)
in sub-layers where the advection-diffusion equation is
solved by the Laplace transform technique. The solution
is given in integral form.
The models accept general profiles for eddy diffusivity
coefficients, as well as the theoretical profiles proposed
in the scientific literature, such as the vertical profiles of
eddy diffusion coefficients predicted by the Similarity
Theory.
2. Puff Models
Puff models were introduced to simulate the behaviour of
pollutants in inhomogeneous and non-stationary mete-
orological and emission conditions [9,10]. The emission
is discretized in a temporal succession of puffs, each of
which shifts into the area of calculus thanks to wind
field.
Puff models assume that each emission of pollutants in
a time interval

t releases into the atmosphere a mass
of pollutants


M
Qt, where Q is the emission rate,
which is variable in time. Each puff contains the mass
M and its centre of mass is transported by the wind,
which may vary in space and time. Continuously emit-
ting sources can be represented by the superposition of a
series of the above clouds.
The puffs considered here are emitted in time intervals
1

t and the calculation of the concentration of pollutants
of each one is made in a time intervals 2. Each puff is
carried in accordance with the trajectory from its centre,
which is determined for velocity vector of the local wind,
while it is enlarged in the time by means of the disper-
sion coefficients. In particular, in our model, the vertical
diffusion of the material carried in accordance with the
trajectory of puff is non-Gaussian and it is described by
general solutions of the following equation:
t

 
,,czt czt
K
z
tz z

S



 


(1)
for 0

zh and the time , subject to the bound-
ary condition
0t
0 for 0;
z
c
K
z
z

h
0
(2)
and the initial condition: . Here,

0cz,


Cz,t
denotes the average crosswind integrated concentration,
h the ABL height,
z
K
the eddy diffusivity coefficient,
the instantaneous point source expressed like: S

 
0
 
s
SQtt zH (3)
In addition,

represents the delta function, z is the
vertical variable, t0 initial time,
s
H
the source height.
In the sequel we solve problem (1) by the GILTT and
ADMM approach.
The main idea of the GILTT approach consist in the
expansion of the pollutant concentration in a truncated
series of eigenfunctions. Replacing this expansion in the
advection diffusion equation and taking moments, we
come out with a first order linear matrix equation, which
is then solved by the Laplace Transform technique. This
procedure leads to a solution expressed in series formula-
tion for more details see the work [6].
The main idea of the ADMM approach relies on the
discretization of the PBL in a multilayer system, where
in each layer the eddy diffusivity and wind profile as-
sume averaged values. The resulting advection-diffusion
equation in each layer is then solved by the Laplace

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere
156
Transform technique. For more details about this meth-
odology see the work [11].
To construct a three-dimensional solution, we assume
the Gaussian model in x and y directions for the pollutant
concentration, therefore Gaussian solution reads like:

2
0
2
0
,,
11
exp
22
1
exp 2
puff
yx x
y
xyt
xx
yy







 










 



(4)
where 0
x
ut, 0 and 0 yvt
x
, 0 are the cen-
troid coordinates (u and v are the components of hori-
zontal velocity of the average wind) and x , y the
lateral dispersion parameters [12] defined as:
y


a
utf tT 


(5)
where

means x and y,
f

is the non-dimensional
function of the travel time tT

:
1
12
 ftT


(6)
where T

is the Lagrangean scale of time for the hori-
zontal (x and y) dispersion and u


is the standard de-
viation of the longitudinal and lateral components of the
wind speed defined as:


23
2035 2
a
S
u* s
H
u. hH

kL

 


 , (7)
where * is friction velocity, k is the Von Kárman con-
stant (k = 0.4), h is the height of the ABL and L is the
Monin-Obukhov length.
u
2.1. The Solution of the One-Dimensional
Transient Problem by the GILTT Method
In order to solve the Equation (1), we rewritten like:
 

2
0
2



S
ccc

K
'zKzQt tzH
tz
z (8)
According the works [6] the solution of problem (1) is
written like:
  
12
0


ii
/
ii
A
tZ z
cz,t N (9)
where
 
cos
ii
Z
zz

and π
iih

 are respect-
tively the eigenfunctions and eigenvalues, and

i
A
t is
the solution of the transformed problem, and is
i
N
expressed by .

d2
ii
v
NZzv
Replacing the Equation (9) in Equation (8) and taking
moments. Thus, after we get the following first order
linear matrix equation



 

0
EY'tBYtQttF (10)
For t > 0, with E, Y, B and F defined as:

0
with d


 
a
ij
ijij 12 12
ij
ZzZz
Ee ez,
(11)
NN
 





j
YtAt, (12)

where ,


 12
is
ij i
i
ZH
Ff f
N
(13)
and the B matrix is expressed by: , with  
ij
Bb
 
12 12
2
00
1
dd









ij
ij
aa
'
ijjij
bNN
k'zZ zZzzkzZ zZzz 
(14)
For the initial condition, the procedure is analogous
and after the substitutions due and integrations we have:

00

j
A (15)
In this work the transformed problem represented by
Equation (10) is solved by the Laplace Transform tech-
nique and diagonalization [13].
Thus, the final solution is given by




aD YtTGt

(16)
where

is the integration constant vector,


D
Gt

0
tT
is
the diagonal matrix witch elements are , a is
the eigenfunction matrix and are the eigenvalues of
the matrix B.

i
dt
e
i
d
The state-of-art the GILTT method can be found in
[14].
2.2. The Solution of the One-Dimensional
Problem Transient by the ADMM
Method
To solve the advection-diffusion Equation (1), for inho-
mogeneous turbulence by the ADMM method, we must
take into account the dependence on the eddy diffusivi-
ties, on the height variable (variable z). To reach this goal
we discretize the height h of the ABL into N sub-inter-
vals in such manner that inside each sub-region


K
z
assume respectively the following average values:

1
1
1d



n
n
z
nz
nn z
K
Kzz
zz (17)

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere157
Obviously, the greater the number o
more accurate the concentration patter
though the relative code running time is consequently
gr
f layers (N), the
n calculated, al-
eater. Moreover, the layers in which the ABL is di-
vided can be not constant in thickness. A more detailed
description is required of wind and diffusion coefficients
in proximity to the ground, where their gradients are high
and more strongly influence pollutant dispersion. There-
fore layers close to the terrestrial surface can be assigned
a smaller thickness than those located higher up. With
the division of the domain into N sub-intervals, the solu-
tion of the Equation (1) is reduced to the solution of N
problems of this type:
2
0
2()()
nn
n
cc
K
QzHs tt
tz


 (18)
for , where, represents the concen-
trationeric subayer. The boun
initial conditions are given by:
1 1n,,N
n in the nth ge
n c
-ldary and
0, for 0,
n
n
c
K
zh
z  (19)
and


e equations represented by the Equation (18) are
the continuity conditions
and flux at the interfaces. Namely:

,0, for 0
n
czt t (20)
Th
joined by for the concentration

1 1, 2,,1, nn
ccn N

 (21)

1 nn
cc
11, 2,,1 nn
K
Kn


N.
zz

  (22)
We apply the Laplace Transform technique in time
variable in Equation (18). We determine the solut
the resulting equation, in a easy manner, using the well
kn
ion of
ow results of second order linear differential equations
with constant coefficients. Indeed, it turns out that by this
procedure, the pollutant concentration in each sub-layer
reads like:

  
2nn RK
fo , whereas s denotes the Lap
formed variable. We are now in position to construct t
global solution for the puff emission. For such, ac- cord-
the Green fun

00
nn
nn
Rz Rz
nnn
RzHtsRzH ts
cz,s AeBe
Qee.




(23)
r 1, , 1nNlace trans-
he
ing ction theory for particular solution, we
write down the solution for a single puff like:

 



00
1
,22
nn
iRzRz
nnn
i
nn
Q
cztAe Be
iRK
 
 





d
nS nS
Rz H tsRzH tsst
s
ee
HzHes
  




(24)
for 1, , 1nN

, where n
nz
RsK,
s
H
is the
heig (located in
that mu is valid
oan
ht of the source
Heaviside function
only in the sub-layer that c
1, , 1
0x
ltiplies the part
ntains the source,
) and H is the
that
An d Bn
(nN

) are the integration costnanhey are
determinate by solving the linear system resulting from
the application of the boundary and interfaces conditions.
More details on the ADMM approach can be found on
[8] and [11].
Finally, we would like to point out that since we suc-
ceed in the task of searching solution for the puff prob-
lem (1), we are confident to affirm that we pave the road
ts, t
to mitigate the previous Gaussian assumptions in the x
and y directions, working out the three-dimensional ad-
vection-diffusion equation with puff source by the ADMM
approach.
Once the solution for single puff is know, we claim
that the puff solution reads like the summation of the
contribution of all puffs emitted by the source. This pro-
cedure leads to the solution:





0
0
1
d



 

puff
p
n
P
pn
t
p
cz,t
M
cz,tHtt t (25)
for p = 1:P, where P is the total number of puffs emitted,
is the mass carried out for the pth puff and

p
M
p
uff
n
c
obtain the is th
search
e one-dimensional puff solution. To
ed three-dimensional solution, we make the as-
hree-
sumption that the solution in the x and y directions are
described by Gaussian solution. Henceforth, the t
dimensional puff solution, assuming point source at
0

xy , has the form:


,,,,, ,
puff
puffn puff
cxyztcxyt (26)
noticing that the function

p
uff is given by Equation (4).
Here


,,,
ff xyzt is the searched puff solution. Fur- pu
C
0
ther,
x
and 0 y
essed in terms of
are the puff centroid coordi
pr
nates ex-
x
ancompond y wind ent as:
,
x
ut

 (27)
,


y
vt
(28)
where u and v are respective the wind components in the
x and y directions. Here

t is the time interval of the
puff emission. In addition, we
are the standard deviation for x
set.
must recall that 
x and

y
and y directions [12].
3. Experimental Data and Vertical
Turbulence Parameterization
The performances of the present models were evaluated
against experimental data of Copenhagen [12,15] data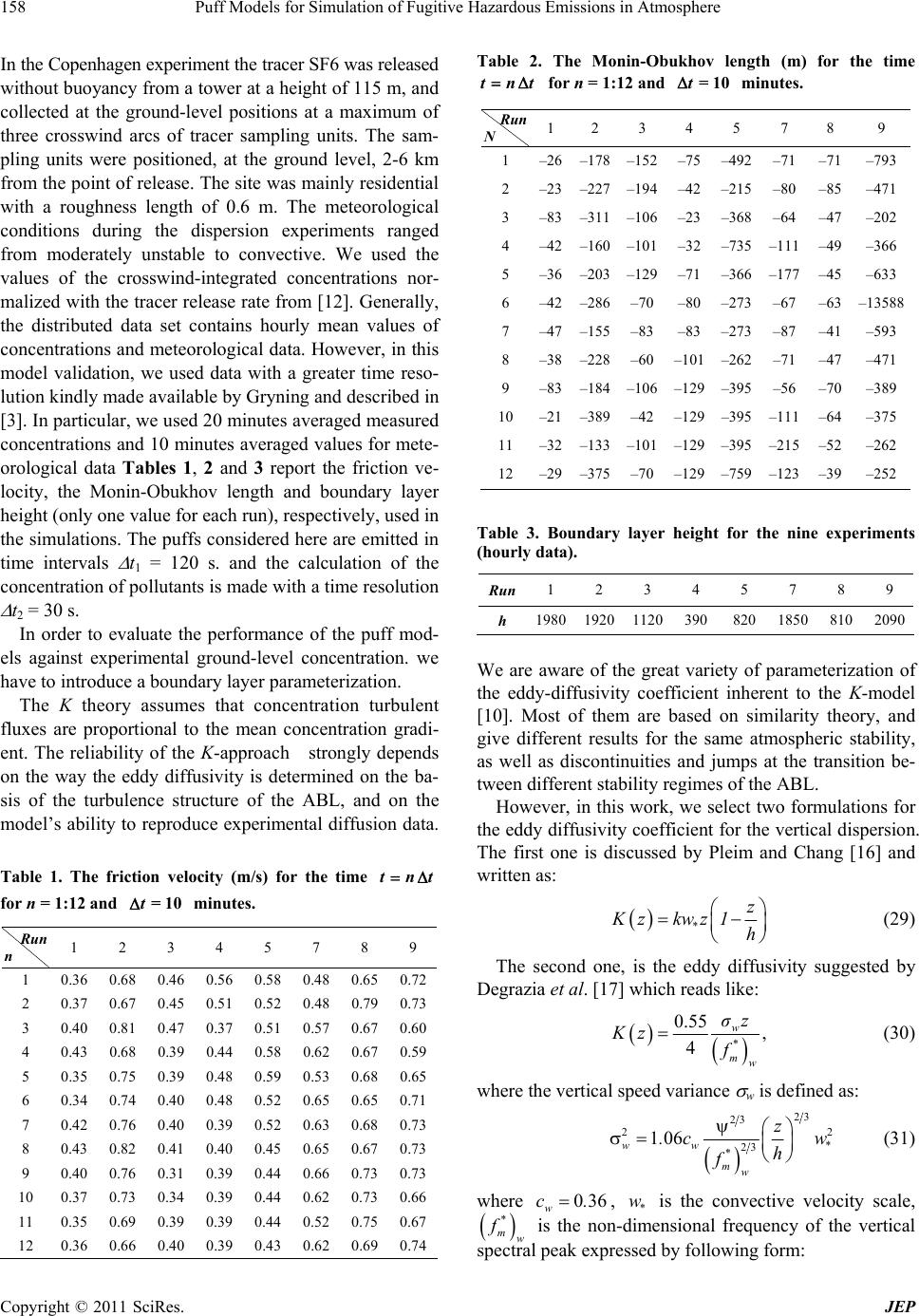

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere
158
Table 2. Theniu fee
In the Copenhagen experiment the tracer SF6 was released
wit of 115 m, and
f
thout buoyancy from a tower at a heigh
collected at the ground-level positions at a maximum of
three crosswind arcs of tracer sampling units. The sam-
pling units were positioned, at the ground level, 2-6 km
from the point of release. The site was mainly residential
with a roughness length of 0.6 m. The meteorological
conditions during the dispersion experiments ranged
from moderately unstable to convective. We used the
values of the crosswind-integrated concentrations nor-
malized with the tracer release rate from [12]. Generally,
the distributed data set contains hourly mean values of
concentrations and meteorological data. However, in this
model validation, we used data with a greater time reso-
lution kindly made available by Gryning and described in
[3]. In particular, we used 20 minutes averaged measured
concentrations and 10 minutes averaged values for mete-
orological data Tables 1, 2 and 3 report the friction ve-
locity, the Monin-Obukhov length and boundary layer
height (only one value for each run), respectively, used in
the simulations. The puffs considered here are emitted in
time intervals  t1 = 120 s. and the calculation of the
concentration of pollutants is made with a time resolution
 t2 = 30 s.
In order to evaluate the performance of the puff mod-
els against experimental ground-level concentration. we
have to introduce a boundary layer parameterization.
The K theory assumes that concentration turbulent
luxes are proportional to the mean concentration gradi-
ent. The reliability of the K-approach strongly depends
on the way the eddy diffusivity is determined on the ba-
sis of the turbulence structure of the ABL, and on the
model’s ability to reproduce experimental diffusion data.
Table 1. The friction velocity (m/s) for the time tnt


for n = 1:12 and t=10 minutes.
Run
n 1 2 3 4 5 7 8 9
1 0.36 0.68 0.46 0.56 0.58 0.48 0.65 0.72
2 0.37 0.67 0. 0.51 0.52 0.4548 0.79 0.73
0.40 0.81 0.47 0.37 0.51 0.57 0.67 0.60
0. 0 0 00. 0 00.
12 0.36 0.66 0.40 0.39 0.43 0.62 0.69 0.74
3
4 43.68.39.4458.62.6759
5 0.35 0.75 0.39 0.48 0.59 0.53 0.68 0.65
6 0.34 0.74 0.40 0.48 0.52 0.65 0.65 0.71
7 0.42 0.76 0.40 0.39 0.52 0.63 0.68 0.73
8 0.43 0.82 0.41 0.40 0.45 0.65 0.67 0.73
9 0.40 0.76 0.31 0.39 0.44 0.66 0.73 0.73
10 0.37 0.73 0.34 0.39 0.44 0.62 0.73 0.66
11 0.35 0.69 0.39 0.39 0.44 0.52 0.75 0.67
Mon-Obkhov length(m) or th tim
tnt

 for n12 = 1: andt=10

minu
n
N
tes.
Ru
1 2 3 4 5 7 8 9
1 –26–––492 –71 ––178152–75 71793
2 –23–227–194–42 –215 –80 –85–471
–83 –311–106368 –64 3 –23 ––47–202
––160–101–32 –735 – ––366
–
4 4211149
5 –36–203–129–71 –366 –177 –45–633
6 –42–286–70–80 –273 –67 –6313588
7 –47–155–83–83 –273 –87 –41–593
8 –38–228–60–101 –262 –71 –47–471
9 –83–184–106–129 –395 –56 –70–389
10 –21–389–42–129 –395 –111 –64–375
11 –32–133–101–129 –395 –215 –52–262
12 –29–375–70–129 –759 –123 –39–252
Tau r the
(hourly data).
R
ble 3. Bondary
layeheigh for te nin experiments
un 1 2 3 4 5 7 89
h 198019201120390 820 1850 8102090
We are aware of the great variety of parameterization of
the eddy-diffusivity coefficient inherent to the K-model
[10]. Most of m ba onmilty try,d
gidit resul tmmrta,
s well as discontinuities and jumps at the transition be-
the aresed siariheo an
ve fferents forhe sae atosphe ic sbility
a
tween different stability regimes of the ABL.
However, in this work, we select two formulations for
the eddy diffusivity coefficient for the vertical dispersion.
The first one is discussed by Pleim and Chang [16] and
written as:


z



*
Kz kwz1h (29)
The second one, is the eddy diffusivity suggested by
Degrazia et al. [17] which reads like:


0.55 ,
4
w
*
mw
σz
Kz f (30)
where the vertical speed variance 
w is defined as:

23
23

22
23
106
ww
*
mw
z
.c
f
 
*
w
h
 (31)
where 036

w
c., * w is the convective velocity scale,


*
mw
f
is the non-dimensional frequency of the vertical
d by following form: spectral peak expresse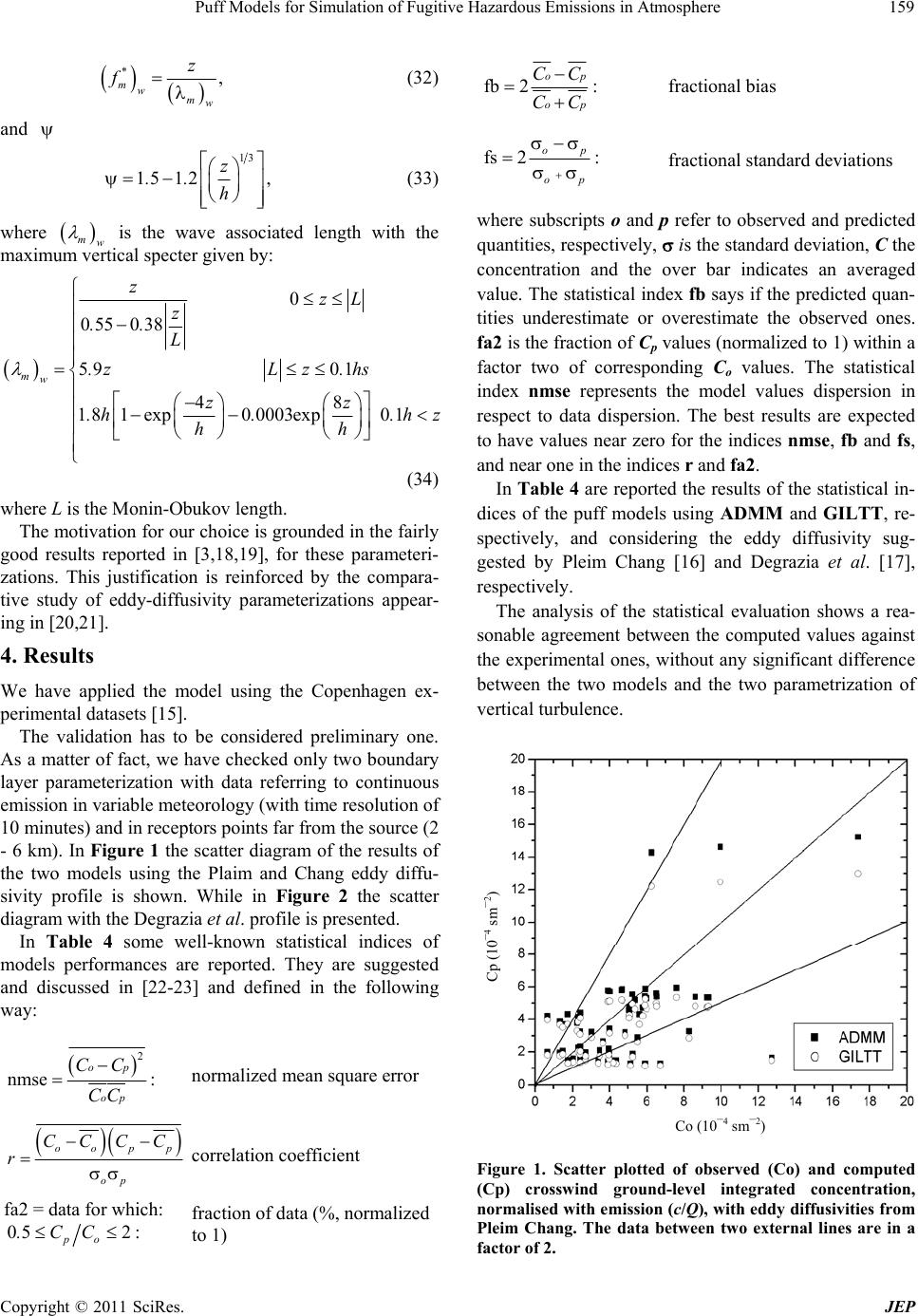

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere159


,
*
mwmw
z
f (32)
and 
13
15 12,
z
..
h


 




(33)
where is the wave
maximcal specter given by:

mw

um verti
associated length with the

0
055 038
5 9 0 1
48
1 81exp0 000
mw
zz
.h .
 




3exp0 1
zzL
z
..
L
.z L z.hs
.hz
hh








 


 



(34)
where L is the Monin-Obukov length.
The motivation for our choice is grounded in the fairly
good results reported in [3,18,19], for these parameteri-
zations. This justification is reinforced by the compara-
tive study of eddy-diffusivity parameterizations appear-
ing in [20,21].
n with data referring to continuous
riable meteorology (with time resolution of
4. Results
We have applied the model using the Copenhagen ex-
perimental datasets [15].
The validation has to be considered preliminary one.
As a matter of fact, we have checked only two boundary
layer parameterizatio
emission in va
10 minutes) and in receptors points far from the source (2
- 6 km). In Figure 1 the scatter diagram of the results of
the two models using the Plaim and Chang eddy diffu-
sivity profile is shown. While in Figure 2 the scatter
diagram with the Degrazia et al. profile is presented.
In Table 4 some well-known statistical indices of
models performances are reported. They are suggested
and discussed in [22-23] and defined in the following
way:

2
nmse  opCC : normalized mean square erro
op CC
r




oo pp
CCCC
r

 correlation coefficient
fraction of data (%, normalized
to 1)
fb 2 
op
op
CC
CC
: fractional bias
fs 2






op
op
: fractional standard deviations
p
quantities, respectiv
concentration and the oan averaged
value. The statistical index e predicted quan-
tities underestate or observed ones.
fa2 is the fraction of Cp values (normalized to 1) within a
factor two of correspondi C
index nmse reesents n
respect to data dispersion. The best results are expected
parametrization of
ve
Figure 1. Scatter plotted of observed (Co) and computed
(Cp) crosswind ground-level integrated concentration,
normalised with emission (c/Q), with eddy diffusivities from
Pleim Chang. The data between two external lines are in a
fact or of 2.
where subscripts o and
ely,
refer to observed and predicted
 is the standard deviation, C the
ver bar indicates
fb says if th
overestimate theim
ng o values. The statistical
the model values dispersion ipr
op

fa2 = data for which:
05 2
po
.CC:
to have values near zero for the indices nmse, fb and fs,
and near one in the indices r and fa2.
In Ta ble 4 are reported the results of the statistical in-
dices of the puff models using ADMM and GILTT, re-
spectively, and considering the eddy diffusivity sug-
gested by Pleim Chang [16] and Degrazia et al. [17],
respectively.
The analysis of the statistical evaluation shows a rea-
sonable agreement between the computed values against
the experimental ones, without any significant difference
between the two models and the two
rtical turbulence.
Cp (10–4 sm–2)
Co (10–4 sm–2)

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere
160
Figure 2. Scatter plotted of observed (Co) and computed
(Cp) crosswind ground-level integrated concentration, nor-
malised with emission (c/Q), with eddy diffusivities from
Degrazia. The data between two external lines are in a fac-
tor of 2.
Table 4. Statistical evaluation of model results.
Model Edyy
diffusivity nmse r fa2 fb fs
ADMM Eq. (41) 0.42 0.58 0.72 0.16 0.01
ADMM
G
G
Eq. (42) 0.40 0.58 0.75 0.14 0.02
ILTT Eq. (41) 0.48 0.57 0.70 0.28 0.16
ILTT Eq. (42) 0.48 0.57 0.72 0.29 0.17
5. Conclusions
We presented a puff model where the vertical concentra
tion distribution is not Gaussian but is describe by
new solutions of the advection-diffusion equation that
accept eddy diffusion co any restriction in
the well-known Copenhagen data set, but with
greater time resolution respect to the original one.
Anon of
well-known statistical indices show that both ap-
pr cp aodfoe ground
level concenare not significant dif-
fbete tos w
dy erizs hri-
mental data.
elimsulnfelicabilityhe
app prond prsing fr rerk:
n offityeri
nd using the ADMM and GILTT solutions in the lat-
-
two
efficient with
their height function.
As preliminary evaluation of the model performances,
the results predicted by the puff model, using two differ-
ent turbulence parameterizations where compared with
data from
a
alysis of the results obtained and the applicati
oachesonsidered
tration data. There
roduce go fit r th
erences ween thwo slution and the to eddy
iffusivitparametationin te range of expe
The prinary rets coirm th app of t
roach
valuatio
posed a
f other ed
are
dy di
omi
usiv
o
para
futu
met
wo
zations e
a
eral dispersion also.
6. Acknowledgements
The authors are gratefully indebted to CNPq, FAPERGS,
CNR and ENVIREN for the partial financial support of
this work.
Cp (14 s) 0–m–2
REFERENCES
[1] R. Lupini and T. Tirabassi, “Solution of the Advection-
Diffusion Equation by the Moments Method,” Atmos-
pheric Environment, Vol. 17, No. 5, 1983, pp. 965-971.
doi:10.1016/0004-6981(83)90248-2
[2] T. Tirabassi and U. Rizza, “A Practical Model for the
Dispersion of Skewed Puffs,” Journal of Applied Meteor-
ology, Vol. 34. No. 4, 1995, pp. 989-99.
doi:10.1175/1520-0450(1995)034<0989:APMFTD>2.0.C
O;2
[3] T. Tirabassi and U. Rizza, “Boundary Layer Parameteri-
zation fo
Co (10–4 sm–2)
r a Non-Gaussian Puff Model,” Journal of
Applied Meteorology, Vol. 36, No. 8, 1997a, pp.
1031-1037.
doi:10.1175/1520-0450(1997)036<1031:BLPFAN>2.0.C
O;2
[4] T. Tirabassi and U. Rizza, “A Non-Gaussian Puff
Model,” Nuovo Cimento, Vol. 20C, 1997b, pp. 453-460.
ilhena, D. D. Moreira and D.
1016/j.atmosenv.2005.01.003
[5] S. Wortmann, M. T. M. V
Buske, “A New Analytical Approach to Simulate the
Pollutant in the PBL,” Atmospheric Environment, Vol. 39,
No. 34, 2005, pp. 2171-2178.
doi:10.
[6] D. M. Moreira, M. T. Vilhena, D. Buske and T. Tirabassi,
“The GILTT on-Diffusion Equa
tion for an Inhoy PBL,” At-
Solution of the Advecti
mogeneous and Nonstationar
mospheric Environment, Vol. 40, No. 17, 2006, pp. 3186-
3194. doi:10.1016/j.atmosenv.2006.01.035
[7] M. T. Vilhena, U. Rizza, G, Degrazia, C. Mangia, D. M
Moreira and T. Tirabassi, “An Ana
.
lytical Air Pollution
. Tirabassi, C. P
in the Atmosphere by the Laplace Transform: The
Model: Development and Rvalution,” Contribution At-
mospheric Physics, Vol. 71, 1998, pp. 818-827.
[8] D. M. Moreira, M. T. Vilhena, M. T. T
Costa and B. Bodmann, “Simulation of Pollutant Disper-
sion
ADMM Approach,” Water, Air and Soil Pollution, Vol.
177, No. 1-4, 2006a, pp. 411-439.
doi:10.1007/s11270-006-9182-2
[9] P. Zannetti, “
nology Publications, Southampton, UK, 1990.
[10] J. H. Seinf
Air Pollution Modeling,” Computer Tech-
eld and S. N. Pandis, “Atmospheric Chemistry
and Physics,” John Wiley & Sons, New York, 1998, pp.
1326.
[11] C. P. Costa, M. T. Vilhena, D. M. Moreira and T. Tira-

Puff Models for Simulation of Fugitive Hazardous Emissions in Atmosphere
161
c Environment, Vol. 40,
bassi, “Semi-Analytical Solution of the Steady Three-
Dimensional Advection-Diffusion Equation in the Planetari
Boundary Layer,” Atmospheri
2006, pp. 5659-5669.
doi:10.1016/j.atmosenv.2006.04.054
[12] S. E. Gryning, A. A. M. Holtslag, J. S. Irwin and B.
Siversten, “Applied Dispersion Modelling Based on Me-
teorological Scaling Parameters,” Atmospheric Environ-
ment, Vol. 21, 1987, pp. 79-89.
doi:10.1016/0004-6981(87)90273-3
[13] C. F. Segatto and M. T. M. B. Vilhena, “The State-
of-the-Art of the LTSN Method,” Proceeding of M&C'99
Conference on Mathematics and Computation, Reactor
ere,” Atmospheric Re-
Physics and Environmental Analysis in Nuclear Applica-
tions, Vol. 3, No. 2, 1999, pp. 1618-1631.
[14] D. M. Moreira, M. T. Vilhena, D. Buske and T. Tirabassi,
“The State-of-Art of the GLTT Method to Simulate Pol-
lutant Dispersion in the Atmosph
search, Vol. 92, 2009, pp. 1-17.
doi:10.1016/j.atmosres.2008.07.004
[15] S. E. Gryning and E. Lyck, “Atmospheric Dispersion
from Elevated Sources in an Urban Area: Comparison
between Tracer Experiments and Model Calculations,”
Journal of Climate Applied Meteorology, Vol. 23, No. 4,
1984, pp. 651-660.
doi:10.1175/1520-0450(1984)023<0651:ADFESI>2.0.C
O;2
[16] J. Pleim and J. S. Chang, “A Non-Local Closure Model
for Vertical Mixing in the Convective Boundary Layer,”
Atmospheric Environment, Vol. 26, No. 6, 1992, pp. 965-
981.
[17] G. A. Degrazia, D. M. Moreira and M. T. M. B. Vilhena,
“Derivation of an Eddy Diffusivity Depending on Source
Distance for Vertically in Homogeneous Turbulence in a
Convective Boundary Layer,” Journal of Applied Mete-
orology, 2001, pp. 1233-1240.
doi:10.1175/1520-0450(2001)040<1233:DOAEDD>2.0.
CO;2
[18] C. Mangia, D. M. Moreira I. Schipa G. A. Degrazia, T. T
Tirab
.
assi and U. Rizza. “Evaluation of a New Eddy Dif-
016/S1352-2310(01)00469-1
fusivity Parameterisation from Turbulent Eulerian Spectra
in Different Stability Conditions,” Atmospheric Environ-
ment, Vol. 36, No. 1, 2002, pp. 67-76.
doi:10.1
[19] D. M. Moreira, J. C. Carvalho, A. G. Goulart and T.
Tirabassi, “Simulation of the Dispersion of Pollutants
Using Two Approaches for the Case of a Low Source in a
SBL: Evaluation of Turbulence Parameterisations,” Water
Air and Soil Pollution, Vol. 161, No. 1-4, 2005, pp.
285-297. doi:10.1007/s11270-005-4287-6
[20] T. Tirabassi, F. Baffo and D. M. Moreira, “Eddy Diffu-
and T. Tirabassi,
terisations by an
3, No. 6, 1989,
sivity Parameterizations and Improve Features in an
Analytical Multilayer Dispersion Model,” Proceeding of
XIII Brazilian Congress of Meteorology, Fortaleza (Br),
August 2004.
[21] D. Buske, M. T. Vilhena, D. M. Moreira
“Evaluation of Eddy Diffusivity Parame
Analytical Solution of the Advection-Diffusion Equa-
tion,” Proceeding of XIV Brazilian Congress of Meteorology,
Florianopolis (Br), November 2006.
[22] S. R. Hanna, “Confidence Limit for Air Quality Models
as Estimated by Bootstrap and Jackknife Resampling
Methods,” Atmospheric Environment, Vol. 2
pp. 1385-1395. doi:10.1016/0004-6981(89)90161-3
[23] J. C. Chang and S. R. Hanna. “Air Quality Model Per-
formance Evaluation,” Meteorological Atmosphere Physics,
Vol. 87, No. 1-3, 2004, pp. 167-196.