J. Software Engineering & Applications, 2009, 2: 44-49
Published Online April 2009 in SciRes (www.SciRP.org/journal/jsea)
1
QoS-Aware Reference Station Placement for Regional
Network RTK
Maolin Tang
1
1
Cooperative Research Centre for Spatial Information, Faculty of Science and Technology, Queensland University of Technology
2 George Street, Brisbane, Australia
Received December 24
th
, 2008; revised January 30
th
, 2009; accepted February 26
th
, 2009.
ABSTRACT
Network RTK (Real-Time Kinematic) is a technology that is based on GPS (Global Positioning System) or more gener-
ally on GNSS (Global Navigation Satellite System) measurements to achieve centimeter-level accuracy positioning in
real-time. Reference station placement is an important problem in the design and deployment of network RTK systems
as it directly affects the quality of the positioning service and the cost of the network RTK systems. This paper identifies
a new reference station placement for network RTK, namely QoS-aware regional network RTK reference station
placement problem, and proposes an algorithm for the new reference station placement problem. The algorithm can
always produce a reference station placement solution that completely covers the region of network RTK.
Keywords: Reference Station, Placement, Regional Network RTK, QoS
1. Introduction
Network RTK (Real-Time Kinematic) is a technology
that is based on GPS (Global Positioning System) or
more generally on GNSS (Global Navigation Satellite
System) measurements to achieve centimeter-level accu-
racy positioning in real-time. It involves a network of
reference stations that are used to take and transmit their
raw GPS or GNSS measurements [1,2,3,4].
The success of network RTK in recent years has re-
sulted in the establishment of network RTK positioning
services to anyone who is willing to pay for them. In
order to provide network RTK services to an area, such
as a state or a country, many reference stations must be
set up and maintained. However, setting-up and main-
taining reference stations is costly, typically tens of
thousands of Australian dollars each with annual op-
erational cost of approximately 10% of the reference
station cost. Therefore, it is desirable to minimize the
total number of reference stations without compromis-
ing the QoS of network RTK. However, the reference
station placement problem has not drawn enough atten-
tion from the community, and little research has been
done.
In our preliminary research, we have identified a sig-
nificant reference station placement problem, namely
location-oriented reference station placement problem,
and proposed an effective and efficient algorithm for the
reference station placement problem [5]. That reference
station placement problem is described as: Given a set of
potential locations where reference stations can be set up
and the locations of the users, select reference station
locations among the potential reference station locations
such that the total number of reference stations is mini-
mum subject to a constraint, that is, the maximal distance
between any user to the closest reference station does not
exceed a parameter
max
D . This maximum distance con-
straint must be satisfied in order to guarantee the accu-
racy of the positioning services.
Recently, we identified and proposed an algorithm for
an area-oriented reference station placement problem for
network RTK [6]. Given a service area that a network
RTK needs to cover, the area-oriented reference station
placement problem strives to find a reference placement
such that the service area is completely covered by the
reference stations. The major deficiency of the algorithm
is that it cannot provide a reference placement solution
that can guarantee to provide QoS because the algorithm
cannot guarantee to generate a reference station place-
ment solution that completely covers the service area
although in most cases it does. As a result, those users
who are located in an area where is not covered by the
reference stations may not receive quality positioning
service.
In this paper we propose a new reference station
placement problem, namely, QoS-aware regional network
RTK reference station problem, and extend the area-ori-
ented reference station placement problem to guarantee to
generate a reference station placement solution that cov-
ers the whole service area. The proposed algorithm has
been implemented and tested by simulation. Experimen-
tal results show that the algorithm is efficient and effec-
tive.

QoS-Aware Reference Station Placement for Regional Network RTK 45
The remaining paper is organized as follows. Section 2
formulates the QoS-aware regional network RTK refer-
ence station placement problem. Section 3 discusses re-
lated work. Section 4 presents our approach to the new
reference station placement problem in detail. The simu-
lation results are presented in Section 5. Finally we con-
clude the proposed approach in Section 6.
2. Problem Formulation
Given an area and the maximal distance constraint from
any user to its closest reference station, the QoS-aware
regional network RTK reference station placement prob-
lem is to find locations on the area such that all the users
at any location within the area can receive real-time cen-
timeter accuracy positioning services.
In order to guarantee a user can get the real-time cen-
timeter accuracy positioning services, it must be guaran-
teed that the maximum distance between the user to its
closest reference station is less than or equals to the
maximum distance constraint. Because the user can be
distributed at any position on the area, the maximum dis-
tance constraint implies that the maximum distance be-
tween any position in the area and its closest reference
station must not exceed the maximum distance constraint.
Thus, the QoS-aware network RTK reference station
placement is formulated as:
Given an area A and the maximal distance constraint
D
max
, find a set of reference stations
{
}
n
rrrR ,,,
21
…=
such that R is minimum, subject to
Ayxp
pp
∈=∀ ),( ,
(
)
Ryxr
iii
∈=∃ ,, where, and
maxrprp
D)yy()xx( ≤−+−
22
. The constraint guar-
antees that the QoS, or the accuracy of positioning ser-
vices, is satisfied.
3. Related Work
In our preliminary research on network RTK, we have
identified a so-called location-oriented reference station
placement problem. The location-oriented reference sta-
tion placement problem is stated as below:
Given a set of reference station candidates
{
}
n
rrrR ,,,
21
…= , a set of users
{
}
m21
,,, uuuU …= , and
the maximal distance between any user and its closest refer-
ence station
max
D, the location-oriented reference stations
placement problem is to find RR ⊆
0
, such that
0
R is
minimal, subject to U)y,x(u
iii
∈=∀,
(
)
Ryxr
jjj
∈=∃ , and
max
22
)()( Dyyxx
jiji
≤−+− , where mi
≤
≤
1 and
nj
≤
≤
1.
The location-oriented reference stations placement
problem can be represented in a so-called graph
),( EVG = , where RUV U=. An edge
(
)
Evv ∈
21
, , if
and only if
(
)
Uyxv ∈=
111
, ,
(
)
Ryxv∈=
222
, , and
max
D)yy()xx( ≤−+−
2
21
2
21
, where
(
)
11
, yx and
(
)
22
, yx represent the location of v
1
and the location of
2
v , respectively. Therefore, the location-oriented refer-
ence station placement problem can be transformed into
the following graph-theoretic problem:
Given a RTK graph
(
)
EVG , = , where RUV U=,
find RR ⊆
0
, such as that
0
VV = , where
(
)
{
}
00
&,RrEvrvV∈∈= .
A RTK graph can be represented by an m × n adja-
cency matrix
nmij
aA
×
= ][ , where


∈
=otherwise
Eruif
a
ji
ij
,0
).(,1
For example, for the RTK graph shown in Figure 1.
The adjacent matrix
















=
1000
1110
0011
1100
0011
A
The location-oriented reference stations placement
problem is a constrained version of the problem of find-
ing a minimum dominating set of an arbitrary graph,
which is an NP-hard [7].
It is conjectured that this reference stations placement
problem is also NP-hard. Thus, we proposed a heuristic
algorithm in [5].
The heuristic algorithm starts with an initial refer-
ence station placement that uses all the reference sta-
tion candidates. Then, the number of reference station
candidates is gradually reduced by iteratively removing
redundant reference stations. A reference station is re-
dundant if all the users that can be covered by the ref-
erence station can also be covered by other reference
stations. A user is said to be covered by a reference
station if the distance between the user and the refer-
ence station does not exceed
max
D . A redundant refer-
ence station
i
r can be identified in the matrix repre-
sentation by checking if there is a second non-zero en-
try in the
th
j column of the matrix. Algorithm III is
the high-level description of the location-oriented ref-
erence station placement algorithm.
Figure 1. A RTK graph

46 QoS-Aware Reference Station Placement for Regional Network RTK
Algorithm 1: Location-oriented placement algorithm
Require: Locations of reference station candidates, loca-
tions of users and the maximal distance allowed between
a user and its reference station
max
D
Ensure: Return the location of reference stations
generate its RTK graph
(
)
EVG ,= ;
for each reference station candidate
R
r
∈
do
if r is redundant then
remove it from R;
remove its associated edges from E;
end if
end for
Output the location of the reference station candi-
dates left in R.
It has been proved in [5] that the computational com-
plexity of the algorithm is
(
)
mnO∗
3
, where m is the
number of reference station candidates and n represents
the number of users. Details about the algorithm analysis
can be found in [5].
4. Approach
The QoS-aware network RTK reference station place-
ment problem is a continuous optimization problem and
it is difficult to be tackled directly. Thus, we transform
the QoS-aware network RTK reference station placement
problem into the location-oriented reference station
placement problem discussed in the Related Work, and
use the location-oriented reference station placement al-
gorithm to tackle the QoS-aware network RTK reference
station placement problem.
In the following, we will discuss how to transform the
QoS-aware network RTK reference station placement
problem into the location-oriented reference station
placement problem. Then, we will present an algorithm
for the QoS-aware network RTK reference station
placement problem, and then we analyses the optimality
and efficiency of the new algorithm.
4.1 Transformation
The QoS-aware network RTK reference station place-
ment problem is a continuous optimization problem,
where the locations of reference stations are on a con-
tinuous two-dimensional region. Thus, it is difficult to be
handled directly as its search space is infinite. However,
the continuous optimization problem can be transformed
into the location-oriented reference station placement
problem using the following procedure.
First of all, a two-dimensional grid graph is generated to
completely cover the whole region of the network RTK A.
This idea is illustrated in Figure 2. In the figure, the filled
enclosed area represents the network RTK service area A.
Then, we select those grid nodes on or outside the
boundary such that the area of the polygon formed by con-
necting those grid nodes is minimal, but can completely
cover the network RTK service area A. Figure 3 shows
such a polygon based on the grid graph shown in Figure 2.
Figure 2. A grid graph that completelly covers the network
RTK service area A
Figure 3. A minimal polygon that completelly covers the
network RTK service area A
And then, we create a sub-graph of the grid graph by
selecting all the grid nodes and arcs enclosed by the
polygon. Figure 4 shows the sub-graph generated from
the grid graph and the polygon shown in Figure 3.
In order to make use of the location-oriented reference
station placement algorithm discussed in the Related
Work section, we need to create dummy users and initial
reference stations (reference station candidates). The se-
lection of users and initial reference stations is very im-
portant because if they are not well chosen, then the loca-
tion-oriented reference station placement algorithm may
not produce a solution that can completely cover the
whole service area of the regional network RTK. Thus, in
the following, we will introduce rules for selecting
dummy users and initial reference stations. We will prove
that by selecting dummy users and initial reference sta-
tions it is guaranteed that the algorithm can always pro-
duce a solution that can completely cover the given ser-
vice area of the regional network RTK.
Given a grid graph
(
)
EVG ,= , all the nodes whose
degree is greater than one are selected as reference sta-
tions and on each edge we create three dummy users: one
at each end of the edge and one at the middle of the edge.
The rules for selecting initial reference stations and the
rules for selecting dummy users are illustrated in Figure 5

QoS-Aware Reference Station Placement for Regional Network RTK 47
and Figure 6, respectively. It will be proven in the paper
that by selecting reference station candidates and user
positions using the above rules, our algorithm can always
produce a reference placement solution that can 100%
covers the given service area A.
Using the rules, we can create a set of initial reference
stations
{
}
n
rrrR ,,,
21
…= and a set of users
{
}
m21
u,,u,uU …= , and have transformed the QoS-aware
regional network RTK reference station problem into the
location-oriented reference station placement problem.
4.2 Algorithm Description
Once we have transformed the QoS-aware regional net-
work RTK reference station placement problem into the
location-oriented reference station placement problem,
we can make use of the ideas of the location-oriented
reference station placement algorithm presented in the
Related Work section to tackle the QoS-aware regional
network RTK reference station placement problem. Al-
gorithm 2 gives a high-level description of the algorithm
for the QoS-aware regional network RTK reference sta-
tion placement problem.
Algorithm 2: QoS-aware regional network RTK place-
ment station placement algorithm
Figure 4. The subgraph enclosed by the minimal polygon
Figure 5. Initial reference stations selection rule
Figure 6. Dummy users selection rule
Require : Network RTK service area A and the maximal
distance allowed between a user and its reference station
max
D .
Ensure: Return the location of reference stations
generate a grid graph of grid size g;
generate the minimal polygon covering the network
RTK service area A;
generate the sub-graph enclosed by the minimal
polygon;
use the rules to create reference station candidate set
R and user set U;
generate its RTK graph
(
)
ERUG ,U= ;
for each reference station candidate
R
r
∈
do
if r is redundant then
remove it from R;
remove its associated edges from E;
end if
end for
Output the location of the reference station candi-
dates left in R.
4.3 Algorithm Analysis
This subsection provides theoretic analysis of the algo-
rithm for the QoS-aware regional network RTK reference
station placement problem presented in the previous sub-
section.
Lemma 1: Algorithm 2 always produces a reference
placement station placement solution in which every
generated user is covered by at least one of the reference
stations.
Proof: Algorithm 2 starts with generating a set of users
and a set of reference stations, and then iteratively re-
duces redundant reference stations. It can be guaranteed
by the rules for identifying users and initial reference
stations that every generated user can be covered by at
least reference station initially, and that during the itera-
tive process of reducing redundant reference stations only
redundant reference stations are removed, which means
all the users that is covered by a removed redundant ref-
erence station can also be covered by another reference
station. Thus, after removing all the redundant reference
stations, every generated user is covered by at least one
of the reference stations.
Theorem 1: Given an area A and the maximum dis-
tance constraint
max
D . algorithm 2 always produces a
reference station placement solution that completely cov-
ers A.
Proof: The given area A is enclosed by a polygon. If
we can prove that the polygon is completely covered by
the reference station placement solution produced by Al-
gorithm 2, then we have proved that the given area A is
completely covered by the solution. In addition, it has
been proved in Lemma 1 that Algorithm 2 can always
produce a solution that covers all the dummy users. Thus,
all we need to prove in the following is that when all the
dummy users are covered, the polygon is 100% covered.

48 QoS-Aware Reference Station Placement for Regional Network RTK
The area of the enclosing polygon is composed of two
basic types of two-dimensional areas, squares and isos-
celes right triangles. For each of the squares as shown in
Figure 7, it will be completely covered by the solution
because in order to cover all the eight user position on the
square as shown in Figure 6 at least two diagonal ref-
erence station candidates must be selected. When any
two of the diagonal candidates on a square are selected,
the whole area of the square will be covered. Note that
the coverage of the reference station is always the length
of the square. Thus, it can be concluded that all the
square areas will be covered by the solution. Figure 7
illustrates the idea. In the figure, two diagonal candidates
A and C are selected. The shadow circles display the
coverage of the reference stations at candidate A and
candidate C.
For each of the isosceles right triangles as shown in
Figure 8, it will also be completely covered by the solu-
tion because according to the reference station candidate
and user selection rules, the only possibility to cover all
the three users on the line from A to B is to select the
reference station candidate at position A, and when that
reference candidate is selected, the isosceles right triangle
ABC will be completely covered by the reference station.
This is illustrated in Figure 8.
The quality of solutions obtained by the algorithm and
the computation time of the algorithm are both dependent
Figure 7. The square case
Figure 8. The isosceles right triangle case
on the grid size g, which is an important parameter used
by the algorithm. In the following section, we present our
empirical study results on the impact of g on the optimal-
ity and performance of the algorithm.
5. Experiment
The proposed algorithm has been implemented in Mi-
crosoft Visual C#. In order to test the optimality and per-
formance of the algorithm, we used the implemented al-
gorithm to find a reference station placement solution for
the network RTK area shown in Figure 2. The value of
max
D . was fixed to 140km, but the values used for the
gird size g varied from 10 to 140 with an increment of 10.
All experiments were conducted on desktop computers
with an Intel Core 2 Duo 6300 CPU (1.86GHz) and 2 GB
of RAM. Table I records the experimental results.
Figure 9 shows the trend of the quality of the solutions
obtained by the algorithm when the grid size increases. It
can be seen from the figure that the grid size used by the
algorithm directly affects the quality of the solutions ob-
tained by the algorithm, and that the smaller the grid size
the better solution the algorithm produces. For example,
when the grid size is 20 the solution produced by the al-
gorithm needs only 23 reference stations. However, when
the grid size increases to 140 the solution generated by
the algorithm needs 34 reference stations.
Figure 10 shows the trend of the computation time of
the algorithm when the grid size increases. It can be seen
from the figure that the computation time of the algo-
rithm decreases dramatically when the grid size increase.
For example, when the grid size is 20 the computation
time is 47.81 seconds. When the grid size increases to
140 the computation time is only 0.02 seconds.
The experimental results reveal that the smaller the
grid size is, the better the quality of the solution is. How-
ever, the computation time increases very quickly when
the grid size decreases. Figure 11 displays the result for
the area-oriented station placement problem obtained by
the implemented algorithm when the grid size g=20. In
the figure, the small filled squares represent reference
stations and the circles are the coverage of the corre-
sponding reference stations.
Table 1. Experimental results on the impact of g on the
optimality and computation time of the algorithm
Grid Size
(g) Reference Station Number Time (second)
20 23 47.81
40 26 2.32
60 27 0.45
80 28 0.15
100 31 0.06
120 33 0.03
140 34 0.02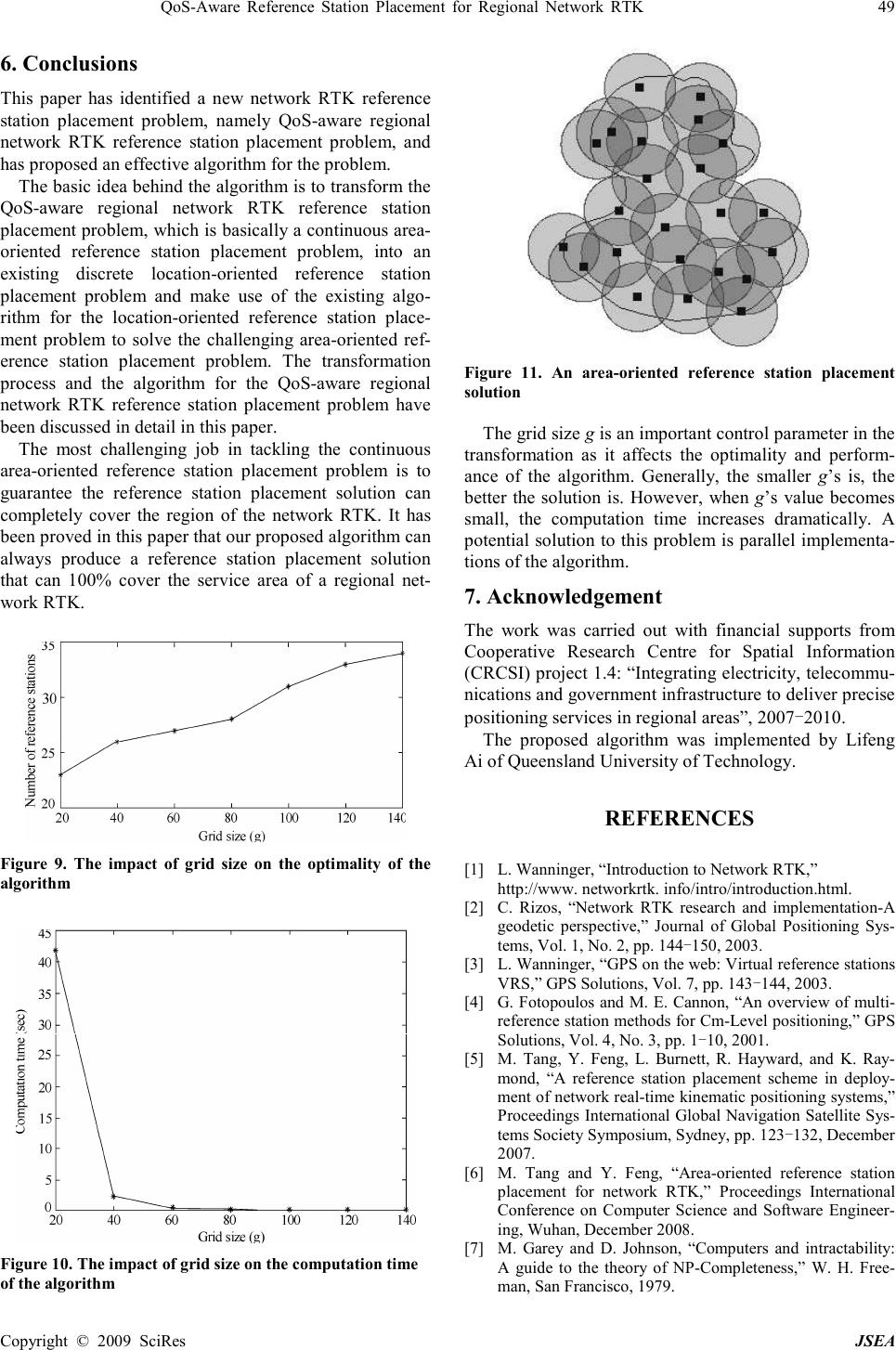

QoS-Aware Reference Station Placement for Regional Network RTK 49
6. Conclusions
This paper has identified a new network RTK reference
station placement problem, namely QoS-aware regional
network RTK reference station placement problem, and
has proposed an effective algorithm for the problem.
The basic idea behind the algorithm is to transform the
QoS-aware regional network RTK reference station
placement problem, which is basically a continuous area-
oriented reference station placement problem, into an
existing discrete location-oriented reference station
placement problem and make use of the existing algo-
rithm for the location-oriented reference station place-
ment problem to solve the challenging area-oriented ref-
erence station placement problem. The transformation
process and the algorithm for the QoS-aware regional
network RTK reference station placement problem have
been discussed in detail in this paper.
The most challenging job in tackling the continuous
area-oriented reference station placement problem is to
guarantee the reference station placement solution can
completely cover the region of the network RTK. It has
been proved in this paper that our proposed algorithm can
always produce a reference station placement solution
that can 100% cover the service area of a regional net-
work RTK.
Figure 9. The impact of grid size on the optimality of the
algorithm
Figure 10. The impact of grid size on the computation time
of the algorithm
Figure 11. An area-oriented reference station placement
solution
The grid size g is an important control parameter in the
transformation as it affects the optimality and perform-
ance of the algorithm. Generally, the smaller g’s is, the
better the solution is. However, when g’s value becomes
small, the computation time increases dramatically. A
potential solution to this problem is parallel implementa-
tions of the algorithm.
7. Acknowledgement
The work was carried out with financial supports from
Cooperative Research Centre for Spatial Information
(CRCSI) project 1.4: “Integrating electricity, telecommu-
nications and government infrastructure to deliver precise
positioning services in regional areas”, 2007 - 2010.
The proposed algorithm was implemented by Lifeng
Ai of Queensland University of Technology.
REFERENCES
[1] L. Wanninger, “Introduction to Network RTK,”
http://www. networkrtk. info/intro/introduction.html.
[2] C. Rizos, “Network RTK research and implementation-A
geodetic perspective,” Journal of Global Positioning Sys-
tems, Vol. 1, No. 2, pp. 144-150, 2003.
[3] L. Wanninger, “GPS on the web: Virtual reference stations
VRS,” GPS Solutions, Vol. 7, pp. 143-144, 2003.
[4] G. Fotopoulos and M. E. Cannon, “An overview of multi-
reference station methods for Cm-Level positioning,” GPS
Solutions, Vol. 4, No. 3, pp. 1-10, 2001.
[5] M. Tang, Y. Feng, L. Burnett, R. Hayward, and K. Ray-
mond, “A reference station placement scheme in deploy-
ment of network real-time kinematic positioning systems,”
Proceedings International Global Navigation Satellite Sys-
tems Society Symposium, Sydney, pp. 123-132, December
2007.
[6] M. Tang and Y. Feng, “Area-oriented reference station
placement for network RTK,” Proceedings International
Conference on Computer Science and Software Engineer-
ing, Wuhan, December 2008.
[7] M. Garey and D. Johnson, “Computers and intractability:
A guide to the theory of NP-Completeness,” W. H. Free-
man, San Francisco, 1979.