 Current Urban Studies 2013. Vol.1, No.4, 117-129 Published Online December 2013 in SciRes (http://www.scirp.org/journal/cus) http://dx.doi.org/10.4236/cus.2013.14013 Open Access 117 Socio-Spatial Inequality in Education Facilities in the Concepción Metropolitan Area (Chile) Helen De la Fuente1, Carolina Rojas1,2*, María Jesús Salado3, Juan Antonio Carrasco1,4, Tijs Neutens5 1Centre of Urban Sustainable Development CEDEUS, Concepción, Chile 2Department of Geography, Universidad de Concepción, Concepción, Chile 3Department of Geography and Geology, Universidad de Alcalá, Alcalá de Henares, Spain 4Department of Civil Engineering, Universidad de Concepción, Concepción, Chile 5Department of Geography, Ghent University, Krijgslaan, Ghent, Belgium Email: *crojasq@udec.cl Received September 13th, 2013; revised October 14th, 2013; accepted October 22nd, 2013 Copyright © 2013 Helen De la Fuente et al. This is an open access article distributed under the Creative Com- mons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, pro- vided the original work is properly cited. In Concepción Metropolitan Area (CMA), the uneven geographical distribution of population, exacerbat- ed by the recent spread of urban growth, has promoted a clear spatial inequity in the provision of quality educational facilities. The objective of this research is to systematically compare the 493 schools of exist- ing educational opportunities in the CMA with the aim to evaluate the spatial equity in order to improve a most inclusive urban planning. Statistical and graphical analysis revealed that nearest units to the center of the metropolitan area (Concepción) had better conditions than the farthest with respect to students- teacher ratio, teaching quality and academic outcomes assessment. This center-periphery pattern shows clearly the challenges to be faced in the CMA with respect to equitable access to quality educational re- sources. Keywords: Spatial Equity; Inequality; Educational Facilities; Accessibility; Concepción Metropolitan Area (Chile) Introduction According to recent reports by the Organization for the Co- operation and Economic Development (OCDE), Chile is the country where private funding has increased weight in both primary and secondary education, and where the lowest degree of socioeconomic inclusion of the students within a school is found (OCDE, 2012). To this student segregation according to income level is added, presumably, a spatial segregation that according to free market laws, it concentrates best quality cen- ters in urban sectors in which middle-high socioeconomic sec- tors predominate. This situation would be feeding a growing social polarization in which lower class groups located in pe- ripheral areas have more difficult access to quality services and facilities (Sabatini & Brain, 2008). Research seems to corroborate this disparity of opportunities of social mobility. According to data from the Chilean Ministry of Education, for 2010 the best performance was concentrated in urban spaces occupied by middle higher classes, whereas less advanced schools, generally of public nature are found in spaces with high presence of lower income economic classes. In other words, a close relation seems to exist between the so- cioeconomic aspects of the families and the performance of an educational center (Ministerio de Educación, 2010; Oberty, 2007). In this situation, the question is how to describe statisti- cally and geographically the spatial distribution of the educa- tional centers, how to measure the accessibility of the school population to those centers, or how to establish the degree of spatial correlation between location of educational facilities and population strata according to their quality and level of income, respectively. As study case, Concepción Metropolitan Area (CMA) is pro- posed. This city represents the second urban concentration in Chile, located in the coastal plains of the Biobío Region and subject to recent processes of population dispersion and urban growth, comparable to mid-size metropolitan areas of Latin America (Rojas et al., 2013). Despite the wide range of educa- tional facilities in its 11 municipalities, coverage degrees and differential levels of spatial accessibility can be identified. Ba- sically, in the most urbanized areas (Concepción and Talca- huano) relocation phenomena are of educational centers previ- ously located in central sectors towards more distant places are being produced, thus favoring the use of private transport as mode of travel and the clustering of specific and homogeneous groups of population. On the other hand, least populated mu- nicipalities continue concentrating their schools in the urban center, whereas their urban growths are increasingly peripheral and distant, involving large displacements. So, assuming that education represents a crucial factor to re- duce inequities and improve the quality of life of the population (Fundación para la superación de la pobreza, 2006), this article pretends to be an essay on the integration of spatial distribution measures of educational facilities, with their own quality and *Corresponding author.  H. DE LA FUENTE ET AL. socioeconomic situation indicators of the population close to every one of the schools. The aim is to enrich the assessment on the spatial equity in the distribution of the education opportuni- ties and hence facilitate better and more inclusive planning. The present work starts by briefly presenting the state of the issue and its geographic framework. Among the methods of statistical and cartographic analysis, the generation of an indi- cator of educational quality that summarizes the rate students- teacher will be considered, as well as the learning results col- lected by the SIMCE (Measurement System of Quality Educa- tion of the Chilean Ministry of Education), and Moran’s Local and Global Index, used to diagnose the spatial grouping of schools in CMA. Results present a spatial diagnose of the educational quality in the area of study, as well as in the zones of low and high concentration of facilities. Finally both strengths and weak- nesses of the investigation are discussed in order to improve the accessibility to a quality education, considering a more equita- ble spatial distribution (Ministerio de Educación, 2010). Principles of Equity, Equality and Spatial Justice in the Location of Facilities There is a way to understand these concepts beyond their merely textual meaning, mainly applied to social sciences and geography. These expressions arose on the basis of Radical Geography, which illustrates the insufficiency of the theoretical models of the Quantitative Geography, which were intended to explain both location of activities and land uses, to move to- wards measuring, quantifying and assessing geographic situa- tions. It involves measuring the degree of injustice, equity or equality of distributions or spatial configurations (Moreno, 2007). Some authors coincide on the close relation among Equality, Justice and Equity. Despite this, it is possible to obtain a dif- ferentiation, as explained by Bosque (2004), who pointed out that the meaning of equity can manifest itself as equality, but not necessary as synonyms, because equity is understood as justice, impartiality of treatment, opportunities, etc. Geographi- cally, something is fair in the sense that distribution among areas has its own proportional differences and these differences are not seen as needs or difficulties, but acceptable for the pop- ulation. Equality, on the other hand, starts from the basis that everyone must have the same opportunities, same health level, education and opportunities, creating a difficult application both in social and geographic terms, regarding that both people and spaces are different. On the other hand, spatial justice can have two approaches: one that decreases differences among areas or distances, and one in which the required opportunity is reached. For the spe- cific case of desirable facilities (Hospitals, Schools or other services), spatial justice is concerned are not unevenly distrib- uted over the space, so there are no differences or. At least, they are not excessively big in the access of the population to these facilities (Flores, 2009). In the case of non-desirable facilities (industries, landfills), the issue is that the distances between population and facilities are not too dissimilar, so some people are not too affected, whereas others are not affected at all (Bosque & Moreno, 2005). Another author that recognizes similarities among terms of equality, justice and equity is Moreno (1999), who pointed out that justice corresponds to the “set of methods used by authori- ties to reduce inequalities among socio-spatial classes”. On the other hand, equality would be sustained on democratic ideas and on egalitarian ideals of philosophy and alludes to the fact that a person has identical rights and obligations, so individuals must be treated in the same way, nevertheless it must be recog- nized that not all individuals are equal. For this reason, an as- sessment on situations, and profit sharing and disutility in a fair, impartial and equitable way must be carried out. It is possible to make a distinction between arithmetic and proportional equality. Arithmetic equality is referred to a per- fect equality, equality of treatment, where exactly the same amount of benefits is destined to everyone, regardless of the circumstances. Justice assumes an unequal distribution, so its aim is to improve the situation of the most disadvantaged. As postulated by Harvey (1977): “The geographic problem con- sists in elaborating a spatial organization mechanism that maximizes the perspectives of the most disadvantaged region”. For Moreno, the terms of spatial equity and equality are almost synonyms, being differentiated from the justice, because ideal justice consists in the suppression of all disadvantages. In other words, justice encompasses both equality and equity. For this reason, justice mixes both social and spatial features. In other words, involves public authorities to attenuate inequalities and the notion of equality would be mixed with the scope of equity. A similar version was presented by Pitarch Garrido (2000) for the elaboration of planning models of educational services, where five fundamental aspects must be considered, such as social equity, indicating that all public activity must be ad- dressed to whole of the society excluding any discrimination on the basis of social differences. On this basis, education as pub- lic service must look for social equity as a right for every citi- zen. On the other hand, locational equity takes into account that the space always introduces inequalities and therefore, is a con- figurative factor, closely related to social equity. Educational System in CMA: Institutional and Geographic Framework The Chilean Educational system is divided into four levels: preschool education (4 to 5 years of age), primary education (6 to 15 years), secondary education (15 to 18 years) and higher education. This study is focused on the evaluation of the first three levels. In theses levels the Chilean Ministry of Education have ap- plied a number of assessment indicators, organized in five groups (Ministerio de Educación, 2008): Context indicators: They reflect the potential demand for educational services and the growth trend of such demand, as well as the relative size of the enrolment. Participation indicators: They are related to the access to education, participation and internal efficiency of the sys- tem. They are calculated by means of levels and include the net rate enrolment (total amount of students of the official age group in a specific level of primary or secondary educa- tion—6 - 13 and 14 - 17 years of age, respectively, regard- ing the total population of that age group); and gross rate enrolment (total amount of students in a specific teaching level of primary or secondary education, in relation to the total amount of students for that education level). Age dis- tribution by age and its growth rate show the trends in the different levels and institutions. Particularly, the distribu- tion of the enrolment reflects important variations since Open Access 118 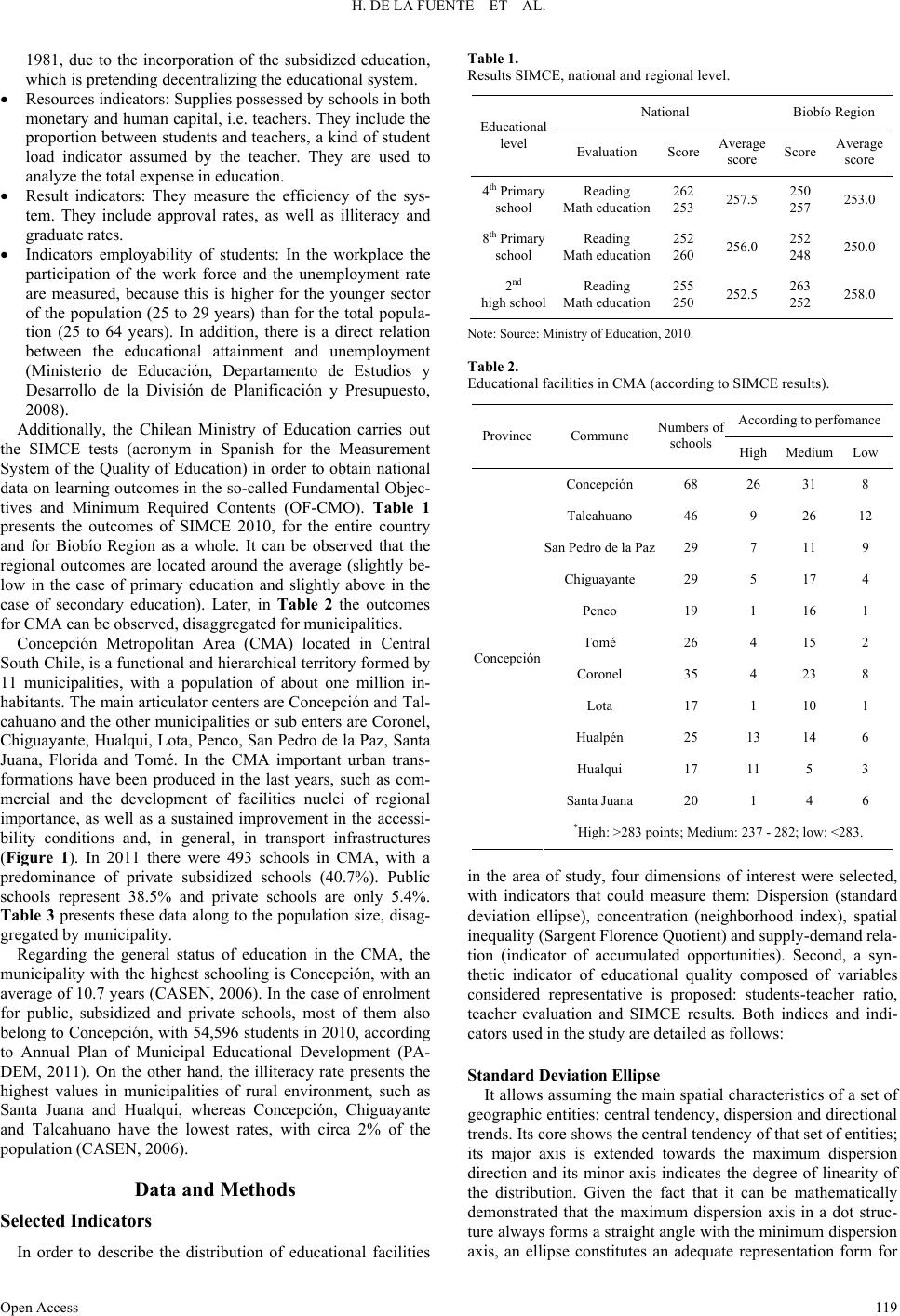 H. DE LA FUENTE ET AL. 1981, due to the incorporation of the subsidized education, which is pretending decentralizing the educational system. Resources indicators: Supplies possessed by schools in both monetary and human capital, i.e. teachers. They include the proportion between students and teachers, a kind of student load indicator assumed by the teacher. They are used to analyze the total expense in education. Result indicators: They measure the efficiency of the sys- tem. They include approval rates, as well as illiteracy and graduate rates. Indicators employability of students: In the workplace the participation of the work force and the unemployment rate are measured, because this is higher for the younger sector of the population (25 to 29 years) than for the total popula- tion (25 to 64 years). In addition, there is a direct relation between the educational attainment and unemployment (Ministerio de Educación, Departamento de Estudios y Desarrollo de la División de Planificación y Presupuesto, 2008). Additionally, the Chilean Ministry of Education carries out the SIMCE tests (acronym in Spanish for the Measurement System of the Quality of Education) in order to obtain national data on learning outcomes in the so-called Fundamental Objec- tives and Minimum Required Contents (OF-CMO). Table 1 presents the outcomes of SIMCE 2010, for the entire country and for Biobío Region as a whole. It can be observed that the regional outcomes are located around the average (slightly be- low in the case of primary education and slightly above in the case of secondary education). Later, in Table 2 the outcomes for CMA can be observed, disaggregated for municipalities. Concepción Metropolitan Area (CMA) located in Central South Chile, is a functional and hierarchical territory formed by 11 municipalities, with a population of about one million in- habitants. The main articulator centers are Concepción and Tal- cahuano and the other municipalities or sub enters are Coronel, Chiguayante, Hualqui, Lota, Penco, San Pedro de la Paz, Santa Juana, Florida and Tomé. In the CMA important urban trans- formations have been produced in the last years, such as com- mercial and the development of facilities nuclei of regional importance, as well as a sustained improvement in the accessi- bility conditions and, in general, in transport infrastructures (Figure 1). In 2011 there were 493 schools in CMA, with a predominance of private subsidized schools (40.7%). Public schools represent 38.5% and private schools are only 5.4%. Table 3 presents these data along to the population size, disag- gregated by municipality. Regarding the general status of education in the CMA, the municipality with the highest schooling is Concepción, with an average of 10.7 years (CASEN, 2006). In the case of enrolment for public, subsidized and private schools, most of them also belong to Concepción, with 54,596 students in 2010, according to Annual Plan of Municipal Educational Development (PA- DEM, 2011). On the other hand, the illiteracy rate presents the highest values in municipalities of rural environment, such as Santa Juana and Hualqui, whereas Concepción, Chiguayante and Talcahuano have the lowest rates, with circa 2% of the population (CASEN, 2006). Data and Methods Selected Indicators In order to describe the distribution of educational facilities Table 1. Results SIMCE, national and regional level. National Biobío Region Educational level Evaluation Score Average score Score Average score 4th Primary school Reading Math education 262 253 257.5 250 257 253.0 8th Primary school Reading Math education 252 260 256.0 252 248 250.0 2nd high school Reading Math education 255 250 252.5 263 252 258.0 Note: Source: Ministry of Education, 2010. Table 2. Educational facilities in CMA (according to SIMCE results). According to perfomance ProvinceCommune Numbers o schools High MediumLow Concepción 68 26 31 8 Talcahuano 46 9 26 12 San Pedro de la Paz29 7 11 9 Chiguayante 29 5 17 4 Penco 19 1 16 1 Tomé 26 4 15 2 Coronel 35 4 23 8 Lota 17 1 10 1 Hualpén 25 13 14 6 Hualqui 17 11 5 3 Santa Juana 20 1 4 6 Concepció n *High: >283 points; Medium: 237 - 282; low: <283. in the area of study, four dimensions of interest were selected, with indicators that could measure them: Dispersion (standard deviation ellipse), concentration (neighborhood index), spatial inequality (Sargent Florence Quotient) and supply-demand rela- tion (indicator of accumulated opportunities). Second, a syn- thetic indicator of educational quality composed of variables considered representative is proposed: students-teacher ratio, teacher evaluation and SIMCE results. Both indices and indi- cators used in the study are detailed as follows: Standard Deviation Ellipse It allows assuming the main spatial characteristics of a set of geographic entities: central tendency, dispersion and directional trends. Its core shows the central tendency of that set of entities; its major axis is extended towards the maximum dispersion direction and its minor axis indicates the degree of linearity of the distribution. Given the fact that it can be mathematically demonstrated that the maximum dispersion axis in a dot struc- ture always forms a straight angle with the minimum dispersion xis, an ellipse constitutes an adequate representation form for a Open Access 119  H. DE LA FUENTE ET AL. Open Access 120 Table 3. Census districts CMA. Code Name Code Name Code Name Code Name 0 Intendencia 39 Bannen 20 Plaza Perú 59 San Vicente 1 Liceo de Hombres 40 Lota Bajo 21 Observatorio 60 Estadio 2 La Cárcel 41 Cementerio 22 Larenas 61 Huachipato 3 Plaza España 42 Colcura 23 Pedro de Valdivia 62 Ramuntcho 4 Estación Central 43 Penco 24 Palomares 63 Hualpencillo 5 Cerro Amarillo 44 Fábrica 25 Lo Pequén 64 Carriel 6 Plaza Cruz 45 Lirquén 26 Municipalidad 65 Las Salinas 7 Cementerio 46 Margaritas 27 Villa Mora 66 Barranquilla 8 Laguna Redonda 47 Batro 28 Schwager 67 Zunico 9 Pajonal 48 Boca Sur 29 Buen Retiro 68 Estadio Higueras 10 Manuel Rodríguez 49 Los Acacios 30 Corcovado 69 San Miguel 11 Escuela Argentina 50 San Pedro 31 Escuadrón 70 Club Hípico 12 General Cruz 51 Lomas Coloradas 32 Lonco 71 Bremen 13 Estación Tucapel 52 Santa Juana 33 Matadero 72 Cerro Verde 14 Lo Méndez 53 El Portón 34 Fábrica 73 El Puerto 15 La Toma 54 Valdivieso 35 Chiguayante 74 Ralihue 16 La Pólvora 55 Cerro Fuentes 36 La Leonera 75 El Morro 17 Población Baquedano 56 La Aduana 37 Hualqui 76 Dichato 18 Plaza Condell 57 Cerro Buenavista 38 Lota Alto 19 Hospital 58 Tumbes Note: Source: INE 2002. such dispersion by providing a perceived “mean” location and thus it allows perceiving the whole systematic delocation of the places. Neighborhood Index Neighborhood index or nearest neighbor analysis is simply the calculation of the average distance divided by the expected average distance to the nearest neighbor, in the case of a ran- dom disposition. If the index is greater than 1, dispersion is the tendency. On the contrary, the pattern will show a conglomer- ate distribution and its calculation results from the following: obs ran R where R is the neighborhood index, obs is the observed dis- tance to the nearest neighbor and ran is the expected average distance to the nearest neighbor, in a random dot arrangement. Neighborhood index can have values between 0, which indi- cates a fully grouped structure and 2.15, which indicates a fully disperse structure. This indicator provides a very useful de- scriptive measure of specific structures, especially for identify- ing the increase or decrease of both dispersion or grouping of a structure (Ebdon, 1982). The index has used the centroid points of each census unit population. Sargent Florence Quotient This index basically measures the degree of inequality among territories. The interpretation considers with value 1 to an egalitarian country condition. On the other hand, values higher than 1 correspond to a surplus of schools. Finally, values lower than 1, correspond related to a deficit of educational in- stitutions. In the study carried out by Fuenzalida (2010) on dis- tribution of hospitals, it is concluded that this index is an un- avoidable complement for the comprehension of the spatial inequalities. Table 4 clarifies its interpretation, being estab- lished the numerical thresholds to facilitate the assessment of results. The index is applied in the following equation: 1 1 n i i in ii i OO CL dd i (1) where CLi = location quotient of the territorial i subunit; i··· n = subunits of the j set; Oi = educational service offering in i sub- unit and di = educational service demand in i. In this case, i subunits are represented by the census districts  H. DE LA FUENTE ET AL. Figure 1. Concepción Metropolitan Area. of every municipality of CMA, in which Oi educational offer- ing corresponds to the sum of the students registered by the Ministry of Education that attend each school in the i district. On the other hand, the demand variable is referred to the poten- tial population to attend, whereas the demand variable is related to the potential population that attends to an educational facility in the subunit. In other words, they correspond to people be- tween 0 to 17 years, according to data from Census (2002). Subsequently, results obtained from the index are plotted in five main categories. These are: important deficit, moderate deficit, moderate surplus, important surplus and country condition (Ta- ble 5). Hence, a value close to 1 will mean that the proportion of the offering in the i subunit respect to the total CMA is similar to the proportion of demand in i respect to the total. Values higher than 1 indicate that in the i subunit there is a relative oversupply respect to the resident demand; and values lower than 1 indicate that there is a deficit in the supply respect to the demand regis- tered in I, which is greater as farther away from the unit. Resident Population Indicator in an Area of Specific Radius/Indicator of Accumulated Opportunities Although several limitations and possible improvements have been pointed out (Bisonnette et al., 2012; Chen et al., 2012; Langford et al., 2008), the method called Two Step Float- ing Catchment Areas (2SFCA) has been frequently used in the recent literature on the assessment of spatial inequities in the Table 4. Qualitative and quantitative classification of educational quality indi- cators. Low quality Medium quality High quality Partial indicators Weight −1 0 1 Student- Teacher ratio2 >34 students 17 - 34 students <17 students Teacher evaluation 3 Satisfactory and basic performance Competent performance Outstanding performance SIMCE results5 Initial Achievement level Intermediate achievement level Advanced achievement level Table 5. Sargent Florence assessment. Level of locator coeffciencient Value Important deficit <0.49 Moderate deficit 0.50 - 0.99 Moderate surplus 1.01 - 1.87 Important superplus 1.88 - 2.73 Country situation 1 Note: Source: Fuenzalida, 2010. distribution of public facilities (Cervigi et al., 2008; Chen et al., 2012; Gualiardo, 2004; Luo, 2004; Luo & Qi, 2009; Luo & Whippo, 2012; Wang, 2012). The first step establishes a buffer around every supply center and it counts how much population resides inside them. The second step the buffer is sketched from every point of demand and the centers or facilities located in- side the center are added. Both start from the delimitation of an influence area of de- termined extent from these points. If these points represent the supply, it can be accounted the volume of resident population within such area, besides quantifying the population covered by the service. In this case, the service is educational. The Geo- graphic accessibility of the facility is also measured (Gutiérrez & García, 2002). If the points that originate the influence area represent the demand, the number of available schools or hos- pital beds can be quantified within that range of distance from each demand point, an indicator of accumulated opportunities will be used as an accessibility measure (Salado, 2012). In any case, in order to use one and another, it is necessary to consider at least three elements: points of supply, distribution of population (potential demand) and the gap among the poten- tial demand of the points of supply, according to areas of influ- ence. In order to determine the areas of influence, two methods that consider the location of educational centers have been taken into account. The first method consists in modeling dif- ferent areas of influence or buffers of 500 and 1000 m, ranges commonly used as more accessible (Ramírez, 2008; Villanueba, 2010; Sabuda, 2007; Yi, 2004) and Pizzolato, Broseghini, & Noguera, 2002). The second method uses areas of influence from the análisis through Thiessen polygons. It must be noted that both GIS operations are carried out by means of the ArcGis Open Access 121  H. DE LA FUENTE ET AL. software. Later, buffers are intersected with the area of influ- ence from Thiessen polygons (geometric construction of the schools). For the calculation of the population variable within the range of geographic accessibility (buffers intersected with Thi- essen polygons), an inconvenient is presented by how deter- mining the amount of potential population between 0 and 17 years, because of its irregular distribution, which many times covers not completely the census blocks. This information is required to determine the approximate number of people cov- ered by the educational service. Therefore, for the solution to this problem the method proposed by Gutiérrez, Pinto & Gómez (2000) is used. This method is nothing but the ratio between the total population of the block and the population covered by the area of influence, as detailed in the following equation: 11 * nn if aj Ppipj aj (2) Being P = total population estimated in the area of influence of any facility; i··· n = sectors entirely included in the coverage area; pi = population entirely included in the coverage area; j··· m = sectors partially included in the coverage area; pj = population of the j sector; aj = area of the j sector which is within the area of influence; and aj = area of the j sector. Educational Quality Indicator (EQI) This synthetic indicator summarizes three partial indicators. From these results, a qualitative evaluation scale was carried out (low, middle and high quality), as well as a quantitative scale (between −1 and 1). Both balance of these partial indica- tors and the definitive classification are presented in Table 5. Student-Teacher ratio: It is equivalent to the number of students in relation to the total amount of teachers accord- ing to education level, administrative dependency, region and geographic area. Carried out by the Chilean Ministry of Education, it allows studying the endowment of teacher per student and outlines the school situation per school. Teacher evaluation: The Ministry of Education carries out the performance evaluation of school teacher, establishing four degrees: outstanding (it indicates a professional per- formance that clearly and consistently stands out with re- spect to expected), competent (proper professional perform- ance, it fulfils the requirements), basic (it fulfils with what is expected in the indicator, but irregularly), and unsatis- factory (it presents clear weaknesses in the teaching per- formance). SIMCE results (of learning outcomes in Fundamental objectives and Minimum Required Contents): Disag- gregated results are presented in Table l. This is the indica- tor granted with the greatest weight, because it counts on a methodologically solid system, it is widely used as tool for education policies and it has been in use for long time. From every variable, a qualitative evaluation scale is per- formed, with variables such as: High, Medium and Low quality. On the other hand, a quantitative sale was also performed, as- signing minimums that range from −1 to 1 as maximum. The evaluation scale used to measure the descriptive correlation statistics of variables is presented in Table 5. This scale fulfills with the condition of being a scale of comparable values that allows assessing different factors, variables or criteria, inde- pendently of the method to be used (Moreno, 1999). The assessment favors the fact that all values are expressed in a comparable scale of values (−1 to 1). Therefore, by means of a simple calculation procedure the proportion applied through maximum and minimum values of each variable under study is applied, as observed as follows: min min max 21XYX XX (3) where X corresponds to the value assigned by the scale, Xmin is the minimum value of the data set, Xmax is the maximum value of the data set, and Y represents the data value to convert. By means of this equation it is possible to convert all con- tinuous data into a scale of values between −1 and 1. Thus, a data matrix or basic input for the construction of educational quality index is obtained. The synthetic index, product if every one of the dimensions (Teacher evaluation, SIMCE test and teacher student ratio) gives more weight to the SIMCE results, then to the teacher evaluation and finally to the student teacher ratio. This propor- tional order is given to the fact that for the Chilean Ministry of Education. SIMCE has greater “legitimacy and credibility”. This test has allows focusing the attention of the public opinion and the teachers into the learning results, by means of a meth- odologically solid system , as well as widely used tool for edu- cational policies, making clear that this is a reliable indicator in time. In Table 6 three indicators of educational quality and their different relative weights for obtaining the synthetic index of educational quality can be observed. The index allows a first approach to the distribution of the phenomenon under study, assuming that every spatial unit have weighted values of each variable, being 10 the maximum value of the scale and repre- senting an educational quality of excellent level. On the other hand, −10 is the minimum value, demonstrating the opposite situation, i.e. an education with multiple deficiencies (Table 6). Geostatistical Analysis The result from the previous indicators was later assigned to cells in a 100 × 100 m grid (the size of the grid has been estab- lished regarding that the average size of a census block, in the CMA fluctuates around 10,000 m2). The aim of this assignment was to find out if the distribution of the results corresponded to a condensed, scattered or random pattern by GeoDa Software. In order to achieve this, a spatial auto-correlation analysis that studies the variation mode of the thematic values among the different points of the space is carried out (Góngora Gómez, 2007). Spatial auto-correlation reflects the degree in which objects or activities in a geographic unit are similar to other objects or Table 6. Weighting of quality indices. Variable Ponderación SIMCE 5 Evaluación docente 3 Tasa Alumno profesor 2 Total 10 Open Access 122  H. DE LA FUENTE ET AL. activities in close geographic units (Goodchild & Haining, 1992). Basic property of spatial auto-correlated data is that val- ues are not random in space. In other words, data values are spatially correlated each other and become redundant (Lee & Wong, 2001). This kind of models supposes that finding a spe- cific observation in a point of an area it is possible to find simi- lar observations in points close to it. On the contrary, distant points would have totally dissimilar characteristics. Specifically, the Moran’s Statistical Global index (I Moran) was applied. This index determines the kind of grouping exist- ing between neighbor spatial units in order to obtain some known distribution model, or to study the spatial segregation of a characteristic. The complexity of the problem increases as a result of possible multidirectional interdependencies that may arise in the space. Its formulation is as follows: 11 2 1 nn ij ij ij n i i WZZ n ISZ (4) where n is the number of geographic observation units, wij are the elements of a binary contiguity matrix, x is the attribute of this variable and the mean of the cross product. The measurement of a correlation with the same variable has in different spatial contiguous units in a horizontal perspective, originates one out of these three possibilities: Positive spatial auto-correlation: neighbor spatial units pre- sent close values and indicate for the spatial units a ten- dency to grouping. Spatial negative correlation: Neighbor spatial units present very dissimilar values and indicate for the spatial units a tendency to dispersion. No correlation: any of the above situations take place. Therefore, values of neighbor spatial units present values randomly produced. Moran’s index is grounded in an auto-covariance model and, after the mean and the variance, is the most important property of any geographic variable. Unlike the previous ones, it is ex- plicitly linked to spatial patterns. These observations can be discrete or continuous and they may be associated to a point on a specific surface, or associated to a surface on which a parti- tion has been performed. This partition may be regular or ir- regular and commonly recognized as reticule (López Her- nández & Palacios Sánchez, 2000). In general, geographic data are presented in a continuous map. The contiguity respect to the central location (e) can be defined in three ways, by means of chess terminology: 1) Rooks criteria: cells b, d, f and h are considered adjacent to the location of “e”. 2) Bishops criteria: cells a, c, g and i would be considered neighbors to the location “e”. 3) Queen criteria: It combines the above two and thus cells a, b, c, d, f, g, h and i would be considered contiguous to “e”. The kind of contiguity on which the work was carried out was Rooks, one of the most used, because of its simplicity (Celemin, 2009). Outcomes from this index vary from −1 to 1, representing minimum (maximum dispersion) and maximum (maximum concentration) correlations, respectively. Zero means totally random spatial pattern. In order to know if an auto-correlation is significant, a null hypothesis test is carried out, checking whether the spatial configuration of the variable occurs ran- domly or it responds to a spatial pattern. In other words, if the assumptions of model whether or not are satisfied from the estimation if a sampling statistic significantly differs from the randomly expected. This test is carried out by locating Moran’s coefficient inside a normal probability curve (Buzai & Baxen- dale, 2008). In order to perform this kind of tests, both null and alterna- tive hypotheses must be clearly formulated. When working on socio spatial projects, as null hypothesis the following claim is considered: “The spatial configuration is randomly produced and as alternative hypothesis, the opposite claim: the spatial configuration is NOT randomly produced” (Celemin, 2009). Once both hypotheses have been established, the significance level (α) must be defined. This indicates the probability for the null hypothesis to be rejected. In other words, if the occurrence probability of a particular value obtained in a test is equal or lower than α, the null hypothesis is rejected and the alternative hypothesis is accepted. Habitually, the significance level is chose according to the importance of the problem. In the socio- spatial analysis is usually 5% (0.05) and 1% (0.01) (Buzai & Pineda, 2007). P-value is the result reported by the hypothesis test. Then, if a significance level of 0.05 is established in general, p-value presents values lower than 0.05. This allows rejecting the null hypothesis and accepting the alternative hypothesis, taking into account that with this decision there is a risk of making a mis- take in 5% of the cases. On the contrary, if the p-value presents results over 0.05, the alternative hypothesis is not accepted, because the risk on the decision exceeds the established limit, and the null hypothesis must be accepted. In other words, the “spatial configuration is occurs randomly”. Moran’s I value represents the spatial correlation degree ei- ther univariate or bivariate of variables and every point of the diagram represents a specific different spatial unit, with X and Y coordinates. In the case of a univariate correlation, on the X axis of the diagram, standardized values of the considered variables and on the Y axis standardized values of “average” values of the neighbor spatial units for such variable will be placed. Moran’s I index value is equivalent to the slope of the regression line. The slope of the line represents the association degree between the variable considered on the horizontal axis and the values of the variable on the vertical axis, in relation to the location of their neighbors (Sabuda, 2007). Description and Analysis of Results Spatial Distribution of the Educational Facilities The standard deviation ellipses reveal a location model con- centrated in every column due to a greater proportion of schools in urban centers consolidated in the cities of the CMA (Figure 2). This map evidences that out of the ellipses area lower qual- ity schools are found, especially in the cities of San Pedro de la Paz, Coronel and Penco. Regarding the directional tendency of the ellipses, these are ruled by a linear organization pattern (Penco, Talcahuano, Coronel and Chiguayante), providing an elongated and disperse shape leaned towards the most hierar- chic urban center, which corresponds to Concepción. In relation of the spatial indicators, the neighborhood analy- sis, the average distance observed between centers is 369.2 meters, a short distance indeed that represents no obstacle to access to a school by walking (Gutiérrez & García, 2002). The main difficulty is given by values far from average. Values far rom average are constituted by distances among private f Open Access 123  H. DE LA FUENTE ET AL. Open Access 124 Figure 2. Distribution of educational quality index and Sargent Florence Quotient in CMA (Source: Own). schools, due to their tendency of being located in peripheral areas. On the contrary, minimum distances are given among municipal schools. The expected distance, product of the den- sity of points in a specific area is 369.4 meters. Therefore, the neighborhood index offers a result of 1005 m that can be inter- preted as a random pattern far from both ends (0 and 2.15). Index of accumulated opportunities (Table 7) shows the population represented by centroids of census blocks which are covered by three ranges of buffers distance: Less than 500 meters (Pedestrian proximity distance to fa- cilities (Gutiérrez García, 2002) low density census block are found (50 inhabitants). Exceptions are presented in Hualpén, Chiguayante Sur and in Agüita de la Perdiz sector in Concep- ción. Total population grouped in this range reaches 201,438 inhabitants for CMA (40.9% coverage). When people between 0 and 17 years of age, the coverage increases up to 213,869 inhabitants. In the second service ring (500 to 1000 meters) census blocks with more than 50 inhabitants are located, reaching more than 100 inhabitants per sample unit (census blocks). Most distant sectors are Collao Sector, Barrio Norte, Tucapel Bajo, Chepe Hill and Agüita de la Perdiz. These places are located approxi- mately 1 km from the nearest school and in some cases, the acilities are low quality. In San Pedro de la Paz the disadvan- f 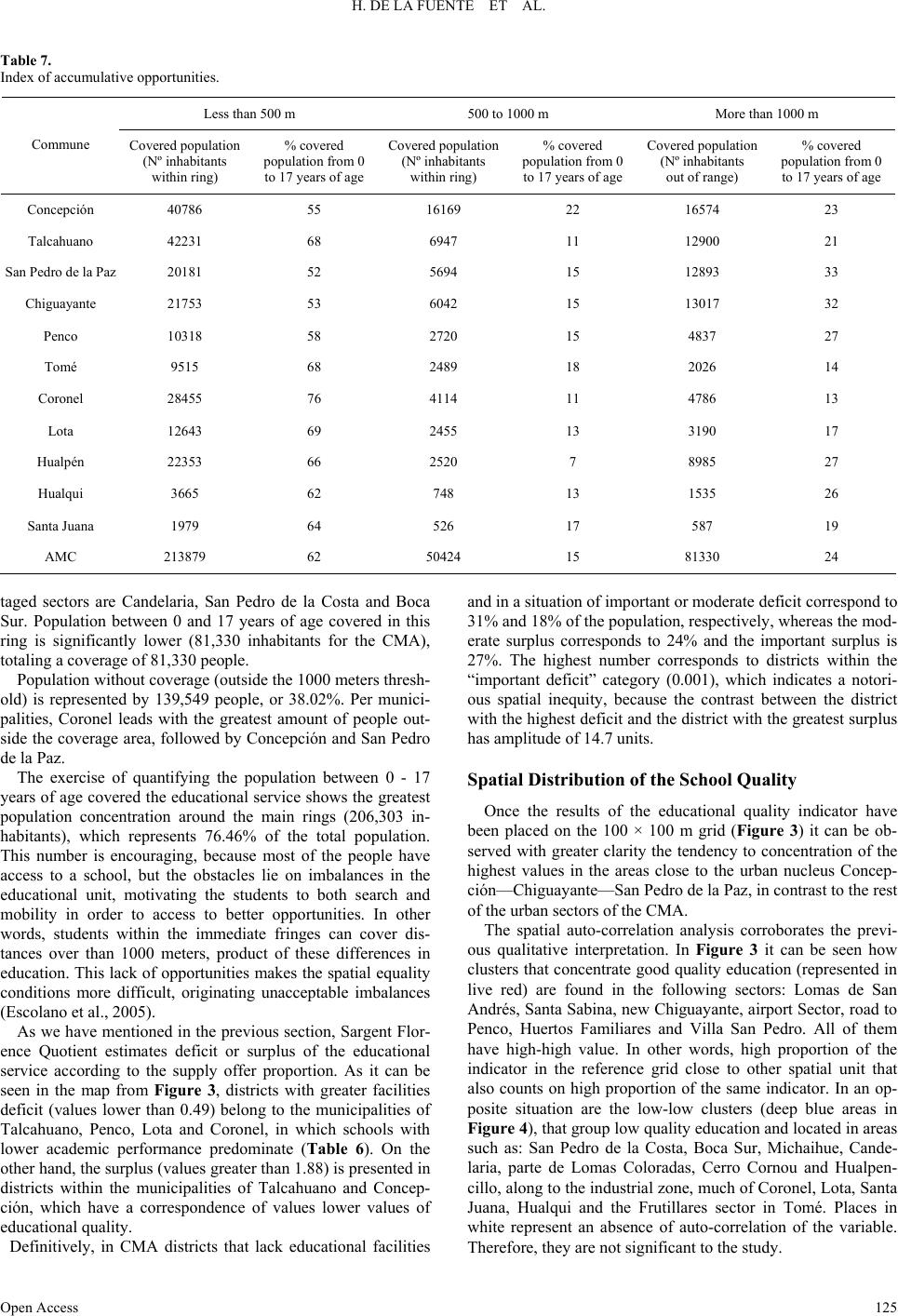 H. DE LA FUENTE ET AL. Table 7. Index of accumulative opportunities. Less than 500 m 500 to 1000 m More than 1000 m Commune Covered population (Nº inhabitants within ring) % covered population from 0 to 17 years of age Covered population (Nº inhabitants within ring) % covered population from 0 to 17 years of age Covered population (Nº inhabitants out of range) % covered population from 0 to 17 years of age Concepción 40786 55 16169 22 16574 23 Talcahuano 42231 68 6947 11 12900 21 San Pedro de la Paz 20181 52 5694 15 12893 33 Chiguayante 21753 53 6042 15 13017 32 Penco 10318 58 2720 15 4837 27 Tomé 9515 68 2489 18 2026 14 Coronel 28455 76 4114 11 4786 13 Lota 12643 69 2455 13 3190 17 Hualpén 22353 66 2520 7 8985 27 Hualqui 3665 62 748 13 1535 26 Santa Juana 1979 64 526 17 587 19 AMC 213879 62 50424 15 81330 24 taged sectors are Candelaria, San Pedro de la Costa and Boca Sur. Population between 0 and 17 years of age covered in this ring is significantly lower (81,330 inhabitants for the CMA), totaling a coverage of 81,330 people. Population without coverage (outside the 1000 meters thresh- old) is represented by 139,549 people, or 38.02%. Per munici- palities, Coronel leads with the greatest amount of people out- side the coverage area, followed by Concepción and San Pedro de la Paz. The exercise of quantifying the population between 0 - 17 years of age covered the educational service shows the greatest population concentration around the main rings (206,303 in- habitants), which represents 76.46% of the total population. This number is encouraging, because most of the people have access to a school, but the obstacles lie on imbalances in the educational unit, motivating the students to both search and mobility in order to access to better opportunities. In other words, students within the immediate fringes can cover dis- tances over than 1000 meters, product of these differences in education. This lack of opportunities makes the spatial equality conditions more difficult, originating unacceptable imbalances (Escolano et al., 2005). As we have mentioned in the previous section, Sargent Flor- ence Quotient estimates deficit or surplus of the educational service according to the supply offer proportion. As it can be seen in the map from Figure 3, districts with greater facilities deficit (values lower than 0.49) belong to the municipalities of Talcahuano, Penco, Lota and Coronel, in which schools with lower academic performance predominate (Table 6). On the other hand, the surplus (values greater than 1.88) is presented in districts within the municipalities of Talcahuano and Concep- ción, which have a correspondence of values lower values of educational quality. Definitively, in CMA districts that lack educational facilities and in a situation of important or moderate deficit correspond to 31% and 18% of the population, respectively, whereas the mod- erate surplus corresponds to 24% and the important surplus is 27%. The highest number corresponds to districts within the “important deficit” category (0.001), which indicates a notori- ous spatial inequity, because the contrast between the district with the highest deficit and the district with the greatest surplus has amplitude of 14.7 units. Spatial Distribution of the School Quality Once the results of the educational quality indicator have been placed on the 100 × 100 m grid (Figure 3) it can be ob- served with greater clarity the tendency to concentration of the highest values in the areas close to the urban nucleus Concep- ción—Chiguayante—San Pedro de la Paz, in contrast to the rest of the urban sectors of the CMA. The spatial auto-correlation analysis corroborates the previ- ous qualitative interpretation. In Figure 3 it can be seen how clusters that concentrate good quality education (represented in live red) are found in the following sectors: Lomas de San Andrés, Santa Sabina, new Chiguayante, airport Sector, road to Penco, Huertos Familiares and Villa San Pedro. All of them have high-high value. In other words, high proportion of the indicator in the reference grid close to other spatial unit that also counts on high proportion of the same indicator. In an op- posite situation are the low-low clusters (deep blue areas in Figure 4), that group low quality education and located in areas such as: San Pedro de la Costa, Boca Sur, Michaihue, Cande- laria, parte de Lomas Coloradas, Cerro Cornou and Hualpen- cillo, along to the industrial zone, much of Coronel, Lota, Santa Juana, Hualqui and the Frutillares sector in Tomé. Places in white represent an absence of auto-correlation of the variable. Therefore, they are not significant to the study. Open Access 125  H. DE LA FUENTE ET AL. Figure 3. Distribution of educational quality in the CMA (Source: Own). Figure 4. Cluster of educational quality in the CMA (Source: Own). Regarding the significance degree of the analysis, this is jus- tified with the map that represents the distribution of the p value in the CMA (Figure 4). This map reveals a significance of 0.05, so the null hypothesis on the random distribution of the variable in the territory is rejected and the alternative hypothe- sis is accepted (this variable does not present a random distri- bution, but it corresponds to a particular spatial pattern). The index clearly shows how the best schools are located in zones of high economic level. The spatial evidence is enhanced with results from the Chilean Ministry of Education, where in both reading and math tests, the percentage of students with scores over 300 points increases as the socioeconomic level increases. However, in all groups there are students with scores over 300 points. For instance, from the students of the low group that undertakes both reading and Math tests, 5% and 4%, respectively obtain scores that exceed 300 points. Results from every one of the variables analyzed by means of Moran’s univariate spatial auto-correlation show the relation between educational quality and location. Specifically, results from Moran global index indicate excellent correlation degrees of the variables, all close to 0.9. Namely, there is a strong rela- tion, considering that 1 is the perfect correlation value. SIMCE variable is the one that obtains the highest correlation, followed by Teacher Evaluation and finally, Student-Teacher ratio that equally have a good correlation degree (Table 8). Discussion and Conclusions: Characterization of the Spatial Inequity in the CMA Results already presented seem to confirm that there are sig- nificant differences in the spatial distribution of the pre-univer- sity schools in the CMA area and, therefore, notable contrasts in the access to this kind of facilities, especially if we consider the access to quality schools. Moran’s I spatial auto-correlation analysis has become a valuable method to know and prove the situation of every territorial unit, in relation to the other geo- graphic surrounding entities, indicating the dissimilar spatial configuration of the educational facilities within the territory. Identifying spatial inequity patterns in educational issues is generally grounded on a specialized description of both cover- age and quality of the service (estimated on teacher competence indicators and/or academic performance). Nevertheless, in many studies the correlation between these indicators and those of environmental quality and/or socioeconomic level is ignored (Talen, 2001). Likewise, the location of such schools is appar- ently unresponsive to a logical inclusive territorial planning (Pitarch Garrido, 2000). In the CMA, educational quality is presented unequally. Spe- cifically, the most disadvantaged places are located in Tomé, Hualpén, some places in San Pedro de la Paz, Coronel, Lota and Santa Juana. The singularity of this case is that most of its population belongs to low socioeconomic classes. Thus, the gap among different zones has a strong spatial relation between geographic distance and educational quality, as well as a noto- rious downtown—periphery spatial pattern and providing clearly differentiated social benefits. Distance becomes in a factor that clearly determines the access to quality facilities, especially damaging lower socioeconomic strata and moving in detriment to a desirable equity and social cohesion. From the methodological point of view, the analyses used have allowed us to describe both distribution and spatial cov- erage of these facilities and their relation with the distribution of the demand and with some parameters of quality usually used by the Chilean Ministry of Education. However, this first approach opens gates to multiple questions. We could ask, for example: What other components and factors would be relevant Open Access 126 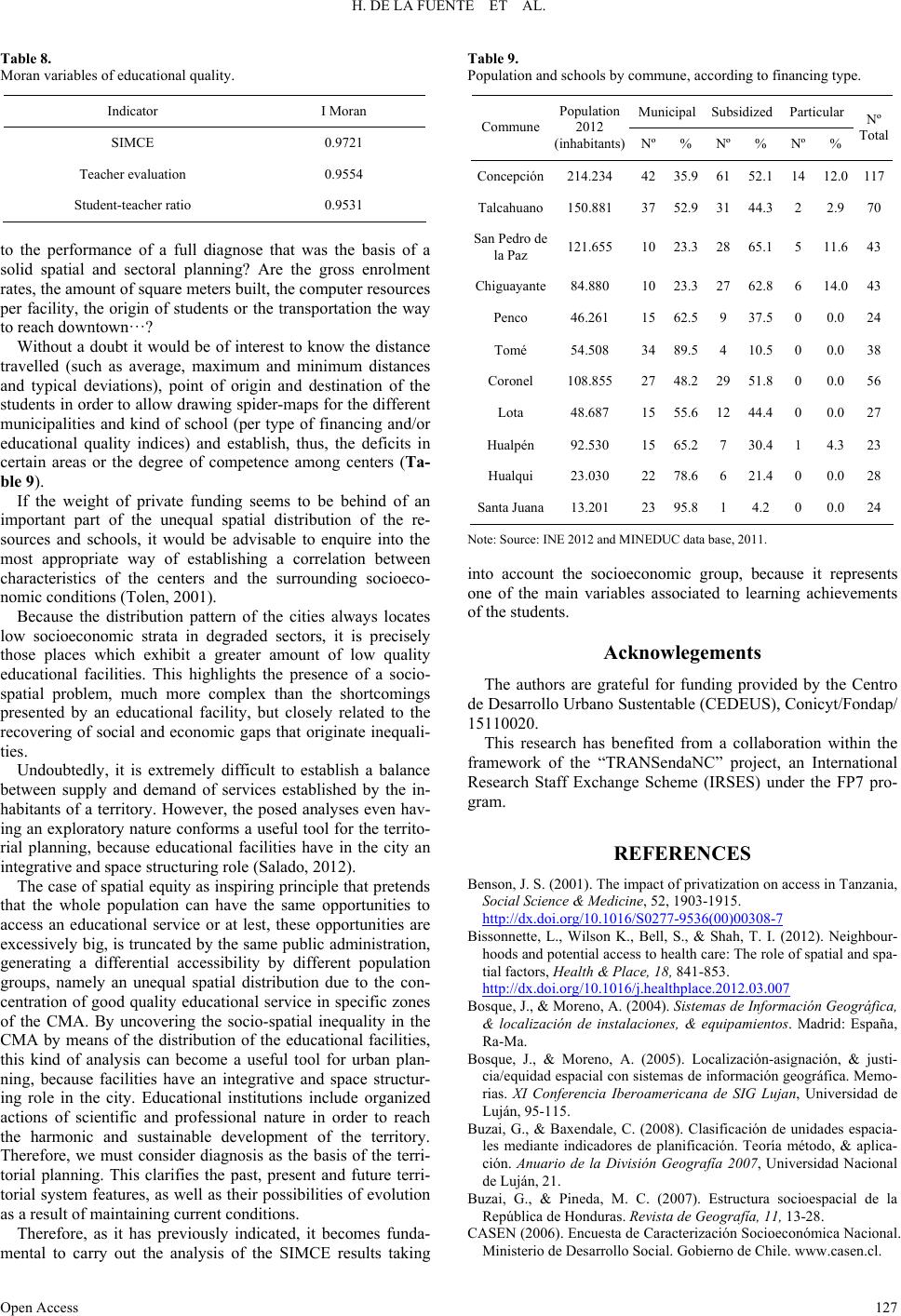 H. DE LA FUENTE ET AL. Table 8. Moran variables of educational quality. Indicator I Moran SIMCE 0.9721 Teacher evaluation 0.9554 Student-teacher ratio 0.9531 to the performance of a full diagnose that was the basis of a solid spatial and sectoral planning? Are the gross enrolment rates, the amount of square meters built, the computer resources per facility, the origin of students or the transportation the way to reach downtown···? Without a doubt it would be of interest to know the distance travelled (such as average, maximum and minimum distances and typical deviations), point of origin and destination of the students in order to allow drawing spider-maps for the different municipalities and kind of school (per type of financing and/or educational quality indices) and establish, thus, the deficits in certain areas or the degree of competence among centers (Ta- ble 9). If the weight of private funding seems to be behind of an important part of the unequal spatial distribution of the re- sources and schools, it would be advisable to enquire into the most appropriate way of establishing a correlation between characteristics of the centers and the surrounding socioeco- nomic conditions (Tolen, 2001). Because the distribution pattern of the cities always locates low socioeconomic strata in degraded sectors, it is precisely those places which exhibit a greater amount of low quality educational facilities. This highlights the presence of a socio- spatial problem, much more complex than the shortcomings presented by an educational facility, but closely related to the recovering of social and economic gaps that originate inequali- ties. Undoubtedly, it is extremely difficult to establish a balance between supply and demand of services established by the in- habitants of a territory. However, the posed analyses even hav- ing an exploratory nature conforms a useful tool for the territo- rial planning, because educational facilities have in the city an integrative and space structuring role (Salado, 2012). The case of spatial equity as inspiring principle that pretends that the whole population can have the same opportunities to access an educational service or at lest, these opportunities are excessively big, is truncated by the same public administration, generating a differential accessibility by different population groups, namely an unequal spatial distribution due to the con- centration of good quality educational service in specific zones of the CMA. By uncovering the socio-spatial inequality in the CMA by means of the distribution of the educational facilities, this kind of analysis can become a useful tool for urban plan- ning, because facilities have an integrative and space structur- ing role in the city. Educational institutions include organized actions of scientific and professional nature in order to reach the harmonic and sustainable development of the territory. Therefore, we must consider diagnosis as the basis of the terri- torial planning. This clarifies the past, present and future terri- torial system features, as well as their possibilities of evolution as a result of maintaining current conditions. Therefore, as it has previously indicated, it becomes funda- mental to carry out the analysis of the SIMCE results taking Table 9. Population and schools by commune, according to financing type. Municipal Subsidized Particular Commune Population 2012 (inhabitants) Nº % Nº % Nº % Nº Total Concepción214.234 42 35.9 61 52.1 14 12.0117 Talcahuano150.881 37 52.9 31 44.3 2 2.970 San Pedro de la Paz 121.655 10 23.3 28 65.1 5 11.643 Chiguayante84.880 10 23.3 27 62.8 6 14.043 Penco 46.261 1562.5 9 37.5 0 0.024 Tomé 54.508 3489.5 4 10.5 0 0.038 Coronel 108.855 27 48.2 29 51.8 0 0.056 Lota 48.687 15 55.6 12 44.4 0 0.027 Hualpén 92.530 1565.2 7 30.4 1 4.323 Hualqui 23.030 2278.6 6 21.4 0 0.028 Santa Juana13.201 2395.8 1 4.2 0 0.024 Note: Source: INE 2012 and MINEDUC data base, 2011. into account the socioeconomic group, because it represents one of the main variables associated to learning achievements of the students. Acknowlegements The authors are grateful for funding provided by the Centro de Desarrollo Urbano Sustentable (CEDEUS), Conicyt/Fondap/ 15110020. This research has benefited from a collaboration within the framework of the “TRANSendaNC” project, an International Research Staff Exchange Scheme (IRSES) under the FP7 pro- gram. REFERENCES Benson, J. S. (2001). The impact of privatization on access in Tanzania, Social Science & Medicine, 52, 1903-1915. http://dx.doi.org/10.1016/S0277-9536(00)00308-7 Bissonnette, L., Wilson K., Bell, S., & Shah, T. I. (2012). Neighbour- hoods and potential access to health care: The role of spatial and spa- tial factors, Health & Place, 18, 841-853. http://dx.doi.org/10.1016/j.healthplace.2012.03.007 Bosque, J., & Moreno, A. (2004). Sistemas de Información Geográfica, & localización de instalaciones, & equipamientos. Madrid: España, Ra-Ma. Bosque, J., & Moreno, A. (2005). Localización-asignación, & justi- cia/equidad espacial con sistemas de información geográfica. Memo- rias. XI Conferencia Iberoamericana de SIG Lujan, Universidad de Luján, 95-115. Buzai, G., & Baxendale, C. (2008). Clasificación de unidades espacia- les mediante indicadores de planificación. Teoría método, & aplica- ción. Anuario de la División Geografía 2007, Universidad Nacional de Luján, 21. Buzai, G., & Pineda, M. C. (2007). Estructura socioespacial de la República de Honduras. Revista de Geografía, 11, 13-28. CASEN (2006). Encuesta de Caracterización Socioeconómica Nacional. Ministerio de Desarrollo Social. Gobierno de Chile. www.casen.cl. Open Access 127  H. DE LA FUENTE ET AL. Celemin, J. P. (2009). Autocorrelación espacial e indicadores locales de asociación espacial. Importancia, estructura, & aplicación. Revista Universitaria de Geografía, 18, 11-31. Cervigni, F., Suzuki, Y., Ishii, T., & Hata, A. (2008). Spatial accessibil- ity to pediatric services. Journal of Community Health, 33, 444-448. http://dx.doi.org/10.1007/s10900-008-9112-x Cheng, Y., Wang, J., & Rosenberg, M. W. (2012). Spatial access to residential care resources in Beijing, China. International Journal of Health Geographics, 1 1 , 32-43. http://dx.doi.org/10.1186/1476-072X-11-32 Departamento Administrativo de Educación Municipal (2011). Plan Anual de Educación M u n i c i p al (PADEM). Escolano, S., Ruiz, E., & Climent, E. (2005). Red de centros educativos, & desequilibrios territoriales: El caso de Aragón. Geographicalia, 47, 153-176. Flores, V. (2009). Localización de instalaciones no deseables: Aportes desde la geografía a la instalación de rellenos sanitarios en el Área Metropolitana de Concepción. Tesis para optar al título de Geógrafo. Concepción: Universidad de Concepción, 128. Fuenzalida, M. (2010). Análisis de desigualdad territoriales en la oferta de equipamientos públicos: El caso de los hospitales en la red asis- tencial del sistema público de salud en Chile. Geografía, & Sistemas de Información Geográfica, 2 , 111-125. Fundación para la Superación de la Pobreza (2006). Umbrales sociales 2006. Propuesta para la futura política social. Santiago, 13. Góngora Gómez, J. (2007). Dimensión espacial de las remesas de migrantes internacionales en México. Tesis para optar al título de Maestro en estudios de población, & desarrollo regional. Cuernavaca, M. (2007). Universidad Autónoma del Estado de Morelos, 105. Goodchild, M., & Haining, S. (1992). Integrating GIS and spatial data analysis problem and possibilities. Geographical Information Sys- tems, 6, 407-423. http://dx.doi.org/10.1080/02693799208901923 GORE/UGIT-Gobierno Regional Región del Bío Bío/Unidad de Ges- tión de Información Territorial (2011). Información georreferenciada, Unidad de Gestión de Información Territorial. Gobierno Regional del Bío Bío. Gualiardo, M. F. (2004). Spatial accessibility of primary care: Concepts, methods and challenges. International Journal of Health Geograph- ics, 3, 1-13. http://dx.doi.org/10.1186/1476-072X-3-1 Gutiérrez, J., & García, J. (2002). Accesibilidad peatonal a la red sani- taria de asistencia primaria en Madrid. Anales de Geografía de la Universidad Complutense, 269-280. Gutiérrez, J., & García, J. (2005). Cambios en la movilidad en el área metropolitana de Madrid: El creciente uso del transporte privado. Anales de Geografía de la Universidad Complutense de Madrid, 25, 331-351. Gutiérrez, J., Pinto, C., & Gómez, G. (2000). Accesibilidad peatonal a la red de metro de Madrid: Efectos del plan de ampliación 1995-99. Anales de Geografía de la Universidad Compluten se, 20, 451-464. Harvey, D. (1977). Urbanismo, & desigualdad social. Madrid. España, Siglo: XXI Editores S.A. INE-Instituto Nacional de Estadísticas (2002). XVII CENSO de po- blación, & VI de vivienda. Gobierno de Chile. www.ine.cl. INE-Instituto Nacional de Estadísticas (2012). XVII CENSO de po- blación, & VII de vivienda. Gobierno de Chile. www.ine.cl. Langford, M., Higgs, G., Radcliffe, J., & White, S. (2008). Urban population distribution models and service accessibility estimation, Computers. Environment and Urban Systems, 3 2 , 66-80. http://dx.doi.org/10.1016/j.compenvurbsys.2007.06.001 Lee, J., & Wong, D. (2001). Statistical analysis with ArcView GIS. New York: John Wiley and Sons. López Hernández, F., & Palacios Sánchez, M. A. (2000). Distintos modelos de dependencia espacial. Análisis de autocorrelación. Ana- les de Economía Aplicada. Oviedo, España, 1-17. Luo, W. (2004). Using a GIS-based floating catchment method to as- sess areas with shortage of physicians. Health Place, 10, 1-11. http://dx.doi.org/10.1016/S1353-8292(02)00067-9 Luo, W., & Qi, Y. (2009). An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place, 15, 1100-1107. http://dx.doi.org/10.1016/j.healthplace.2009.06.002 Luo, W., & Whippo, T. (2012). Variable catchment sizes for the two-step floating catchment area (2SFCA) method. Health Place, 18, 789-795. http://dx.doi.org/10.1016/j.healthplace.2012.04.002 MINEDUC-Ministerio de Educación (2010). Sistema de Medición de Calidad de la Educación (SIMCE). Gobierno de Chile. www.mineduc.cl. MINEDUC-Ministerio de Educación (2011). Establecimientos Educa- tivos en la Región del Bío Bío. Gobierno de Chile. www.mineduc.cl. Ministerio de Educación-Departamento de estudios y desarrollo de la División de Planificación y Presupuesto (2008). Indicadores de la Educación en Chile 2007-2008. Estudios y estadísticas del sistema del escolar chileno, 5, 140. Moreno, A. (1999). Justicia y eficiencia espacial como principios para la planificación: Aplicación en la provisión de servicios colectivos con SIG. IX Conferencia Iberoamericana de Sistemas de Informa- ción Geográfica, 197-230. Moreno, A. (2007). En torno a los conceptos de equidad, justicia e igualdad especial. Huellas, 11, 133-142. Oberty, M. (2007). Social and school differentiation in urban space: Inequalities and local configurations. Environment and Planning A, 39, 208-227. http://dx.doi.org/10.1068/a39159 Organisation for Economic Co-operation and Development, OECD (2012). Education at a Glance 2012: OECD Indicators, OECD Pub- lishing. URL (last checked 10 Jan 2012). http://dx.doi.org/10.1787/eag-2012-en http://dx.doi.org/10.1787/eag-2012-en Pitarch Garrido, M. D. (2000). Los modelos de planificación espacial de los servicios públicos: El caso de los servicios educativos. Cuad- ernos de Geografía, 67- 68 , 119-136. Pizzolato, N., Broseghini, F., & Noguera, L. (2004). School location methodology in urban areas of developing countries. International Transactions in Operational Research, 11, 667-681. http://dx.doi.org/10.1111/j.1475-3995.2004.00483.x Ramírez, L. (2008). Estudio de la accesibilidad de la población del Gran Resistencia a los centros de salud. Serie Geográfica, 14, 235- 248. Rojas, C., Muñiz, I., & Pino, J. (2013). Understanding the urban sprawl in the mid-size Latin American cities through the urban form: Analy- sis of the concepcion metropolitan area (Chile). Journal of Geo- graphic Information System, 5, 222-234. http://dx.doi.org/10.4236/jgis.2013.53021 Sabatini, F., & Brain, I. (2008). La segregación, los guetos y la inte- gración social urbana: Mitos y claves. Revista latinoamericana de estudios urbanos regionales EURE (Santiago), 34, 5-26. www.scielo.cl/scielo.php?script=sci_arttext&pid=S0250-716120080 00300001&lng=es&nrm=iso. Sabuda, F. (2007). Autocorrelación espacial aplicada al análisis de la vulnerabilidad educativa en la ciudad de Mar del Plata. XI Conferen- cia Iberoamericana de Sistema de Información Geográfica, Buenos Aires, Argentina, 20. Sabuda, F., Ares, S., & Mikkelsen, C. (2005). Calidad de vida y acce- sibilidad geográfica en la ciudad de Mar del Plata, primeros aportes (pp. 1-7). Mar del Plata, Argentina: X Jornadas Argentinas de Estu- dios de Población. Salado, M. J. (2012). Localización de los equipamientos colectivos, accesibilidad y bienestar social, en Bosque, J. y Moreno, A. (coords): Sistemas de Información Geográfica y localización óptima de insta- laciones y equipamientos (2ª ed.). Madrid, España: Ra-Ma, Revisada y ampliada, 41-65. Talen, E. (2001). School, community and spatial equity: An empirical investigation of access to elementary schools in West Virginia. An- nals of the Association of American Geographers, 91, 465-486. http://dx.doi.org/10.1111/0004-5608.00254 Tsou, K. W., Hung, Y. T., & Chang, Y. L. (2005). An accessibility- based integrated measure of relative spatial equity in urban public facilities. Cities, 22, 424-435. http://dx.doi.org/10.1016/j.cities.2005.07.004 Villanueba, A. (2010). Accesibilidad geográfica a los sistemas de salud y educación. Análisis espacial de las localidades de Necochea y Quequén. Revista Terri torio y Transporte, 2, 23. Open Access 128  H. DE LA FUENTE ET AL. Open Access 129 Wang, F. H. (2012). Measurement, optimization, and impact of health care accessibility: A methodological review. Annals of the Associa- tion of American Geographers, 102, 1104-1112. http://dx.doi.org/10.1080/00045608.2012.657146 Yi, L. (2004): Evaluation of accessibility to primary schools. The case of Yuhua, Changsha, China (p. 81). Tesis para optar al título de mas- ter of science in urban planning and land administration. Enschede: Utrecht University and ITC.
|