 Applied Mathematics, 2013, 4, 1647-1650 Published Online December 2013 (http://www.scirp.org/journal/am) http://dx.doi.org/10.4236/am.2013.412224 Open Access AM New Implementation of Legendre Polynomials for Solving Partial Differential Equations Ali Davari*, Abozar Ahmadi Department of Mathematics, Faculty of Science, University of Isfahan, Isfahan, Iran Email: *a_davari@sci.ui.ac.ir Received May 25, 2013; revised June 25, 2013; accepted July 2, 2013 Copyright © 2013 Ali Davari, Abozar Ahmadi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT In this paper we present a proposal using Legendre polynomials approximation for the solution of the second order lin- ear partial differential equations . Our approach consists of reducing the problem to a set of linear equations by expand- ing the approximate solution in terms of shifted Legendre polynomials with unknown coefficients . The performance of presented method has been compared with other methods , namely Sinc-Galerkin , quadratic spline collocation and Liu- Lin method . Numerical examples show better accuracy of the proposed method . Moreover , the computation cost de- creases at least by a factor of 6 in this method . Keywords: Legendre Polynomials; Partial Differential Equations ; Collocation Method 1. Introduction There are several applications of partial differential equations (PDEs) in science and engineering [1,2]. Many physical processes can be modeled using PDEs . Ana- lytical solution of PDEs , however , either does not exist or is difficult to find . Recent contribution in this regard includes meshless methods [3], finite-difference methods [4], Alternating-Direction Sinc-Galerkin method (ADSG) [5] , quadratic spline collocation method (QSCM) [6] , Liu and Lin method [7] and so on . Orthogonal functions and polynomials have been em- ployed by many authors for solving various PDEs. The main idea is using an orthogonal basis to reduce the problem under study to a system of linear algebraic equations. This can be done by truncated series of or- thogonal basis functions for the solution of problem and using the collocation method. In this paper, we have applied a method based on Legendre polynomials basis on the unit square. This method is simple to understand and easy to implement using computer packages and yields better results. Com- parative studies of CPU time of present method and other methods such as Sinc-Galerkin method, quadratic spline collocation method and Liu-Lin method are also pre- sented. Numerical tests exhibit better accuracy of our proposed method based on Legendre polynomials. Moreover, time for computation decreases at least more than 6 folds. This paper is organized as follows. In Section 2, we present some properties of Legendre polynomials. Sec- tion 3 describes the proposed technique for solution of PDEs. Section 4 is devoted to some experimental results and the paper is concluded with a summery in Section 5. 2. Preliminaries and Notation The Legendre polynomials ; are the eigenfunctions of the singular Sturm-Liouville prob- lem m Lx 0,1,2,,m 2 110, mm xLxmm Lxx 1,1. The Legendre polynomials satisfy the recursion rela- tion 11 21 ; 0,1,2, 11 mmm mm LxxLx Lxm mm where 01Lx and 1 Lx x. In order to use Leg- endre polynomials on the interval 0,1 we use the so-called shifted Legendre polynomials by introducing the change of variable 21tx . The shifted Legendre polynomials 12Lx m are denoted by m Px and can be obtained by the following triple recursion relation: *Corresponding author.  A. DAVARI, A. AHMADI 1648 11 21 21; 0,1,2, 11 mmm mm Pxx PxPxm mm where 01 1, 21.PxPx x A square integrable function , x in 0,1, may be expanded in terms of shifted Legendre polynomials as 0 , mm m xaPx where the coefficients are given by m a 1 0 21d; 1,2, mm am fxPxxm In practice, only the first 1-Mterms shifted Leg- endre polynomials are considered. Then we set 0 . M mm m xaPx Similarly a function , xy 0,xy of two independent variables defined for may be expanded in terms of double shifted Legendre polynomials as 1 00 ,; MM ij ij ij xyaP xPy where the coefficient are given by ij a 11 00 212 1,dd; ,0,1,2,,. iji j ai jfxyPxPyx ij M y For further properties of Legendre polynomials re- ferred to [8,9]. 3. Solution of Second-Order Linear PDEs Consider the following second-order linear PDEs on the unit square, 2 0,1 : 22 22 ,,, ,,, uu axybxycxy u xy u d xyg xyufxy y (1) where and ,,, ,abcdg are known functions. With Dirichlet boundary conditions: 12 0,, 1,,uygyuygy 3 ,0, ,1,uxg xuxgx 4 1 (2) where are known functions. We intro- duce the following notations: ; 1,2,3,4 i gi 12 00 11 0 d, d, d. xx iii i ii Px PttPx Ptt CPtt (3) We assume that the second order partial derivatives can be expressed by Legendre polynomials series as given below: 2 2 00 ,, MM ij ij ij u yaPxP x y (4) 2 2 00 ,, MM ij ij ij u ybPxP y y (5) The following collocation points are considered: 0.5 ; 1,2,,1 1 cc xc M M 0.5 ; 1,2,,1 1 ss ys M M (6) After integrating from “Equation (4)” we obtain 1 11 ,0, MM ij ij ji uu , yyaPxP xx y (7) or 1 11 0, ,, MM ij ij ji uu yxy aPxP xx y (8) Now by integrating from “Equation (8)” in the interval 0, , we get 11 0,1,0,, MM iji j ji uyuyuyaCPy x (9) Substituting “Equation (9)” in “Equation (7)”, yields 1 11 ,1,0, MM ij jii ji u. yuyuyaPyPxC x Now by integrating this equation from to 0 , we have 2 11 ,0, 1,0, , MM ij jii ji uxyu yxuyu y aP yPxxC (10) Thus by substituting “Equation (2)” in this equation, we obtain 121 2 11 , . MM ij jii ji uxyg yxgyg y aP yPxxC (11) Similarly for “Equation (5)”, we have 1 ,1 ,,1,0 M ij ijj ij uxyuxuxbPxPyC y ; and 343 2 ,1 , . M ij iji ij uxygyygxg x bP xPyyC (12) Open Access AM 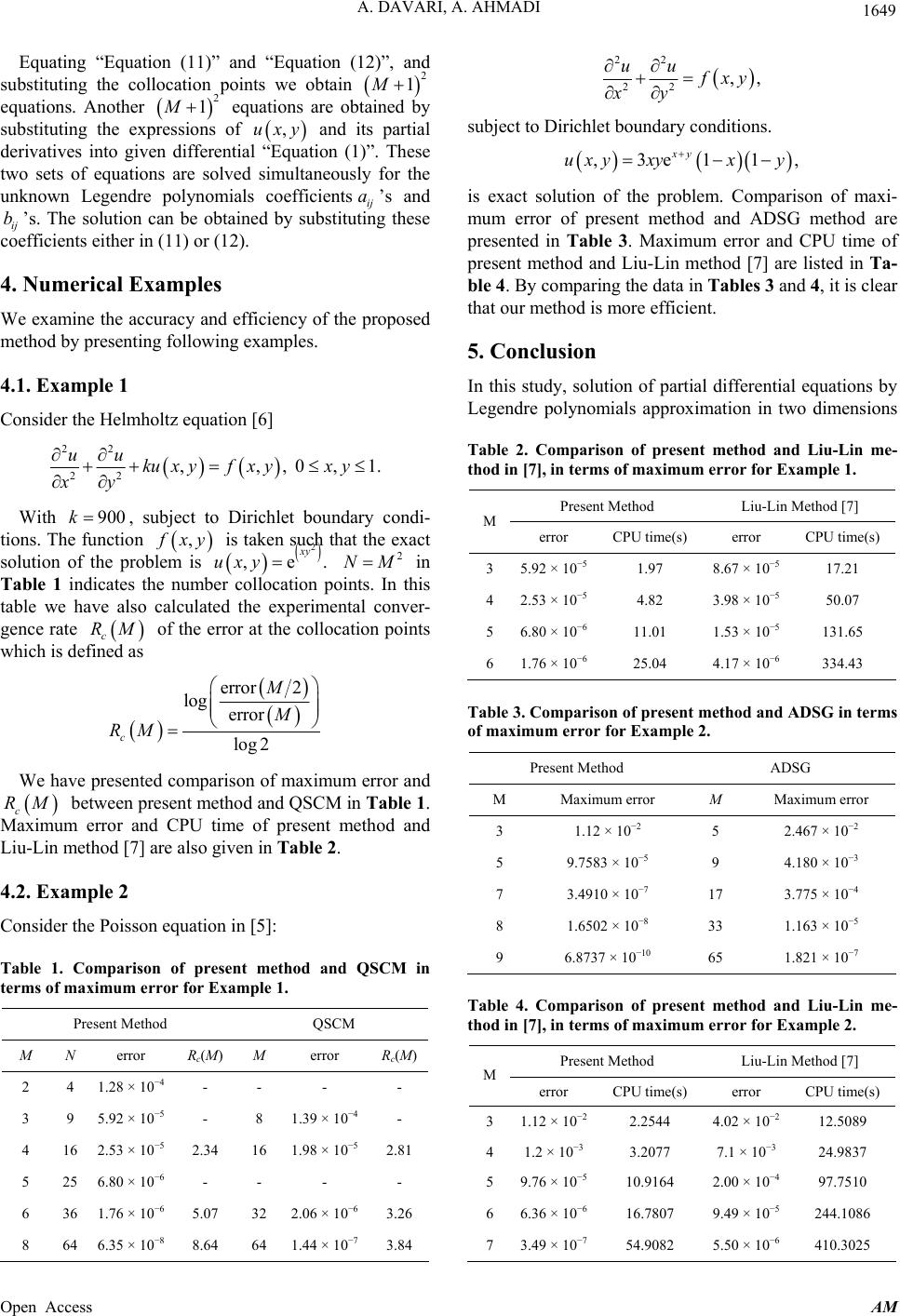 A. DAVARI, A. AHMADI 1649 Equating “Equation (11)” and “Equation (12)”, and substituting the collocation points we obtain 2 1M equations. Another equations are obtained by substituting the expressions of and its partial derivatives into given differential “Equation (1)”. These two sets of equations are solved simultaneously for the unknown Legendre polynomials coefficientsij’s and ij ’s. The solution can be obtained by substituting these coefficients either in (11) or (12). 2 1M ,uxy a b 4. Numerical Examples We examine the accuracy and efficiency of the proposed method by presenting following examples. 4.1. Example 1 Consider the Helmholtz equation [6] 22 22 ,,, 0, uu kux yfx yx y xy 1. With , subject to Dirichlet boundary condi- tions. The function 900 k , xy is taken suat the exact solution of the problem is in Table 1 indicates the number collocation points. In this table we have also calculated the experimental conver- gence rate c of the error at the collocation points which is defined as ch th 2 ,e xy uxy.2 NM RM error 2 log error log 2 c M M RM We have presented comparison of maximum error and between present method and QSCM in Table 1 . Maximum error and CPU time of present method and Liu-Lin method [7] are also given in Table 2. c RM 4.2. Example 2 Consider the Poisson equation in [5]: Table 1. Comparison of present method and QSCM in terms of maximum error for Example 1. Present Method QSCM M N error Rc(M) M error Rc(M) 2 4 1.28 × 10−4 - - - - 3 9 5.92 × 10−5 - 8 1.39 × 10−4- 4 16 2.53 × 10−5 2.34 16 1.98 × 10−52.81 5 25 6.80 × 10−6 - - - - 6 36 1.76 × 10−6 5.07 32 2.06 × 10−63.26 8 64 6.35 × 10−8 8.64 64 1.44 × 10−73.84 22 22 ,, uu xy xy subject to Dirichlet boundary conditions. ,3e11 xy uxy xyxy , is exact solution of the problem. Comparison of maxi- mum error of present method and ADSG method are presented in Table 3. Maximum error and CPU time of present method and Liu-Lin method [7] are listed in Ta- ble 4. By comparing the data in Tables 3 and 4, it is clear that our method is more efficient. 5. Conclusion In this study, solution of partial differential equations by Legendre polynomials approximation in two dimensions Table 2. Comparison of present method and Liu-Lin me- thod in [7], in terms of maximum error for Example 1. Present Method Liu-Lin Method [7] M error CPU time(s) error CPU time(s) 3 5.92 × 10−51.97 8.67 × 10−5 17.21 4 2.53 × 10−54.82 3.98 × 10−5 50.07 5 6.80 × 10−611.01 1.53 × 10−5 131.65 6 1.76 × 10−625.04 4.17 × 10−6 334.43 Table 3. Comparison of present method and ADSG in terms of maximum error for Example 2. Present Method ADSG M Maximum error M Maximum error 3 1.12 × 10−2 5 2.467 × 10−2 5 9.7583 × 10−5 9 4.180 × 10−3 7 3.4910 × 10−7 17 3.775 × 10−4 8 1.6502 × 10−8 33 1.163 × 10−5 9 6.8737 × 10−10 65 1.821 × 10−7 Table 4. Comparison of present method and Liu-Lin me- thod in [7], in terms of maximum error for Example 2. Present Method Liu-Lin Method [7] M error CPU time(s) error CPU time(s) 3 1.12 × 10−22.2544 4.02 × 10−2 12.5089 4 1.2 × 10−33.2077 7.1 × 10−3 24.9837 5 9.76 × 10−510.9164 2.00 × 10−4 97.7510 6 6.36 × 10−616.7807 9.49 × 10−5 244.1086 7 3.49 × 10−754.9082 5.50 × 10−6 410.3025 Open Access AM  A. DAVARI, A. AHMADI Open Access AM 1650 is investigated. Results show better accuracy of the pro- posed method based on Legendre polynomials. Experi- mental results on various problems show that in com- parison with the previous method (Sinc-Galerkin method, quadratic spline collocation method and Liu-Lin me- thod), the computation cost of the proposed methods has decreased noticeably, the CPU time for computation falls at least more than 6 folds. 6. Acknowledgements Thanks the Center of Excellence for Mathematics, Uni- versity of Isfahan for Financial support. REFERENCES [1] Q. Wang, “Numerical Solutions for Fractional KdV-Bur- gers Equatin by Adomian Decomposition Method,” Ap- plied Mathematics and Computation, Vol. 182, No. 2, 2006, pp. 1048-1055. http://dx.doi.org/10.1016/j.amc.2006.05.004 [2] X. Chen and J. Xiang, “Solving Diffusion Equation Using Wavelet Method,” Applied Mathematics and Computa- tion, Vol. 217, No. 13, 2011, pp. 6426-6432. http://dx.doi.org/10.1016/j.amc.2011.01.042 [3] Q. N. Yang, J. J. Zheng, Y. Miao and Y. Z. Sima, “An Improved Hybrid Boundary Node Method for Solving Steady Fluid Flow Problems,” Engineering Analysis with Boundary Elements, Vol. 35, No. 1, 2011, pp. 18-24. http://dx.doi.org/10.1016/j.amc.2011.01.042 [4] K. W. Morton and D. F. Mayers, “Numerical Solution of Partial Differential Equations,” Cambridge University Press, Cambridge, 2005. http://dx.doi.org/10.1017/CBO9780511812248 [5] N. Alonso and K. L. Bowers, “An Alternating-Direction Sinc-Galerkin Method for Elliptic Problems,” Journal of Complexity, Vol. 25, No. 3, 2009, pp. 237-252. http://dx.doi.org/10.1016/j.jco.2009.02.006 [6] G. Fairweather, A. Karageorghis and J. Maack, “Compact Optimal Quadratic Spline Collocation Methods for the Helmholtz Equation,” Journal of Computational Physics, Vol. 230, No. 8, 2011, pp. 2880-2895. http://dx.doi.org/10.1016/j.jcp.2010.12.041 [7] N. Liu and E. B. Lin, “Legendre Wavelet Method for Numerical Solutions of Partial Differential Equations,” Numerical Methods for Partial Differential Equations, Vol. 26, No. 1, 2010, pp. 81-94. http://dx.doi.org/10.1002/num.20417 [8] C. Canuto, M. Y. Hussaini, A. Quarteroni and T. A. Zang, “Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamiccs,” Springer, New York, 2007. [9] A. Saadatmandi and M. Dehghan, “Numerical Solution of the Higher-Order Linear Fredholm Integro Differential Difference Equation with Variable Coefficients,” Com- puters and Mathematics with Applications, Vol. 59, No. 8, 2010, pp. 2996-3004. http://dx.doi.org/10.1016/j.camwa.2010.02.018
|