Journal of Software Engineering and Applications
Vol.08 No.03(2015), Article ID:54795,9 pages
10.4236/jsea.2015.83014
Optimizing Software Effort Estimation Models Using Firefly Algorithm
Nazeeh Ghatasheh1, Hossam Faris2, Ibrahim Aljarah2, Rizik M. H. Al-Sayyed2
1Department of Business Information Technology, The University of Jordan, Aqaba, Jordan
2Department of Business Information Technology, The University of Jordan, Amman, Jordan
Email: n.ghatasheh@ju.edu.jo, hossam.faris@ju.edu.jo, i.aljarah@ju.edu.jo, r.alsayyed@ju.edu.jo
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 February 2015; accepted 16 March 2015; published 18 March 2015
ABSTRACT
Software development effort estimation is considered a fundamental task for software development life cycle as well as for managing project cost, time and quality. Therefore, accurate estimation is a substantial factor in projects success and reducing the risks. In recent years, software effort estimation has received a considerable amount of attention from researchers and became a challenge for software industry. In the last two decades, many researchers and practitioners proposed statistical and machine learning-based models for software effort estimation. In this work, Firefly Algorithm is proposed as a metaheuristic optimization method for optimizing the parameters of three COCOMO-based models. These models include the basic COCOMO model and other two models proposed in the literature as extensions of the basic COCOMO model. The developed estimation models are evaluated using different evaluation metrics. Experimental results show high accuracy and significant error minimization of Firefly Algorithm over other metaheuristic optimization algorithms including Genetic Algorithms and Particle Swarm Optimization.
Keywords:
Software Quality, Effort Estimation, Metaheuristic Optimization, Firefly Algorithm

1. Introduction
Effort estimation of software development has been a crucial task for software engineering community. Reliable effort estimation makes it more dependable to schedule project activities, allocate resources, estimate costs, and reduce the probability of project failures or delays. According to the survey in [1] , most of the projects face overruns of effort or schedules. The survey also claimed that the lack of accurate estimation models is a main reason for project overruns.
Usually projects seem to be vague at the beginning and become less vague as they progress. At the same time, each project has its special nature that makes it much harder to estimate the required effort for completion. Due to the uncertain nature of projects, authors in [2] [3] suggested developing models that can adapt to a wide range of projects. But for the fact that software project data sets are typically small and the underlying relations are inaccurate or missing, the task of prediction becomes more challenging.
Several effort estimation models have been developed and improved over time for better prediction accuracy and thus better development quality [1] [4] - [8] . Such models range from complex calculations and statistical analysis of project parameters, to advanced machine learning approaches.
Heuristic optimization [9] is a method that relies on several attempts to find an optimal solution. Heuristic optimizers have been used in software effort estimation [10] as the use of genetic programming in [11] for model optimization. Another example is the part that Particle Swarm Optimization took in [12] as a heuristic optimizer. Moreover, the hybrid approaches encompass a combination of heuristic algorithms like the use of Genetic Algorithm and Ant Colony [13] .
Despite a large number of experiments on finding the best prediction model, there is no clear evidence of a highly accurate or efficient approach. At the same time it is important to develop a prediction method that is less complex and much more useful. For instance, in some prediction models, a large number of variables that are used to construct the model do not reflect or improve the accuracy of the prediction model. Thus, collecting extra or unrelated variables is time-consuming with no significance. It would be more efficient to build a model with a minimum number of variables, hopefully finding the most important and common variables for generic project development efforts.
This work presents a study of how Firefly Algorithm improves the overall estimation of the software effort estimation. Where the main contributions are:
・ Proving the suitability of Firefly Algorithm as predictor towards a generic prediction model for software effort estimation.
・ The significant improvement in performance over previously reported methods.
・ The suitability of machine learning approaches for effort prediction using a small number of input variables and data set instances.
2. Related Work
Many of Machine Learning (ML) approaches in the literature have been applied to improve the software effort estimation [2] . ML optimization algorithms that are inspired from nature have received much attention to find more accurate estimation for software effort. Nature-inspired ML algorithms include Cuckoo Search [14] , Particle Swarm Optimization (PSO) [15] , Bat Algorithm [16] , Firefly Algorithm [17] , and many others.
In [18] , the authors compared the performance of different soft computing techniques such as PSO-Tuned COCOMO, Fuzzy Logic with traditional effort estimation structures. Their results showed that the proposed model outperformed traditional effort estimation structures for NASAs software effort data set. In [7] , decision trees based algorithm was used to perform the software effort estimation. In addition, the authors presented an empirical proof of performance variations for several approaches that include Linear Regression, Artificial Neural Networks (ANN), and Support Vector Machines (SVM). Also the authors pointed to the suitability of the experimented ML approaches in the area of effort estimation. From their performance comparison results with other traditional algorithms, their results in terms of the error rate were better than other techniques.
A hybrid approach was adopted in [19] for parameter selection and model optimization. The authors used Genetic Algorithms (GA) for optimizing a Support Vector Regression model. The authors clarified the impact of using GA in feature selection and parameter optimization of the effort estimation model. The results of their approach showed that GA is applicable to improve the performance of the SVR model compared to other approaches. A generic framework is proposed in [20] for software effort estimation. The framework tries to simulate the human way of thinking to resolve the effort estimation by adopting fuzzy rules modeling. Therefore the generated models take advantage of experts knowledge, interoperable, and could be applied to various problems as risk analysis or software quality prediction. ANNs gained noticeable attention by researchers for effort estimation as illustrated by the review in [21] , but it is insufficient to generalize the applicability of ANN in effort estimation. The authors stated that it is required to have further thorough investigation. The authors in [22] relied on seven evaluation measures to assess the stability of 90 software effort predictors over 20 data sets. According to the empirical results it was found that analogy-based methods or regression trees outperformed in terms of stability. Such conclusions open the door for extensive research towards a superior and generic prediction approach regarding the software effort estimation issue.
3. Firefly Algorithm
Firefly Algorithm (FA) is a multimodal optimization algorithm, which belongs to the nature-inspired field, is inspired from the behavior of fireflies or lightning bugs [17] . FA was first introduced by Xin-She at Cambridge University in 2007 [17] . FA is empirically proven to tackle problems more naturally and has the potential to over-perform other metaheuristic algorithms.
FA relies on three basic rules, the first implies that all fireflies are attracted to each other with disregard to gender. The second rule states that attractiveness is correlated with brightness or light emission such that bright flies attract less bright ones, and for absence of brighter flies the movement becomes random. The last main rule implies that the landscape of the objective function determines or affects the light emission of the fly, such that brightness is proportional to the objective function.
Algorithm 1. Pseudo-code of firefly algorithm.
The attractiveness among the flies in FA has two main issues that are; the modeling of attractiveness and the various light intensities. For a specific firefly at location X brightness I is formulated as 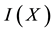
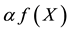 . While attractiveness b is proportional to the flies and is related to the distance
. While attractiveness b is proportional to the flies and is related to the distance 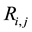 between fireflies i and j. Equation (1) shows the inverse square of light intensity
between fireflies i and j. Equation (1) shows the inverse square of light intensity 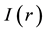 in which
in which 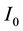 represents the light intensity at the source.
represents the light intensity at the source.
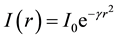 (1)
(1)
Assuming an absorption coefficient of the environment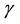 , intensity is represented in Equation (2) in which
, intensity is represented in Equation (2) in which 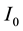 is the original intensity.
is the original intensity.
 (2)
(2)
Generally the Euclidean distance is illustrated in Equation (3), which represents the distance between a firefly at location 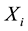 and another at location
and another at location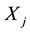 . In which
. In which 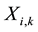 is the
is the  component of the spatial coordinate
component of the spatial coordinate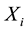 .
.
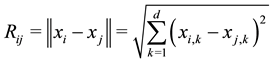 (3)
(3)
A firefly i attracted to a brighter one j as illustrated in Equation (4) where attraction is represented by
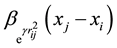
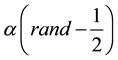
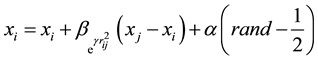
Furthermore, variations of attractiveness are determined by γ which on its turn affects the behavior and convergence speed of FA.
4. Effort Estimation Models
One of the Famous and widely used effort estimation models is the Constructive Cost Models COCOMO and its extension COCOMOII. COCOMO is used as cost, effort, and schedule estimation model in the process of planning new software development activity, also known as COCOMO 81. COCOMO was defined between the late 1970s and early 1980s [23] . Where COCOMOII is a later extension of the previously defined model. This research work tries to optimize the parameters of three variations of the COCOMO model. The first is the basic COCOMO model which is represented in Equation (5).
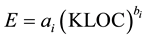
E is the effort in person-months, KLOC represents the thousand (K) lines of code included in a software project. Typically, the coefficient ai and the exponent bi are chosen based on COCOMO pre-set parameters that depend on the software project details.
The other two models are extensions of the basic COCOMO model which are proposed by A. Sheta in [24] . Both models consider the effect of methodologies (ME) as supposed to be linearly related to the software effort. These models are represented in Equations (6) and (7) and named Model I and Model II respectively.
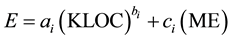
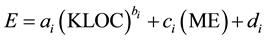
This work tries empirically to optimize the constants ai, bi, ci and di using FA, GA and PSO.
5. Data Set and Evaluation Measures
This research considers a famous and public data set in order to produce comparable results; namely NASA projects' effort data set. The data set is challenging due to the small number of instances and limited number of analyzed variables. However, regarding the objectives of this research the data set is considered to be adequate. The data set is split into two parts; training set of about 60% and testing set of about 30% instances.
NASA data set [6] consists of 18 software projects for which this research considers three main variables that are the project size in thousand Lines of Code (KLOC), Methodology (ME), and Actual Effort (AE). Training data set has 13 instances and the records from 14 till 18 are for testing the model. Table 1 shows the actual values of the training and testing data sets.
In order to check the performance of the developed models, the computed measures are the Correlation Coefficient (R2),

the Mean Squares Error (MSE),
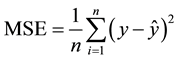
Table 1. NASA data set.
the Mean Absolute Error (MAE),
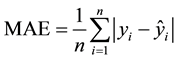
the Mean Magnitude of Relative Error (MMRE),
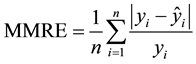
and the Variance-Accounted-For (VAF).
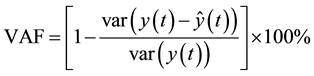
These performance criteria are used to measure how close the predicted effort to the actual values, where y is the actual value, 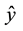
6. Experiments and Results
The experiments apply FA, GA and PSO for optimizing the coefficients of the basic COCOMO model, COCOMO Model I and COCOMO Model II based on the training part of NASA data set. For FA, the Matlab implementation developed by X.-S. Yang [9] is applied. Number of flies, particles and population size is unified and set to 100 in all the algorithms. The number of iterations is set to 500. The rest of the parameters of FA, GA and PSO are set as listed in Tables 2-4. MAE criteria are used as an objective function which is shown in Equation (10). In order to carry out meaningful evaluation results, each algorithm is applied 25 times then the average of the evaluation results is reported. In each run, the optimized models are evaluated based on the testing data using VAF, MSE, MAE, MMRE, RMSE and R2 evaluation metrics.
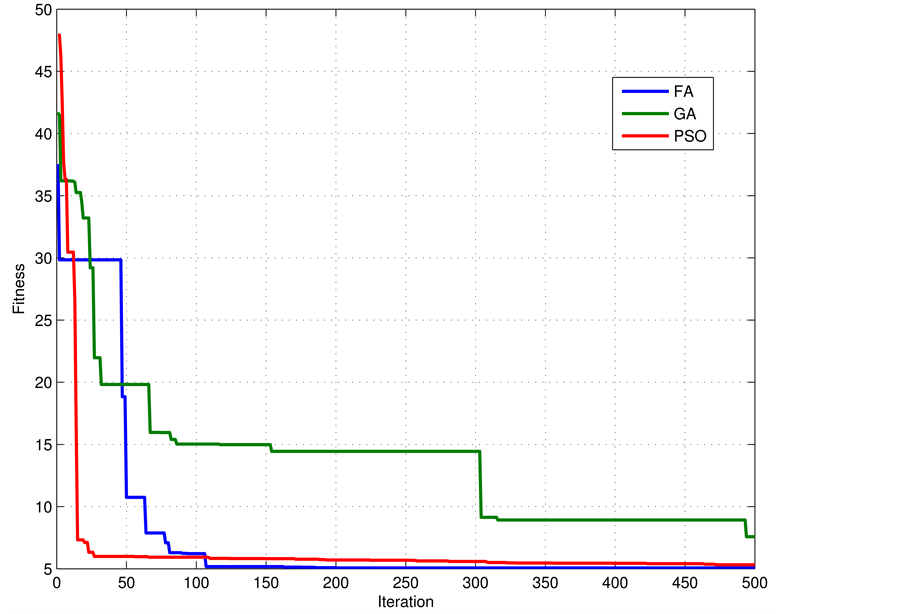
Carrying out the experiments, the average convergence curves for FA, GA and PSO are shown in Figures 1-3 respectively for the three variations of COCOMO model.
Table 2. Firefly algorithm parameter settings.
Table 3. GA parameter settings.
Table 4. PSO parameter settings.
Figure 1. Convergence of FA, GA and PSO in optimizing the basic COCOMO model.
Figure 2. Convergence of FA, GA and PSO in optimizing Model I.
Figure 3. Convergence of FA, GA and PSO in optimizing Model II.
The evaluation results for training and testing cases are shown in Tables 5-7. Based on Table 5 and Table 6 it can be noticed that Firefly outperforms GA and PSO in optimizing the basic COCOMO model and the Model I by means of all evaluation metrics. For the Model II, Firefly and PSO are very competitive and have very close results. On the other hand GA has the lowest results and it has the slowest convergence.
In summary, FA as a metaheuristic optimization algorithm over-performs GA and PSO in terms of higher estimation accuracy for the software effort COCOMO based models.
Table 5. Basic COCOMO model.
Table 6. COCOMO Model I.
Table 7. COCOMO Model II.
7. Conclusion and Future Work
This work investigated the efficiency of applying the Firefly Algorithm as a metaheuristic optimization technique to optimize the parameters of different effort estimation models. These models are three variations of the Constructive Cost Model COCOMO which are the basic COCOMO model, and other two extensions of the basic model that were proposed previously in the literature. The optimized models are assessed according to different evaluation criteria and compared with models optimized using other metaheuristic algorithms which are Genetic Algorithm and Particle Swarm Optimization. Evaluation results show that developed models using the Firefly Algorithm have higher accuracy in estimating software effort. Further future work is intended to overcome the instability issues, a more generic prediction model that is not highly affected by the size and the type of data set, and preferably an enhancement to the Firefly Algorithm itself. Moreover, it would be important to work towards a hybrid approach that encompasses the best characteristics of different prediction schemes.
References
- Molokken, K. and Jorgensen, M. (2003) A Review of Software Surveys on Software Effort Estimation. 2003 International Symposium on Empirical Software Engineering, 30 September-1 October 2003, 223-230.
- Song, Q. and Shepperd, M. (2011) Predicting Software Project Effort: A Grey Relational Analysis Based Method. Expert Systems with Applications, 38, 7302-7316. http://dx.doi.org/10.1016/j.eswa.2010.12.005
- Khatibi, V. and Jawawi, D.N. (2011) Software Cost Estimation Methods: A Review. Journal of Emerging Trends in Computing and Information Sciences, 2, 21-29.
- Afzal, W. and Torkar, R. (2011) On the Application of Genetic Programming for Software Engineering Predictive Modeling: A Systematic Review. Expert Systems with Applications, 38, 11984-11997. http://dx.doi.org/10.1016/j.eswa.2011.03.041
- Albrecht, A. and Gaffney, J.E. (1983) Software Function, Source Lines of Code, and Development Effort Prediction: A Software Science Validation. IEEE Transactions on Software Engineering, SE-9, 639-648. http://dx.doi.org/10.1109/TSE.1983.235271
- Bailey, J.W. and Basili, V.R. (1981) A Meta-Model for Software Development Resource Expenditures. Proceedings of the 5th International Conference on Software Engineering, Piscataway, 107-116.
- Ruchika Malhotra, A.J. (2011) Software Effort Prediction Using Statistical and Machine Learning Methods. International Journal of Advanced Computer Science and Applications (IJACSA), 2.
- Yadav, C.S. and Singh, R. (2014) Tuning of Cocomo ii Model Parameters for Estimating Software Development Effort Using GA for Promise Project Data Set. International Journal of Computer Applications, 90, 37-43. http://dx.doi.org/10.5120/15542-4367
- Wang, F.-S. and Chen, L.-H. (2013) Heuristic Optimization. In: Dubitzky, W., Wolkenhauer, O., Cho, K.-H. and Yokota, H., Eds., Encyclopedia of Systems Biology, Springer, New York, 885-885.
- Uysal, M. (2010) Estimation of the Effort Component of the Software Projects Using Heuristic Algorithms. INTECH Open Access Publisher, Croatia.
- Alaa, F. and Al-Afeef, A. (2010) A GP Effort Estimation Model Utilizing Line of Code and Methodology for NASA Software Projects. IEEE 10th International Conference on Intelligent Systems Design and Applications (ISDA), Cairo, 29 November-1 December 2010, 290-295.
- Bhattacharya, P., Srivastava, P. and Prasad, B. (2012) Software Test Effort Estimation Using Particle Swarm Optimization. In: Satapathy, S., Avadhani, P. and Abraham, A., Eds., Proceedings of the International Conference on Information Systems Design and Intelligent Applications 2012 (INDIA 2012), Visakhapatnam, January 2012, Vol. 132 of Advances in Intelligent and Soft Computing, 827-835. Springer, Berlin and Heidelberg.
- Maleki, I., Ghaffari, A. and Masdari, M. (2014) A New Approach for Software Cost Estimation with Hybrid Genetic Algorithm and Ant Colony Optimization. International Journal of Innovation and Applied Studies, 5, 72-81.
- Yang, X.-S. and Deb, S. (2009) Cuckoo Search via Levy Flights. World Congress on Nature Biologically Inspired Computing, NaBIC 2009, Coimbatore, 9-11 December 2009, 210-214.
- Kennedy, J. and Eberhart, R. (1995) Particle Swarm Optimization. IEEE International Conference on Neural Networks, 4, 1942-1948.
- Yang, X.-S. (2010) A New Metaheuristic Bat-Inspired Algorithm. In: Gonzlez, J., Pelta, D., Cruz, C., Terrazas, G. and Krasnogor, N., Eds., Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), Vol. 284 of Studies in Computational Intelligence, 65-74. Springer, Berlin and Heidelberg.
- Yang, X.-S. (2009) Firefly Algorithms for Multimodal Optimization. In: Watanabe, O. and Zeugmann, T., Eds., Stochastic Algorithms: Foundations and Applications, Vol. 5792 of Lecture Notes in Computer Science, 169-178. Springer, Berlin and Heidelberg.
- Sheta, A., Rine, D. and Ayesh, A. (2008) Development of Software Effort and Schedule Estimation Models Using Soft Computing Techniques. IEEE Congress on Evolutionary Computation, CEC 2008 (IEEE World Congress on Computational Intelligence), Hong Kong, 16 June 2008, 1283-1289.
- Oliveira, A.L.I., Braga, P.L., Lima, R.M.F. and Cornélio, M.L. (2010) GA-Based Method for Feature Selection and Parameters Optimization for Machine Learning Regression Applied to Software Effort Estimation. Information and Software Technology, 52, 1155-1166. http://dx.doi.org/10.1016/j.infsof.2010.05.009
- Huang, X., Ho, D., Ren, J. and Capretz, L. (2006) A Soft Computing Framework for Software Effort Estimation. Soft Computing, 10, 170-177. http://dx.doi.org/10.1007/s00500-004-0442-z
- Dave, V. and Dutta, K. (2014) Neural Network Based Models for Software Effort Estimation: A Review. Artificial Intelligence Review, 42, 295-307. http://dx.doi.org/10.1007/s10462-012-9339-x
- Keung, J., Kocaguneli, E. and Menzies, T. (2013) Finding Conclusion Stability for Selecting the Best Effort Predictor in Software Effort Estimation. Automated Software Engineering, 20, 543-567. http://dx.doi.org/10.1007/s10515-012-0108-5
- Boehm, B., Abts, C., Clark, B. and Devnani-Chulani, S. (1997) COCOMO II Model Definition Manual. University of Southern California, Los Angeles.
- Sheta, A.F. (2006) Estimation of the COCOMO Model Parameters Using Genetic Algorithms for NASA Software Projects. Journal of Computer Science, 2, 118-123. http://dx.doi.org/10.3844/jcssp.2006.118.123