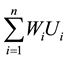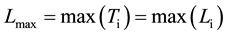Received 10 January 2015; accepted 27 January 2015; published 28 January 2015

ABSTRACT

This paper discusses review of literature of open shop scheduling problems. First, the problem is classified as per different measures of performance, viz., minimization of makespan, minimization of sum of completion times of jobs, minimization of sum of weighted completion times of all jobs, minimization of total tardiness of all jobs, minimization of sum of weighted tardiness of all jobs, minimization of weighted sum of tardy jobs, and miscellaneous measures of the open shop scheduling problem. In each category, the literature is further classified based on approaches used and then the contributions of researchers in the respective categories are presented. Directions for future research are discussed in the end.

Keywords:

Open Shop Scheduling, Measures of Performance, Meta-Heuristics, Heuristics

1. Introduction

Production scheduling is a key for organizational productivity, which prepares a calendar for producing components/products. The scheduling problems are classified into single machine scheduling, flow shop scheduling, job shop scheduling, open shop scheduling, and hybrid scheduling. In this paper, the open shop scheduling problem is considered. The open shop scheduling problem is alternatively called as moderated job shop scheduling problem (Panneerselvam [1] ), which is between the flow shop scheduling problem and job shop scheduling problem.

The flow shop scheduling problem consists of “n” jobs, each with “m” operations. The process sequences of these jobs are one and the same for this problem. The job shop scheduling problem consists of n jobs, each with m operations. The process sequences of the jobs are not the same for this problem. The open shop scheduling problem consists of n jobs, each with at most m operations. The operations of each job can be processed in any sequence. If a job consists of three operations, viz., 1, 2 and 3, then this job can be processed using any one of the following six sequences, which is n:

Sequence 1: 1 - 2 - 3;

Sequence 2: 1 - 3 - 2;

Sequence 3: 2 - 1 - 3;

Sequence 4: 2 - 3 - 1;

Sequence 5: 3 - 1 - 2;

Sequence 6: 3 - 2 - 1.

If a problem consists of n jobs, each with at most m operations of the open shop scheduling problem, then a generalized data format of the processing times is shown in Table 1. In Table 1, if t_ij is positive, then the job i requires t_ij units of processing time for the operation j; if it is zero, then the job i does not require the operation j.

In open shop scheduling problem (OSSP), there is a finite set J which consists of n jobs and a set M which consists of m machines. Each Job J_i (i = 1 to n) is to be processed on machine M_j (j = 1 to m) for t_ij processing time, where ij stands for i^th job on a j^th machine. Each job J_i consists of at most m tasks. At a time, each job can be processed only on one machine and each machine can process only one job.

In this paper, a 3-field notation 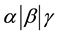(Graham et al. [2] ) is used to classify open shop scheduling problems:

・ α indicates the machine environment [O2 for open shop with 2 machines, O3 for open shop with 3 machines or O (without any suffix number) for m machines];

・ β indicates job characteristics [r_i for release date of every job, ord for ordered jobs, pmtn for preemption allowed, non-preempt for jobs where preemption cannot be allowed, t_ij = 1 for all jobs with unit processing time, etc.];

・ γ indicates optimality criteria or objectives [minimization of total completion time or flow time or makespan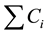, total tardiness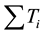, weighted completion time or weighted flow time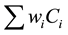, total number of tardy jobs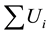, maximum lateness L_max, etc.].

2. Measures of Performance of Open Shop Problem

In practice, the scheduling of the jobs in the open shop scheduling has several measures of performance which are as listed below:

・ Minimize the makespan;

・ Minimize the sum of completion time of all the jobs;

・ Minimize the weighted sum of completion times of all jobs;

・ Minimize the total tardiness of all jobs;

・ Minimize the weighted total tardiness of all jobs;

・ Minimize the number of tardy (late) jobs;

・ Minimize the number of weighted sum of tardy (late) jobs;

・ Minimize the maximum lateness.

Let

・ n be the number of jobs;

・ m be the number of machines (operations);

・ d_i is the due date of the job i;

・ C_i be the completion time of the last operation in the assumed sequence for processing of the job i;

・ W_i be the weight of the job i;

・ T_i (also called L_i) be the tardiness (lateness) of the job i.

The makespan (C_max) is the maximum of the completion times of all the jobs and it is given by the following formula. It is the measure, which indicates the earliest time at which the given batch of jobs can be fully completed, which is known as makespan. The objective is to minimize the makespan.

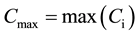, where.

The sum of the completion times of the jobs is given by the following formula and it should be minimized. This objective minimizes the total flow time which amounts to minimizing the mean flow time of the jobs in the system. This in turn minimizes the in-process inventory.

Sum of the completion times of the jobs =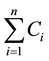

The weighted sum of completion times of the jobs is given by the following formula. This measure should be minimized. If the jobs differ in terms of importance (priority) for processing, then the jobs are assigned with weights W_i, 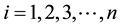, which will be fixed by the company processing the jobs.

Weighted sum of the completion times of the jobs =

The sum of the tardiness of the jobs is given by the following formula and it should be minimized.

Sum of the tardiness of all the jobs =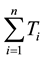

The tardiness (T_i) of the job i is given by the following formula.

The sum of the weighted tardiness is given by the following formula and this measure is to be minimized.

Sum of weighted tardiness of all the jobs =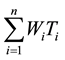

The number of tardy/late jobs is given by the following formula and this measure is to be minimized.

The number of tardy/late jobs =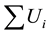, where, U_i = 1 if C_i is more than d_i; U_i = 0, otherwise.

The formula for the sum of the weighted number of tardy jobs is given by the following formula and it should be minimized.

Sum of weighted number of tardy jobs =

The formula for the maximum lateness (tardiness) [L_max] is given by the following formula and it should be minimized.

3. Problem Statement

The main objective of this research paper is to classify the research papers on open shop scheduling problem in different ways. The other objectives of this review are to study the recent trends in the area of open shop scheduling and critically review the research papers. Many researchers earlier studied different open shop scheduling problems. Kubiak et al. [3] studied the complexity aspect of open shop scheduling problems solved till 1990. Roemer [4] presented a note on the complexity problems related with concurrent open shop problem in which it is proved that even the simplest of the dedicated parallel machine problem with the objective of minimizing the average completion time, 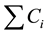_, is strongly NP-hard. Brucker et al. [5] presented about the complexity results for open shop problems with transportation delay. The summary of review of literature under each of the measures of performance of the open shop scheduling problem is shown in Table 2.

3.1. Minimization of Makespan

This section presents the review of literature in which the objective is to minimize the makepsan. The literature under this category is classified as given below:

・ Theoretical study;

・ Mathematical models;

・ Exact algorithms;

・ Heuristics;

・ Genetic algorithms;

・ Tabu search algorithms;

・ Simulated annealing algorithms;

・ ACO algorithms;

・ Bee colony optimization algorithms;

・ Hybrid algorithms.

3.1.1. Theoretical Study

This section presents the review of literature of the theoretical study conducted in the open shop scheduling problem.

Brasel et al. [6] discussed the theory behind the irreducible sequences of the open shop scheduling problem. Irreducible sequences are set of sequences, which are structurally optimal in the sense that there is at least one optimal sequence in the set for each instance of processing times. They provided necessary and sufficient conditions for irreducibility and also the test results conducted for different isomorphism classes like structure isomorphism, permutation isomorphism and graph isomorphism. Akker et al. [7] studied two-machine open shop scheduling problem and proposed at most two non-dominated points D1 and D2 that exist and a feasible schedule that is possible for these points. The objective of this study is to minimize the makespan. They considered the algorithm by Gonzalez-Sahni [8] as a pre-requisite to the conditions that are proposed in their reserach. Kubale and Nadolski [9] considered the computational complexity of a cyclic open shop scheduling problem and also a modification of cyclic open shop called as compact cyclic open shop with the objective of minimizing the makespan (C_max). They showed that two-machine cyclic open shop problem to minimize makespan is polynomially solvable but three machines cyclic open shop problem is NP-hard. Also, they showed that two-machine compact cyclic open shop problem to minimize the makespan is NP-hard. Finally, they compared the computational complexity results of cyclic open shop problem and compact cyclic open shop problem.

3.1.2. Mathematical Models

Masuda and Ishii [10] showed that there exists a unique optimal solution when bi-criteria are considered for a two-machine open shop scheduling problem. The two criteria which are considered are to minimize maximum completion time (makespan) and maximum lateness. They developed a linear programming model to meet the objective of minimizing the stated bi-criteria. Kis et al. [11] studied multiprocessor (multi-machines) extension of the preemptive open shop scheduling problems, where set of processors (machines) are partitioned into groups. The objective here is to minimize the makespan which is polynomially solvable for two multiprocessor groups even if preemptions are restricted to integral times. They developed a special integer program in two dimensions and proved that in the vicinity of the optimal solution of its LP relaxation, there are always integral lattice points which form an optimal solution of the integer program. Schuurman and Woeginger [12] considered a hybrid open shop scheduling problem in which each machine has identical parallel machines with an objective of minimizing the makespan. They developed 2 approximation results for this NP-hard problem. They illustrated the existence of a polynomial time approximation algorithm with the worst case ratio of 2 for the case that the number of “s” stages is a part of the input. For the two-machine open shop scheduling problem with identical machines, they derived family of polynomial time approximation algorithms, whose worst case ratio is closer to 3/2. Kyparisis and Koulamas [13] developed a polynomial algorithm for the open shop scheduling problem to minimize the makespan with three machines and also with number of arbitrary machines and when certain conditions are imposed on job processing times.

3.1.3. Exact Algorithms

Brucker et al. [14] considered the open shop scheduling problem with the objective of minimizing the makespan. They developed a branch-and-bound algorithm using disjunctive graph model. They compared the results with that of the benchmark problems of Taillard [15] with new harder instances of open shop problems. Gueret and Prins [16] considered the open shop scheduling problem with the objective of minimizing the makespan. Since the open shop problem lacks tighter bounds while using branch-and-bound method, they proposed an improved bound which is defined as the optimal makespan of a relaxed OS_k problem. Gueret et al. [17] presented improving technique for branch-and-bound method applied to Brucker et al. method [14] for open shop problems involving 3 machines and 2 jobs with the objective of minimizing the makespan. The authors mainly dealt with intelligent backtracking method, when a node is eliminated. They tested the method on benchmark problems of Taillard [15] . Cheng and Shakhlevich [18] considered two-machine open shop scheduling problem in which the processing times are controlled but at some costs. They dealt with the objective of minimizing both the makespan and the cost which is incurred while compressing the processing times. The authors developed an algorithm with complexity function O(nlogn) to provide a schedule whose makespan is optimal.

3.1.4. Heuristics

Gonzalez and Sahni [8] studied the open shop scheduling problem with two machines and preemptive jobs with the objective of minimizing the makespan. They provided a linear time algorithm to solve this problem. Further, they showed that the open shop scheduling problem with more than two machines and with non-preemptive jobs is NP-complete. Jurisch and Kubiak [19] provided a O(n³) algorithm for the two-machine open shop scheduling problem with single renewable resource and non-preemptive schedule. Based on this aspect, they developed a polynomial time algorithm to minimize the makespan. They further showed that the two-machine open shop with two different resources is NP-hard. They also showed that the optimal non-preemptive schedules are not longer than optimal preemptive schedules. Lu and Posner [20] considered open shop scheduling problem with two machines. They examined the average case complexity of this problem for minimizing the makespan on two machines with two distinct release dates. They also presented linear-time algorithms for two variations of the two-machine open shop scheduling problem, viz. minimizing the weighted sum of machine completion times and minimizing the makespan, when one machine is unavailable for processing. They provided guidelines to use variation of the second problem for solving the problem of minimizing the makespan, when there is rolling horizon. Chen and Strusevich [21] considered three-machine open shop scheduling problem in which the objective is to minimize the makespan. They showed that the worst-case performance ratio of a greedy algorithm to solve this problem is 5/3. Then, they presented a linear time heuristic with the worst-case performance ratio of 3/2. Giaro et al. [22] considered the open shop scheduling problem with no-wait scheduling without allowing inserted idle time, where execution times of operations are either zero or one. Such schedules, where inserted idle times are not allowed are also called as compact schedules and the objective is to minimize the maximum completion time (makespan). They used bipartite graph to derive polynomially solvable algorithms. This is equal to coloring problem. When the number of machines is more than 3, it is not possible to color consecutively the edges of the respective graph. So, they concentrated on special families of scheduling graphs, which can be colored in polynomial time. Drobouchevitch and Strusevich [23] considered three-machine open shop scheduling problem to minimize the makespan with a special case of two operations per job and with a bottleneck machine, which means that one of the operations of each job is to be performed on one specific machine and the other operation can be performed on any one of the other two machines. They devised a new lower bound on the optimal makespan and developed a linear time algorithm to find the optimal non-preemptive schedule. Kononov et al. [24] considered the open shop scheduling problem with two machines, in which the objective is to minimize the makespan. They studied the effect of difference in machine loads with reference to maximum machine load on the optimality of the solution. They developed a linear time algorithm for this problem together with a polynomial algorithm to minimize the makespan. Further, they proved that this problem becomes NP complete, when the number of machines is more than 2. Rebaine and Strusevich [25] considered open shop scheduling problem with n jobs and two machines without preemption but with a special case of transportation times and with the objective of minimizing the makespan. The author developed a linear time algorithm that provides the optimal solution for a case where the largest transportation time does not exceed the smallest processing time and also provided a heuristic for job-independent but route dependent transportation times. Panneerselvam [1] considered n jobs and m machines case of the open shop scheduling problem in which the objective is to minimize the makespan. The author has developed a heuristic to achieve the objective. Further the author has tested the efficiency of the heuristic and found that it gives optimal solution for 84% of the problem. Gupta and Werner [26] dealt with two-machine flow shop and open shop scheduling problems with secondary criteria in which the prime objective is to minimize the makespan. Using 3-field standard notation, the bi-criteria scheduling problem can be represented as follows:

・ indicates that efficient solution relative to criteria C1 & C2 are being examined;

・ , where Fw(C1, C2) means the weighted sum of two criteria C1 and C2;

・ , where Fh(C1, C2) represents the hierarchical optimization of criteria C2 given that criteria C1 is at its optimal value.

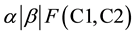
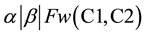
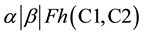
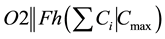
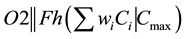
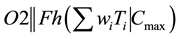
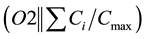
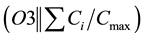
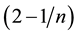
The authors developed a constructive and iterative heuristics to solve approximately the problems, , and corresponding counterparts for the flow-shop problem. The authors adopted neighborhood search method to find the optimal solution. Kyparisis and Koulamas [27] studied the two-machine open shop scheduling problem with the primary objective of minimizing the makespan and the secondary objective of minimizing the total completion time. They developed polynomial time algorithms for three special cases. Also, they extended some of their results to three-machine case. Lorigeon et al. [28] have studied the two-machine open shop scheduling problem with an availability constraint, which means that a machine is not always available and processing of interrupted jobs can be resumed when the machine becomes available again. They developed a pseudo-poly- nomial time dynamic programming algorithm to minimize the makespan. Further, they proposed a mixed integer linear programming model to minimize the makespan. Kononov and Sviridenko [29] demonstrated “m” machines open shop scheduling problem with a polynomial time approximation scheme (PTAS) to minimize the makespan when release dates are given and preemption is not allowed. They used the work of Sevastianov and Woeginger [30] to divide the whole set of jobs into three subsets of “large”, “small” and “tiny” jobs. The big jobs in terms of time are scheduled followed by fitting “tiny” operations into the gaps of the partial schedule in a greedy way. Finally, the small jobs are scheduled by using greedy algorithm. Murugesan et al. [31] illustrated a heuristic algorithm for n jobs, m machines open shop scheduling problems to identify a rank minimal optimal sequence. The algorithm is based on the concepts such as cyclic machine orders and cyclic associates of a machine order matrix. They tested the proposed algorithm with the Taillard [15] benchmark problems and also compared the optimal sequences with the solutions of the branch-and-bound algorithm developed by Brucker et al. [14] . Breit et al. [32] studied two-machine open shop scheduling problem with non-preemptive condition and when the machines are not continuously available for processing with the objective of reducing the makespan. They developed 2-approximation algorithm for a problem with two holes (idle times) one on each machine and further developed 4/3 approximation algorithm for a problem with one hole only. Gupta et al. [33] considered the open shop scheduling problem with each of the secondary criteria, viz. minimize flow time, minimize total weighted flow time and minimize total weighted tardiness time, combined with the primary criterion of minimizing C_max, which is the makespan. They developed three different constructive heuristics based on insertion techniques for 2 polynomially solvable special cases. They derived a strongly connected neighborhood structure and used it to develop an effective two iterative heuristics, viz., Simulated Annealing (SA) and multi-start procedure. They compared the result of insertion technique with that of iterative procedures. But, they did not use any statistical tool in their comparison. Rebaine [34] considered “n” jobs, two-machine open shop scheduling problem with the time delay between the completion of an operation and start of another for the same job with the objective of minimizing the makespan. The author presented two heuristics for non-symmetric time delays with the worst case performance ratios of and. Su et al. [35] studied two models for the flow shop and open shop scheduling problems. The first model involves multiple machines at the first stage and two machines at the second stage and the other model involves multiple machines at both the stages. They considered two-stage processing involving flow shop at the first stage followed by open shop at the second stage. In both the models, the objective is to minimize the makespan. For the first model, a mixed integer programming model is formulated but when the number of jobs increases, the computing time increases drastically for which they presented a branch-and-bound algorithm. Then, a heuristic algorithm is presented for the first model which is a combination of CDS procedure and Longest Available Processing Time (LAPT) rule. For second model, an integer programming model is presented to minimize the makespan and again a heuristic algorithm that combines CDS and LAPT rule is provided.

Alcaide et al. [36] studied the open shop scheduling problem with stochastic processing times subject to random machine breakdowns in which the objective is to minimize the makespan. They developed a heuristic for each of the cases, viz., all the jobs are available at time zero (r_j = 0) and all jobs have different release dates r_j. Zhang and Velde [37] presented online two machine open shop scheduling problem to minimize makespan, using greedy algorithm as the technique. They considered time lag condition between the completion of first job and starting of next job. The quality of online algorithm is measured by its competitive ratio, that is “ρ―com- petitive” if online algorithm is at most ρ times value of an offline solution. They proved that this competitive ratio for greedy algorithm is 2 and is 5/3 in case of small time-lags. Yu et al. [38] considered generalization of classical open shop and flow shop scheduling problem where the jobs are located at the vertices of undirected graph and the machines travel along the graph to process the jobs. Since the problem involves deciding the routing and scheduling of machines, these are called routing-scheduling problems. There are three types of graphs, viz., general graph, tree and line. The objective is to minimize the makespan. In tour-version, makespan means the time by which each machine is used by the jobs assigned to it and returned to its initial location, while in path-version the makespan represents the maximum completion time of all jobs. They developed an approximation algorithm Tour-O2 for tour-version of two-machine case and an approximation algorithm Tour-O_m(ρ) for m-machine case. Similarly, they provided an approximation algorithm Path-O2(σ) for path-version of 2-machine case and an approximation algorithm Path-Om for m-machine case of path-version. Bai and Tang [38] investigated that Dense Schedules (DS) is asymptotically optimal for m machines, when number of jobs “n” goes to infinity with the objective of minimizing the makespan with given release dates. They developed an on-line heuristic “Dynamic Shortest Processing Time” (DPST). They provided asymptotically optimal lower bound and conducted several experiments to verify the effectiveness of the heuristic. Gupta et al. [40] developed a heuristic for n jobs, 2-stage open shop scheduling problem with stochastic processing times when transportation delay times are given with the objective of minimizing the makespan.

Chung and Mohanty [41] discussed two-machine preemptive open-shop scheduling problem with probabilistic arrivals of jobs following Poisson distribution and processing of any job on a machine following an exponential service time. They concluded using Markov process and dynamic programming with Longest Expected Processing Time (LEPT) policy minimizes the makespan most. Kubale [42] provided two polynomial-time algorithms, one for all mn unit tasks and another for at most m + n unit tasks, for n-jobs and m-machines open shop scheduling problem and with zero-one execution times. The execution time will be zero if the task does not exist and it will be 1 if it exists. The author constructed a non-preemptive schedule that minimizes the makespan with given release date r_i and deadline d_i. Liaw [43] developed an algorithm for non-preemptive ‘m’ machines open shop scheduling problem with the objective of minimizing the makespan. This algorithm is an iterative procedure that uses Benders’ decomposition to separate sequencing and scheduling operations which in turn uses dual of the longest path problem. Breit et al. [44] studied a two-machine open shop scheduling problem when one machine is not available for processing (hole) to minimize the makepsan. They presented a linear time approximation algorithm with a worst case ratio of 4/3. They presented three procedures for three different conditions. Sevastianov and Woeginger [30] studied r-stage open shop problem with identical parallel machines at each stage and with the objective of minimizing makespan. They constructed an approximation scheme that is almost like an FPTAS―Fully Polynomial Time Approximation Scheme. Colak and Agarwal [45] proposed a non-greedy heuristics and also developed an Augmented Neural Networks (AugNN) to minimize the makespan of the open shop scheduling problem. They have tested their algorithm against 3 sets of problems, viz., Taillard [15] benchmark instances, Gueret and Prins [16] benchmark instances and randomly generated problem instances of sizes 25 × 25, 30 × 30, 50 × 50 and 100 × 100. They observed that their algorithm performs better than other techniques in almost all of these instances. Kubzin and Strusevich [46] dealt with two-machine open shop scheduling problem to minimize the maximum completion times of all activities to be scheduled, where each machine is to be maintained exactly once during the planning period. They assumed that the length of the maintenance period on a machine is of the form α + f(t), where “t” is the start time, “α” is a given positive constant (the duration of standard tests) and f(t) is the non-decreasing function (duration of maintenance activities that depends on the state of the equipment). Normally, this is called as “deteriorating”. They showed that open- shop scheduling problem with preventive maintenance schedule for each machine can be solved in polynomial time. Sedeno-Noda et al. [47] considered preemptive open-shop scheduling problem with time windows. That is, for each job, there is specified time window defined by its release time and due date. They considered the optimization problem, for which the objective function is to minimize the makespan. They used network flow approaches and Accumulated Processing Time Units (APTU) algorithm to find whether the feasible schedule exists for the optimization problem. They further used Max-Flow Parametrical Algorithm to minimize the makespan.

Modarres and Ghandehari [48] applied the concept of graph circular coloring to develop a model for “m” machines, non-preemptive open shop scheduling problems. They considered dedicated resources which can be executed in more than one cycle. The number of cycles is a positive integer. In each cycle, there are “n” independent jobs with each job consisting of several tasks. A task may be present in more than one job. Each task needs a set of resources to be executed. During the process of a task, preemption is not allowed. The objective is to determine the minimum number of cycles and a proper schedule of tasks such that makespan is minimized. They initially considered unit processing times and later generalized it by relaxing this restriction. Malapret et al. [49] developed an optimal constraint programming approach for the open shop scheduling problems to minimize the makespan. They showed that randomization and restart strategies combined with strong propagation and scheduling heuristics can lead to a very efficient approach for solving this problem. They compared their results with state-of-the-art methods available in literature. The experimental results showed that the efficiency and robustness of the proposed heuristics match with the results of best meta-heuristics of Taillard [15] benchmarks and outperforms other exact methods like Gueret and Prins [16] and Brucker et al. [14] benchmarks.

Naderi et al. [50] discussed the case of redundancy in the permutation list of open shop scheduling problem with the objective of minimizing the makespan. They developed efficient theorems to avoid the occurrence of redundancy of permutation list, which means that despite the change in positions of the operations in the sequence, the situation might end up with the same solution (previous solution). They further proposed four Insertion and Reinsertion Heuristics (IRH 1, IRH 2, IRH 3 and IRH 4) and evaluated these four heuristics on three benchmarks problems, viz., Taillard [15] Benchmark, Gueret and Prins [16] Benchmark and Brucker et al. [14] benchmark.

3.1.5. Genetic Algorithms

Fang et al. [51] considered a generalized open shop scheduling problem, for which they attempted the development of hybrid genetic algorithm based heuristic to minimize makespan. Louis and Xu [52] developed genetic algorithm for open shop scheduling with re-scheduling. They combined the genetic algorithm with Case-Based Reasoning (CBR) principles to find optimally directed solutions that minimize the makespan. Khuri and Miryala [53] compared three different genetic algorithms that minimize the makespan. They have tested the proposed algorithm against 36 Taillard’s benchmark instances. They have compared permutation genetic algorithm, hybrid genetic algorithm and selfish-gene algorithm and found that hybrid genetic algorithm outperforms the other two algorithms for larger problem instances. Prins [54] presented genetic algorithm solution for a generalized open shop scheduling problem with non-preemptive job in which the objective is to minimize makespan. They developed several genetic algorithms (GAs) for the open shop problem and compared the results with the Brucker [14] and Taillard’s [15] benchmark problems. Senthilkumar and Shahabudeen [55] developed a heuristic for the open shop scheduling problem using genetic algorithm (GA) to minimize the makespan. The parameters ‘Crossover’ and ‘Mutation Operator’ of genetic algorithm are suitably modified to maintain feasibility. Five test problems with the new heuristic based on GA are compared with an earlier work using a complete factorial experiment and found that their genetic algorithm based heuristic performs better than the earlier heuristic proposed by Panneerselvam [1] .

Liaw [56] developed a hybrid genetic algorithm (HGA) that incorporates tabu search (TS) algorithm for local improvement values to minimize the makespan of the open shop scheduling problem. The performance of HGA is tested by three sets of problems, viz., randomly generated, benchmark problems by Taillard [15] and benchmark problems by Brucker [14] .

Zobolas et al. [57] developed a hybrid genetic algorithm that solves the open shop scheduling problem to minimize the makespan. In the first phase, they developed a variable neighborhood search (VNS) algorithm in which the initial population is generated using NEH heuristic (Nawaz-Enscore-Ham Heuristic). In the next phase, they combined GA and VNS algorithm to improve the solution. They tested their heuristic with several Taillard [15] benchmark instances and Brucker [14] benchmark instances where it turns out to give best solutions in most of the benchmark problems. Matta [58] studied proportionate multi-processor open shop (MPOS) scheduling problem to minimize the makespan. They developed two different mixed integer linear programming formulations for proportionate MPOS to minimize makespan. While the first formulation is time-based model, second formulation is sequence-based model. Then, they proposed Genetic Algorithm (GA) for proportionate MPOS and finally presented its computational performance analysis.

3.1.6. Tabu Search Algorithms

Liaw [59] developed an efficient local search algorithm based on tabu search algorithm to the minimize makespan. The author compared the results of the proposed algorithm with that obtained using dispatching rule DS/RANDOM. Aguirre-Solis [60] considered “n” jobs with “m” operations to be processed on “m” machines open shop scheduling problem to minimize the makespan. The author dealt with sequence-dependent jobs. Tabu Search Algorithm has been used to solve the scheduling problem, in which a dispatching rule has been proposed to generate an initial feasible solution.

3.1.7. Simulated Annealing Algorithms

This section gives the review of literature of the simulated annealing algorithm used to obtain solution for the open shop scheduling problem.

Roshanaei et al. [61] considered non-preemptive open shop scheduling problem, where set-up times are sequence dependent (SDST) on each machine to minimize the makespan. They have developed constructive heuristics (CH) so as to consider SDST. Longest Total Processing Time (LTPT) is modified to Longest Total Modified Processing Time which is used as a dispatching rule.

3.1.8. ACO Algorithms

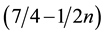
Panahi and Tavakkoli-Moghaddam [62] considered the open shop scheduling problem to minimize twin objectives of minimizing the makespan and total tardiness. They developed Hybrid Ant Colony Optimization (HACO) algorithm. Simulated annealing algorithm is used to initialize the search. The authors compared the results obtained by HACO with NSGA―Non Dominated Sorting Genetic Algorithm and concluded that HACO outperforms NSGA most or all of the cases. Chernykh et al. [63] studied hybrid problem of two classical discrete optimization problems, viz., OSSP and Metric TSP. Here, the jobs are located at the nodes of an undirected transportation network and the machines have to travel between jobs and the makespan is the length of the time interval between the instant the first machine starts and moves from node to node to an instant when the last machine returns to the depot. The objective is to minimize the makespan. They have used Greedy algorithm to find makespan for ‘m’ machines routing open shop problem. They further presented a new 7/4 approximation algorithm for two-machines routing problem and easy-TSP to handle Hamiltonian tour in polynomial time.

3.1.9. Bee Colony Optimization Algorithms

This section presents a review of literature of the open shop scheduling problem using bee colony optimization algorithms.

Huang and Lin [64] proposed bee-colony optimization algorithm with an idle-time based filtering (ITBF) scheme that automatically stops searching a partial solution with insufficient profitability thus saving time-cost for the remaining partial solution. The logic behind this, as per them is that “the smaller the idle time, the smaller the partial solution” and thus “the smaller the makespan C_max will be”.

3.1.10. Hybrid Algorithms

Liu and Ong [66] proposed a meta-heuristic to solve job shop problem, open shop problem and mixed shop problem, which is a combination of job shop problem and open shop problem. They used three meta-heuristics viz. Simulated Annealing (SA), Threshold Accepting (TA) and Tabu Search (TS) to get the results of job shop problem, open shop problem and mixed shop problem. Kokosinski and Studzienny [68] proposed sequential and parallel hybrid genetic algorithm to solve m machines, n jobs open shop scheduling problems with the objective of reducing the makespan. Two greedy algorithms LPT-Task and LPT-Machine are proposed for decoding chromosomes by permutations with repetitions. Modarres and Ghandehari [69] studied generalized cyclic open shop scheduling (GCOSS) problem to minimize the makespan. They used developed a hybrid algorithm consisting of ant colony optimization technique, beam search and local search technique.

The review of literature of the open shop scheduling problem with the objective of minimizing the makespan reveals that more researchers developed several heuristics and genetic algorithms to solve the problem. So, future researchers may attempt to develop other meta-heuristics and hybrid algorithms to minimize the makespan of this problem. Further, comparisons of the proposed algorithms with existing algorithms have been carried out using mean and percentage analysis. Instead, in future researchers may follow a complete factorial experiment for comparison purpose by taking several factors of importance, out of which “algorithm” must be a factor. This will help to study the effects of the main factors as well as those of interaction terms in ANOVA model on the response variable, namely performance measure(s) of interest.

3.2. Minimization of Sum of Completion Times of Jobs

This sections presents review of literature on the minimization of the sum of completion time of all the jobs under the following subdivisions:

・ Exact algorithm;

・ Heuristics;

・ Tabu search algorithm;

・ Particle swarm optimization algorithm;

・ Hybrid algorithm;

・ Multiple algorithm;

・ Miscellaneous algorithm.

3.2.1. Exact Algorithms

Dror [70] examined the open shop problem with machine dependent processing time with the objectives of minimizing the makespan and minimizing the mean flow time. For the problem of minimizing the makespan and n ≥ m, the author presented an optimal algorithm with the complexity function O(mn). For the same problem, it is proved that the problem becomes NP-hard if n < m but ≥3. The author developed an optimal algorithm with a complexity function of O(n) for this open shop scheduling problem with two machines to minimize the mean flow time.

3.2.2. Heuristics

Achugbue and Chin [71] considered the open shop scheduling problem with the objective of minimizing the mean flow time. They showed that this problem is NP-complete. In addition, they derived bounds for mean flow times of arbitrary schedules and SPT first schedules for m-process and n-job systems in terms of the mean flow time of the optimal schedule. Werra and Blazewicz [72] presented an edge coloring model for preemptive open- shop problem, in which additional constraints generated by the presence of resource R are considered, where resource “R” can be nonrenewable resource (money, fuel, etc.) or a renewable resource (manpower, tools, etc.). The objective of this problem is to minimize the total completion time. They provided edge coloring of bipartite graph for both problems, viz., Preemptive with Renewable Resource Open Shop (PROS) and Preemptive with Nonrenewable Resource Open Shop (PNOS). They further provide basic properties of edge colorings.

Tautenhahn [73] considered the open shop problem with unit processing times and due dates. The author developed a polynomial time algorithm to minimize the completion time of all the jobs when a deadline is imposed for each job. The existence of open shop scheduling with unit execution time (UET) in reality is very rare. Lin et al. [74] addressed a multi-processing-stage open shop scheduling problem with characteristics of movable dedicated machines and no-wait restrictions. They developed a descriptive linear programming model to minimize the total completion times. Further, they developed a heuristic algorithm which has two phases. In the first phase, an initial sequence is developed and in the second phase, the sequence is improved iteratively. Tang and Bai [75] investigated the open shop scheduling problem to minimize the sum of the completion times. They proposed a shortest process time block (SPTB) heuristic for a situation, where number of jobs is multiple times the number of machines. When the size of job goes infinity, it is proved that the heuristic is asymptotically equal to the optimal result. Brasel et al. [76] proposed several constructive algorithms, like matching algorithm, beam insert and beam append procedures with beam search, which generate active and non-active delay schedules to minimize the sum of completion times or mean flow times. Brasel, Kluge and Werner [77] dealt open shop scheduling problem with arbitrary number of machines, unit processing times and out-tree between the jobs. 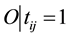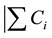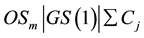They dealt with, Outtree. They presented polynomial algorithm that divides the problem into sub- problems to minimize the total completion time. Lann et al. [78] developed a polynomial heuristic and a lower bound for “n” jobs with “m” machines open shop problem where job overlaps. The objective is to minimize the sum of jobs’ completion time. They have simulated with 2 machines and with varying number of jobs Liaw et al. [79] studied the open shop scheduling problem for “m” machines to minimize the sum of the completion times when sequences of jobs is given for one machine. The three field notation for the problem handled is (where GS (1) means given sequence for 1 machine). They developed a one-pass heuristic with an adjustment strategy to adjust the parameter in each of the iterations. They then derived a lower bound followed by branch-and-bound algorithm to obtain optimal value.

3.2.3. Tabu Search Algorithms

Seraj and Tavakkoli-Moghaddam [80] developed a bi-objective mixed integer linear programming model in which mean tardiness and mean completion time are minimized. Further, they developed Tabu Search (TS) algorithm. They have then compared its results with those obtained using LINGO software which gives optimal solutions. They observed that the solutions of TS are very close to the corresponding optimal solutions. But statistical comparison using factorial experiment was not carried out by the authors.

3.2.4. Particle Swarm Optimization Algorithms

Sha et al. [65] proposed a multi-objective particle swarm optimization technique with modified parameters like particle position, particle movement and particle velocity. They conducted the experiment and reported the results. This algorithm has not been compared with any of the existing algorithm.

3.2.5. Hybrid Algorithms

This section presents a review of literature of hybrid algorithms to solve the open shop scheduling problem. Naderi et al. [81] explored scheduling open shops with parallel machines at each stage of processing, which is a more realistic variant of OSSP. The objective is to minimize total completion time. They proposed a Mixed-Integer Linear Programming (MILP) model to formulate an open shop with parallel machine with the objective to minimize the total completion time. Also, they developed a hybrid of genetic algorithm.

3.2.6. Multiple Algorithms

This section presents a review of literature involving more than one algorithm used to solve the open shop scheduling problem.

Andresen et al. [82] considered “n” jobs and “m” machines open shop scheduling problem to minimize the sum of completion times or mean flow time. They proposed and compared two iterative algorithms, viz., simulated annealing algorithm and genetic algorithm. They have presented extensive computational results for problems with n = 50 jobs and m = 50 machines and also tested under different conditions like n < m, n = m, n > m and 30,000 generated schedules/solutions. They concluded that for most of the problems, genetic algorithm is superior.

3.2.7. Miscellaneous Algorithm/Study

Leung et al. [83] revisited and presented a counter example to the model already presented in an earlier paper where they had earlier showed a proof that the minimization of total completion time in a two-machine open shop scheduling problem with jobs overlap is NP-hard. This is in contrast to the classical open shop problem and here the two operations of any given job may overlap in time. Their proof is based on Numerical Matching with Target Sum (NMTS) problem. They showed that the earlier proof is not correct and further provided a counterexample to show that complexity of two-machine open-shop problem with job overlap remains open.

The review of the open shop problem with the objective of minimizing the sum of completion times of jobs shows that more research have been carried out using heuristics. So, future researchers may concentrate in developing meta-heuristics and hybrid algorithms for this problem. As mentioned in the previous section, a complete factorial experiment may be used for comparison of proposed algorithms with existing algorithms. Further, it is advisable to randomly generate data as per the complete factorial experiment so that a perfect balance will be there under all levels of the factors.

3.3. Minimization of Sum of Weighted Completion Times of All Jobs

This section presents the review of literature on the minimization of the sum of the weighted completion times of all the jobs under the sub-classifications heuristics, genetic algorithm and particle swarm optimization algorithm.

3.3.1. Heuristics

Gandhi et al. [84] mapped the data migration problem as open shop scheduling problem. The objective of data migration problem is to compute the efficient plan to move the data stored on devices in a network from one configuration to another configuration. Here, the objective is to minimize the completion time of all storage devices. This problem is modeled by a transfer graph in which vertices represent storage devices and edges represent data transfer required between pairs of devices. The objective is to minimize the sum of weighted completion time of all vertices. They have improved Kim’s 9-approximation algorithm for the problem when the edges have arbitrary processing times and gave 5.06 approximation algorithm. Queyranne and Sviridenko [85] considered generalized preemptive open shop problem with the objective of minimizing the sum of weighted job completion times. They presented a (2 + ε) approximation algorithm with general minsum criteria. They developed interval-indexed formulation of LP model with the objective to minimize the sum of the weighted job completion times. They used randomized approximation algorithm that takes an optimum LP solution to construct a feasible schedule by using Gonzalez-Sahni’s algorithm [8] . Finally they de-randomize the randomized algorithm.

3.3.2. Genetic Algorithm

Doulabi et al. [86] proposed a mixed integer linear programming model to minimize weighted flow time and also the intermediate storage cost of the open shop scheduling problem. They have considered time-dependent weights in order to represent the reality of time value of money in many major projects. Further, they proposed a genetic algorithm to solve time-dependent weighted completion times that yields better results in comparison to the one with constant weights.

3.3.3. Particle Swarm Optimization Algorithm

Noori-Darvish et al. [87] proposed bi-objective probabilistic mixed-integer LP model for OSSP where sequence-dependent set-up times are considered along with fuzzy processing times and fuzzy due dates. The objectives are “sum of the weighted tardiness” and “sum of the weighted completion times of all the jobs”. They converted the results to an Equivalent Auxiliary Crisp Model for defuzzification of data and finally solved the problem. They solved medium to large size problems using Multi-objective Particle Swarm Optimization (MOPSO) algorithm and finally conducted Design of Experiments (DOE) using ANOVA test to confirm the significant effect and better performance of MOPSO algorithm in comparison with Strength Pareto Evolutionary Algorithm II (SPEA II) and reported the result.

The review under this section clearly shows that less works have been carried out to minimize the sum of weighted completion times of all the jobs of the open shop scheduling problem. So, future researchers may concentrate in developing heuristics, meta-heuristics and hybrid algorithms for this problem. As mentioned in Section 3.1, a complete factorial experiment may be used for comparison of proposed algorithms with existing algorithms.

3.4. Minimization of Total Tardiness of All Jobs

This section gives a review of literature of the minimization of total tardiness of all the jobs of the open shop scheduling problem under the sub-classification heuristics.

Heuristics

Liu and Bulfin [88] considered the open shop problem with identical processing times for jobs, specifically unit processing times or unit execution times (UET). They provided two algorithms, viz., Algorithm 1 and Algorithm 2 to minimize total tardiness and the number of tardy jobs, respectively. Liaw [89] addressed the open shop scheduling problem, for 2 machines with a special case of allowed preemption and with the objective of minimizing the total tardiness. An optimal timing algorithm is used to generate optimal or near optimal job completion sequence. Naderi et al. [90] dealt with open shop scheduling problem to minimize total tardiness. They provided four mixed integer linear programming (MILP) models. Then, they proposed a VNS with two types of Neighborhood Search Structure (NNS) based on insertion neighborhoods. They also proposed a genetic algorithm (GA) and finally evaluated MILP and other proposed heuristics on small-sized instances and as well on some well known benchmarks, like Taillard [15] , Brucker et al. [14] , and Gueret and Prins [16] .

From the review of this section, one can infer that very fewer researches have been carried out to minimize the total tardiness of all jobs of the open shop scheduling problem. So, future researchers may concentrate in developing heuristics, meta-heuristics and hybrid algorithms for this problem. As mentioned in Section 3.1, a complete factorial experiment may be used for comparison of proposed algorithms with existing algorithms.

3.5. Minimization of Sum of Weighted Tardiness of All Jobs

This section gives review of literature on the minimization of the sum of weighted tardiness of the open shop scheduling problem under the sub-classifications mathematical model, heuristic and simulated annealing algorithm.

3.5.1. Mathematical Model

Doulabi [91] proposed a mixed integer linear programming descriptive model to minimize the weighted earliness and weighted tardiness of jobs of the open shop scheduling problem. Though, the author provided computational results, they are not compared with any of the previous results.

3.5.2. Heuristics

Blazewicz et al. [92] proposed a linear programming model to minimize the weighted tardiness (T_w) with a special case of preemption allowed for open shop scheduling problem. Later, they proposed an algorithm to minimize weighted tardiness (T_w) and total tardiness (T) in two-machine open shop with a common due date for all the jobs.

3.5.3. Simulated Annealing Algorithm

Andresen et al. [93] discussed the application of simulated annealing to open shop scheduling problems with the objective of minimizing total weighted tardiness subject to given release dates.

From the review of this section, it is clear that few researchers contributed to minimize the sum of weighted tardiness of all jobs of the open shop scheduling problem. So, future researchers may concentrate in developing heuristics, meta-heuristics and hybrid algorithms for this problem.

3.6. Minimization of Weighted Sum of Tardy Jobs

This section presents the review of literature on the minimization of the weighted sum of tardy jobs of the open shop scheduling problem under the sub-classification heuristic.

Heuristic

Ng et al. [94] studied concurrent open shop scheduling problem to minimize the weighted number of tardy jobs with 0 - 1 processing times and common due date “d”. They provided in-approximate algorithm, an approximation algorithm and linear programming approximation algorithm to minimize the number of weighted tardy jobs. But the existence of this kind of problem in reality is very rare.

Under this measure of minimizing the weighted sum of tardy jobs of the open shop scheduling problem, only article is presented. In fact, this measure is considered to be an important measure. So, researchers may select this measure for their researches and develop heuristics/meta-heuristics/hybrid algorithms.

3.7. Miscellaneous Problems

Cho and Sahni [95] studied open, flow and job shop problems with feasible preemptive scheduling of independent jobs with each job accompanied with its release and due dates. They developed a linear programming model for the open shop scheduling problem with release and due dates of independent jobs. Werra et al. [96] presented a graph-theoretical model for a periodic scheduling in an open shop where infinite time horizon is divided into k time units and there is a cyclic schedule that guarantees that in each period all jobs 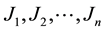are completed. They considered schedules with preemptions and schedules without preemptions. Konno and Ishii [97] presented a model for preemptive open shop scheduling problem with bi-criteria of maximizing the minimal satisfaction degree regarding the time intervals of jobs (total completion time) and minimal satisfaction degree of resource amounts used in the processing intervals. They proposed a solution procedure based on network flow algorithm to solve the open shop scheduling problem. Werra et al. [98] studied a variation of preemptive open shop schedule corresponding to finding a feasible edge coloring in a bi-partite multigraph with some cardinality constraints imposed by fixing the number of times each color can be used. They used Dynamic Programming procedure to show that given a graph G, the problem is polynomially solvable for trees with bounded degrees. The objective discussed in the paper is to minimize the cost c_i for each edge and each color i. Giaro et al. [99] studied the complexity results of single machine total cost open shop and conclude that it is NP-hard. They also studied total cost open shop using cyclic nature of scheduling graphs and length of operations with both arbitrary time tasks and unitary time tasks. Cheng and Shakhlevich [100] studied open shop scheduling problem with unit-time operations, with both preemptive and non-preemptive, “m” identical parallel machines and “n” identical jobs to minimize a given function arbitrary non-decreasing function. They constructed a linear description of scheduling polyhedron for the unit-time open shop scheduling problem. They also provided mathematical formulation for the scheduling functions. Werra, Kis and Kubaik [101] addressed multiprocessor generalization of preemptive open shop scheduling problem. Here, the set of processors are partitioned into two groups and each operation of a job might require single processor in either group or simultaneously all the processors from the same group. The results are obtained using strongly polynomial time algorithm for the two-multiprocessor open-shop scheduling problem with both, fractional preemptions (preemptions at any time) and integral preemptions (preemptions only at integer time points). For the fractional problem, a linear programming model is developed to minimize w - r, where w is the length of individual operations or idling on all processors and r is length of group operations on both processors. For the integral problem, rounding technique is shown but the authors suggest that this needs further investigation.

6. Conclusions

Open shop scheduling problem is a special kind of scheduling problem, which has n jobs, each with m operations, similar to follow shop, but the operations of each job can be processed in any order. So, this problem comes under combinatorial category, which warrants the use of meta-heuristic to find good solution. In this paper, a comprehensive review of literature has been carried out under the categories, viz., minimization of makespan, minimization of sum of completion times of jobs, minimization of sum of weighted completion times of all jobs, minimization of total tardiness of all jobs, minimization of sum of weighted tardiness of all jobs, minimization of weighted sum of tardy jobs, and miscellaneous measures. It is observed that the researchers have used theoretical study, mathematical models, exact algorithms, heuristics, genetic algorithms, tabu search algorithms, simulated annealing algorithms, ACO algorithms, bee colony optimization algorithms, and hybrid algorithms for the open shop scheduling problem to minimize the makespan. The literature to minimize the sum of completion times of jobs of the open shop scheduling problem is presented under exact algorithm, heuristics, tabu search algorithm, particle swarm optimization algorithm, hybrid algorithm, multiple algorithm, and miscellaneous algorithms. It is observed that heuristics, genetic algorithm and particle swarm optimization algorithm are used to minimize the sum of weighted completion times of all jobs. From literature, it is found that only heuristics are used to minimize the total tardiness of all the jobs. The sum of weighted tardiness of all jobs is minimized using mathematical model, heuristic and simulated annealing algorithm. Only one article discusses the minimization of the weighted sum of tardy jobs of the open shop scheduling problem.

From the review, it is clear that wherever comparison of the proposed algorithm with existing algorithm(s) has been carried out, it is done using mean and percentage analysis. In future, researchers may follow a complete factorial experiment for comparison purpose by taking several factors of importance, out of which “algorithm” must be a factor. This will help to study the effects of the main factors, as well as those of interaction terms in ANOVA model on the response variable, namely, performance measure(s) of interest. Further, randomly generated data may be used for comparison purpose, so that the problems under the levels of the factorial experiment are in balanced nature.

From the literature, it is clear that many researchers have contributed to the minimization of the makespan, as well as minimization of the sum of completion times of jobs of the open shop problem, in terms of several approaches, including meta-heuristics. For other measures of performance, the number of contributions, as well as applications of different meta-heuristics, is less in number. So, future researchers may focus on developing meta-heuristics for the other measures of performance. Since the minimization of makespan is considered to be a dominant measure of performance, development of varied hybrid algorithms to minimize the makespan may also be attempted by researchers in future.

Acknowledgements

The authors thank the anonymous referees for their constructive suggestions, which have improved the paper.

References