Natural Science
Vol.06 No.16(2014), Article ID:51819,6 pages
10.4236/ns.2014.616115
The Gap Labelling Integrated Density of States for a Quasi Crystal Universe Is Identical to the Observed 4.5 Percent Ordinary Energy Density of the Cosmos
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Academic Editor: Leila Marek-Crnjac, Technical School Center of Maribor, Slovenia
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 August 2014; revised 29 September 2014; accepted 15 October 2014
ABSTRACT
Condense matter methods and mathematical models used in solving problems in solid state physics are transformed to high energy quantum cosmology in order to estimate the magnitude of the missing dark energy of the universe. Looking at the problem from this novel viewpoint was rewarded by a rather unexpected result, namely that the gap labelling method of integrated density of states for three dimensional icosahedral quasicrystals is identical to the previously measured and theoretically concluded ordinary energy density of the universe, namely a mere 4.5 percent of Einstein’s energy density, i.e. E(O) = mc2/22 where E is the energy, m is the mass and c is the speed of light. Consequently we conclude that the missing dark energy density must be E(D) = 1 − E(O) = mc2(21/22) in agreement with all known cosmological measurements and observations. This result could also be interpreted as a strong evidence for the self similarity of the geometry of spacetime, which is an expression of its basic fractal nature.
Keywords:
E-Infinity Theory, Fractal-Witten M-Theory, Gap Labelling Theorem, Density of States, Dark Energy Density, Noncommutative Geometry, K-Theory, Dimension Group

1. Introduction
It is well known that many models and mathematical techniques that proved to be valuable in the low energy domain of condense matter physics were found to be of considerable usefulness in clarifying basic questions in high energy physics [1] -[7] . Symmetry breaking and phase transition [3] are well known examples for the above, which resulted in the major discovery of the Higgs boson [4] . The hypothesis is also well known that the universe is a gigantic self similar structure [6] [7] as partially evidenced by the planetary system of the Rutherford- Bohr atom model [5] . Nevertheless the result of the present paper goes far beyond what the preceding fact could have led us to believe and it was rather a delightful unexpected result to find that the methods of solid state physics and the suspected self similarity of a fractal universe [6] [7] could lead to accurate results setting the gap labelling integrated density of states for a 3-D quasicrystals [8] - [12] equal to the ordinary energy density of the cosmos as found by COBE, WMAP and the Planck measurements [13] - [18] . In fact these various accurate measurements which lead to several Nobel prizes in physics [13] - [20] are in complete accordance with the theoretical results obtained in the last three years or so [21] - [25] and in turn these theoretical energy density derivations give identical results to the present one [16] - [25] as will be expanded upon in the following sections. In short the main objective of the present paper is to show that the methods of high energy physics and that of low energy solid state physics converge in a clear way leading to the same dark energy density.
2. Integrated Density of States
2.1. Background Information
It is well known that electronic band theory is a very useful and successful theory in the physics of solids that solved difficult problems connected to the design of solar cells and transistors as well as illuminating fundamental properties of solids such as optical absorption and electrical resistance [8] . In this respect the density of states and the Brillouin zone plays a central role [8] . Thus the said density function is defined as the number of electronic states per unit energy for nearby electron energy while the Brillouin zone is polyhedron in Schrö- dinger wave vector space, which is related to a corresponding crystal lattice [8] - [12] .
Now with a somewhat unconventional but well motivated idea in the back of our minds, namely that of draw- ing an instructive analogy between the zero density inside a band gap and the geometry and topology of the crystal lattice on the one side and ordinary energy and dark energy density contained in the structure of our cosmos on the other side, we will start here by extending the above concepts and notions to quasi periodic crystalline [8] [10] [11] . Luckily we already have at our disposal a gap labelling theorem to lean on as well as many results obtained notably by J. Bellisard [8] , A. Connes and many others who applied the powerful mathematical machinery of K-theory and noncommutative geometry [26] to the problem. For example an extensively used standard model is the Fibonacci sequence of two letters a and b in which the frequency of the “a” is given by the golden mean [8] [11] . This we consider next.
2.2. Gap Labelling Density of States of One Dimensional Discrete System
Probably the simplest group of one dimensional systems to illustrate the theory at hand is an automatic sequences such as period doubling, the Rudin-Shapiro sequence and Thue-Morse sequence [8] . However the Fibonacci sequence is the most appropriate for our purpose here not only because it is the simplest but also because it constitutes in the limit a one dimensional Cantorian space with a Hausdorff dimension equal
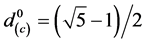 and a Menger-Urysohn topological dimension
and a Menger-Urysohn topological dimension  while displaying a remarkable inte-
while displaying a remarkable inte-
grated density of states having the same information as that of a higher dimensional model. Let the two letters alphabet be given by 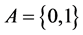 and let the substitution be
and let the substitution be
 (1)
(1)
Following Bellissard’s general exposition and his notation we find two matrices [8]
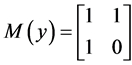 (2)
(2)
and
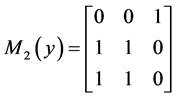 (3)
(3)
The largest Eigenvalue of the above is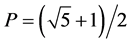 , i.e.
, i.e. 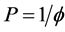 where
where 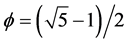 is the golden mean. Using the same notation and abbreviations of [8] the corresponding Eigenvectors are consequently
is the golden mean. Using the same notation and abbreviations of [8] the corresponding Eigenvectors are consequently
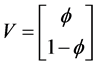
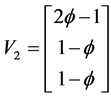 (4)
(4)
and the integrated density of states (IDS) is given by [8]
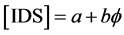 (5)
(5)
where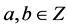 . It is almost impossible for anyone familiar with noncommutative geometry or E-infinity theory to overlook that the preceding density is at a minimum formally identical to that of the compactified Penrose tiling dimensional function [7] [11] [26] as well as the bijection formula of Cantorian spacetime [7] [26] [27] . Thus as simple as the preceding analysis may be, it has far reaching consequences which we discuss next in the context of a K-analysis of the famous Penrose fractal tiling [11] [12] [26] .
. It is almost impossible for anyone familiar with noncommutative geometry or E-infinity theory to overlook that the preceding density is at a minimum formally identical to that of the compactified Penrose tiling dimensional function [7] [11] [26] as well as the bijection formula of Cantorian spacetime [7] [26] [27] . Thus as simple as the preceding analysis may be, it has far reaching consequences which we discuss next in the context of a K-analysis of the famous Penrose fractal tiling [11] [12] [26] .
2.3. Landi’s K-Analysis of the Penrose Tiling
As noted by Landi [12] , the K-theory of Penrose universe treated as x-space by Connes [26] is straight forward and leads via Bratteli diagram and the fact that {0} is the only primitive ideal to the inclusion [12]
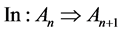 (6)
(6)
which is reminiscent of the previous recursive Fibonacci example. Proceeding in the usual way Landi can then prove the proposition that the c star algebra of the Penrose tiling gives rise to a group given by [12]
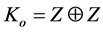 (7)
(7)
and
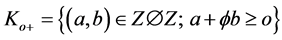 (8)
(8)
This result is again identical to that obtained by Connes and noting the one to one correspondence between the bijection formula of E-infinity Cantorian spacetime [7] [19] [26] - [29]

and von Neumann-Connes dimensional function it follows that ko+ as well as [IDS] are simply mathematical tautology, albeit an extremely instructive one bringing various theories for the micro cosmos and the large structure of spacetime [29] to come together and reveal their quintessentially identical nature. One must add however that the bijection formula is a far more compact notation and one could deduce 


exactly as should be while the zero set is given clearly by [7] [27]

so that 

Next we discuss the vital physical and cosmological implication of the preceding results.
3. Ordinary and Dark Energy from Integrated Density of States and Gap Labelling
One of the most important conclusions arrived at from the preceding Section 2 is that what we called topological probability 
Hardy’s quantum probability of entanglement [19] - [22] is an ideal starting point for various very good reasons. First it is an exact solution of two quantum particles using orthodox quantum mechanics a la Dirac [19] - [22] . Second this exact solution turned out to be a most surprizing quantitative answer with a strong qualitative flavour being the golden mean 

Being a probability we could look upon it as being the inverse of a dimension, i.e. un-normed probability given by the bijection formula [7] [27] . Taking the dimensionality n to be n = 6 one finds [7] [27] [19] - [22]

Therefore we have the normed probability [19] - [22]

Alternatively we could see P(Hardy) as living in a negative four dimensional space 

Here we tacitly made use of the notion of the degree of emptiness of an empty set introduced first by the late inventor of the word fractals, B. Mandelbrot [7] . This is so because the zero set n = 0 is the surface of the empty set 






Let us return to 









where the 22 may be viewed as the compactified dimensional subset of the 26 dimensions of the bosonic string theory [19] - [21] . In other words, for a normed m = 1, c = 1 we have E(Einstein) = 1 and the measurable energy density is simply 

4. Conclusions
There is one aspect of theoretical physics that is so incredibly beautiful that one cannot find the right words to describe it. This is a first hand experience of the present author which happens whenever he notices that two totally different fields can be directly connected and analogies established simply because the same stringent logic, i.e. the same mathematical pattern and schemes are obeyed by both fields. One such case is the connection between super conductivity and the high energy physics of elementary particles [1] - [4] . This is truly the unreasonable effectiveness of mathematics which on deeper still reflection, is truly reasonable.
The present work reveals a similar situation where the extremely small and large ultra obeys basically the same subgroup of R generated by Z and the golden mean number 




From all of the above we have considerable renewed confidence in our proposal made some two decades ago that the universe as a whole can be regarded as huge quasicrystals [37] - [43] . Clearly the proposal is indirectly implied by the work of Penrose [38] as well as a powerful but largely unsung work of a Russian school [41] . The idea was then given new impulse by the work of a leading physicist and cosmologist, P. Steinhardt [43] and it may be possible to explain the origin of the forbidden 5-D symmetry of the found meteorite remnants by the effect of the quasicrystalline geometry of quantum spacetime on its initial quantum formation [36] . In fact all recent astrophysical observations indicate a quasi self-similar universe as exposed in an excellent 2008 paper by R. Murdzek [44] , which we give here together with the superb historical account in [6] as recommended reading. We think that future research following the ideas presented here may lead to a possible harnessing of dark energy using some innovative nanotechnological devices.
References
- Aoki, H. (Chairman) (2010) Condensed Matter Physics Meets High Energy Physics. IPMU, 1st International Conference, Tokyo, 8-12 February 2010.
- El Naschie, M.S. (1977) The Logic of Interdisciplinary Research. Chaos, Solitons & Fractals, 8, vi-x.
- Sachder, S. (2011) Quantum Phase Transition. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511973765
- El Naschie, M.S. (2005) Experimental and Theoretical Arguments for the Number and the Mass of the Higgs Particle. Chaos, Solitons & Fractals, 23, 1091-1098. http://dx.doi.org/10.1016/j.chaos.2004.08.001
- French, A. and Kennedy, P., Eds. (1985) Niels Bohr—A Centenary Volume. Harvard University Press, Cambridge- Mass.
- Baryshev, Y. and Teerikorpi, P. (2002) Discovery of Cosmic Fractals. World Scientific, Singapore.
- El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- Bellissard, J. (1992) Gap Labelling Theorems for Schrödinger’s Operators. In: Waldschmidt, M., et al., Eds., From Number Theory to Physics, Springer, Heidelberg, 538-630. http://dx.doi.org/10.1007/978-3-662-02838-4_12
- Sze, S. (1981) Modern Physics of Semiconductors. John Wiley & Sons, New York.
- El Naschie, M.S. (1998) Fredholm Operator and the Wave-Particle Duality. Chaos, Solitons & Fractals, 9, 975-978. http://dx.doi.org/10.1016/S0960-0779(98)00076-9
- El Naschie, M.S. (1998) Penrose Universe and Cantorian Spacetime as a Model for Noncommutative Quantum Geometry. Chaos, Solitons & Fractals, 9, 931-933. http://dx.doi.org/10.1016/S0960-0779(98)00077-0
- Landi, G. (1997) An Introduction to Noncommutative Spaces and Their Geometrics. Springer, Berlin.
- El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
- Corda, C. (2011) Cosmology of Einstein-Vlasov System in a Weak Modification of General Relativity. Modern Physics A, 26, 362-370.
- Corda, C. (2008) A Repulsive Force from a Modification of General Relativity. International Journal of Theoretical Physics, 47, 2679-2685. http://dx.doi.org/10.1007/s10773-008-9705-2
- Tang, W., Li, Y., Kong, H.Y. and El Naschie, M.S. (2014) Nonlocal Elasticity to Nonlocal Spacetime and Nanoscience. Bubbfil Nanotechnology, 1, 3-12.
- El Naschie, M.S. (2014) From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
- He, J.H. (2014) A Tutorial Review on Fractal Spacetime and Fractional Calculus. International Journal of Theoretical Physics, 53, 3698-3718. http://dx.doi.org/10.1007/s10773-014-2123-8
- Marek-Crnjac, L. and He, J.H. (2013) An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471. http://dx.doi.org/10.4236/ijaa.2013.34053
- He, J.H. and Marek-Crnjac, L. (2013) The Quintessence of El Naschie’s Theory of Fractal Relativity and Dark Energy. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 3, 130-137.
- Helal, M.A., Marek-Crnjac, L. and He, J.H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145.
- El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and ‘tHooft’s 4-e Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37.
- El Naschie, M.S. (2014) Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity. World Journal of Mechanics, 4, 153-156. http://dx.doi.org/10.4236/wjm.2014.46017
- El Naschie, M.S. (2014) From Chern-Simon Holography and Scale Relativity to Dark Energy. Journal of Applied Mathematics and Physics, 2, 634-638.
- El Naschie, M.S. (2014) Why E Is Not Equal mc2. Journal of Modern Physics, 5, 743-750. http://dx.doi.org/10.4236/jmp.2014.59084
- Connes, A. (1994) Noncommutatie Geometry. Academic Press, San Diego.
- El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646. http://dx.doi.org/10.1016/j.chaos.2008.09.059
- Auffray, J.P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436. http://dx.doi.org/10.4236/jmp.2014.515144
- Hawking, S.W. and Ellis, G.F.R. (1973) The Large Scale Structure of Spacetime. Cambridge University Press, Cambridge.
- Karpenkov, O. (2013) Geometry of Continued Fractions. Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-39368-6
- Jacobsen, L., Ed. (1989) Analytic Theory of Continued Fractions. Lecture Notes No. 1406 in Mathematics. Springer, Berlin.
- Khanin, K., Dias, J.L. and Marklof, J. (2007) Multidimensional Continued Fractions, Dynamical Renormalization and KAM Theory. Communications in Mathematical Physics, 270, 197-231. http://dx.doi.org/10.1007/s00220-006-0125-y
- El Naschie, M.S. (2013) A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light. International Journal of Modern Nonlinear Theory and Application, 2, 43-54.
- El Naschie, M.S. (2013) Nash Embedding of Witten’s M-Theory and the Hawking-Hartle Quantum Wave of Dark Energy. Journal of Modern Physics, 4, 1417-1428. http://dx.doi.org/10.4236/jmp.2013.410170
- El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic ‘tHooft-Veltman- Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221. http://dx.doi.org/10.4236/wjnst.2014.44027
- El Naschie, M.S. and Helal, A. (2013) Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography. International Journal of Astronomy and Astrophysics, 3, 318-343.
- El Naschie, M.S. (2000) Branching Polymers, Knot Theory and Cantorian Spacetime. Chaos, Solitons & Fractals, 11, 453-463. http://dx.doi.org/10.1016/S0960-0779(98)00092-7
- El Naschie, M.S. (1993) Penrose Tiling, Semi-Conduction and Cantorian
Spectra in Four and Five Dimensions. Chaos, Solitons & Fractals, 3, 489-491. >http://html.scirp.org/file/4-8302499x59.png" class="200" /> Spectra in Four and Five Dimensions. Chaos, Solitons & Fractals, 3, 489-491. http://dx.doi.org/10.1016/0960-0779(93)90033-W
- El Naschie, M.S. (1994) Forbidden Symmetries, Cantor Sets and Hypothetical Graphite. Chaos, Solitons & Fractals, 4, 2269-2272. http://dx.doi.org/10.1016/0960-0779(94)90046-9
- Iovane, G., Laserra, E. and Tortoriello, F.S. (2004) Stochastic Self-Similar and Fractal Universe. Chaos, Solitons & Fractals, 20, 415-426. http://dx.doi.org/10.1016/j.chaos.2003.08.004
- Ivanenko, D.D. and Gailuin, R.V. (1995) Quasicrystal Model of the Universe. (TpXVIIMexΔyHap.ceMnHapano fn3.Bblaconx) (In Russian)
- Iovane, G. (2005) Mohamed El Naschie’s E-Infinity Cantorian Spacetime and Its Consequence in Cosmology. Chaos, Solitons & Fractals, 25, 775-779. http://dx.doi.org/10.1016/j.chaos.2005.02.024
- Wolchover, N. (2014) Quasicrystal Meteorite Exposes Novel Processes in Early Solar System. Scientific American, 18 June, and Quanta Magazine. www.quantamagazine.org/20140613-quasicrystal-meteorite-posses-age-old-questions/
- Murdzek, R. (2008) Hierarchical Cantor Set in the Large Scale Structure with Torus Geometry. Chaos, Solitons & Fractals, 38, 1269-1273. http://dx.doi.org/10.1016/j.chaos.2007.01.150


 Spectra in Four and Five Dimensions. Chaos, Solitons & Fractals, 3, 489-491. >http://html.scirp.org/file/4-8302499x59.png" class="200" /> Spectra in Four and Five Dimensions. Chaos, Solitons & Fractals, 3, 489-491.
Spectra in Four and Five Dimensions. Chaos, Solitons & Fractals, 3, 489-491. >http://html.scirp.org/file/4-8302499x59.png" class="200" /> Spectra in Four and Five Dimensions. Chaos, Solitons & Fractals, 3, 489-491.