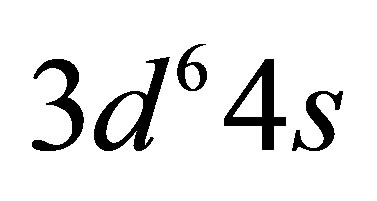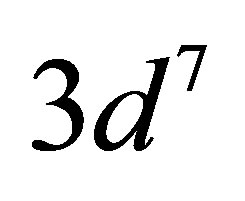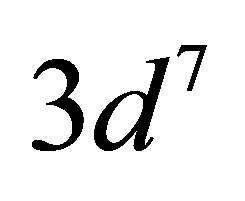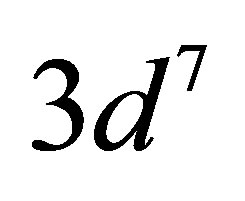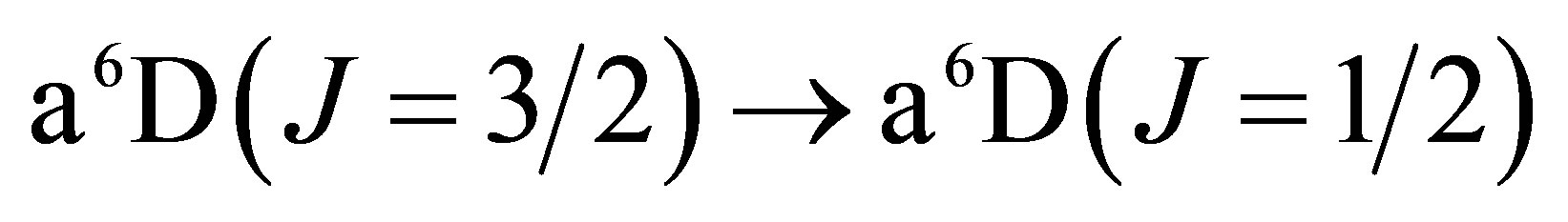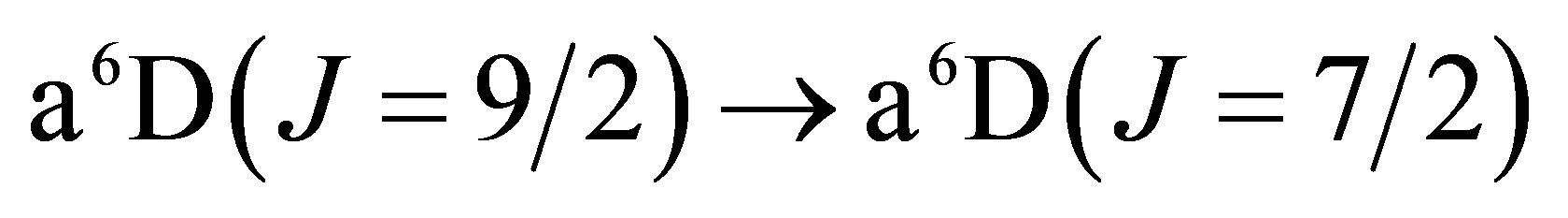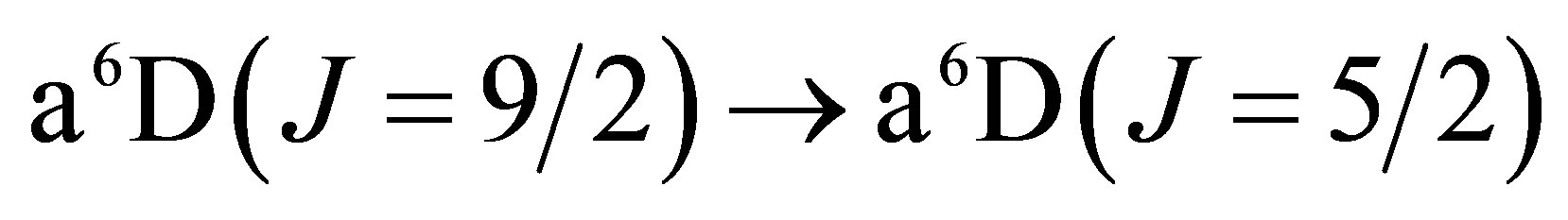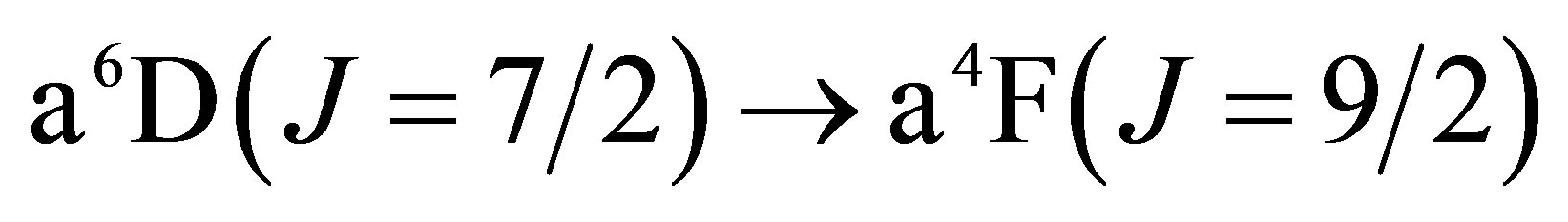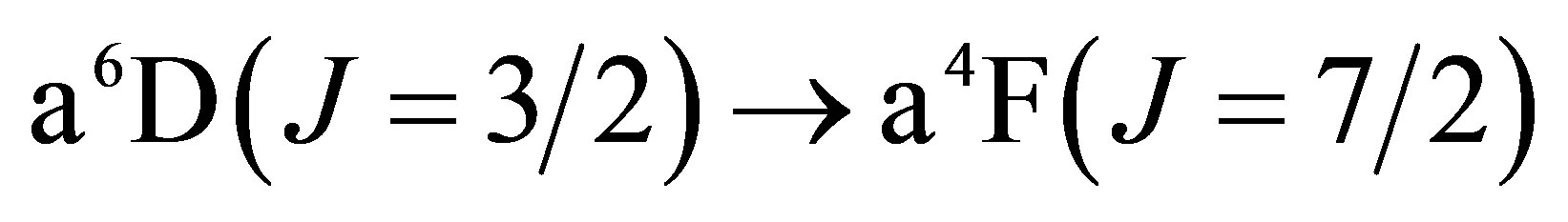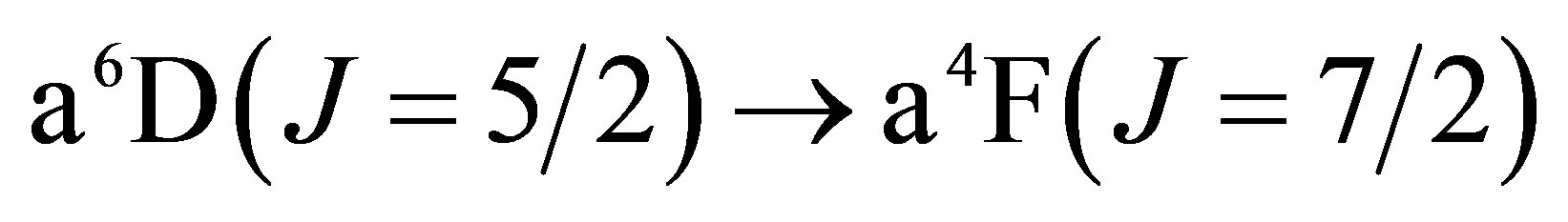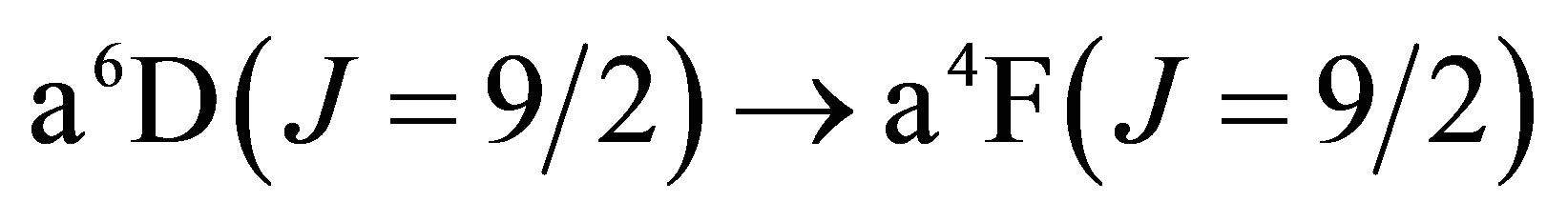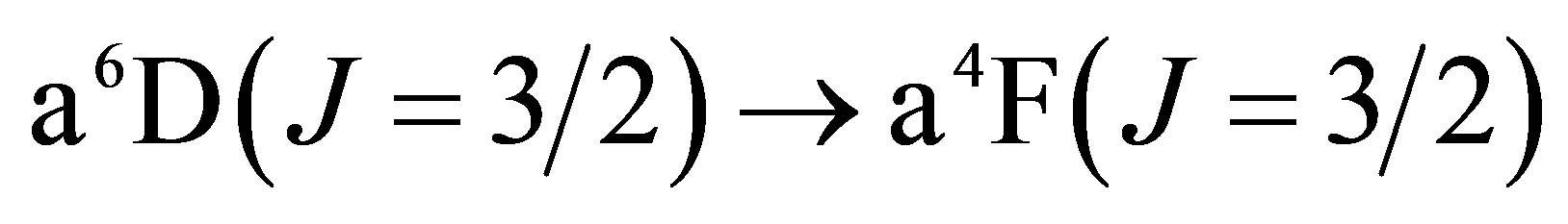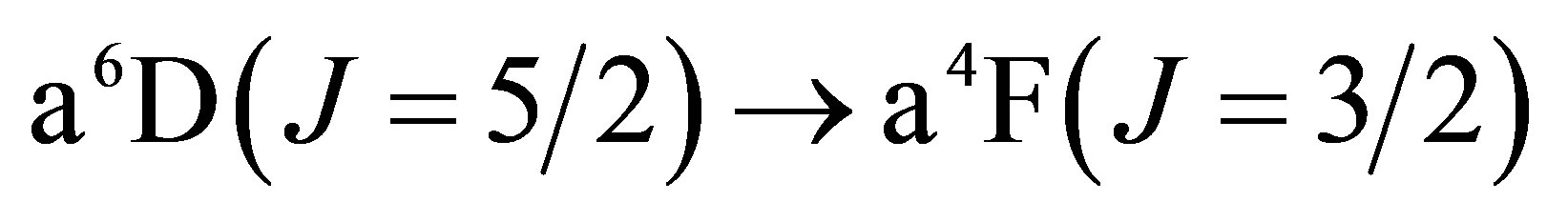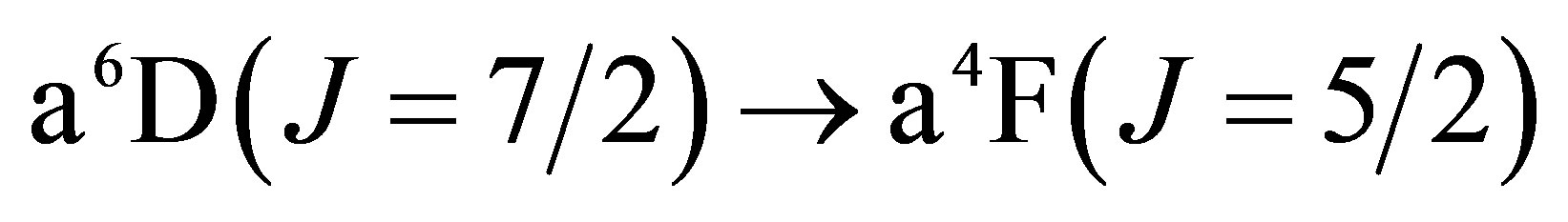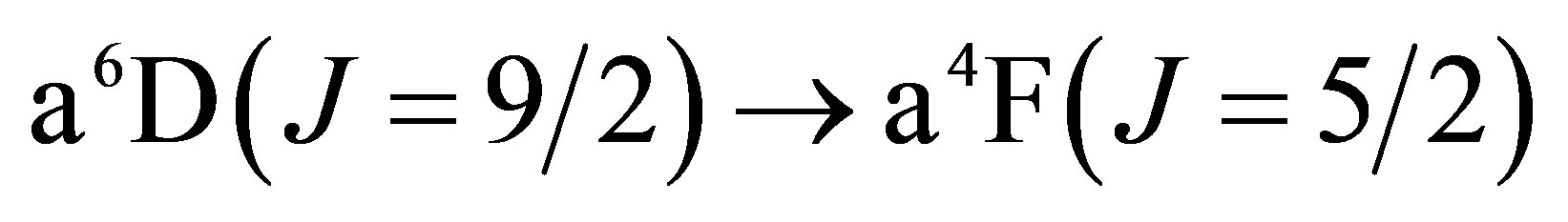Journal of Modern Physics
Vol.4 No.12A(2013), Article ID:41504,28 pages DOI:10.4236/jmp.2013.412A1004
Planetary Heating by Neutrinos: Long-Term Habitats for Aquatic Life if Dark Energy Decays Favourably
School of Biological Sciences, Bangor University, Bangor, United Kingdom
Email: y.gofod@gmail.com
Copyright © 2013 R. J. Spivey. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2013 are reserved for SCIRP and the owner of the intellectual property R. J. Spivey. All Copyright © 2013 are guarded by law and by SCIRP as a guardian.
Received October 1, 2013; revised November 4, 2013; accepted November 27, 2013
Keywords: Neutrinos; Dark Matter; Dark Energy; Sterile Neutrinos; Oceanic Planets; Astrobiology; Cosmology
ABSTRACT
The potential cosmological and astrobiological implications of neutrinos are considered. Dark energy drives the current phase of accelerating cosmic expansion. Like inflation, it may decay in time to matter and radiation. However, since its energy density is minuscule in comparison, decay would be unlikely to inject such a rich variety of particles into the universe, and may instead be limited to the lowest energy fermions. Nonrelativistic neutrinos have the capacity to form stable, galaxy-engulfing haloes supported by degeneracy pressure, much like white dwarves and neutron stars. Conversely, bodies of mass  can indefinitely rely on Coulomb forces for weight support. Opportunities for the mutual annihilation of electron neutrinos are largely confined to planets containing iron in the hcp phase. If dark energy decays primarily to neutrinos in 40 ~ 100 Gyr, then oceanic planets orbiting within the resulting haloes could provide long-term habitats for aquatic life with only lax constraints on the neutrino mass,
can indefinitely rely on Coulomb forces for weight support. Opportunities for the mutual annihilation of electron neutrinos are largely confined to planets containing iron in the hcp phase. If dark energy decays primarily to neutrinos in 40 ~ 100 Gyr, then oceanic planets orbiting within the resulting haloes could provide long-term habitats for aquatic life with only lax constraints on the neutrino mass, . Various considerations now favour the possibility that neutrinos are Majorana particles with an inverted mass hierarchy and an electron neutrino mass in the vicinity of 50 meV. Sterile neutrinos of eV-mass may already be a significant component of dark matter, and could enhance planetary heating when active neutrino haloes become heavily depleted. An intriguing mechanism capable of regulating oceanic heat flux over a wide range of planetary masses is also described.
. Various considerations now favour the possibility that neutrinos are Majorana particles with an inverted mass hierarchy and an electron neutrino mass in the vicinity of 50 meV. Sterile neutrinos of eV-mass may already be a significant component of dark matter, and could enhance planetary heating when active neutrino haloes become heavily depleted. An intriguing mechanism capable of regulating oceanic heat flux over a wide range of planetary masses is also described.
1. Introduction
Life on Earth inefficiently harnesses the Sun’s energy but dark matter represents a much larger energy resource than all the stars combined. Of the particles of the standard model, those in the first generation are the most commonly encountered in nature and the most stable. Living organisms are reliant on biochemistry and, with the possible exception of the electron neutrino, biological functions can be readily ascribed to all first generation particles. Electromagnetism ensures attraction between electrons and protons, without which atoms would be unstable. The strong interaction binds nucleons, allowing elements heavier than hydrogen to form. Gravity enables planets to stably orbit stars at habitable distances. The weak interaction, which is responsible for the radioactive decay of certain isotopes, appears to be a force of instability rather than stability. It creates deuterium during the proton-proton cycle, generating solar neutrinos as it does so, but its biological significance may not end there. The weak interaction is the only means by which neutrinos participate in particle interactions. Moreover, neutrinos are the only non-baryonic dark matter particles whose existence is in no doubt.
The former solar neutrino problem was resolved when it was found that neutrinos undergo flavour oscillations. Hence, contrary to the expectations of the standard model, neutrinos must possess mass [1]. Tritium beta decay experiments currently provide the most robust upper bound to the neutrino mass scale,  [2], though cosmological limits are considerably tighter with
[2], though cosmological limits are considerably tighter with  [3-5]. Observations of neutrino oscillations have inferred useful information concerning the differences between their mass eigenstates. Since
[3-5]. Observations of neutrino oscillations have inferred useful information concerning the differences between their mass eigenstates. Since  [6], the mass hierarchy is unlikely to be degenerate. Anomalies in short baseline experiments imply the existence of eV-scale sterile neutrinos: a mini-seesaw mechanism may link active and sterile species, strongly favouring an inverted mass hierarchy [7]. Data from LEP [8] and nucleosynthesis [9] establishes that there are three species of active neutrinos. These considerations seem to constrain the effective mass of electron neutrinos to the range 0.045 - 0.066 eV.
[6], the mass hierarchy is unlikely to be degenerate. Anomalies in short baseline experiments imply the existence of eV-scale sterile neutrinos: a mini-seesaw mechanism may link active and sterile species, strongly favouring an inverted mass hierarchy [7]. Data from LEP [8] and nucleosynthesis [9] establishes that there are three species of active neutrinos. These considerations seem to constrain the effective mass of electron neutrinos to the range 0.045 - 0.066 eV.
The accelerating expansion of the universe [10,11] has revealed that dark energy is increasingly dominating the cosmos. The value of the cosmological constant  is at least 120 orders of magnitude smaller than theory can explain, a fact historically referred to as the cosmological constant problem [12]. Thus, dynamical dark energy caused by an exotic negative pressure fluid is the most theoretically plausible explanation for the accelerating expansion of the universe [13]. Often modeled as a scalar field evolving along a potential [14], when imitating a cosmological constant
is at least 120 orders of magnitude smaller than theory can explain, a fact historically referred to as the cosmological constant problem [12]. Thus, dynamical dark energy caused by an exotic negative pressure fluid is the most theoretically plausible explanation for the accelerating expansion of the universe [13]. Often modeled as a scalar field evolving along a potential [14], when imitating a cosmological constant  the equation of state of the dark energy field
the equation of state of the dark energy field  is
is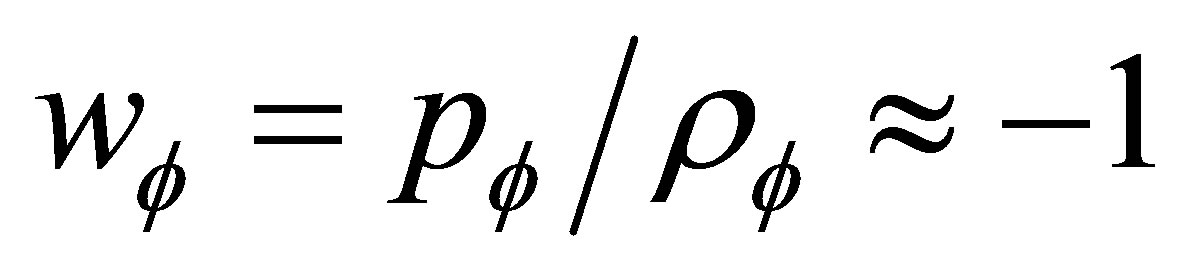 . Its energy density then remains approximately constant at
. Its energy density then remains approximately constant at  so that dark energy’s totality increases as the cube of the universal scale factor, growing exponentially at late times if dark energy does not decay.
so that dark energy’s totality increases as the cube of the universal scale factor, growing exponentially at late times if dark energy does not decay.
Inflation, now an integral part of big bang cosmology, posits that the early universe underwent exponential expansion [15] terminating with the decay of a dynamical energy field into matter during inflationary reheating [16]. Remarkably, the decay of dark energy to matter and radiation was suggested decades before inflation was advanced [17]. If dark energy is a low-energy analogue of the inflationary field, one would not expect the accelerating expansion to persist forever. It is possible that dark energy can only decay into matter once some threshold is exceeded. Since its energy density is minute [18-20], its decay might proceed predominantly via the copious discharge of the lowest energy fermions. Thus, nonrelativistic neutrinos might become the most prevalent form of matter in the future universe. Self-gravitating clouds of neutrinos can be supported indefinitely against collapse by mutual repulsion arising due to Pauli’s exclusion principle. Since neutrinos have a tiny yet non-zero mass, these quantum structures could engulf the largest galaxies [21-23].
The cosmic neutrino background (CνB) froze out during primordial nucleosynthesis ~2 seconds after the big bang. The momentum of these relic neutrinos decreases inversely with the universal scale factor, their median velocity at redshift z being  [24]. If their mass exceeds ~0.16 eV then galaxy clusters, which typically have velocity dispersions of ~1000 km/s and are the most massive bound structures of the universe, would already be trapping them [25]. It was long ago appreciated that galaxy clusters are rich in dark matter and will gravitationally lens light from background objects [26]. The distribution of mass within the Abell 1689 galaxy cluster has now been reconstructed using gravitational lensing data [27]. Recent modelling has inferred that ~97% of this cluster’s mass can be accounted for by a degenerate halo of 1.5 eV fermions [28], which seems incompatible with our knowledge of ordinary, active neutrinos. However, short-baseline and reactor experiments are now uncovering evidence for eV-scale sterile neutrinos [29]. Interestingly, if more than one species of sterile neutrino exists then the cosmological constant could be ruled out as an explanation for accelerating expansion [30].
[24]. If their mass exceeds ~0.16 eV then galaxy clusters, which typically have velocity dispersions of ~1000 km/s and are the most massive bound structures of the universe, would already be trapping them [25]. It was long ago appreciated that galaxy clusters are rich in dark matter and will gravitationally lens light from background objects [26]. The distribution of mass within the Abell 1689 galaxy cluster has now been reconstructed using gravitational lensing data [27]. Recent modelling has inferred that ~97% of this cluster’s mass can be accounted for by a degenerate halo of 1.5 eV fermions [28], which seems incompatible with our knowledge of ordinary, active neutrinos. However, short-baseline and reactor experiments are now uncovering evidence for eV-scale sterile neutrinos [29]. Interestingly, if more than one species of sterile neutrino exists then the cosmological constant could be ruled out as an explanation for accelerating expansion [30].
The fate of virtually all stars is to gravitationally contract to form black dwarves or neutron stars supported by fermionic repulsion between electrons or neutrons. Following the loss of thermal energy, however, planets of mass  acquire sufficient weight support from Coulomb repulsion with most of their electrons remaining bound to atoms. Within comets, asteroids and dwarf planets, internal pressures are insufficient to appreciably change the density of matter. Hence, beyond the stelliferous era, planets will be the only bodies containing nondegenerate atomic matter at a diverse range of pressures and densities. Hydrostatic equilibrium will ensure these objects are highly spherical.
acquire sufficient weight support from Coulomb repulsion with most of their electrons remaining bound to atoms. Within comets, asteroids and dwarf planets, internal pressures are insufficient to appreciably change the density of matter. Hence, beyond the stelliferous era, planets will be the only bodies containing nondegenerate atomic matter at a diverse range of pressures and densities. Hydrostatic equilibrium will ensure these objects are highly spherical.
Given sufficient time, the matter of the universe is expected to transform into leptons and photons [31]. Photons of lesser energy than the lowest mass particles do not represent a particularly useful form of energy. Conversely, though neutrinos have a tiny mass, their energy is potentially useful. From the perspective of the gradual heat-death of the universe, processes transforming low energy neutrinos, which cluster gravitationally on galactic scales, into photons are thus very interesting. Special attention will be drawn here to the 4s electrons of iron as targets for mutually annihilating electron neutrinos and antineutrinos belonging to a dark matter halo. Stellar nucleosynthesis remains exothermic up until nickel but 56Ni radioactively decays via 56Co to 56Fe, the most stable of all nuclides. Thus, iron is already and will continue to be an abundant element. Its 3d and 4s electrons have remarkably similar ground state energies, offering almost unique opportunities for low energy transitions comparable to the neutrino annihilation energy. Iron’s hcp phase (hexaferrum) exists at pressures between 0.06 and 57 Mbar, corresponding to the density range 9 ~ 34 g/cm3 common within planets [32].
Following the original proposal that neutrino dark matter might sustain aquatic life within oceans encased in ice surrounding iron-cored planets [33], this work describes the circumstances in which this would be viable and what it might imply for the properties of active and sterile neutrinos. The work is organised in sections as follows. The future abundance, composition, heating requirements and internal thermal structure of oceanic planets are first considered. Opportunities for annihilation of neutrinos to be mediated by various forms of matter are then assessed. Reasons why iron-cored planets would be the primary recipients of neutrino energy are detailed and a mechanism is identified capable of sustaining a remarkably consistent oceanic heat flux over a wide range of planet masses. The performance of neutrino haloes is then analysed. An adjuvant role for eV-scale sterile neutrinos acting in concert with active species in prolonging planetary heating and boosting overall energetic efficiency is then illustrated. The constraints this might impose on the timing of dark energy’s decay are subsequently investigated. This work concludes with a brief discussion contextualising the findings.
2. Iron-Cored Oceanic Planets
2.1. Abundance
The homogeneity of type Ia supernovae (SNIa) was instrumental to the discovery of accelerating cosmic expansion and has now been confirmed by direct observations [34]. The consistent luminosity exhibited by SNIa is thought to be due to a common explosion mechanism involving carbon/oxygen white dwarf progenitors of mass approaching the Chandrasekhar limit, 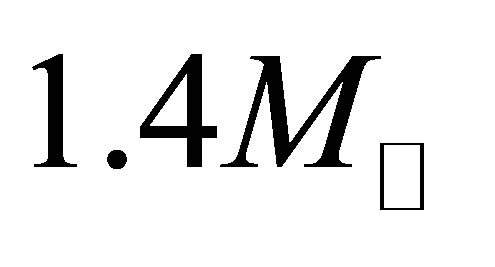
 , triggered by the accretion of matter e.g. from binary companions [35]. White dwarves of mass
, triggered by the accretion of matter e.g. from binary companions [35]. White dwarves of mass  are capable of fusing helium to carbon and oxygen, those of lower mass being degenerate helium dwarves. Due to their compact size and intense gravity, white dwarves attract matter, causing their mass to increase with time. With some 97% of stars ending their lives as white dwarves [36], this offers many opportunities for SNIa. Since supernovae other than SNIa only occur in stars of mass exceeding
are capable of fusing helium to carbon and oxygen, those of lower mass being degenerate helium dwarves. Due to their compact size and intense gravity, white dwarves attract matter, causing their mass to increase with time. With some 97% of stars ending their lives as white dwarves [36], this offers many opportunities for SNIa. Since supernovae other than SNIa only occur in stars of mass exceeding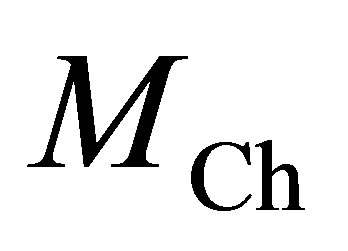 , by the end of the stelliferous era SNIa will have been responsible for the production of almost all the heavier elements of the cosmos.
, by the end of the stelliferous era SNIa will have been responsible for the production of almost all the heavier elements of the cosmos.
Observations have determined that the ejecta of a typical SNIa are, by mass, 18% oxygen, 15% silicon, 13% iron, and 49% nickel (almost all in the unstable form 56Ni which decays radioactively to 56Fe), along with smaller amounts of carbon, calcium, sulphur and magnesium [37]. Elements emerge from SNIa in strata, with the lightest occupying the outermost layers. This provides the oxygen-rich outermost shell with the best opportunities for reacting with hydrogen in the interstellar medium, resulting in the formation of water molecules. On cooling to temperatures found in deep space, ice XI is obtained, whose ferroelectric self-aggregation may be relevant to comet formation [38-40]. The bombardment of protoplanets with comets would be important to the formation of oceanic planets, deferring the delivery of water to their surfaces.
Thus, SNIa ejecta are eminently suitable for the formation of oceanic planets having an inner silicate mantle, an outer mantle of ice VII/ice VI and, if the temperature permits, a deep liquid ocean enveloping the entire surface. Pressure would typically cause these oceans to solidify at depths of tens of km. Oceanic planets have attracted much interest in the last decade [41-44]. Note that since SNIa progenitors have a mass of , the ejecta of a single supernova could yield up to 105 oceanic planets of
, the ejecta of a single supernova could yield up to 105 oceanic planets of . Such planets are already likely to greatly outnumber stars and, due to continued accretion of mass onto white dwarves, they may be so abundant by the end of the stelliferous era that their combined mass rivals that of stellar remnants in some regions of the universe. Comets and asteroids played an important role in the formation of the Earth’s oceans so the stelliferous era provides ample time for comets to transform initially arid planets into oceanic planets. It is apparent that oceanic planets will only attain their maximal abundance as the stelliferous era draws to a close and supernova activity has ceased.
. Such planets are already likely to greatly outnumber stars and, due to continued accretion of mass onto white dwarves, they may be so abundant by the end of the stelliferous era that their combined mass rivals that of stellar remnants in some regions of the universe. Comets and asteroids played an important role in the formation of the Earth’s oceans so the stelliferous era provides ample time for comets to transform initially arid planets into oceanic planets. It is apparent that oceanic planets will only attain their maximal abundance as the stelliferous era draws to a close and supernova activity has ceased.
2.2. Heating Requirements
An estimate will now be derived for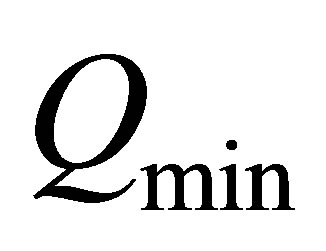 , the minimum heat flux through the surface of an oceanic planet necessary for the presence of a liquid ocean. It will be conservatively assumed that oceanic planets lack any significant atmosphere that might otherwise temper radiative heat losses. A crust of ice can provide handsome thermal insulation without encroaching significantly on the volume of an underlying ocean.
, the minimum heat flux through the surface of an oceanic planet necessary for the presence of a liquid ocean. It will be conservatively assumed that oceanic planets lack any significant atmosphere that might otherwise temper radiative heat losses. A crust of ice can provide handsome thermal insulation without encroaching significantly on the volume of an underlying ocean.
If comets and asteroids deliver at least half the oxygen content of each oceanic planet then extrapolating from the composition of SNIa ejecta suggests that a typical Earth-sized oceanic planet would have H2O deposits at the surface approximately 375 km in depth. Since water at temperatures above 273 K transitions to the solid ice VI phase at pressures exceeding 632 MPa, the maximum depth of an ocean is limited to some 64 - 100 km on planets with a surface gravity resembling that of the Earth. Consideration is restricted here to worlds with a radius  and a mass
and a mass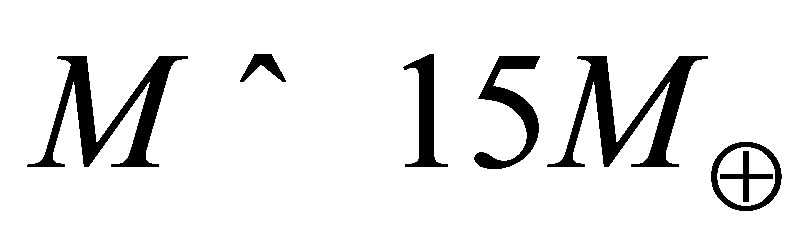 , see Appendix A. Beyond this size, the central pressure would exceed ~57 Mbar and iron would experience a hcp®fcc phase transition [32]. For the largest planets of interest, the oceans would solidify at depths of around 40 km. In these circumstances, the upper 10 km of the ocean could freeze without impinging unduly on the volume of water beneath. The heat lost per unit area from the ice surface due to black body radiation,
, see Appendix A. Beyond this size, the central pressure would exceed ~57 Mbar and iron would experience a hcp®fcc phase transition [32]. For the largest planets of interest, the oceans would solidify at depths of around 40 km. In these circumstances, the upper 10 km of the ocean could freeze without impinging unduly on the volume of water beneath. The heat lost per unit area from the ice surface due to black body radiation, 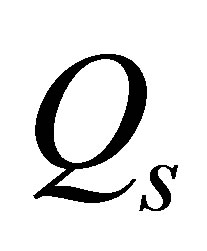 , is given by the StefanBoltzmann law:
, is given by the StefanBoltzmann law:
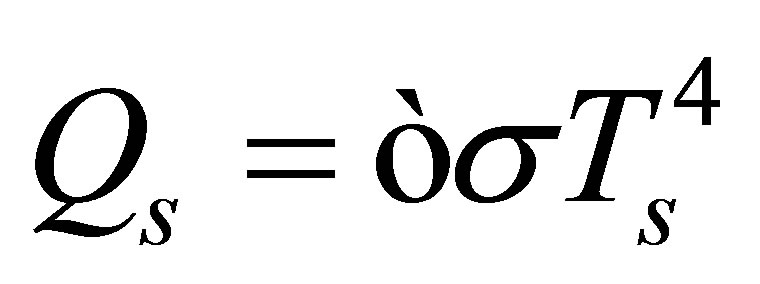 (1)
(1)
where the temperature of the surface is  , the radiant emissivity of the ice crust is
, the radiant emissivity of the ice crust is 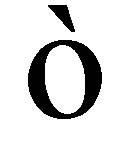 and
and  is the StefanBoltzmann constant. For pure ice at relevant infrared wavelengths,
is the StefanBoltzmann constant. For pure ice at relevant infrared wavelengths, 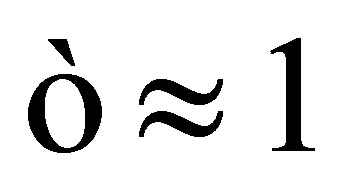 , which maximizes radiant heat losses. The thermal conductivity,
, which maximizes radiant heat losses. The thermal conductivity, 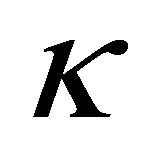 , of hexagonal ice Ih is inversely related to temperature but is relatively constant with pressure and can be approximated by
, of hexagonal ice Ih is inversely related to temperature but is relatively constant with pressure and can be approximated by  in units of W
in units of W (m
(m K)-1 [45]. As pressure shifts the melting point of ice slightly, the temperature at the boundary between the surface ice and the underlying ocean is taken to be ~265 K. Heat will pass through the crust of ice almost entirely by thermal conduction. The heat flux,
K)-1 [45]. As pressure shifts the melting point of ice slightly, the temperature at the boundary between the surface ice and the underlying ocean is taken to be ~265 K. Heat will pass through the crust of ice almost entirely by thermal conduction. The heat flux, 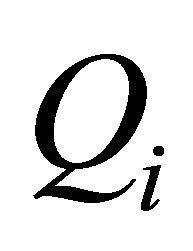 , passing through a unit area of ice is related to the depth of the ice crust,
, passing through a unit area of ice is related to the depth of the ice crust,  , by Fourier’s law:
, by Fourier’s law:
 (2)
(2)
Continuity of heat flux demands that  be matched to
be matched to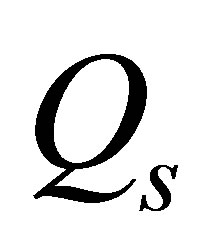 . For an ice depth of 10 km, iteration of the following expression rapidly converges to the surface temperature
. For an ice depth of 10 km, iteration of the following expression rapidly converges to the surface temperature :
:
 (3)
(3)
The result is 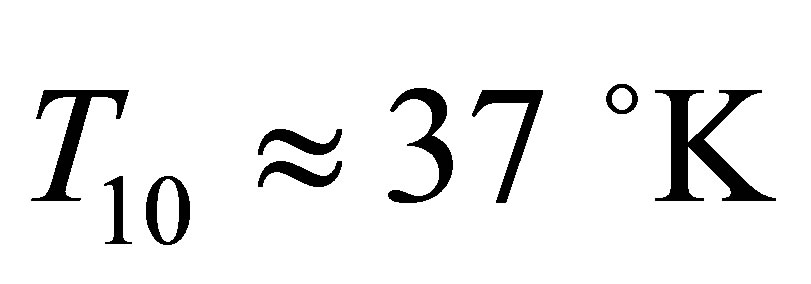 from which the minimum heat flux which can comfortably sustain water in the liquid state for oceanic planets up to
from which the minimum heat flux which can comfortably sustain water in the liquid state for oceanic planets up to 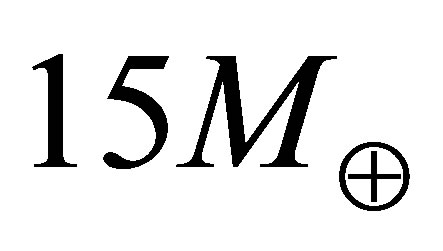 is estimated to be
is estimated to be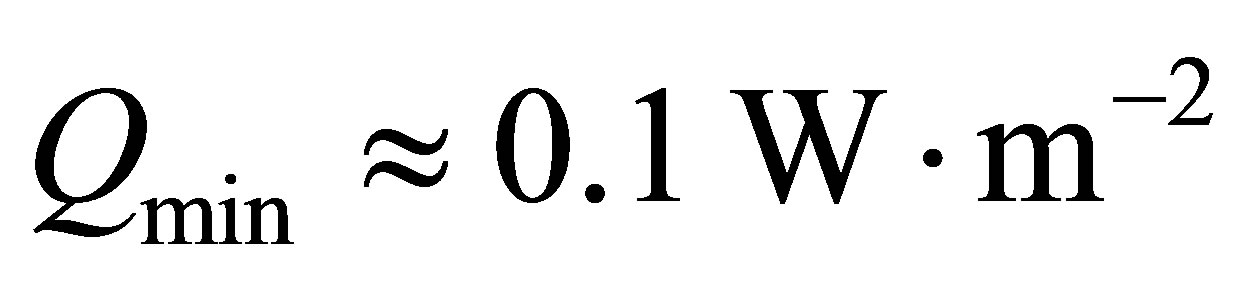 . Note that the core temperature of the Earth is estimated to be around 5800 K, driving heat flow at the surface of ~0.06 W/m2 [46]. For an Earthmass planet, the total power comes to
. Note that the core temperature of the Earth is estimated to be around 5800 K, driving heat flow at the surface of ~0.06 W/m2 [46]. For an Earthmass planet, the total power comes to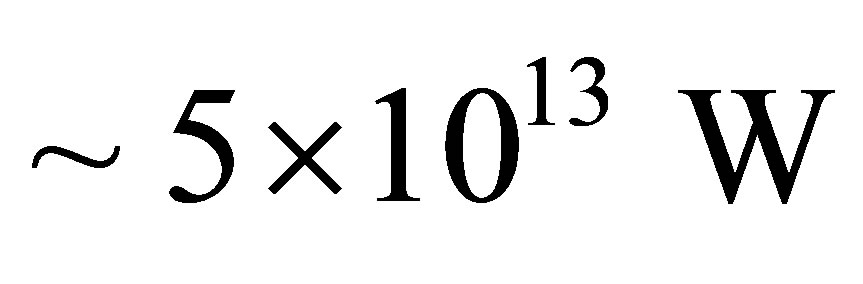 . The thickness of the ice and its surface temperature are plotted as a function of heat flux in Figure 1. In the absence of an atmosphere, the surface ice completely melts
. The thickness of the ice and its surface temperature are plotted as a function of heat flux in Figure 1. In the absence of an atmosphere, the surface ice completely melts  if
if .
.
2.3. Internal Structure
The minimum heat flux required in order to support water in the liquid state determines the thermal profile of a typical oceanic planet, here taken to have a mass equal to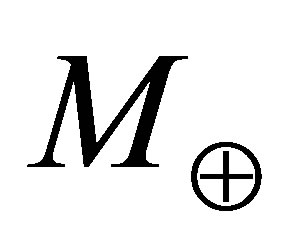 . Since convection is highly effective at transporting heat, the maximum temperature gradient within the ocean can be estimated from the adiabatic case which corresponds to about 0.4 K/km. This suggests that the temperature at the base of a 100 km deep ocean is unlikely to exceed 310 K. For most oceanic planets, it is likely to be very close to 283 K [41]. In contrast, heat is transported by conduction through the ice crust, which will thus have a steep temperature gradient. Depending on depth and surface temperature, this gradient will be in the range 7 ~ 50 K/km. Thus, a crust of ice serves as an effective thermal insulator.
. Since convection is highly effective at transporting heat, the maximum temperature gradient within the ocean can be estimated from the adiabatic case which corresponds to about 0.4 K/km. This suggests that the temperature at the base of a 100 km deep ocean is unlikely to exceed 310 K. For most oceanic planets, it is likely to be very close to 283 K [41]. In contrast, heat is transported by conduction through the ice crust, which will thus have a steep temperature gradient. Depending on depth and surface temperature, this gradient will be in the range 7 ~ 50 K/km. Thus, a crust of ice serves as an effective thermal insulator.
Based on the composition of type Ia supernova ejecta, a hypothetical oceanic planet of one Earth-mass is projected to consist of a large iron core of radius ~4240 km surrounded by a silicate mantle of thickness ~1300 km through which heat would be transported by advection. External to this inner mantle would be an outer mantle of ice consisting of strongly convective ice VI and VII phases of combined depth ~320 km. A liquid ocean ~50 km in depth covered by a solid crust of ice Ih upwards of 50 m in thickness would overlie the hot ice mantles. The temperature gradient would be around 0.05 - 0.1 K/km within the ice mantle [47]. Within a slowly convecting silicate mantle the thermal gradient is often taken to be 0.3 K/km but, if the inner mantle is subadiabatic, it may be as little as 0.05 - 0.15 K/km [48]. Due to the presence
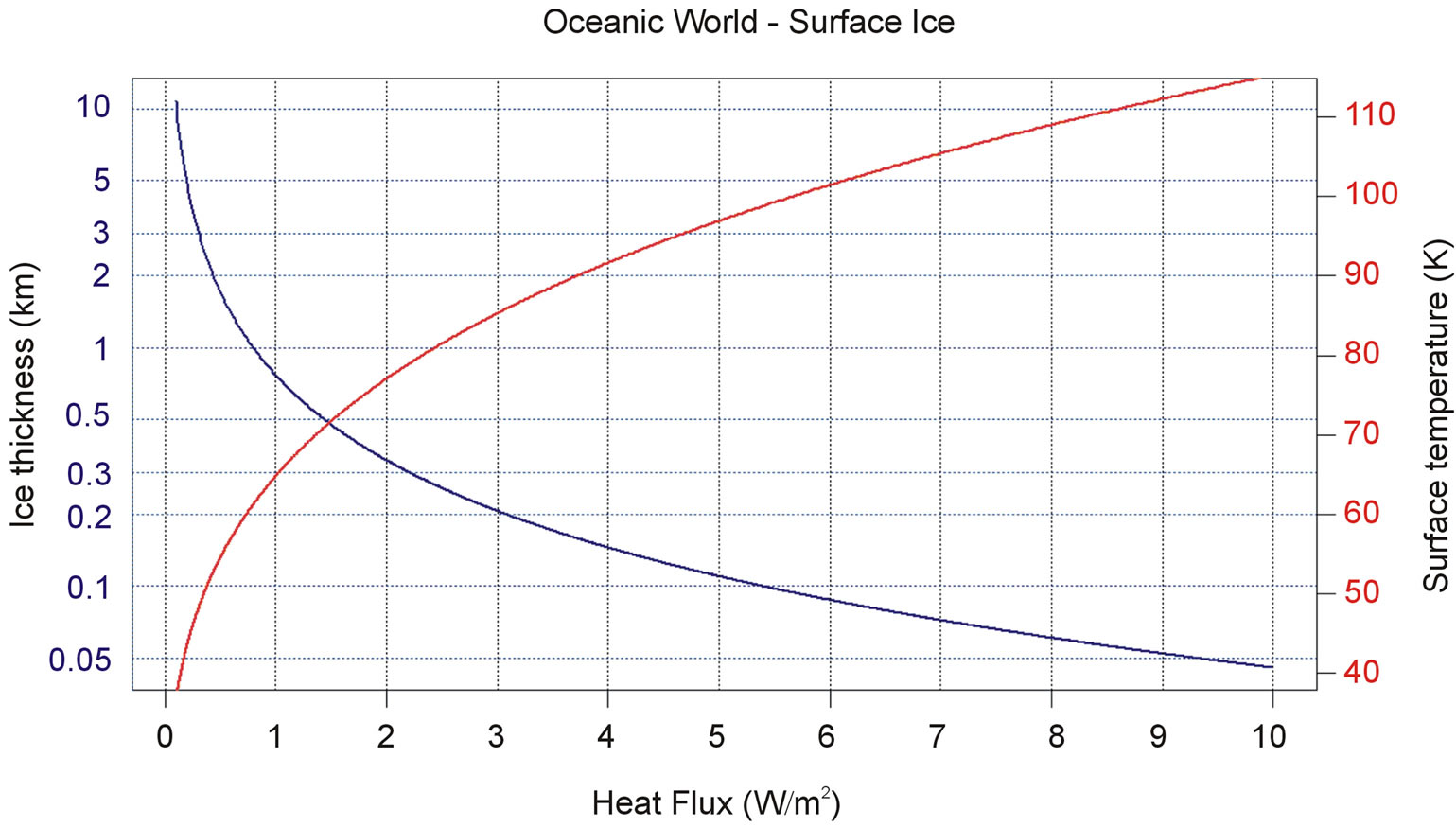
Figure 1. Thickness of surface ice and its surface temperature as functions of the surface heat flux.
of convection in both the inner and outer mantles, some mixing between the two would occur, but stratification would be maintained by gravity. A liquid ocean could in principle be sustained even if the exterior temperature of the iron core were as low as ~800 K. A depiction of the internal structure of such an oceanic planet is presented in Figure 2.
3. Neutrino Annihilation
Nonrelativistic neutrinos are incapable of producing other mass-bearing particles when they mutually annihilate. Impervious to electromagnetic forces, neutrinos cannot directly interact with photons. The transformation of two annihilating neutrinos into a photon would violate the conservation of linear momentum. In a vacuum, a neutrino and an antineutrino can only annihilate into a short-lived virtual Z boson which must swiftly decay into a fermion and an antifermion. If the original neutrinos were not ultrarelativistic, the only possibility is a pair of neutrinos with precisely the same properties as the original pair. Thus, the mutual annihilation of low energy neutrinos and antineutrinos is essentially prohibited in a vacuum.
Annihilation is possible in the presence of other leptons, in particular when electrons act as receptors of the annihilation energy. For momentum and energy to be conserved demands that the electrons interact with other matter [49]. Providing this condition is satisfied, neutrinos can annihilate either via neutral or charged current interactions. Charged currents are of most interest to this discussion because electron densities within oceanic planets are far higher than neutrino densities within neutrino haloes. Annihilation is thus anticipated to proceed primarily via:
 (4)
(4)
This reaction is closely related to the photoneutrino

Figure 2. Internal structure of a typical oceanic planet undergoing internal heating due to neutrino annihilation.
process in which  [50-56]. Note that energy can only be conserved if the final electron is able to emit a photon so the intermediate electron is a virtual particle. Effectively the time-reversal of the photoneutrino process, the annihilation of low energy neutrinos shall be referred to here as the inverse photoneutrino process (IPP). Unlike interactions where neutrinos scatter from other particles, the ambient neutrino concentration is an important rate-determining factor for IPP. Thus, the opacity of matter to neutrinos is a function of neutrino density. This work is primarily concerned with active neutrinos of a mass in the vicinity of 0.05 eV. An IPP energy of
[50-56]. Note that energy can only be conserved if the final electron is able to emit a photon so the intermediate electron is a virtual particle. Effectively the time-reversal of the photoneutrino process, the annihilation of low energy neutrinos shall be referred to here as the inverse photoneutrino process (IPP). Unlike interactions where neutrinos scatter from other particles, the ambient neutrino concentration is an important rate-determining factor for IPP. Thus, the opacity of matter to neutrinos is a function of neutrino density. This work is primarily concerned with active neutrinos of a mass in the vicinity of 0.05 eV. An IPP energy of 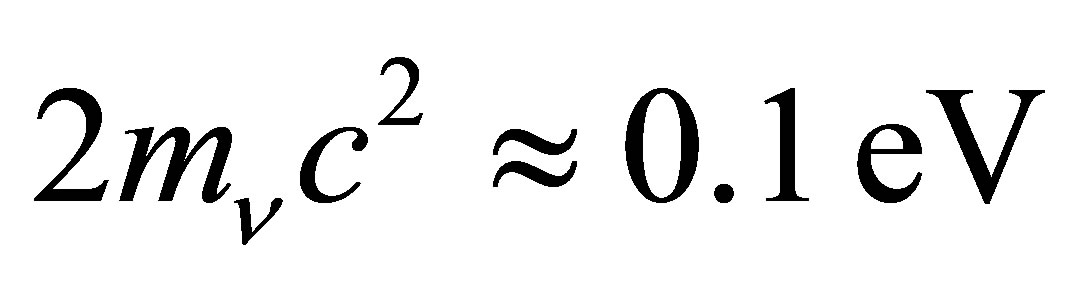 thus corresponds to 12 μm long-wavelength infrared radiation which is readily absorbed in matter.
thus corresponds to 12 μm long-wavelength infrared radiation which is readily absorbed in matter.
3.1. Opportunities for IPP in Iron
Owing to radioactive decay of 56Ni and 56Co about 58% of the mass of the ejecta of SNIa is transformed into iron within a matter of months. Due to its 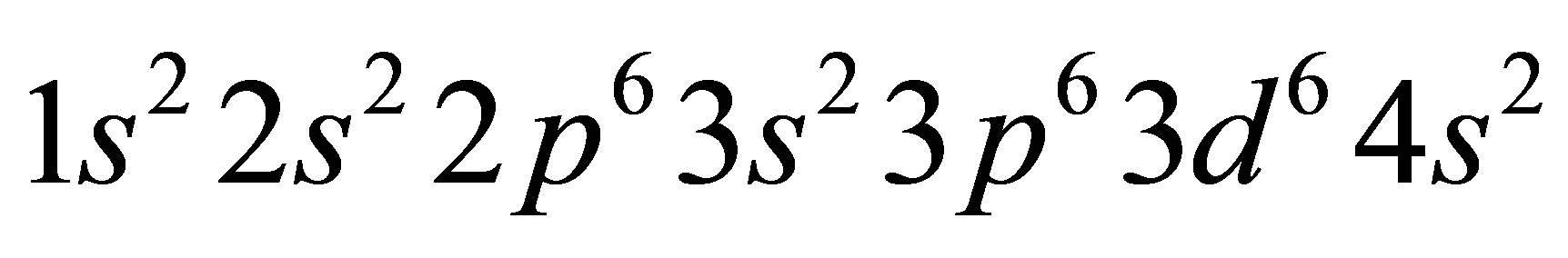 configuration and the similarity in energy between the 3d and 4s subshells, iron has a particularly rich electronic structure. When iron condenses to form a metal each atom donates one 4s electron to the conduction band, leaving one 4s electron in place. The smallest energy transitions in the remaining 4s electron of the Fe II ground state are comparable to the IPP energy of 0.1 eV, involving either promotion of the remaining 4s electron to the 3d subshell or 4s to 4s excitation. The lowest energy transitions near the ground state in the other common elements hydrogen to calcium involve much larger energy changes than the IPP energy. Iron’s core electrons require energies of at least 30 eV to be excited as they are more tightly bound to the nucleus.
configuration and the similarity in energy between the 3d and 4s subshells, iron has a particularly rich electronic structure. When iron condenses to form a metal each atom donates one 4s electron to the conduction band, leaving one 4s electron in place. The smallest energy transitions in the remaining 4s electron of the Fe II ground state are comparable to the IPP energy of 0.1 eV, involving either promotion of the remaining 4s electron to the 3d subshell or 4s to 4s excitation. The lowest energy transitions near the ground state in the other common elements hydrogen to calcium involve much larger energy changes than the IPP energy. Iron’s core electrons require energies of at least 30 eV to be excited as they are more tightly bound to the nucleus.
Being a transition metal, iron’s 4s electron normally, though not always, possesses lower energy than the paired electrons of the 3d subshell. For IPP to proceed within iron, the presence of a 4s target electron is required. While Fe II has numerous energy levels, as is apparent from the density histogram of Figure 3, transitions between them are constrained by quantum-mechanical selection rules. IPP involves the destruction and recreation of an electron via the W boson. The near simultaneous emission of a photon is mandatory if energymomentum conservation is to be satisfied. The net spin of a neutrino and antineutrino is zero so the total angular momentum  of an atom must change by
of an atom must change by 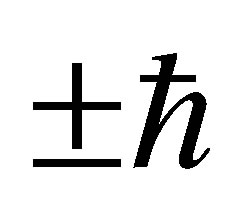 when a spin 1 photon is emitted, while the spin of the final electron may or may not differ from that of the initial electron. However, if neutrinos are Majorana particles then
when a spin 1 photon is emitted, while the spin of the final electron may or may not differ from that of the initial electron. However, if neutrinos are Majorana particles then  [57] and lepton number need not be conserved. Neutrino annihilation could then change the total angular momentum
[57] and lepton number need not be conserved. Neutrino annihilation could then change the total angular momentum  of an iron atom by 0,
of an iron atom by 0, 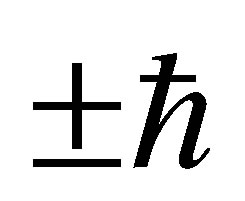 or
or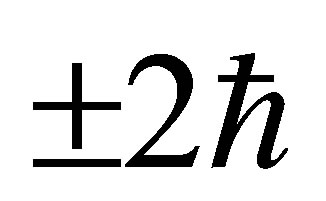 , thereby increasing opportunities for IPP.
, thereby increasing opportunities for IPP.
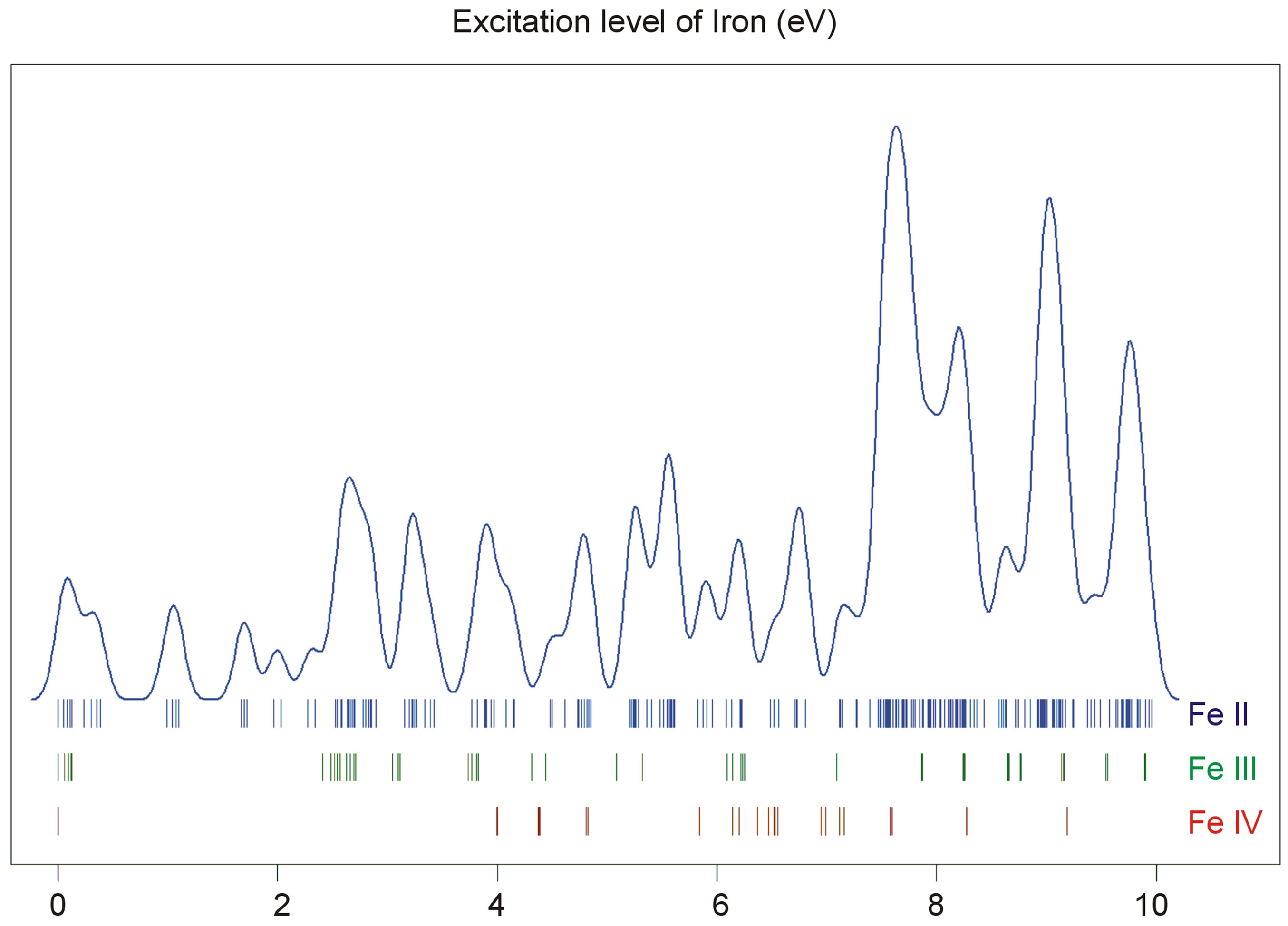
Figure 3. Excitation levels for iron species in the range 0 - 10 eV. Vertical bars denote energy levels (Fe II—blue; Fe III— green; Fe IV—red). A density curve is provided for Fe II simulating pressure-broadening in metallic iron. In this range of energies, Fe II has 247 distinct excitation levels whereas hydrogen and helium have none. No element has an ionisation energy below that of Caesium’s, 3.9 eV (Source: NIST).
The lowest energy states of Fe II correspond to the 3d6(5D)4s configurations (Russell-Saunders a6D terms) with J = 1/2, 3/2, 5/2, 7/2 or 9/2. These energies lie 0 - 0.121 eV above the ground state [58]. At marginally higher energies, 0.232 - 0.387 eV, Fe II can take on the 3d7 configurations (Russell-Saunders a4F terms) with J = 3/2, 5/2, 7/2 or 9/2. These levels and the permissible transitions between them are detailed in Appendix B. Roughly speaking, it therefore requires temperatures of 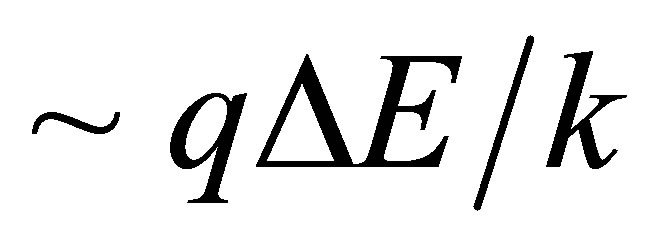 or several thousand Kelvin for atoms of metallic iron to be stripped of their remaining 4s electrons. The hcp®fcc phase transition in iron has been attributed to the transferral of the 4s electron to the 3d subshell [59]. The energy of the ground state a4F term will therefore match that of the ground state a6D term at the hcp®fcc transition. Thus, the transitions listed in Appendix B will be significantly suppressed at high pressures and temperatures, whose combined influence determines whether iron exists in the hcp phase or fcc phase. Once the 4s electron is lost there is an abrupt decrease in atomic volume precipitating the phase transition.
or several thousand Kelvin for atoms of metallic iron to be stripped of their remaining 4s electrons. The hcp®fcc phase transition in iron has been attributed to the transferral of the 4s electron to the 3d subshell [59]. The energy of the ground state a4F term will therefore match that of the ground state a6D term at the hcp®fcc transition. Thus, the transitions listed in Appendix B will be significantly suppressed at high pressures and temperatures, whose combined influence determines whether iron exists in the hcp phase or fcc phase. Once the 4s electron is lost there is an abrupt decrease in atomic volume precipitating the phase transition.
A relatively large energy is required to promote a 3d electron to an unoccupied 4s orbital. The lowest energy configuration in Fe II that possesses two 4s electrons is the  configuration (a6S term with J = 5/2). Located almost 3 eV above the ground state, it is out of reach of the IPP energy. No 4s electrons remain in fcc iron so the 3d electrons become the outermost valence electrons and seamlessly merge with the conduction band. Promotion of iron’s outermost electrons is then blocked by the degeneracy of the valence/conduction band. This is biologically favourable, as the hcp®fcc transition thus prevents the overheating of oceanic planets by neutrinos. Indeed, in conjunction with the presence of a dense neutrino halo, this arrangement constitutes a mechanism for thermally regulating a planet’s internal temperature.
configuration (a6S term with J = 5/2). Located almost 3 eV above the ground state, it is out of reach of the IPP energy. No 4s electrons remain in fcc iron so the 3d electrons become the outermost valence electrons and seamlessly merge with the conduction band. Promotion of iron’s outermost electrons is then blocked by the degeneracy of the valence/conduction band. This is biologically favourable, as the hcp®fcc transition thus prevents the overheating of oceanic planets by neutrinos. Indeed, in conjunction with the presence of a dense neutrino halo, this arrangement constitutes a mechanism for thermally regulating a planet’s internal temperature.
Since IPP necessarily involves the emission of a photon, the electron cannot receive all the energy of the annihilating neutrinos. Choosing a reference frame in which the neutrino and antineutrino initially approach one another at identical speeds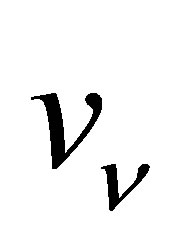 , their total momentum is zero. Assigning initial and final velocities of
, their total momentum is zero. Assigning initial and final velocities of 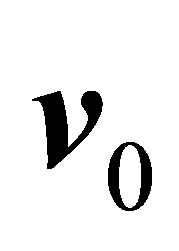 and
and  respectively to the electron, its energy gain is maximised when the direction of motion is unchanged between final and initial states. A photon is emitted with energy
respectively to the electron, its energy gain is maximised when the direction of motion is unchanged between final and initial states. A photon is emitted with energy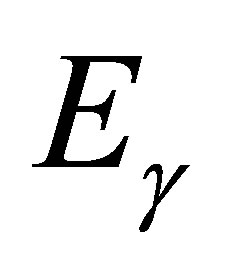 , absorbing the remaining energy of the annihilating neutrinos. Energy-momentum conservation then gives:
, absorbing the remaining energy of the annihilating neutrinos. Energy-momentum conservation then gives:
 (5)
(5)
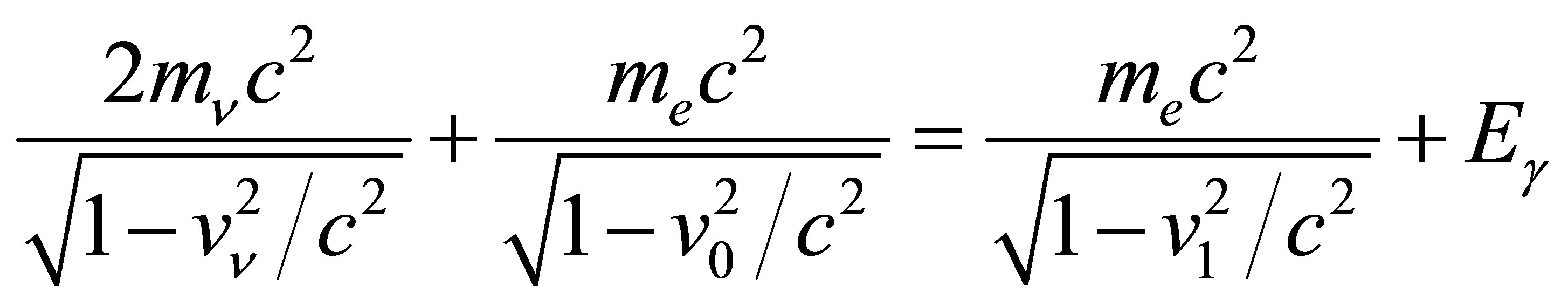 (6)
(6)
Eliminating  leaves a quadratic equation involving
leaves a quadratic equation involving .
.
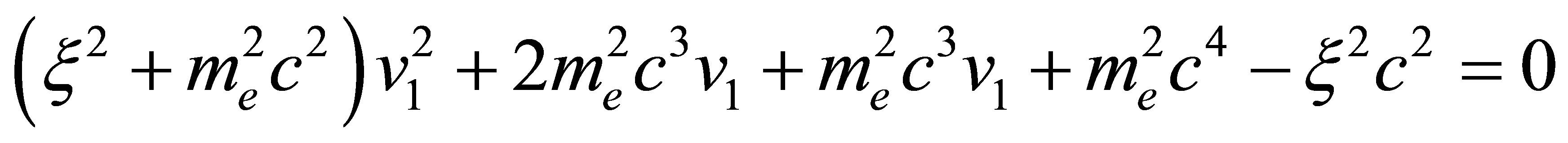 (7)
(7)
where . Assuming
. Assuming  and using
and using 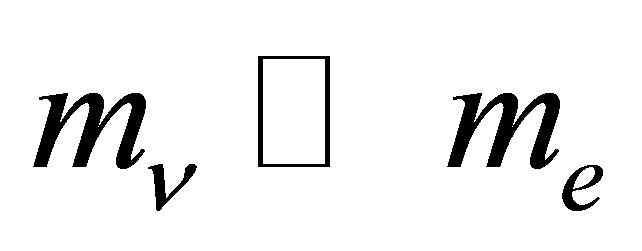 it can be shown that
it can be shown that
 (8)
(8)
The ratio 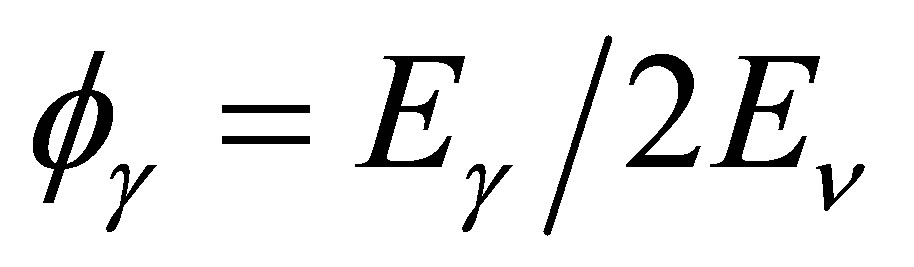 represents the fraction of the annihilation energy passed on to the photon:
represents the fraction of the annihilation energy passed on to the photon:
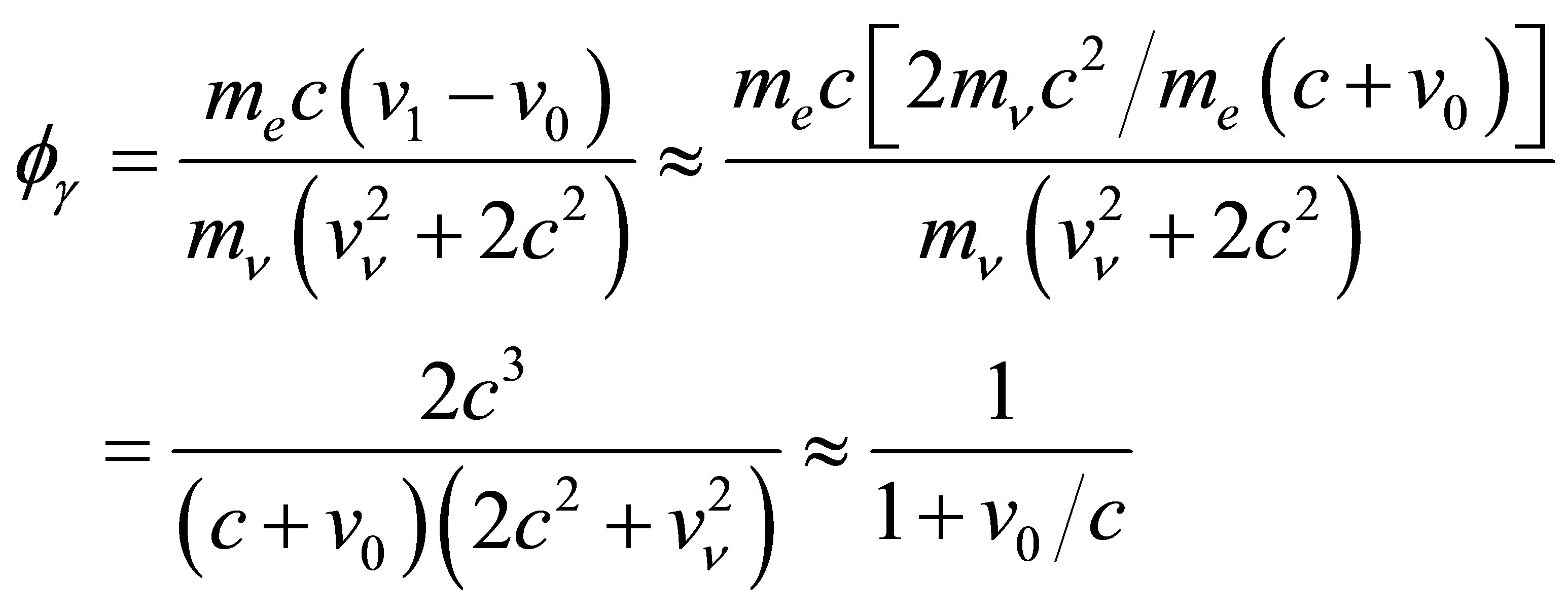 (9)
(9)
It is apparent that 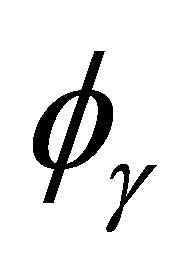 is a simple sigmoidal function of
is a simple sigmoidal function of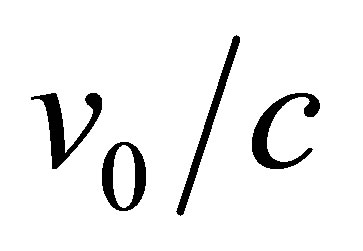 . The 4s electrons of iron move with a mean velocity given by
. The 4s electrons of iron move with a mean velocity given by , which yields the estimate
, which yields the estimate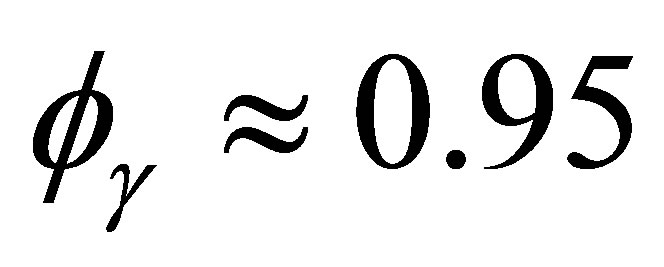 . Thus, this analysis finds that no more than 5% of the IPP energy can go to the final electron, regardless of likely variations in
. Thus, this analysis finds that no more than 5% of the IPP energy can go to the final electron, regardless of likely variations in 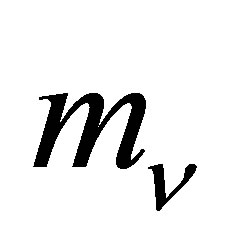 and
and . Hence, the annihilation of 50 meV neutrinos involves electron excitations no larger than 5 meV in energy. Avoidance of the smallest energy transition within iron at zero pressure (see Appendix B) therefore requires an electron neutrino mass smaller than 0.142 eV for the Majorana case or 0.383 eV for the Dirac case. Both are compatible with existing cosmological limits.
. Hence, the annihilation of 50 meV neutrinos involves electron excitations no larger than 5 meV in energy. Avoidance of the smallest energy transition within iron at zero pressure (see Appendix B) therefore requires an electron neutrino mass smaller than 0.142 eV for the Majorana case or 0.383 eV for the Dirac case. Both are compatible with existing cosmological limits.
Due to the proximity of electrons from neighbouring atoms, in metallic iron the energy of 4s electrons becomes closer to the energies of 3d electrons. At constant pressure or planetary depth, iron’s hcp®fcc phase transition occurs due to rising temperature and coincides with the ground state energies of the 4s and unoccupied 3d orbitals becoming equal. Thus, opportunities for IPP will inevitably arise within planets containing hcp iron at suitable temperatures i.e. those close to the hcp®fcc boundary where one expects the energy transitions listed in Appendix B to be shifted downwards towards the range 0 to 5 meV.
Interactions of 4s electrons with those in adjacent atoms leads to the formation of a valence band. The 4s electrons shield internal electrons and so 3d electrons have a comparatively narrow band structure though hybridization of the 3d and 4p orbitals can somewhat broaden the 3d band under pressure [60]. This would only enhance opportunities for  electron transfer, assisting heating over a wide range of planetary radii.
electron transfer, assisting heating over a wide range of planetary radii.
The temperature at which the hcp®fcc phase transition occurs tends to increase with pressure, attaining a maximum of about 19,000 K at pressures encountered at the cores of  planets [32]. The hcp phase of iron can exist at the cores of planets of mass
planets [32]. The hcp phase of iron can exist at the cores of planets of mass 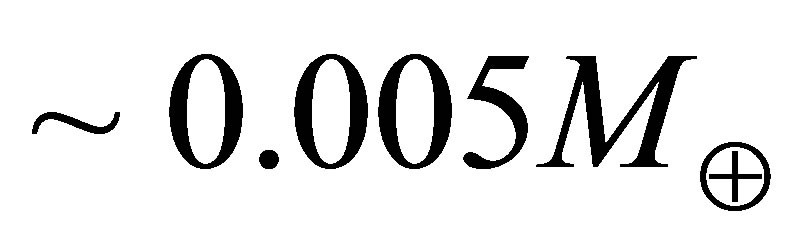
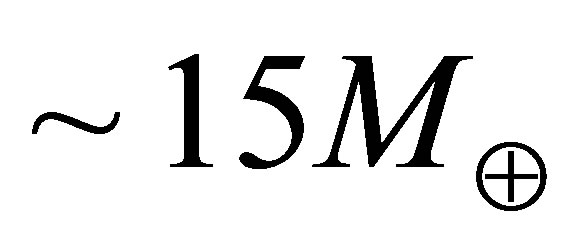 (Appendix A). Such planets all possess sufficient gravity to attain hydrostatic equilibrium and spherical symmetry, supporting their own weight via Coulomb forces even if all internal heat is lost. In order to sustain liquid oceans, larger planets require higher core temperatures to maintain the same thermal flux through thicker mantles. Assuming oceanic planets to be of a consistent composition and mean density, a constant heat flux requires that planetary radius scales with core temperature. Since core pressure, P, scales as
(Appendix A). Such planets all possess sufficient gravity to attain hydrostatic equilibrium and spherical symmetry, supporting their own weight via Coulomb forces even if all internal heat is lost. In order to sustain liquid oceans, larger planets require higher core temperatures to maintain the same thermal flux through thicker mantles. Assuming oceanic planets to be of a consistent composition and mean density, a constant heat flux requires that planetary radius scales with core temperature. Since core pressure, P, scales as 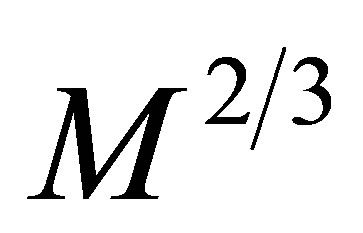 and
and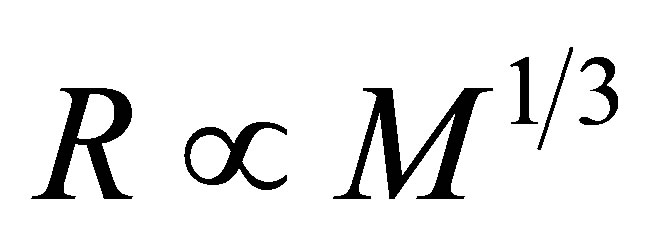 , then the core temperature would preferably scale as
, then the core temperature would preferably scale as . The hcp-fcc boundary in the phase diagram of iron, depicted in Figure 4, conforms remarkably well to this ideal, which can be seen to run almost parallel to the diagonal dashed line.
. The hcp-fcc boundary in the phase diagram of iron, depicted in Figure 4, conforms remarkably well to this ideal, which can be seen to run almost parallel to the diagonal dashed line.
3.2. Selective Delivery of Energy to Iron via IPP
With the exception of the 4s electrons of iron, under modest pressures and temperatures matter offers relatively few opportunities for the annihilation of low energy neutrinos. Transitions of the ground state electrons of almost all elements require energies well in excess of the IPP energy, less than 5% of which is available for electron excitation. In order to assess whether opportuni-

Figure 4. Phase diagram for iron at pressures and temperatures relevant to planetary heating. The hcp-fcc boundary has a very similar slope to that of a 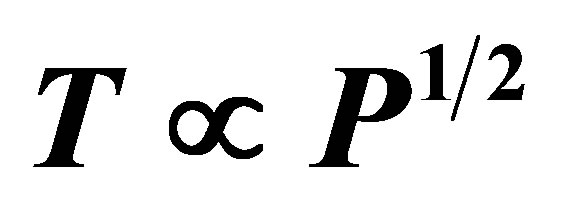 relationship (with the same slope as the dashed line shown). Since planetary heating would approximately track the hcp-fcc transition, it would be well-suited to the heating of a wide range of planetary masses
relationship (with the same slope as the dashed line shown). Since planetary heating would approximately track the hcp-fcc transition, it would be well-suited to the heating of a wide range of planetary masses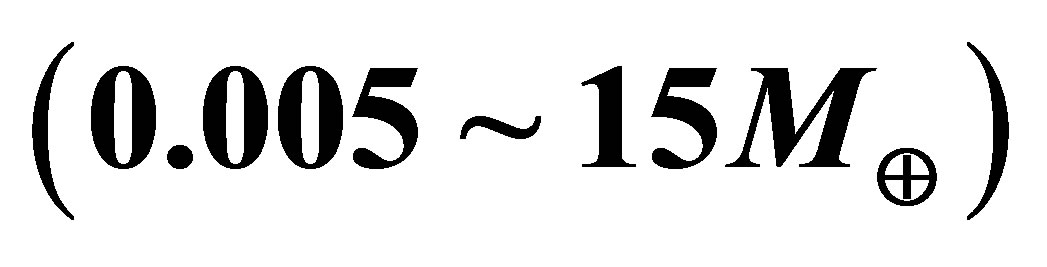 . It is currently uncertain whether hcp iron can coexist with fcc iron in the chequered region. The highest temperature at which hcp iron can exist is ~19,000 K, corresponding to planets of a mass around
. It is currently uncertain whether hcp iron can coexist with fcc iron in the chequered region. The highest temperature at which hcp iron can exist is ~19,000 K, corresponding to planets of a mass around .
.
ties for IPP might exist in the future universe, other than in the case of iron’s 4s electrons, there is a need to carefully consider what neutrino annihilation involves.
IPP commences when an electron antineutrino encounters an electron, transforming these particles into a virtual W boson. If the wavefunction of this W boson overlaps the wavefunction of an electron neutrino, the annihilation process can proceed, resulting in the creation of a virtual electron. The electron is virtual since both energy and momentum cannot be conserved in the reaction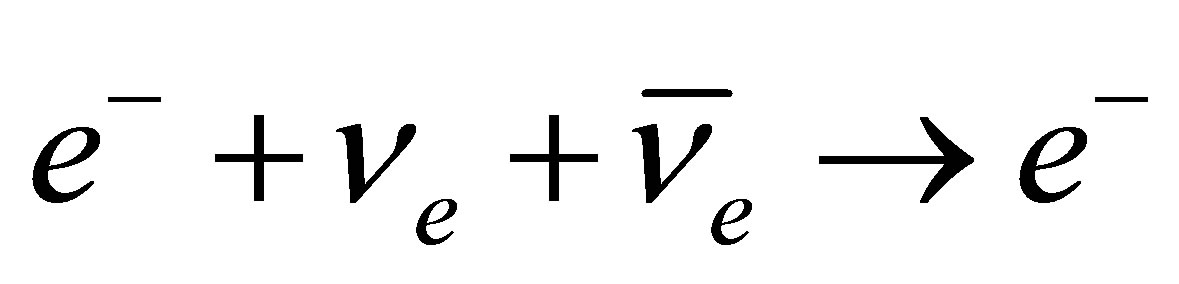 . This is apparent if one considers the interaction from the reference frame in which the total momentum of the incoming neutrinos is zero. A contradiction arises since the solitary final electron must have more energy than the initial electron, yet their momenta should be equal. Thus, IPP is a cascade process first involving a weak interaction followed almost immediately by an electromagnetic interaction in which a photon is created to satisfy the demands of energy-momentum conservation. Due to the time-energy uncertainty principle,
. This is apparent if one considers the interaction from the reference frame in which the total momentum of the incoming neutrinos is zero. A contradiction arises since the solitary final electron must have more energy than the initial electron, yet their momenta should be equal. Thus, IPP is a cascade process first involving a weak interaction followed almost immediately by an electromagnetic interaction in which a photon is created to satisfy the demands of energy-momentum conservation. Due to the time-energy uncertainty principle, 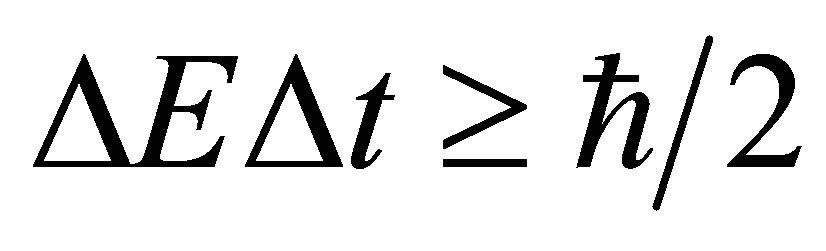 , the photon must be emitted within several femtoseconds of the weak interaction. The prompt emission of a photon would occur quite naturally when a bound electron is excited to a different orbital. Note that the intermediate virtual electron does not occupy any orbital as such, it simply seeks a means of shedding a photon in order to settle into the orbital of the final electron. Should it fail to do so, its own existence would come to an abrupt end and the original neutrino, antineutrino and electron would be restored, as though this possibility had not been explored.
, the photon must be emitted within several femtoseconds of the weak interaction. The prompt emission of a photon would occur quite naturally when a bound electron is excited to a different orbital. Note that the intermediate virtual electron does not occupy any orbital as such, it simply seeks a means of shedding a photon in order to settle into the orbital of the final electron. Should it fail to do so, its own existence would come to an abrupt end and the original neutrino, antineutrino and electron would be restored, as though this possibility had not been explored.
Most of the baryonic matter of the universe currently exists in the form of a rarefied plasma, only a small fraction of which is accounted for by stars. However, the future universe will be much cooler, allowing charged particles to readily combine into atoms via electrostatic attraction. Indeed, the Milky Way has already reprocessed most of the interstellar medium in this way. Thus, in time, there will be very few electrons drifting through space capable of mediating IPP. In the meantime, we might occasionally train the eyes of our infra-red telescopes on regions of space where hot plasma exists, such as the intracluster medium of local galaxy clusters. There may be a discernible hump in the infrared spectrum in the vicinity of ten microns due to an overdensity of relic neutrinos there.
Objects supported by electron degeneracy pressure are extremely ill-suited to receiving energy via IPP. In very cold degenerate matter, states below the Fermi energy are completely occupied. Thus, the only electrons potentially receptive to neutrino annihilation would be those within 5% of the IPP energy. Within a black dwarf the Fermi energy of the electrons will be:
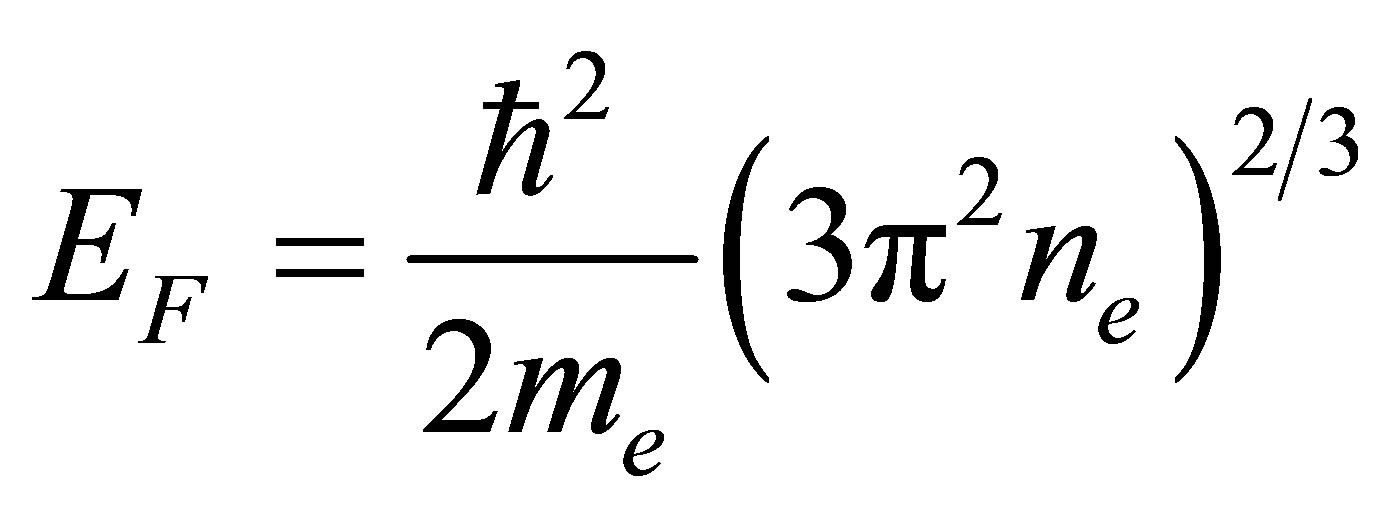 (10)
(10)
This is typically ~200 keV, more than a million times the IPP energy. Hence, the strong degeneracy within black dwarves is highly effective at obstructing neutrino heating. However, for those rare electrons capable of being excited above the Fermi energy, there may be further obstructions. Firstly, these electrons may not be able to emit photons as swiftly as electrons bound to atoms undergoing orbital transitions, and if energy-momentum cannot be immediately assured then it may prohibit IPP. Secondly, if one regards these particles as essentially free electrons due to their lack of interaction with other particles then, in their rest frame, the subsequent emission of a photon would cause the electron’s energy to increase through recoil, apparently violating energy conservation once more. A better understanding of the exotic physics of neutrinos beyond the standard model might be required here.
At present, the internal temperatures of white dwarves are several thousand times higher than their surface temperatures. Their compact size further inhibits radiative heat losses. Surrounded by thin surface layers of nondegenerate matter, the lightest elements hydrogen and helium, their interiors are well-insulated. Above a temperature of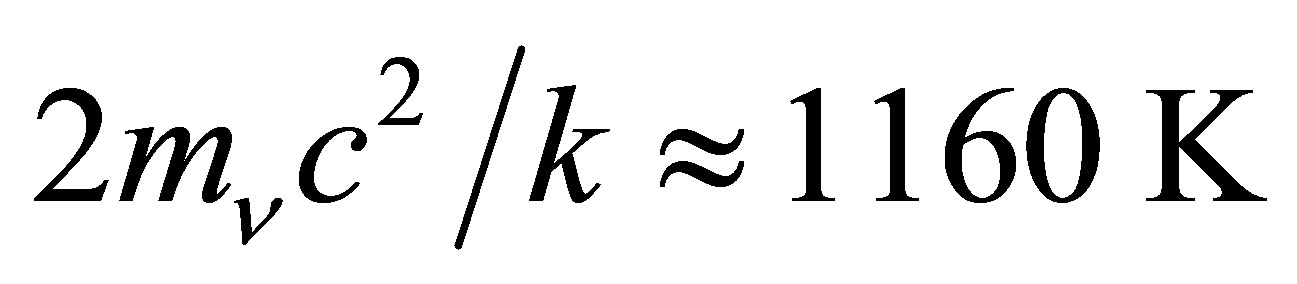 , equivalent to the IPP energy, their cores can spontaneously emit neutrinos, tending to resist further heating. It is therefore likely that the core temperatures of black dwarves passing through a dense neutrino halo would be very modest compared to the ~107 K internal temperatures of white dwarves.
, equivalent to the IPP energy, their cores can spontaneously emit neutrinos, tending to resist further heating. It is therefore likely that the core temperatures of black dwarves passing through a dense neutrino halo would be very modest compared to the ~107 K internal temperatures of white dwarves.
The gas giants Jupiter and Saturn are currently supported in large part by degeneracy pressure since metallic hydrogen forms through pressure ionisation above  Mbar [59]. As gas giants cool, their interiors become increasingly degenerate but their surface layers, which also consist of the lightest elements hydrogen and helium, remain non-degenerate. Neither hydrogen nor helium have excited states within 10 eV of their ground state. The dissociation energy for molecular hydrogen is 4.5 eV, which also lies far above the IPP energy. Therefore, the non-degenerate surface layers of gas giants present few opportunities for IPP.
Mbar [59]. As gas giants cool, their interiors become increasingly degenerate but their surface layers, which also consist of the lightest elements hydrogen and helium, remain non-degenerate. Neither hydrogen nor helium have excited states within 10 eV of their ground state. The dissociation energy for molecular hydrogen is 4.5 eV, which also lies far above the IPP energy. Therefore, the non-degenerate surface layers of gas giants present few opportunities for IPP.
Conduction electrons in a metal lattice are largely degenerate but their Fermi energy in iron is around 11 eV, far smaller than that of black dwarves. Very few would be receptive to IPP; only those with an energy within 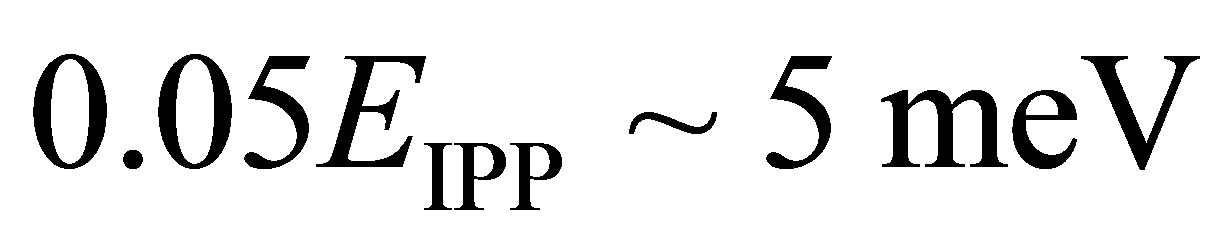 of the top of the conduction band need be considered, amounting to less than approximately one in every 2000 conduction electrons. As in the case of the black dwarf, even these electrons may face further obstructions such as being too slow to emit a photon swiftly enough to persuade the weak interaction to proceed.
of the top of the conduction band need be considered, amounting to less than approximately one in every 2000 conduction electrons. As in the case of the black dwarf, even these electrons may face further obstructions such as being too slow to emit a photon swiftly enough to persuade the weak interaction to proceed.
Could baryonic particles mediate IPP? All but the most massive stars end their lives as black dwarves or neutron stars. Within neutron stars, electrons and protons combine to form neutrons whose Fermi energy of ~30 MeV is enormous. The smallest energy transitions of atomic nuclei are tens of keV, also far beyond the IPP energy. Lone baryons do not present significant opportunities for neutrino decay either. Free neutrons have a short half-life of around ten minutes, undergoing beta decay to protons, electrons and antineutrinos. Lone protons are stable, attracting electrons to form hydrogen. However, they cannot be transformed by halo neutrinos into neutrons through inverse beta decay since the rest mass deficit 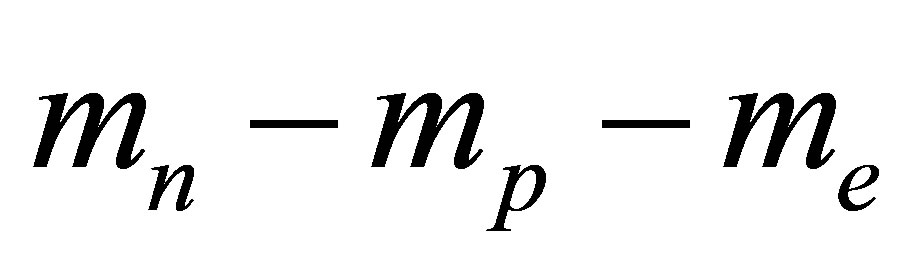 is almost 8 million times the IPP energy
is almost 8 million times the IPP energy . Inverse beta decay involving stable isotopes
. Inverse beta decay involving stable isotopes 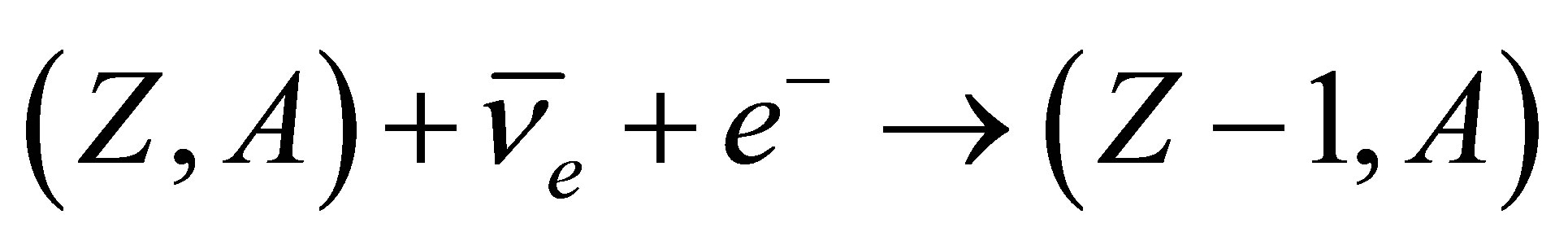 and capture of orbiting electrons also requires strongly relativistic neutrinos. One can therefore disregard the sapping of neutrino haloes by neutron stars, atomic nuclei and isolated baryons.
and capture of orbiting electrons also requires strongly relativistic neutrinos. One can therefore disregard the sapping of neutrino haloes by neutron stars, atomic nuclei and isolated baryons.
Intense pressures are required in order to substantially increase the density of solids and liquids and it is only then that the energy levels of electrons bound to atoms are altered significantly. The core pressure of a planet scales approximately as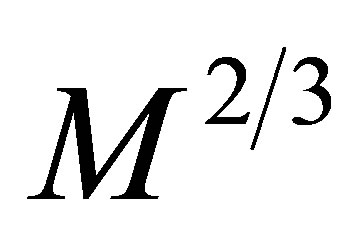 . Hence, the pressure at the core of the Earth is ~360 times that within Pluto, a body of insufficient mass to contain hcp iron at its core [32]. Coulomb forces cannot support the weight of spent stars but they are adequate to resist the gravitational collapse of oceanic planets, even after an arbitrarilty lengthy cooling period. Pressures within oceanic planets at moderate temperatures are insufficient to appreciably ionise heavier elements, but compression and pressure-shifting will significantly shift the electron energy and transition levels. The inverse Stark and inverse Zeeman effects might also exert some influence but pressure is the primary mechanism by which electronic energy bands would broaden [60] because the mean separation between atoms reduces under compression, increasing the degree of overlap of the wave functions of the outermost electrons of adjacent atoms. For illustration purposes, this effect was simulated in the blue curve of Figure 3.
. Hence, the pressure at the core of the Earth is ~360 times that within Pluto, a body of insufficient mass to contain hcp iron at its core [32]. Coulomb forces cannot support the weight of spent stars but they are adequate to resist the gravitational collapse of oceanic planets, even after an arbitrarilty lengthy cooling period. Pressures within oceanic planets at moderate temperatures are insufficient to appreciably ionise heavier elements, but compression and pressure-shifting will significantly shift the electron energy and transition levels. The inverse Stark and inverse Zeeman effects might also exert some influence but pressure is the primary mechanism by which electronic energy bands would broaden [60] because the mean separation between atoms reduces under compression, increasing the degree of overlap of the wave functions of the outermost electrons of adjacent atoms. For illustration purposes, this effect was simulated in the blue curve of Figure 3.
In summary, the low energy transitions involving the 4s electrons of hcp iron appear to be particularly receptive to IPP in environments encountered within planets. It is interesting, therefore, to know whether neutrino annihilation might be capable of delivering sufficient energy to iron-cored oceanic planets that aquatic life could be sustained over the long-term within subglacial oceans. Before this question can be answered, it is necessary to determine theoretical limits to the ambient neutrino concentration within degenerate neutrino haloes.
4. Neutrino Haloes
4.1. Gravitational Clustering
Pauli’s exclusion principle forbids fermions from occupying identical quantum states, giving rise to an internal degeneracy pressure within a neutrino halo even at arbitrarily low temperatures. Neutrinos are far less massive than other elementary fermions which range from  for the electron to
for the electron to  for the top quark. This allows low energy neutrinos to form large, stable structures whose self-gravity is counteracted by degeneracy. The radius
for the top quark. This allows low energy neutrinos to form large, stable structures whose self-gravity is counteracted by degeneracy. The radius  of a quantum degenerate neutrino halo is related to its total mass
of a quantum degenerate neutrino halo is related to its total mass  and
and  as follows [61]:
as follows [61]:
 (11)
(11)
Since 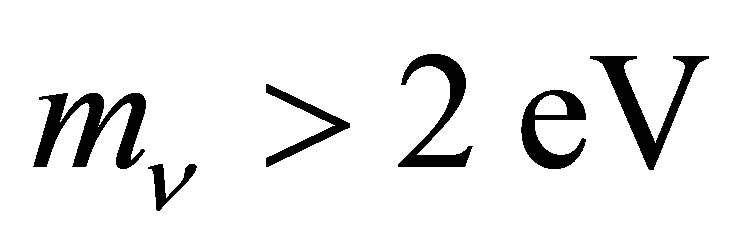 has been experimentally excluded, neutrino haloes possessing the mass of a galaxy cluster,
has been experimentally excluded, neutrino haloes possessing the mass of a galaxy cluster, 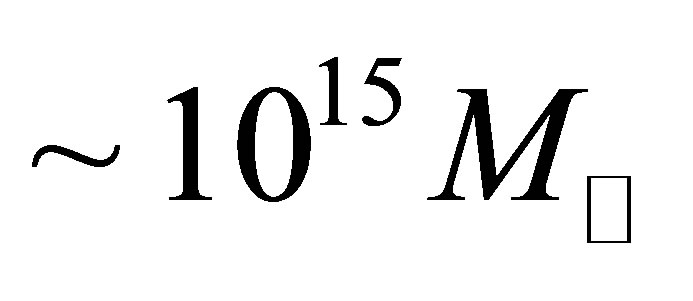 , will have radii upwards of 250 kpc, easily sufficient to completely enshroud the largest galaxies. The same cannot be said of bosonic or cold dark matter particles, which rules them out as an effective means of achieving the galaxy-wide heating of planets over the long-term. The first work to consider neutrinos as a component of the dark matter of galaxy clusters happened to illustrate the possibility using neutrinos of a mass coincidentally matching the current upper experimental bound [21]. Rough estimates of
, will have radii upwards of 250 kpc, easily sufficient to completely enshroud the largest galaxies. The same cannot be said of bosonic or cold dark matter particles, which rules them out as an effective means of achieving the galaxy-wide heating of planets over the long-term. The first work to consider neutrinos as a component of the dark matter of galaxy clusters happened to illustrate the possibility using neutrinos of a mass coincidentally matching the current upper experimental bound [21]. Rough estimates of  and
and 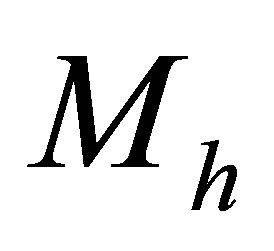 can yield relatively accurate estimates of
can yield relatively accurate estimates of 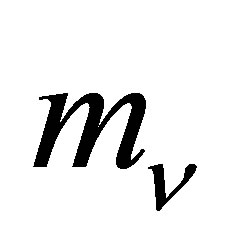 due to the small magnitude of the exponents of
due to the small magnitude of the exponents of  and
and 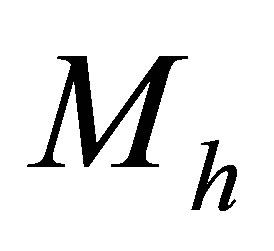 in the following expression:
in the following expression:
 (12)
(12)
Low energy neutrinos have minute scattering crosssections and hence barely impede the orbits of galaxies, stars and planets orbiting within their haloes. As with white dwarves and neutron stars, neutrino haloes have a maximal mass beyond which degeneracy pressure is insufficient to resist gravitational implosion. To estimate this limit, consider a uniform spherical halo containing a total of  neutrinos. The number density of the neutrinos will be approximately:
neutrinos. The number density of the neutrinos will be approximately:
 (13)
(13)
If the neutrinos form an ultra-relativistic degenerate gas, their Fermi energy will be:
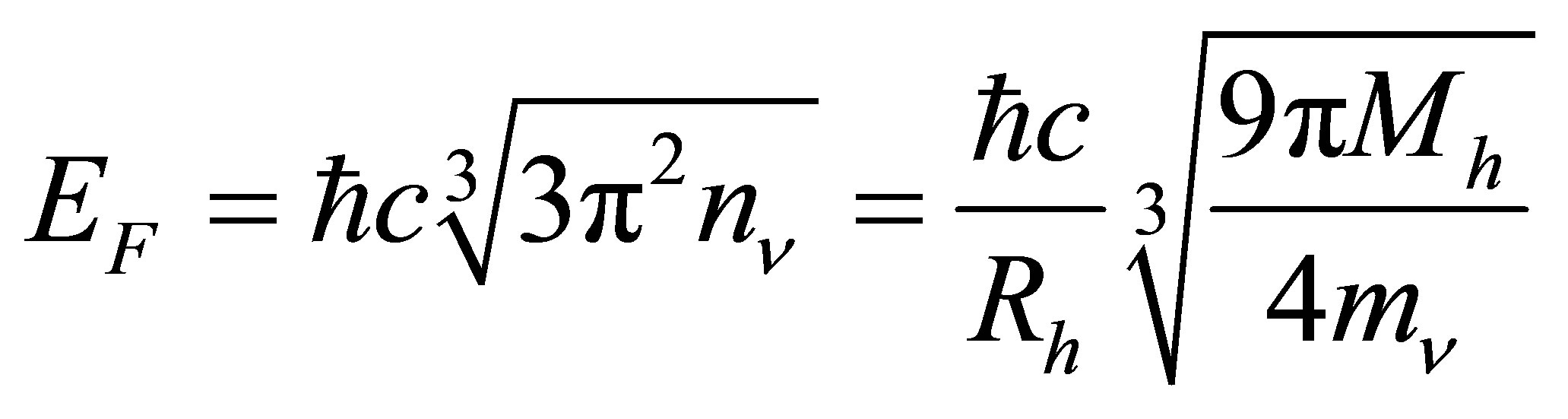 (14)
(14)
The total kinetic energy of the halo of non-relativistic neutrinos is given by:
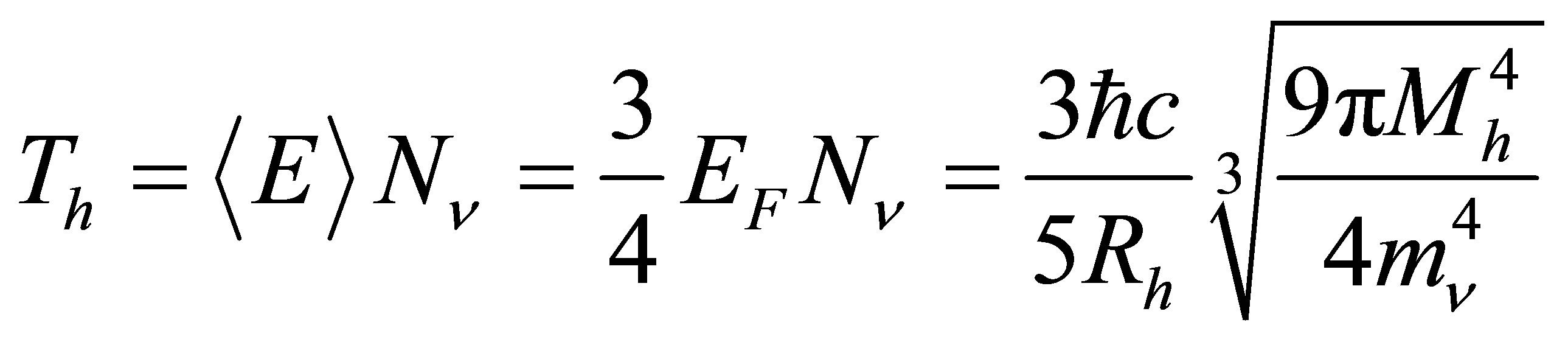 (15)
(15)
Whereas this grows as , the gravitational potential energy of the halo,
, the gravitational potential energy of the halo, 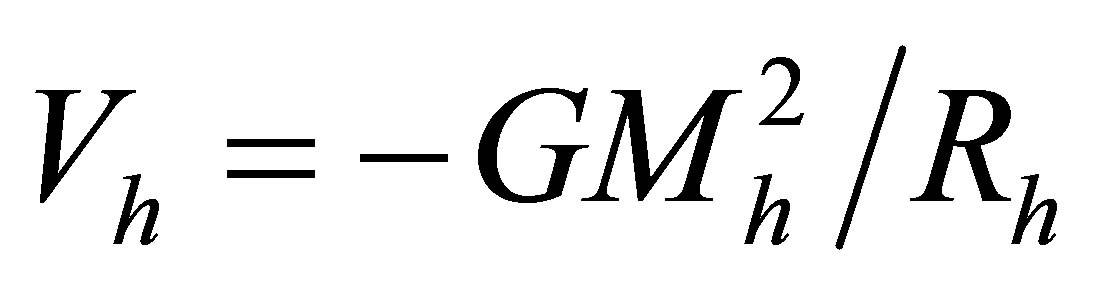 declines quadratically with halo mass. If the total energy of the system
declines quadratically with halo mass. If the total energy of the system  becomes negative, gravitational implosion will occur. Equating
becomes negative, gravitational implosion will occur. Equating 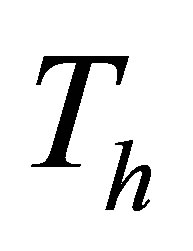 and
and  leads to the following estimate for the limiting mass of a neutrino halo:
leads to the following estimate for the limiting mass of a neutrino halo:
 (16)
(16)
This result agrees with an independent argument that
 which leads to an estimate of the total mass of
which leads to an estimate of the total mass of 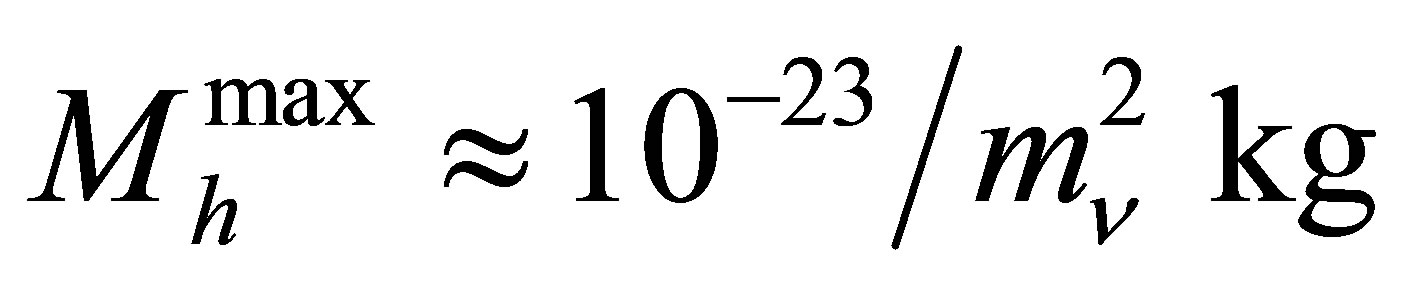 [62]. This expression can be substituted in Equation (11) to leave a similar expression in which
[62]. This expression can be substituted in Equation (11) to leave a similar expression in which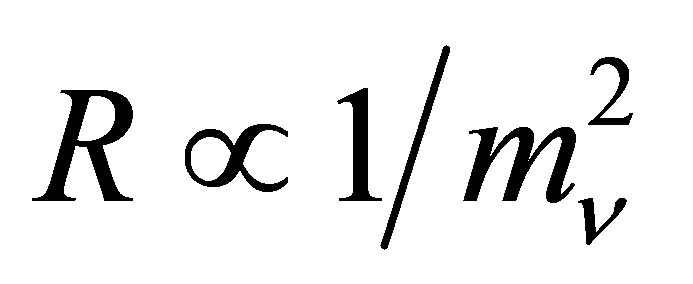 . For
. For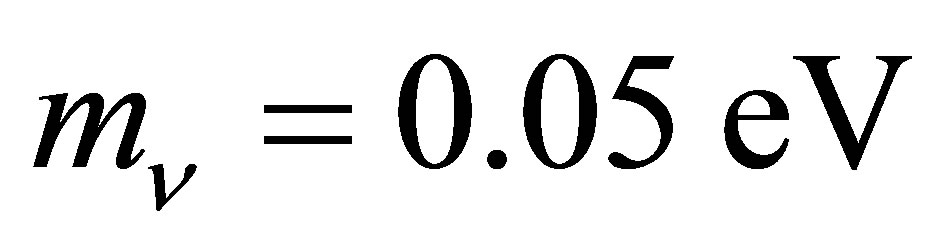 ,
,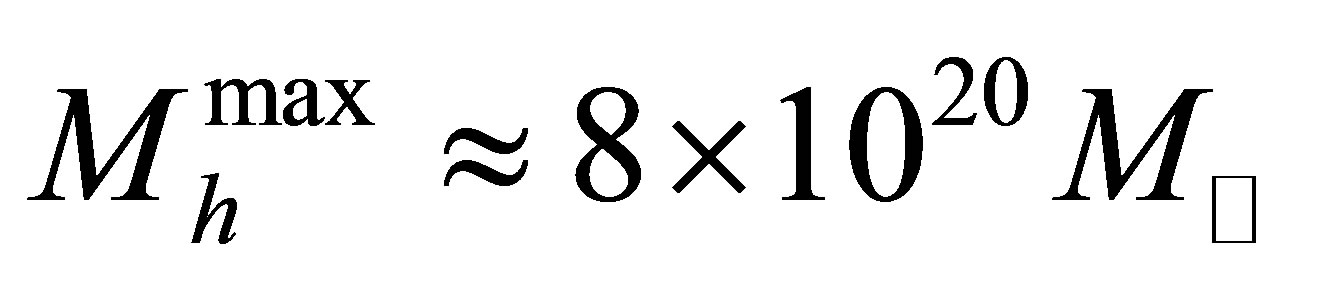 . The radius of a neutrino halo reaches a stable minimum when its mass is maximal. For the same neutrino mass,
. The radius of a neutrino halo reaches a stable minimum when its mass is maximal. For the same neutrino mass, 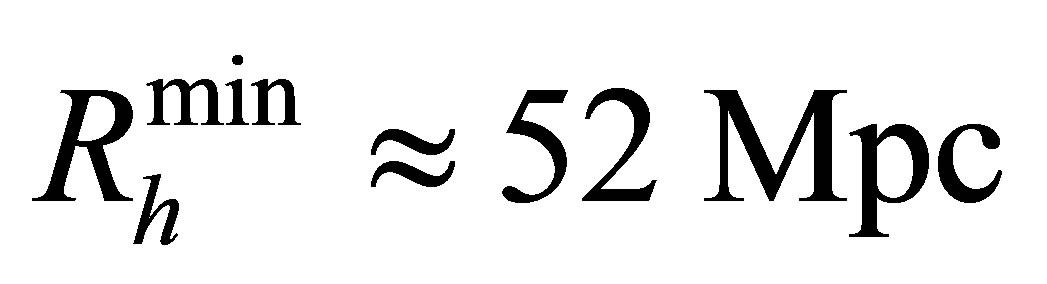 , easily large enough to accommodate the largest galaxies. The dependency of maximal halo mass and minimal halo radius upon neutrino mass are conveniently summarised below
, easily large enough to accommodate the largest galaxies. The dependency of maximal halo mass and minimal halo radius upon neutrino mass are conveniently summarised below
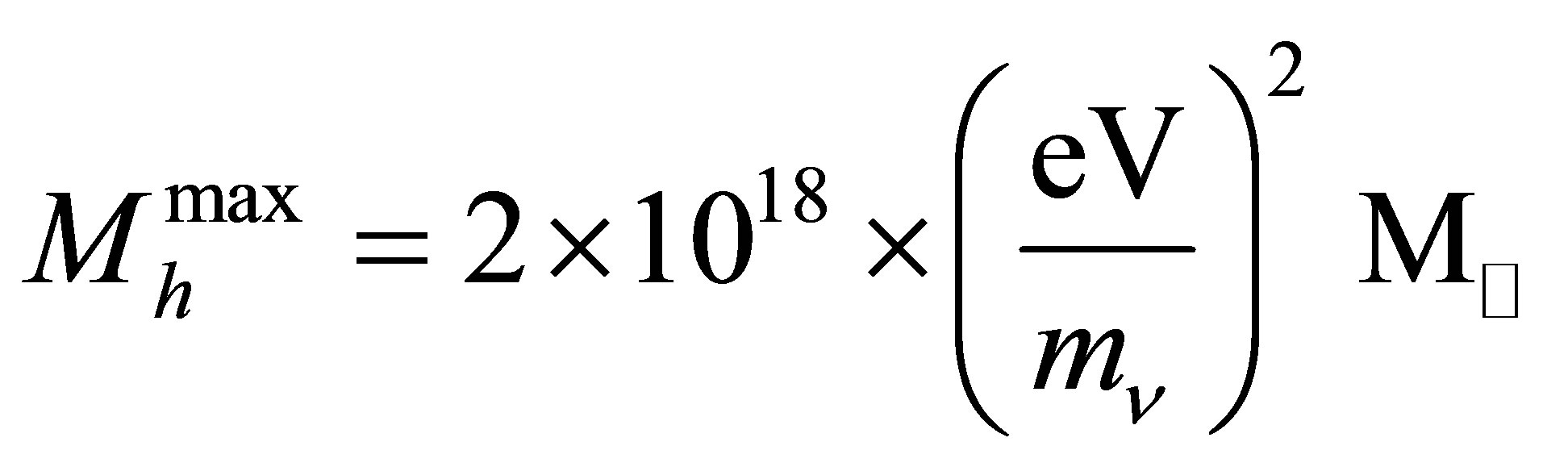 (17)
(17)
 (18)
(18)
4.2. Scaling of Neutrino Haloes
Degenerate haloes consisting of sub-relativistic neutrinos are well-described by a polytrope of index 3/2 [23]. The neutrino haloes of interest here will envelop and greatly outweigh the galaxies they contain. Therefore, the gravity of the galaxies themselves can be neglected and neutrino haloes will obey the scaling laws of polytropes. The scaling relationships described here pertain to a fixed neutrino mass: the influence of altering the neutrino mass will be addressed later.
The central density of a polytrope is proportional to the square of its total mass,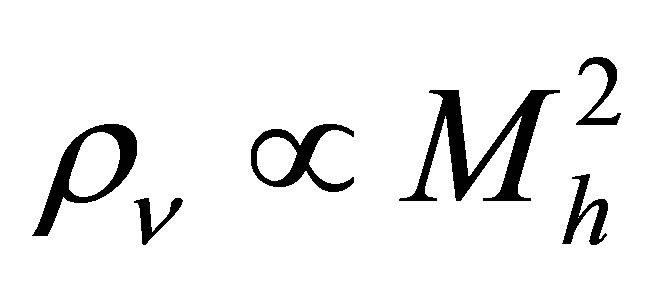 . Density varies little in the central regions of a degenerate halo. The radius
. Density varies little in the central regions of a degenerate halo. The radius  within which quantum behaviour is important decreases with mass as
within which quantum behaviour is important decreases with mass as  and the central pressure varies with the central density according to
and the central pressure varies with the central density according to . There is a transition to
. There is a transition to  when the neutrinos become relativistic, which occurs only if
when the neutrinos become relativistic, which occurs only if . The mean momentum of a neutrino within a strongly degenerate halo is:
. The mean momentum of a neutrino within a strongly degenerate halo is:
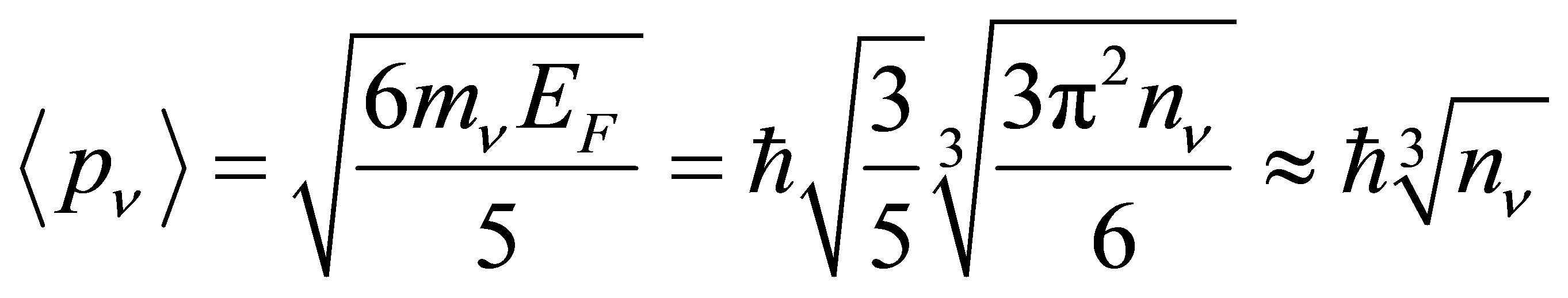 (19)
(19)
The mean velocity of a halo neutrino is therefore:
 (20)
(20)
Modelling of Abell 1689 inferred that the 1.5 eV fermions there had a temperature of 0.045 K [28]. Their thermal velocity would then be 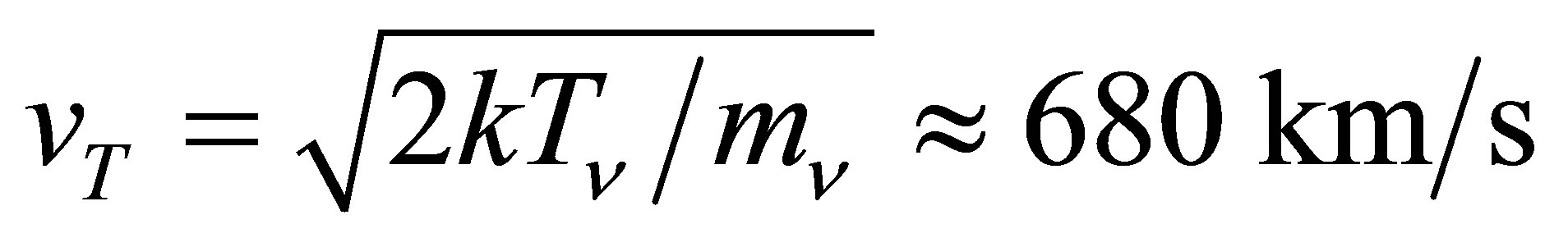 , well below
, well below 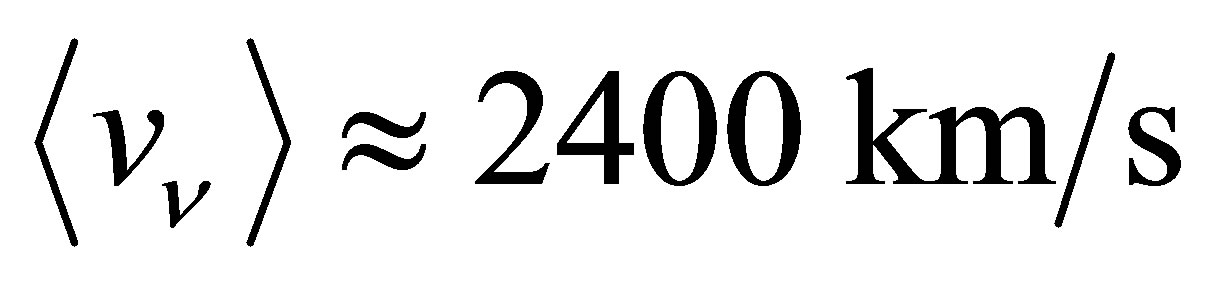
 and consistent with the presence of a degenerate halo. This analysis neglects any residual thermal energy the neutrinos may possess since very massive haloes for which
and consistent with the presence of a degenerate halo. This analysis neglects any residual thermal energy the neutrinos may possess since very massive haloes for which  are of particular interest here. In the non-relativistic case, the neutrino velocity scales with halo density and mass as:
are of particular interest here. In the non-relativistic case, the neutrino velocity scales with halo density and mass as:
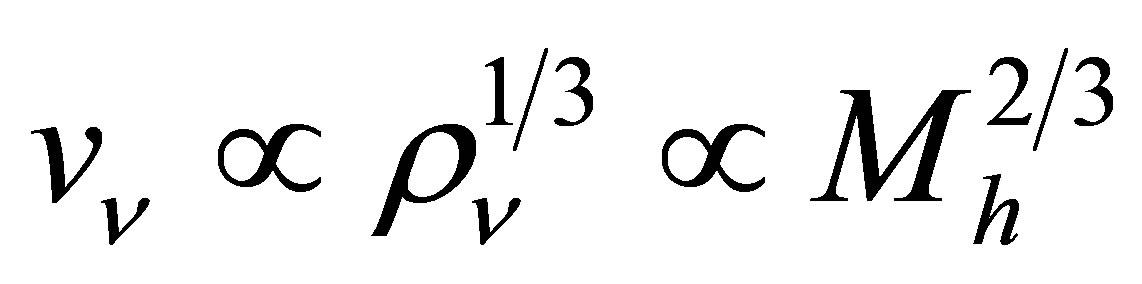 (21)
(21)
The neutrino velocity imposes a weak constraint on planetary heating by limiting the rate at which neutrinos can stream inwardly. In order for an Earth-mass planet to sustain a liquid ocean, the power supplied must exceed , equivalent to half a gram of neutrinos annihilating per second. The neutrino flux
, equivalent to half a gram of neutrinos annihilating per second. The neutrino flux  scales as the product of the neutrino velocity and the neutrino density such that
scales as the product of the neutrino velocity and the neutrino density such that .
.
5. Planetary Heating via IPP
A remarkable feature of the interaction whereby neutrinos annihilate, 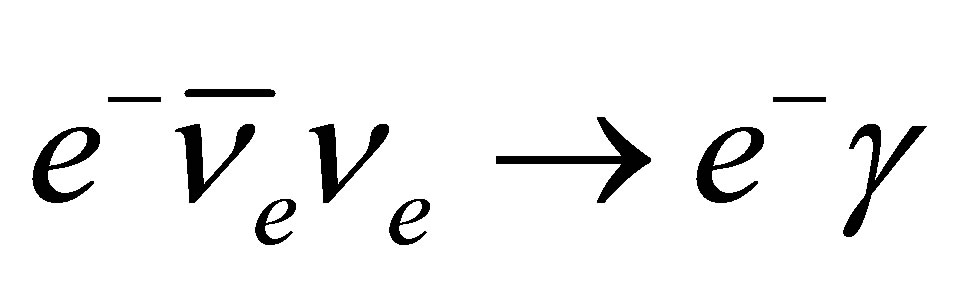 , is that there are fewer particles in the final state than were present in the initial state. This distinguishes it from reactions intensively studied in particle accelerators. In order to demonstrate the viability of planetary heating by neutrinos, the power available from neutrino annihilation within iron-cored planets shall be calculated here using a straightforward approximation method in which the physics remains transparent throughout. This will allow estimates of the minimum halo mass
, is that there are fewer particles in the final state than were present in the initial state. This distinguishes it from reactions intensively studied in particle accelerators. In order to demonstrate the viability of planetary heating by neutrinos, the power available from neutrino annihilation within iron-cored planets shall be calculated here using a straightforward approximation method in which the physics remains transparent throughout. This will allow estimates of the minimum halo mass 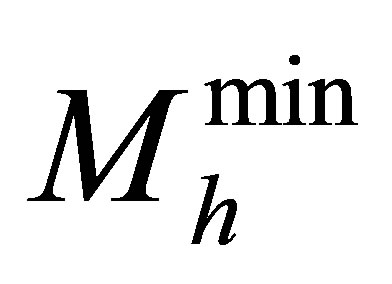 and minimum neutrino density
and minimum neutrino density  required to sustain liquid oceans.
required to sustain liquid oceans.
Since neutrinos possess mass, their helicity is not Lorentz invariant. One therefore expects low energy neutrinos and antineutrinos of both helicities to be equally abundant within neutrino haloes. Although the photoneutrino process and the plasma process play important roles in the physics of stellar interiors, and the importance of energy redistribution by high energy neutrinos has been appreciated within supernovae, the annihilation of non-relativistic neutrinos, as might belong to a dark matter halo, has not been considered before. While neutrinos possess some exotic properties whose physics lies beyond the standard model, it is possible to confirm the feasibility of planetary heating by neutrinos using a semiclassical approach.
The proposal of wave-particle duality [63] led to the development of a relativistic wave equation [64]. A consequence of this equation, 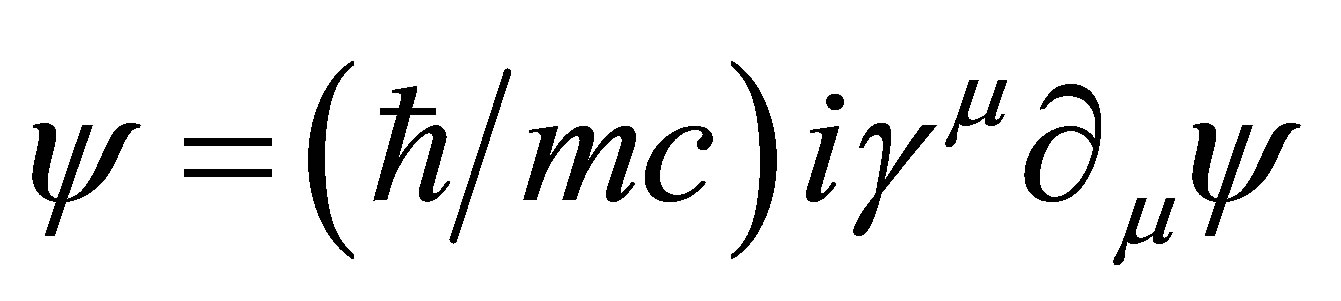 , is that particles cannot be localised on scales smaller than
, is that particles cannot be localised on scales smaller than 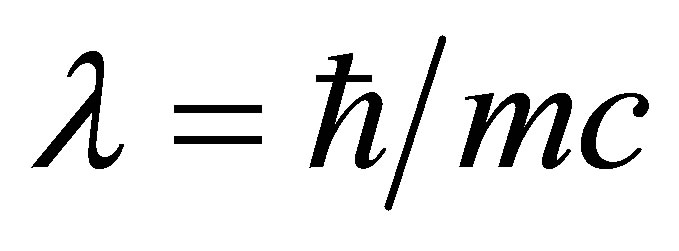 , the reduced Compton wavelength. Below this scale, quantum effects cause classical physics to break down [65]. The reduced Compton wavelength also crops up in other contexts including the Schrödinger and KleinGordon equations, representing a fundamental scale for the size of a particle from a quantum-mechanical perspective. Thus, a particle’s mass is essentially inversely related to its size, and vice versa. Yukawa interactions also have a range set by the reduced Compton wavelength of the gauge bosons. In general, the effective radius of a particle
, the reduced Compton wavelength. Below this scale, quantum effects cause classical physics to break down [65]. The reduced Compton wavelength also crops up in other contexts including the Schrödinger and KleinGordon equations, representing a fundamental scale for the size of a particle from a quantum-mechanical perspective. Thus, a particle’s mass is essentially inversely related to its size, and vice versa. Yukawa interactions also have a range set by the reduced Compton wavelength of the gauge bosons. In general, the effective radius of a particle  which governs its cross section,
which governs its cross section,  , involves scaling of
, involves scaling of 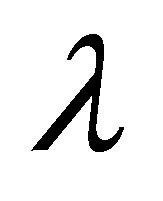 by a coupling constant
by a coupling constant 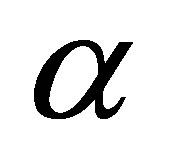 of the interaction concerned according to the relationship
of the interaction concerned according to the relationship . This can be seen in low energy processes such as Thomson scattering,
. This can be seen in low energy processes such as Thomson scattering, 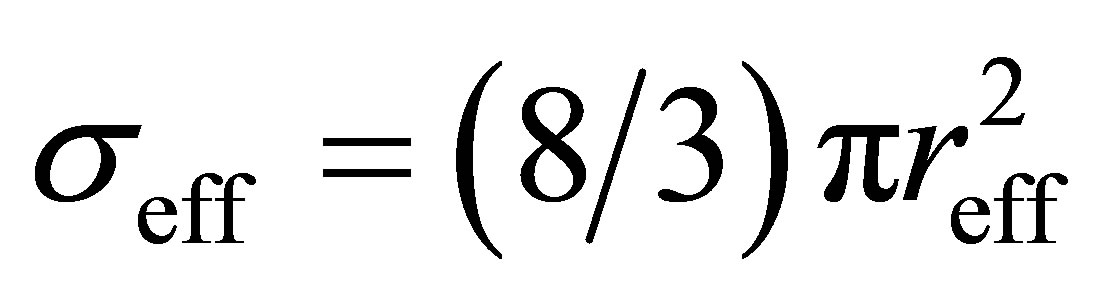 , and the Ramsauer approximation,
, and the Ramsauer approximation, 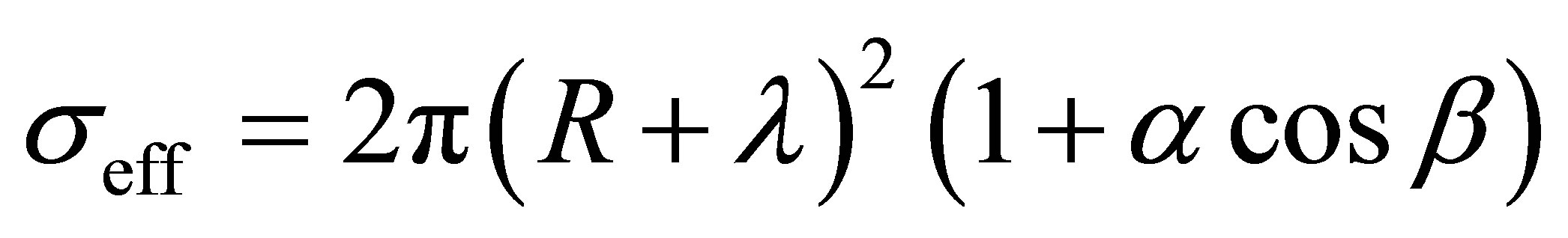 which accurately describes the strong force mediated scattering of low energy neutrons,
which accurately describes the strong force mediated scattering of low energy neutrons,  being the particle radius. In the case of the weak interaction one has
being the particle radius. In the case of the weak interaction one has 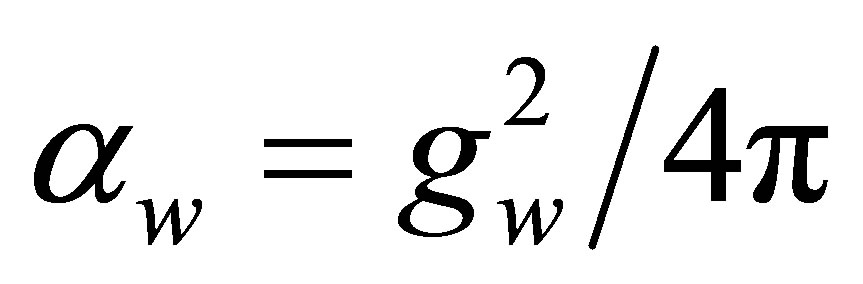 where, for historical reasons,
where, for historical reasons, 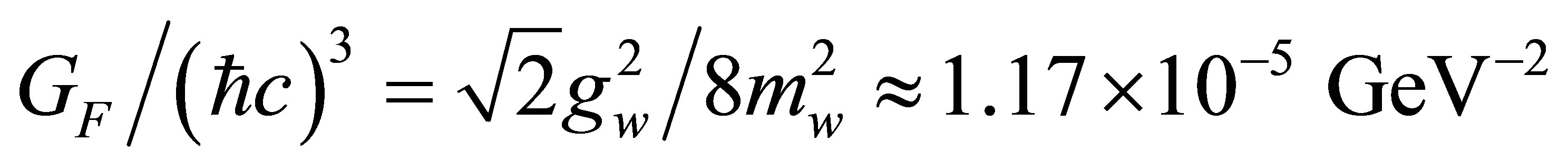 . Hence,
. Hence,  and
and , a factor associated with each weak vertex in a Feynman diagram. This is almost five times larger than the electromagnetic coupling constant
, a factor associated with each weak vertex in a Feynman diagram. This is almost five times larger than the electromagnetic coupling constant , otherwise known as the fine-structure constant.
, otherwise known as the fine-structure constant.
Owing to the large mass of the W boson,  , its reduced Compton wavelength is tiny,
, its reduced Compton wavelength is tiny,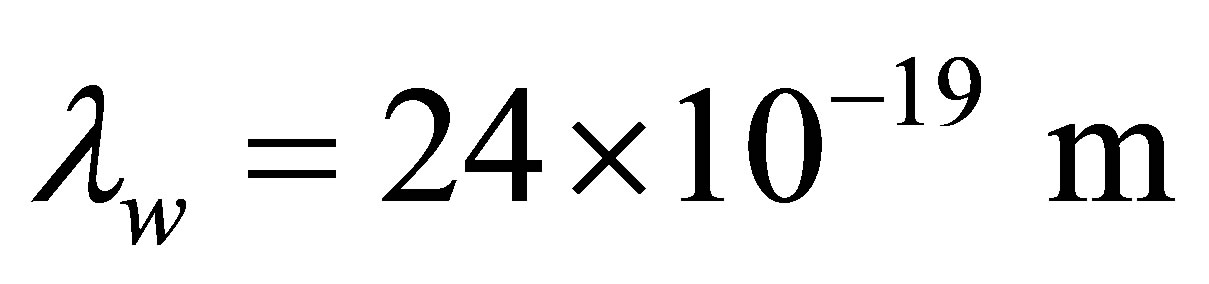 . When an electron antineutrino
. When an electron antineutrino  and an electron
and an electron 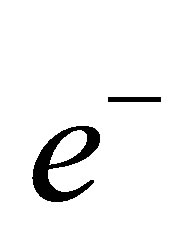 are within a range comparable to
are within a range comparable to , a virtual W boson can couple to them both. Due to the uncertainty principle, virtual W bosons have a lifespan of
, a virtual W boson can couple to them both. Due to the uncertainty principle, virtual W bosons have a lifespan of . In comparison, the mean lifespan of a real W boson is some
. In comparison, the mean lifespan of a real W boson is some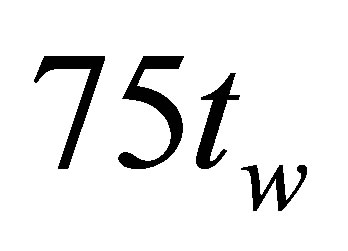 . On a timescale of
. On a timescale of 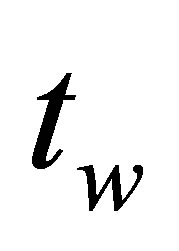 a W boson cannot travel farther than a millionth of an electron’s Compton wavelength and thus, in this analysis, virtual W bosons are regarded as essentially stationary.
a W boson cannot travel farther than a millionth of an electron’s Compton wavelength and thus, in this analysis, virtual W bosons are regarded as essentially stationary.
Inelastic scattering of neutrinos with electrons involves a point-like interaction whose cross section is given by 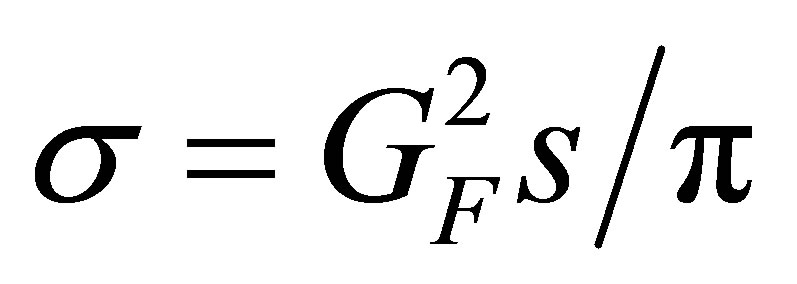 [66]. Here, s is a Mandelstam variable which is the square of the sum of the 4-momenta of the incoming neutrino and incoming electron. When the neutrino energy
[66]. Here, s is a Mandelstam variable which is the square of the sum of the 4-momenta of the incoming neutrino and incoming electron. When the neutrino energy  is much larger than the rest mass of the electron, but small compared to the mass of the W boson,
is much larger than the rest mass of the electron, but small compared to the mass of the W boson,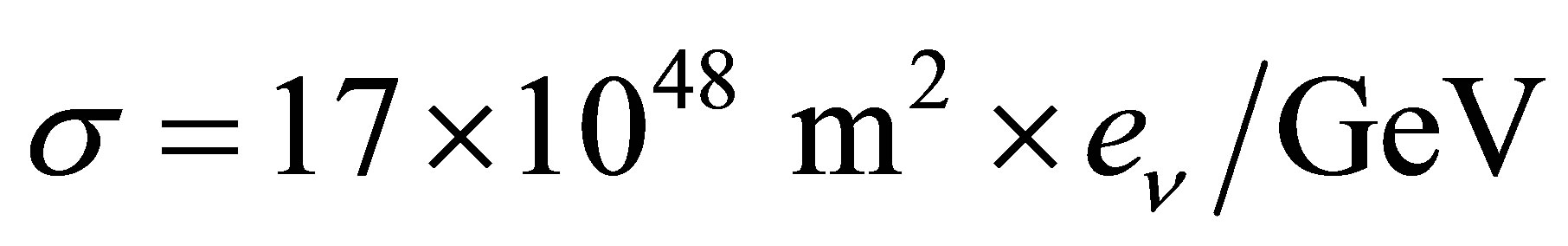 . However, in the case of nonrelativistic neutrinos, it holds that
. However, in the case of nonrelativistic neutrinos, it holds that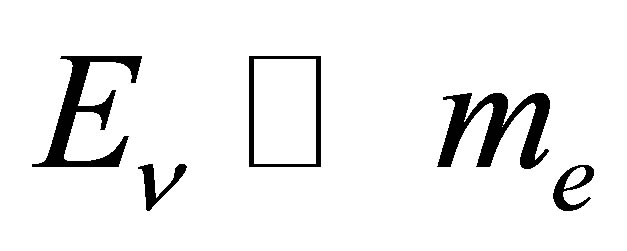 , and the result has to be multiplied by
, and the result has to be multiplied by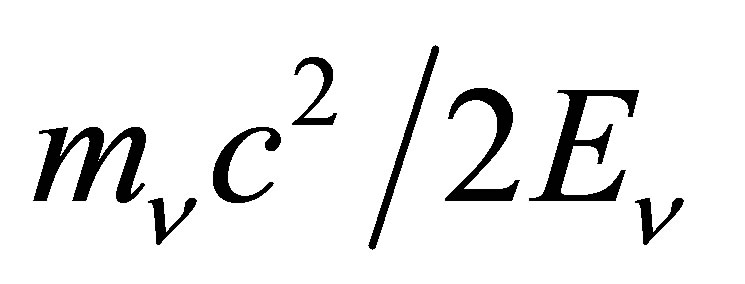 . There is then no dependency on the neutrino energy with the cross section coming to
. There is then no dependency on the neutrino energy with the cross section coming to  = 44 × 10−50 m2. By writing
= 44 × 10−50 m2. By writing , these low energy scattering events typically occur when the initial particles approach one another to distances smaller than
, these low energy scattering events typically occur when the initial particles approach one another to distances smaller than . Notice that this is several million times smaller than the reduced Compton wavelength of the W boson,
. Notice that this is several million times smaller than the reduced Compton wavelength of the W boson, 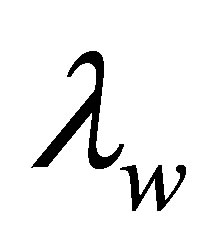 = 24 × 10−19 m.
= 24 × 10−19 m.
The mutual annihilation of neutrinos is not the same as scattering between a neutrino and a charged lepton. Firstly, annihilation opportunities are swiftly taken in nature: it allows entropy to increase. Secondly, whereas a W boson serves as a propagator of force during scattering, in the case of IPP it functions as a mediator for annihilation and so its Compton wavelength becomes relevant. This can be readily appreciated if one considers a stationary electron antineutrino 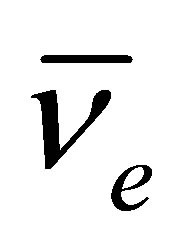 separated by a small distance from a stationary electron
separated by a small distance from a stationary electron 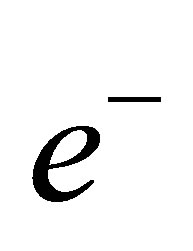 receptive to IPP. A virtual W boson spontaneously created by the vacuum can only couple to them both if its wavefunction simultaneously overlaps the location of the electron and the antineutrino. Roughly speaking, this is likely to occur if the particle separation is comparable to or less than
receptive to IPP. A virtual W boson spontaneously created by the vacuum can only couple to them both if its wavefunction simultaneously overlaps the location of the electron and the antineutrino. Roughly speaking, this is likely to occur if the particle separation is comparable to or less than . However, a relatively remote electron neutrino can sense an opportunity for annihilation if its matter wave overlaps with the virtual W boson. This follows from experiments in which particles are diffracted by the walls of a narrow slit whose width is smaller than their de Broglie wavelength. Since neutrinos have a much smaller mass than W bosons, their de Broglie wavelengths will be at least
. However, a relatively remote electron neutrino can sense an opportunity for annihilation if its matter wave overlaps with the virtual W boson. This follows from experiments in which particles are diffracted by the walls of a narrow slit whose width is smaller than their de Broglie wavelength. Since neutrinos have a much smaller mass than W bosons, their de Broglie wavelengths will be at least  times larger than the Compton wavelength of the W boson. Hence, the electron neutrino could initially be a good distance from both the W boson and the antineutrino when IPP occurs. Due to the antineutrino and electron being stationary, annihilation is sure to proceed given sufficient time. If these particles are all permitted to move, the range over which neutrino annihilation can occur is unchanged in the low velocity limit. This is the regime pertinent to planetary heating.
times larger than the Compton wavelength of the W boson. Hence, the electron neutrino could initially be a good distance from both the W boson and the antineutrino when IPP occurs. Due to the antineutrino and electron being stationary, annihilation is sure to proceed given sufficient time. If these particles are all permitted to move, the range over which neutrino annihilation can occur is unchanged in the low velocity limit. This is the regime pertinent to planetary heating.
The weak interaction only couples to left-handed fermions and right-handed antifermions. Thus, the initial electron is receptive to IPP if it has left-handed helicity and the final electron is not quantum-mechanically prohibited from accepting its share of the annihilation energy or incapable of emitting a photon necessary for energy-momentum conservation. In the following analysis it shall be assumed that half the 4s electrons of hcp iron within planets are receptive to IPP due to a favourable combination of pressure and temperature near the hcp/fcc transition. Before proceeding to calculate the heating available due to IPP, there are two issues to first address: 1) the availability of an electron neutrino from the halo and 2) the question of the effective range of the virtual W boson over which it can couple to the electron and the antineutrino.
5.1. Neutrino Degeneracy and Availability
Consider a neutrino trapped within a cube of volume  so that it is compelled to take on stationary states. The time-independent Schrödinger equation requires that the neutrino’s wave-function,
so that it is compelled to take on stationary states. The time-independent Schrödinger equation requires that the neutrino’s wave-function, 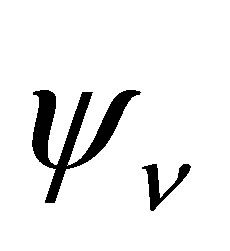 , obeys the relationship
, obeys the relationship
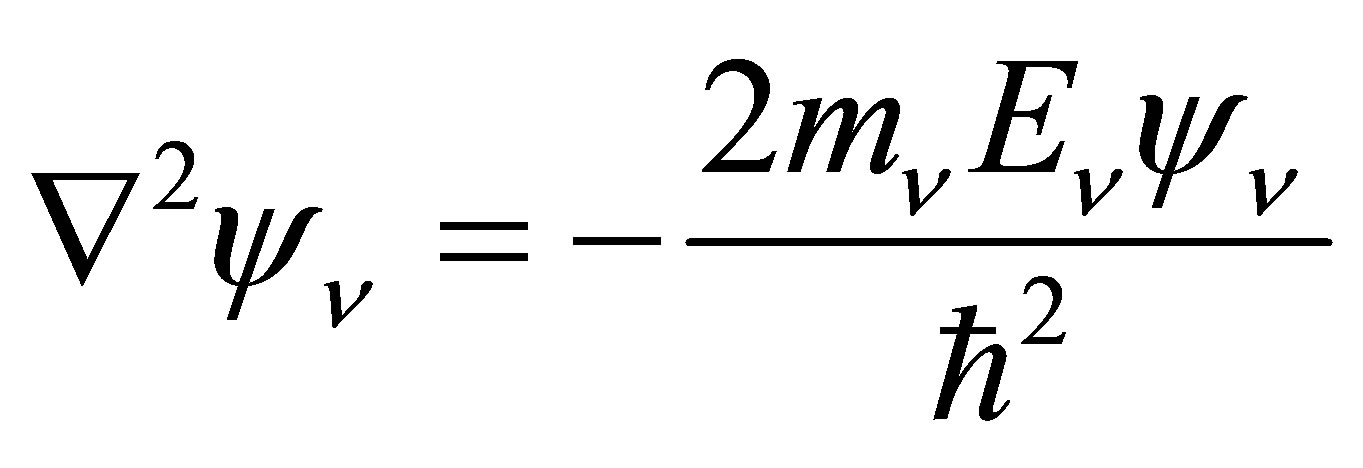 (22)
(22)
The solution is given by
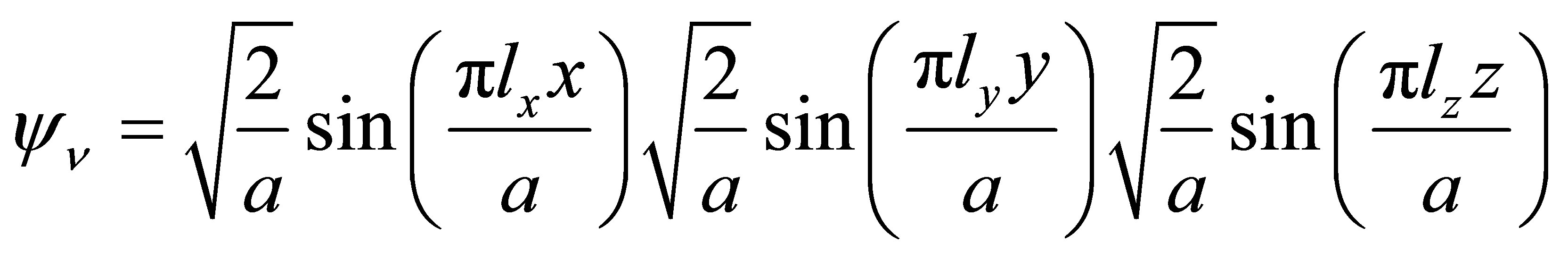 (23)
(23)
where, in order to satisfy boundary conditions, 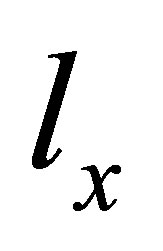 ,
,  and
and  are positive integers, thereby imposing quantisation. The energy of the neutrinos hence comes to
are positive integers, thereby imposing quantisation. The energy of the neutrinos hence comes to
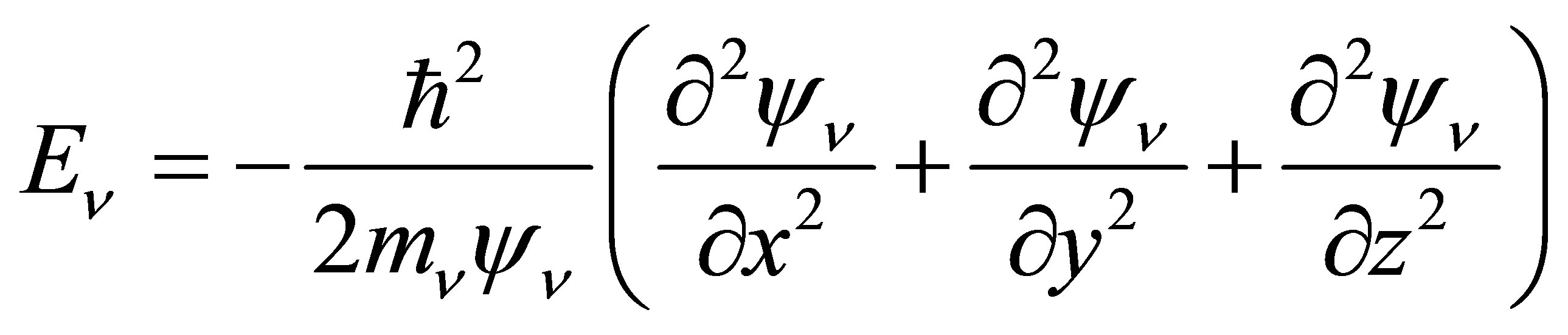 (24)
(24)
 (25)
(25)
 (26)
(26)
Since neutrinos are fermions, only one neutrino of a given helicity can have any given set of ,
, 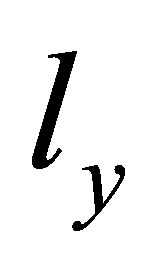 and
and 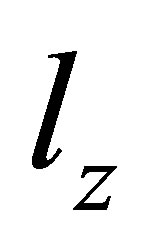 values. A cold, degenerate halo containing
values. A cold, degenerate halo containing  neutrinos of each flavour and helicity is now considered. The neutrinos occupy all the energy states
neutrinos of each flavour and helicity is now considered. The neutrinos occupy all the energy states  up to the Fermi energy but none above, in accordance with the Fermi-Dirac distribution
up to the Fermi energy but none above, in accordance with the Fermi-Dirac distribution 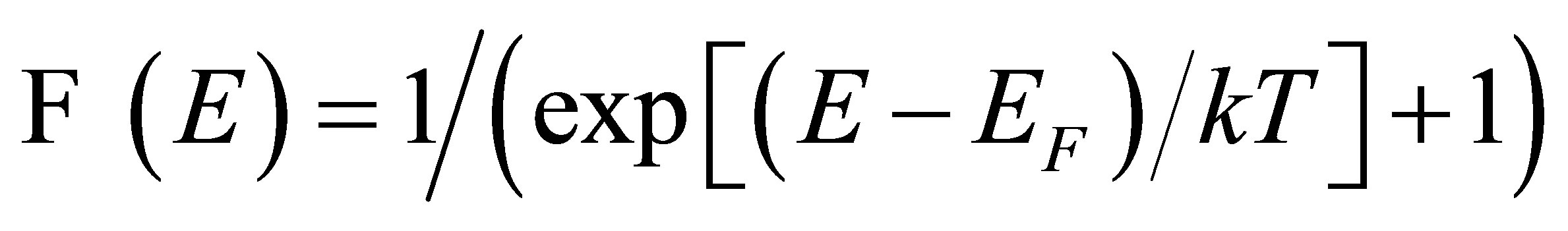 when
when .
.
With the energy of each neutrino being proportional to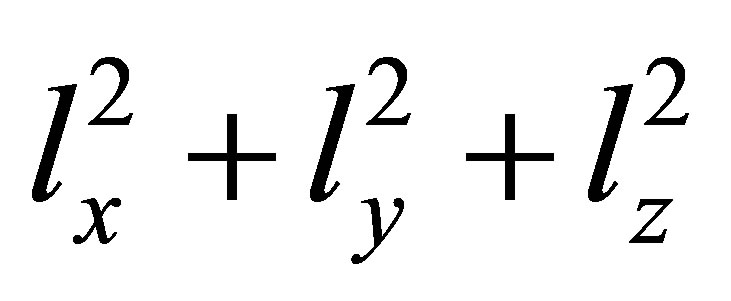 , and each quantum number being positive, the distinct states occupy a spherical octant in
, and each quantum number being positive, the distinct states occupy a spherical octant in  -space whose radius
-space whose radius  is obtained from the Fermi energy
is obtained from the Fermi energy . This octant contains
. This octant contains 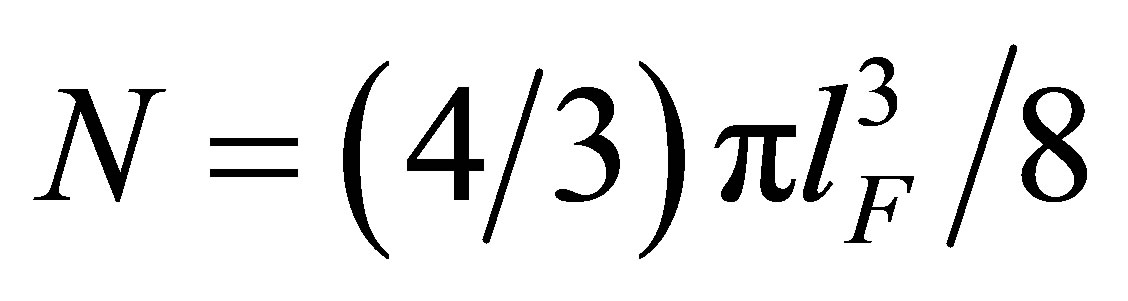 states so that
states so that  and therefore
and therefore
 (27)
(27)
where  is the number of neutrinos of each flavour and helicity per unit volume. Thus, the Fermi energy is a simple function of the neutrino density
is the number of neutrinos of each flavour and helicity per unit volume. Thus, the Fermi energy is a simple function of the neutrino density , taken here to be equal to
, taken here to be equal to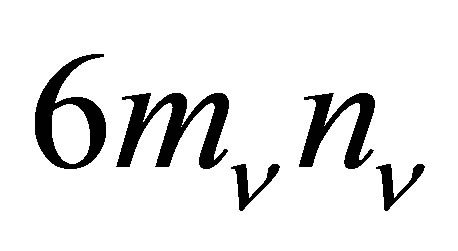 . The mean kinetic energy of the neutrinos,
. The mean kinetic energy of the neutrinos, 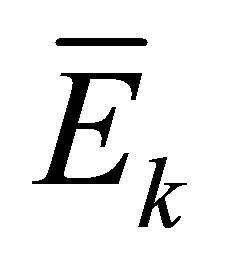 , is obtained by integrating their energies
, is obtained by integrating their energies  over the uniformly distributed quantum states of the octant
over the uniformly distributed quantum states of the octant
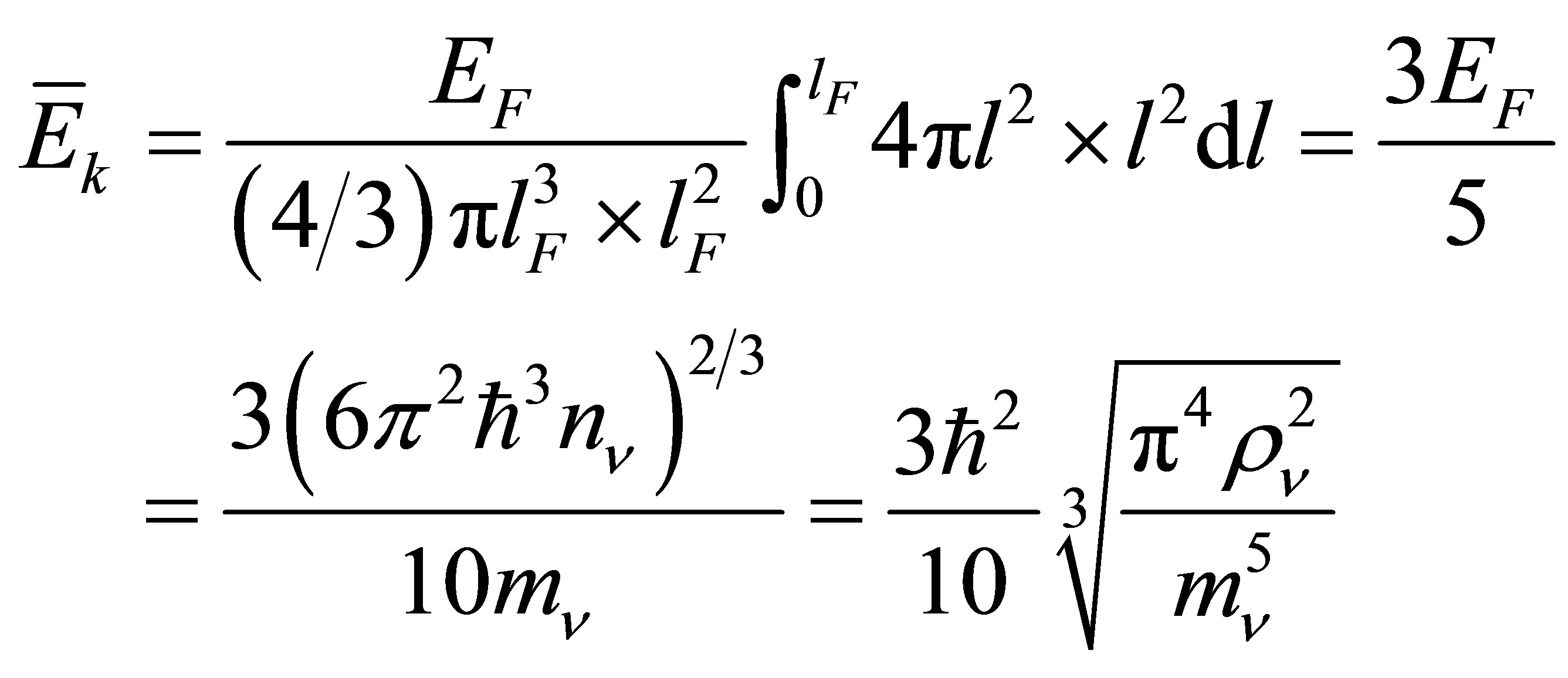 (28)
(28)
The mean volume occupied by a neutrino is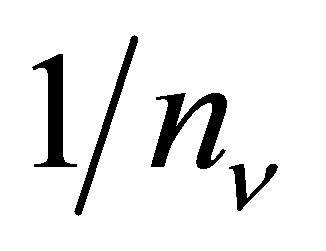 . A sphere of radius
. A sphere of radius  has volume
has volume  if
if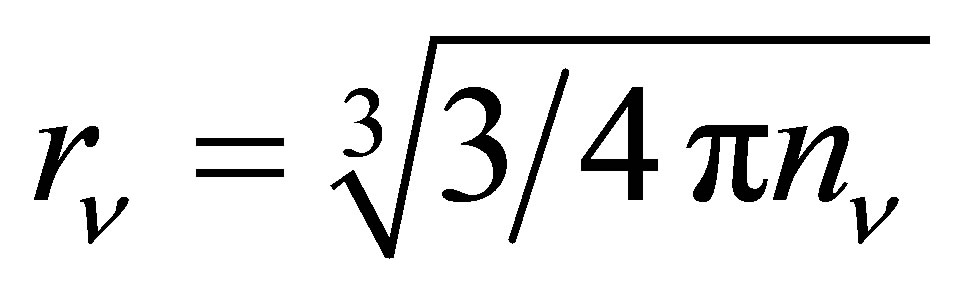 . It can be seen from Equation (27) that
. It can be seen from Equation (27) that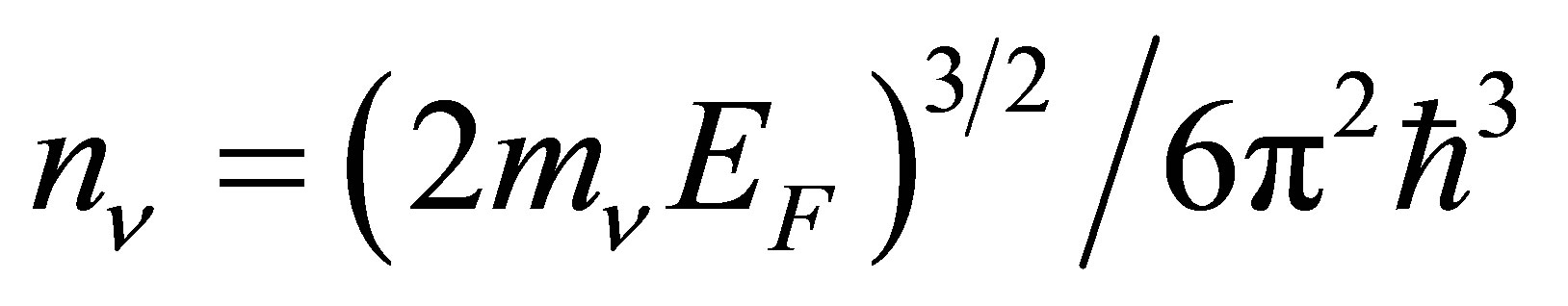 . Therefore, the radius of the mean volume occupied by a neutrino comes to
. Therefore, the radius of the mean volume occupied by a neutrino comes to
 (29)
(29)
Thus, the degeneracy of the halo causes the neutrinos to adjust their momenta in such a way that the mean separation between adjacent neutrinos is a fixed fraction of the mean de Broglie wavelength. This will hold providing relativistic effects can be neglected and the halo remains degenerate.
The intensity of the Airy diffraction pattern produced by a circular aperture of radius  is given by
is given by
 (30)
(30)
where  is a first order Bessel function of the first kind and
is a first order Bessel function of the first kind and 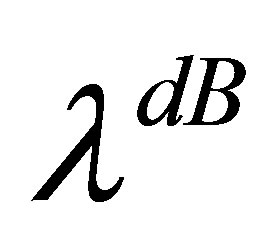 is the de Broglie wavelength of the radiation. If
is the de Broglie wavelength of the radiation. If  then half the emergent radiation is diffracted by an angle exceeding 22˚. Hence, the wave-functions of the neutrinos in a degenerate halo will essentially fully saturate the space there. Due to this collective permeation of space by both neutrinos and antineutrinos, there will always be a high degree of overlap between the wave-function of any antineutrino and its nearest neutrino,
then half the emergent radiation is diffracted by an angle exceeding 22˚. Hence, the wave-functions of the neutrinos in a degenerate halo will essentially fully saturate the space there. Due to this collective permeation of space by both neutrinos and antineutrinos, there will always be a high degree of overlap between the wave-function of any antineutrino and its nearest neutrino, . Though these would normally be oblivious of each other, when a W boson forms due to the collision of an antineutrino with a receptive electron, a communication channel is effectively established between two ostensibly distinct haloes, and a pair of neutrinos may thereby annihilate. This simplifies the calculation of the IPP rate, allowing it to be estimated from the rate at which electron antineutrinos encounter 4s electrons.
. Though these would normally be oblivious of each other, when a W boson forms due to the collision of an antineutrino with a receptive electron, a communication channel is effectively established between two ostensibly distinct haloes, and a pair of neutrinos may thereby annihilate. This simplifies the calculation of the IPP rate, allowing it to be estimated from the rate at which electron antineutrinos encounter 4s electrons.
The analysis here shall also be used to justify the assumption that IPP occurs when the antineutrino and electron approach one another to within a distance of 0.385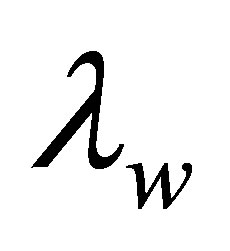 . This result shall be conservatively rounded down to
. This result shall be conservatively rounded down to 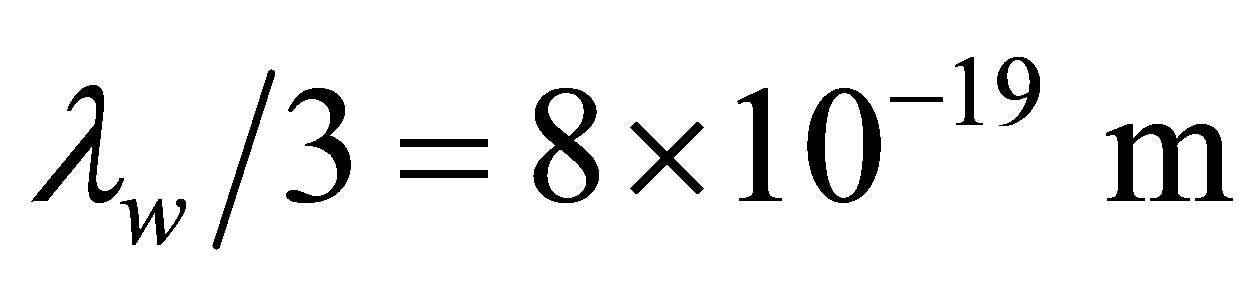 in later calculations. A characteristic timescale for weak interactions is given by
in later calculations. A characteristic timescale for weak interactions is given by  seconds. Particle motions begin to significantly impede IPP when the relative velocity exceeds about
seconds. Particle motions begin to significantly impede IPP when the relative velocity exceeds about . An allowance for this shall be made in forthcoming calculations.
. An allowance for this shall be made in forthcoming calculations.
5.2. Annihilation Rates
Under pressures present within planets of interest the density of iron at the core, 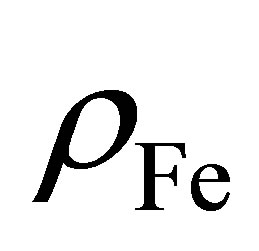 , will usually exceed 104 kg/m3 so the electron number density in iron,
, will usually exceed 104 kg/m3 so the electron number density in iron,  will be at least 28 × 1029 m−3. The 3d subshell will possess four vacancies and six electrons shielded from other atoms by the lone 4s electron. Since electrons can have either left or right handed helicity, only half the 4s electrons of each iron atom are assumed to be capable of accepting the IPP energy. Thus, the density of IPP receptive electrons,
will be at least 28 × 1029 m−3. The 3d subshell will possess four vacancies and six electrons shielded from other atoms by the lone 4s electron. Since electrons can have either left or right handed helicity, only half the 4s electrons of each iron atom are assumed to be capable of accepting the IPP energy. Thus, the density of IPP receptive electrons,  , is conservatively taken to be
, is conservatively taken to be . Similarly, neutrinos of a degenerate halo will lack thermal energy and hence present themselves to IPP interactions with both helicity states, so only half the electron neutrinos are able to experience weak interactions at any given moment in time.
. Similarly, neutrinos of a degenerate halo will lack thermal energy and hence present themselves to IPP interactions with both helicity states, so only half the electron neutrinos are able to experience weak interactions at any given moment in time.
The mean relative velocity,  , between antineutrinos and electrons is required. Mean neutrino velocity
, between antineutrinos and electrons is required. Mean neutrino velocity  and kinetic energy
and kinetic energy 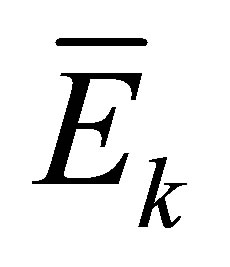 are related by
are related by
 . Inserting the expression for
. Inserting the expression for  obtained earlier in Equation (28) allows the neutrino velocity to be determined from the neutrino density
obtained earlier in Equation (28) allows the neutrino velocity to be determined from the neutrino density
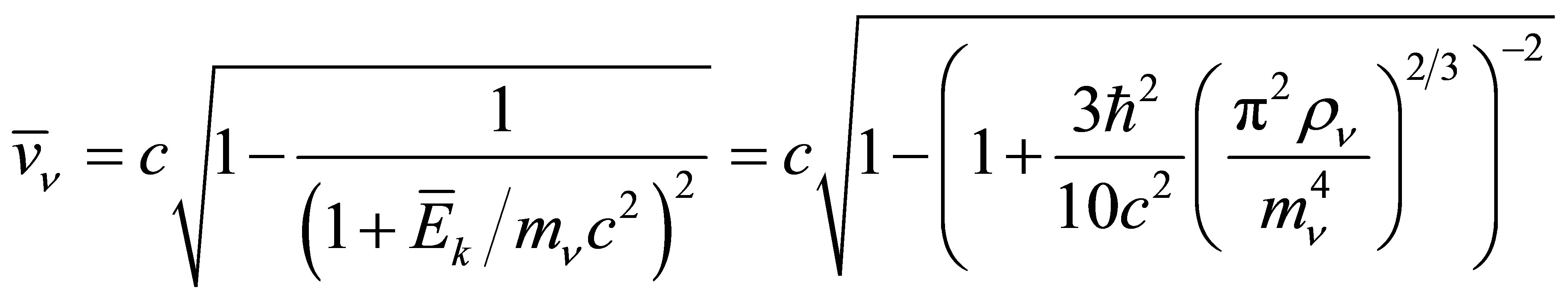 (31)
(31)
If a 4s electron bound to an atom of iron has orbital radius  and mean orbital velocity
and mean orbital velocity  then Newton’s second law and the electrostatic attraction between the electron and the nucleus yields the classical result
then Newton’s second law and the electrostatic attraction between the electron and the nucleus yields the classical result
 (32)
(32)
The angular momentum of the electron,  , will be a multiple of
, will be a multiple of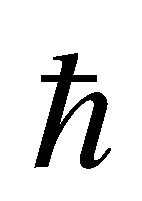 . Since the electron occupies the fourth shell,
. Since the electron occupies the fourth shell, 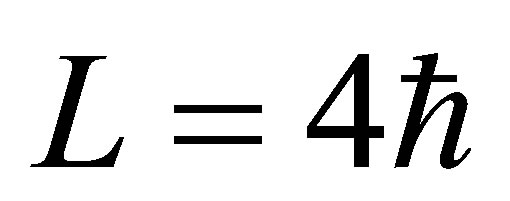 , and
, and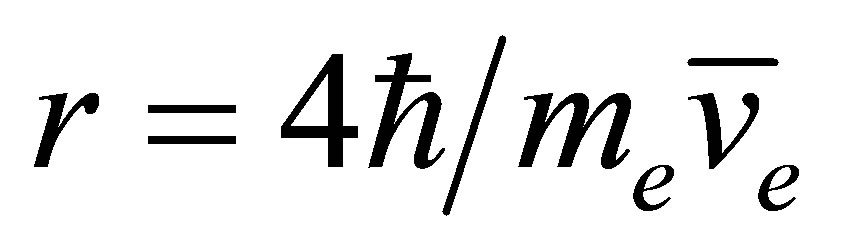 . It therefore follows that
. It therefore follows that
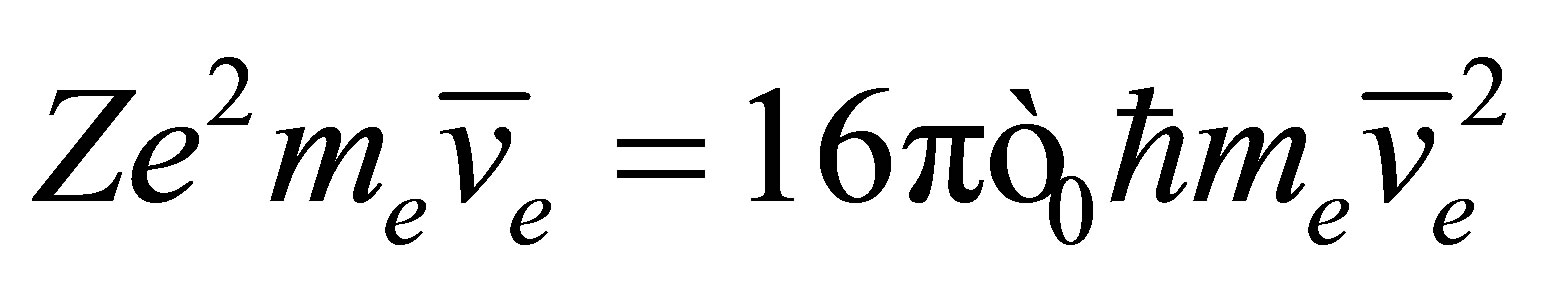 (33)
(33)
 (34)
(34)
where  is the fine-structure constant. In comparison, planets orbit galaxies with modest speeds. The relative velocity
is the fine-structure constant. In comparison, planets orbit galaxies with modest speeds. The relative velocity  between a neutrino and a 4s electron is
between a neutrino and a 4s electron is
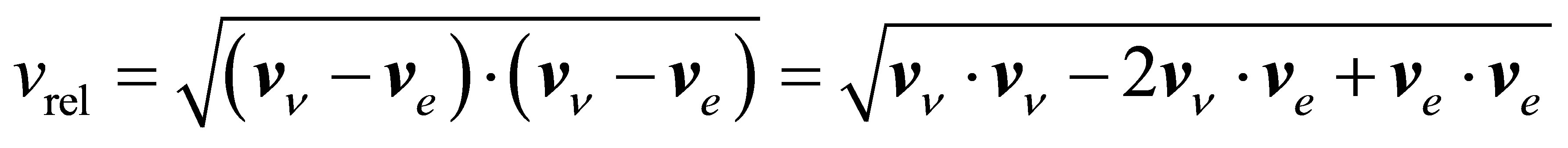 (35)
(35)
Since 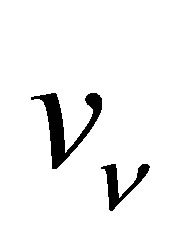 and
and 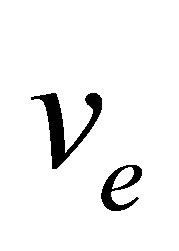 are statistically uncorrelated, the mean value of
are statistically uncorrelated, the mean value of  is zero. Hence, the mean value of the relative velocity between the neutrinos and the electrons is
is zero. Hence, the mean value of the relative velocity between the neutrinos and the electrons is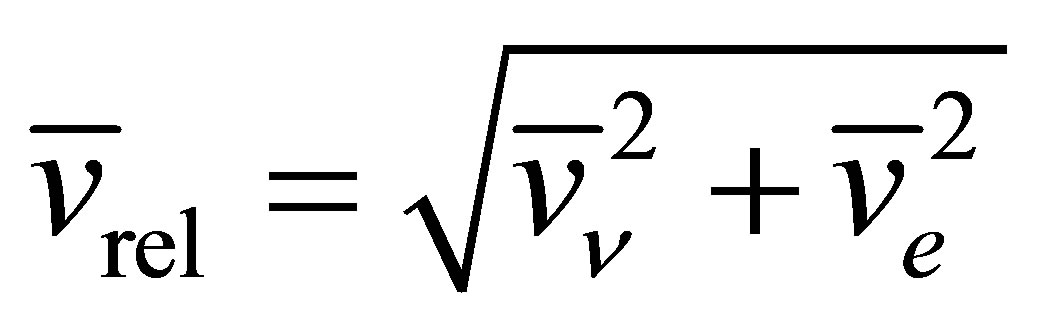 . Electron antineutrinos approach 4s electrons within a distance
. Electron antineutrinos approach 4s electrons within a distance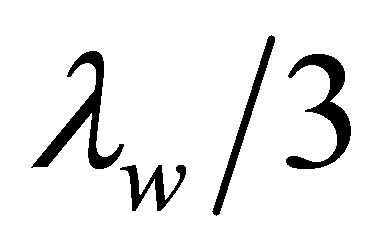 , a range allowing virtual W bosons to couple to them both, after a mean time interval of
, a range allowing virtual W bosons to couple to them both, after a mean time interval of
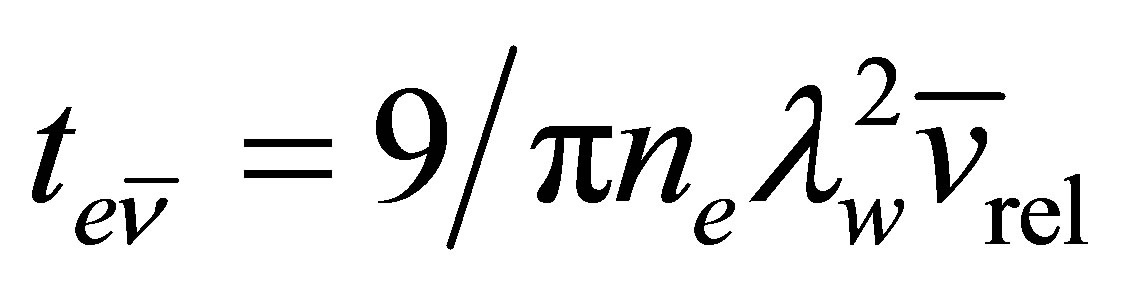 (36)
(36)
Encounters between neutrinos and virtual W bosons offering the opportunity of annihilation have a mean free path of
 (37)
(37)
This is equivalent to a cross-section:
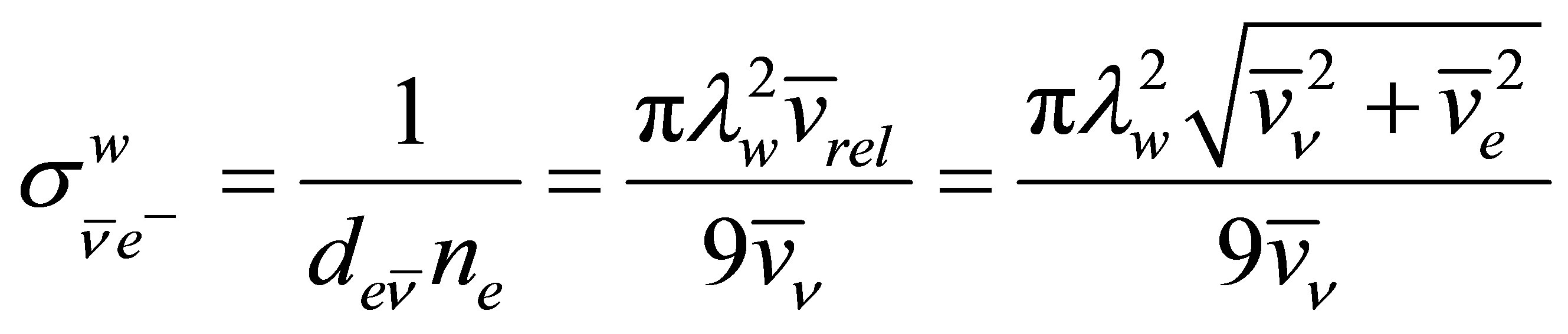 (38)
(38)
When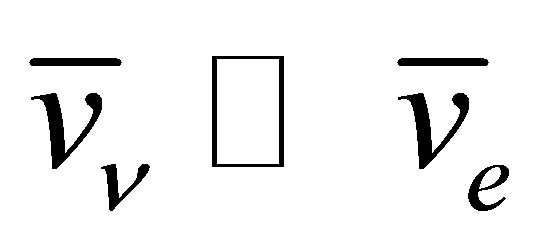 , the cross section is simply
, the cross section is simply  but when
but when  there is enhancement by a factor
there is enhancement by a factor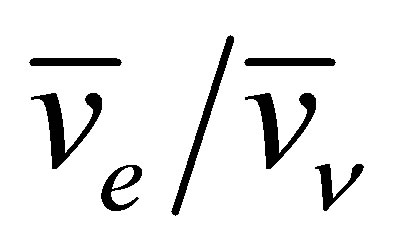 . The rate at which
. The rate at which  collisions occur per unit volume of iron,
collisions occur per unit volume of iron, 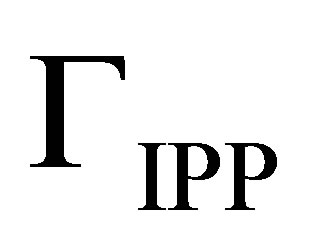 , is given by the ratio of the electron antineutrino number density
, is given by the ratio of the electron antineutrino number density  to the mean time between collisions
to the mean time between collisions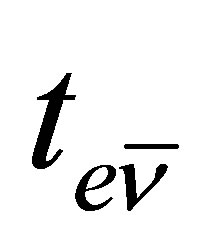 . If one assumes the neutrinos were originally formed as electron neutrinos then their mean survival probability
. If one assumes the neutrinos were originally formed as electron neutrinos then their mean survival probability  comes to about 0.54 (see Appendix C). Taking into account that nonrelativistic neutrinos have both helicities, the electron antineutrino number density is
comes to about 0.54 (see Appendix C). Taking into account that nonrelativistic neutrinos have both helicities, the electron antineutrino number density is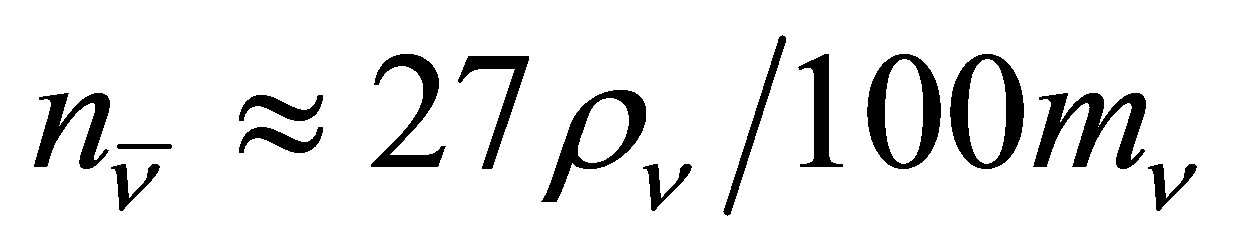 , from which
, from which
 (39)
(39)
The mean distance travelled by a neutrino as it passes within a sphere of radius  of a 4s electron is approximately
of a 4s electron is approximately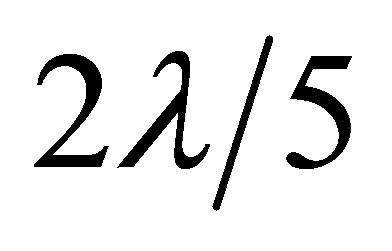 . The sphere crossing time,
. The sphere crossing time, 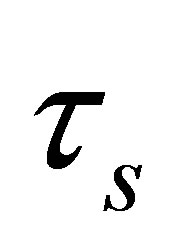 , is therefore
, is therefore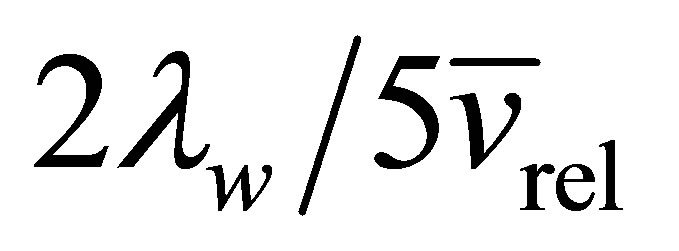 . This can be compared to the characteristic timescale of the weak interaction,
. This can be compared to the characteristic timescale of the weak interaction,  . In order to model the reduction in IPP due to restricted interaction time for rapidly moving particles, an attenuation factor
. In order to model the reduction in IPP due to restricted interaction time for rapidly moving particles, an attenuation factor 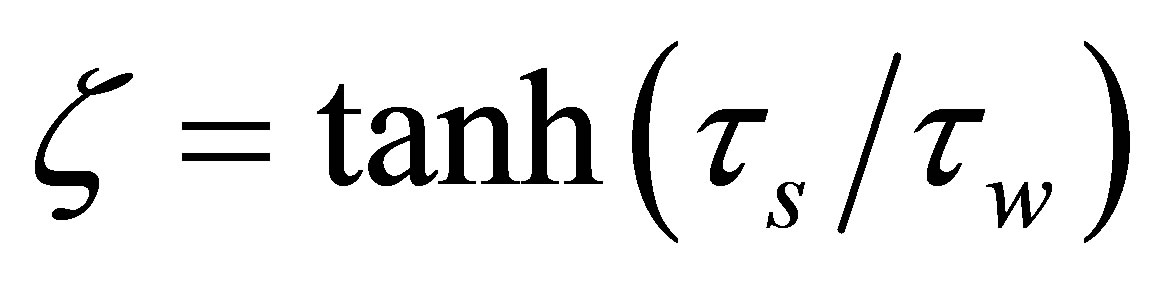 occupying the interval
occupying the interval 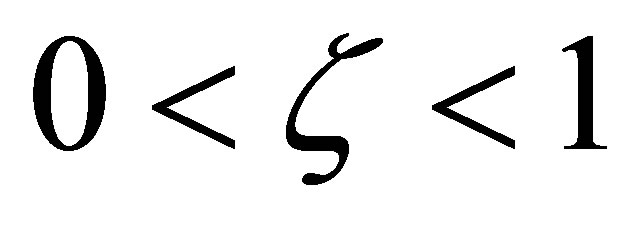 can be calculated
can be calculated
 (40)
(40)
This has the desirable property of yielding 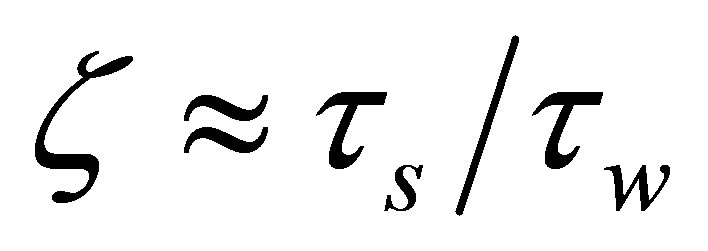 for
for  and
and  for
for . An estimate of the maximum heating power
. An estimate of the maximum heating power  that a neutrino halo can deliver to a planet whose iron core has a radius
that a neutrino halo can deliver to a planet whose iron core has a radius 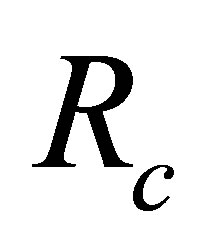 is thus given by the product of the core volume,
is thus given by the product of the core volume,  , the antineutrino-electron collision rate,
, the antineutrino-electron collision rate,  , the attenuation factor,
, the attenuation factor,  , and the combined energy of the annihilating neutrinos, which is
, and the combined energy of the annihilating neutrinos, which is  in the nonrelativistic limit:
in the nonrelativistic limit:
 (41)
(41)
Planetary heating can be determined directly from the ambient density of halo neutrinos and the neutrino mass using
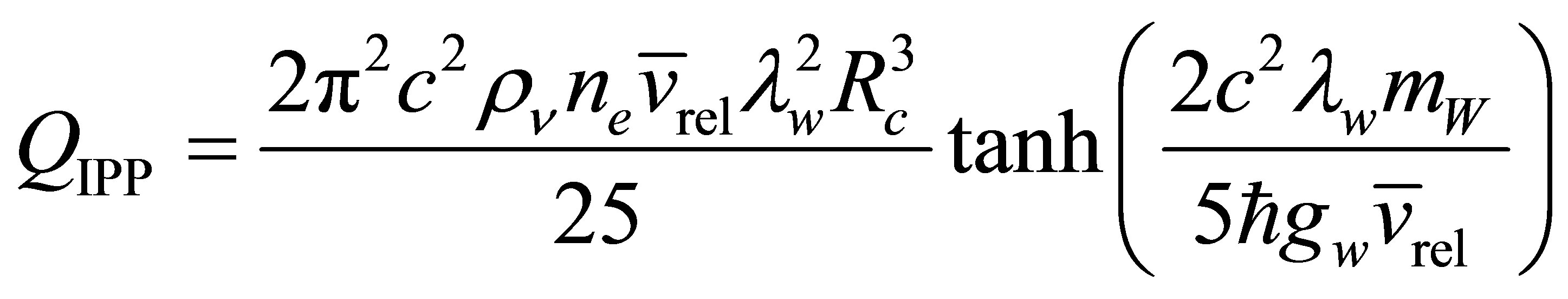 (42)
(42)
where, from Equations (31) and (34), the relative velocity can be obtained as
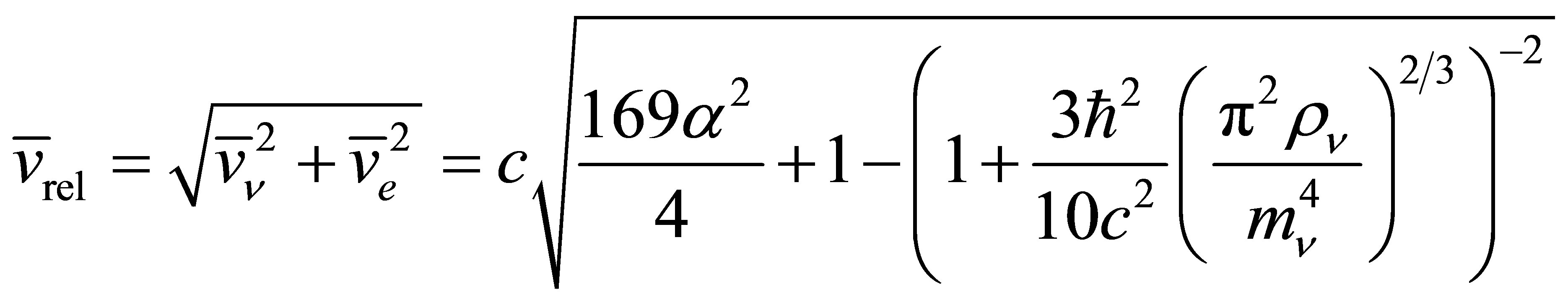 (43)
(43)
Given the abundance of water on oceanic planets, insulating crusts of ice up to 10 km in depth can be easily accommodated. This translates into a requirement that the surface temperature remains above 37 K and the heat flux at the surface exceeds 100 mW/m2. An Earth-mass planet with an iron content resembling that of type Ia supernova ejecta would have a core radius of about 4240 km. A minimal planetary power consumption of 5 × 1013 W requires the mean rate of neutrino energy deposition within the iron core,  , to be 0.15 μW
, to be 0.15 μW m-3. Results for a neutrino mass
m-3. Results for a neutrino mass  are plotted in Figure 5. It can be seen that halo densities of 10−24 ~ 10−21 kg·m−3 would allow aquatic life to be comfortably supported. Much above this, neutrinos would become relativistic and haloes would run the risk of imploding gravitationally. The plot shows power continuing to rise at higher neutrino densities but in reality the hcp®fcc transition would curb this behaviour, thermally regulating core temperatures according to planet size so that a comfortable heat flux
are plotted in Figure 5. It can be seen that halo densities of 10−24 ~ 10−21 kg·m−3 would allow aquatic life to be comfortably supported. Much above this, neutrinos would become relativistic and haloes would run the risk of imploding gravitationally. The plot shows power continuing to rise at higher neutrino densities but in reality the hcp®fcc transition would curb this behaviour, thermally regulating core temperatures according to planet size so that a comfortable heat flux
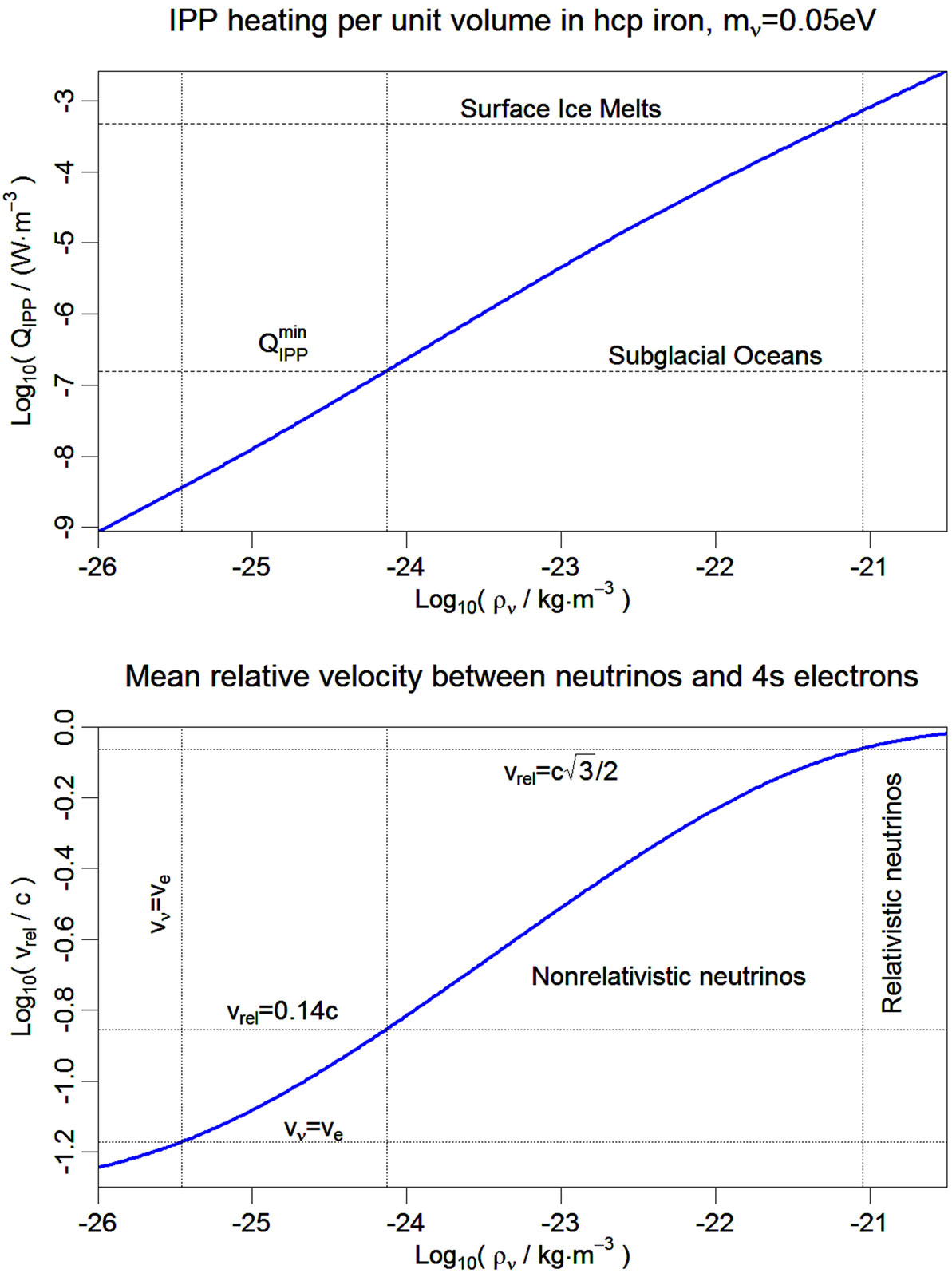
Figure 5. Heating due to IPP and neutrino velocity as predicted for neutrinos of mass 0.05 eV. Non-relativistic neutrinos span more than three orders of magnitude in neutrino density and are habitable for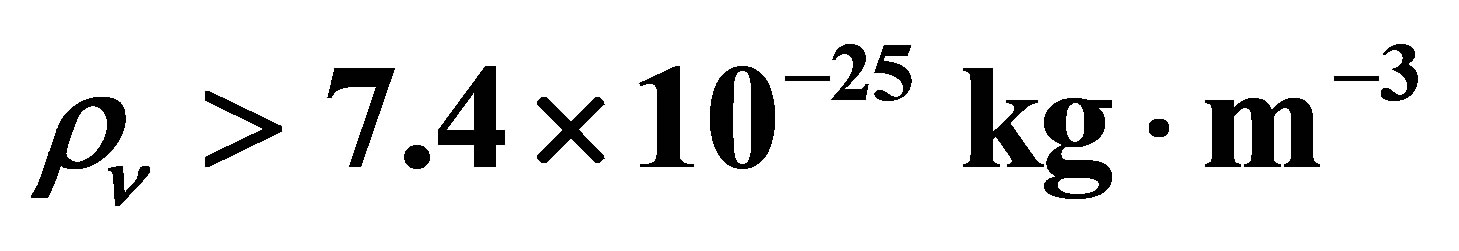 .
.
would be maintained through the oceans.
The total energy of a neutrino doubles relative to its rest mass energy when its velocity reaches . At
. At , this occurs at a neutrino density of
, this occurs at a neutrino density of 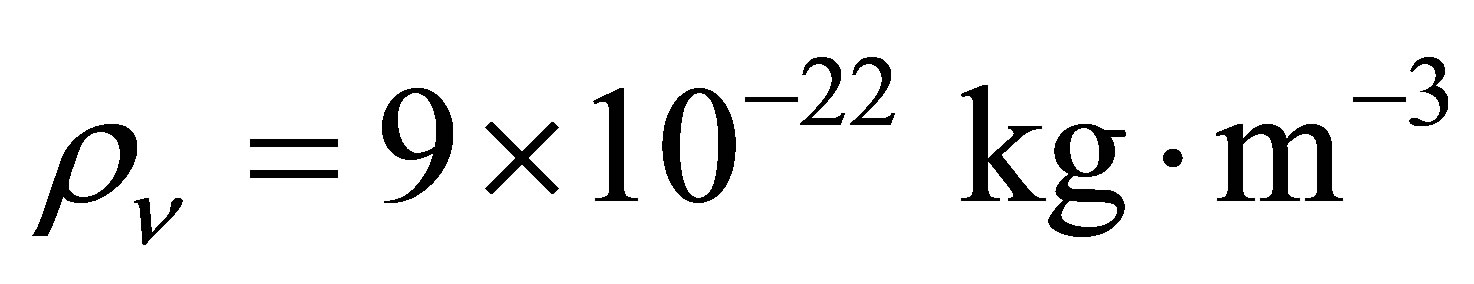 which is more than three orders of magnitude greater than
which is more than three orders of magnitude greater than , the minimum halo density capable of comfortably sustaining liquid oceans. Using the criterion
, the minimum halo density capable of comfortably sustaining liquid oceans. Using the criterion  to define the onset of the relativistic regime, it can be shown using Equation (31) that the neutrino density
to define the onset of the relativistic regime, it can be shown using Equation (31) that the neutrino density  at which this occurs is related to the neutrino mass by
at which this occurs is related to the neutrino mass by
 (44)
(44)
The neutrino density  at which
at which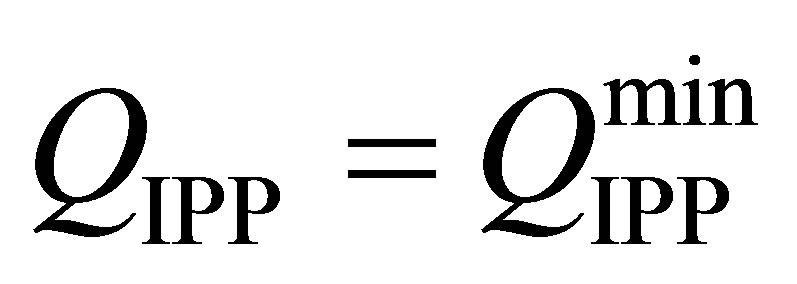 , is a far more complicated function of neutrino mass. It is plotted along with
, is a far more complicated function of neutrino mass. It is plotted along with 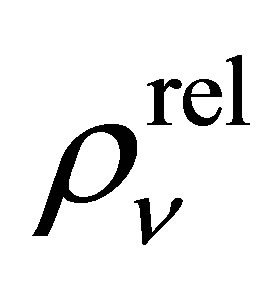 in Figure 6. If the dynamic range in the neutrino density,
in Figure 6. If the dynamic range in the neutrino density,  exceeds unity, aquatic habitats can be supported.
exceeds unity, aquatic habitats can be supported. 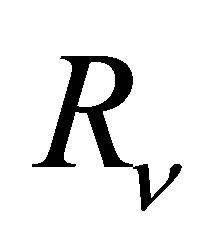 declines rapidly at smaller neutrino masses, pinching off completely at
declines rapidly at smaller neutrino masses, pinching off completely at 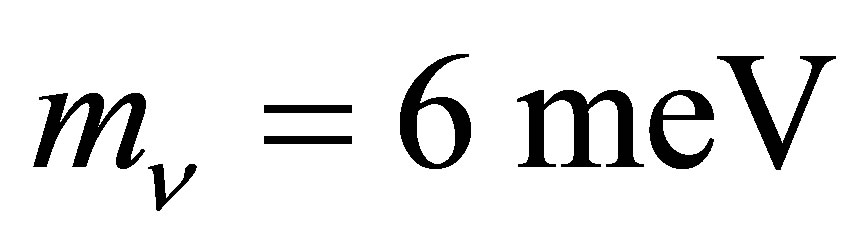 as
as . Even the densest haloes would then be incapable of sustaining liquid oceans. The maximum mass of a neutrino halo scales as
. Even the densest haloes would then be incapable of sustaining liquid oceans. The maximum mass of a neutrino halo scales as 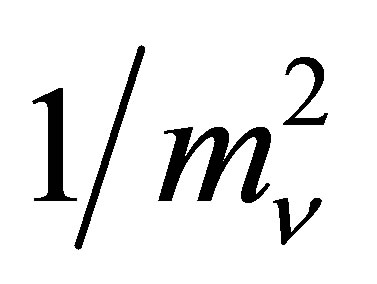 so a low mass is biologically advantageous but comes at the expense of reduced dynamic range. For
so a low mass is biologically advantageous but comes at the expense of reduced dynamic range. For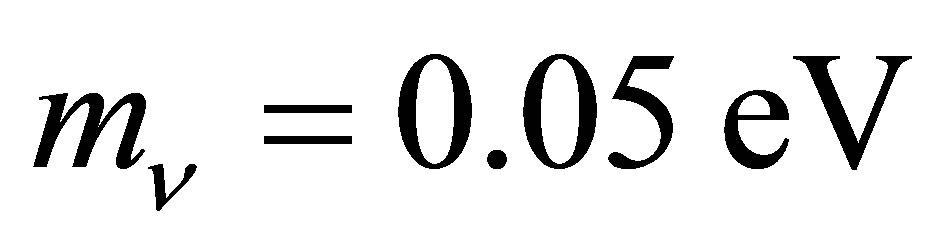 ,
, . Since
. Since  at fixed neutrino mass, this translates into a 42-fold dynamic range in the total mass of the halo,
at fixed neutrino mass, this translates into a 42-fold dynamic range in the total mass of the halo, . This would limit the energetic efficiency of nonrelativistic haloes to 97.6% or less for 0.05 eV neutrinos. However, peculiar results from some neutrino oscillation experiments hint at a possible mechanism that could improve upon this, as discussed next.
. This would limit the energetic efficiency of nonrelativistic haloes to 97.6% or less for 0.05 eV neutrinos. However, peculiar results from some neutrino oscillation experiments hint at a possible mechanism that could improve upon this, as discussed next.

Figure 6. Top: neutrino densities that support liquid oceans as a function of neutrino mass: habitable haloes are impossible for neutrino masses below 6 meV. Bottom: halo dynamic range,  , increases with neutrino mass though total mass declines as
, increases with neutrino mass though total mass declines as .
.
6. Sterile Haloes
Neutrino haloes expand as their total mass decreases, which reduces the ambient concentration of neutrinos. Inevitably, at some stage planetary heating becomes inadequate to sustain liquid oceans. Provided that  , the maximum mass of a neutrino halo, and therefore the amount of aquatic life it might support, increases as
, the maximum mass of a neutrino halo, and therefore the amount of aquatic life it might support, increases as 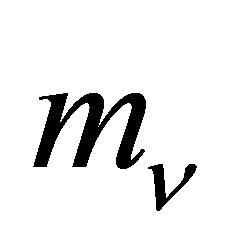 is reduced. However, the ratio
is reduced. However, the ratio 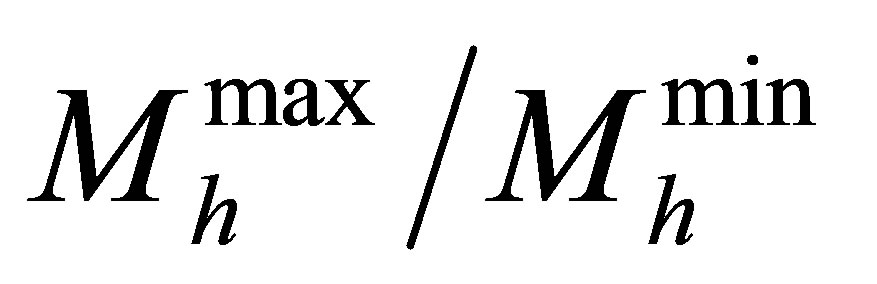 is thereby decreased, which reduces overall energetic efficiency. This section describes a possible natural mechanism that might alleviate this compromise and perhaps shed some light on the current composition of dark matter.
is thereby decreased, which reduces overall energetic efficiency. This section describes a possible natural mechanism that might alleviate this compromise and perhaps shed some light on the current composition of dark matter.
A near-maximal halo of 0.05 eV neutrinos could readily accommodate a supergiant galaxy with a radius of some 400 thousand light years. Consider now the influence of a secondary, inner halo of size comparable to the internal galaxy which only interacts gravitationally with the outer halo. Its mass could be small compared to the neutrino halo within which it is immersed, even though its mean density may be far greater. The additional gravity of this relatively compact inner halo would have the effect of attracting neutrinos of the larger halo, locally enhancing their concentration. This would boost neutrino annihilation in the central region of a heavily depleted neutrino halo.
The inner halo could be structurally stable over the long-term if it were composed of highly inert fermions: particles ideally possessing no electrical charge and interacting with other particles only through gravity and the exclusion principle. In order to yield haloes just large enough to envelop supergiant galaxies, fermions of ~eV mass would be required. Participation in weak interactions could be avoided if these fermions have zero weak isospin. This can be arranged if the particles have positive chirality. All these demands can potentially be met by sterile neutrinos. It is therefore encouraging that the LSND, MiniBooNE and reactor anomalies appear to imply the existence of one or more sterile neutrino species with a mass at the eV-scale [67]. Furthermore, cosmology is capable of accommodating extra radiation from eV-scale sterile neutrinos with only minor revisions [68]. Modelling of the Abell 1689 galaxy cluster inferred the existence of a dark matter halo of 1.5 eV fermions [28]. For these to be active neutrinos would defy current cosmological constraints. However, this leaves open the possibility that sterile neutrinos may comprise almost all the dark matter within galaxy clusters.
To assess the influence of a sterile inner halo on an active halo, it is now assumed that sterile neutrinos have a mass of 1.5 eV. Any mixing between active and sterile neutrino states is taken to be negligible. The mass of the sterile halo shall be fixed here at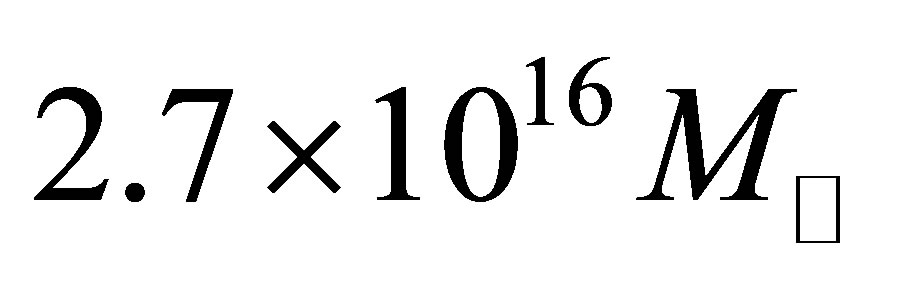 , approximately 3% of the
, approximately 3% of the  maximal mass according to (18). This halo mass shall be justified later. Both haloes shall be described by polytropes of index
maximal mass according to (18). This halo mass shall be justified later. Both haloes shall be described by polytropes of index 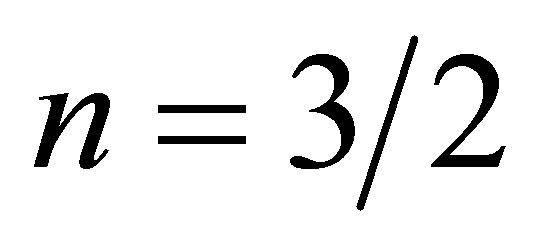 and spherical symmetry shall be assumed. Such polytropes attain maximum gravity at a radius about 48.6% of their outer surface. Thus, it would be interesting to consider a sterile halo roughly twice the diameter of the supergiant galaxy it contains.
and spherical symmetry shall be assumed. Such polytropes attain maximum gravity at a radius about 48.6% of their outer surface. Thus, it would be interesting to consider a sterile halo roughly twice the diameter of the supergiant galaxy it contains.
The pressure and density within these haloes is related by  where
where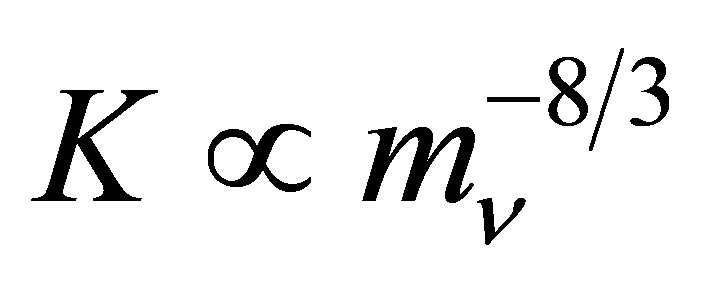 . Hence,
. Hence,
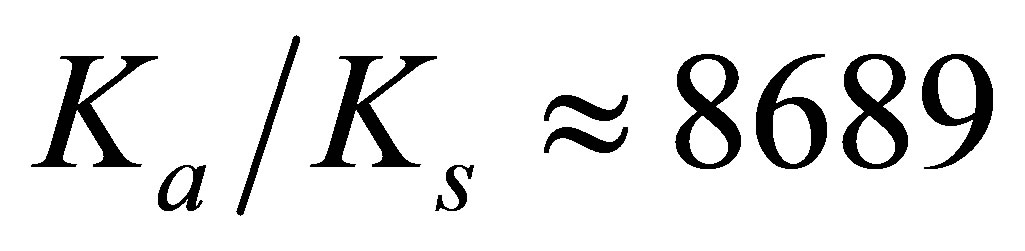 , where the subscripts a and s respectively denote the active and sterile haloes. Analytical solutions do not exist to the Lane-Emden equation for polytropes of index 3/2, so their structure must be numerically determined. The situation is no simpler for the double polytrope considered here. In hydrostatic equilibrium, the pressure gradients within the active and sterile haloes are
, where the subscripts a and s respectively denote the active and sterile haloes. Analytical solutions do not exist to the Lane-Emden equation for polytropes of index 3/2, so their structure must be numerically determined. The situation is no simpler for the double polytrope considered here. In hydrostatic equilibrium, the pressure gradients within the active and sterile haloes are
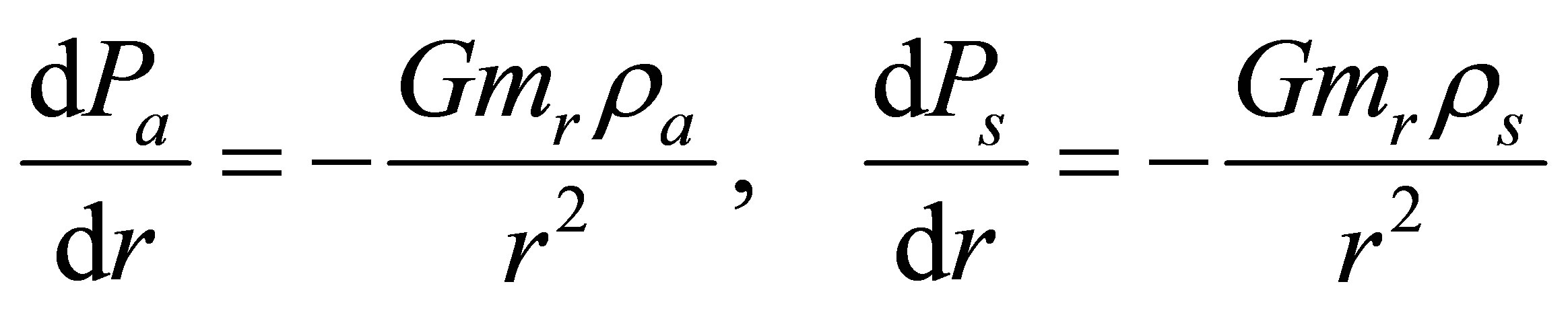 (45)
(45)
where  is the internal mass at radius r. Upon differentiation one obtains
is the internal mass at radius r. Upon differentiation one obtains
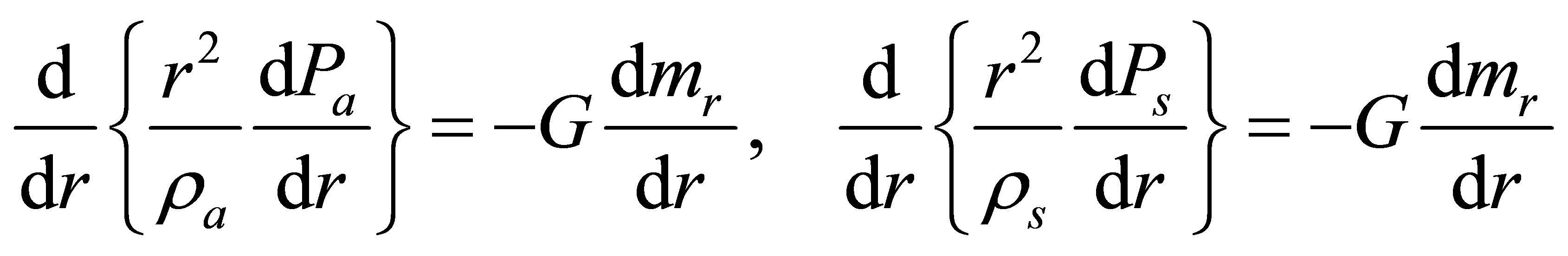 (46)
(46)
A thin shell of radius r and thickness 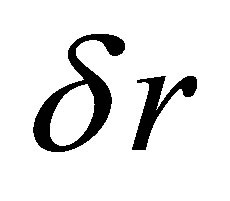 has a mass
has a mass  and thus
and thus
 (47)
(47)
Differentiation of the pressure-density relationships gives
 (48)
(48)
Using these results, one finds for the active halo that
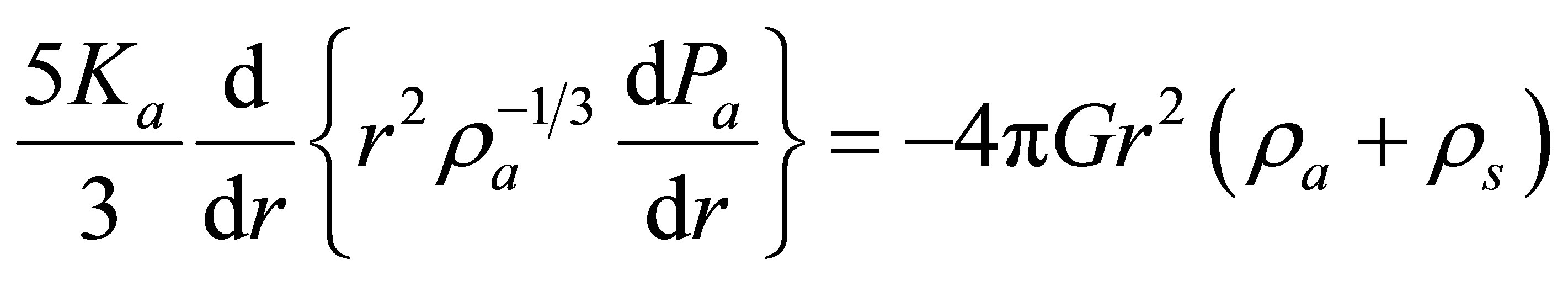 (49)
(49)
 (50)
(50)
 (51)
(51)
The difference equation 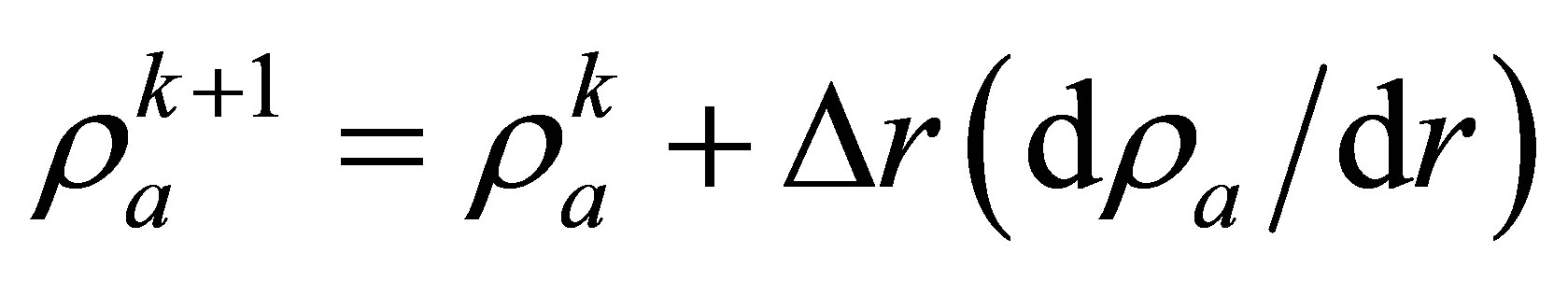 can be used to numerically integrate the density. The
can be used to numerically integrate the density. The 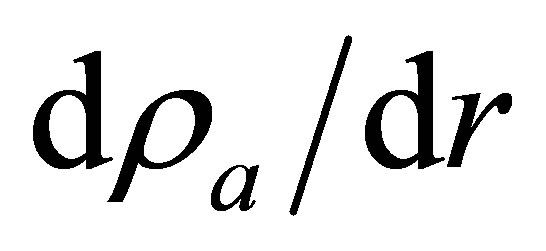 term is obtained by differentiating and substituting the previous expression for the second derivative:
term is obtained by differentiating and substituting the previous expression for the second derivative:
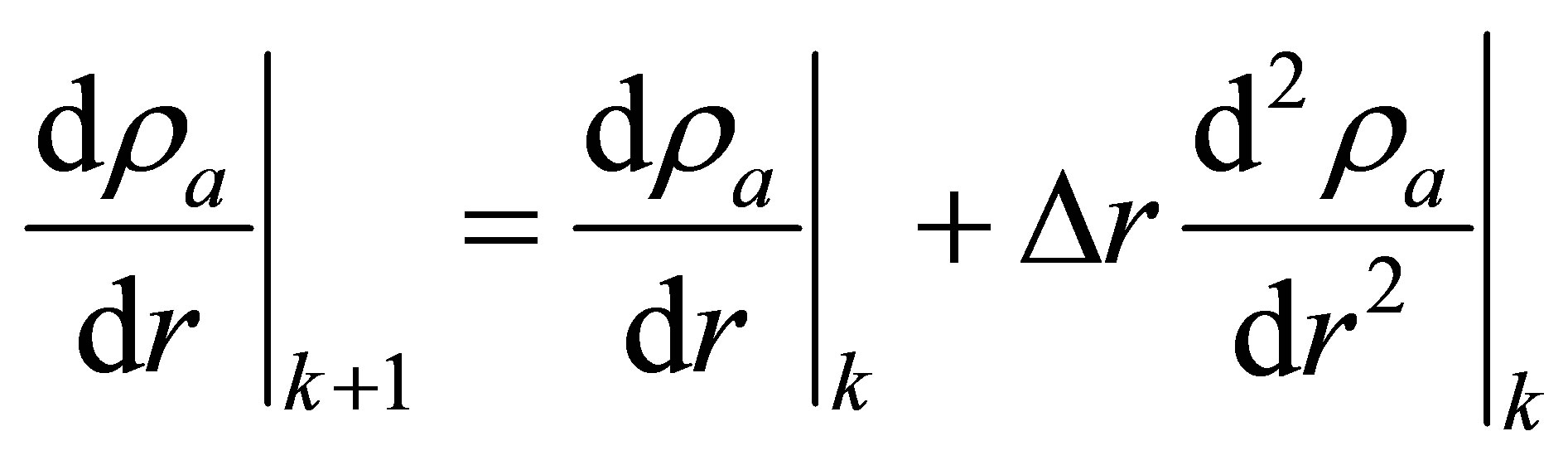 (52)
(52)
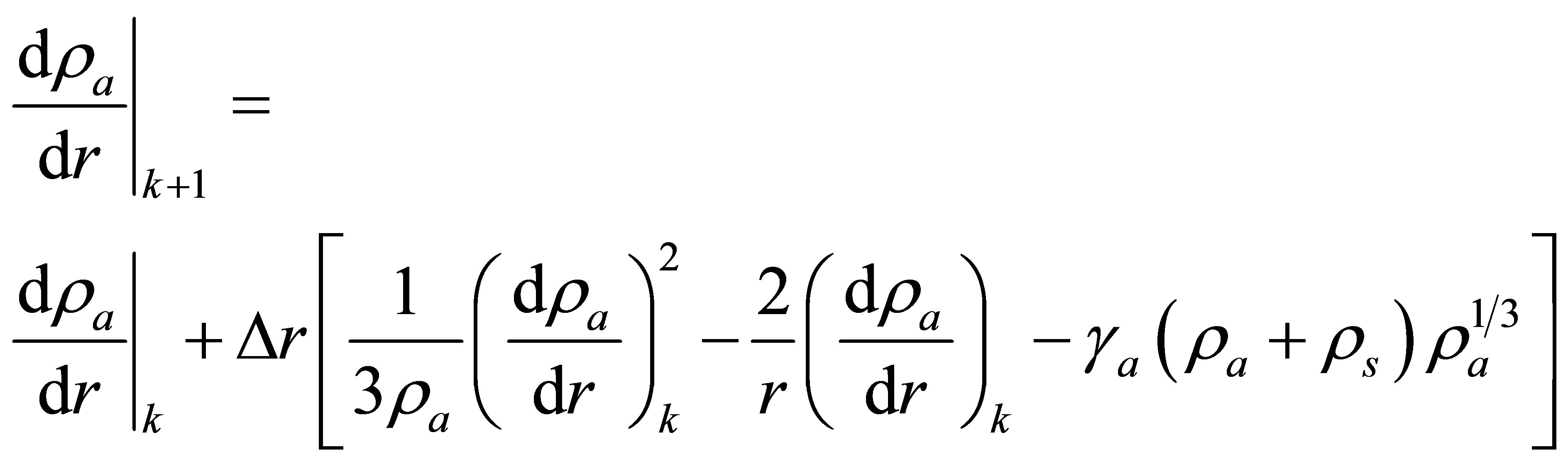 (53)
(53)
where . Likewise, the density of the sterile halo is simultaneously obtained by numerical integration using both
. Likewise, the density of the sterile halo is simultaneously obtained by numerical integration using both 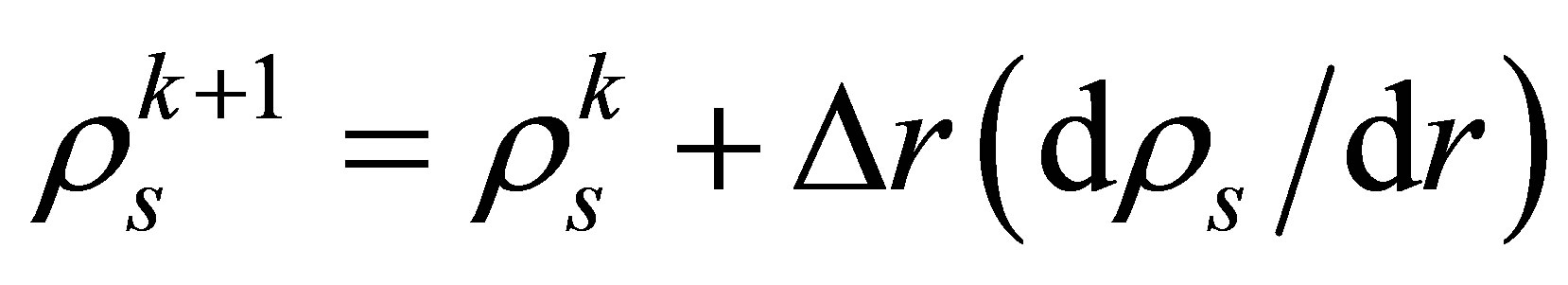 and
and
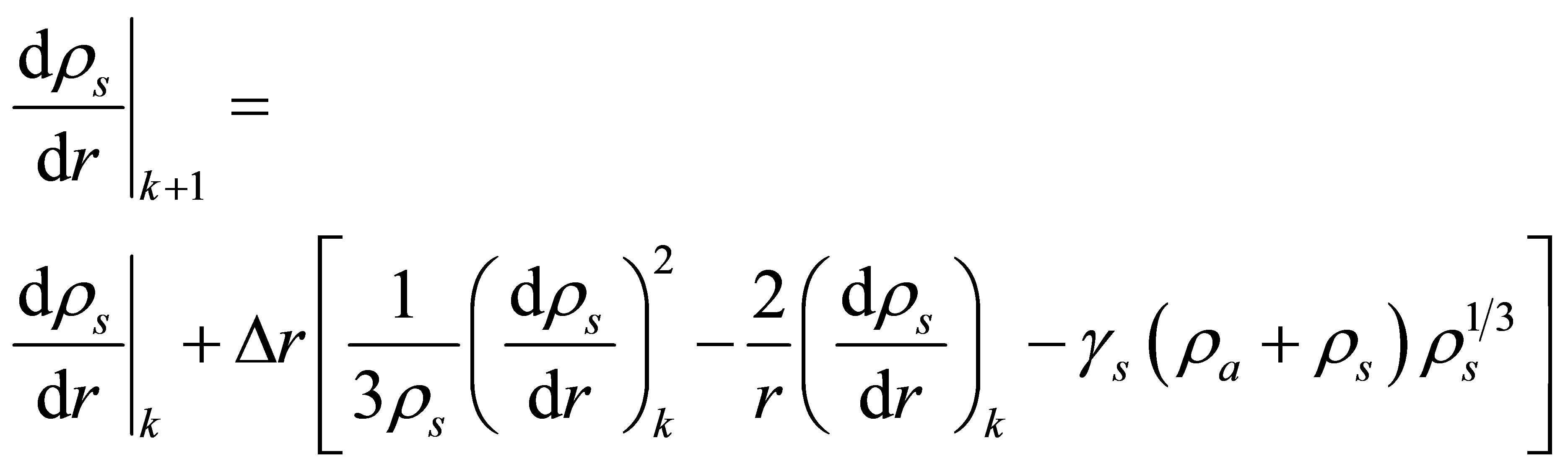 (54)
(54)
Physically realistic solutions are obtained when the boundary conditions 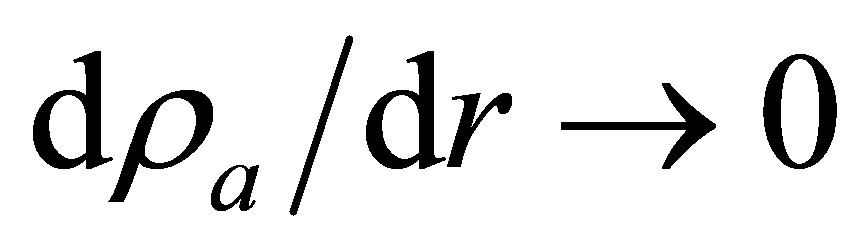 and
and 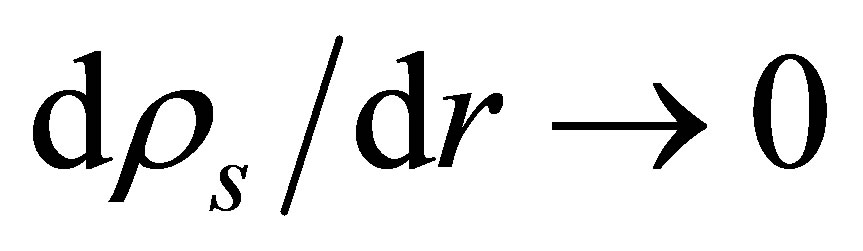 at small r are imposed, providing initial conditions when integrating outwards from the centre. Once
at small r are imposed, providing initial conditions when integrating outwards from the centre. Once 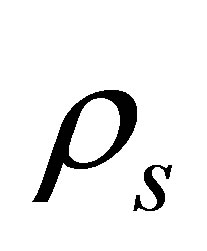 reaches zero, the outer surface of the sterile halo is reached, and
reaches zero, the outer surface of the sterile halo is reached, and  is thereafter held at zero until the outer surface of the active halo is attained, where integration is halted. Masses are calculated by summing shell masses at each iteration,
is thereafter held at zero until the outer surface of the active halo is attained, where integration is halted. Masses are calculated by summing shell masses at each iteration,  and
and 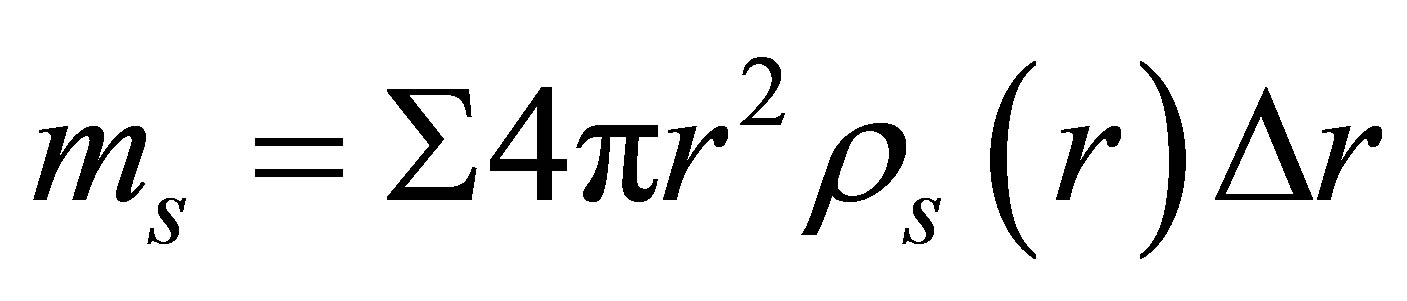 . Due to the disparity in scale between the sterile and active haloes, integration was performed here using radial increments of 0.1% starting from an initial radius of 100 light years. There is freedom to select the central densities
. Due to the disparity in scale between the sterile and active haloes, integration was performed here using radial increments of 0.1% starting from an initial radius of 100 light years. There is freedom to select the central densities 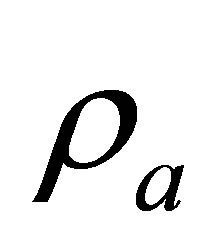 and
and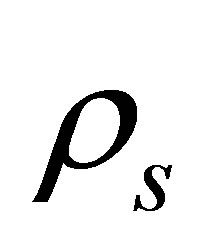 , which control the total mass of each halo. The target mass of the sterile halo,
, which control the total mass of each halo. The target mass of the sterile halo, 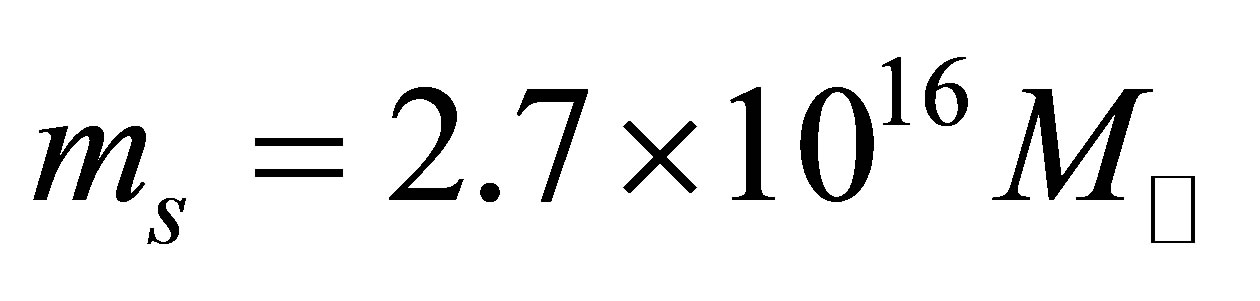 , was achieved by setting
, was achieved by setting  . The central density of the active halo is typically three or more orders of magnitude smaller, so the active halo barely has any gravitational influence on the sterile halo. Results are presented in Figure 7 for active haloes of different total mass both with and without assistance from a sterile halo. In the case of no assistance, planets would only be habitable over a 42-fold range of active halo mass. However, when the sterile neutrino halo is present, the total mass of the active halo can still support life even though it varies by 9 orders of magnitude. The active neutrino density then remains above the critical threshold of
. The central density of the active halo is typically three or more orders of magnitude smaller, so the active halo barely has any gravitational influence on the sterile halo. Results are presented in Figure 7 for active haloes of different total mass both with and without assistance from a sterile halo. In the case of no assistance, planets would only be habitable over a 42-fold range of active halo mass. However, when the sterile neutrino halo is present, the total mass of the active halo can still support life even though it varies by 9 orders of magnitude. The active neutrino density then remains above the critical threshold of 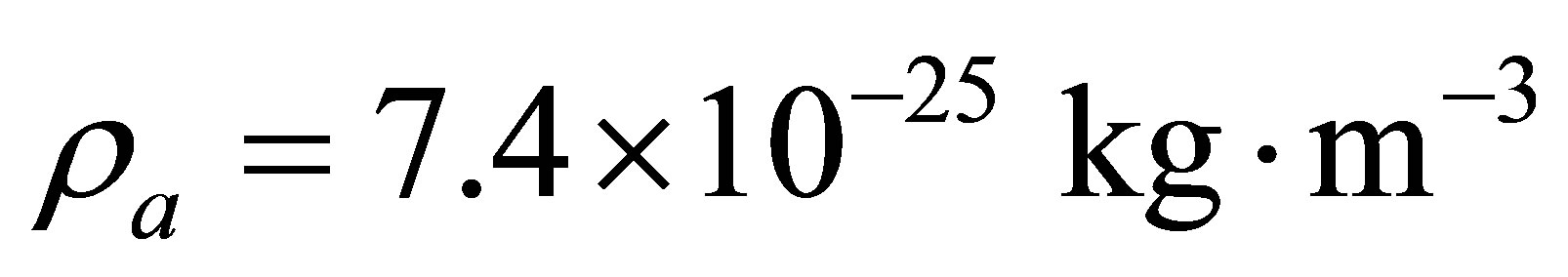 at galactic radii up to 400 thousand light years. A sterile halo of modest total mass was chosen as it reduces the energetic cost, provides a good safety margin against implosion and can accommodate larger galaxies.
at galactic radii up to 400 thousand light years. A sterile halo of modest total mass was chosen as it reduces the energetic cost, provides a good safety margin against implosion and can accommodate larger galaxies.
If the decay of dark energy will augment the number of active neutrinos in the cosmos, might it also deliver more sterile neutrinos? This seems unlikely if dark energy can only decay to the lowest mass fermions. Since sterile neutrinos are not strictly required until active neutrino haloes become depleted, it would be acceptable for them to accumulate very gradually with time. This might
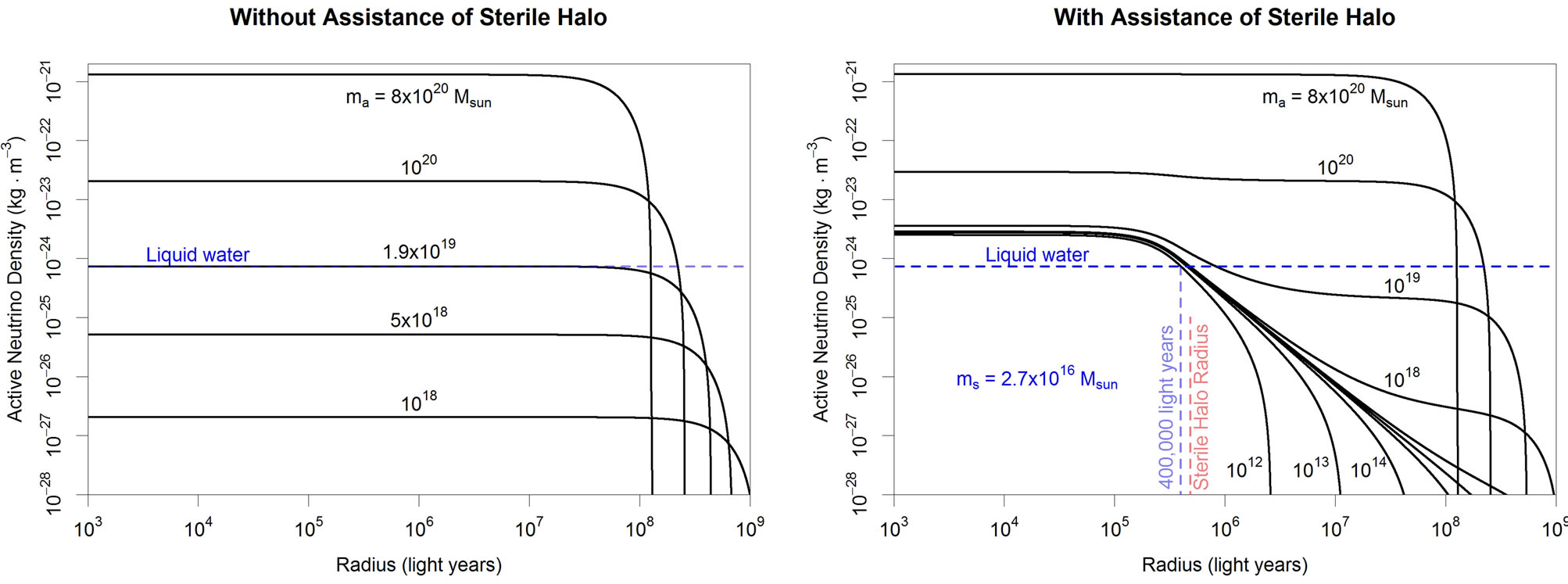
Figure 7. Left: active neutrino density with no assistance from sterile neutrinos. Once the halo mass declines below , the active neutrino density enters the regime
, the active neutrino density enters the regime  which is insufficient to comfortably support liquid oceans. Right: active neutrino density with assistance of an internal halo of 1.5 eV sterile neutrinos of central density 10-18 kg·m-3, total mass
which is insufficient to comfortably support liquid oceans. Right: active neutrino density with assistance of an internal halo of 1.5 eV sterile neutrinos of central density 10-18 kg·m-3, total mass  and halo radius 484 thousand light years. The gravity of the sterile halo locally enhances the galactic density of active neutrinos, especially apparent for lower mass haloes,
and halo radius 484 thousand light years. The gravity of the sterile halo locally enhances the galactic density of active neutrinos, especially apparent for lower mass haloes, . Planetary heating can thereby proceed at radii up to 400 thousand light years even when the active halo is heavily depleted. Despite the relatively small mass of the sterile halo, the assistance available is impressive.
. Planetary heating can thereby proceed at radii up to 400 thousand light years even when the active halo is heavily depleted. Despite the relatively small mass of the sterile halo, the assistance available is impressive.
be possible if black dwarves, which are extremely well insulated thermally, maintain a moderate internal temperature sustained by a minimal degree of active neutrino annihilation mediated by electrons very close to the Fermi energy. If the core temperatures of black dwarves exceed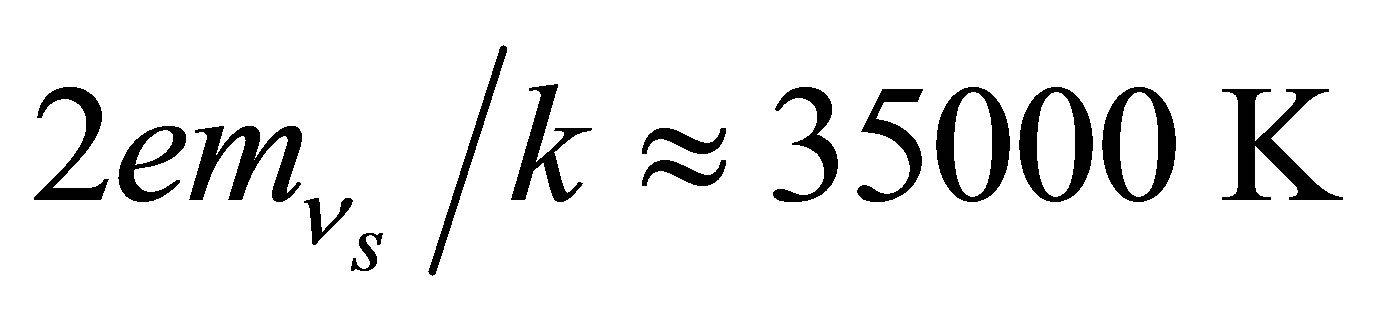 , they would be capable of the pair-production of 1.5 eV sterile neutrinos. In general, the probability of emitting neutrinos of abnormal chirality is proportional to
, they would be capable of the pair-production of 1.5 eV sterile neutrinos. In general, the probability of emitting neutrinos of abnormal chirality is proportional to 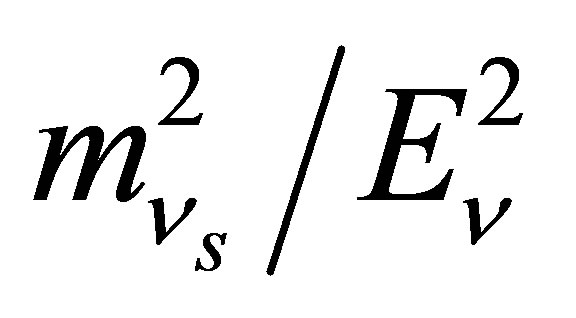 and so becomes far more frequent at low energies. Therefore, it may not be necessary for the decay of dark energy to yield sterile neutrinos, nor for them to have been created in great numbers at the big bang.
and so becomes far more frequent at low energies. Therefore, it may not be necessary for the decay of dark energy to yield sterile neutrinos, nor for them to have been created in great numbers at the big bang.
White dwarves cool primarily through the emission of neutrinos via the plasma process [69]. In the low-mass, low-temperature limit the cooling rate is 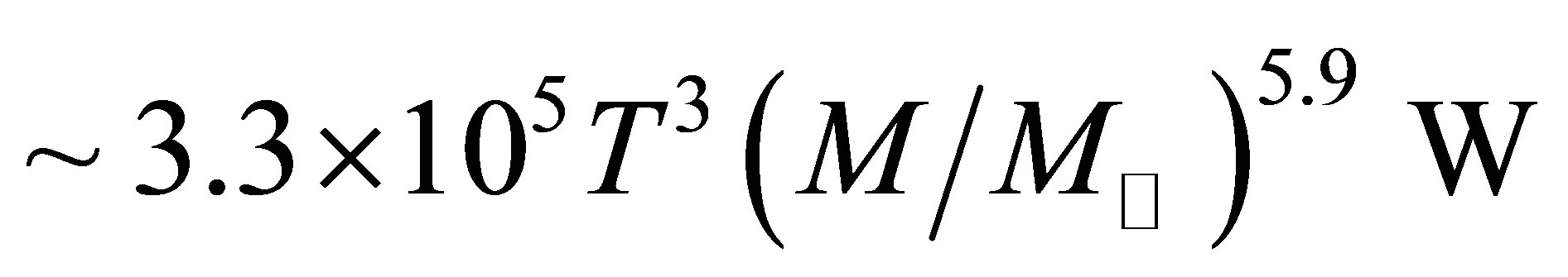 . For a black dwarf of stellar mass with an internal temperature of 35,000 K, this equates to a luminosity of ~1019 W which may be adequate in the long-term for reprocessing active neutrinos into sterile neutrinos. Within non-degenerate matter at sub-keV energies, the photoneutrino process has a more extreme temperature dependency and, for an iron-cored planet, the power radiated by the photoneutrino process per cubic metre can be estimated by the expression
. For a black dwarf of stellar mass with an internal temperature of 35,000 K, this equates to a luminosity of ~1019 W which may be adequate in the long-term for reprocessing active neutrinos into sterile neutrinos. Within non-degenerate matter at sub-keV energies, the photoneutrino process has a more extreme temperature dependency and, for an iron-cored planet, the power radiated by the photoneutrino process per cubic metre can be estimated by the expression  [49]. For a planet of mass
[49]. For a planet of mass  and internal temperature 105 K, this mechanism results in a total active neutrino luminosity of less than a Watt. Clearly, the formation of a sterile halo could not rely entirely on the heat possessed by newly-formed neutron stars and white dwarves, not least because their total mass falls short of what is required. If the dark matter haloes of galaxy clusters currently consist of sterile neutrinos they almost certainly originated at the big bang.
and internal temperature 105 K, this mechanism results in a total active neutrino luminosity of less than a Watt. Clearly, the formation of a sterile halo could not rely entirely on the heat possessed by newly-formed neutron stars and white dwarves, not least because their total mass falls short of what is required. If the dark matter haloes of galaxy clusters currently consist of sterile neutrinos they almost certainly originated at the big bang.
This analysis has found that aquatic life could be sustained even when the active halo is so depleted that it contains far less mass than the sterile halo. In this example, the mass of the sterile halo was smaller by a factor of ~30,000 than the maximum initial mass of the active halo. Therefore, appropriately sized haloes consisting of 1.5 eV sterile neutrinos would have the potential to greatly reduce the wastage of active neutrinos on processes which lack possible biological importance. It is also apparent that the energetic cost of the assistance they could provide is rather minimal.
Oceanic planets might be regarded as heat engines whose efficiency is given by 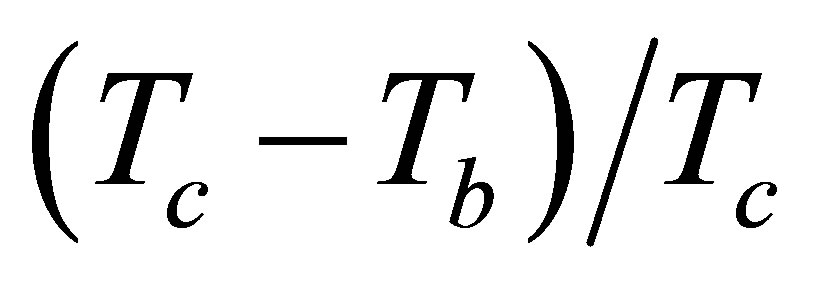 where
where 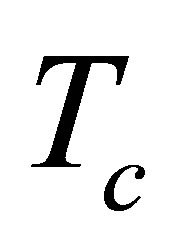 is the core temperature (1000 ~ 19000 K, depending on planet mass) and
is the core temperature (1000 ~ 19000 K, depending on planet mass) and 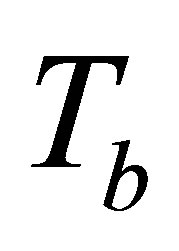 the effective temperature for black body radiation (roughly 37 K in the absence of an insulating atmosphere). Due to the favourable slope of the hcp-fcc boundary, heating can be remarkably efficient even down to the dwarf planet scale, but super-Earth planets where hcp iron exists at higher temperatures would be most efficient. Overall efficiencies exceeding 99% may not be unrealistic. Heating of smaller planets is only likely to be sustained when their core temperatures are already elevated, whether due to latent heat, collisions or some artificial stimulus.
the effective temperature for black body radiation (roughly 37 K in the absence of an insulating atmosphere). Due to the favourable slope of the hcp-fcc boundary, heating can be remarkably efficient even down to the dwarf planet scale, but super-Earth planets where hcp iron exists at higher temperatures would be most efficient. Overall efficiencies exceeding 99% may not be unrealistic. Heating of smaller planets is only likely to be sustained when their core temperatures are already elevated, whether due to latent heat, collisions or some artificial stimulus.
Since the central density of a sterile halo is relatively constant and can strongly dominate the gravitational potential within the contained galaxy, the angular velocities of orbiting bodies could be largely independent of orbital radius. This would help reduce dynamical friction between planets and be conducive to the long-term stability of their galactic orbits. It is conceivable that the presence of sterile neutrinos could allow triaxial galactic morphologies to be sustained over the long-term, inhibiting relaxation to planar distributions. The brightest cluster galaxies are observed to be giant elliptical galaxies. While this can be explained in terms of recent galaxy mergers, the influence of dark matter there would not seem to be irrelevant.
7. Dark Energy Decay
For all permissible values of the electron neutrino mass, neutrinos are presently too scarce to allow appreciable heating of oceanic planets. However, most of the energy of the cosmos is associated with its current accelerating expansion, and that energy is increasing with time. Apart from a simple cosmological constant, a plethora of mechanisms have been proposed to account for cosmic acceleration including quintessence (axions, dilatons), k-essence, tachyon fields, conformal symmetry breaking, Chaplygin gas, neutrino mixing, mass-varying neutrinos (MaVaNs), various modifications of gravity (GaussBonnet gravity, scalar-tensor theory, f(R) models), dark fluid and possibilities motivated by string theory. The fundamental energy scale of dark energy is ~10-3 eV, much closer to the mass of the neutrino than other particles [70,71]. Hinting at a possible connection between the two, this has understandably led to speculations that the physics of neutrinos and dark energy might be linked in various ways [18-20,72-81]. In MaVaN scenarios, the neutrino masses are tied to dark energy and evolve cosmologically [20,82-85]. The present model, however, requires no time sensitivity of the physical constants.
While a physical comprehension of dark energy remains elusive, it is possible to consider its ultimate fate. Decay to a true vacuum resulting in the injection of matter into the cosmos is plausible due to its resemblance to inflation. Such a possibility can be characterised by 1) the time of the decay,  2) the fraction
2) the fraction 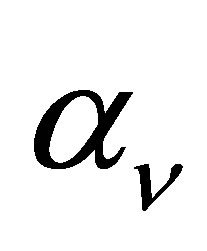 of dark energy transformed into neutrinos 3) the fraction
of dark energy transformed into neutrinos 3) the fraction  of those neutrinos having a sufficiently low kinetic energy to form haloes and 4) the fraction
of those neutrinos having a sufficiently low kinetic energy to form haloes and 4) the fraction 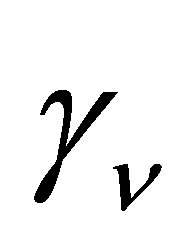 of low energy neutrinos captured by galaxy clusters. If dark energy can only decay into fermions once some energy threshold is met, the exclusive decay of dark energy to low energy neutrinos would be anticipated. This would imply that
of low energy neutrinos captured by galaxy clusters. If dark energy can only decay into fermions once some energy threshold is met, the exclusive decay of dark energy to low energy neutrinos would be anticipated. This would imply that 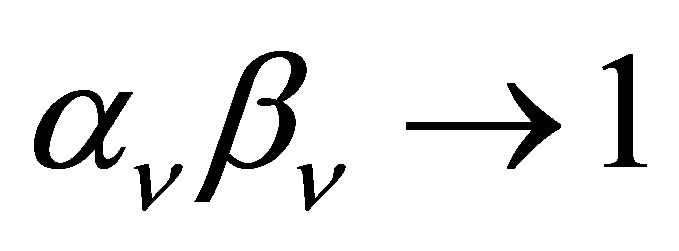 but these parameters are left free in the following analysis.
but these parameters are left free in the following analysis.
For simplicity, the equation of state for dark energy is taken here to be 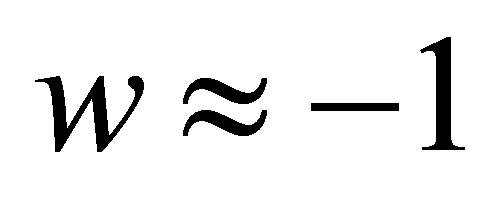 up until
up until  when it is assumed that dark energy abruptly decays into matter, the scale factor of the universe having grown by then from its present value
when it is assumed that dark energy abruptly decays into matter, the scale factor of the universe having grown by then from its present value  to
to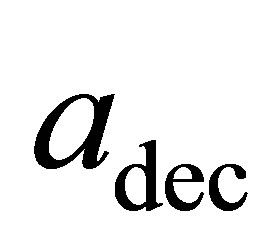 . Since the spatial energy density of dark energy remains constant until
. Since the spatial energy density of dark energy remains constant until , the energy represented by dark energy at the time of decay will have increased by a factor of
, the energy represented by dark energy at the time of decay will have increased by a factor of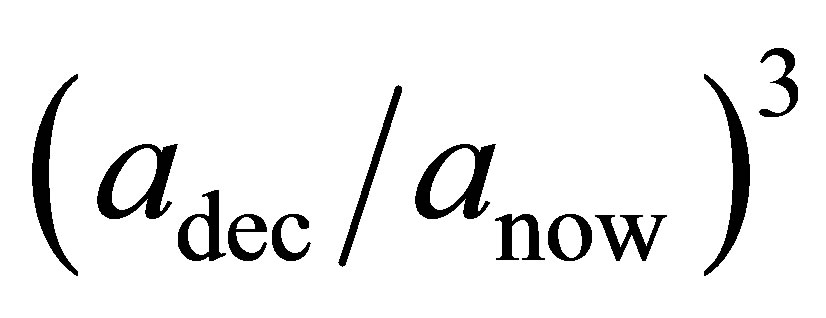 . Galaxy clusters are especially rich in dark matter, still assimilating galaxy groups and about 15% of galaxies currently belong to clusters [86]. They represent sites where neutrinos are most likely to condense [25]. It is assumed here that galaxy clusters will in time come to account for about half the matter of the universe (
. Galaxy clusters are especially rich in dark matter, still assimilating galaxy groups and about 15% of galaxies currently belong to clusters [86]. They represent sites where neutrinos are most likely to condense [25]. It is assumed here that galaxy clusters will in time come to account for about half the matter of the universe ( as
as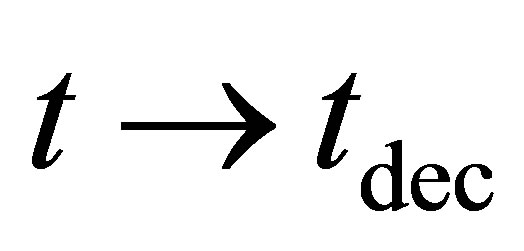 ) and that neutrinos captured by clusters subsequent to
) and that neutrinos captured by clusters subsequent to  will dominate the mass of each cluster and increase their mass as follows:
will dominate the mass of each cluster and increase their mass as follows:
 (55)
(55)
The largest known galaxy cluster has a mass  [87]. Galaxy clusters are at risk of gravitational implosion when dark energy decays unless:
[87]. Galaxy clusters are at risk of gravitational implosion when dark energy decays unless:
 (56)
(56)
This can be used to obtain a constraint on universal expansion:
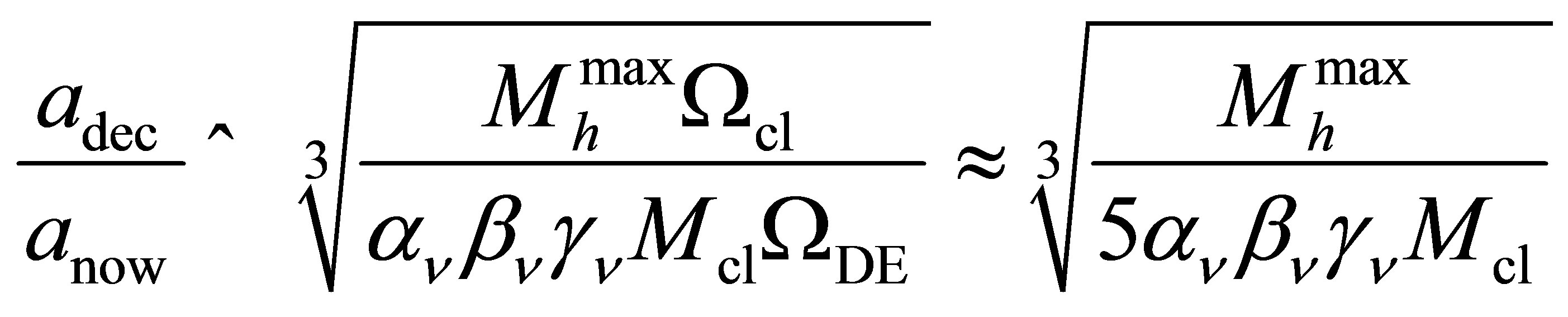 (57)
(57)
If the universe is flat, this ratio can be used to obtain the time of dark energy’s decay:
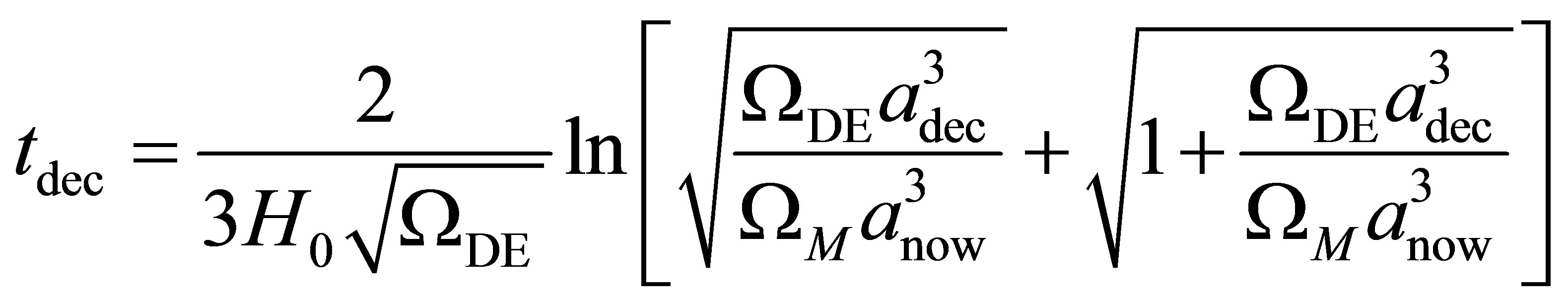 (58)
(58)
where 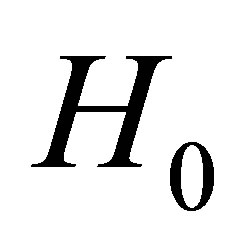 is the current value of the Hubble constant. Therefore, the largest galaxy clusters are not anticipated to implode if:
is the current value of the Hubble constant. Therefore, the largest galaxy clusters are not anticipated to implode if:
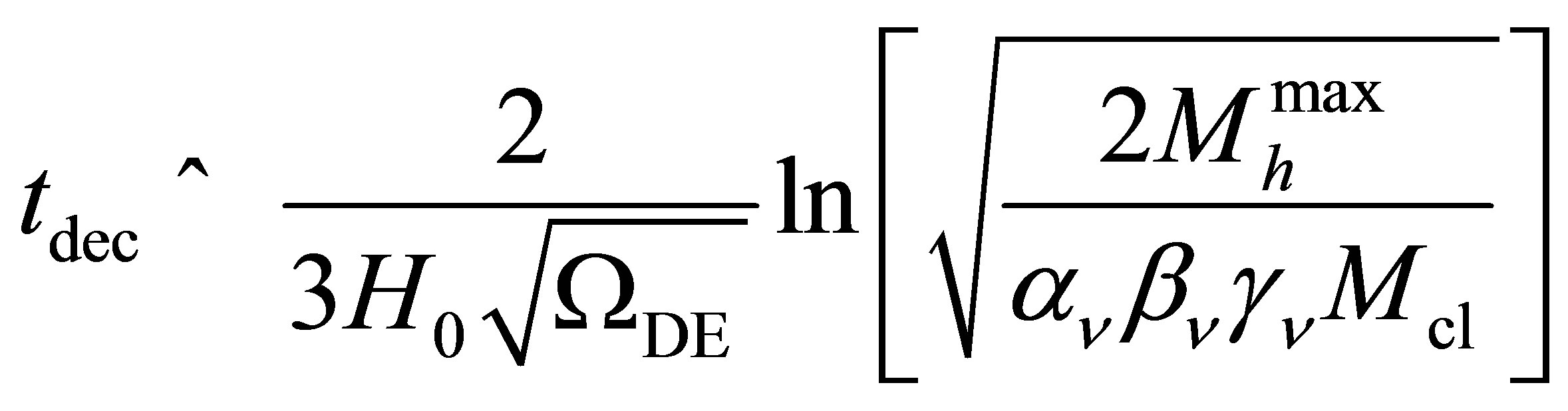 (59)
(59)
How soon would dark energy have to decay in order to avoid the implosion of galaxy clusters if ? Taking
? Taking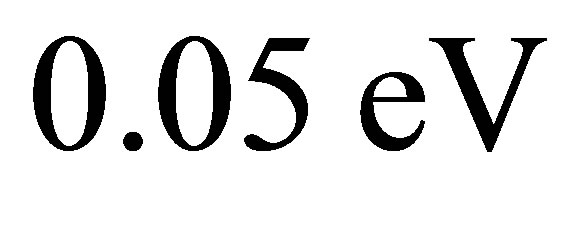
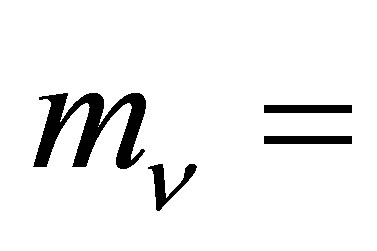 ,
, 
 and
and  one finds that
one finds that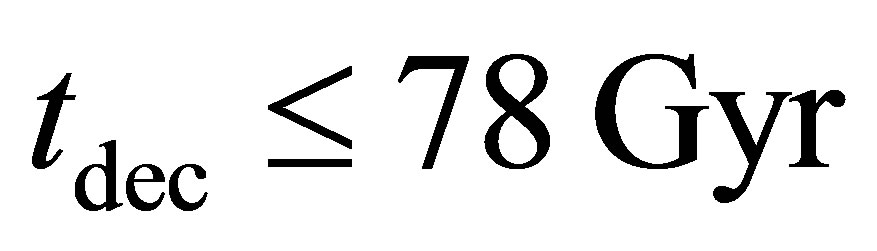 , with
, with  when
when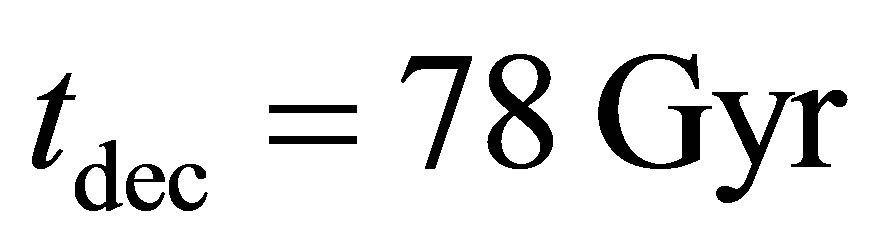 .
.
Stellar lifespans are limited, scaling as . Thus, the life-cultivating class F, G and K stars
. Thus, the life-cultivating class F, G and K stars  only remain active for 4 ~ 74 Gyr, a small fraction of the stelliferous era. Since planets are drawn into synchronous rotation with their host stars at a rate inversely proportional to the sixth power of orbital radius [88], otherwise habitable planets orbiting red dwarves become tidally-locked on timescales much shorter than was required for the evolution of the Earth’s biosphere. Tidally-heated planetary satellites also suffer from the same complication. While planets that remain habitable until dark energy decays may be rare, there should be many examples in each galaxy.
only remain active for 4 ~ 74 Gyr, a small fraction of the stelliferous era. Since planets are drawn into synchronous rotation with their host stars at a rate inversely proportional to the sixth power of orbital radius [88], otherwise habitable planets orbiting red dwarves become tidally-locked on timescales much shorter than was required for the evolution of the Earth’s biosphere. Tidally-heated planetary satellites also suffer from the same complication. While planets that remain habitable until dark energy decays may be rare, there should be many examples in each galaxy.
For neutrino haloes to sustain liquid oceans, dark energy must not decay too soon, otherwise the concentration of neutrinos will be insufficient to effectively support planetary heating even in the densest haloes. This condition is satisfied if
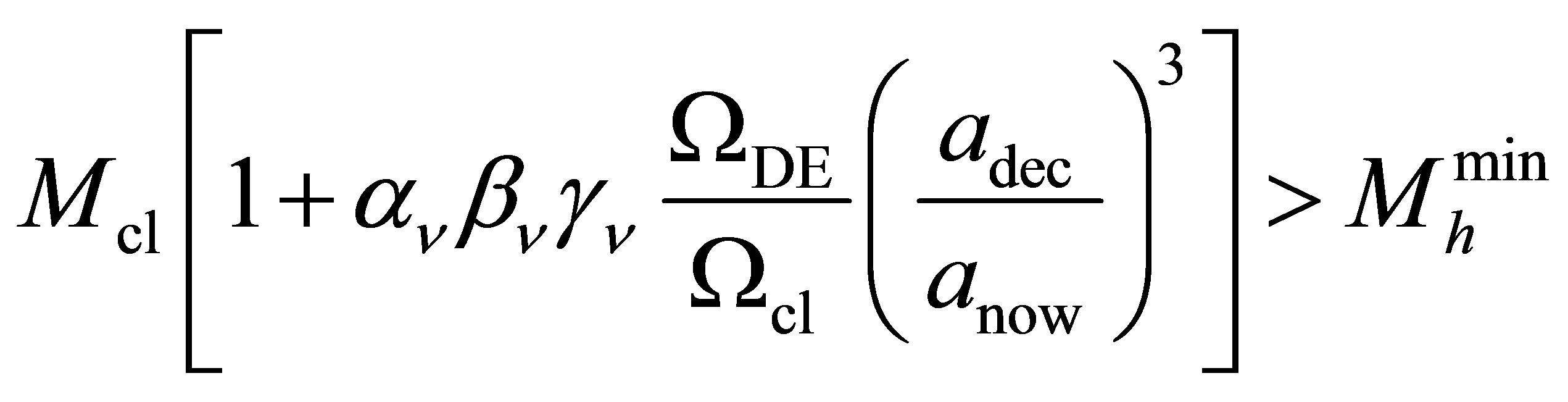 (60)
(60)
This in turn requires
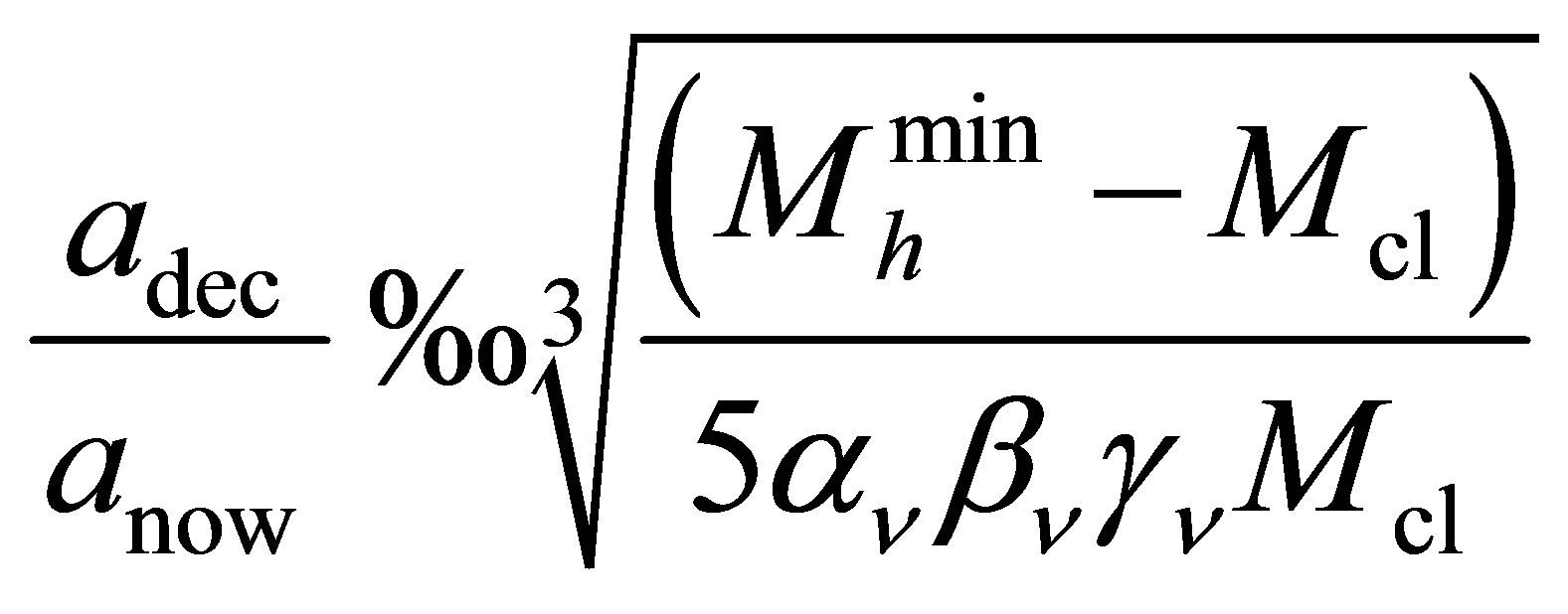 (61)
(61)
Hence, it is necessary that
 (62)
(62)
If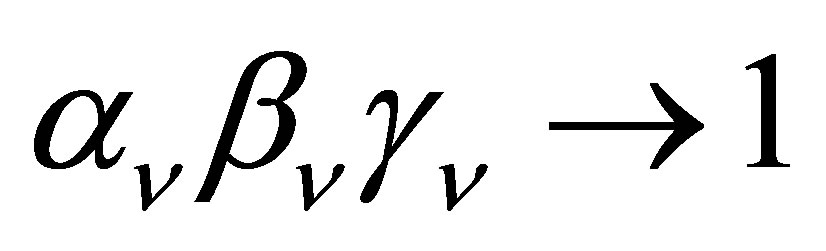 ,
,  and enhancement due to sterile neutrinos is ignored, dark energy would need to decay in 40 ~ 64 Gyr. The universe would be no more than six times its current age and so the anti-gravitational action of dark energy would not have had time to cause solar systems or galaxies to disperse which, roughly speaking, starts to occur after ~100 Gyr.
and enhancement due to sterile neutrinos is ignored, dark energy would need to decay in 40 ~ 64 Gyr. The universe would be no more than six times its current age and so the anti-gravitational action of dark energy would not have had time to cause solar systems or galaxies to disperse which, roughly speaking, starts to occur after ~100 Gyr.
The increasing dominance of dark energy with time causes an asymptotically exponential growth 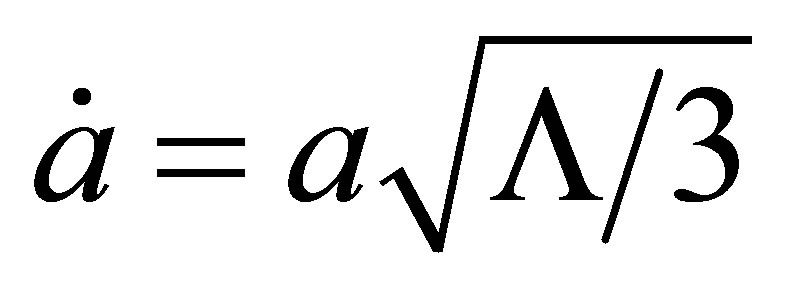 . In terms of the scale factor ratio, this can be expressed as
. In terms of the scale factor ratio, this can be expressed as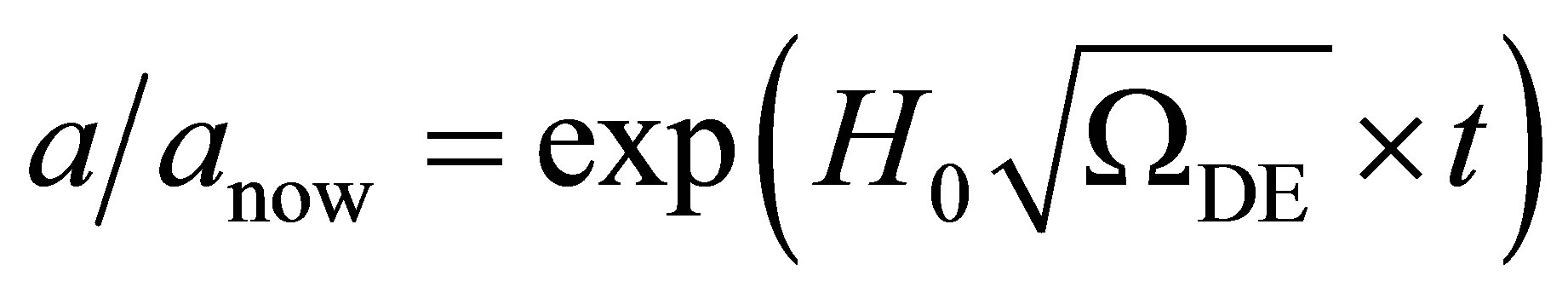 . Taking
. Taking  for 0.05 eV neutrino haloes, whatever the neutrino yield, the decay of dark energy would need to occur within a time window of width
for 0.05 eV neutrino haloes, whatever the neutrino yield, the decay of dark energy would need to occur within a time window of width  . Figure 8 illustrates the space of possibilities concerning the timing of dark energy’s decay
. Figure 8 illustrates the space of possibilities concerning the timing of dark energy’s decay 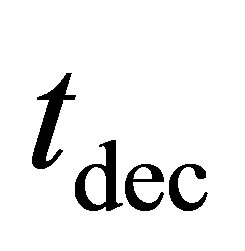 and the neutrino yield
and the neutrino yield 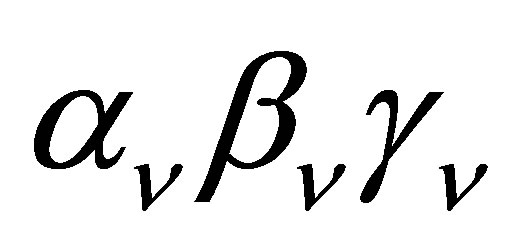 for a neutrino mass of 0.05 eV. While there is scope for
for a neutrino mass of 0.05 eV. While there is scope for  to be far smaller than one if decay occurs at later times, this runs an increased risk of galactic disintegration due to dark energy. Possible assistance from ster-
to be far smaller than one if decay occurs at later times, this runs an increased risk of galactic disintegration due to dark energy. Possible assistance from ster-

Figure 8. The relationship between the timing of the decay of dark energy and the galaxy cluster halo augmentation fraction 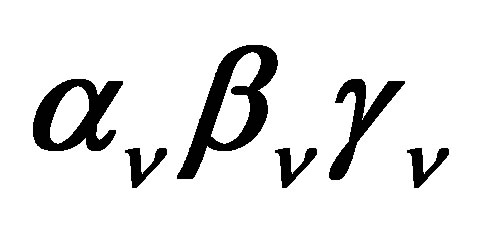 for 0.05 eV neutrinos and
for 0.05 eV neutrinos and 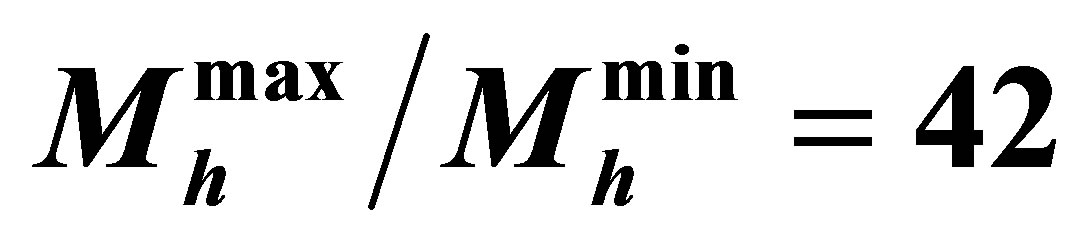 . Liquid oceans can be sustained if decay occurs within the shaded region. The left-most edge of this zone (dashed line) shifts further left if sterile neutrinos are able to provide significant assistance. A minority of life-cultivating stars are able to remain active for the necessary time period, though the Sun will not be amongst them.
. Liquid oceans can be sustained if decay occurs within the shaded region. The left-most edge of this zone (dashed line) shifts further left if sterile neutrinos are able to provide significant assistance. A minority of life-cultivating stars are able to remain active for the necessary time period, though the Sun will not be amongst them.
ile neutrino haloes has been ignored here, but could significantly relax the constraints obtained and reduce the need for haloes to be initially pushed close to their maximal masses.
8. Discussion
The traditional view has been that the stelliferous era will be followed by a highly inert degenerate era [31]. However, this work brings to attention an alternative possibility involving an aquatic era fostered by the decay of dark energy into neutrinos fuelling oceanic planets of a mass intermediate between that of the Moon and Uranus. It has previously been claimed that there is no biological necessity for the weak interaction: life-cultivating stars could still arise in a universe lacking it, albeit with carefully chosen initial conditions [89]. The need for three generations of fermions has also been questioned since everyday matter is composed of only first generation particles. Planetary heating by flavour-oscillating neutrinos could put a rather new complexion on these issues, lending weight to the notion that nature may not be devoid of purpose [90]. Anthropic reasoning may now be a bona fide topic of discussion [91], but its utility has until now been retrodictive, as in Hoyle’s deduction of a previously unknown nuclear resonance in 12C [92]. Since neutrinos and the weak interaction have not positively contributed to human evolution, our existence cannot explain their potential to 1) annihilate almost exclusively within iron-cored planets 2) regulate the core temperatures of planets via the favourable hcp/fcc boundary in iron 3) ensure consistent oceanic heat fluxes over a wide range of ambient concentrations and planetary masses or 4) sustain aquatic life efficiently into the distant future.
If hcp iron is almost uniquely capable of mediating neutrino annihilation, the difficulty of accurately predicting the future abundance of oceanic planets is largely circumvented. Whether or not one accepts that ferroelectricity in ice and ferromagnetism in iron, cobalt and nickel are able to regulate the formation of consistently sized oceanic planets from supernova ejecta is not crucial to this scenario. Should oceanic planets be unexpectedly rare, neutrinos would be consumed less rapidly and aquatic life sustained for longer. In the run-up to the putative decay of dark energy, there would be ample time for asteroids and comets to bombard planets and deliver water to their surfaces. Before the composition of the ejecta of SNIa had been studied in detail, microlensing data prompted the suggestion that oceanic planets might already be very abundant, even within the Milky Way [93]. Neither the Milky Way nor the Local Group have sufficient gravity to retain all supernova ejecta, but galaxy clusters do. If some galaxies provide better long-term habitation opportunities than others, and there is a certain urgency attached to relocation, it may cast light on the lingering mystery concerning extraterrestrial silence.
Indeed, it was this enduring puzzle that originally spurred investigation into a possible biological role for dark matter [33]. Galaxy clusters are the likeliest sites for neutrinos to condense [25]. Should dark energy decay in a favourable manner, habitable planets may be confined to clusters beyond the stelliferous era. Galactic mergers are a frequent occurrence there, leading to the formation of a dominant supergiant galaxy [94]. Computer simulations have observed the process operating on a timescale of 20 - 40 Gyr [95]. Hence, if dark energy decays in  60 Gyr, the formation of supergiant galaxies would be complete while satellite galaxies now orbiting on the periphery are likely to have spiralled away due to the repulsive influence of dark energy on larger scales. Extraterrestrial civilisations may have compelling reasons to believe that the remnant supergiant galaxies of galaxy clusters afford the best long-term opportunities for life. Even if they are uncertain, relocation would seem to be a wise precaution. Reasons for contact avoidance by any remnant civilisations shall be elucidated in forthcoming work.
60 Gyr, the formation of supergiant galaxies would be complete while satellite galaxies now orbiting on the periphery are likely to have spiralled away due to the repulsive influence of dark energy on larger scales. Extraterrestrial civilisations may have compelling reasons to believe that the remnant supergiant galaxies of galaxy clusters afford the best long-term opportunities for life. Even if they are uncertain, relocation would seem to be a wise precaution. Reasons for contact avoidance by any remnant civilisations shall be elucidated in forthcoming work.
Some 16 Mpc distant, Virgo is the nearest rich cluster to us. Figure 9 illustrates X-ray emissions from the high temperature plasma of its intracluster medium. It has a mass of  and a radius of ~2.2 Mpc [96]. Already containing ~2000 galaxies, it is still devouring galaxy groups. The Local Group and neighbouring galaxy groups typically have masses of
and a radius of ~2.2 Mpc [96]. Already containing ~2000 galaxies, it is still devouring galaxy groups. The Local Group and neighbouring galaxy groups typically have masses of 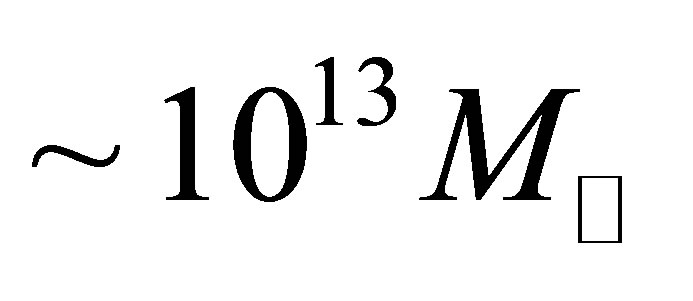 [86]. The Local Group was once thought to be caught up in the so-called Virgocentric flow, but the discovery of dark energy has changed this picture. The cosmic repulsion is already 4 ~ 7× the gravitational attraction of the Virgo cluster and though the Milky Way currently has an anomalous velocity towards it of 220 ± 70 km·s−1, it is nevertheless receding at 1004 ± 70 km·s−1 [97]. Only galaxies within 9 ~ 11 Mpc have any realistic chance of eventually merging with it.
[86]. The Local Group was once thought to be caught up in the so-called Virgocentric flow, but the discovery of dark energy has changed this picture. The cosmic repulsion is already 4 ~ 7× the gravitational attraction of the Virgo cluster and though the Milky Way currently has an anomalous velocity towards it of 220 ± 70 km·s−1, it is nevertheless receding at 1004 ± 70 km·s−1 [97]. Only galaxies within 9 ~ 11 Mpc have any realistic chance of eventually merging with it.
Relocation to the Virgo cluster need not entail an exodus or even a small-scale migration; it could be accomplished by means of autonomous probes that spawn life upon arrival. This may demand some sophistication in genetics, as would the adaptation of land-based animals to aquatic habitats. Heat released by long-term gravitational contraction has transformed the intergalactic gas of the Virgo cluster into a plasma. Magnetic braking of arriving spacecraft could utilise the plasma for deceleration with the scattering of charged particles offering a convenient cushion at the destination. This would avoid the need to transport enormous quantities of fuel for deceleration which might otherwise greatly prolong the voyage. A modest acceleration of 1-g is sufficient to attain a relativistic velocity within a year, and does not seem at all unrealistic using an antimatter-fuelled rocket. Acceleration would be followed by a period of coasting lasting several hundred million years with gradual deceleration at the destination being accomplished in, say, a million years.
According to the present analysis, planetary heating proceeds due to transitions involving the 4s electrons of
Figure 9. X-ray emitting plasma of the Virgo galaxy cluster. By the time dark energy is anticipated to decay, the plasma of the intracluster medium will have condensed into gas. Credit: Max-Planck-Institute für extraterrestrische Physik.
iron. The necessity of this 4s electron is satisfied in hcp iron but not in fcc iron. This is a crucial finding as the loss of the 4s electron not only prevents overheating but also provides thermoregulation at core temperatures ensuring a comfortable heat flux through the oceans. If neutrinos are Majorana fermions then opportunities for IPP would be approximately doubled. Observation of neutrinoless double-beta decay  would betray the non-conservation of lepton number but the present model does not demand that neutrinos be Majorana fermions.
would betray the non-conservation of lepton number but the present model does not demand that neutrinos be Majorana fermions.
Since liquid oceans can be sustained for a time  , near-maximal haloes of 0.05 eV neutrinos might permit an aquatic era lasting ~1025 years. Astoundingly lengthy as this is, there is no evidence that protons or leptons are unstable over this time period. Although
, near-maximal haloes of 0.05 eV neutrinos might permit an aquatic era lasting ~1025 years. Astoundingly lengthy as this is, there is no evidence that protons or leptons are unstable over this time period. Although  tapers off as the neutrino mass is reduced until planetary heating becomes impossible, sterile neutrinos have the potential to greatly boost this ratio at relatively little expense.
tapers off as the neutrino mass is reduced until planetary heating becomes impossible, sterile neutrinos have the potential to greatly boost this ratio at relatively little expense.
The maximum mass of a neutrino halo scales as 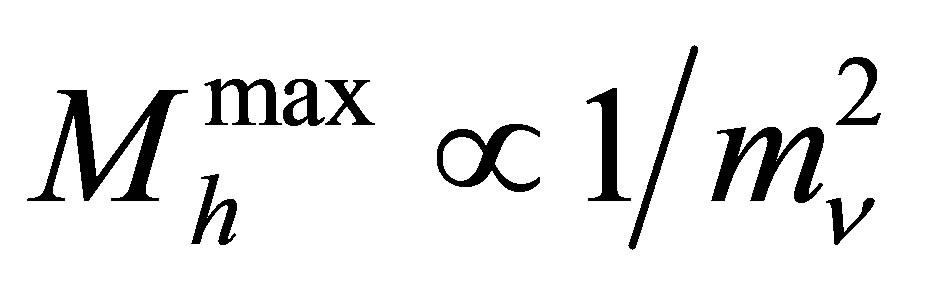 and determines the duration of the aquatic era that can be supported. In terms of the neutrino mass hierarchy, it is known that
and determines the duration of the aquatic era that can be supported. In terms of the neutrino mass hierarchy, it is known that 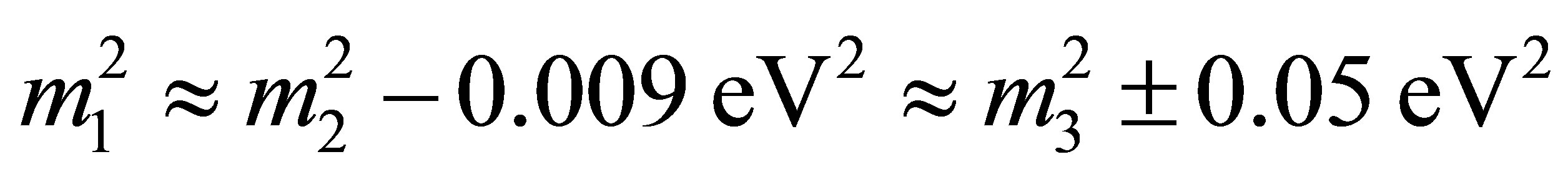 [6] and that the mass of the electron neutrino is primarily associated with
[6] and that the mass of the electron neutrino is primarily associated with  and
and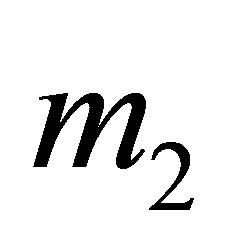 . In the inverted hierarchy
. In the inverted hierarchy 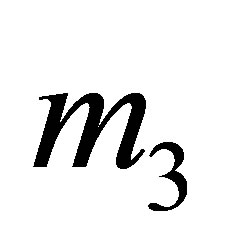 is smaller than
is smaller than 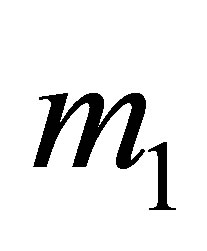 and
and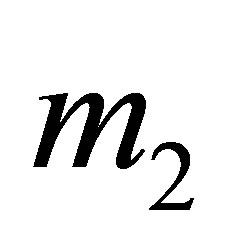 , allowing the maximum halo mass to be increased. This would not unduly compromise the ability of electron neutrinos to heat oceanic planets. Even if
, allowing the maximum halo mass to be increased. This would not unduly compromise the ability of electron neutrinos to heat oceanic planets. Even if 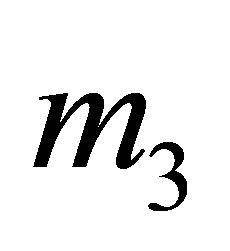 were to approach zero, the mass of the muon and tau neutrinos would only be halved. As the lighter neutrino flavours would move faster at a given momentum, the influx of neutrinos towards iron cores would be enhanced, partially compensating for the reduction in ambient neutrino densities. Thus, liquid oceans could be maintained for longer and hence more aquatic life would be supported if neutrinos have a strongly inverted mass hierarchy. As mentioned previously, experimental data is already hinting at an inverted mass hierarchy [7].
were to approach zero, the mass of the muon and tau neutrinos would only be halved. As the lighter neutrino flavours would move faster at a given momentum, the influx of neutrinos towards iron cores would be enhanced, partially compensating for the reduction in ambient neutrino densities. Thus, liquid oceans could be maintained for longer and hence more aquatic life would be supported if neutrinos have a strongly inverted mass hierarchy. As mentioned previously, experimental data is already hinting at an inverted mass hierarchy [7].
Due to the assistance of a sterile halo, the lone 4s electron in each atom of hcp iron is perfectly adequate for planetary heating to proceed. Iron is better suited as a mediator of planetary heating than other transition elements of the same period. Its sole challenger would be titanium, which also has a 4s electron in the ground state only a small fraction of one eV lower in energy than the 3d orbital it could instead occupy. Just as 56Ni decays radioactively to the highly stable 56Fe nuclide, boosting the abundance of iron, 48Cr could decay radioactively to 48Ti, which is stable. Note, however, that titanium, vanadium and chromium are not ferromagnetic, unlike iron, cobalt and nickel—and magnetism is of vital importance to the thermally-regulated formation of iron-rich protoplanets in the aftermath of supernovae. Furthermore, iron is far denser than titanium, important during planetary differentiation.
Annihilation of low energy neutrinos and antineutrinos is not altogether prohibited in vacuum. It proceeds mainly via the emission of three photons and has a cross section of 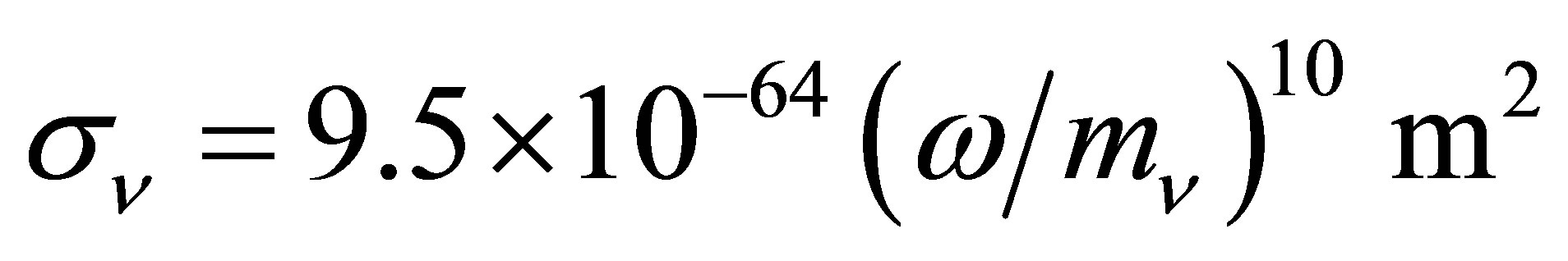 [98]. The mean time required for neutrinos to annihilate in vacuum is hence
[98]. The mean time required for neutrinos to annihilate in vacuum is hence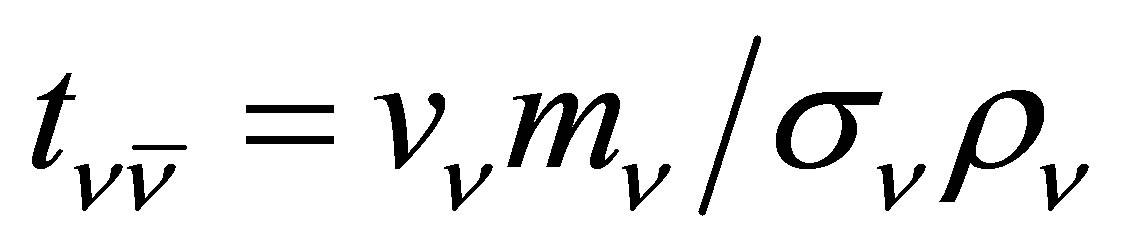 . Since
. Since , vacuum annihilation proceeds more slowly for low mass neutrinos with
, vacuum annihilation proceeds more slowly for low mass neutrinos with . For a halo of sub-relativistic 0.05 eV neutrinos, this is of order 1030 years, comfortably longer than the maximum duration of the aquatic era.
. For a halo of sub-relativistic 0.05 eV neutrinos, this is of order 1030 years, comfortably longer than the maximum duration of the aquatic era.
In some supersymmetric theories, the cosmological constant is required to be zero. Inflation sets a precedent for the current phase of accelerating expansion being due to dynamical dark energy and its decay into matter. As the energy density of dark energy is much lower than that of the inflationary field, there is a distinct possibility that dark energy is unable to decay until a threshold is met above which the production of low energy fermions occurs, i.e. nonrelativistic active neutrinos. The decay of dark energy to dark matter via unknown microphysics is a possibility that has been considered elsewhere [13] and it could already be happening [99]. If so, the neutrino haloes surrounding galaxy clusters may not be a direct legacy of the big bang but the result of actively ongoing dark energy decay. This would evade cosmological constraints on sterile neutrinos and leave room for (the still undetected) cold dark matter particles to play a role in structure formation. Nature may have other ways of gradually producing sterile neutrinos in the numbers required to concentrate active neutrinos, and the reprocessing of active neutrinos into sterile forms by black dwarves merits closer attention. However, the physics of sterile neutrinos remains unclear at present, clouding theoretical predictions of their production processes and cosmological abundance.
The unbridled growth of black holes capable of devouring neutrinos and even their host galaxies is of course a possible complication. Black holes of initial mass  immersed in a halo of mass
immersed in a halo of mass  would fully deplete a neutrino halo in a time:
would fully deplete a neutrino halo in a time:
 (63)
(63)
Halo mass influences 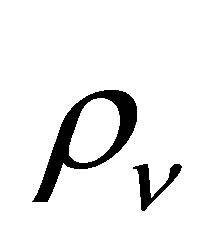 and
and  in such a way that
in such a way that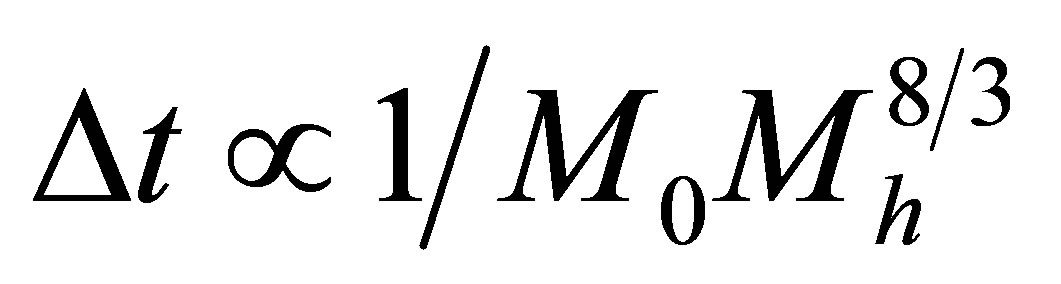 . Thus, the largest supermassive black holes located within the densest haloes might absorb neutrinos of a surrounding halo on timescales capable of substantially curtailing the aquatic era. Hawking evaporation can lead to the eradication of black holes, but is too slow to be relevant, taking ~1085 years for a
. Thus, the largest supermassive black holes located within the densest haloes might absorb neutrinos of a surrounding halo on timescales capable of substantially curtailing the aquatic era. Hawking evaporation can lead to the eradication of black holes, but is too slow to be relevant, taking ~1085 years for a 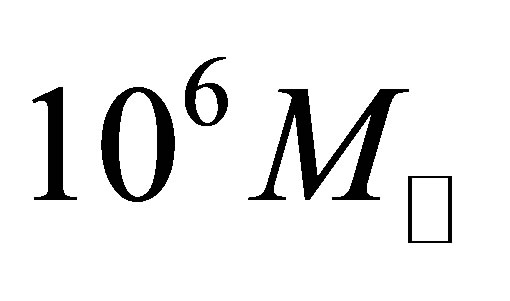 supermassive black hole. However, the accretion of phantom dark energy, whether gradually [100] or through the sudden onset of instabilities [101], is also able to erase black holes. It seems relevant to mention that the latest WMAP estimates marginally favour phantom dark energy with equation of state
supermassive black hole. However, the accretion of phantom dark energy, whether gradually [100] or through the sudden onset of instabilities [101], is also able to erase black holes. It seems relevant to mention that the latest WMAP estimates marginally favour phantom dark energy with equation of state  [3]. Could it be that the decay of dark energy will predominantly occur in the vicinity of the most massive black holes within galaxy clusters by mechanisms currently beyond our ken? Might black holes be transformed into white holes following some vacuum transition, allowing dark energy to be discharged? Perhaps this new cosmological vista implies that our comprehension of black hole physics is incomplete.
[3]. Could it be that the decay of dark energy will predominantly occur in the vicinity of the most massive black holes within galaxy clusters by mechanisms currently beyond our ken? Might black holes be transformed into white holes following some vacuum transition, allowing dark energy to be discharged? Perhaps this new cosmological vista implies that our comprehension of black hole physics is incomplete.
Much has been learnt about neutrinos in recent years. They undergo vacuum oscillations, allowing all flavours to participate in planetary heating. Their mass scale is simultaneously small enough that their haloes can completely enshroud galaxies, yet compatible with the lowest energy excitations of 4s electrons in hcp iron. The calculations presented here for the power neutrino annihilation can deliver to iron-cored planets are approximate yet adequate to demonstrate the feasibility of the proposal. Due to the brevity of this work and the need for its rapid dissemination, some of the important topics touched upon here have only been superficially investigated. There remains considerable scope to further refine these calculations, consolidate the findings and conduct more thorough research into the new avenues of investigation opened up by this work.
Neutrinos are ghostly particles, rarely scattering off matter. Hence, the densest neutrino haloes would barely impede planetary orbits, a useful quality for a planetary fuel. This is especially so of sterile neutrinos, whose existence now has to be taken very seriously. The major lingering uncertainties concerning the characteristics of neutrinos are likely to be resolved in coming years. Longer baseline oscillation experiments will settle the issue of the neutrino mass hierarchy, closer scrutiny of neutrino observations will help clarify whether sterile neutrinos exist and if so, what their properties are, and neutrinoless double beta decay searches are capable of determining whether neutrinos are Majorana particles. KaTriN will be able to rule out electron neutrino masses above 0.2 eV and may also yield useful information concerning sterile neutrinos [102-105].
The selective heating of habitable oceanic planets seems possible for electron neutrinos of a mass between 6 and 140 meV. Furthermore, if cosmological limits are correct and neutrinos have an inverted mass hierarchy, then constraints from oscillation experiments require that the electron neutrino mass lies between 45 and 66 meV. This range seems especially well-suited to long-term planetary heating. One therefore wonders whether the stelliferous era could be a fleeting prelude to a universe whose entropy-increasing processes are dominated by energy exchanges within oceanic planets. Might the cosmos currently be evolving towards a stable long-term configuration capable of sustaining aquatic life for a very protracted period? Water has been dubbed the matrix of life and is a superb biological medium: it affords comfortable accommodation requiring no shelter, buoyancy provides weight support, motion is possible in all three axes of space and, since ice has the peculiar property of being less dense than water, it can thermally insulate oceans. As ours is not an aquatic species, perhaps we are glimpsing here further vindication for the Copernican Principle. Neutrinos do not abide by the expectations of the standard model, possessing mass and undergoing flavour oscillations. The underlying physics responsible for these departures remains unclear at present but the potential importance of these particles to life not only here but throughout the universe insists that furthering our understanding of their exotic physics should be prioritised as a matter of urgency.
9. Acknowledgements
This work has benefited from sources of publicly accessible information including Wikipedia, NASA’s Astrophysics Data Service (ADS), the NIST website and the science library at Bangor University.
REFERENCES
- Y. Fukuda and the Super-Kamiokande Collaboration, Physical Review Letters, Vol. 81, 1998, p. 1158. http://dx.doi.org/10.1103/PhysRevLett.81.1158
- E. W. Otten and C. Weinheimer, Reports on Progress in Physics, Vol. 71, 2008, Article ID: 086201. http://dx.doi.org/10.1088/0034-4885/71/8/086201
- E. Komatsu, et al., Astrophysical Journal Letters, Vol. 192, 2011, p. 18.
- U. Seljak, A. Slosar and P. McDonald, Journal of Cosmology and Astroparticle Physics, Vol. 0610, 2006, Article ID: 014.
- S. A. Thomas, F. B. Abdalla and O. Lahav, Physical Review Letters, Vol. 105, 2010, Article ID: 031301. http://dx.doi.org/10.1103/PhysRevLett.105.031301
- K. Nakamura, et al, Journal of Physics G: Nuclear and Particle Physics, Vol. 37, 2010, Article ID: 075021. http://dx.doi.org/10.1088/0954-3899/37/7A/075021
- J. J.Fan and P. Langacker, Journal of High Energy Physics, Vol. 04, 2012, Article ID: 083.
- J. Drees, International Journal of Modern Physics A, Vol. 17, 2002, p. 3259. http://dx.doi.org/10.1142/S0217751X02012727
- R. H. Cyburt, B. D. Fields, K. A. Olive and E. Skillman, Astroparticle Physics, Vol. 23, 2005, pp. 313-323. http://dx.doi.org/10.1016/j.astropartphys.2005.01.005
- S. Perlmutter, G. Aldering, G. Goldhaber, et al., The Astrophysical Journal, Vol. 517, 1999, p. 565. http://dx.doi.org/10.1086/307221
- A. Riess, et al., The Astrophysical Journal, Vol. 116, 1998, p. 1009.
- S. E. Rugh and H. Zinkernagel, Studies in History and Philosophy of Modern Physics, Vol. 33, 2002, p. 663.
- P. J. E. Peebles and B. Ratra, Review Modern Physics, Vol. 75, 2003, pp. 559-606. http://dx.doi.org/10.1103/RevModPhys.75.559
- D. F. Mota and D. J. Shaw, Physical Review D, Vol. 75, 2007, Article ID: 063501. http://dx.doi.org/10.1103/PhysRevD.75.063501
- S. Ilic, M. Kunz, A. R. Liddle and J. A. Frieman, Physical Review D, Vol. 81, 2010, Article ID: 103502. http://dx.doi.org/10.1103/PhysRevD.81.103502
- L. Kofman, A. Linde and A. A. Starobinsky, Physical Review Letters, Vol. 73, 1994, pp. 3195-3198. http://dx.doi.org/10.1103/PhysRevLett.73.3195
- M. Bronstein, Physikalische Zeitschrift der Sowjetunion, Vol. 3, 1933, p. 73.
- A. W. Brookfield, C. van de Bruck, D. F. Mota and D. Tocchini-Valentini, Physical Review D, Vol. 73, 2006, Article ID: 083515. http://dx.doi.org/10.1103/PhysRevD.73.083515
- D. B. Kaplan, A. E. Nelson and N. Weiner, Physical Review Letters, Vol. 93, 2004, Article ID: 091801. http://dx.doi.org/10.1103/PhysRevLett.93.091801
- R. D. Peccei, Physical Review D, Vol. 71, 2005, Article ID: 023527. http://dx.doi.org/10.1103/PhysRevD.71.023527
- R. Cowsik and J. McClelland, The Astrophysical Journal, Vol. 180, 1973, pp. 7-10. http://dx.doi.org/10.1086/151937
- R. Fabbri, R. T. Jantzen and R. Ruffini, Astronomy & Astrophysics, Vol. 114, 1982, p. 219.
- B. M. Lewis, Proceedings of ASA, Vol. 4, 1981, p. 182.
- S. Singh and C.-P. Ma, Physical Review D, Vol. 67, 2003, Article ID: 023506. http://dx.doi.org/10.1103/PhysRevD.67.023506
- A. Ringwald and Y. Y. Y. Wong, Journal of Cosmology and Astroparticle Physics, Vol. 0412, 2004, Article ID: 005.
- F. Zwicky, The Astrophysical Journal, Vol. 86, 1937, p. 217. http://dx.doi.org/10.1086/143864
- J. A. Tyson and P. Fischer, Astrophysical Journal Letters, Vol. 446, 1995, p. L55. http://dx.doi.org/10.1086/187929
- Th. M. Nieuwenhuizen, Europhysics Letters, Vol. 86, 2009, Article ID: 59001. http://dx.doi.org/10.1209/0295-5075/86/59001
- C. Giunti and M. Laveder, Physical Review D, Vol. 84, 2011, Article ID: 093006. http://dx.doi.org/10.1103/PhysRevD.84.093006
- J. R. Kristiansen and O. Elgaroy, Astronomy & Astrophysics, Vol. 532, 2011, p. A67. http://dx.doi.org/10.1051/0004-6361/201117025
- F. C. Adams and G. Laughlin, Reviews of Modern Physics, Vol. 69, 1997, pp. 337-372. http://dx.doi.org/10.1103/RevModPhys.69.337
- L. Stixrude, Physical Review Letters, Vol. 108, 2012, Article ID: 055505. http://dx.doi.org/10.1103/PhysRevLett.108.055505
- R. J. Spivey, 2011. arXiv: 1101.4172.
- C. Blake, K. Glazebrook, T. M. Davis, et al., Monthly Notices of the Royal Astronomical Society, Vol. 418, 2011, pp. 1725-1735. http://dx.doi.org/10.1111/j.1365-2966.2011.19606.x
- P. A. Mazzali, F. K. Röpke, S. Benetti and W. Hillebrandt, Science, Vol. 315, 2007, pp. 825-828. http://dx.doi.org/10.1126/science.1136259
- G. Fontaine, P. Brassard and P. Bergeron, Publications of the Astronomical Society of the Pacific, Vol. 113, 2001. http://dx.doi.org/10.1086/319535
- M. Tanaka, et al., Monthly Notices of the Royal Astronomical Society, Vol. 410, 2011, p. 1725.
- H. Fukazawa, A. Hoshikawa, Y. Ishii, B. C. Chakoumakos and J. A. Fernandez-Baca, The Astrophysical Journal Letters, Vol. 652, 2006, p. L57. http://dx.doi.org/10.1086/510017
- M. J. Iedema, M. J. Dresser, D. L. Doering, J. B. Rowland, W. P. Hess, A. A. Tsekouras and J. P. Cowin, The Journal of Physical Chemistry B, Vol. 102, 1998, pp. 9203-9214. http://dx.doi.org/10.1021/jp982549e
- H. Wang, R. C. Bell, M. J. Iedema, A. A. Tsekouras and J. P. Cowin, The Astrophysical Journal, Vol. 620, 2005, p. 1027. http://dx.doi.org/10.1086/427072
- R. Fu, R. J. O’Connell and D. D. Sasselov, The Astrophysical Journal, Vol. 708, 2010, p. 1326. http://dx.doi.org/10.1088/0004-637X/708/2/1326
- M. J. Kuchner, The Astrophysical Journal, Vol. 596, 2003, p. L105. http://dx.doi.org/10.1086/378397
- A. Leger, F. Selsis, C. Sotin, T. Guillot, D. Despois, D. Mawet, M. Ollivier, A. Labèque, C. Valette, F. Brachet, B. Chazelas and H. Lammer, Icarus, Vol. 169, 2004, pp. 499-504. http://dx.doi.org/10.1016/j.icarus.2004.01.001
- F. Selsis, B. Chazelas, P. Bordé, M. Ollivier, F. Brachet, M. Decaudin, F. Bouchy, D. Ehrenreich, J.-M. Grieß- meier, H. Lammer, C. Sotin, O. Grasset, C. Moutou, P. Barge, M. Deleuil, D. Mawet, D. Despois, J. F. Kasting and A. Léger, Icarus, Vol. 191, 2007, pp. 453-468. http://dx.doi.org/10.1016/j.icarus.2007.04.010
- N. H. Fletcher, “Chemical Physics of Ice,” Cambridge University Press, Cambridge, 1970. http://dx.doi.org/10.1017/CBO9780511735639
- A. M. Hofmeister and R. E. Criss, Tectonophysics, Vol. 395, 2005, pp. 159-177. http://dx.doi.org/10.1016/j.tecto.2004.09.006
- M. Monnereau and D. A.Yuen, Earth and Planetary Science Letters, Vol. 202, 2002, pp. 171-183. http://dx.doi.org/10.1016/S0012-821X(02)00756-2
- B. Yan, T. Hua and J. Fu-Qian, Journal of Physics: Condensed Matter, Vol. 14, 2002, Article ID: 10849. http://dx.doi.org/10.1088/0953-8984/14/41/316
- H.-Y. Chiu, “Stellar Physics,” Vol. I, Blaisdell, Waltham, 1968, pp. 261-264.
- G. Beaudet, V. Petrosian and E. E. Salpeter, Astrophysical Journal, Vol. 150, 1967, p. 979. http://dx.doi.org/10.1086/149398
- H.-Y. Chiu and R. Stabler, Physical Review, Vol. 122, 1961, pp. 1317-1322. http://dx.doi.org/10.1103/PhysRev.122.1317
- D. A. Dicus, Physical Review D, Vol. 6, 1972, pp. 941- 949. http://dx.doi.org/10.1103/PhysRevD.6.941
- S. I. Dutta, S. Ratković and M. Prakash, Physical Review D, Vol. 69, 2004, Article ID: 023005. http://dx.doi.org/10.1103/PhysRevD.69.023005
- N. Itoh, T. Adachi, M. Nakagawa, Y. Kohyama and H. Munakata, Astrophysical Journal, Vo. 339, 1989, pp. 354-364. http://dx.doi.org/10.1086/167301
- V. I. Ritus, Soviet Physics-JETP, Vol. 14, 1962, p. 195.
- P. J. Schinder, D. N. Schramm, P. J. Wiita, S. H. Margolis and D. L. Tubbs, Astrophysical Journal, Vol. 313, 1987, pp. 531-542. http://dx.doi.org/10.1086/164993
- E. Majorana, Nuovo Cimento, Vol. 14, 1937, pp. 171-184. http://dx.doi.org/10.1007/BF02961314
- J. Sugar and C. Corliss, Journal of Physical and Chemical Reference Data, Vol. 14, 1985, 664 p.
- S. A. Bonev, E. Schwegler, T. Ogitsu and G. Galli, Nature, Vol. 431, 2004, p. 669. http://dx.doi.org/10.1038/nature02968
- [61] V. Iota, J.-H. Park Klepeis, C.-S. Yoo, J. Lang, D. Haskel and G. Srajer, Applied Physics Letters, Vol. 90, 2007, Article ID: 042505. http://dx.doi.org/10.1063/1.2434184
- [62] L. D. Landau and E. M. Lifshitz., “Statistical Physics,” Pergamon Press, Oxford, pp. 324-342.
- [63] F. De Paolis, G. Ingrosso, A. A. Nucita, D. Orlando, S. Capozziello and G. Iovane, Astronomy & Astrophysics, Vol. 376, 2001, pp. 853-860. http://dx.doi.org/10.1051/0004-6361:20010929
- [64] L. de Broglie, Nature, Vol. 112, 1923, p. 540. http://dx.doi.org/10.1038/112540a0
- [65] P. A. M. Dirac, Proceedings of the Royal Society of London A, Vol. 117, 1928, p. 778. http://dx.doi.org/10.1098/rspa.1928.0023
- [66] P. A. M. Dirac, “Principles of Quantum Mechanics,” Clarendon Press, Oxford, 1958.
- [67] K. McFarland, 2008, arXiv: 0804.3899
- [68] J. Kopp, M. Maltoni and T. Schwetz, Physical Review Letters, Vol. 107, 2011, Article ID: 091801. http://dx.doi.org/10.1103/PhysRevLett.107.091801
- [69] J. Hamann, S. Hannestad, G. Raffelt and Y. Wong, Journal of Cosmology and Astroparticle Physics, Vol. 09, 2011, Article ID: 034.
- [70] E. M. Kantor and M. E. Gusakov, Monthly Notices of the Royal Astronomical Society, Vol. 381, 2007, pp. 1702- 1710. http://dx.doi.org/10.1111/j.1365-2966.2007.12342.x
- [71] P.-H. Gu and U. Sarkar, Physical Review D, Vol. 81, 2010, Article ID: 033001. http://dx.doi.org/10.1103/PhysRevD.81.033001
- [72] R. J. Michney and R. R. Caldwell, Journal of Cosmology and Astroparticle Physics, Vol. 01, 2007, Article ID: 014.
- [73] L. Amendola, Physical Review D, Vol. 62, 2000, Article ID: 043511. http://dx.doi.org/10.1103/PhysRevD.62.043511
- [74] J. R. Bhatt, B. R. Desai, E. Ma, G. Rajasekaran and U. Sarkar, Physics Letters B, Vol. 687, 2010, pp. 75-78. http://dx.doi.org/10.1016/j.physletb.2010.02.079
- [75] M. Blasone, A. Capolupo, S. Capozziello, S. Carloni and G. Vitiello, Physics Letters A, Vol. 323, 2004, pp. 182- 189. http://dx.doi.org/10.1016/j.physleta.2004.02.004
- [76] A. Capolupo, S. Capozziello and G. Vitiello, Physics Letters A, Vol. 363, 2007, pp. 53-56. http://dx.doi.org/10.1016/j.physleta.2006.10.084
- [77] S. Das, P. S. Corasaniti and J. Khoury, Physical Review D, Vol. 73, 2006, Article ID: 083509. http://dx.doi.org/10.1103/PhysRevD.73.083509
- [78] P.-H. Gu, H.-J. He and U. Sarkar, Journal of Cosmology and Astroparticle Physics, Vol. 11, 2007, Article ID: 016.
- [79] M. Kaplinghat and A. Rajamaran, Physical Review D, Vol. 75, 2007, Article ID: 103504. http://dx.doi.org/10.1103/PhysRevD.75.103504
- [80] M. Li, X. D. Li, S. Wang and Y. Wang, Communications in Theoretical Physics, Vol. 56, 2011, pp. 525-604. http://dx.doi.org/10.1088/0253-6102/56/3/24
- [81] A. de la Macorra, Astroparticle Physics, Vol. 28, 2007, pp. 196-204. http://dx.doi.org/10.1016/j.astropartphys.2007.05.005
- [82] W. Zimdahl and D. Pavon, Physics Letters B, Vol. 521, 2001, pp. 133-138. http://dx.doi.org/10.1016/S0370-2693(01)01174-1
- [83] S. Antusch, S. Das and K. Dutta, Journal of Cosmology and Astroparticle Physics, Vol. 10, 2008, Article ID: 016.
- [84] O. E. Bjaelde and S. Hannestad, Physical Review D, Vol. 81, 2010, Article ID: 063001. http://dx.doi.org/10.1103/PhysRevD.81.063001
- [85] R. Fardon, A. E. Nelson and N. Weiner, Journal of High Energy Physics, Vol. 03, 2006, Article ID: 042.
- [86] R. Horvat, Journal of Cosmology and Astroparticle Physics, Vol. 01, 2006, Article ID: 015.
- [87] I. D. Karachentsev, Astronomical Journal, Vol. 129, 2005, p. 178. http://dx.doi.org/10.1086/426368
- [88] M. Gitti and S. Schindler, Astronomy & Astrophysics, Vol. 427, 2004, pp. L9-L12. http://dx.doi.org/10.1051/0004-6361:200400086
- [89] B. Gladman, D. D. Quinn, P. Nicholson and R. Rand, Icarus, Vol. 122, 1996, pp. 166-192. http://dx.doi.org/10.1006/icar.1996.0117
- [90] R. Harnik, G. D. Kribs and G. Perez, Physical Review D, Vol. 74, 2006, Article ID: 035006. http://dx.doi.org/10.1103/PhysRevD.74.035006
- [91] E. R. Harrison, The Quarterly Journal of the Royal Astronomical Society, Vol. 36, 1995, p. 193.
- [92] M. Livio and M. J. Rees, Science, Vol. 309, 2005, pp. 1022-1023. http://dx.doi.org/10.1126/science.1111446
- [93] F. Hoyle, Astrophysical Journal Supplement, Vol. 1, 1954, p. 121. http://dx.doi.org/10.1086/190005
- [94] D. Ehrenreich and A. Cassan, Astronomische Nachrichten, Vol. 88, 2006, p. 789.
- [95] J. P. Ostriker, Proceedings of Tallin Symposium, D. Reidel Publishing Co, Dordrecht,1977, pp. 357-374.
- [96] J. Dubinski, The Astrophysical Journal, Vol. 502, 1998, p. 141. (for simulations see http://www.cita.utoronto.ca/
 dubinski/bigcluster.html)
dubinski/bigcluster.html) - [97] J. L. Tonry, J. P. Blakeslee, E. A. Ajhar and A. Dressler, The Astrophysical Journal, Vol. 530, 2000, p. 625. http://dx.doi.org/10.1086/308409
- [98] A. D. Chernin, et al., Astronomy & Astrophysics, Vol. 520, 2010, p. A104.
- [99] T. De Graaf and H. A. Tolhoek, Nuclear Physics, Vol. 81, 1966, p. 596.
- [100] U. Alam, V. Sahni and A. Starobinsky, Journal of Cosmology and Astroparticle Physics, Vol. 04, 2003, Article ID: 002.
- [101] E. Babichev, V. Dokuchev and Yu. Eroshenko, Physcial Review Letters, Vol. 93, 2004, Article ID: 021102. http://dx.doi.org/10.1103/PhysRevLett.93.021102
- [102] X. He, B. Wang, S.-F. Wu and C.-Y. Lin, Physics Letter B, Vol. 673, 2009, pp. 156-160. http://dx.doi.org/10.1016/j.physletb.2009.02.002
- [103] C. Weinheimer and the KATRIN collaboration, Progress in Particle and Nuclear Physics, Vol. 48, 2002, pp. 141- 150. http://dx.doi.org/10.1016/S0146-6410(02)00120-5
- [104] C. Tachinami, H. Senshu and S. Ida, The Astrophysical Journal, Vol. 726, 2011, p. 70. http://dx.doi.org/10.1088/0004-637X/726/2/70
- [105] F. P. An, et al., Physcial Review Letters, Vol. 108, 2012, Article ID: 171803. http://dx.doi.org/10.1103/PhysRevLett.108.171803
- [106] P. C. de Holanda and A. Yu. Smirnov, Physcial Review D, Vol. 83, 2011, Article ID: 113011. http://dx.doi.org/10.1103/PhysRevD.83.113011
Appendix A: Maximal Mass of Planets Containing Hcp Iron
Using a Vinet equation of state, the structure of terrestrial planets in the mass range 0.1 - 10 MÅ with a realistic thermal profile has been calculated [103]. This appendix shall extrapolate from these results an estimate for the planetary mass at which the density of iron at the core approaches that of the hcp-fcc phase transition at 57 Mbar. The limiting density at the phase transition is 33.9 g·cm-3 [32] and central densities in 0.1 - 10 MÅ planets range between 10 and 29 g·cm-3 [103].
By taking logs of planetary masses and central densities, and fitting a fourth order polynomial to the data, it is estimated that planets with a core pressure of 57 Mbar have a mass of ~13.5 MÅ. Using linear interpolation from the two nearest points, the estimate ~15.3 MÅ is obtained. Planets whose central pressures marginally exceed 57 Mbar are anticipated to contain significant quantities of hcp iron at radii where the pressure falls below the hcp-fcc phase transition threshold. Therefore, this work adopts a mass of 15 MÅ as the upper limit for oceanic planets receiving heat from neutrino annihilation which, as can be seen from the plot of Figure A1, has an acceptably small uncertainty.
Appendix B: Low Energy Electron Excitations in Iron
Within 0.98 eV of the ground state, the available energy states for singly ionized atomic iron (Fe II) are the following:
| Configuration | Term | | Energy (eV) |
| | a6D | 9/2 | 0.0000 |
| | a6D | 7/2 | 0.0477 |
| | a6D | 5/2 | 0.0828 |
| | a6D | 3/2 | 0.1069 |
| | a6D | 1/2 | 0.1211 |
| | a4F | 9/2 | 0.2322 |
| | a4F | 7/2 | 0.3013 |
| | a4F | 5/2 | 0.3519 |
| | a4F | 3/2 | 0.3865 |
Only left-handed electrons are able to participate in weak interactions. If neutrinos are not Majorana fermions then lepton number must be conserved during neutrino annihilation. When a left-handed 4s electron receives the annihilation energy and transitions to a different orbital, energy-momentum conservation demands the emission of a photon so the total angular momentum  of the atom must change by
of the atom must change by . However, if neutrinos and antineutrinos are indistinguishable then their spins need not cancel for annihilation to occur, allowing
. However, if neutrinos and antineutrinos are indistinguishable then their spins need not cancel for annihilation to occur, allowing  to change by
to change by 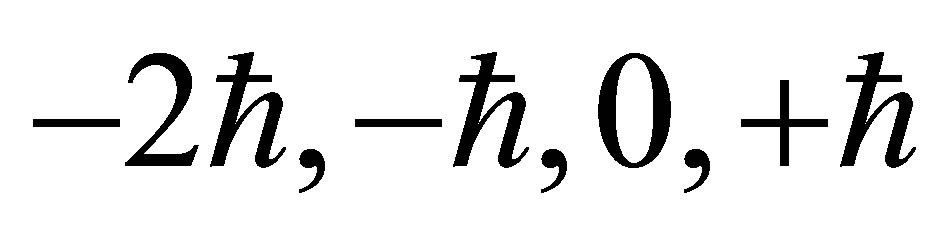 or
or  . This limits the possible transitions capable of mediating neutrino annihilation to those plotted in Figure B1 and listed below:
. This limits the possible transitions capable of mediating neutrino annihilation to those plotted in Figure B1 and listed below:

Figure A1. Interpolation of the planetary mass at which the core density of iron reaches the limit causing a hcp®fcc transition, irrespective of core temperature.
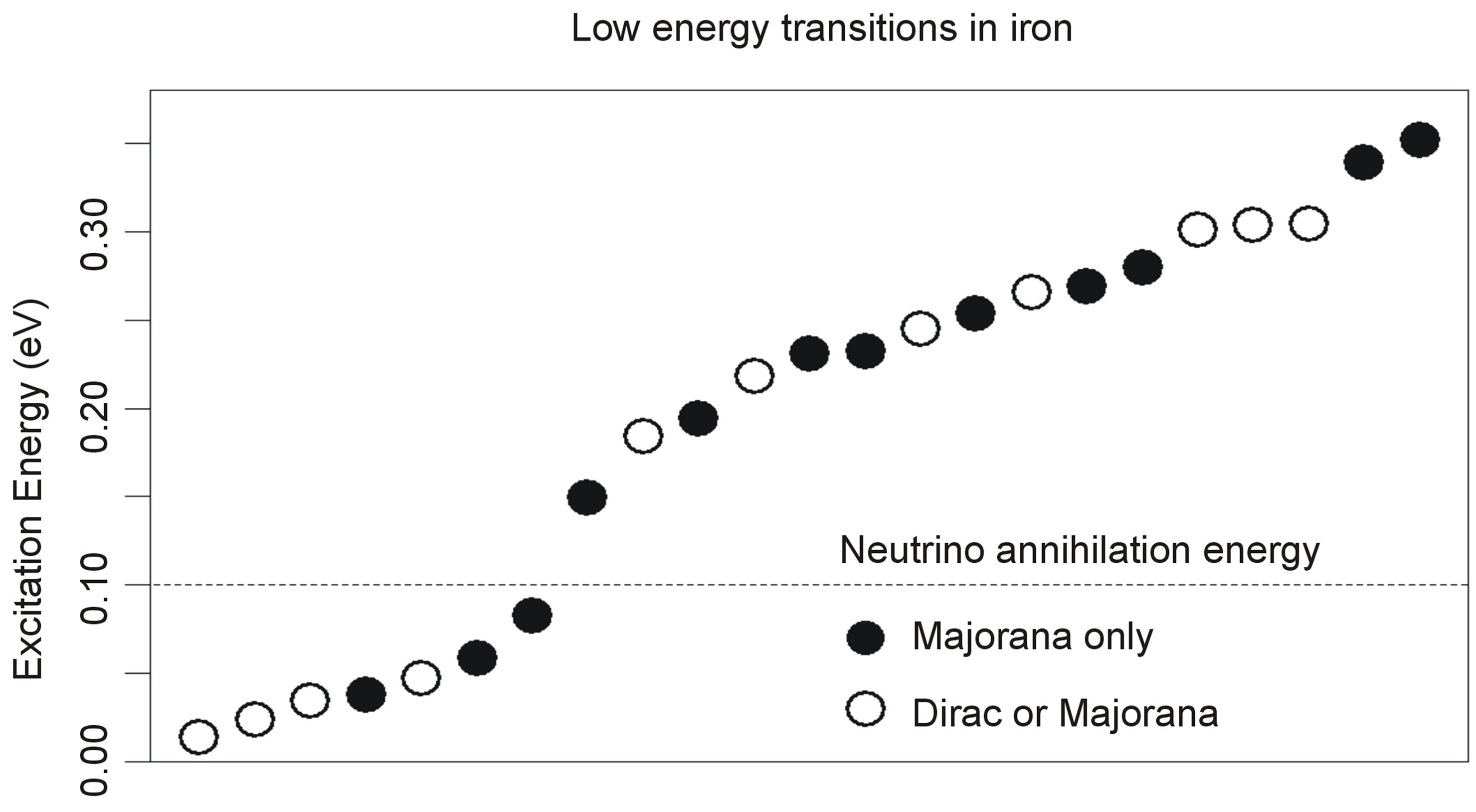
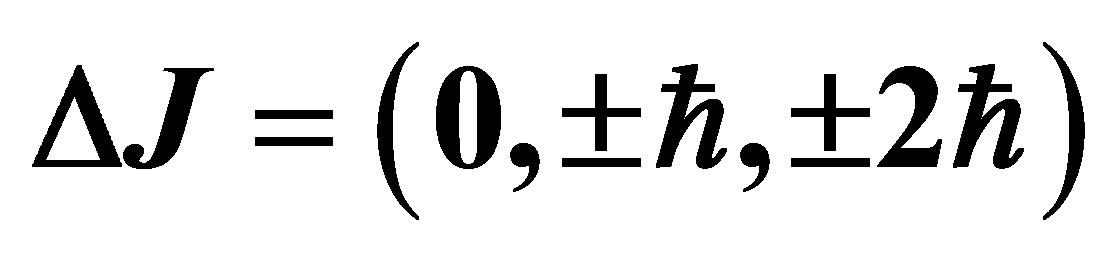 transitions within 0.98 eV of the ground state in Fe II. As increasing pressure is applied to iron these energies tend to decrease towards zero until, at the hcp/fcc phase transition, the energies of the
transitions within 0.98 eV of the ground state in Fe II. As increasing pressure is applied to iron these energies tend to decrease towards zero until, at the hcp/fcc phase transition, the energies of the 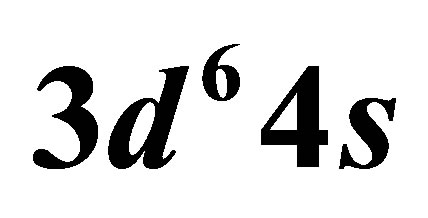 and
and 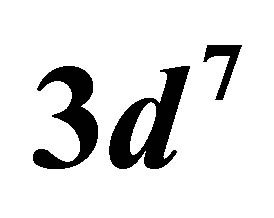 ground states coincide.
ground states coincide.
| Transition | Majorana | Excitation energy (eV) |
| | × | 0.0142 |
| | × | 0.0241 |
| | × | 0.0351 |
| | ü | 0.0383 |
| | × | 0.0477 |
| | ü | 0.0592 |
| | ü | 0.0828 |
| | ü | 0.1494 |
| | × | 0.1845 |
| | ü | 0.1944 |
| | × | 0.2185 |
| | ü | 0.2308 |
| | ü | 0.2322 |
| | × | 0.2450 |
| | ü | 0.2536 |
| | × | 0.2654 |
| | ü | 0.2691 |
| | ü | 0.2796 |
| | × | 0.3013 |
| | × | 0.3037 |
| | × | 0.3042 |
| | ü | 0.3388 |
| | ü | 0.3519 |
Appendix C: Effect of Flavour Oscillation on Electron Neutrino Availability
Neutrinos undergo vacuum oscillations due to differences between the mass eigenstates, an interference effect caused by propagation velocities being a function of mass. Experiments have now succeeded in measuring the mixing angles allowing the impact of oscillations on the availability of neutrinos to be estimated. The probability that a neutrino of momentum  initially in eigenstate
initially in eigenstate 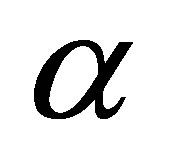 is later observed in eigenstate
is later observed in eigenstate 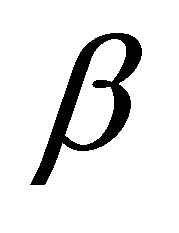 having travelled a distance
having travelled a distance  through a vacuum is given by:
through a vacuum is given by:
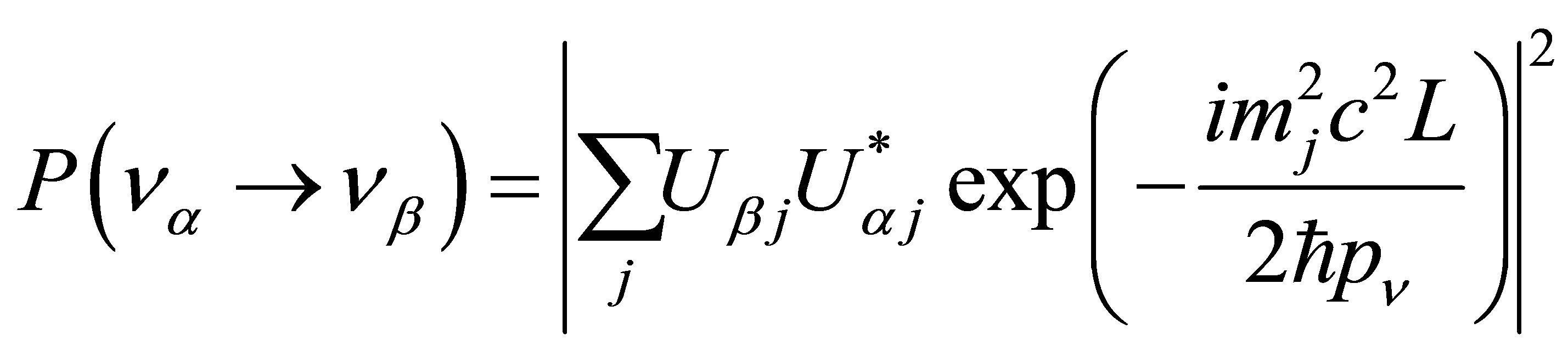 (C1)
(C1)
where 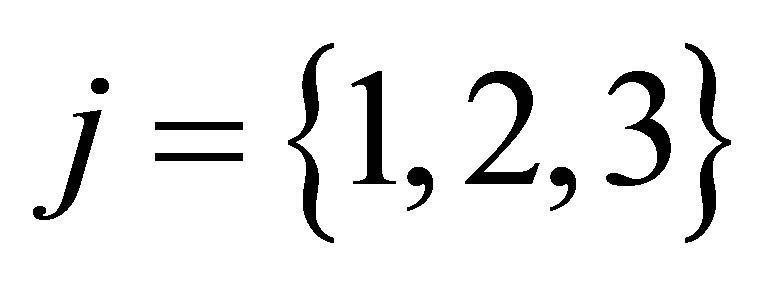 for three generations of neutrinos and
for three generations of neutrinos and  is the PMNS matrix. Oscillation probabilities are independent of any Majorana phases in
is the PMNS matrix. Oscillation probabilities are independent of any Majorana phases in  and depend only on distance travelled, neutrino energy and differences in the squared neutrino masses. Using this prescription, and letting
and depend only on distance travelled, neutrino energy and differences in the squared neutrino masses. Using this prescription, and letting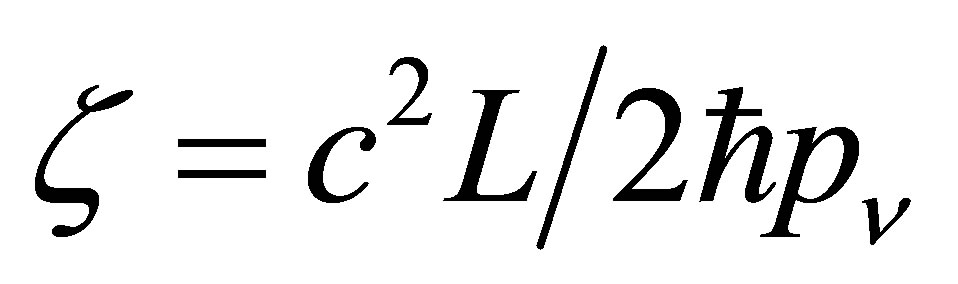 , the survival probability
, the survival probability  for an electron neutrino can be expressed as shown in Equation C2 (see foot of page).
for an electron neutrino can be expressed as shown in Equation C2 (see foot of page).
The mean value of 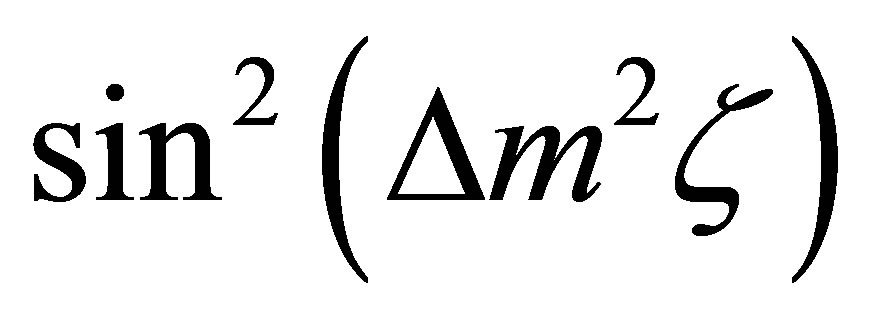 as L varies is:
as L varies is:
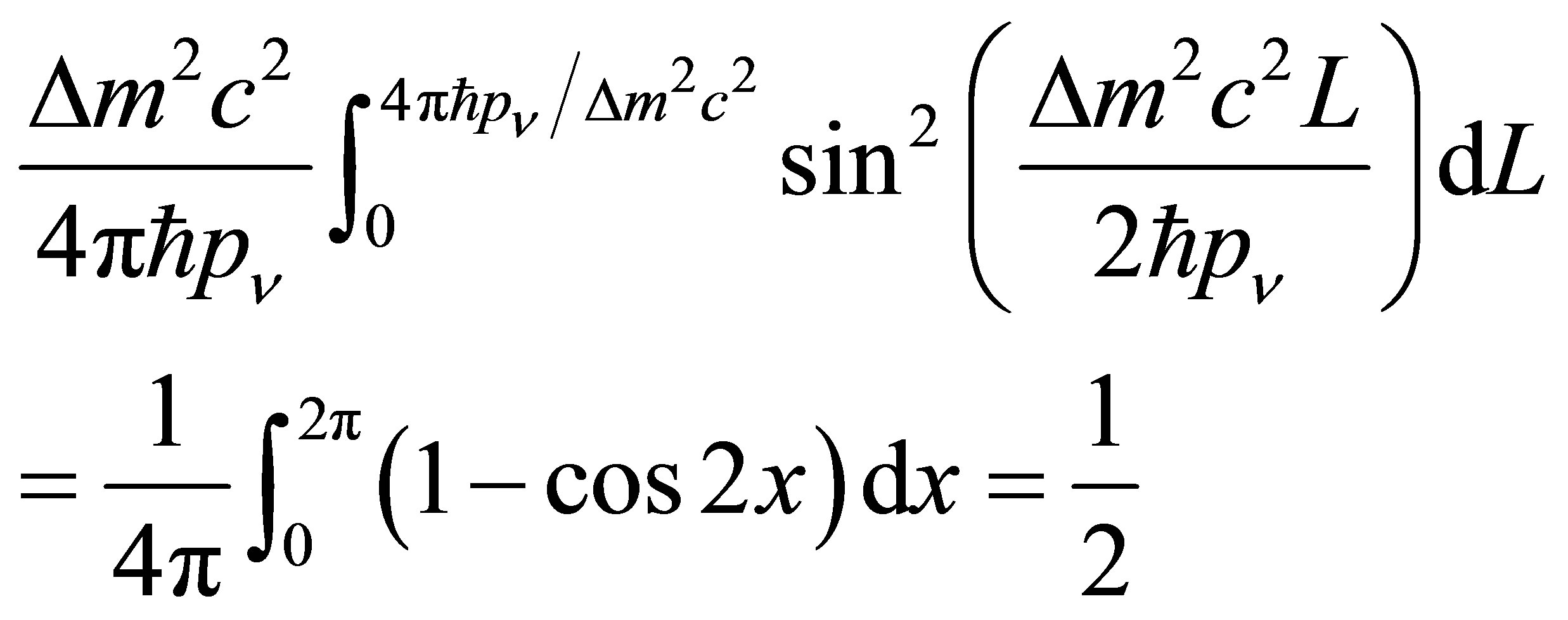 (C3)
(C3)
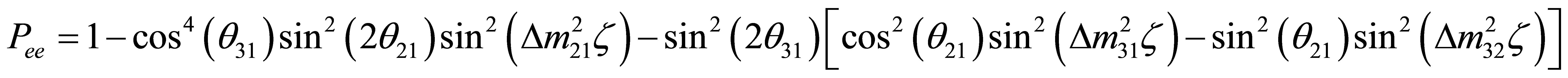 (C2)
(C2)
Therefore, the mean value of  simplifies to:
simplifies to:
 (C4)
(C4)
Taking  [6] and
[6] and 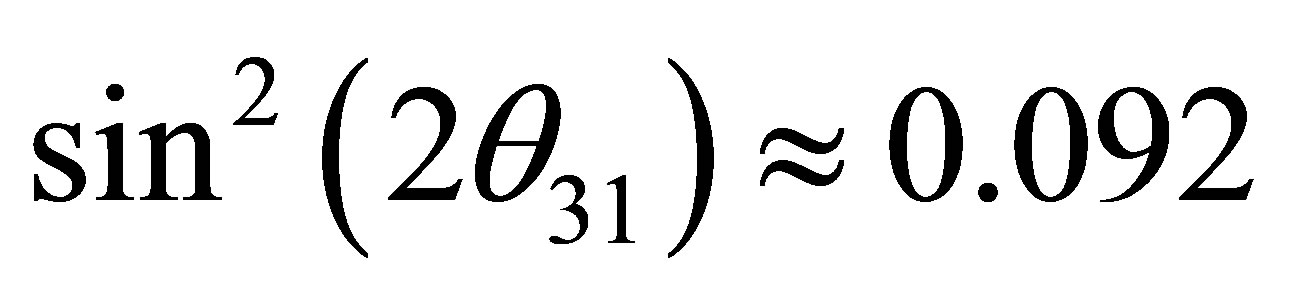 [104], one has
[104], one has  and
and 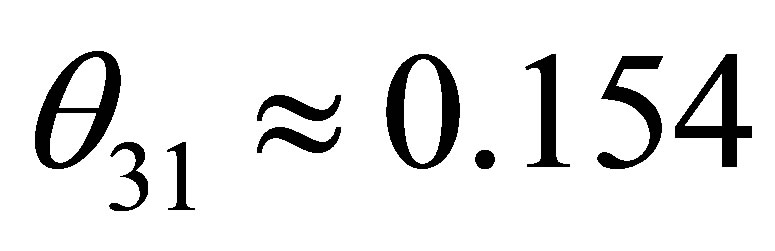 giving:
giving:
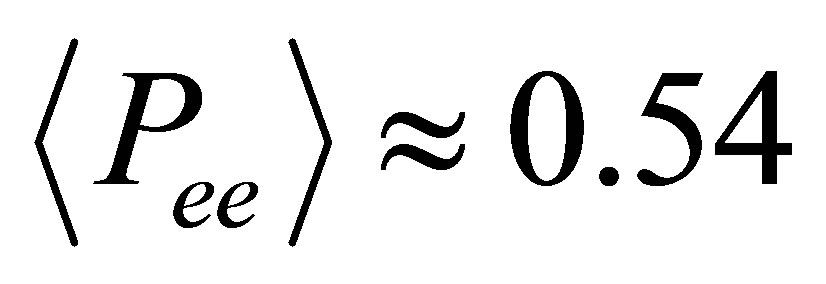 (C5)
(C5)
This result is in good agreement with an independent estimate of  for the low energy regime [105] and would be expected to boost planetary heating by a modest factor of
for the low energy regime [105] and would be expected to boost planetary heating by a modest factor of  compared neutrinos spending equal amounts of time as each flavour. Note also that the largest amplitude oscillations also have the longest wavelength and are associated with
compared neutrinos spending equal amounts of time as each flavour. Note also that the largest amplitude oscillations also have the longest wavelength and are associated with 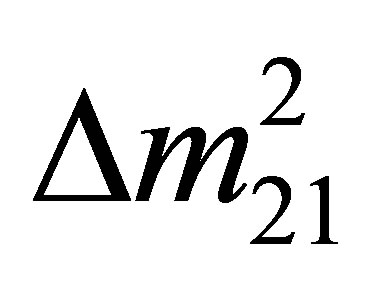 since
since 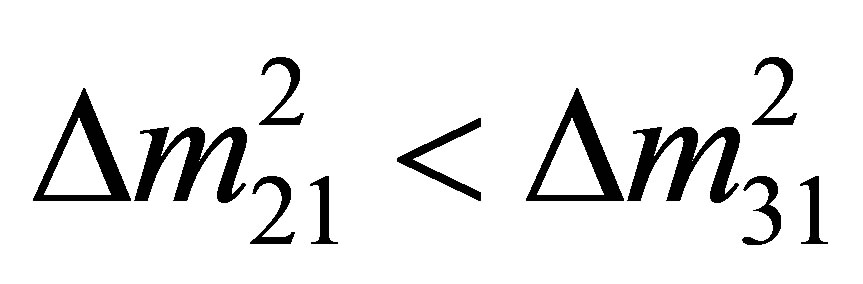 and
and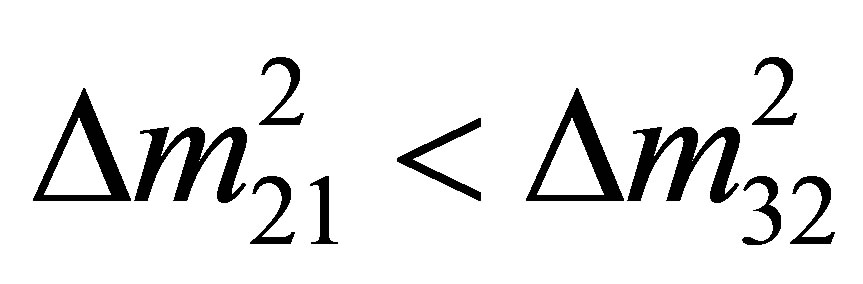 . Taking
. Taking  , in the nonrelativistic regime where
, in the nonrelativistic regime where  this wavelength is:
this wavelength is:
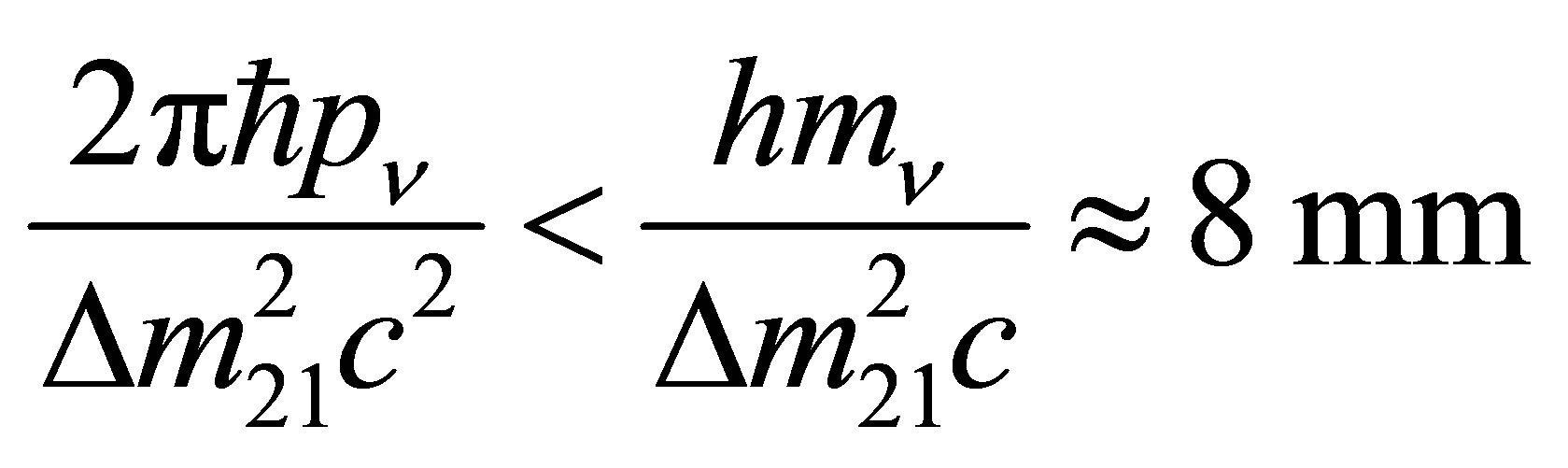 (C6)
(C6)
Hence, oscillation wavelengths of halo neutrinos will all be much smaller than a planetary radius. In typical circumstances, because  and
and  , shorter wavelength oscillations will occur on micron scales.
, shorter wavelength oscillations will occur on micron scales.