Applied Mathematics
Vol.06 No.10(2015), Article ID:59732,15 pages
10.4236/am.2015.610151
Epidemiological Model and Public Health Sensitization in Mali
Mahamadou Alassane
Département de Mathématiques et d’Informatique, Faculté des Sciences et Techniques, Bamako, Mali
Email: alassanemaiga@yahoo.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 August 2015; accepted 15 September 2015; published 18 September 2015
ABSTRACT
In this paper we propose a mathematical model to evaluate the impact of public health sensitization campaign on the spread of HIV-AIDS in Mali. We analyse rigorously this model to get insight into its dynamical features and to obtain associated epidemiological thresholds. If R0 < 1, we show that the disease-free equilibrium of the model is globally asymptotically stable when the public health sensitization program is 100% effective. The impact of public health sensitization strategies is assessed numerically by simulating the model with a reasonable set of parameter values (mostly chosen from the literature) and initial demographic data from Mali.
Keywords:
HIV-AIDS, Basic Reproduction Number, Global Stability, Public Health

1. Introduction
AIDS is the most deadly disease caused by a human immunodeficiency virus (HIV). The virus destroys all the immune system and leaves individuals susceptible to any other infections. It multiplies inside lymphocytes and finally destroys them. When the lymphocytes are reduced to a certain numbers, the immune system stops functioning correctly. Therefore, the individual can catch any kind of disease that might kill him easily because of the failure of the immune system. However, there exist drugs that can slow down the evolution of the virus. HIV is usually transmitted in three different ways: sexual contacts, blood transfusion, and exchange between mother and child during pregnancy, childbirth and breastfeeding.
Many mathematical models are used to study the impact of preventive control strategies on the spread of HIV-AIDS in given populations (cf. [1] -[11] , etc.). Some of these models showed that a change in risky behaviour was necessary to prevent the spread of HIV even in the presence of a treatment (see for example [12] -[16] ). Thus, it is instructive to study models that focus on non-pharmaceutical interventions, such as the use of public health sensitization campaign.
The models developed in [15] [17] -[19] study the impact of public health sensitization campaign on the spread of HIV-AIDS. In this paper we propose and study a mathematical model to estimate the impact of public health sensitization campaign on the spread of HIV-AIDS in Mali. We divide for it the population into two classes: “class with high-risk behavioral or class without public health sensitization” and “class with low risk behavioral or class with public health sensitization”. Every class consists of susceptible individuals and infected individuals. The class of the individuals at high-risk behavioral is split into susceptibles individuals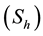 , indi-
, indi-
viduals who are in stage 1 of the infection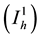 , individuals who are in stage 2 of the infection
, individuals who are in stage 2 of the infection 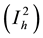 and
and
individuals who are in stage AIDS 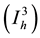 while the class of the individuals at low-risk behavioral is split into susceptibles individuals
while the class of the individuals at low-risk behavioral is split into susceptibles individuals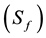 , individuals who are in stage 1 of the infection
, individuals who are in stage 1 of the infection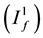 , individuals who are in
, individuals who are in
stage 2 of the infection  and individuals who are in stage AIDS
and individuals who are in stage AIDS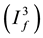 . The total population (Figure 1) at
. The total population (Figure 1) at
time t is denoted by 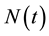 and can be expressed as the following sum:
and can be expressed as the following sum:
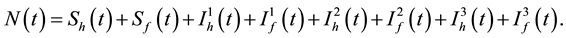 (1)
(1)
Our model is given by the following system of ODEs with constant coefficients:
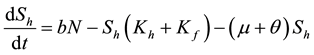 (2)
(2)
 (3)
(3)
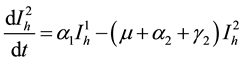 (4)
(4)
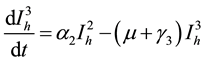 (5)
(5)
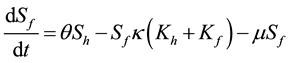 (6)
(6)
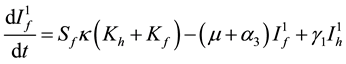 (7)
(7)

Figure 1. Behavioral representation of the HIV-AIDS model.

with

By adding of (2) to (9), we obtain: 
Our mathematical model is an extension of the models developed in [15] [17] -[19] . In our model, we suppose:
H1: that he mode of transmission of the virus is the horizontal transmission;
H2: that every individual is susceptible at high risk before his recruitment in the compartment 
H3: that

















2. Analysis of the Complete Model
2.1. Existence of Solutions
To show that the model is mathematically and biologically possible, we begin by rewriting it in terms of proportions. So, we introduce the following scalings:

Consequently:

By using what precedes, the rates of infection (10) become:

If we introduce the following parameters:

In the new variables, (2)-(9) reduces to:


Table 1. Model parameters.






We suppose that the initial conditions belong in 

Now we can enounce the following result:
Theorem 1. For any initial condition in


Before giving the proof of this theorem, we give at first a technical result which we shall use after.
Lemma 1. Let a(t) and y(t) be n X n matrices of bounded measurable functions on

with 




Proof. Indeed, this follows from the integrated form of the differential Equation (24),

We rewrite the system (15)-(22) in the form

Now we can give the proof of the theorem 1.
Proof. Step 1: Local existence of the solutions.
The local existence of the solutions ensues directly from the regularity of the function 


Step 2: We show that 
A.


















By Lemma 1, 






We next show that 


Proceding by contradiction:
We suppose that 



Then, 








By Lemma 1, 






Now we consider the Equations (16) and (20) in time


which is a contradiction, Consequently 


B. The following inequalities hold:
Adding all the equations of (15), we obtain:

By integrating (40) between 0 and t, we have:
So if the initial condition verifies
then the relation
will be verified for all
This second stage shows that the solutions are limited for everything

2.2. Desease Free Equilibruim
There will be absence of desease in the population if the proportions









Theorem 2. The model of HIV-SIDA (2)-(9) or (15)-(22) possesses a unique desease free equilibruim in 


and


Proof. Let be 











Let be 

where

2.3. Local Stability of Disease Free Equilibrium
By using the method of Van den Drissche and Watmough, we denote by F the rate of appearance of new infections in compartments of the infectious, and by Vs the rate of transfer of individuals in and out the compartments of the infectious by all other means. Then
The next-generation matrix is defined by:
where













Proposition 3. The basic reproduction ratio for HIV-SIDA model (15)-(22) is explicitly given by the formula (52) where



Theorem 4. The disease free equilibrium 


2.4. Global Stability of the Disease Free Equilibrium
We have the following theorem.
Theorem 5. For the system (15)-(22), if 
Proof. We begin by rewriting the system (15)-(22) in the form:








where 



Now, let us consider the following function:
If






We can also write
Algebraic manipulations give
or
If



2.5. Numerical Simulations
Before closing this section, we verify numerically the theoretical results obtained in subsections 2, 2 and 2 for an initial condition







First case: the disease goes extinct in the population (see Figure 2).
Second case: the disease persists in the population (see Figure 3).
These parameters are obtained in the literature and are summarized in the Table 2.


Figure 2. Dynamics of the system (15)-(22) in case where the disease goes extinct in the population. With the parameters of the Table 2 (first case), we have R0 = 0.5826. Figure 2(a) shows the evolution of susceptibles individuals, whereas Figures 2(b)-(d) show the evolution of infected individuals. The system converges towards the desease free equilibruim (0.226, 0, 0, 0, 0.774, 0, 0, 0). The simulation was realized with the MATLAB logiciel.
3. Model without Public Health Sensitization
In this section all sensitization-related parameters and variables are fixed to zero in order to understand the dynamic behavior of the population without public health sensitization campaign.
So, we pose






Figure 3. Dynamics of the system (15)-(22) in case where the disease persists in the population. With the parameters of the Table 2 (second case), we have R0 = 1.2928. Figure 3(a) shows the evolution of susceptibles individuals, whereas Figures 3(b)-(d) show the evolution of infected individuals. The system converges towards the endemic equilibrium (0.6609, 0.0423, 0.021, 0.0206, 0.2251, 0.0072, 0.007, 0.0158). The simulation was realized with the MATLAB logiciel.
Table 2. Biological parameters.
where
with




3.1. Local Stability of Disease Free Equilibrium
The desease free equilibruim 
By using the method of Van den Drissche and Watmough, we denote by F the rate of appearance of new infections in compartments of the infectious, and by Vs the rate of transfer of individuals in and out the compartments of the infectious by all other means. Then:
the next-generation matrix is defined by:
Proposition 6. The basic reproduction ratio for the sub-model (61)-(64) is given by the formula (66):

Theorem 7. The disease free equilibrium 


3.2. Global Stability of the Disease Free Equilibrium
Theorem 8. For the system (61)-(64), if 

Proof. We begin by rewriting the system (61)-(64) in the form:




where
The disease free equilibrium 

Now, let us consider the following function:
The function V is positive, and it nulle at the disease free equilibrium. The derivative of this Lyapunov function V along the trajectories of the ordinary differentiel system is:
We can also write
Algebraic manipulations give
or
If

3.3. Existence and Uniqueness of an Endemic Equilibrium
It is found that an unique endemic equilibrium of (61)-(64) for




From (72), we have:

From (73), we have:

From (74) et (76), we have:

From (75), (76) and (77), we have:

(76), (77) and (78) in (71) give:

(79) dans (76) give:

(79) in (77) give

If
3.4. Numerical Simulations
Before closing this section, we verify numerically the theoretical results obtained in this section for an initial condition



First case: the disease goes extinct in the population (see Figure 4).
Second case: the disease persists in the population (see Figure 5).
These parameters are obtained in the literature and are summarized in the Table 3.
4. Evaluation of Impact of Public Health Sensitization
Before using the model (15)-(22) to evaluate the impact of public health sensitization in combatting HIV-AIDS spread in a population, it is instructive to evaluate the behaviour of the model under the worst case scenario (i.e., the case where no public health sensitization is provided in the population). By setting all sensitization related parameters to zero (i.e.,
We resume in Table 4 and Table 5, data of Mali concerning the spread of the HIV-AIDS.

Figure 4. Dynamics of the system (61)-(64) in case where the disease goes extinct in the population. With the parameters of the Table 3 (first case), we have Rh0 = 0.3077. Figure 4(a) shows the evolution of susceptibles individuals, whereas Figures 4(b)-(d) show the evolution of infected individuals. The system converges towards the desease free equilibruim (1, 0, 0, 0). The simulation was realized with the MATLAB logiciel.

Figure 5. Dynamics of the system (61)-(64) in case where the disease persists in the populationn. With the parameters of the Table 3 (second case), we have Rh0 = 1.6. Figure 5(a) shows the evolution of susceptibles individuals, whereas Figures 5(b)-(d) show the evolution of infected individuals. The system converges towards the endemic equilibrium (0.6298, 0.038, 0.0195, 0.0111). The simulation was realized with the MATLAB logiciel.
Table 3. Biological parameters.
Table 4. Mali epidemiological data for the model (15).
Table 5. Mali demographic data of 2001 used as initial conditions.

Figure 6. Dynamics of the system (15)-(22) in the nose of the cases, Rh0 = 1.6. Figure 6(a) shows the evolution of susceptibles individuals, whereas Figure 6(b) shows the evolution of infected individuals. We use the parameters of the Table 4. The simulation was realized with the MATLAB logiciel.


Figure 7. Dynamics of the system (15) in case the population of Mali is submitted to Public Health sensitization compaign on the spread of HIV-AIDS, R0 = 0.5109. Figure 7(a) shows the evolution of susceptibles individuals, whereas Figures 7(b)-(d) show the evolution of infected individuals. We use the parameters of the Table 4. The simulation was realized with the MATLAB logiciel.
We evaluate now the behavior of the model (15)-(22) by considering the impact of Public Health sensitization compaign on the spread of HIV-AIDS in Mali. Using the data in Table 4 and Table 5, simulations of the model (15)-(22) show that in Mali the proportion of infected individuals would reach approximately 0.0137 (soit 100020 cas) in 9 years from 2001 (Figure 6(b)). These projections of the model are compatible with the data found in the literature (Source CIA factbook). According to this source, in Mali the individuals infected by the HIV-AIDS in 2010 were 100000 (see Figure 7).
Cite this paper
MahamadouAlassane, (2015) Epidemiological Model and Public Health Sensitization in Mali. Applied Mathematics,06,1696-1711. doi: 10.4236/am.2015.610151
References
- 1. Lounes, R. and De Arazoza, H. (1999) A Two-Type Model for the Cuban National Programme on HIV-AIDS. IMA Journal of Mathematics Applied in Medicine and Biology, 16, 143-154.
http://dx.doi.org/10.1093/imammb/16.2.143 - 2. McCluskey, C.C. (2003) A Model of HIV/AIDS with Staged Progressionv and Amelioration. Mathematical Biosciences, 181, 1-16.
http://dx.doi.org/10.1016/S0025-5564(02)00149-9 - 3. Gumel, A.B., McCluskey, C.C. and van den Driessche, P. (2006) Mathematical Study of a Staged-Progression HIV Model with Imperfect Vaccine. Mathematical Biosciences, 68, 2105-2128.
http://dx.doi.org/10.1007/s11538-006-9095-7 - 4. Smith, R.J., Li, J., Gordon, R. and Heffernan, J.M. (2009) Can We Spend Our Way out of the AIDS Epidemic? A World Halting AIDS Model. BMC Public Health, 9, S15.
http://dx.doi.org/10.1186/1471-2458-9-s1-s15 - 5. Mukandavire, Z., Garira, W. and Chiyaka, C. (2007) Asymptotic Properties of an HIV/AIDS Model with a Time Delay. Journal of Mathematical Analysis and Applications, 330, 916-933.
http://dx.doi.org/10.1016/j.jmaa.2006.07.102 - 6. Hyman, J.M. and Stanley, E.A. (1998) Using Mathematical Models to Understand the AIDS Epidemic. Mathematical Biosciences, 90, 415-473.
http://dx.doi.org/10.1016/0025-5564(88)90078-8 - 7. Alfonseca, M., Martinez-Bravo, M.T. and Torrea, J.L. (2000) Mathematical Models for the Analysis of Hepatitis B and AIDS Epidemics. Simulation, 74, 219-226.
http://dx.doi.org/10.1177/003754970007400403 - 8. Srinivasa, A.S.R. (2003) Mathematical Modelling of AIDS Epidemic in India. Current Science, 84, 1193-1197.
- 9. Luboobi, L.S. (1991) Mathematical Models for the Dynamics of the AIDS Epidemic. In: Patel, M.S. and Noke, S., Eds., Biometry for Development, ICIPE, Science Press, Nairobi, 76-83.
- 10. Mugisha, J.Y.T. (1997) The Mathematical Dynamics of HIV-AIDS Epidemic in Age-Structured Population. Proceedings XI SAMSA Symposium on the Potential of Mathematical Modeling of Problems from the SAMSA Region, 8-23.
- 11. Anderson, R.M., Medley, G.F., May, R.M. and Johnson, A.M. (1986) A Preliminary Study of the Transmission Dynamics of the Human Immunodeficiency Virus (HIV), the Causative Agent of AIDS. IMA Journal of Mathematics Applied in Medicine and Biology, 3, 229-263.
http://dx.doi.org/10.1093/imammb/3.4.229 - 12. Alassane, M., Diallo, O. and Pousin, J. (2011) Individual Behavior and Epidemiological Model. Journal of Applied Mathematics and Bioinformatics, 1, 57-74.
- 13. Anderson, R.M. (1988) The Role of Mathematical Models in the Study of HIV Transmission and the Epidemiology of AIDS. Journal of Acquired Immune Deficiency Syndromes, 1, 241-256.
- 14. Blower, S.M. and Dowlatabadi, H. (1994) Sensitivity and Uncertainty Analysis of Complex Models of Disease Transmission. International Statistical Review, 62, 229-243.
http://dx.doi.org/10.2307/1403510 - 15. Del Valle, S., Ecangelista, A.M., Velasco, M.C., Kribs-Zaleta, C.M. and Hsu Schmitz, S.-F. (2004) Effects of Sensitization, Vaccination and Treatment on HIV Transmission in Homosexuals with Genetic Heterogeneity. Mathematical Biosciences, 187, 111-133.
http://dx.doi.org/10.1016/j.mbs.2003.11.004 - 16. Kribs-Zaleta, C. and Halesco-Hernandez, J. (2000) A Simple Vaccination Model with Multiple Endemic States. Mathematical Biosciences, 164, 183-201.
http://dx.doi.org/10.1016/S0025-5564(00)00003-1 - 17. Mukandavire, Z., Garira, W. and Tchuenche, J.M. (2009) Modelling Effects of Public Health Sensitizational Campaigns on HIV-AIDS Transmission Dynamics. Applied Mathematical Modelling, 33, 2084-2095.
http://dx.doi.org/10.1016/j.apm.2008.05.017 - 18. Mukandavire, Z. and Garira, W. (2007) Effects of Public Health Sensitizational Campaigns and the Role of Sex Workers on the Spread of HIV-AIDS among Heterosexuals. Theoretical Population Biology, 72, 346-365.
http://dx.doi.org/10.1016/j.tpb.2007.07.002 - 19. Hussaini, N., Winter, M. and Gumel, A.B. (2010) Qualitative Assessment of the Role of Public Health Sensitization Program on HIV Transmission Dynamics. Mathematical Medicine and Biology: A Journal of the IMA, 28, 245-270.
http://dx.doi.org/10.1093/imammb/dqq009


































