Applied Mathematics
Vol.3 No.10A(2012), Article ID:24090,7 pages DOI:10.4236/am.2012.330180
An Interactive Fuzzy Satisficing Method for Multiobjective Stochastic Integer Programming with Simple Recourse
Faculty of Engineering, Hiroshima University, Hiroshima, Japan
Email: sakawa@hiroshima-u.ac.jp, tak-matsui@hiroshima-u.ac.jp
Received May 29, 2012; revised June 25, 2012; accepted July 3, 2012
Keywords: Multiobjective Programming; Stochastic Programming; Fuzzy Programming; Interactive Methods; Simple Recourse Model
ABSTRACT
This paper considers multiobjective integer programming problems involving random variables in constraints. Using the concept of simple recourse, the formulated multiobjective stochastic simple recourse problems are transformed into deterministic ones. For solving transformed deterministic problems efficiently, we also introduce genetic algorithms with double strings for nonlinear integer programming problems. Taking into account vagueness of judgments of the decision maker, an interactive fuzzy satisficing method is presented. In the proposed interactive method, after determineing the fuzzy goals of the decision maker, a satisficing solution for the decision maker is derived efficiently by updating the reference membership levels of the decision maker. An illustrative numerical example is provided to demonstrate the feasibility and efficiency of the proposed method.
1. Introduction
In actual decision making situations, we must often make a decision on the basis of imprecise information or uncertain data. For such decision making problems involveing uncertainty, there exist two typical approaches: stochastic programming and fuzzy programming. Stochastic programming, as an optimization method on the basis of the probability theory, has been developing in various ways [1-5], including two stage problem by [6], and chance constrained programming by [7]. Fuzzy mathematical programming representing the vagueness in decision making situations by fuzzy concepts has been studied by many researchers [8-12].
In most practical situations, however, it is natural to consider that the uncertainty in real world decision making problems is often expressed by a fusion of fuzziness and randomness rather than either fuzziness or randomness. For handling not only the decision maker’s vague judgments in multiobjective problems but also the randomness of the parameters involved in the objectives and/or constraints, Sakawa and his colleagues incorporated their interactive fuzzy satisficing methods for deterministic problems [9,13] into multiobjective stochastic programming problems. Through the introduction of several stochastic programming models such as expectation optimization [14,15], variance minimization [14], probability maximization [14,16,17] and fractile criterion optimization [14] together with chance constrained programming techniques, they introduced several interactive fuzzy satisficing methods to derive a satisficing solution for a decision maker from Pareto optimal solution sets.
It should be stressed here that in the chance constrained problems, for random data variations, a mathematical model is formulated such that the violation of the constraints is permitted up to specified probability levels. Compared with this, in a two-stage [18] or multistage [19] model including a simple recourse model as a special case, a shortage or an excess arising from the violation of the constraints is penalized, and then the expectation of the amount of the penalties for the constraint violation is minimized [20,21].
Furthermore, it is often found that in real-world decision making situations, decision variables in a multiobjective stochastic programming problem are not continuous but rather discrete. From this observation, we discuss interactive fuzzy multiobjective stochastic integer programming which is a natural extension of multiobjective stochastic programming with continuous variables. To deal with practical sizes of multiobjective stochastic nonlinear integer programming problems formulated for decision making problems in the real-world, we employ genetic algorithms to derive a satisficing solution to the decision maker.
Under these circumstances, in this paper, we consider multiobjective integer programming problems involving random variables in constraints. The main contribution of this paper is to provide a novel decision making methodology including a new model, solution concept and solution algorithm to deal with more realistic problems in the real world, by simultaneously considering various concepts such as fuzziness, randomness, integer decision variables and interactive fuzzy programming, while most of previous papers dealt with either of the concepts or a part of them. Using the concept of simple recourse [20], the formulated multiobjective stochastic simple recourse problems are transformed into deterministic ones. For solving transformed deterministic problems efficiently, genetic algorithms with double strings for nonlinear integer programming problems are introduced. Assuming that a decision maker has a fuzzy goal for each of the objective functions, we present an interactive fuzzy satisficing method to derive a satisficing solution for the decision maker by updating the reference membership levels for fuzzy goals represented by the membership functions. An illustrative numerical example is provided to demonstrate the feasibility and efficiency of the proposed method.
2. Multiobjective Stochastic Integer Programming with Simple Recourse
We consider a simple recourse model for the multiobjective stochastic integer programming problems
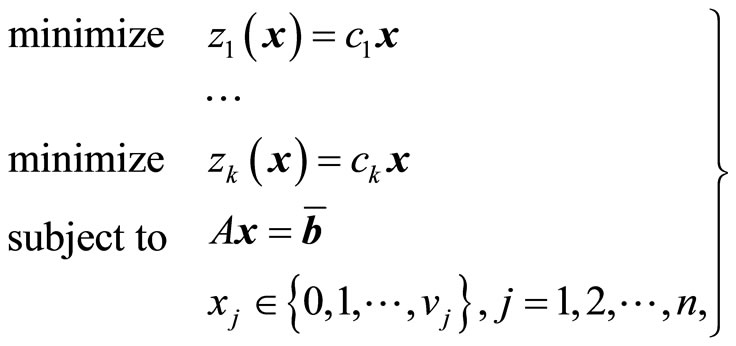 (1)
(1)
where x is an n dimensional integer decision variable column vector, cl, l = 1, 2, ···, k are n dimensional coefficient row vectors, A is an m × n coefficient matrix, and 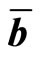 is an m dimensional random variable column vector. It should be noted here that, in a simple recourse model, the random variables are involved only in the right-hand side of the constraints.
is an m dimensional random variable column vector. It should be noted here that, in a simple recourse model, the random variables are involved only in the right-hand side of the constraints.
To understand an idea of the formulation in the simple recourse model, consider a decision problem of a manufacturing company where the decision variables actually make sense only if they are integer values. Suppose that the company makes m types of products which requires n kinds of working processes, and a decision maker (DM) in the company desires to optimize the total profit and the total production cost simultaneously.
Let 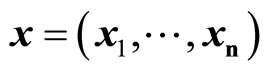 denote activity levels for the n kinds of working processes which are integer decision variables, and then Tx denotes the amount of products, where T is an m × n matrix transforming the n kinds of activity levels of the working processes into the m types of products. The total profit is expressed as c1Tx, where an m dimensional coefficient vector c1 is a vector of unit product profits for the m types of products, and the total production cost is represented by c2x, where an n dimensional coefficient vector c2 is a vector of unit costs for the n kinds of activity levels of the working processes. Assume that the demand coefficients
denote activity levels for the n kinds of working processes which are integer decision variables, and then Tx denotes the amount of products, where T is an m × n matrix transforming the n kinds of activity levels of the working processes into the m types of products. The total profit is expressed as c1Tx, where an m dimensional coefficient vector c1 is a vector of unit product profits for the m types of products, and the total production cost is represented by c2x, where an n dimensional coefficient vector c2 is a vector of unit costs for the n kinds of activity levels of the working processes. Assume that the demand coefficients 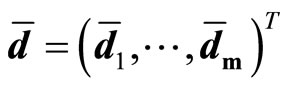 for the m products are uncertain, and they are represented by random variables. The demand constraints are expressed as
for the m products are uncertain, and they are represented by random variables. The demand constraints are expressed as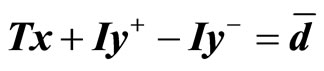 , where y+ and y– represent the errors for estimating the demands, and I is the m dimensional identity matrix. These two objectives are optimized under the demand constraints
, where y+ and y– represent the errors for estimating the demands, and I is the m dimensional identity matrix. These two objectives are optimized under the demand constraints 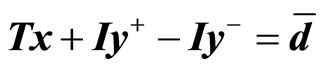 together with the ordinary constraints Bx ≤ e without uncertainty for the activity levels such as the capacity, budget, technology, etc. The constraints
together with the ordinary constraints Bx ≤ e without uncertainty for the activity levels such as the capacity, budget, technology, etc. The constraints 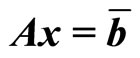 in (1) can be interpreted as the combined form of the demand constraints with random variables and the ordinary constraints without uncertainty.
in (1) can be interpreted as the combined form of the demand constraints with random variables and the ordinary constraints without uncertainty.
Let us return to a general case of the recourse model. It is assumed that, in this model, the DM must make a decision before the realized values of the random variables involved in (1) are observed, and the penalty of the violation of the constraints is incorporated into the objective function in order to consider the loss caused by random date variations.
To be more specific, by expressing the difference between 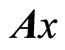 and
and 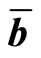 in (1) as two vectors
in (1) as two vectors
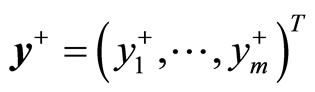
and
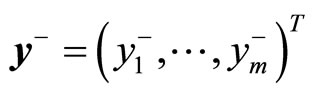
the expectation of a recourse for the lth objective function is represented by
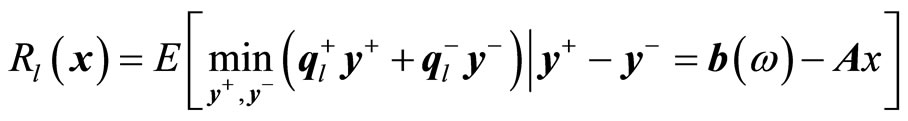 (2)
(2)
where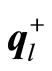 and
and 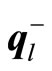 are m dimensional constant row vectors, and b(ω) is an m dimensional realization vector of
are m dimensional constant row vectors, and b(ω) is an m dimensional realization vector of 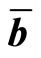 for an elementary event ω. Thinking of each element of
for an elementary event ω. Thinking of each element of
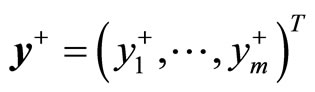
and
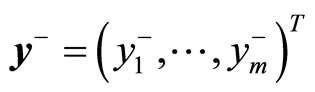
as a shortage and an excess of the left-hand side, respectively, we can regard each element of 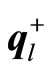 and
and 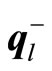 as the cost to compensate the shortage and the cost to dispose the excess, respectively.
as the cost to compensate the shortage and the cost to dispose the excess, respectively.
Then, for the multiobjective stochastic programming problem, the simple recourse problem is formulated as
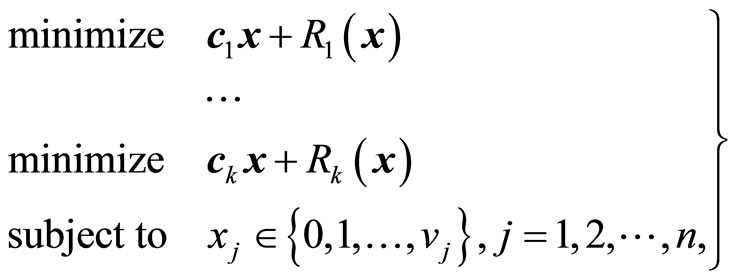 (3)
(3)
Because 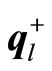 and
and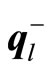 are interpreted as penalty coefficients for shortages and excesses, it is quite natural to assume that
are interpreted as penalty coefficients for shortages and excesses, it is quite natural to assume that 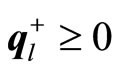 and
and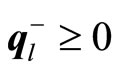 , and then, it is evident that, for all i = 1, ···, m, the complementary relations
, and then, it is evident that, for all i = 1, ···, m, the complementary relations
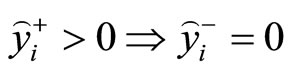 ,
,
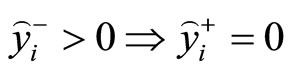
should be satisfied for an optimal solution. With this observation in mind, we have
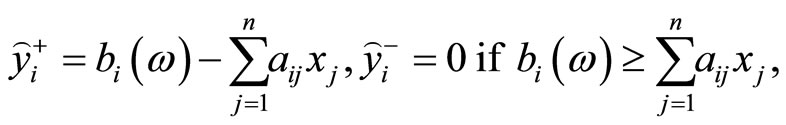
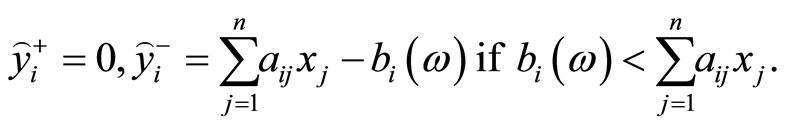
Recalling that 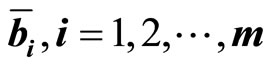 are mutually independent, (2) can be explicitly calculated as
are mutually independent, (2) can be explicitly calculated as
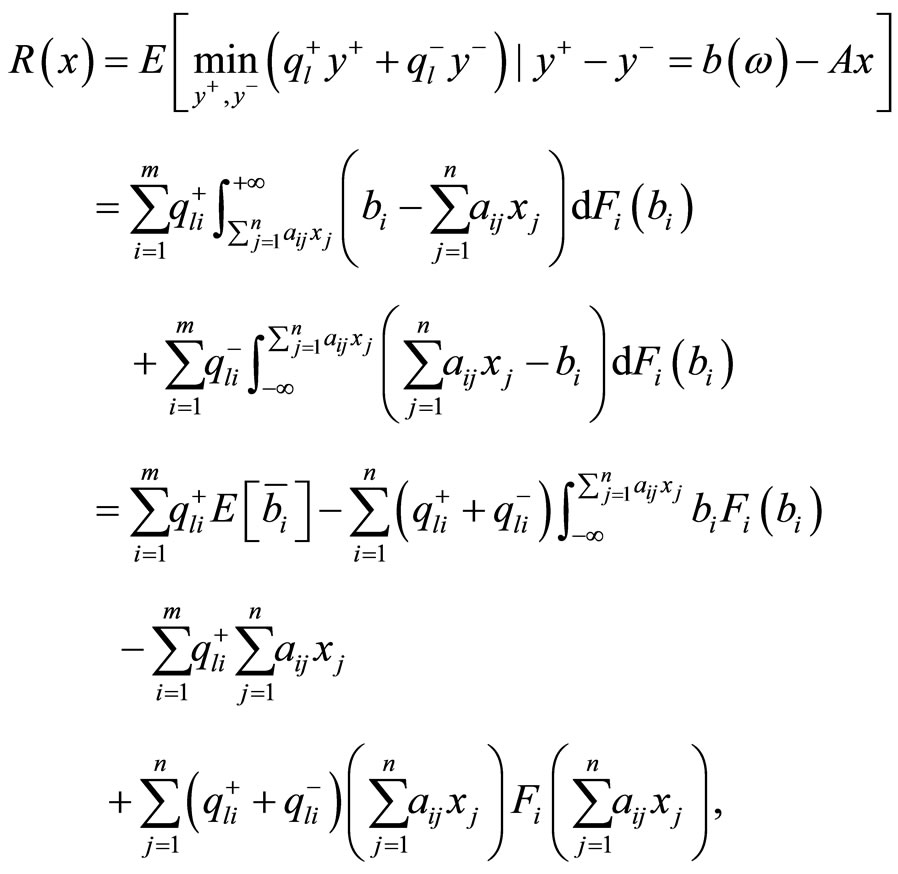 (4)
(4)
where Fi is the probability distribution function of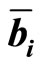 . Then, (3) can be rewritten as
. Then, (3) can be rewritten as
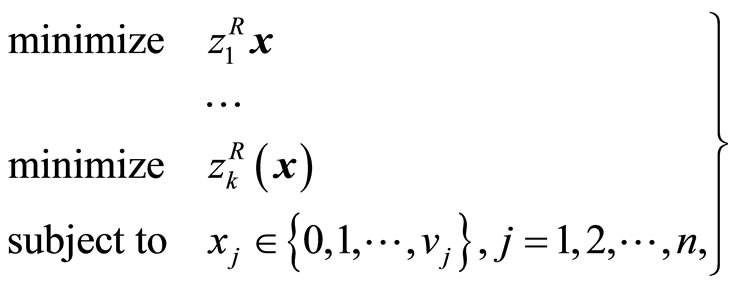 (5)
(5)
where
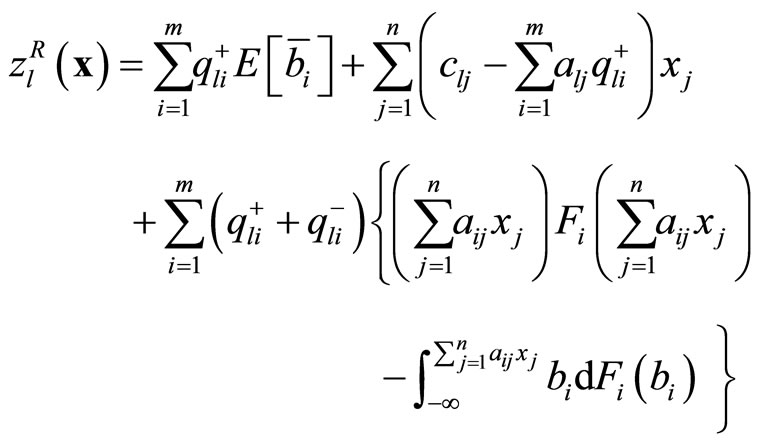
3. Fuzzy Goals
In order to consider the imprecise nature of the DM’s judgments for each objective function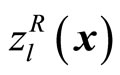 in (5), by introducing the fuzzy goals such as “
in (5), by introducing the fuzzy goals such as “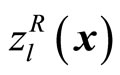 should be substantially less than or equal to a certain value,” (5) can be interpreted as
should be substantially less than or equal to a certain value,” (5) can be interpreted as
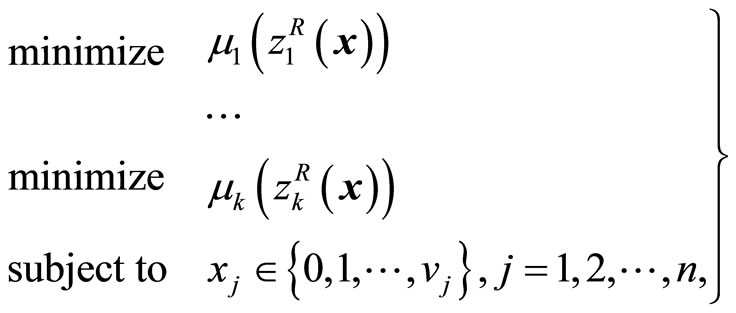 (6)
(6)
where μl is a membership function to quantify a fuzzy goal for the lth objective function in (5) as shown in Figure 1.
It should be noted here that (6) is regarded as a multiobjective decision making problem, and that there rarely exists a complete optimal solution that simultaneously optimizes all the objective functions. By directly extending Pareto optimality in ordinary multiobjective programming problems, Sakawa et al. defined M-Pareto optimality on the basis of membership function values as a reasonable solution concept for the fuzzy multiobjective decision making problem [9,13].
Definition 1 (M-Pareto optimal solution). A point 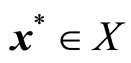 is said to be an M-Pareto optimal solution if and only if there does not exist another
is said to be an M-Pareto optimal solution if and only if there does not exist another 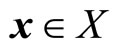 such that
such that
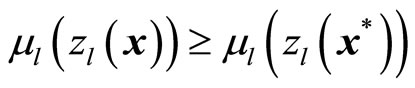
for all 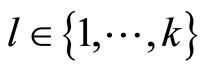 and
and
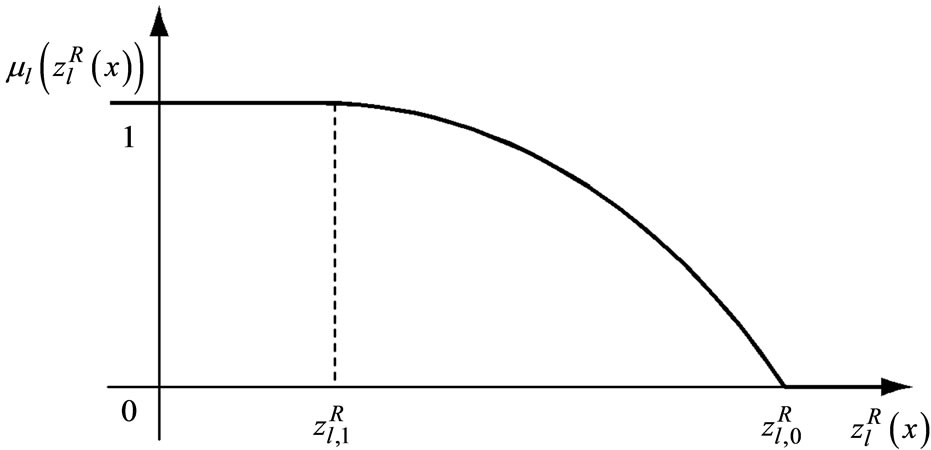
Figure 1. Example of a membership function .
.
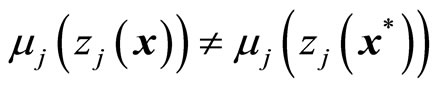
for at least one , where X denotes the feasible region of the problem.
, where X denotes the feasible region of the problem.
To help the DM specify the membership functions, it is recommended to calculate the individual minima of 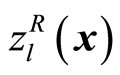 by solving the nonlinear integer programming problems
by solving the nonlinear integer programming problems
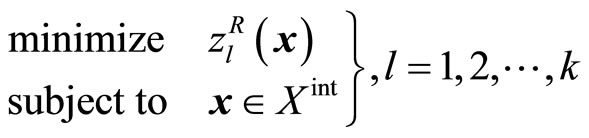 (7)
(7)
where 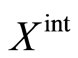 denotes the feasible region of (6).
denotes the feasible region of (6).
In order to find a candidate for the satisficing solution, the DM specifies the reference membership levels 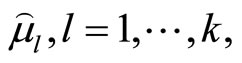 and then by solving the augmented minimax problem
and then by solving the augmented minimax problem
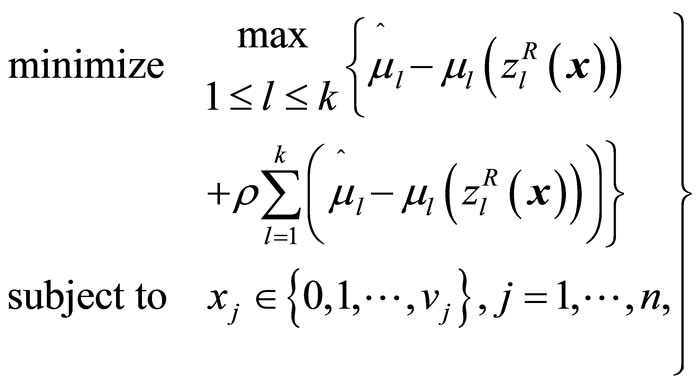 (8)
(8)
an M-Pareto optimal solution corresponding to 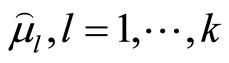 is obtained, and (8) is equivalently expressed by
is obtained, and (8) is equivalently expressed by
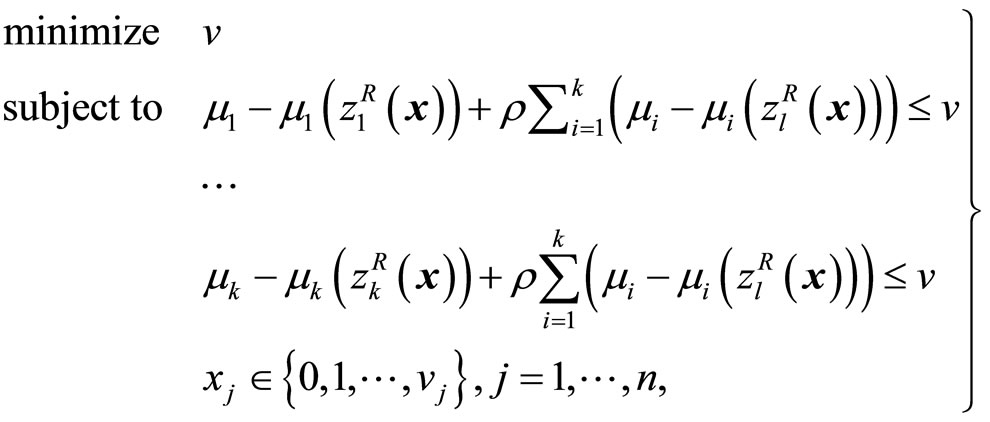 (9)
(9)
where ρ is a sufficiently small positive number.
Observing that (7) and (9) are nonlinear integer programming problems, we cannot directly apply GADSLPRRSU [11] for solving them.
4. Genetic Algorithms for Nonlinear Integer Programming
For solving linear integer programming problems on the framework of genetic algorithms, Sakawa proposed GADSLPRRSU [11]. GADSLPRRSU is an abbreviation for genetic algorithms with double strings based on linear programming relaxation and reference solution updating. This method includes three key ideas: double strings (DS), linear programming relaxation (LPR), and reference solution updating (RSU). Unfortunately, however, due to nonlinearity, we cannot directly apply GADSLPRRSU for solving (7) and (9). However, we can introduce the revised GADSLPRRSU where GENOCOPIII [22,23] is employed for solving a nonlinear continuous relaxation problem.
As an efficient approximate solution method, the revised GADSLPRRSU are designed for nonlinear integer programming problems formulated as:
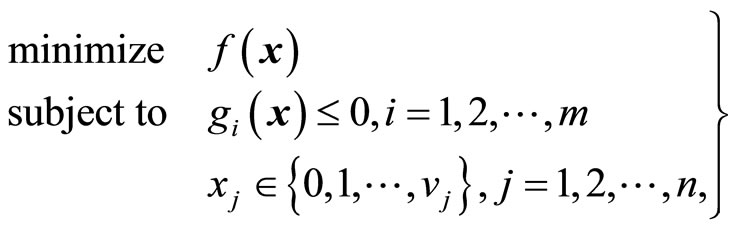 (10)
(10)
where x is an n dimensional integer decision variable column vector. Furthermore, 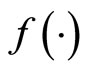 and
and 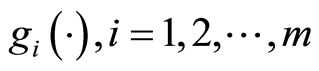 may be nonlinear.
may be nonlinear.
Quite similar to genetic algorithms with double (GADS) [11], an individual is represented by a double string shown in Figure 2. In Figure 2, for a certain j, 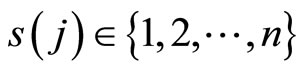 represents an index of a decision variable
represents an index of a decision variable 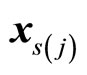 in the solution space, while
in the solution space, while 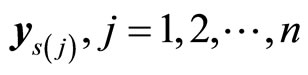 does the integer value among
does the integer value among 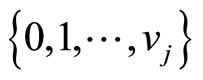 of the
of the 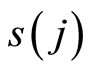 th decision variable
th decision variable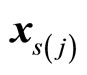 .
.
Now we can summarize the computational procedures of the revised GADSLPRRSU as follows.
Computational procedures of the revised GADSLPRRSU
Step 0: Determine values of the parameters used in the genetic algorithm.
Set the generation counter t at 0.
Step 1: Generate the initial population consisting of N individuals based on the information of the optimal solution to the continuous relaxation problem.
Step 2: Decode each individual in the current population and calculate its fitness based on the corresponding solution.
Step 3: If the termination condition is fulfilled, stop. Otherwise, let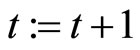 .
.
Step 4: Apply reproduction operator using elitist expected value selection after linear scaling.
Step 5: Apply crossover operator, called PMX (Partially Matched Crossover) for double string.
Step 6: Apply mutation based on the information of a solution to the continuous relaxation problem.
Step 7: Apply inversion operator, return to Step 2.
Further details of GADSLPRRSU and the revised GADSLPRRSU can be found in [11,24].
5. Interactive Fuzzy Satisficing Method
We can now construct the interactive algorithm for

Figure 2. Double string.
deriving a satisficing solution for the DM where (9) for the updated reference membership levelsis repeatedly solved until the DM is satisfied with an obtained optimal solution.
Interactive Fuzzy Satisficing Method for the Simple Recourse Model with Integer Decision Variables
Step 1: Calculate the individual minima 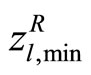 of
of 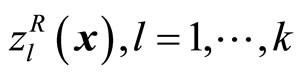 by solving (7) through the revised GADSLPRRSU.
by solving (7) through the revised GADSLPRRSU.
Step 2: Ask the DM to specify the membershipfunctions 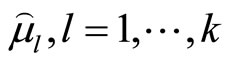 taking into account the individual minima obtained in step 1.
taking into account the individual minima obtained in step 1.
Step 3: Set the initial reference membership levels at 1s, which can be viewed as the ideal values, i.e.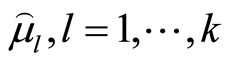 .
.
Step 4: Solve the augmented minimax problem (9) for the current reference membership levels 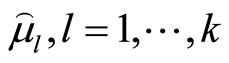 by using the revised GADSLPRRSU.
by using the revised GADSLPRRSU.
Step 5: The DM is supplied with the corresponding M-Pareto optimal solution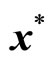 . If the DM is satisfied with the current membership function values
. If the DM is satisfied with the current membership function values
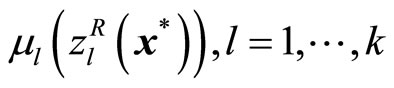
stop the algorithm. Otherwise, ask the DM to update the reference membership levels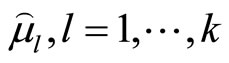 , in consideration of the current membership function values, and return to step 4.
, in consideration of the current membership function values, and return to step 4.
Here it should be stressed for the DM that any improvement of one membership function value can be achieved only at the expense of at least one of the other membership function values.
6. Numerical Example
In order to demonstrate the feasibility and efficiency of the interactive fuzzy satisficing method for the simple recourse model, as a numerical example of (1), consider the multiobjective stochastic integer programming problem formulated as
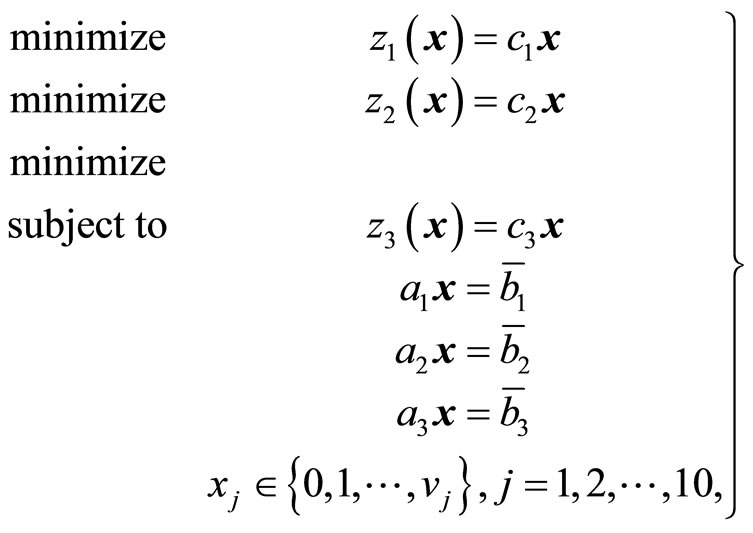 (11)
(11)
where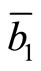 ,
, 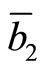 and
and 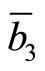 are Gaussian random variables N(230, 12), N(345, 18) and N(437, 22), respectively. Each element of coefficient vectors
are Gaussian random variables N(230, 12), N(345, 18) and N(437, 22), respectively. Each element of coefficient vectors 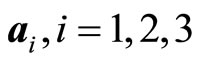 is randomly chosen from among a set of integers
is randomly chosen from among a set of integers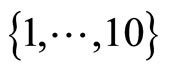 , and each element of
, and each element of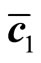 ,
, 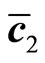 an d
an d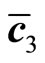 is also randomly chosen from among sets of integers
is also randomly chosen from among sets of integers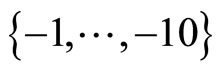 ,
, 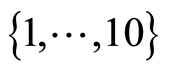 and
and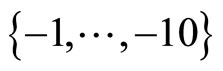 , respectively. These values are shown in Table 1. The penalty coefficient row vectors
, respectively. These values are shown in Table 1. The penalty coefficient row vectors 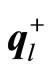 and
and 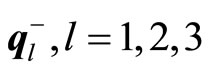 for violating the constraints are given in Table 2.
for violating the constraints are given in Table 2.
By using the revised GADSLPRRSU, the individual minima 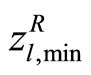 are calculated as
are calculated as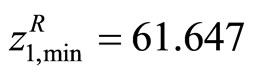 ,
, 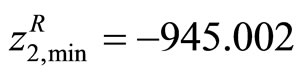 and
and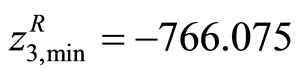 . Taking these values into account, suppose that the DM determines the linear membership functions as
. Taking these values into account, suppose that the DM determines the linear membership functions as
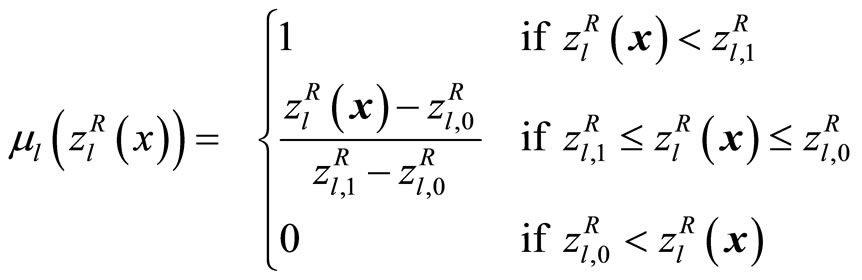 (12)
(12)
where 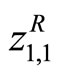 and
and 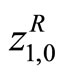 are calculated as
are calculated as 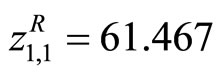 ,
,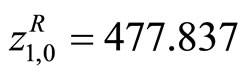 ,
,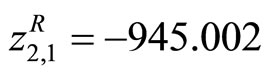 ,
,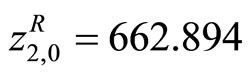 ,
, 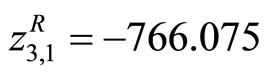 and
and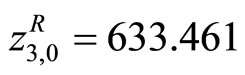 by using the Zimmermann method [25].
by using the Zimmermann method [25].
For the initial reference membership levels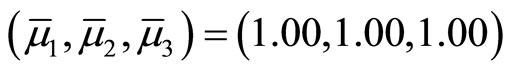 , the corresponding augmentedminimax problem (8) is solved by using the revised GADSLPRRSU, and the DM is supplied with the membership function values of the first iteration shown in Table 3.
, the corresponding augmentedminimax problem (8) is solved by using the revised GADSLPRRSU, and the DM is supplied with the membership function values of the first iteration shown in Table 3.
Assume that the DM is not satisfied with these membership function values, and the DM updates the reference membership levels as 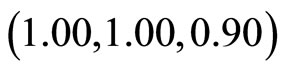 for improving the satisfaction levels μ1 and μ2 at the expense of μ3. For the updated reference membership levels, the corresponding augmented minimax problem is solved
for improving the satisfaction levels μ1 and μ2 at the expense of μ3. For the updated reference membership levels, the corresponding augmented minimax problem is solved
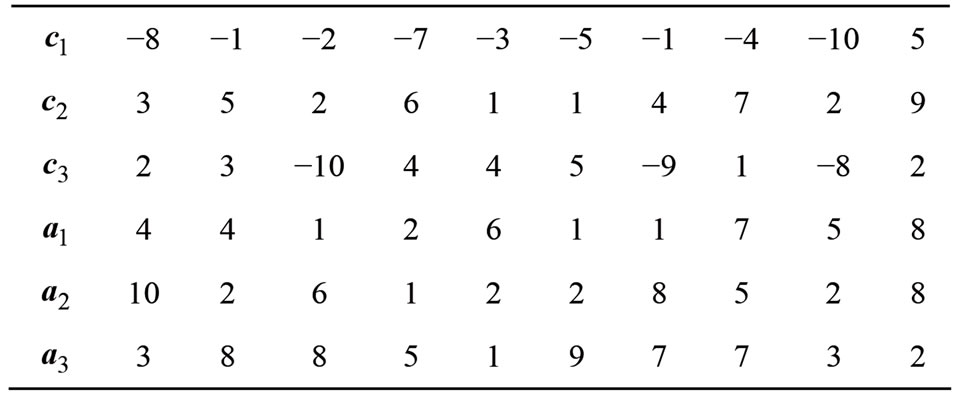
Table 1. Value of each element of ci, i = 1, 2, 3 and ai, i = 1, 2, 3.

Table 2. Value of each element of  and
and 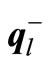 , l = 1, 2, 3.
, l = 1, 2, 3.
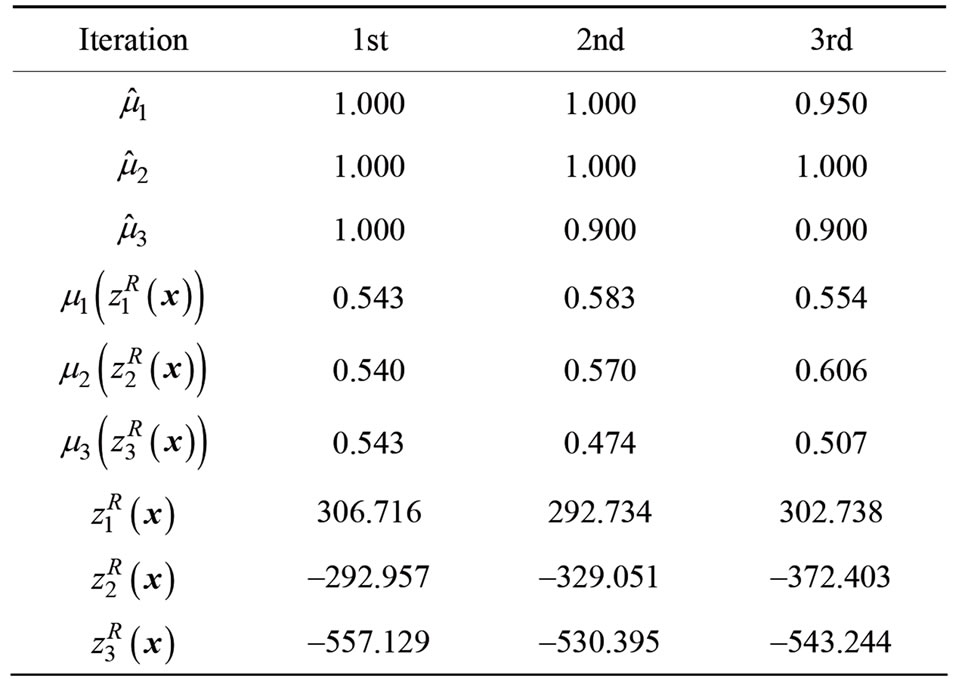
Table 3. Process of interaction.
again, and the membership function values calculated in the second iteration are shown in Table 3.
A similar procedure continues until the DM is satisfied with the membership function values. In this example, we assume that the satisficing solution for the DM is derived in the third interaction.
7. Conclusion
In this paper, we focused on multiobjective integer programming problems with random variables in in the right-hand side of the constraints. Through the use of the simple recourse model, the formulated multiobjective stochastic integer programming problems with simple recourse are transformed into deterministic ones. Assuming that the DM has fuzzy goals for the objective functions, an interactive fuzzy satisficing method for deriving a satisficing solution for the decision maker from among the M-Pareto optimal solution set has been proposed. In the proposed interactive method, after determining the fuzzy goals of the DM, a satisficing solution is derived efficiently by updating the reference membership levels of the DM. Genetic algorithm for nonlinear integer programming, called the revised GADSLPRRSU were introduced for solving transformed deterministic ones efficiently.An illustrative numerical example was provided to demonstrate the feasibility and efficiency of the proposed method. Extensions to other stochastic programming models will be considered elsewhere.
REFERENCES
- J. R. Birge and F. Louveaux, “Introduction to Stochastic Programming,” Springer, London, 1997.
- P. Kall, “Stochastic Linear Programming,” SpringerVerlag, Berlin, 1976. doi:10.1007/978-3-642-66252-2
- P. Kall and J. Mayer, “Stochastic Linear Programming Models, Theory, and Computation,” Springer, New York, 2005.
- I. M. Stancu-Minasian, “Stochastic Programming with Multiple Objective Functions,” D. Reidel Publishing Company, Dordrecht, 1984.
- I. M. Stancu-Minasian, “Overview of Different Approaches for Solving Stochastic Programming Problems with Multiple Objective Functions,” In: R. Slowinski and J. Teghem, Eds., Stochastic Versus Fuzzy Approaches to Multiobjective Mathematical Programming under Uncertainty, Kluwer Academic Publishers, Dordrecht/Boston/ London, 1990, pp. 71-101. doi:10.1007/978-94-009-2111-5_5
- G. B. Dantzig, “Linear Programming under Uncertainty,” Management Science,Vol. 1, No. 3-4, 1955, pp. 197-206. doi:10.1287/mnsc.1.3-4.197
- A. Charnes and W. W. Cooper, “Chance Constrained Programming,” Management Science, Vol. 6, No. 1, 1959, pp. 73-79. doi:10.1287/mnsc.6.1.73
- Y. J. Lai and C. L. Hwang, “Fuzzy Mathematical Programming,” Springer-Verlag, Berlin, 1992. doi:10.1007/978-3-642-48753-8
- M. Sakawa, “Fuzzy Sets and Interactive Multiobjective Optimization,” Plenum Press, New York, 1993.
- M. Sakawa, “Large Scale Interactive Fuzzy Multiobjective Programming,” Physica-Verlag, Heidelberg, 2000. doi:10.1007/978-3-7908-1851-2
- M. Sakawa, “Genetic Algorithms and Fuzzy Multiobjective Optimization,” Kluwer Academic Publishers, Boston, 2001. doi:10.1007/978-1-4615-1519-7
- H.-J. Zimmermann, “Fuzzy Sets, Decision-Making and Expert Systems,” Kluwer Academic Publishers, Boston, 1987. doi:10.1007/978-94-009-3249-4
- M. Sakawa and H. Yano, “Interactive Fuzzy Satisficing Method Using Augumented Minimax Problems and Its Application to Environmental Systems,” IEEE Transactions on Systems, Man and Cybernetics, Vol. 15, No. 6, 1985, pp.720-729. doi:10.1109/TSMC.1985.6313455
- M. Sakawa and K. Kato, “Interactive Fuzzy MultiObjective Stochastic Linear Programming,” In: C. Kahraman, Ed., Fuzzy Multi-Criteria Decision Making— Theory and Applications with Recent Developments, Springer, New York, 2008, pp. 375-408.
- M. Sakawa, K. Kato and I. Nishizaki, “An Interactive Fuzzy Satisficing Method for Multiobjective Stochastic Linear Programming Problems through an Expectation Model,” European Journal of Operational Research, Vol. 145, No. 3, 2003, pp. 665-672. doi:10.1016/S0377-2217(02)00150-9
- M. Sakawa and K. Kato, “An Interactive Fuzzy Satisficing Method for Multiobjective Stochastic Linear Programming Problems Using Chance Constrained Conditions,” Journal of Multi-Criteria Decision Analysis, Vol. 11, No. 3, 2002, pp. 125-137. doi:10.1002/mcda.322
- M. Sakawa, K. Kato and H. Katagiri, “An Interactive Fuzzy Satisficing Method for Multiobjective Linear Programming Problems with Random Variable Coefficients through a Probability Maximization Model,” Fuzzy Sets and Systems, Vol. 146, No. 2, 2004, pp. 205-220. doi:10.1016/j.fss.2004.04.003
- K. Frauendorfer, “Stochastic Two-Stage Programming,” Springer-Verlag, Berlin/New York, 1992. doi:10.1007/978-3-642-95696-6
- P. Olsen, “Multistage Stochastic Programming with Recourse: The Equivalent Deterministic Problem,” SIAM Journal on Control and Optimization, Vol. 14, No. 3, 1976, pp. 495-517. doi:10.1137/0314033
- D. W. Walkup and R. J. B. Wets, “Stochastic Programming with Recourse,” SIAM Journal on Applied Mathematics, Vol. 15, No. 5, 1967, pp. 1299-1314. doi:10.1137/0115113
- R. Wets, “Stochastic Programs with Fixed Recourse: The Equivalent Deterministic Program,” SIAM Review, Vol. 16, No. 3, 1974, pp. 309-339. doi:10.1137/1016053
- S. Koziel and Z. Michalewicz, “Evolutionary Algorithms, Homomorphous Mapping, and Constrained Parameter Optimization,” Evolutionary Computation, Vol. 7, No. 1, 1999, pp. 19-44. doi:10.1162/evco.1999.7.1.19
- Z. Michalewicz and G. Nazhiyath, “Genocop III: A Co-Evolutionary Algorithm for Numerical Optimization Problems with Nonlinear Constraints,” Proceedings of the Second IEEE International Conference on Evolutionary Computation, Perth, 29 November-1 December 1995, pp. 647-651. doi:10.1109/ICEC.1995.487460
- M. Sakawa, K. Kato, H. Sunada and T. Shibano, “Fuzzy Programming for Multiobjective 0-1 Programming Problems through Revised Genetic Algorithms,” European Journal of Operational Research, Vol. 97, No. 1, 1997, pp. 149-158. doi:10.1016/S0377-2217(96)00023-9
- H.-J. Zimmermann, “Fuzzy Programming and Linear Programming with Several Objective Functions,” Fuzzy Sets and Systems, Vol. 1, No. 1, 1978, pp. 45-55. doi:10.1016/0165-0114(78)90031-3

