Received 22 December 2015; accepted 25 January 2016; published 29 January 2016

ABSTRACT

In this paper, our focus is to investigate the notion of irresolute topological vector spaces. Irresolute topological vector spaces are defined by using semi open sets and irresolute mappings. The notion of irresolute topological vector spaces is analog to the notion of topological vector spaces, but mathematically it behaves differently. An example is given to show that an irresolute topological vector space is not a topological vector space. It is proved that: 1) Irresolute topological vector spaces possess open hereditary property; 2) A homomorphism of irresolute topological vector spaces is irresolute if and only if it is irresolute at identity element; 3) In irresolute topological vector spaces, the scalar multiple of semi compact set is semi compact; 4) In irresolute topological vector spaces, every semi open set is translationally invariant.

Keywords:

Topological Vector Space, Irresolute Topological Vector Space, Irresolue Mapping, Semi Open Set

1. Introduction

If a set is endowed with algebraic and topological structures, then by means of a mathematical phenomenon, we can construct a new structure, on the bases of an old structure which is well known. This is the case we have introduced and discussed for beautiful interaction between linearity and topology in this paper. Although the new notion is similar to the notion of topological vector spaces, mathematically it behaves differently. To define irresolute topological vector space, we keep the algebraic and topological structures unaltered on a set but continuity conditions of vector addition and scalar multiplication are replaced by one of the characterizations of irresolute mappings.

A topological vector space [1] is a structure in topology in which a vector space X over a topological field F(R or C) is endowed with a topology such that the vector space operations are continuous with respect to.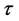

The axioms for a space to become a topological vector space or linear topological space have been given and studied by Kolmogroff [2] in 1934 and von Neumann [3] in 1935. The relation between the axioms of topological vector space has been discussed by Wehausen [4] in 1938 and Hyers [5] in 1939. Also, Kelly [6] has done classical work on topological vector spaces. In the last decade, we can see the work of Chen [7] , on fixed points of convex maps in topological vector spaces. Bosi et al. [8] and Clark [9] have researched on conics in topological vector spaces. More work, in recent years, has been done by Drewnowski [10] , Alsulami and Khan [11] and Kocinac et al. [12] . In 2015, Moiz and Azam [13] defined and investigated s-topological vector spaces, which is a generalization of topological vector spaces.

The motivation behind the study of this paper is to investigate such structures in which the topology is endowed upon a vector space which fails to satisfy the continuity condition for vector addition and scalar multiplication or either. We are interested to study such structures for irresolute mappings in the sense of Levine. The concept of irresolute was introduced by Crossely and Hildebrand in 1972 as a consequence of the study of semi open sets and semi continuity in topological spaces, defined by Levine [14] . In this paper, several new facts concerning topologies of irresolute topological vector spaces are established.

2. Preliminaries

Throughout in this paper, X and Y are always representing topological spaces on which separation axioms are not considered until and unless stated. We will represent field by F and the set of all real numbers by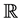. 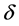and are assumed negligible small but positive real numbers.

Semi open sets in topological spaces were firstly appeared in 1963 in the paper of N. Levine [14] . With invent of semi open sets and semi continuity, many interesting concepts in topology were further generalized and investigated by number of mathematicians. A subset A of a topological space X is said to be semi open if, and only if, there exists an open set O in X such that, or equivalently if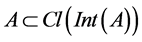. 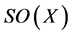denotes the collection of all semi open sets in the topological space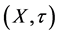. The complement of a semi open set is said to be semi closed; the semi closure of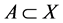, denoted by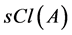, is the intersection of all semi closed subsets of X containing A [15] . It is known that 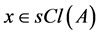if, and only if, for any semi open set U containing , 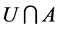is non-empty. Every open set is semi open and every closed set is semi closed. It is known that union of any collection of semi open sets is semi open set, while the intersection of two semi open sets need not be semi open. The intersection of an open set and a semi open set is semi open set. A subset A of a topological space X is said to be semi compact if for every cover of A by semi open sets of X, there exists a finite sub cover.

Remember that, a set 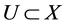is a semi open neighbourhood of a point 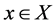if there exists such that. A set is semi open in X if, and only if, A is semi open neighbourhood of each of its points. If a semi open neighbourhood U of a point is a semi open set, we say that U is a semi open neighbourhood of . If and, then, where and are topological spaces and is a product space. It is worth mentioning that a set semi open in the product space cannot be expressed as product of semi open sets in the components spaces. Basic properties of semi open sets are given in [14] , and of semi closed sets in [15] [16] , and references therein.

If is a vector space then e denotes its identity element, and for a fixed, , and, , denote the left and the right translation by x, respectively. The addition mapping is defined by, and the scalar multiplication mapping is defined by.

Definition 1. Let be single valued function between topological spaces (continuity not assumed). Then:

1) is termed as semi continuous [14] , if and only if, for each V open in Y, there exists.

2) is termed as irresolute [15] , if, and only if, for each, there exists . Note that the function is irresolute at, if for each semi open set V in containing, there exists a semi open set U in X containing x such that.

Recall that a topological vector space is a vector space over a topological field F (most often the

real or complex numbers with their standard topologies) that is endowed with a topology such that:

1) Addition mapping defined by is continuous function.

2) Multiplication mapping defined by. is continuous function (where the domains of these functions are endowed with product topologies).

Equivalently, we have a topological vector space X over a topological field F (most often the real or complex numbers with their standard topologies) that is endowed with a topology such that:

1) for each, and for each open neighbourhood W of in X, there exist neighbourhoods U and V of x and y respectively in X, such that.

2) for each and for each open neighbourhood W in X containing, there exist neighbourhoods U of in F and V of x in X such that. Or equivalently, we have: topological Vector Space X over the field with a topology on X such that is a topological group and is a continuous mapping.

3. Irresolute Topological Vector Spaces

In this section we will define and investigate basic properties of irresolute topological vector spaces. Examples are given to show that topological vector spaces are independent of irresolute topological vector spaces in general.

Definition 2. A space is said to be an irresolute topological vector space over the field F if the

following two conditions are satisfied:

1) for each and for each semi open neighbourhood W of in X, there exist semi open neighbourhoods U and V in X of x and y respectively, such that.

2) for each and for each semi open neighbourhood W of in X, there exist semi open neigh- bourhoods U of in F and V of x in X, such that.

Remark 1. Topological vector spaces are independent of irresolute topological vector spaces.

The following example shows that is neither a topological vector space nor an irresolute topological vector space.

Example 1. Consider the vector space R_(R) endowed with the lower limit topology on, generated by

the base, then is neither a topological vector space nor an irre-

solute topological vector space.

Example 2. Let be a topology on generated by the base, then

is a topological vector space as well as irresolute topological vector space over the field.

The next example shows that is an irresolute topological vector space which fails to be a topological

vector space.

Example 3. Consider the field with standard topology on F. Let, where topology defined on

X be generated by the base. Then is not a topological vector

space, because for but, if we choose an open neighbourhood of in X, then, there does not exist any open neighbourhoods U and V of x and y respectively in X, which satisfy the relation.

Now, we show that is an irresolute topological vector space. To verify the first condition, let

.

Case I: Let Consider a semi open neighbourhood (or, ) of in X. Then, for the selection of semi open neighbourhoods (resp.) and (resp.) of x and y respectively in X, we have for each.

Case II: Let, for or. Consider a semi open neighbourhood (or,) of in X. Then, for the selection of semi open neighbourhoods (resp.) and (resp.) of x and y respectively in X, we have for each.

Now, we have to verify the second condition. For this we have four cases,

Case I: Let and. Then for each semi open neighbourhood (or,) of in X, we can choose semi open neighbourhoods (resp.) and (resp.) containing and x in F and X respectively. Then, for every (resp.).

Case II: Let, and. Then for each semi open neighbourhood (or,) of in X, we can choose semi open neighbourhoods (resp.) and, (resp.) containing and x in F and X respectively. Then,

for every (resp.).

Case III: Let and. Then for each semi open neighbourhood (or,) of in X, we can choose semi open neighbourhoods (resp.) and (resp.) containing and x in F and X respectively. Then,

for every (resp.).

Case IV: Let and. Then for each semi open neighbourhood (or,) of in X, we can choose semi open neighbourhoods (resp.) and (resp.) containing and x in F and X respectively. Then, for every (resp.).

Since, both conditions for irresolute topological vector spaces are satisfied, therefore, is an irreso-

lute topological vector space.

Theorem 1. Let be an irresolute topological vector space. Then:

1) The (left) right translation defined by; for all, is irresolute.

2) The translation, defined by; for all, is irresolute.

Proof. 1. Let W be a semi open neighbourhood of. Then by definition, there exist semi open neighbourhoods U and V in X containing y and x respectively, such that. Or . This proves that, is irresolute mapping.

2. Let, then. Let W be any semi open neighbourhood of, then by definition, there exist semi open neighbourhoods U in F of and V in X of x, such that. This gives that

. This proves that is an irresolute mapping.

Remark 2. In topological vector spaces, every open set is translationally invariant whereas in irresolute topological vector spaces, every semi open set is translationally invariant.

Theorem 2. Let be an irresolute topological vector space. If, then:

1) for every.

2) for every.

Proof 1. Let, and let, then we have to prove that z is a semi-interior point of. Now, , where x is some point in A. We can write. By the right translation

, we have. Since, X is irresolute topological vector space and is

irresolute, by Theorem 1 , we have for any semi open neighbourhood A containing, there exists

semi open neighbourhood of z such that, that is. Thus for any

, we can find a semi open neighbourhood such that. Hence.

2. Let and. This means, for some, so we can write

and. Then we can define mapping by. Since, X is an irresolute

topological vector space and by Theorem 1(2), is irresolute mapping, so, we have for any semi open neighbourhood containing, there exists semi open neighbourhood of z such that

. This gives. That is, for any, we can find a semi open neighbourhood

, such that. Hence.

Theorem 3. Let be an irresolute topological vector space. If and B is any subset of

X, then is semi open in X.

Proof. Suppose and. Then, for each and by Theorem 2 (1), We have

. Now, for each. Because arbitrary union of

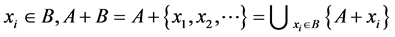
semi open sets is semi open, therefore is semi open in X.

Corollary 1. Suppose is an irresolute topological vector space. If, then the set

is semi open in X.

Theorem 4. Let be an irresolute topological vector space. Then is an irresolute mapping.

Proof. Let and. The. Let W be a semi open neighbourhood of in X.

Since is an irresolute topological vector space, therefore there exist semi open neighbourhoods U of

in F and V of x in X such that,. Or. Since, and, therefore,. This proves that is an irresolute mapping.

Theorem 5. Let be an irresolute topological vector space. The defined by

is an irresolute mapping.

Proof. Let and. Let W be a semi open neighbourhood of in X. Since is an Irresolute topological vector space, therefore, there exist semi open neighbourhoods U of x and

V of y in X such that,. Or. Since, and

, therefore,. This proves that is an irresolute mapping.

Let A be semi open in X. Then, by Theorem 3, and. Similarly, we can prove that each set is semi open in X. Thus the set is semi open in X.

Definition 3. A mapping f form a topological space to itself is called irresolute-homeomorphism [15] , if it is bijective, irresolute and pre-semi open.

Theorem 6. Let be an irresolute topological vector space. For given and with

, each translation mapping and multiplication mapping, where is irresolute homeomorphism onto itself.

Proof. First, we show that is an irresolute homeomorphism. It is obviously bijective. By Theorem 1, is irresolute. Moreover, is pre-semi open because for any semi open set U, by Theorem 2 (1), is semi open.

Similarly, we can prove that is an irresolute homeomorphism.

Definition 4. An irresolute topological vector space is said to be irresolute homogenous space, if

for each, there exists irresolute homeomorphism f of the space X onto itself such that.

Theorem 7. Every irresolute topological vector space is an irresolute homogenous space.

Proof. Let be an irresolute topological vector space. Take, put. Define,

by. By Theorem 6, is irresolute homeomorphism, therefore

is an irresolute homogenous space.

Theorem 8. Suppose that is an irresolute topological vector space and S is a subspace of X. If S

contains a non-empty semi open subset of X, then S is semi open in.

Proof. Suppose U is a non-empty semi open subset in X, such that. By Theorem 2 (1),

is semi open subset of X for each. Thus is semi open in X being union of semi open

sets.

In general, intersection of two semi open sets is not semi open; however we have the following lemma.

Lemma 1. [17] Let be a topological space and. If A is open and U is semi open, then.

Lemma 2. [17] Suppose is a topological space., where, then if, and only if,.

Theorem 9. Every open subspace S of an irresolute topological vector space is also an irresolute topological vector space.

Proof. Suppose is an irresolute topological vector space and S is an open subspace of X. Then, it

satisfies the following properties.

1) For all, we have.

2) For any and, we have. We define topology on S as,. We show that is itself an irresolute topological vector space.

Now, let, and W be any semi open neighbourhood of in S, then W is semi open neighbor-

hood of in X. As is an irresolute topological vector space, therefore, there exist semi open

neighbourhoods of x and of y such that. Now, the sets and are semi open in X containing x and y respectively. By Lemma, 2, , and.

Again, for, and, let W be a semi open neighbourhood of in S and hence semi open in X.

As is an irresolute topological vector space, therefore there exist semi open neighbourhoods A of in F and B of in X such that. Now, the sets and are semi open in F and

X respectively. Since, S is open, therefore by Lemma 2, V is semi open in S. Hence for each semi open neighbourhood W of in S, there exist semi open neighbourhoods U in F of and V in S of x such that

. This proves that is an irresolute topological vector space.

Theorem 10. In irresolute topological vector spaces, for any semi open neighbourhood U of 0, there exists a semi open neighbourhood V of 0 such that.

Proof. The proof is trivial, therefore omitted.

Theorem 11. Let A and B be subsets of an irresolute topological vector space. Then .

Proof. Let and, and let W be a semi open neighbourhood of. Then there exist semi open neighbourhoods U and V of x and y respectively, such that. Since, , , there are and. Then,. This implies. That is,.

Theorem 12. Let be an irresolute topological vector space, then every semi open subspace of X is

semi closed in X.

Proof. Let H be a semi open subspace of X. As right translation is irresolute homeomorphism,

therefore, is semi open. Then, is also semi open. Hence, is semic-

losed.

Theorem 13. Let be a homomorphism of irresolute topological vector spaces. f is

irresolute on X if it is irresolute at.

Proof. Let. Suppose W is semi open neighbourhood of in Y. Since, is irresolute, therefore, there is a semi open neighbourhood V of 0 such that. Now, since f is irresolute at, there exists semi open neighbourhood U of 0 in X such that. Since is irresolute, therefore, is semi open neighbourhood of x. Thus, . This proves that, f is irresolute at x and hence on X.

Theorem 14. Let be an irresolute topological vector space and are subsets of X. If B is

semi open, then for any set A, we have.

Proof. As we know that so. Conversely, let and write where and. There exists a semi open neighbourhood V of zero such that. Now, V is semi open neighbourhood of 0 in X, this gives that is also semi open neighbourhood of 0 in X. Since, , so,. We know that . Therefore,. Hence,.

Theorem 15. Let be an irresolute topological vector space. Then the scalar multiple of semi closedset is semi closed.

Proof. Let, then.. Therefore,.

Theorem 16. Let be an irresolute topological vector space. Then scalar multiple of semi-compact

set is semi-compact.

Proof. Let A be a semi-compact subsets of X. Let be a semi open cover of for some non

zero, then. This gives. Since, and is an irresolute topological vector space, therefore, for each αÎ. Since, A is semi-compact therefore, there exist a finite subset of such that This implies that. Hence is semi-compact in X.

Definition 5. [18] A space is said to be P-regular, if for each semi closed set F and, there exist disjoint open sets U and V such that and.

Theorem 17. Let be a P-regular and irresolute topological vector space. Then the algebraic sum of

a semi-compact set A and semi-closed set B is semi-closed.

Proof. Let, then for some,. Since, the translation mapping is irresolute homeomorphism so, where is semi closed. Since X is P-regular space, therefore, there exist

open sets and such that and. Also is semi open and contains a. Hence,. Since, A is semi-compact, therefore there exists a finite subset of elements of A, such that. Let, then U is a neighbourhood

of x. We claim that. If not, then, then for some i and, which is contradiction to the fact that.

Cite this paper

Moizud Din Khan,Muhammad Asad Iqbal, (2016) On Irresolute Topological Vector Spaces. Advances in Pure Mathematics,06,105-112. doi: 10.4236/apm.2016.62009

References