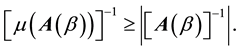Received 29 July 2015; accepted 23 August 2015; published 26 August 2015

ABSTRACT

The theory of Schur complement plays an important role in many fields such as matrix theory, control theory and computational mathematics. In this paper, some new estimates of diagonally, α-diagonally and product α-diagonally dominant degree on the Schur complement of matrices are obtained, which improve some relative results. As an application, we present several new eigenvalue inclusion regions for the Schur complement of matrices. Finally, we give a numerical example to illustrate the advantages of our derived results.

Keywords:

Schur Complement, Gerschgorin Theorem, Diagonally Dominant Degree, Eigenvalue

1. Introduction

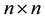Let denote the set of all complex matrices, 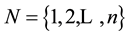and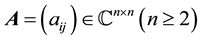. We write

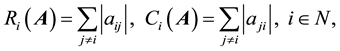
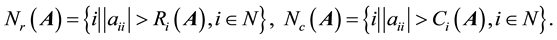
We know that A is called a strictly diagonally dominant matrix if

A is called an Ostrowski matrix (see [1] ) if

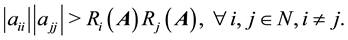
and will be used to denote the sets of all 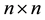strictly diagonally dominant matrices and the sets all 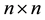Ostrowski matrices, respectively.

As shown in [2] , for 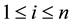and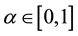, we call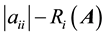, 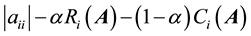and the i-th diagonally, α-diagonally and product α-diagonally dominant degree of A, respectively.

For, denote by the cardinality of β and. If, then is the submatrix of A with row indices in β and column indices in. In particular, is abbreviated to. If is nonsingular,

is called the Schur complement of A with respect to.

The comparison matrix of A, , is defined by

A matrix is called an M-matrix, if there exist a nonnegative matrix B and a real number, where is the spectral radius of B, such that. It is known that A is an h-matrix if and only if is an m-matrix, and if A is an m-matrix, then the Schur complement of A is also an m-matrix and (see [3] ). We denote by H_n and M_n the sets of h-matrices and m-matrices, respectively.

The Schur complement of matrix is an important part of matrix theory, which has been proved to be useful tools in many fields such as control theory, statistics and computational mathematics. A lot of work has been done on it (see [4] -[8] ). We know that the Schur complements of strictly diagonally dominant matrices are strictly diagonally dominant matrices, and the Schur complements of Ostrowski matrices are Ostrowski matrices. These properties have been used for deriving matrix inequalities in matrix analysis and for the convergence of iterations in numerical analysis (see [9] -[12] ). More importantly, studying the locations for the eigenvalues of the Schur complement is of great significance, as shown in [2] [6] [13] -[18] .

The paper is organized as follows. In Section 2, we give some new estimates of diagonally dominant degree on the Schur complement of matrices. In Section 3, we present several new eigenvalue inclusion regions for the Schur complement of matrices. In Section 4, we give a numerical example to illustrate the advantages of our derived results.

2. The Diagonally Dominant Degree for the Schur Complement

In this section, we present several new estimates of diagonally, α-diagonally and product α-diagonally dominant degree on the Schur complement of matrices.

Lemma 1. [3] If, then.

Lemma 2. [3] If or, then, i.e.,.

Lemma 3. [6] If or and, then the Schur complement of A is in or, where is the complement of β in N and is the cardinality of.

Lemma 4. [16] Let, , and. Then

Theorem 1. Let, , , and. Then for all,

(1)

and

(2)

where

Proof. Since, then and. From Lemma 1 and Lemma 2, we have

Thus, for any and, we obtain

For any, denote

If

then there exists sufficiently small positive number such that

(3)

Construct a positive diagonal matrix, where

Let. For, by (3), we have

And for, by, , we obtain

Thus, , and so. Note that, then

(4)

Let x be in. Then

Since, by (4), we have

Let. Then we obtain (1). Similarly, we can prove (2). □

Remark 1. Note that

This shows that Theorem 1 improves Theorem 2 of [17] and [2] , respectively.

Next, we present some new estimates of α-diagonally and product α-diagonally dominant degree of the Schur complement.

Theorem 2. Let, , , and. Then for all, ,

(5)

and

(6)

where for any,

Proof. By Lemma 1 and Lemma 2, we have. Thus, for all, , we have

Let

Similar as the proof of Theorem 1, we can prove

Similarly, we have

By Lemma 4, we have

Hence, (5) holds. Similarly, we can prove (6).

Remark 2. Note that

This shows that Theorem 3 improves Theorem 4 of [2] .

Similar as the proof of Theorem 2, we can prove the following theorem immediately, which improves Theorem 2 of [2] .

Theorem 3. Let, , , and. Then for all, ,

and

3. Eigenvalue Inclusion Regions of the Schur Complement

In this section, based on these derived results in Section 2, we present new eigenvalue inclusion regions for the Schur complement of matrices.

Theorem 4. Let, , , and and be eigenvalue of. Then there exists such that

(7)

Proof. By Gerschgorin Circle Theorem, we know that there exists such that. Thus, by Lemma 1 and Lemma 2, we have

i.e.,

Thus, (7) holds.

Lemma 5. [2] Let and. Then for any eigenvalue of A, there exists such that

Theorem 5. Let, , , , and be eigenvalue of. Then for any, there exists such that

(8)

Proof. By Lemma 5, we know that there exists such that

Therefore,

Similar as the proof of Theorem 2, we can prove

Thus, we have

Further, we obtain (8).

4. A Numerical Example

In this section, we present a numerical example to illustrate the advantages of our derived results.

Example 1. Let

By calculation with Matlab 7.1, we have that

Since, by Theorem 4, the eigenvalue inclusion set of is

From Theorem 4 of [2] , the eigenvalue inclusion set of is

We use Figure 1 to illustrate. And the eigenvalues of are denoted by “+” in Figure 1. The blue dotted line and green dashed line denote the corresponding discs and respectively.

Meanwhile, since, by taking in Theorem 5, the eigenvalue inclusion set of is

From Theorem 5 of [2] , the eigenvalue inclusion set of is

We use Figure 2 to illustrate. And the eigenvalues of are denoted by “+” in Figure 2. The blue dotted line and green dashed line denote the corresponding discs and respectively. It is clear that and.

Cite this paper

DongjieGao, (2015) The Estimates of Diagonally Dominant Degree and Eigenvalue Inclusion Regions for the Schur Complement of Matrices. Advances in Pure Mathematics,05,643-652. doi: 10.4236/apm.2015.510058

References