Received 11 May 2015; accepted 7 July 2015; published 10 July 2015

ABSTRACT

The aim of this paper is to introduce the concept of generalized topological molecular lattices briefly GTMLs as a generalization of Wang’s topological molecular lattices TMLs, Császár’s set- point generalized topological spaces and lattice valued generalized topological spaces. Some notions such as continuous GOHs, convergence theory and separation axioms are introduced. Moreover, the relations among them are investigated.

Keywords:

Generalized Topological Molecular Lattices, Generalized Order Homomorphisms, Convergence of Molecular Nets, Separation Axioms

1. Introduction

In 1992 Wang [1] , introduced his important theory called topological molecular lattice (briefly, TML) as a generalization of ordinary topological and fuzzy topological spaces in tools of molecules, remote neighborhoods and generalized order homomorphisms GOHs. Then many authors characterized some topological notions in such TMLs, such as convergence theories of molecular nets or ideals [1] - [3] , separation axioms [1] [4] and other notions.

In this paper, we aim to introduce a generalization of TMLs under the name of generalized topological molecular lattice (briefly, GTML). In the same manner, we study several notions in these GTMLs, investigate some properties and set the relations among these notions including GOHs, convergence theories and separation axioms.

Throughout this work, 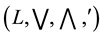is a complete lattice with an order-reversing involution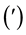, and with the smallest element 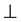and the largest element .

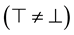By an L-generalized topology [5] , on a non-empty ordinary set X, we mean a subfamily 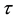of 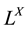with the following axioms:

(T₁) For all;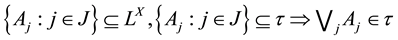

(T₂).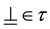

The pair 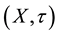is called an L-generalized topological space. Every element A of 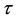is called t-open L-set and the pseudo complement 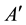is called t-closed L-set. The concept of L-generalized co-topological space can be defined dually.

For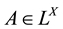, the L-generalized interior of A is the largest L-open subset contained in A and denoted by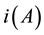, so A is open if and only if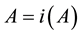. The L-generalized closure of A is the smallest L-closed subset contains A and denoted by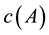, so A is closed if and only if.

Let be an ordinary mapping. The corresponding L-fuzzy mapping is defined as follows:

and its inverse defined as:

A mapping between two L-generalized topological spaces is said to be an L-genera- lized continuous mapping if and only if. The mapping is called an L-generalized open (resp. L-generalized closed) mapping if (resp. is m-closed for all t-closed set F). The category of L-generalized topological spaces and their L-generalized continuous mappings is denoted by L-GTop.

Let us recall that a non-zero element a in a lattice L is said to be a molecule, if for every such that, implies or. Denote the set of all molecules of L by or M for short, clearly, every element in L can be constructed by elements of M, since each element in L is a union of molecules.

Definition 1.1. [1] Let L ba a complete lattice,. The subset is called a minimal family of a if the following two conditions are hold:

(i).

(ii) If and, then such that.

Denote the greatest minimal family of a by. Hence, let.

It is easily to see that both and are minimal families of a.

Definition 1.2. [1] Let and be complete lattice. A mapping is called a generalized order homomorphism or GOH for short if

(i) if and only if.

(ii) f is join preserving, i.e.;.

(iii) is join preserving, where for all,.

Theorem 1. [1] Let be GOH, then the following properties are hold:

(1) f and are order preserving, i.e.:

.

.

(2), for all.

(3), for all.

(4).

(5), for all.

(6) is meet preserving, i.e.:.

Theorem 2. [1] Let be a GOH, then:

(i) If, then.

(ii) If B is a minimal family of a in, then is a minimal family of in.

Proposition 3. [1] Let, be a mapping between complete lattices. The following are equivalent:

(1) f is an isomorphism.

(2) f is a bijective GOH.

(3) is a bijective GOH.

2. Main Notions in GTMLs

This section is devoted to introduce the concept of generalized topological molecular lattices and other concepts which play an essential role in these GTMLs.

To denote a molecular lattice, the entry is used: it indicates both the lattice itself and the set of its molecules.

Definition 2.1. Let be a molecular lattice. A subfamily is said to be a generalized closed topology, or briefly, generalized co-topology, if

(T₁) is closed under arbitrary intersections;

(T₂).

A generalized co-topology is said to be a closed topology (or co-topology) [1] , if it satisfies the following additional conditions:

(T₃) is closed under finite union;

(T₄).

The pair is called a generalized topological molecular lattice, or briefly, GTML.

Example 1. Let be a generalized topological space [6] . Then it is clear that is a molecular lattice and is a GTML, where.

Example 2. Let be an L-generalized topological space [5] . Then we have that is a GTML, where is a molecular lattice and.

Definition 2.2. [7] Let be a GTML, , and. Then F is said to be a generalized remote neighborhood of a. The set of all generalized remote neighborhoods of a will be denoted by.

In a GTML, if and such that, then we get. However, for, need not to be in, since it does not necessary be closed element because is not necessary be closed under finite joins.

Definition 2.3. [8] Let L be a complete lattice. A non empty subset I of L is said to be an ideal, if it satisfies the following conditions:

(i) For and.

(ii) For all.

(iii).

Generally, one can get that is not necessary be an ideal in GTMLs. So, let us define the following:

Then is an ideal in GTMLs.

Definition 2.4. Let be a GTML and. The intersection of all h-elements containing A will be called the generalized closure of A denoted by. i.e.,

.

By the definition of, one can obtain that A is a closed element if and only if.

Proposition 4 Let be a GTML, then the following statements are hold:

(1), if, then;

(2);

(3).

Proof.

(1) For, with, we have

i.e.,.

(2) For all. obvious;

(3) For all, we have.

Since any generalized co-topology is not necessarily closed under finite join, then the finite join is not necessarily be a closed L-fuzzy set, so some relations that are valid in topological molecular lattices do not remain true in generalized topological ones, for example the equation

is not necessarily true in generalized topological lattice as shown in the following example:

Example 3. Let, and be a generalized topology on X. The class is a generalized co-topology on. So for and, we have that, and. But implies that which means that.

Definition 2.5. Let be a GTML, , then a is said to be an adherence point of A, if for all, we have.

Since is a GTML with L equipped with an order reversing involution, we can define the generalized interior by

Proposition 5. Let be a GTML, then the following statements are hold:

(1).

(2), if, then

(3).

Proof.

(1) For all. obvious;

(2) For, with, we have

i.e.,.

(3) For all,.

The relation which is true in TMLs, it is not true in GTMLs as shown in the following example:

Example 4. For and the generalized co-topology on as given in Example 3. Let and, we have that, and. But implies that which means that.

Definition 2.6. Let and be GTMLs. An GOH is called:

(1) continuous GOH, if for every, we have.

(2) continuous at a molecule, if for every, we have.

It is clear that the generalized topological molecular lattices GTMLs and the continuous GOHs form a category denoted by GTML.

Theorem 6. Let and be GTMLs, be a GOH, then the following statements are equivalent:

(i) f is a continuous GOH.

(ii).

(iii).

Proof. The proof the same as given for Theorem 5.2 [1] .

For an L-generalized continuous mapping, it is well-known that induced by an ordinary mapping, and satisfied many useful properties ([9] [10] ). Hence, the continuous GOHs can be regarded as a generalization of L-generalized continuous mappings.

Definition 2.7. Let be an isomorphism and f and be continuous. A GOH is said to be a homeomorphism.

Definition 2.8. Let and be GTMLs. A GOH is said to be:

(1) closed, if for every, we have

(2) open, if for every and every such that, there exists such that and.

Remark 1. In the case and are equipped with order reversing involutions, we can say that a GOH is open if it maps open elements in into open elements in. Clearly, every L-generalized closed (resp. open) mapping is a closed GOH (resp. an open GOH).

As given in [1] , we have the following easily established result.

Proposition 7 The compositions of closed (resp.,open) GOHs are closed (resp.,open) GOHs.

Definition 2.9. [1] Let be a molecular lattice, and D is a directed set, then the mapping is called a molecular net and denoted by. S is said to be in A, if.

Definition 2.10. [1] Let be a molecular lattice, and be two molecular nets, then T is said to be a subnet of S, if there exists a mapping such that

(i).

(ii) such that.

Definition 2.11. Let be a GTML, be a molecular net and, then:

(1) a is called a limit point of S, if eventually true, and denoted by. The join of all limit points of S will be denoted by.

In symbol,.

(2) a is called a cluster point of S, if frequently true, and denoted by. The join of all cluster points of S will be denoted by.

In symbol,.

Corollary 1 [1] Suppose that (resp.,) and. Then (resp.,).

From the Definition 1.1, similarly to the case of TMLs, the following proposition is hold:

Proposition 8. Let be a GTML, be a molecular net and, then:

(1) if and only if.

(2) if and only if.

Proposition 9. Let be a GTML, be a molecular net and, then:

(1) if and only if.

(2) if and only if.

Proof.

(1) We only prove the sufficiency. Suppose that and is a standard minimal family of a. Since. Then for all, there exists a limit point x of S such that. By Corollary 1, and therefore.

(2) The proof is similar to that of (1) and is omitted.

Remark 2. Let be a molecular lattice, S be a molecular net and, then

(1) If is a constant net, i.e., , then.

(2) If and T be a subnet of S, then.

Theorem 10 [8] Let be a GTML, and, then:

(1) If, then there exists a molecular net in A, such that.

(2) If is a molecular net in A, such that, then.

Corollary 2 [8] Let be a GTML, and, then if and only if there exists a molecular net in A, such that.

3. Separation Axioms in GTMLs

In this section, we introduce some kinds of separation axioms in GTMLs and investigate their properties. Moreover, we discuss the relations among them, isomorphic GOHs.

Definition 3.1. Let be a GTML, then

(1) is called, if, there exists such that.

(2) is called, if, there exists such that or there exists such that.

(3) is called, if, there exists such that.

(4) is called, if, there exists and such that.

According to the above definitions, we can directly obtain the following results:

Corollary 3 For a GTML, we have the following implications:

.

.

In general, we have that does not imply. The next example [1] is clear.

Example 5. Take and, then clearly that is not and hence it is not. But there are no disjoint points, so is.

Definition 3.2. [1] Let be a molecular lattice, with, then m is called a component of A, if and with and imply that.

Lemma 1. [1] Let be a molecular lattice, with and, then A has at least one component m such that.

Theorem 11. Let be a GTML, then it is, if and only if, we have a is a component of.

Proof.

Assume that there exists such that a is not a component of, then by the preceding lemma, we can choose a component b of such that. Since is a, then such that. Hence and so. a contradiction.

Let with, then by the assumption, we have a is a component of and hence. Then and.

Therefore, is.

Theorem 12. Let be a GTML, then it is, if and only if, we have or.

Proof.

Let be, then, there exists such that or there exists such that. Hence, a is not an adherence point of b or b is not an adherence point of a which implies that or.

Let with, then we have or. Hence, we get with or with which complete the proof.

Theorem 13. Let be a GTML, then it is, if and only if, a is closed.

Proof.

Let be and, if, then there exists such that. Hence, a is not an adherence point of b. Thus, b contains all its adherence points and hence, b is closed.

Let. By the assumption, b is closed and then with. Therefore, is.

Theorem 14. Let be a GTML, then it is, if and only if for every molecular net S, contains no disjoint molecules.

Proof.

Let be a molecular net such that with. Let and, since, then eventually, i.e.; such that we have. Similarly, we have, but D is a directed set, hence such that and. Then. Therefore, , then is not.

Assume that is not, then with and, we have. Thus, we can choose a molecule such that. Put

Then S is a molecular net with both a and b are limit points of S. Hence, contains at least two disjoint molecules.

Theorem 15. Let and be GTMLs. If is a and be a homeomorphism, then so is.

Proof. We only show the case of and the others are similar. Let be a and with. Since f is bijective, then there exist such that and. Then there exist and such that. But f is isomorphic GOH, so and.

Thus,.

Therefore, is also a.

Similarly, one can check the other cases.

Analogously to [4] , we give the next definitions:

Definition 3.3. Let be a GTML, then is said to be, if and only if with, there exists and such that.

Clearly, if is a, then it is. Furthermore, we have the following:

Definition 3.4. Let be a GTML, then is called an interior additive if, we have.

Theorem 16. Let be a GTML, if it is both and an interior additive, then is a.

Proof. Let with. Since is, then there exists and such that. Hence,.

But is an interior additive, then.

Therefore, is a.

4. Conclusion

The concept of generalized topological molecular lattices GTMLs has been defined. Some notions have been extended to such spaces namely continuous GOHs, convergence theory in terms of molecular nets and and separation axioms.

References