Received 26 March 2015; accepted 22 May 2015; published 25 May 2015

ABSTRACT

The main purpose of this article is to define the super characteristic classes on a super vector bundle over a superspace. As an application, we propose the examples of Riemann-Roch type formula. We also introduce the helicity group and cohomology with respect to coefficient of the helicity group. As an application, we propose the examples of Gauss-Bonnet type formula.

Keywords:

Superspace, Super Characteristic Class, Complex Supercurve with Genus g, SUSY Structure, Cohomology of Helicity Group

1. Introduction

In this paper, we define various characteristic classes on a super vector bundle over a superspace, so called super characteristic classes. We also propose the super Riemann-Roch formulas and the super Gauss-Bonnet formulas as its application. In contrast, it is justified the definition of the super characteristic classes by establishing those formulas. In [1] , we defined the super Chern classes with values in the super number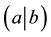, 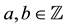and we succeeded in applying the super ADHM construction of the super Yang-Mills instantons. But essentially the super Chern classes ought to take with values in an integer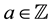. Meaning like it, we introduce the new definition of the super Chern classes with values in integer. In general, the characteristic classes consider that given the vector bundles it corresponds to some cohomology class of the base manifolds. Hence, we need the cohomology reflecting the properties of superspaces. Therefore, we will define the cohomology with respect to coefficient of the some finitely generated group, which is called the helicity group.

This article is organized as follows. After a brief sketch on the definition and examples of superspaces and its cohomology in Section 2 ([1] -[6] ), main result in this paper is that we define the Chern class, Chern character, Todd class, Pontrjagin class, Eular class, 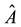-genus and L-genus as in the case of super category in Section 3. In Section 4, as an application, we have the Riemann-Roch type formula of super structure sheaf on the complex supercurves of dimension with genus g. Moreover, it generalizes the structure sheaf to any super line sheaves. In particular, in the case of dimension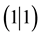, with supersymmetric structure, we obtain the Atiyah-Singer index type formula for any super line bundles. In Section 5, we attempt to define the helicity group and cohomology with respect to coefficient of the helicity group. In Section 6, we give the Gauss-Bonnet type formula on the complex supercurves of dimension with genus g and the complex super projectve space of dimension.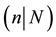

2. Supermanifolds

We will summarize the definitions here in order to establish terminology and notation ([1] -[6] ).

Definition 2.1 A superspace is defined to be a local ringed space 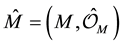consisting a topological

space M and a sheaf of 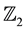-graded supercommutative rings 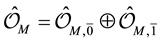on it such that the stalk 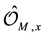at any point 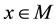is a local ring.

In particular case of a superspace, a supermanifold is defined by the following.

Definition 2.2 A supermanifold of dimension 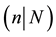is a ringed space with the following properties:

1) the structure sheaf is a sheaf of -graded supercommutative rings,

2) Let be the ideal sheaf of nilpotents in. Then is a classical manifold M of dimension n, so also called body.

3) Let be the locally free -module of rank. Then is locally isomorphic to the exterior algebra.

A supermanifold is said to be split if the isomorphism 3) holds globally.

A local section can be expressed as follows:

(1)

where, is a local coordinate function on and a local

generator of. We refer to as a local coordinate of a supermanifold.

Example 2.1 1) The typical example is the real (or complex) linear superspace (or) which can be defined by

where (or) is the sheaf of the ring of differential functions on (or). It is easy to see that

the is isomorphic to.

2) A real super sphere of dimension is defined by

where is the sheaf of the ring of differential functions on.

3) A complex super projective space of dimensin is defined by

We denote by the structure sheaf of. A super holomorphic function 1) on should be a function of total homogeneity 0 in even variables and N odd variables, that is has homogeneity. Let be the even line sheaf of degree d on and be the odd line sheaf of degree d on.

4) A quaternionic super projective space of dimension is defined by

The above are examples of the supermanifolds in Definition 2.2.

5) We have a new example of superspace in Definition 2.1 as follows. The complex supercurves of dimension with genus g is defined by

where is the canonical line bundle on the classical Riemann surfaces and. In the case of, it becomes the super Riemann surfaces with SUSY structure (c.f. [7] , p.162). In the case of, we do not kown whether or not there exists a SUSY structure.

We can construct the super Euler sequence as follows ([1] ).

Tensoring this with, we have

Considering the super determinant ( so called Berezin bundle ) of the super Euler sequence, we obtain

Dualizing this, we can write

where calls the canonical super line bundle of and is the parity change functor. The fol- lowing is given by Manin ([5] ).

Lemma 2.1

where and.

The following is given by Penkov ([8] ).

Theorem 2.1 (Super Serre Duality) Let E be a complex super vector bundle over. Suppose that is the canonical super line bundle of. Then we have the following.

3. Super Characteristic Class

In this section, we will give a main result in this paper. Let denote the structure sheaf on. Then we have an exact sequence (cf. [2] , p.166 Lemma 2.1)

where is the natural injection and exp is defined by

The implies,. Hence. This induces the exact sequence of cohomology groups:

We can identify with the equivalence classes of or -super line bundles over. Then we can define the super first Chern class of -super line bundle L and -super line bundle by

Remark 3.1 Note that we can define. We consider the line sheaf over the complex super projective space. This line sheaf is decomposed into

The super first Chern calss and the classical first Chern class denote by and, respectively. Then we have

Hence, we see that for the superline bundle L

We will propose the axiomatic definition of super Chern classes (cf. [1] [2] [9] -[15] ). We consider the category of complex -super vector bundles over an -superspace.

Axiom 1 For each complex super vector bundle E over and for each positive integer i, the i-th super Chern class is given, and.

We set and call the total super Chern class of E.

Axiom 2 (Naturality)

Let E be a complex super vector bundle over a superspace and a morphism of superspaces. Then

where is the pull-back bundle over.

Axiom 3 (Whitney sum formula)

Let be complex line bundles of rank or and be their Whitney sum. Then

Axiom 4 (Normalization)

We put and. Then it can be axiomatically as follows:

In order to explicitly define the super characteristic classes we need the splitting principle ([2] Proposition 3.7) as follows.

Proposition 3.1 (Bartocci, Bruzzo, Hernandez-Ruiperez) Let E be a complex -super vector bundle over an -supermanifold. Then there exists a supermanifold and a proper fibration such that

1) The homomorphism is injective.

2) The pull-back bundle splits into a direct sum of even complex line bundles of rank and odd complex line bundles of rank:

We will explicitly give the super characteristic classes.

Definition 3.1 1) The total super Chern class is defined by

2) The total super Chern character is defined by

3) The super Todd class is defined by

4) The super Eular class is defined by

5) Let be a real vector bundle of rank. The i-th super Pontrjagin class and the total super Pontrjagin class are defined by

6) The super -genus is defined by

7) The super L-genus is defined by

We can consider that it is justified these definitions by the following (cf. [13] [14] ).

Lemma 3.1 The first few terms of and are given by the following.

Proof. Let E be a complex rank- super vector bundle over a complex -dimensional supermanifold. Then, total super Chern class is written by

Hence, we have

The total super Chern character is written by

Hence we have

,

,

,

.

It is well-known thtat

Hence the total super Todd class is written by

Therefore we have

,

,

,

.

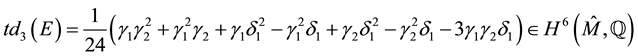
Then, they satisfy that

W

Lemma 3.2 The first few terms of, and are given by the following.

Proof., and similarly form in the classical case. Therefore and are of same argument (cf. [13] ).

Let E be a complex rank- super vector bundle over a complex -dimensional supermanifold. The total super Chern class is written by

Hence, we have

,

,

,

.

The total super Pontrjagin class is written by

Hence, we have

,

.

Then, they satisfy that

W

4. Riemann-Roch Type Formula

Let be the complex supercurves with genus g, where, ,

in Example 2.1 (5). Then the canonical super line bundle on is explicitly written by

Hence we have.

Note that for any object E and F the parity change functor satisfies

In general, if is a supermanifold, then its tangent bundle can be written by (cf. [16] ). Hence we have

Using this decomposition, Euler number of get

Note that.

Theorem 4.1 Let be the complex -dimensional supercurves with genus g. Then, we have a Noether type formula as follows.

Proof. Let be the genus on the classical Riemann surfaces and be

the number of linear independent Dirac zero modes or harmonic spinors which is not topologically invariant.

The structure sheaf of the complex supercurves have decomposition

.

In the case of genus, we have (cf. ([17] ))

In the case of genus, it always satisfies for any p. In the case of genus, it satisfies

In the case of genus, we have the following.

Note that equal of second make use of the classical Serre duality. Hence we obtain

In the case of genus and, we can prove similarly. W

Corollary 4.1 Let be the complex -dimensional supercurves with genus g. Then we have a Riemann- Roch type formula as follows.

where is the fundamental homology class.

Proof.

From Theorem 4.1, this completes the proof of Corollary 4.1. W

The following Corollary essentially has been obtained by [18] . It needs the supersymmetric structure on the super Riemann surfaces (cf. [7] [19] [20] ). The following rewrite the result of [21] to the super characteristic classes.

Corollary 4.2 Let be the complex -dimensional super Riemann surfaces and be any super line bundles of rank on. Then we have a Atiyah-Singer index type formula as follows.

where is the fundamental homology class.

Proof. The canonical super line bundle of a super Riemann surface can be defined by splitting the Berezin bundle using the super complex structure. We get an exact sequence ([21] [22] )

We can define the operator, , ,. Note that the

operator is supersymmetric anti-holomorphic vector fields. Tensoring this exact sequence with any super line bundles, we have

We can define the operator, ,. We can describe

as the space of sections s of satisfying the condition. The group can be described as

the space of sections modulo the image of the operator. Hence

and. W

Let be distinct points and,. Then the super meromorphic functions

is coresponding to the super Weil divisor (cf. [18] [20] )

where is a super holomorphic function. We put, , and

. Then the inverse element of, which is unique, is given by the formula (cf. [23] ). As an application, we have a main theorem as follows.

Theorem 4.2 Let be the complex -dimensional supercurves with genus g and be

any super line bundles of rank on. Then we have a Riemann-Roch type formula as follows.

where is the fundamental homology class.

Proof. Let us consider the super divisor on. The local equation on D is defined by on a open set of. If, then. The super Weil divisor can be considered as the super Cartier divisor. Then there is the exact sequence

The line sheaf corresponding to is defined by the transition functions

on. The sheaf which is defined by

is the coherent ideal sheaf. The fiber of is of zero in and in. The sheaf is called the super skyscraper sheaf. Tensoring this with, we have

The map is defined by on an open set of. Taking co-

homology, this gives a long exact sequence

Taking the alternative sum, we have

Noting that and, we have

From and, we have

We also take the exact sequence

This gives rise to a long exact sequence

Taking also the alternative sum, we have

Hence, we havet

Note that. So adding in both side, we see that

Therefore, is independent of, so that we can put.

From Theorem 6.1,. This completes the proof of

Theorem 4.2. W

5. Helicity Group

Definition 5.1 The helicity rank of finitely generated group G is defined by the positive generator of linearly independent itself. The helicity rank is denoted by. The helicity rank of is defined by the negative generator of linearly independent itself. The helicity rank of also is defined by twice the positive generator of linearly independent itself of G.

We define the finitely generated group of two type as follows.

Note that, and are isomorphic to, and as abelian groups, respectively.

But its helicity rank is differently as follows.

Example 5.1, , ,

, , , ,

, ,.

Definition 5.2 Let be a -dimensional complex supermanifold. Then the helicity group is defined by the following.

The helicity rank of can be represented by

The super cohomology with coefficient in of an -dimensional supermanifold is isomorphic to the -valued cohomology with coefficient in of the classical manifold M using the universal coefficient theorem. That is to say, we have the following.

This isomrphism is applied in section 6.

6. Gauss-Bonnet Type Formula

In this section, we will apply the super cohomology with coefficient in helicity group.

Theorem 6.1 Let be the complex -dimensional supercurves with genus g. Then we have a Gauss- Bonnet type formula as follows.

Proof. Euler number of get

Note that. On the other hand, the right hand side is

.

Both sides coincide. W

Theorem 6.2 Let be the complex -dimensional super projective space. Then, we have

Proof.

From the super Euler sequence, we can compute the total Chern class of holomorphic tangent bundle. Setting for simplicity’s sake and, we have

The sum of coefficient of x is the first super Chern number.

W.

References