Advances in Pure Mathematics
Vol.04 No.12(2014), Article ID:52464,15 pages
10.4236/apm.2014.412074
Compactness of Composition Operators from the p-Bloch Space to the q-Bloch Space on the Classical Bounded Symmetric Domains
Jianbing Su*, Huijuan Li, Xingxing Miao, Rui Wang
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou, China
Email: *sujb@jsnu.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 October 2014; revised 30 November 2014; accepted 12 December 2014
ABSTRACT
In this paper, we introduce the weighted Bloch spaces  on the first type of classical bounded symmetric domains
on the first type of classical bounded symmetric domains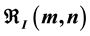 , and prove the equivalence of the norms
, and prove the equivalence of the norms 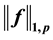 and
and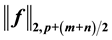 . Furthermore, we study the compactness of composition operator
. Furthermore, we study the compactness of composition operator 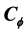 from
from 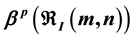 to
to , and obtain a sufficient and necessary condition for
, and obtain a sufficient and necessary condition for  to be compact.
to be compact.
Keywords:
Bloch Space, Classical Bounded Symmetric Domains, Composition Operators, Compactness, Bergman Metric

1. Introduction
Let  be a bounded homogeneous domain in
be a bounded homogeneous domain in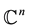 . The class of all holomorphic functions on
. The class of all holomorphic functions on 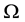 will be denoted by
will be denoted by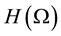 . For
. For 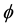 a holomorphic self-map of
a holomorphic self-map of  and
and , the composition
, the composition  is denoted by
is denoted by


The composition operators as well as related operators known as the weighted composition operators between the weighted Bloch spaces were investigated in [1] [2] in the case of the unit disk, and in [3] - [7] for the case of the unit ball. The study of the weighted composition operators from the Bloch space to the Hardy space 
In 1930s all irreducible bounded symmetric domains were divided into six types by E. Cartan. The first four types of irreducible domains are called the classical bounded symmetric domains, the other two types, called exceptional domains, consist of one domain each (a 16 and 27 dimensional domain).
The first three types of classical bounded symmetric domains can be expressed as follows [19] :

where 




Let 




matrix 





where 



Following Timoney’s approach (see [18] ), a holomorphic function 

Now we define a holomorphic function 


where
We can prove that 

with the case on
Let 


Let 


In Section 2, we prove the equivalence of the norms defined in this paper and in [20] .
In Section 3, we state several auxiliary results most of which will be used in the proofs of the main results.
Finally, in Section 4, we establish the main result of the paper. We give a sufficient and necessary condition for the composition operator Cf from the p-Bloch space 



Theorem 1.1. Let 





for all 


The compactness of the composition operators for the weighted Bloch space on the bounded symmetric domains of 

2. The Equivalence of the Norms
Denote [20] 
Lemma 2.1. (Bloomfield-Watson) [21] Let 


where 


Theorem 2.1. 

Proof. The metric matrix of 
For any


Denote 


Thus
Hence
Furthermore,
Since
Thus

For
then we have

Combining (2.2) and (2.3),
Next,
and
Therefore, the proof is completed. □
3. Some Lemmas
Here we state several auxiliary results most of which will be used in the proof of the main result.
Lemma 3.1. [18] Let 



for each 


on


Lemma 3.2. Let 





for all 

Proof. For
For any compact





Thus

Combining Lemma 3.1 with (3.3) shows that (3.2) holds. □
Lemma 3.3. (Hadamard) [21] Let 


and equality holds if and only if 
Lemma 3.4. Let

Proof. For any
Thus we have
It follows from Lemma 3.3 that 
Lemma 3.5. Let 





If (3.6) holds, then

Proof. We can get the conclusion by the process of the proof on Theorem 2.1. □
Lemma 3.6. [18] Let
where 

Denote

(1)
(2)
(3)
(4) 

(5) 

(6) 

Lemma 3.7. 


any bounded sequence 


Proof. The proof is trial by using the normal methods. □
4. Proof of Theorem 1.1
Proof. Let 




Suppose (1.3) holds. Then for any


for all 


By the chain rule, we have
If 





It follows from (4.1) and (4.2) that


whenever 

On the other hand, there exists a constant 
So if
We assume that 






for any





whenever 

Combining (4.4) and (4.6) shows that 


For the converse, arguing by contradiction, suppose 
the condition (1.3) fails. Then there exist an







for all
Now we will construct a sequence of functions 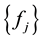
(I) 

(II) 

(III)
The existence of this sequence will contradict the compactness of
We will construct the sequence of functions 
Part A: Suppose that
where 






Denote 

Denote
then

We construct the sequence of functions 
Case 1. If for some

then set

where 
Case 2. If for some

then set

where





Case 3. If for some

then set

Next, we will prove that the sequences of functions 
To begin with, we will prove the sequence of functions 
It follows from Lemma 3.5 that
This proves that the sequence of functions 
Let 



for any
Since
But 







Now (4.8) and (4.9) mean that

Combining (4.7) and (4.16), we have
Since
This proves that 


We can prove that the sequence of functions 
Part B: Now we assume that
It is clear that 





If

Using formula (1.1), we have
Denote
Then,

We construct the sequence of functions 
Case 1. If for some
then set

Case 2. If for some
then set

Case 3. If for some
then set

Case 4. If for some
then set

Case 5. If for some
then set

Case 6. If for some
then set

By using the same methods as in Part A, we can prove the sequences of functions 
Now, as an example,we will prove that the sequence of functions 
For any

Thus
By Lemma

It follows from Lemma 3.5 and (4.25) that

Let 




Since
So 


formly on E. Therefore,the sequence of 



For case 2,

Combining (4.7) and (4.26), we have
Since
This proves that 


If



If we denote


Denote


where 

and
It is clear that



We prove that the sequence of functions 

Since
So 
Next we prove that 




It is clear that 


Since 







morphic on








by the definition of


Hence 

Part C: Assume that
where







Just as in Part B, we can use the same methods to prove the conclusion. And for


Using formula (1.1), we have
Denote
then,

We construct the sequence of functions 
Case 1. If for some
then set

Case 2. If for some
then set

Case 3. If for some
then set

Using the same methods as in Part A and Part B, we can prove the sequences of functions 
Part D: In the general situation. For




We may assume that 





that 










verges uniformly to 

Let


From the same discussion as that in Part B, we know that 



set 












Acknowledgements
We thank the Editor and the referee for their comments. Research is funded by the National Natural Science Foundation of China (Grant No. 11171285) and the Postgraduate Innovation Project of Jiangsu Province of China (CXLX12-0980).
Cite this paper
JianbingSu,HuijuanLi,XingxingMiao,RuiWang, (2014) Compactness of Composition Operators from the p-Bloch Space to the q-Bloch Space on the Classical Bounded Symmetric Domains. Advances in Pure Mathematics,04,649-664. doi: 10.4236/apm.2014.412074
References
- 1. Ramos-Fernández, J. C. (2011) Composition Operators between μ-Bloch Spaces. Extracta Mathematicae, 26, 75-88.
- 2. Wolf, E. (2011) Weighted Composition Operators between Weighted Bloch Type Spaces. Bulletin de la Société Royale des Sciences de Liège, 80, 806-816.
- 3. Dai, J.N. (2012) Compact Composition Operators on the Bloch Space of the Unit Ball. Journal of Mathematical Analysis and Applications, 386, 294-299. http://dx.doi.org/10.1016/j.jmaa.2011.07.067
- 4. Li, J.F. (2010) Composition Operators from p-Bloch Spaces to Little q-Bloch Spaces on the Unit Ball of Cn. Acta Mathematica Sinica (Series B), 30, 1013-1020.
- 5. Zhang, M.Z. and Xu, W. (2007) Composition Operators on α-Bloch Spaces of the Unit Ball. Acta Mathematica Sinica (Series B), 23, 1991-2002.
- 6. Zhang, X.J. and Li, J.X. (2009) Weighted Composition Operators Between μ-Bloch Spaces over the Unit Ball of Cn. (Chinese). Acta Mathematica Sinica (Series A), 29, 573-583.
- 7. Zhou, Z.H. and Zeng, H.G. (2003) Composition Operators between p-Bloch Space and q-Bloch Space in the Unit Ball. Progr. Progress in Natural Science (Engl. Ed.), 13, 233-236.
- 8. Stevo, S. (2008) Norm of Weighted Composition Operators from Bloch Space to on the Unit Ball. Ars Combinatoria, 88, 125-127.
- 9. Tang, X.M. and Zhang, R.J. (2013) Weighted Composition Operator from Bloch-Type Space to H∞ Space on the Unit Ball. Mathematical Inequalities and Applications, 16, 289-299. http://dx.doi.org/10.7153/mia-16-22
- 10. Li, S.X. and Zhu, X.L. (2004) Essential Norm of Weighted Composition Operator between α-Bloch Space and β-Bloch Space in Polydiscs. International Journal of Mathematics and Mathematical Sciences, 69-72, 3941-3950.
- 11. Zhou, Z.H. and Shi, J.H. (2001) Compact Composition Operators on the Bloch Space in Polydiscs. Science in China Series A, 44, 286-291. http://dx.doi.org/10.1007/BF02878708
- 12. Zhou, Z.H. and Wei, Z.Q. (2005) Weighted Composition Operators on the Bloch Space in Polydiscs (Chinese). Journal of Mathematics (Wuhan University), 25, 435-440.
- 13. Allen, R.F. and Colonna, F. (2010) Weighted Composition Operators on the Bloch Space of a Bounded Homogeneous Domain. In: Operator Theory: Advances and Applications, Volume 1. Operators, Matrices and Analytic Functions, Oper. Theory Adv. Appl., 202, Birkh?user Verlag, Basel, 11-37.�
- 14. Allen, R.F. and Colonna, F. (2009) Multiplication Operators on the Bloch Space of Bounded Homogeneous Domains. Computational Methods and Function Theory, 9, 679-693. http://dx.doi.org/10.1007/BF03321751
- 15. Deng, F.W. and Ouyang, C.H. (2006) Bloch Spaces on Bounded Symmetric Domains in Complex Banach Spaces. Science in China Series A, 49, 1625-1632. http://dx.doi.org/10.1007/s11425-006-2050-0
- 16. Shi, J.H. and Luo, L. (2001) Composition Operators on the Bloch Space of Several Complex Variables (Chinese). Acta Mathematica Sinica (Chinese Series), 44, 1-10.
- 17. Timony, R.M. (1980) Bloch Functions in Several Complex Variables, I. Bulletin of the London Mathematical Society, 12, 241-267. http://dx.doi.org/10.1112/blms/12.4.241
- 18. Zhou, Z.H. and Shi, J.H. (2002) Compactness of Composition Operators on the Bloch Space in Classical Bounded Symmetric Domains. Michigan Mathematical Journal, 50, 381-405.
http://dx.doi.org/10.1307/mmj/1028575740 - 19. Lu, Q.K. (1963) The Classical Manifolds and the Classical Domains (Chinese). Shanghai Scientific and Technical Publishers, Shanghai.
- 20. Pan, W.Q. (2012) Composition Operators between p-Bloch Space and q-Bloch Space in the First Classical Bounded Symmetric Domain. Master’s Thesis, Jiangsu Normal University, Xuzhou.
- 21. Kuang, J.C. (2004) Applied Inequalities (Chinese). 3nd Edition, Shandong Science and Technology Press, Shandong.
NOTES
*Corresponding author.






































































