ABSTRACT

In the presence of a strong magnetic field, accretion discs surrounding neutron stars, black holes, and white dwarfs have their inner edges at their Alfvén radii, i.e., at the distance where magnetic energy density becomes equal to the kinetic energy density. Young stars, X-ray binaries, active galactic nuclei possess discs which could generate jets. Jets arise at the inner boundary of the disc at the Alfvén radius when magnetic field is sufficiently strong. We emphasize here that not only accretion discs possess this feature. The inner edge of the heliospheric current sheet is located at the solar Alfvén radius. The inner edges of the Jovian magnetodisc and Saturnian ring current are also placed close to their Alfvén radii. Thus, in the presence of a strong magnetic field the inner edges of a lot of astrophysical discs are located at Alfvén radii regardless of the nature of their origin, material, and motion direction. This means that discs under such conditions are well described by MHD theory.

1. Introduction

We consider a wide range of astrophysical objects surrounded by discs such as neutron stars, pulsars, white draws, black holes, X-ray binaries, active galaxy nuclei, young stars, Sun, giant planets in the solar system (Jupiter and Saturn), and note that many of them in the presence of magnetic field have the inner edges at the Alfvén radii independent of the nature of their origin, the motion direction inside the disc (towards the central body or out of it, or in the azimuthal direction), and the sort of material in the disc. Of course, other types of discs, for which the inner edges do not coincide with the Alfvén radii also exist. That is the case, for example, for the discs around stars, white dwarfs, or neutron stars with a weak magnetic field or without it, the cold non-magnetized matter undergoing free radial equatorial infall to a nonrotating black hole from the initial rest state, etc. However, we do not consider these objects in the present review.

Position of the inner edge of astrophysical discs plays a crucial role in different physical processes. It is one of the parameters which determine the total luminosity of an accretion disc, the position of powerful jets origin and maximum temperature in the discs, the location of the main emissions and the wave diapason of emissions, the location of strong field-aligned currents in the heliosphere and in the Jovian magnetosphere (in the last case these currents generate bright auroras in the main ovals). It also coincides with the last stable orbit near a black hole and determines the magnetospheric size for the outer planets in the solar system. Therefore, we pay the main attention to this subject. As we show in this paper, the inner edges of astrophysical discs in the presence of strong magnetic field are close to Alfvén radii.

Khodachenko et al. [1] constructed the magnetospheric model for a magnetized giant exoplanet at a close orbit around its host star (“Hot Jupiter”). Weak intrinsic magnetic dipole moments of tidally locked close-in giant exoplanets have been shown in previous studies to be unable to provide an efficient magnetospheric protection for their expanding upper atmospheres against the stellar plasma flow, which should lead to significant non-thermal atmosphere mass loss. In [1] besides the intrinsic planetary magnetic dipole, in the paraboloid magnetospheric model (PMM) [2-4] for an exoplanet, the current systems of the magnetotail, magnetopause currents, and the ring current of a magnetodisc are included. In the PMM, the magnetopause is represented by a paraboloid surface co-axial with the direction of the ambient stellar wind plasma. It is supposed in the PMM that the inner edge of the magnetodisc is located at the place where rigid corotation of plasma is braked down. This happens in the magnetospheric equatorial plane at the Alfvén radius, determined from the equality of energy densities of the plasma rotational motion and the dipole magnetic field. Beyond the Alfvén radius an outflow of the subcorotating plasma begins. The escaping along the magnetic field lines, plasma deforms the original planetary magnetic dipole field by stretching the field lines and creating the magnetodisc.

The real discs are very complicated and strongly stratified objects. However, here we would like to emphasize that in the presence of a strong magnetic field the location of the inner boundary of the disc at the Alfvén radius occurs in numerous forms in the universe. This relates not only to the accretion discs, but also to the heliospheric current sheet, the Jovian magnetodisc, and Kronian ring current. In the following sections this phenomenon is discussed in details.

2. Accretion Discs

2.1. Discs around Neutron Stars, Pulsars and White Dwarfs

Neutron stars arise as a result of gravitational collapse of cores of normal stars after exhaustion of all thermonuclear energy sources. At the end of a star evolution the envelope is thrown away during explosion and forms a planetary nebula, or a supernova remnant depending on the mass of the dying star. The neutron star masses range from 1.4 to 3 M_Sun, where M_Sun = 2×10³⁰ kg is a solar mass, 1.4 M_Sun is a Chandrasekhar limit, and 3 M_Sun is an Oppenheimer-Volkoff limit. The neutron stars consist mainly of neutrons. Radius of a neutron star is ~10 - 20 km. The material density in neutron stars could be up to 10¹⁷ - 10¹⁸ kg·m^–3. If a neutron star has a strong magnetic field, the external plasma flows to its auroral zones generating X-rays.

Pulsar is a rapidly rotating (the typical period 0.1 - 5 s) small, extremely dense neutron star that emits brief, sharp pulses of energy (not all neutron stars are pulsars). Pulsar has a very strong dipole-type magnetic field (10¹¹ - 10¹⁵ G), and the beams of radiation are emitted along its magnetic dipole axis which does not coincide with the spin axis. Radio-pulsars are the mostly numerous class of pulsars. Most of radio pulsars are single neutron stars [5]. Istomin [6] stated that the source of pulsar’s radio emission could be, for example, the stream of the relativistic electron-positron plasma generated in the magnetosphere of a neutron star.

There is a group of pulsars called millisecond pulsars with the spin period 1 - 10 ms and magnetic field 10⁸ - 10⁹ G. About a half of millisecond pulsars are in binaries, i.e. in the stellar systems containing two stars orbiting around their common center of mass. Observations and theory of binary systems are summarized in [7-9]. If one star in a binary system is a neutron star, then the period of pulsar is the spin period of the accreting neutron star.

A part of the ejected matter, after a supernova explosion, may remain bound to the remnant and fall back. This falling back material can form a disc surrounding the remnant star. Some of neutron stars possess accretion discs, while the others are accreting directly from the stellar wind. A disc can be formed of this material if its specific angular momentum l exceeds the Keplerian value at the surface of  a newly born neutron

starl_K = (GM_*R_*)^1/2(1)

where M_* is the mass of the star and R_* is its radius, G is Newton’s gravitational constant (G = 6.673 × 10^{–11 m3}·kg^–1·s^–2).

The character of material motion at the inner edge of the accretion disc depends on the magnetic field of the neutron star. In the case of a neutron star without magnetic field, the disc extends until its surface. Ghosh and Lamb [10,11] described the interaction of a dipolar stellar magnetic field with a surrounding disc. The authors found that the inner edge of the disc is located at the distance where the integrated magnetic stress acting on the disc becomes comparable to the integrated material stress associated with plasma inward radial drift and orbital motion (at Alfvén radius). Later Cheng et al. [11] considering the neutron star—accretion disc system also stated that the position of the inner edge of the accretion disc is of the order of Alfvén radius.

In the Ghosh and Lamb model [10,12] the corotation radius, defined as

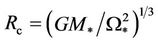(2)

where the angular velocities of the disc and the star (W_*) are the same, also plays a key role. The magnetic field lines penetrating the disc inside the corotation radius spin up the star, whilst those penetrating the accretion disc outside the corotation radius brake the star down. The spin evolution of the star is therefore the result of a balance between the angular momentum carried by the accreting matter from the disc to the star, the magnetic spin-up torque from the accretion disc inside the corotation radius, and the magnetic spin-down torque from the accretion disc outside the corotation radius. The position of the inner edge of the accretion disc varies with the accretion rate so, that it becomes closer to the star when the accretion rate increases. Thus, it is expected that the star spins up, or at least spins down more slowly, when the accretion rate (or equivalently, the luminosity) is high [13].

A neutron star can interact with a surrounding disc in a variety of modes. In this interaction the inner part of an accretion disc plays a significant role leading to different observational properties of X-ray pulsars and low-mass X-ray binaries [14]. These different modes of interaction can have various astrophysical manifestations [14]. The mode of interaction is determined by the location of the inner radius of the disc with respect to the major characteristic radii: the corotation radius, and the light cylinder radius, R_L

R_L = c/W_*(3)

where c is light velocity. There are three basic modes of interaction of a neutron star with a surrounding disc: accretor, propeller, and ejector [15-17]. If the inner radius of the disc is beyond the corotation radius, but smaller than the light cylinder radius, the system is expected to be in the propeller stage (a neutron star rotation is strong enough to prevent the accreting matter from the falling to the star). The ejector stage is assumed to take place when the inner radius is beyond the corotation radius and the light cylinder radius. For the accretor mode, the inner radius of the disc has to be smaller than the light cylinder radius, and accretion to the central object occurs when the corotation radius becomes larger than Alfvén radius.

Shvartsman [15,16] argued in the context of wind-fed, mass-exchange binaries, that a fast-rotating neutron star at first appears as an ejector (radio pulsar), in which the disc remains outside the light cylinder. After the star slows down, the inflowing matter can penetrate the light cylinder, allowing the propeller stage to commence. For a fallback disc, a fixed amount of mass is available in the disc, rather than a continuous supply as in the case of a mass-exchange binary. Finally, for a slowly rotating neutron star, the ejection changes to accretion.

The relativistic outflowing momentum flux in ejectors is always larger than the ram pressure of the surrounding material, therefore they never accrete. This is typical for either active or dead pulsars, which are still spun down by dipole losses. In propellers the incoming matter can penetrate down to the Alfvén radius, R_A, but not further (because of the centrifugal barrier), and a stationary inflow cannot occur. For accretors the falling to the central object flow stops at the distance where the object’s magnetic pressure becomes equal to the kinetic flow pressure (e.g., at Alfvén radius) [15,16].

The accretion to a rotating neutron star with the magnetic dipole axis inclined relative the rotation axis, can lead to the phenomenon of an X-ray pulsar [18]. When describing discs around magnetars (neutron stars with very strong magnetic field > 10¹⁵ - 10¹⁶ G), Zhang and Dai [19] note, that the magnetized disc is always viscously stable outside the Alfvén radius, whereas it is thermally unstable near the Alfvén radius. At this distance, the magnetic field plays more important role than the viscous stress in transferring the angular momentum and heating the disc. Zhang and Dai [19] defined Alfvén radius as a distance, at which the magnetic pressure equals the ram pressure of the accreting material. They have shown that the thermally-driven outflow wind can exist also beyond the Alfvén radius in the magnetized discs, where the material pressure dominates over the magnetic pressure. Besides the thermally-driven outflow in the disc outer region, a strong magnetic field inside the Alfvén radius causes the accretion flow to co-rotate with the stellar magnetic field. That results in driving of an MHD wind along the field lines [20].

Bednarek [21] studied a strongly magnetized rotating neutron star (magnetar) and a massive OB type companion star inside a close binary system. It was assumed that the material of the stellar wind is effectively captured by the strong gravitational potential of the magnetar in the propeller phase. The distance at which the magnetic field starts to dominate the dynamics of the in-falling matter was estimated by assuming the equilibrium between the magnetic field energy density and the kinetic energy density of the wind (e.g., at the Alfvén radius). The matter in this region is very turbulent and strongly magnetized. This provides good conditions for acceleration of electrons up to TeV energies. These electrons produce gamma-ray emission.

Quite often X-ray pulsars reside in the binary systems built of a rotating magnetized neutron star (pulsar) and a normal star. Due to accretion from the normal star to the neutron star, plasma is accelerated up to very high velocities, which then brake dawn near the neutron star surface. That results in the increase of plasma temperature up to T ³ 10⁷ - 10⁸ K [22]. As a consequence, the electromagnetic emission in the UV, g-ray and mainly X-ray bands is generated. If the magnetic field of a neutron star is weak or absent, the material from the inner parts of the disc reaches the neutron star equatorial region, forming at its surface a hot boundary layer where thermo-nuclear reactions may occur. That could lead to short powerful irregular X-ray flashes, which form the major feature of an X-ray burster of 1st type. An X-ray burster of the 2nd type is connected with instabilities in the disc. Quickly rotating magnetized neutron star without accretion could act as a radio pulsar emitting short periodic pulses produced due to transformation of the rotation energy into the energy of radio emission in the strong magnetic field.

In the Keplerian rotating highly turbulent inner parts of the accretion disc (i.e., where Kepler’s laws of motion are valid due to the dominance of a massive body at the disc centre) the magnetic fields are strongly amplified and expelled from the disc. This leads to the formation of a magnetically structured accretion disc corona, sandwiching the disc, to which it is electrodynamically coupled. The interaction of inner parts of an accretion disc with a neutron star leads to a channeled accretion onto the magnetic pole zones, resulting in the phenomenon of an X-ray pulsar with the associated spin variations due to angular momentum transfer. Kuperus [23] stated that interaction of the disc coronal structures with the relatively weak magnetic field of an old fast spinning neutron star leads to a new form of interaction around the so called beat frequency that can be used as a model for quasiperiodic oscillations in low-mass X-ray binaries (binary stars which radiate X-rays).

In models for disc accretion onto magnetized objects, the inner radius R₀ of the Keplerian disc is conventionally expressed as R₀ = xR_A, where R_A is the Alfvén radius for the spherical accretion and the parameter x, which depends on the fraction of the stellar magnetic flux threading the disc, is usually taken to be 0.5 (e.g., [24]). In the disc-fed X-ray pulsars, the inner radius R₀ of the accretion disc is also expressed in terms of the Alfvén radius R_A for spherical accretion, R₀ = xR_A [14]. Application of the beat frequency model to the binary X-ray pulsars showing quasi-periodic oscillations suggests strongly that for these objects the stellar dipole field fully threads the disc, and x @ 1 [25], while the plasma velocity in the inner part of the accretion disc could be close to the light speed.

Eksi and Alpar [14] note regarding the discs around radio pulsars, that the position of the inner radius of a thin disc around a neutron star is determined by the balance of stresses. It can be estimated by comparison of the electromagnetic energy density, generated by the neutron star as a rotating magnetic dipole in vacuum, with the kinetic energy density of the disc. In the inner zone, i.e., inside the light cylinder, the electromagnetic field is essentially the dipole magnetic field, and the disc inner radius is the conventional Alfvén radius, which is a stable equilibrium point. Shvartsman [16] showed, that in the radiation zone (R > R_L) the stable equilibrium outside the light cylinder is only possible beyond the gravitational capture radius (R_G = 2GM_*/V², where V is the velocity of the rotator’s environment). The gravitational capture radius R_G is derived by an equalizing the sum of potential and kinetic energies to zero.

Bednarek and Pabich [26] studied high-energy processes in the intermediate polar cataclysmic variables (IPCVs). These objects have been recently established by the INTEGRAL (observatory at the near-Earth orbit) as a class of the hard X-ray sources with evidences of nonthermal components. Quite often, the cataclysmic variables (CVs) are white dwarfs within compact binary systems which accrete matter from their companion normal stars.

While stars with normal mass after they have exhausted their nuclear fuel are transferred to neutron stars, less massive stars (like the Sun) become white dwarfs. The mass of a white dwarf is M_* < 1.4 M_Sun. The radius R_* of a typical white dwarf with a mass M_* = M_Sun is of the order of ~10^–2 R_Sun, where R_Sun = 7×10⁵ km is the solar radius. If the mass of a celestial body is less than 0.08 M_Sun, the hydrogen burning fusion does not take place in its center. Such objects are called “brown dwarfs”, they represent an intermediate class of objects between stars and planets.

The stars in compact binary systems could be so close to each other that the gravity of a white dwarf distorts the secondary star, and the white dwarf accretes the matter from its companion. If after some time a sufficiently large amount of material from the companion star is accumulated on the white dwarf surface, so that the thermo-nuclear reactions suddenly begin, this would correspond to “a new star flash”. Such flash may be repeated again after tens-thousands years. In intermediate polar systems, the accretion disc is disrupted by the magnetic field of the white dwarf star. Due to the instabilities arising in the disc, the flashes inside the disc (with periodicity from a week up to a year) also could be seen. As the material in the accretion disc approaches the magnetic white dwarf, it is swept up by the magnetic field of the white dwarf forming accretion curtains along the magnetic field lines.

All active cataclysmic binary systems are semi-detached. In the semi-detached binary one component fills its Roche lobe, and mass transfer occurs from this star to the other. While in some systems the gas stream falls directly to the surface of the second star, in most cases it forms an accretion disc. Zhilkin and Bisikalo [27] using the three-dimensional MHD numerical simulations investigated the characteristic properties of the magneticfield structures in the accretion discs of semi-detached binary systems. The intrinsic magnetic field of the accretor star was assumed to be dipolar. Turbulent diffusion of the magnetic field in the disc was taken into account. Their result showed the intense generation of a predominantly toroidal magnetic field in the accretion disc. Magnetic zones with well defined structure were separated by current sheets in which magnetic reconnection and current dissipation take place.

Depending on the strength of the surface magnetic field of a white dwarf, the accretion rate, and the angular momentum of matter, the accretion process can occur in different modes. Specific modes correspond to different types of accreting white dwarf systems, such as polars (direct accretion on a magnetic pole), intermediate polars (accretion on a magnetic pole from the accretion disc), and nonmagnetic white dwarfs (the accretion disc extends to the surface of the white dwarf). The physical processes in CVs are expected to be similar to those taking place in the X-ray binaries with the accreting neutron stars [26]. Due to significantly larger radii, white dwarfs accreting in the accretor phase have typical magnetic moments two to three orders of magnitude larger than those of the neutron stars. The distance, at which the magnetic field begins to dominate the dynamics of matter (the Alfvén radius), can be estimated again by comparison of the magnetic field energy density with the material kinetic energy density. Bednarek and Pabich [26] also used the relation R₀ = xR_A, and assumed x = 1 at the disc inner radius (R₀) for the chosen in their paper parameters.

Alfvén radius coincides with the so-called magnetosphere radius for the magnetized neutron star or pulsar. Thus, as it was shown above, the inner edges of the discs around magnetized neutron stars, the X-ray pulsars, radio pulsars, and white dwarfs with intrinsic magnetic field are located near their Alfvén radii. If a neutron star has so week magnetic field, that its pressure cannot stop the falling plasma, the inner edge of accretion disc coincides with the neutron star surface.

In a result of the core-collapse of a massive star at the end of its life after it has exhausted its nuclear fuel, a compact object with a mass > 3 M_Sun could be formed. It is called a “black hole” (for example, in the center of our Galaxy there is a supermassive black hole with mass ~ 3.5 × 10⁶ M_Sun). It should be noted that the mass of a star is not a single parameter which determines its evolution. The stellar mass loss, in particular, is also important. Ginzburg [22] noted that quasar (quasi-stellar radio source) or galactic nuclear also can evolve to a black hole under certain conditions.

The structure of magnetic fields near the discs around magnetized white dwarfs, neutron stars or magnetars is very different from the black hole case. The origin of a magnetic field in the central compact star determines the initial field topology. An interaction between the star and the surrounding disc makes the stellar magnetic field partially thread the accretion disc. The main difference in the interaction between a central object and the inner part of the disc in the cases of a neutron star and a black hole is caused by different magnetic field structures [19]. The most significant thing is that the intrinsic magnetic field of a black hole is absent beyond the horizon of events.

2.2. Discs around Black Holes and in the Close Binary Systems Containing Black Holes

A black hole is an object, which has so strong gravitational field, that it does not radiate either electromagnetic or gravitational waves (all radiation and matter are confined inside the horizon of events—the effective boundary around the black hole, from which no information can escape to the entire world). The escape speed exceeds the speed of light within the event horizon, while outside it the escape speed is less than the speed of light.

Black holes are characterized by their mass, angular momentum, and electric charge. The radius of the event horizon for a non-rotating uncharged black hole (named as a Schwarzchild black hole) is equal to the gravitation or Schwarzchild radius

R_G = 2GM_*/c²(4)

which marks the point where the escape velocity equals the speed of light. The rotating uncharged black hall is called a Kerr black hole; a non-rotating charged black hall is known as a Reissner-Nordstrom black hall, whereas a charged and rotating black hall is called a KerrNewman black hall. For a rotating black hole the event horizon radius is less than R_G. It follows from the quantum mechanics that all black halls may eventually evaporate.

Beyond R_G the gravitational field of a black hole forces the surrounding gas to fall on it, with formation of a rapidly spinning disc. The gas in the disc has a very high temperature which leads to the generation of strong X-ray radiation. Moreover, under certain conditions the gas near a black hole may become turbulent, and as it flows to r ~ R_G, magnetic field growths in it which leads to particle acceleration. As a result, the synchrotron emission (non-thermal radiation generated by relativistic charged particles in strong magnetic field) arises [22].

A black hole has no intrinsic magnetic field outside of its event horizon, but magnetic fields can be generated by plasma which surrounds the black hole and forms the accretion disc. Interaction of disc’s rotation with these electromagnetic fields may result in the appearance of sub-light narrow and very long jets. The magnetic flux between the black hole and the inner edge of disc is either outgoing towards the asymptotic jet or in-going towards the black hole.

As a confirmation of the existence of black holes, the high-energy phenomena, such as X-ray emissions and jets, and the observed character motions of nearby objects are considered. The identification of an invisible object like a black hole requires an estimation of its mass and size. Methods and results of a search for stellar mass black holes in binary systems and supermassive black holes in galactic nuclei of different types are described by Cherepashchuk [28]. The methods for estimation of supermassive black hole masses are analyzed in [29].

The last stable circular orbit for the pseudo-Newtonian potential is located at 3R_G. Shakura and Sunayev [18] assumed for the Schwarzschild black holes that the inner edge of the disc is at 3R_G, since no stable circular orbits are possible near the black hole at R < 3R_G, and the material motion acquires a radial character without transport of angular momentum and without any external observable effects (in the region R < 3R_G the effects of general relativity (GR) should be taken into account). However, Tomsick et al. [30] have studied the stellar mass black holes at high luminosities, including GX 339-4, and reported the measurement of a smaller R₀ than the radius of the innermost stable circular orbit for a non-rotating black hole (R₀ = 2.4 R_G when GX 339-4 was bright [31]).

There is a space-time singularity in the center of a black hole, where the matter collapses inwards. Penrose and Floyd [32], based on the property of Kerr’s solution for the Einstein’s vacuum equations, stated that the event horizon of a rotating uncharged black hole is surrounded by a stationary limit surface, at which a particle would have to travel with the local light velocity, in order to appear stationary to an observer at infinity. The stationary limit touches the event horizon where they intersect the rotation axis. Both these surfaces coincide in the case of the Schwarzschild solution, which is a limiting case of the Kerr solution for zero angular momentum of a black hole. Penrose and Floyd [32] noted that in the region between the stationary limit and the event horizon (ergosphere) it is possible for the mass-energy of a test particle (as measured from infinity) to be negative (inside the event horizon this can still be true). The so-called Penrose process is connected with the existence of this region. According to this process, a particle with fixed four-momentum which dropped into the relevant region splits into two particles so, that the mass-energy (as measured from infinity) of one of these particles is negative whereas the second particle escapes back to infinity with a higher mass-energy than the original particle possessed. Therefore, some of the rotational energy of the black hole is extracted during this process.

Although the Penrose process shows a possibility of energy extraction from the black hole, it is improbable as an engine for astrophysical jets, because of poor collimation of particles and poor event rate [33]. In that respect, Koide and Arai [33] considered the effects of magnetic field. They emphasized that magnetic reconnection also redistributes angular momentum of the plasma producing a pair of fast outflows from the reconnection region. The authors showed that the magnetic energy at infinity becomes negative when W_H > W_F, where W_H is the angular velocity of the black hole horizon, and W_F is the angular velocity of magnetic field lines. A steady state of electromagnetic field in the force-free condition has been assumed [33]. Chandrasekhar and Woltjer [34] wrote that cosmic magnetic fields which occur in the regions of low density (such as stellar envelopes, gaseous nebulae, and interstellar space) are force-free in the sense that the Lorentz force vanishes, i.e., the current flows parallel to the magnetic field. Koide and Arai [33] stated that the Alfvén velocity near a very rapidly rotating black hole under the force-free condition becomes the speed of light, and therefore the Alfvén surface is located at the event horizon. In the finite pressure case, the Alfvén surface is located inside the ergosphere, and the Alfvén velocity is close to the speed of light. In this case the reconnection occurs in the equatorial current sheet of the accretion disc inside the ergosphere. The plasma at the disc edge falls spirally due to the frame-dragging effect, and the magnetic flux tubes dragged by the plasma are elongated spirally.

Quite often, black holes reside in the binary systems with low-mass star-donors. In a close binary system comprised of a visible star and a black hole, the outflow of matter from the surface of the visible star and its accretion on the black hole should be detectable in observations because the accreting gas releases large amount of energy [35,36]. In particular, black hole in accretion regime could emit X-rays. It should be mentioned that if the matter undergoes the free radial infall (in case if it was initially at rest and there was no magnetic field), it accretes to the black hole without any energy release or observational effects [37]. However, in a binary system, in which the matter flows out from the normal star and falls on the black hole with a considerable angular momentum, the situation is different. If the companion star fills its Roche equipotential lobe, then a narrow stream of gas escapes the star through the inner Lagrangian (L1) point. This gas has a high specific angular momentum and cannot accrete directly onto the black hole. The outward transfer of the angular momentum of the accreting matter leads to the formation of a thin disc around the black hole. Inside the disc, the gas moves in Keplerian orbits, however, viscous dissipation slowly taps energy from the bulk orbital motion, and viscosity transports the angular momentum outward. As a result, the gas gets hotter as it moves deeper in the gravitational field of the black hole. Near the black hole the disc terminates. Due to the energy release there, the black holes could be detected among the optical objects and X-ray sources [18]. In the presence of a strong magnetic field (supported, for example, by currents in external gas) and in the case of a rapidly rotating black hole, the spin and/or electromagnetic effects not only drive the relativistic jets, but also may modify the spectrum of the inner accretion disc. The power, driving the relativistic jet is provided by the magnetic field of an accretion disc and from the rotating black hole.

According to Fendt and Greiner [38], the observations indicate that accretion disc instabilities may be related to jet ejection. The authors demonstrated that the wind/jet is basically magnetically driven and is created by accelerated outgoing plasma. They concluded that acceleration takes place predominantly at the distance of Alfvén radius, as expected from MHD theory. For the relativistic jets with a high magnetization the Alfvén point is always very close to the light surface [38]. General relativity effects are important only if the wind originates very close to the black hole.

For a binary system, in which accretion disc originates due to mass overflow from a primary star onto a compact star, Kuperus [23] noted that when the compact star is a neutron star or a black hole, the inner edge of the thin disc extends till the Alfvén radius which is a few times the Schwarzchild radius.

As it was shown by Tomsick et al. [30], for a stellar mass black hole, the inner edge of disc moves sharply outward, as the luminosity decreases. This could be explained by assuming that the position of R₀ is connected with R_A. By decrease of the luminosity, and correspondingly the mass accretion rate, the location of the place where this velocity equals to the Alfvén velocity

V_A = B₀ (μ₀ρ₀)^–1/2(5)

(where B₀ and ρ₀ are magnetic field and plasma density, respectively) occurs at the distance where V_A is smaller, which accordingly to Equation (5), means mainly that B₀ is smaller, i.e. more far from the central object (as the gas flowing to r ~ R_G becomes near the black hole turbulent and magnetic field in it growths). The fact found by Tomsick et al. [30] that the inner portion of the disc is not present at low luminosity, allowing the possibility, for example, that the inner disc is replaced by magnetically dominated accretion flows, also supports this paradigm.

2.3. Galactic Discs

Disc is the major element of spiral, lenticular (a lensshaped), and some irregular galaxies; it contains stars, gas, and dust orbiting the centre of a galaxy. The thickness of the disc is small in relation to its diameter. The formation of a star is often not an isolated process. Young stars occur in a star-forming region located mainly in the disc. A spiral galaxy, for example, has the disc (with the spiral arms), the halo, and the nucleus (sometime, the central bulge also). The halo and the nucleus are called the spherical component of the galaxy. Assembly of stars can be considered as a collisionless medium (similar to the collisionless gas). Angular velocity decreases in discs with increasing of the distance from the center of a galaxy.

Using the magnetic field model for the heliospheric current system, Alfvén extended it to the galactic scale. It has been proposed that a protogalaxy transfers away the angular momentum similarly to a protostar. As a result the galactic electric circuit is formed, in which the galaxy current should be 10¹⁷ - 10¹⁹ A. The currents flow in the plane of the galaxy, possibly waving up and down, along the spiral arms, and out along the axis of rotation (e.g., [39], and references therein).

Most galaxies with active nuclei host supermassive black holes at their centers. The supermassive black holes with masses ~10⁶ - 10¹⁰ solar masses (quasars) in active galactic nuclei (AGNs) are usually surrounded by rapidly rotating accretion discs [40,41]. Very active quasar could emit more energy than its galaxy. For explanation of this phenomenon the non-spherical accretion to the supermassive black hole was suggested [36]. Emitted by the AGN energy could be taken from the central black hole rotation and from the accreting material [5].

The center of our Galaxy (Milky Way) is located in the direction of the constellation Sagittarius. As the dust becomes thicker to the center of the Galaxy, this region is invisible in optics. It is usually studied by observations in radio and/or in infrared wavelengths. The inner part of the Galaxy is a zone where young stars form. The brightest object in radio waves located in the Galaxy center is called Sgr A (Sagittarius A). Observations in X-rays, which also can penetrate the thick gas and dust, reveal that Sgr A can be further reduced to a few sources, including a mostly bright, small source called Sgr A^*, which is identified with the supermassive black hole. The star S2 is currently closest to Sgr A^*, it moves along an elliptical orbit with Sgr A^* at one focus in accordance with Kepler’s law. It has an orbital period ~15 years, which was determined by the Earth-based IR observations at the European Southern Observatory in Chile.

Levine et al. [42] reported on the observation of 22 GHz H₂O maser in Sgr A West located close to the inner edge of the circumnuclear disc within 2 pc of the Galaxy center. The maser coincides with a luminous M supergiant. The authors emphasized that if this star was formed within the circumnuclear disc, it is the first known case of a recently formed star (10⁷ - 10⁸ years ago) in the central 2 pc which can be associated with the gaseous structure in which it was born (as it is known that stars are formed mainly in the galactic discs from dust and gas. Duschl [43] presented evidence that the sharp inner edge of the circumnuclear disc in the Galactic center is due to a change in the radial gradient of the mass distribution at ~1.8 pc. Volmer and Duschl [44] suggested a mechanism for the formation of the inner edge in the circumnuclear disc in our Galaxy. In their model, the presence of rotation and/or magnetic fields results in an increase of the critical cloud mass with respect to gravitational instability for clouds of a given temperature and external pressure.

Water maser emission at 22 GHz has been detected from more than hundred AGNs (see e.g., [45] and references therein). It could be associated with nuclear activity, the late-type stars, or star formation. Water molecules undergo the population inversion and stimulated emission processes. The water masers are concentrated towards the central axis of the star formation region. It has been established that the physical conditions in massive star-forming regions favor maser emission from the water molecules [46]. The 22 GHz transition of H₂O is one of the best known and most widespread tracers of extremely young and heavily embedded lowand highmass stars. Also maser emission could be connected with a rotating, highly inclined disc, close to the central engines (“disc maser”). Calculations by Wallin and Watson [47] demonstrated that the absorption of IR radiation by dust grains can increase significantly the pumping of the 22 GHz water masers under conditions that may be appropriate for the circumnuclear environment of active galaxies.

Seyfert galaxies (spiral or barred-spiral galaxies with bright compact nuclei) exhibit a strong continuum in the range from IR till X-rays. In some Seyfert galaxies a very asymmetric profile of the iron Ka line (e.g., its extended red wing) indicates that the emission arises in the innermost region of a relativistic accretion disc. The material velocity near the inner edge of accretion disc is close to the speed of light. Tomsick et al. [30] studied the location of the inner edge of the accretion disc using iron emission lines that arise due to fluorescence of iron in the disc. This study reveals that the inner edge of the accretion disc is occurred to be close to the black hole at high and moderate luminosities, while for low luminosity the distance to it significantly increases. Relativistic Doppler broadening (due to motion of the accretion disc material) and gravitational redshifting (due to the black hole’s gravitational field) of the iron lines enables a measurement of R₀. Broad iron lines have been seen from both stellar mass and supermassive black holes. Emission from the Galactic ridge includes iron Ka emission with the most prominent line being due to He-like iron at 6.7 keV. The emission is strongest in the Galactic center. Reynolds et al. [48] from observations of AGN NGC 4258 with low luminosity inferred that R₀ > 3 × 10³ R_G. Camenzind [49] noted that discs in quasars extend most probably down to the marginally stable orbit, while in intermediate luminosity objects, like radio galaxies and normal Seyfert 1 galaxies, the disc most likely exists at distances of a few tens to a few hundreds of Schwarzschild radii.

The central engine in AGNs is surrounded by dusty optically thick clouds which form a clumpy torus. The torus size is of the order of a few parsecs (see e.g., [50] and references therein). Elitzur and Shlosman [50] noted that the water masers detectable in edge-on AGNs, reside in the inner molecular regions of the accretion disc. At smaller radii, the disc composition switches from dusty and molecular to atomic and ionized material. However, when bolometric luminosity of a galaxy decreases below ~10⁴² erg·s^–1, the obscuring torus disappears, because mass accretion from the disc cannot anymore sustain the required cloud outflow rate. The authors concluded that the AGN switches its main dynamic channel for release of accreted mass from the torus outflow at higher luminosities to the radio jets at lower ones.

Beskin [5] noted that usually it is suggested that accretion to the central black hole has a disc form. This determines a characteristic direction—the disc axis—along which the powerful jets are formed. The matter in jets often preserves the relativistic velocity very far from the galactic nuclear. Central galactic objects are active until the accreting material falls to them. Beskin [5] explained the main physical processes leading to generation of jets in AGNs, microquasars, radio pulsars, and young stars by the operation of a unipolar inductor (within the frame of MHD-theory) which creates a strong field-aligned current at the place where rigid-corotation is broken and magnetic field lines change their form.

Livio [51] noted that most of the astrophysical objects which exhibit jets contain accreting central bodies. He considered, particularly, young stellar objects (YSOs), X-ray binaries, black hole transients, AGNs and showed that these objects possess discs which could generate jets. Livio [51] stated that jets are produced at the center of accretion discs, and are accelerated and collimated hydromagnetically. According to Livio [51], the production of powerful jets requires a hot corona or an additional energy source associated with the central object. Suzuki [52] considered the accretion disc wind driven by MHD turbulent pressure and amplified by magneto-rotational instability (instability arising in the presence of an arbitrarily weak poloidal magnetic field when the angular velocity of a magnetized fluid decreases as the distance from the rotation center increases). Such wind is generated when the magnetic energy starts to dominate the gas energy (at the Alfvén radius). Suzuki [52] modeled only the onset region of the disc wind and found that the result is qualitatively similar to what was received in the MHD simulation of the solar and stellar winds. Pudritz et al. [53] mentioned that the place where jets arise is near the Alfvén radius. This conclusion is valid also for AGNs.

According to Camenzind [49], the ergosphere of a black hole is typically a region located inside 3R_G from the singularity, and the Alfvén surface is located within the ergosphere, while the currents across the rotating black hole magnetosphere (and forming disc) arise near the Alfvén surface. Thus, from these estimations it follows that for mostly bright AGNs, connected with the powerful jets, the inner edges of discs could also be located at the Alfvén radii. However, at the present time the definite answer to the question about location of the inner edge of the disc in galactic center is not obtained. That is, in particular, because the modern observational facilities are not able to resolve the plasma flows at the scales comparable to the black hole size, thus, the interaction of a central black hole with the accreting disc could be observed only at essentially larger scale [5].

2.4. Protoplanetary Discs around Young Stars

The values of stellar masses occupy the range from ~0.08 till 100 M_Sun. The lower limit here is determined by the impossibility of thermo-nuclear reaction of the helium synthesis from hydrogen for low mass objects, while the upper limit is due to the instabilities arising for very high stellar masses.

An accretion disc that provides material for planet formation is referred to as a protoplanetary disc. The size of protoplanetary discs could be up to 1000 AU. Usually young stars are surrounded by protoplanetary discs. The interaction between a magnetic star and a surrounding accretion is important for understanding the spin evolution of objects as diverse as T Tauri stars and X-ray pulsars. T Tauri stars are very young (<10 million years old), lightweight (from 0.5 to 2 M_Sun), variable stars with spectral type ranging from F to M, and radius of less than 3 - 4 R_Sun named after their prototype—T Tauri. They are found near gas and dust clouds and are identified by their optical variability, strong emission lines, and broad absorption lines. T Tauri stars are still in the process of gravitational contraction. They may be subdivided on two types: classical T Tauri stars, which are slow rotators and have accretion discs (observed excess ultraviolet and infrared emissions are associated with accretion flows), and weak-lined T Tauri stars, which are fast rotators with no signatures of an accretion disc. The weak-lined T Tauri stars are believed to represent a later evolutionary stage, when the star has got rid of its accretion disc [13]. The circumstellar discs around slowly rotating T Tauri stars left over from stellar formation may be considered as a protoplanet disc. Vidotto et al. [54] wrote that the Alfvén surface plays an essential role in the determination of the magnetic field configuration in the stellar wind.

In the T Tauri classical star stage, when most of the original core has been accreted and the young stellar object is being fed by lower accretion rates through the surrounding Keplerian accretion disc, the high-speed jet becomes optically visible. When the disc disappears in the weak-lined T Tauri star phase, the jet disappears also with it [53]. Jets and discs are closely coupled. The innermost region of the disc i.e., a region, where the stellar magnetosphere interacts with the disc, is the place where jets arise at the Alfvén radius [53].

3. Non-Accretion Current Discs

Above we considered only the accretion discs, however, discs (or some part of disc) formed by the out-flowing gas/plasma could also exist. For example, Bespalov and Zheleznyakov [55] studied the possible formation of plasma discs around hot magnetic stars (a young white dwarf or a young neutron star) under the action of light pressure exceeding the effect of gravitation when an effective outflow of plasma from the surface of a star takes place. Plasma moving along closed field lines is concentrated at the most remote parts of the field lines and forms disc near the magnetic equator. Bespalov and Zheleznyakov [55] called such stellar objects the radiative discons. In radiative discon plasma drift or diffuse slowly to the periphery of disc. The authors noted that at some distance from the star, the magnetic field is incapable of preventing the radial dispersal of the plasma and, accordingly, cannot ensure the matter flow to the disc along a field line.

Bednarek [56] describing two massive (~70 M_Sun) Wolf-Rayet (WR) stars in a compact binary system with the surface magnetic field ~10⁴ G and radii ~20 R_Sun, applied a model for the external magnetic field structure in the presence of a strong gas out-flow. According to this model the magnetic field is a dipole type below the Alfvén radius, and becomes radial above it. This corresponds to the case when the inner boundary of the disc’s current sheet is located at the Alfvén radius, which for the parameters considered by Bednarek [56] was ~1.3 WR star radii. Below we consider the non-accretion current discs.

3.1. Heliospheric Current Sheet

The heliosphere is a region around the Sun through which the solar wind (i.e., the plasma ejected from the Sun) with its magnetic field extends and where the influence of the solar wind is significant. The mass loss rate for the Sun is 2×10^–14 M_Sun/year [18]. The outer boundary of the heliosphere is called the “heliopause”. It separates the heliosphere and the surrounding interstellar medium. The heliosphere contains the global heliospheric current sheet located at the magnetic equatorial plane between sectors of opposite polarity (e.g., [57]). It is usually assumed that the inner boundary of the heliosphere is located at around 10 - 20 solar radii or 0.1 AU from the center of the Sun.

Alfvén considered the heliospheric current sheet (with the electric current 3 × 10⁹ A) to be a part of the heliospheric electric current system, in which the Sun acts as a unipolar inductor producing the current. The current transfers angular momentum from the central body to the surrounding plasma [39]. It has been generally accepted that at large heliocentric distances the heliospheric current sheet is a warped surface. Alfvén and Carlqvist [39] noted that the in-situ measured sector structure of the interplanetary magnetic field can be referred to the waving motion of the current sheet. The electric current in the equatorial plane is supposed to be closed by the fieldaligned currents going to the Sun polar regions and later to the Sun’s atmosphere. The rigid corotation of the solar wind plasma with the Sun, in zero-order approximation, takes place in the region below the Alfvén radius R_A. For typical models of the magnetized solar wind, the Alfvén radius is estimated as 0.11 AU. Inside the Alfvén radius, the solar magnetic field forces plasma to corotate, while outside the Alfvén radius, the magnetic field is passively convected by the solar wind plasma motion. The direction of equatorial heliospheric current depends on the orientation of the solar magnetic dipole moment, which changes during the solar cycle.

Zhao and Hoeksema [58] analyzed the STEREO A and B observations of the radial magnetic field between 1 January 2007 and 31 October 2008. These data show significant evidence that, the radial component of ambient magnetic field, after removal of all dynamic effects, has a uniform distribution in the heliosphere. Ignoring polarity aspect, this configuration is similar to the monopolar field. Based on this monopolar topology of the ambient heliospheric field, the authors argue that the surface beyond which the magnetic fields have the monopolar configuration could be considered as the inner boundary of the heliosphere. Such approach separates the monopole-dominated heliospheric magnetic field from the multipole-dominated coronal magnetic field. The magnetic field at the inner edge of the heliosphere should be a uniform radial field. Zhao and Hoeksema [58] stated that although there is no strict definition of the inner boundary of the heliosphere in the literature, it is generally assumed to be a surface that separates the superAlfvén solar wind from the sub-Alfvénic coronal expansion. In other words, it means that the inner edge of heliospheric current sheet is located at the highest radial Alfvén critical point, where the radial solar wind velocity equals to the Alfvén velocity. Zhao and Hoeksema [58] found that this surface should be set at about 14 solar radii near solar minimum phase.

3.2. Current-Carrying Discs in the Magnetospheres of Jupiter, Saturn, and a Close-In Giant Exoplanet

3.2.1. Jovian Magnetodisc

Jupiter is located at ~5.2 AU from the Sun and possesses the largest magnetic field among the planets in the solar system. Its dipole magnetic moment is 4.28 G× R_J³, where R_J = 7.14 × 10⁷ m is the jovian radius. Magnetodisc of Jupiter is formed due to the fast rotation of the planet (the rotation period is about 10 hours) and the presence of inter-magnetospheric sources of plasma. In particular, the volcanic activity on the jovian satellite Io provides about 1 T of ions per second. The total azimuthal current in the magnetodisc is estimated as ~10⁸ A and the effective magnetic moment of the magnetodisc field exceeds Jovian dipole magnetic moment by a factor ~2.6 (see e.g., [59], and references therein). Thus, the magnetodisc plays a significant role in the Jovian magnetosphere. It was found by observations that beyond ~20 R_J from the planet the equatorial magnetic field lines are stretched into a form typical for discs.

Hill et al. [60] and Hill [61] wrote that beyond the Alfvén radius, the field should assume a disc-like geometry. Barbosa [62] stated that plasma is assumed to emanate from the Alfvén surface and is channelled down-tail at Jupiter. Coroniti and Kennel [63] marked, that for the centrifugally driven “wind” from the Jupiter the outflow commences at the Alfvén radius (according with one of their estimations R_A ~ 20 R_J). The plasma b exceeds unity in the current sheet beyond this distance.

From figure 6 from Delamere and Bagenal [64] it follows that approximately at 18 - 20 R_J the local Alfvén velocity reaches the value ~250 km·s^–1. Alfvén velocity was determined by the authors using the planetary dipole field for estimation of magnetic field at these distances. The authors mentioned that at about 60 ± 20 R_J the radial outflow exceeds the local Alfvén velocity. However, if one looks at the azimuthal velocity, which was assumed in [64] to be a rigid corotation, but not exceeding 250 km·s^–1 consistent with the observed azimuthal flows in the middle and outer magnetosphere (see [64], and references therein), then it can be seen that at ~20 R_J the azimuthal velocity becomes of the order of the Alfvén velocity. For rigid corotation, V_rig = 12.6 L km·s^–1, where L is the jovicentric distance measured in R_J. Therefore, the Alfvén radius determined with respect to the azimuthal velocity is located near 18 - 20 R_J, i.e., at the jovicentric distance of the inner edge of the Jovian magnetodisc.

The dominating motion of plasma in the inner part of the disc around Jupiter takes place in the azimuthal direction, thus the azimuthal velocity determines the Alfvén radius. Using the Alfvén radius (which is one of the input parameters in the paraboloid magnetospheric magnetic field model for Jupiter) for determination of the inner boundary of the disc enables to interpret observations with a good accuracy [3,59]. The distance to the inner edge of magnetodisc in this study was chosen to be 18.4 R_J.

At the inner edge of the Jovian magnetodisc the geometry of magnetic field lines changes from the dipoletype to the disc-type. This is also connected with the appearance of a visible radial outflow of plasma (~10 km·s^–1) [64] and, consequently, to decrease of its azimuthal velocity. As a result, the field-aligned currents arise, which accelerate electrons into Jupiter’s atmosphere/ionosphere and thus can create emissions in the main auroral ovals. The field-aligned mapping of the observed ovals seen in the UV images obtained by the Hubble Space Telescope (HST), fulfilled using the paraboloid magnetospheric magnetic field model, gives the equatorial projection located near 18 R_J, which well supports the idea of the location of the inner edge of the disc at the Alfvén radius defined as described above.

3.2.2. Kronian Ring Current

Saturn is the second largest planet in the solar system. It is a rapidly rotating planet (rotation period is ~10.6 hours) located at 9.5 AU from the Sun. It possesses a strong magnetic field, the dipole magnetic moment of Saturn equals 0.21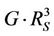, where R_S = 60330 km is Saturn’s radius. A small analog of the Jovian magnetodisc (named a ring current) exists in the Saturn’s magnetosphere. It is also formed due to the fast planetary rotation and the existence of plasma sources inside the magnetosphere (mainly, the kronian satellite Enceladus). The magnetosphere of Saturn may be considered as an intermediate between the terrestrial and the Jovian magnetospheres.

Analyzing the Pioneer 11 plasma data in Saturn’s magnetosphere, Frank et al. [65] found that the plasma outflow occurs there at the radial distance of about 6 - 8 R_S. The ratio of plasma and magnetic field pressures approaches unity in this region for different sorts of plasmas corotating with the planet. The authors stated that this condition assumes that the corotational energy density of the plasma is equal to or greater than the energy density of the dipole magnetic field. Therefore, major reconfiguration of the magnetosphere caused by the disc /ring current, occurs beyond 6 - 8 R_S. The inner radius of the Kronian magnetodisc/ring current determined by Bunce and Cowley [66] for the compressed Pioneer-11 system, is 6.5 R_S (in this time the corresponding distance to the magnetopause subsolar point for Saturn was ~17.5 R_S).

For the Voyager encounters, Connerney et al. [67] determined the location of the inner edge of Saturn’s ring current at around 8 R_S. Later, Kellett et al. [68], based on data from two equatorial passes of the Cassini spacecraft in September 2005, found the inner boundary of the kronian current sheet to be located from 6 to 8 R_S. So, the coincidence of the inner edge of the current-carrying disc with the Alfvén radius (determined for the azimuthal velocity) takes place also for Saturn. This fact has been confirmed for different values of the solar wind dynamic pressure, corresponding to different kronian magnetospheric states, and for different spacecraft passes nearby the planet.

Belenkaya et al. [69] found the input model parameters for the inbound part of the Pioneer 11 trajectory using the approximate formulas for simulation of the magnetic fields of different magnetospheric current systems along the Saturn-Sun line and magnetic field measurements in a few selected points along this line. The obtained set of the input model parameters was used for computation of the magnetospheric magnetic field along the whole inbound Pioneer 11 trajectory. Comparison of the obtained results with the spacecraft measurements showed good accordance (demonstrated in figure 1 from [69]). Among the used parameters there was also a distance from the Kronian center to the inner edge of the Saturn’s ring current, which was estimated to be equal to 6.5 R_S. As it was shown above, this value coincides well with the Alfvén radius, obtained for the azimuthal velocity.

3.2.3. Discs around Close-In Exoplanets (“Hot Jupiters”)

At the present time hundreds of extrasolar exoplanets have been detected. Many of them are located at distances less than 0.5 AU and have masses of the order of the Jovian mass. The upper atmospheres of such planets, located close to their parent stars, are strongly heated by the stellar XUV radiation therefore these planets are called “Hot Jupiters”. Cohen et al. [70] emphasized that for close-in exoplanetary orbits at distances comparable to or less than the stellar Alfvén radius, the star-planet magnetic interaction may be significant. Cohen et al. [70] presented MHD numerical simulations of the star-planet interaction considering the interaction between the stellar and planetary Alfvén surfaces, which modifies the global structure of the stellar corona and stellar wind.

The paraboloid model of a planetary magnetosphere, originally constructed by Alexeev [2] for the case of Earth, and generalized later for Mercury [4], Jupiter [3, 59], and Saturn [69,71-73], recently was also applied to “Hot Jupiters” [1]. In particular, the exoplanetary magnetospheric equatorial current-carrying disc was introduced in [1]. This disc surrounds the planet and significantly enlarges the size of the planetary magnetosphere and increases the total magnetic field. The previous study of exoplanetary magnetospheres were made within a simplifying assumption of a planetary dipole-dominated magnetosphere. Khodachenko et al. [1] made a step forward in construction of a more complete “Hot Jupiter” magnetospheric structure and topology, which has the magnetodisc-dominated character. The formation of such magnetospheres is strongly connected with the significant thermal outflow of the expanding atmospheric material of the close-in “Hot Jupiters”, heated and ionized by the stellar radiation. This expanding material, under the conditions of the rotating planetary intrinsic magnetic dipole field, contributes to the formation of an extended current-carrying plasma disc around a planet. It has been shown that the magnetodisc-dominated magnetospheres in most cases appear to be large enough in order to protect exoplanets against the destructive action of the stellar wind plasma flows.

Khodachenko et al. [1] considered formation of the disc in the exoplanetary magnetosphere. As the gas/ plasma surrounding the rotating magnetized object moves outwards along the magnetic field lines, its angular velocity V_j is approximately constant until it reaches a value of the local Alfvén speed V_A. This happens at the Alfvén radius. At R_A, the field lines become to be distorted by the inertia of the co-rotating gas, and the dipole-type topology of the magnetic field in the inner magnetosphere changes to the magnetodisc-type topology beyond R_A. The expression for R_A in the exoplanet magnetosphere was given in [1]:

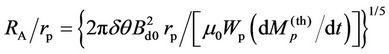(6)

where r_p is the planetary radius, δθ is the angular thickness of the disc, B_d0 is the value of the planetary dipole magnetic field in the equatorial plane at the surface of the planet, μ₀ is a permeability of the vacuum, W_p is the planetary angular rotation rate, and dM_p^(th)/dt is the planetary thermal mass loss. At the inner edge of the disc the azimuthal velocity shift arises due to change of the magnetic field lines form. This results in an electric field along the strongly conducting magnetic field lines, generated in the rest frame of the rotating planet. As a consequence, the field-aligned currents flow there.

Location of the inner edge of magnetodisc around a magnetized exoplanet is a very important parameter. In particular, it determines the substellar magnetopause distance from the exoplanet center which characterizes a scale of the whole magnetosphere. Besides that, it influences the value of the magnetodisc’s magnetic field, which may give a significant contribution to the total magnetospheric field [1]. While in the paraboloid model of an exoplanetary magnetosphere the inner edge of the magnetodisc coincides with the Alfvén radius in the equatorial plane, the outer edge of the magnetodisc is close to the magnetopause substellar distance.

4. Discussion and Conclusions

One of the main tasks of the theory of astronomical discs is to study their structure and location. In the present review we considered different types of astrophysical discs: discs around stars, planets, exoplanets, and compact objects. We also shortly discussed the discs around supermassive black holes in AGNs (quasars) and discs in binary systems (twin sources of X-ray, twin and millisecond radio pulsars) existing due to the mass exchange between two stars-companions realized through the disc.

Beskin and Tchekhovskoy [74] presented analytical results obtained for a large class of axisymmetric stationary flows in the vicinity of compact astrophysical objects. They described the ideal flows in the vicinity of spinning black holes by a kind of the Grad-Shafranov equation. In astrophysics the Grad-Shafranov equation describes axially symmetric stationary flows and the poloidal structure of the magnetic field. This equation was originally related to an equilibrium static configuration. Beskin and Tchekhovskoy [74] mentioned that spherically symmetric accretion (ejection) of matter could be a solution of Grad-Shafranov equation, i.e. the equilibrium equation for magnetic surfaces. They stated that accretion flows to neutron stars and black holes, axisymmetric stellar (solar) winds, jets from young stellar objects, and ejection of particles from magnetospheres of rotating neutron stars with a high accuracy degree are axisymmetric and stationary. The authors noted that the ideal magnetohydrodynamics could be applied to such objects because due to axial symmetry and stationarity, as well as the ideal freezing-in condition: E + V ´ B = 0 (where E and B are electric and magnetic fields, respectively, and V is velocity), it is possible to introduce in the most general case five integrals of motion which are constant at axisymmetric magnetic surfaces. These integrals are an energy flux (integral Bernoulli), the z-component of an angular momentum, electric potential, an entropy per particle, and a ratio of particle flux to magnetic flux [75]. Beskin and Tchekhovskoy [74] noted that this concerns also to the vicinity of the spinning black holes, as the Kerr metric, which describes space-time around a rotating black hole, is also axially symmetric and stationary. Beskin [75] showed that the Alfvén surface (where the radial flow velocity equals to the Alfvén velocity) does represent a singular surface of the second-order GradShafranov equation, and the regularity condition must be satisfied there. All the trajectories with a positive square of energy go through the Alfvén surface. For the hydrodynamic accretion (when magnetic field is negligible) Alfvén surface does not exist [75].

Lery and Frank [76] noted that the general problem of determination of the stationary two-dimensional structure of magnetohydrodynamic outflows requires the solution of the equilibrium of forces perpendicular and parallel to the magnetic surfaces. One can describe the former by using the transfield or Grad-Shafranov equation and the latter by the Bernoulli equation for a polytropic equation of state. We should mention here that while for neutron stars, pulsars, stars, and black holes the Alfvén radius characterizing the inner disc boundary, is calculated using the poloidal flow velocity, for the giant planets of the solar system and exoplanets the Alfvén radius is determined by equality of the azimuthal flow velocity to the Alfvén velocity.

As stated by Lery and Frank [76], for the poloidal motion in the disc, the balance of forces perpendicular to magnetic surfaces is accounted for on the Alfvén surface at the base of the flow. On the Alfvén surface the force balance equation turns into the known Alfvén regularity (nonsingularity) condition. Except the Alfvén point, MHD flows have two other critical points: the slow and fast magnetosonic points. Both of them are located where the poloidal velocity equals one of the two magnetosonic mode speeds. The corresponding fast and slow surfaces, unlike the Alfvén surface, are saddle points, i.e., transonic solutions only exist for a certain relation among the integrals of motion [76].

Abubekerov and Lipunov [77] stated that the size of the magnetosphere of an accreting star (accretor) is close to the Alfvén radius. Such magnetized objects (surrounded by accreting disc beyond the magnetosphere boundary) are found among X-ray pulsars, X-ray-bursters, cataclismic variables (polars, intermediate polars), T Tauri stars. The mentioned above properties of accretors are independent of the nature of the central object, which may be a neutron star, white dwarf, or T Tauri star.

Ferreira and Petrucci [78] noted that the fact that self-confined jets are observed around stellar mass black holes and supermassive black holes (AGNs), neutron stars and young forming stars, points to a jet launching mechanism, independent of the nature of the central object, namely the surrounding accretion disc. Conditions for launching jets are very stringent and require a large scale magnetic field B_z close to equipartition with the total (gas and radiation) pressure. The presence of a large scale vertical magnetic field is an unavoidable ingredient for jet launching, regardless of the nature of the central object. Therefore, the accretion discs around the mentioned above celestial bodies, are interrupted and transfer part of their energy to jets at the Alfvén radius.

In the other systems, the matter can be rotationally ejected at the Alfvén radius. The ejected matter carries away angular momentum and brakes the central rotation magnetized object. This scenario could be realized for a strong magnetic field. As it has been considered in this paper, the Sun, Jupiter, Saturn, and close-in giant exoplanets are surrounded by discs with the outflowing plasmas, and the inner edges of these discs coincide with the corresponding Alfvén radii.

The angular momentum of gas/plasma flowing in or out from the central body prevents the matter from direct fall on the object. Instead, the gas/plasma settles into a disc-like structure whose orientation is defined by its angular momentum. This is a reason for the prevalence of discs in astrophysics [79]. Disc is a configuration possessing minimum of the total energy for the fixed angular momentum.

Discs occur in a wide range of astrophysical contexts, differing in size, in origin, in material and direction of motion inside them. One specific feature common for a large group of astrophysical discs in the presence of a sufficiently strong magnetic field is considered in this paper. It consists in the fact that a lot of discs have their inner edges near Alfvén radii. The reason is that in the presence of magnetic field, the MHD theory describes the plasma motion, and in particular, determines the location where plasma begins to form disc (for outflow) or leave it (for in-fall), thus creating its inner edge. The inner edge of a disc arises in a place, where the external influence becomes significant. The magnetic field may play a role of such an external agent. It could be either a strong magnetic field of the central body, or the magnetic field carried by the disc material and surrounding magnetized plasma.

5. Acknowledgements

Work at the Institute of Nuclear Physics, Moscow State University was supported by the RFBR Grants No 11-05-00894 and 12-05-00219. The authors are thankful to the Ministry of Education and Science of the Russian Federation Grant No 07.514.11.4020 and to EU FP7 projects EUROPLANET/JRA3 and IMPEX for support of their collaboration and to Igor Alexeev and Vladimir Kalegaev for construction of the planetary magnetospheric models. MLK also acknowledges the support from the Austrian Science Foundation (FWF) via the projects P21197-N16 and S11606-N16.

REFERENCES