ABSTRACT

A nonlinear state observer design with sampled and delayed output measurements for variable speed and external load torque estimations of SPMSM drive system has been addressed, successfully. Sampled output state predictor is re-initialized at each sampling instant and remains continuous between two sampling instants. Throughout this study, a positive constant to satisfy an upper limit of the sampling period between sampling instants and allowable timing delay in terms of observer parameters has been prepared such that the exponential stable of the closed-loop system is guaranteed, based on Lyapunov stability tools. In order to validate the theoretical results introduced by main fundamental theorem to prove the observer convergence, the proposed sampled-data observer is demonstrated through a sample study application to variable speed SPMSM drive system.

Keywords:

Stability, SPMSM, Sampled Output Observer, Lyapunov Stability, Intelligent Sensor

1. Introduction

In recent decays, synchronous machines are used in variable speed motoring and the manufacturers had been made synchronous machines based on permanent magnets in wide power range with various categories and structures. On the other hand, an efficient development has been considered in the field of power electronics technology; it has made the task of flexible rotor speed variation a realizable target. In effect, PMSMs are more efficient for applications demanding rotor speed reversion. Synchronous machine is convenient for drive applications, when these applications involve wide power variation. To this end, PMSMs have been made controllable through inverters since these inverters have the possibility of interconnection between electrical grid and three-phase machines and they are capable to ensure smooth output voltage. The latter allow the control of stator phases switching action, depending on the electrical rotor position, so that the PMS motors operate with time-varying speed. The inverters are acted on using controllers, but these need online measurements of the rotor speed and load torque [1] . The point is that mechanical sensors are costly and may not be sufficiently reliable. Accordingly, state observers have been reported in recent years to get online estimates of mechanical variables based on on-line measurements of the electrical variables. Various design approaches had been used to obtain mechanical senseless observers for PMSMs. One of the design approaches dealing with the identification and investigation of eddy current effects on motor rotor position observation had been claimed by [2] . The authors tried to improve high frequency injection approach based on self-sensing control of a PMSM drive system at stand still and low rotor speed. This approach is not recommended for high rotor speed applications and LFI. On the other hand, some of excitation strategies had been recommended by [3] that rely on the detection of the rotor position from the stator voltages and currents without requiring additional test signals. In [4] , the back EMF (waveform of the voltage induced in stator windings) had been used to estimate rotor position by means of state observers or Kalman filters [5] . This approach works well in medium and high speed applications, but it is not accurate at low operation when the back EMF is low. In [6] , Kalman-like interconnected observers have been designed that estimate the machine position and speed. However, these observers are complex (computation time consuming), and their convergence analysis relies on an excitation condition involving the observer signals (e.g. the state estimates). More specifically, an interconnected observer is in fact composed of two observers and the persistent excitation condition of one observer involves the state estimates provided by the other. As a matter of fact, suitable conditions are those involving the system signals (system input and output) not the observer signals.

Recently, the problem of global exponential stabilization of nonlinear systems has received a great deal attention in the world. Consequently, this paper deals with designing of nonlinear sampled-data observers in the presence of sensorless measurements, all the mechanical state variables are considered inaccessible for measurements. As investigated in [7] [8] , some extra growth conditions on the unmeasurable states of the system are usually necessary for the global stabilization of nonlinear time delay systems. A Lyapunov-Krasovskii Functional (LKF) was suggested in [9] , such that the relation between the delayed state variable and the number of cascade observers with specific vector gain were introduced. In [10] [11] claimed that several authors extended the result in [9] to a time-varying delay system with observer and provided a maximum allowable time delay in terms of observer design parameters.

A sampled-data control of nonlinear systems using high-gain observers is introduced by [12] . The state observer is performed in continuous-time mode and then it is discretized for digital implementation using three different discretization methods.

Sufficient conditions for time-varying delays were derived via Razumikhin approach [13] , which leads to more conservative results than Krasovskii method. For systems with constant delays, sufficient conditions were derived in terms of LKF in [14] . Published studies concerning with the design of continuous-time high-gain observers [15] [16] dealing with dynamical high-gain observers for continuous-time systems are designed.

In present paper, one looks for accurate observation of the unmeasured mechanical state variables, which are angular rotated speed and external load torque for surface permanent magnet synchronous motor SPMSM, supposing the stator current and voltage to be accessible for measurements. To this end, a sampled-data nonlinear state observer will be designed with sampled and delayed output measurements coupled with inter-sampled output state prediction. The proposed observer will prove to be exponentially convergent in presence of wide range variations. The proposed observer is capable to ensure efficient tracking response. The proposed observer is formally proved through a main result based on tools of Lyapunov stability approach.

The remainder of this paper is organized as follows. In the next section, the problem formulation of SPMSM will be provided. The Third section is devoted to the observer design and stability analysis with sampled and delayed measurements is provided by using a Lyapunov stability approach. Then the equations of the state observer used for SPMSM are given. In this section, the problem statement which leads us to prove the exponential convergence of the global exponential stabilization and state estimation of nonlinear systems coupled with sampled?data observer design based on main theorem. The forth section is simulation results and verifications. Finally, conclusions are given in section five.

2. Problem Formulation

2.1. Reduced Model of SPMSM

Dynamic modelling is needed for various types of analysis related to system dynamics: stability, control system, and optimization. The SPMSM model is constructed in (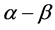) stationary reference frame. Notice that, the time derivative of the external input load torque is considered by an unknown bounded function. The control objective is to determine under what sufficient conditions that all the SPMSM states variables, which are, 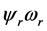and T_L can be determined from the motor input and output measurements, namely the stator current and the motor input command voltage signal, 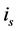and.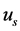

A mathematical model of the synchronous motor is highly desirable to obtain an overview on the complex electromagnetic behavior of the motor, and perform the simulation or controller synthesis. A model based on the electrical and mechanical equations are usually sufficient to synthesize the system model. SPMSM nonlinear system model is given by [17] :

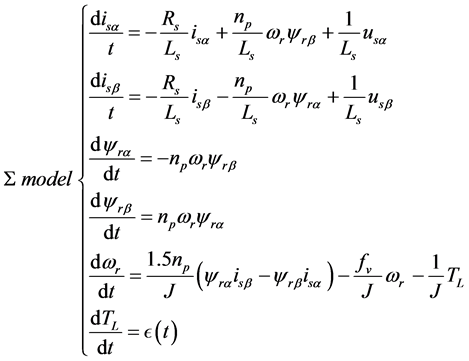(1)

with, 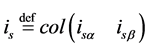, , 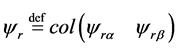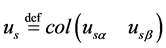are respectively,

the stator vector of currents, the rotor fluxes and the motor input command signals. 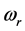and T_L respectively, denote the rotor speed and the load torque, which is unknown but constant and that its upper bound is available. J and are the moment of inertia and viscous friction; 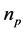is the number of magnetic pole pairs. The electrical parameters, R_s and L_s are the armature resistor and inductance, respectively. The electromagnetic torque, 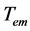, is indirect measurable output state. This can be evaluated through the first term of third subsystem given in (1). One can write the system under study of SPMSM as:

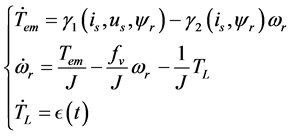(2)

where

This model can be re-written under the form taking into account that the electromagnetic torque is not accessible to measurement all the time, only sampled? data measurements, 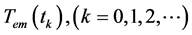are available:

(3)

where, the state vector

, , and

To clarify the general procedure related with this study, a flow block diagram of study method and its application to sensorless SPMSM drive system is shown in Figure 1.

2.2. System Construction in z Benchmark

Let us provide the following state transformation to put the system model in observable normal form as follows:

such that, is diffeomorphism.

Let us put the following system in the z benchmark after doing state transformation is:

(4)

where, , that is,

(5)

where, and,

(6)

(7)

Before the observer synthesis for our physical system model given in (4) is designed, some technical assumptions have to be stated. Such hypothesis have vital role for the next results.

H₁: The functions, are locally Lipschitz and globally bounded with respect to z in domain of interest, uniformly in i.e., , such that, we can easily write the following:

(8)

Note that the functions may contain linear parts and the dynamics depends on all state variables through the Lipchitz function.

H₂: Throughout this paper the function is unknown periodic bounded and the real is the upper bound of such that,.

Lemma [18] : Let us consider that the input is regularly persistent for system given in (4) and assuming the Lyapunov differential equation stated in (10), so that for any symmetric positive definite matrix S(0), , such that. Also, by choosing, one has

3. Observer Structure

In this subsection, the following sampled-data observer is proposed for,. The main difference compared with third class of nonlinear system given in [19] resides in the presentation of state observer with the effect of external disturbance. As a matter of fact, the authors in [20] focused in case of linear systems and without taken into consideration the state predictor.

(9)

(10)

(11)

(12)

The output sampled data observer defined from (9)-(12) consists of a classical observer and output predictor for sampled and delayed measurements where is the continuous estimates of the states. The predictor w is reset (re-initialized) at each sampling instant. S is SPD matrix and continuous in. Now, one shall prove in the next theorem that the proposed observer is a global exponential observer for system given in (4) with the sampled and delayed measurements in output state vector, , where is set of natural numbers. Figure 2 shows single line diagram of proposed study with sampled and time delayed state observer.

Theorem (Main Result): Let us consider the system described by the set of differential equation given by (4), and hypothesis H₁, H₂ hold. This leads us for constant maximum allowable sampling period and upper bound limit of admissible timing delay in output state measurements as follows:

(13)

and,

(14)

The sampled output-data observer given in Equations (9)-(12) is global exponential observer for system (4) as for sufficient large positive value of observer design parameter, satisfying,.

Proof of theorem: The searcher shall give formal analysis of the main theorem using Lyapunov stability approach. For writing convenience, the variable t can be cancelled. Set observation error:, then one shall obtain from Equations (9)-(12) and (4) the following new dynamics error system as follows:

(15)

Throughout this paper, let us define the following quantities:

(16)

(17)

Thanks to Newton Leibniz integration formula that it will be used in next equations:

(18)

Then the error dynamics given by (15) can be re-formulated as:

(19)

Let us define the following LKF, provided by [20] :

(20)

where is a positive design parameter and is a piecewise differentiable positive function designed for the purpose of correcting the error between the predictor and the output such that, satisfies the following conditions:

(21)

To show the exponential convergence of the observation error, it is necessary to prepare conditions for and to guarantee that:

(22)

(23)

Using the fact that the observation error is continuous and the error then it is clear that the inequality defined in (22) is performed.

Now, let us decomposes the Lyapunov function into four functions, which are and, respectively:

(24)

Now, the time derivative of the first Lyapunov function is:

(25)

Combining (10) and (19) for and, respectively, yields

(26)

Using the fact that,

This will give,

(27)

Thanks to Jensen’s inequality, one has:

(28)

This leads us to get the following result,

(29)

In view of Lemma, one deduce

(30)

And, the time derivative of given in (30) is:

(31)

On the other hand from (9)-(12), one can easily conclude that:

(32)

That is, the system (31) becomes:

(33)

Likewise, the time derivative of third Lyapunov function in (24) is:

(34)

The time derivative of the prediction error given in (16) is:

(35)

Using (11) and (29) with the assistance of the Newton Leibniz integration formula stated in (18) and using H₂, one gets:

(36)

Since,

Therefore, the first term of (34) becomes:

(37)

Using once again Jenson’s inequality given in (28), and using, H₃, yields:

(38)

So, combining Equation (38) in (34), one has:

(39)

Thus, from equations (30), (31) and (39), one has the following

(40)

Thus, the exponential convergence of the observation error is guaranteed if the following conditions successfully achieved:

(41)

(42)

(43)

To derive the, and, let us consider, and, , this implies, (41) becomes:

(44)

Furthermore, one selects the function as a saw tooth function for, , , , , and. Consequently, the proposed condition in (42) is performed if,

(45)

This leads us that the sampling interval must be smaller than, ,. Using (45), the proposed maximum admissible sampling interval is:

(46)

On other hand, from condition (43), the corresponding admissible timing delay, is

(47)

It is obvious that if Equations (45), (46) and (47) are performed successfully, the proposed conditions given in Equations (41), (42), (43) and (44) are satisfied in the same way. Thus the observation error of the system under study tends exponentially towards the origin as the time increasing towards infinity. This ends proof of theorem.

4. Simulation Results

In this section, the dynamic performances of the proposed sampled data observer accompanied by sampled and delayed output measurements for online estimation of SPMSM state variables, which are motor rotor speed and external load torque. SPMSM has been implemented under MATLAB/Simulink environment. The tool selected for solving the dynamic equations is the MATLAB function called ODE45.

The system dynamics have been described by third order nonlinear dynamic model given in Equation (2) for SPMSM. A proposed sampled-data observer of the nonlinear system is given by (9) accompanied by sampled and delayed output measurements as a practicable solution for sensorless variable speed control of SPMSM is proposed to get on line estimates of all mechanical state variables in SPMSM. The sampled data observer stated in system (9) is implemented using realistic benchmark MATLAB/Simulink resources. The observer design parameters are and. The dynamic performance depends on the numerical value given to the observer design parameters, constant sampling period, between sampling instants and allowable timing delay. The selection of the tuning parameter is performed using try and error procedure. This value has been bounded to 200 as listed in Table 1 when simulating sampled?data nonlinear observer given in Equation (9). From Table 1, the electrical time constant is accordingly, a suitable value of the allowable timing delay would be 6 ms. A time delay of 6 ms appears be sufficient to exceed transient stability. The summarized results for sampled-data observer design parameters and are listed in Table 2. The nonlinear observer dynamic performances for complete one cycle of (50 s). Figure 3 shows reference rotor speed in (rad/sec) to guarantee control strategy. Figure 4 clarifies the external load torque profile in (N∙m). Figure 5 illustrates real electromagnetic torque and its estimates. On the other hand, the rotor speed and load torque tracking performances are shown in Figure 6 and Figure 7, respectively. The output state prediction error is shown in Figure 8. It is apparent that the output electromagnetic torque and its prediction is decreased and increased simultaneously with variation of angular rotated speed. Thus, the observation errors resulting from technical hypothesis H₁, H₂ are practically acceptable as shown in Figure 9 and Figure 10. It should be mentioned that the dynamic tracking performance of the proposed sampled and delayed observer is quite satisfactory. From these figures, the error dynamics are exponentially convergence to origin and the closed-loop sample study is globally asymptotically stable GAS with time progressive.

The initial conditions of the matrices is set as, , where is identity matrix and is symmetric positive definite matrix and solution of the Lyapunov equation. The initial conditions of the system states are chosen:

and the corresponding observer states are chosen as,. A solution of the Lyapunov equation given by

Equation (10) is: is the binomial coefficient. The simulations have been achieved successfully with stator inputs in stationary reference frame are,

The simulation results for our case study claimed that the proposed sampled-data observer has acceptable transient response, with influence of sampled and delayed output measurement, accurate tracking response and robustness of observer performance for unknown mechanical torque.

5. Conclusion

In this study, synthesis of nonlinear hybrid state observer for a class of MIMO systems accompanied by sampled and delayed output measurements has been achieved successfully. The observer convergence is formally analyzed and clarified by numerical simulation of surface mounted PMSM drive system. As already mentioned, mechanical sensors based solutions are most costly and unreliable. Then, state observers turn out to be a quite natural alternative to get estimates of mechanical variables using only measurable electrical state variables. The proposed observer provides estimates of the mechanical state variables (rotor speed, load torque) using stator currents and voltages measurements. The numerical results presented in this paper are interesting and could be practically useful from the view point of engineers. The searcher provided an upper bound of constant sampling period and allowable timing delay with sufficient large value of observer synthesis parameter that will ensure the global exponential convergence of the observation and prediction errors towards zero using Lyapunov stability theory.

Acknowledgements

I greatly appreciate the financial support given from ministry of higher education and scientific research in Iraq to carry out this research.

Cite this paper

Al-Tahir, A.A.R. (2016) Exponential Stabilization and Estimation for Sampled Observer Design of Surface Mounted Permanent Magnet Synchronous Motor. Journal of Sensor Technology, 6, 122-140. http://dx.doi.org/10.4236/jst.2016.64010

References