Journal of Data Analysis and Information Processing
Vol.04 No.03(2016), Article ID:70381,15 pages
10.4236/jdaip.2016.43012
Missing Data Imputations for Upper Air Temperature at 24 Standard Pressure Levels over Pakistan Collected from Aqua Satellite
Muhammad Usman Saleem1,2, Sajid Rashid Ahmed2,3
1Institute of Geology, University of the Punjab, Lahore, Pakistan
2Collage of Earth and Environmental Sciences, University of the Punjab, Lahore, Pakistan
3Center for Geographic Information System, Punjab University Collage of Information Technology, Lahore, Pakistan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 May 2016; accepted 28 August 2016; published 31 August 2016
ABSTRACT
This research was an effort to select best imputation method for missing upper air temperature data over 24 standard pressure levels. We have implemented four imputation techniques like inverse distance weighting, Bilinear, Natural and Nearest interpolation for missing data imputations. Performance indicators for these techniques were the root mean square error (RMSE), absolute mean error (AME), correlation coefficient and coefficient of determination ( ) adopted in this research. We randomly make 30% of total samples (total samples was 324) predictable from 70% remaining data. Although four interpolation methods seem good (producing <1 RMSE, AME) for imputations of air temperature data, but bilinear method was the most accurate with least errors for missing data imputations. RMSE for bilinear method remains <0.01 on all pressure levels except 1000 hPa where this value was 0.6. The low value of AME (<0.1) came at all pressure levels through bilinear imputations. Very strong correlation (>0.99) found between actual and predicted air temperature data through this method. The high value of the coefficient of determination (0.99) through bilinear interpolation method, tells us best fit to the surface. We have also found similar results for imputation with natural interpolation method in this research, but after investigating scatter plots over each month, imputations with this method seem to little obtuse in certain months than bilinear method.
) adopted in this research. We randomly make 30% of total samples (total samples was 324) predictable from 70% remaining data. Although four interpolation methods seem good (producing <1 RMSE, AME) for imputations of air temperature data, but bilinear method was the most accurate with least errors for missing data imputations. RMSE for bilinear method remains <0.01 on all pressure levels except 1000 hPa where this value was 0.6. The low value of AME (<0.1) came at all pressure levels through bilinear imputations. Very strong correlation (>0.99) found between actual and predicted air temperature data through this method. The high value of the coefficient of determination (0.99) through bilinear interpolation method, tells us best fit to the surface. We have also found similar results for imputation with natural interpolation method in this research, but after investigating scatter plots over each month, imputations with this method seem to little obtuse in certain months than bilinear method.
Keywords:
Missing Data Imputations, Spatial Interpolation, AQUA Satellite, Upper Level Air Temperature, AIRX3STML

1. Introduction
Climate data gather through remote sensing satellites contains missing data i.e. incomplete data matrices. A major cause of this missing data may result from insufficient sampling, errors in measurement or faults in data gathering [1] [2] . Using of missing data may lead to wrong results and analysis in the research [3] - [6] . It is, therefore, important to select the best estimation of these missing data through available sample data points [1] [7] . In literature [1] [7] - [9] we found mean value imputation method to estimate this missing information, but this method may disturb the data integrity. There are a number of interpolation methods that have been proposed for imputation of missing dataset [10] - [15] . The accurate method depends on the missing data mechanism [2] and schemes for interpolation, with spatial variation in air temperature [16] . In literature, there were several extensive spatial interpolation methods that have been used for air temperature data [17] - [22] . Air temperature data at different pressure levels captured by AQUA satellite contain randomly missing data. We employ Inverse Distance Weighting, Bilinear, Nearest and Natural interpolation techniques for filling these missing information accurately. Air temperature data at 24 standard pressure levels have been filled with these interpolation methods. According to [1] [2] , [7] [8] , [23] , [24] , we chose Root Mean Square Error (RMSE), Absolute Mean Error (AME), Correlation coefficient (corrl) and Coefficient of determination (R2) as performance indicators for these imputations. Firstly missing values have been interpolated through these techniques, then 30% of sample data (total of 324) have been predicted through 70% of known datasets over each month. We take an average of each month’s performance parameters over pressure levels. Scatter plots for bilinear and natural interpolation method have been created and investigated for best imputations. There was not a single study for missing air data imputation over Pakistan. So we make a strategy to check the best interpolation method for temperature data set through available data and software.
In Sections 2 and 3, we will describe data set and meteorology of the study area. Then in Sections 4 and 5, we describe methods and results of this study. Discussions and conclusions will be in Sections 6 and 7 respectively.
2. Data Set Used
To conduct this research work, we have used Atmospheric Infrared Sounder (AIRS) STM Lite Version 6 level 3 product monthly mean air temperature (K) from September 2002 to December 2015. AIRS is one of the instrument mounted on AQUA satellite, which was launched in May 2002 by NASA [25] . Goddard Earth Science Data and Information Service Center (GESDISC) provide air temperature data set on 24 hPa atmospheric pressure levels (i.e. 1000, 925, 850, 700, 600, 500, 400, 300, 250, 200, 150, 100, 70, 50, 30, 20, 15, 10, 7, 5, 3, 2, 1.5, 1 hPa). We have averaged each monthly temperature data over the time period. Through intensive programming, this data set has been processed in Matlab software for each pressure level. AQUA satellite has 2378 bands in the thermal infrared region (3.7 um - 15.5 um) and 4 bands in the visible region (0.4 um - 1.0 um) of electromagnetic spectrum [25] . This spectral range of thermal and visible bands provides accuracy of 1˚C in air temperature for 1 km of air mass thickness [25] . The version 6 of AIRS provide very high-resolution data set of 1˚ × 1˚ grid cell and has an advantage of providing good temperature free from atmospheric biases than version 5 [26] . AQUA provides temperature data set ranging from −180 to +180 longitudes and −90 to +90 latitude [25] . Version 6 has some gaps in the data set which we have filled with IDW, bilinear, nearest, natural interpolations techniques.
3. Study Area
Pakistan (60˚E - 78˚E, 20˚N - 38˚N) geographically lies northeast to china, West to Afghanistan, Iran to the south-west, India to east and South to the Arabian-Sea. Its climate varies from arctic like condition on snow covered mountains in northern areas to arid like conditions in hot deserts in the south-west regions. It consists of four provinces, Punjab, Sindh, Khyber Pakhtunkhwa (KPK), and Baluchistan. Punjab being the largest province mostly consists on the fertile region. This province shared its border with Indian Punjab. Both Punjab has same fertile lands due to river flooding. Sindh which bordered with Indian provinces Rajasthan and Gujarat contain the Thar Desert. Baluchistan border with Afghanistan is a drier region. The overall climate of Pakistan is drier [27] . Its coastal areas facing 0.6C to 1.0C rise in temperature since the 1900 s [28] . Average rainfall varies from area to area but overall has about 10 inches of annually. Desert regions of Baluchistan get less than 5 inches of annual rainfall while Punjab got 20 inches of annual rainfall [27] . Northern mountainous areas face average coldest temperature of 23.88˚C in summer while on Baluchistan, it is about 26.66˚C. On the Indus plain, a temperature range of high of 32.22˚C to 48.88˚C [27] in summer, to a low 12.77˚C in winters. Hottest months in a year are May and June where temperature can reach to 50˚C and coldest month is January with temperature of 5˚C. Pakistan face monsoon season in which seasonal reversal of lower tropospheric winds appears [29] . It has four well define seasons: Winter, from November to February; Pre-monsoon (Hot), from March to mid of June; Monsoon, from mid of June to mid of September; Post-monsoon, from mid of September to October. Summer season is extremely hot and the relative humidity ranges from 25% to 50% [30] (see Figure 1).
4. Research Method and Methodology
We have separated air temperature for each 24 atmospheric pressure levels using Matlab software. Through spatial interpolation techniques of Inverse distance weighting, bilinear, nearest, and natural we filled missing data in air temperature at each pressure level. In order to select best interpolation technique in our data set, we randomly make 30% of the sample data to predict from 70% remaining data set. Interpolated value of this 30% sample data set has been compared with its original ones and we calculated the root mean square error (RMSE) for each interpolation method. Besides other performance indicators like mean absolute error (AME), correlation coefficient (Corrl), the coefficient of determinations (R2) and scatter plots have used in this research, to select best imputation method for upper air temperature data. Performance parameters were investigated after taking averaging over each month (Monthly results can be demanded by emailing the author).
Figure 1. Geographical location of Pakistan as study area.
4.1. Inverse Distance Weighting
It is a weighted average deterministic approach, which assumes that things related more which are closer together. It applies weight to each observation in inverse proportion to its distance from the point where prediction is required [9] . More will be the distance of neighbors from a predicted point, less will be its weight in prediction. Here is mathematical formula is given by [23] .
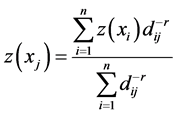 (1)
(1)
where 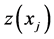 is the interpolated value of missing data through IDW,
is the interpolated value of missing data through IDW, 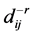 is the weighting factor which was calculated by the Euclidean distance between the neighbor
is the weighting factor which was calculated by the Euclidean distance between the neighbor 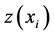 and point to be estimated
and point to be estimated . n is the total no of the sample used (total of 324) and r is the power of distance weighting. Setting search radius of 250 neighbor points and distance power of −2 in IDW algorithm created by [31] we filled the missing data with IDW technique in Matlab software. Extrapolation also has been done with IDW algorithm in data set imputation.
. n is the total no of the sample used (total of 324) and r is the power of distance weighting. Setting search radius of 250 neighbor points and distance power of −2 in IDW algorithm created by [31] we filled the missing data with IDW technique in Matlab software. Extrapolation also has been done with IDW algorithm in data set imputation.
4.2. Nearest Neighbor Interpolation
In the nearest neighbor interpolation method (NNM) missing data imputed directly from the nearest neighbor of the data set [16] [23] . Extrapolation of temperature data was performed with NNM where it requires to extrapolate.
4.3. Bilinear Interpolation
Bilinear interpolation method (BIM) fits a straight line between starting and ending points of the missing data and then enable to interpolate missing values straightforwardly employ this linear equation. Reference [1] provides this formula for linear interpolation.
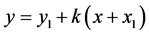 (2)
(2)
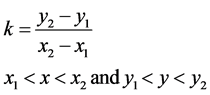 (3)
(3)
Equation (2) is a linear equation of the straight line with 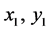 are the coordinates of starting missing data and
are the coordinates of starting missing data and  ending coordinates of the missing values, k being the slope or gradient of line calculated with (3). We have adopted the same scheme of 30% of the sample points as missing to interpolate with bilinear interpolation method. Extrapolation of the missing data has been done with linear interpolation method where it was required.
ending coordinates of the missing values, k being the slope or gradient of line calculated with (3). We have adopted the same scheme of 30% of the sample points as missing to interpolate with bilinear interpolation method. Extrapolation of the missing data has been done with linear interpolation method where it was required.
4.4. Natural Interpolation
The natural interpolation method is based natural neighbor around the missing data. In non-uniformly missing data, selection of natural neighbor is based on Delaunay triangulations method [32] . This interpolation smoothen the surface of the data set.
4.5. Performance Parameters
Several performance indicators were calculated for the best method of imputation. After reading literature, [1] , [2] , [7] , [9] , [16] , [23] , [24] , [33] , we select four performance parameters, root mean square error (RMSE), absolute mean error (AME), correction coefficient (Corrl) and coefficient of determination (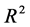 ), as indicators, to select the best method for estimating missing air temperature data.
), as indicators, to select the best method for estimating missing air temperature data.
4.6. Root Mean Square Error (RMSE)
Root mean square error was commutated with Formula (4) given by [7] .
 (4)
(4)
where n is the total no of imputation points [1] , Pi is the imputed data point and Oi is the observed data point. RMSE tells us about a total difference between actual and predicted air temperature data. Lower will be the RMSE, accurate will be imputations [33] .
4.7. Absolute Mean Error (AME)
More residual error in comparison with RMSE can be investigated from absolute mean error (AME). It can be calculated from Equation (5) given by [1] and [7] .
 (5)
(5)
where n is the total no of imputation points [1] , Pi is the imputed data point and Oi is the observed data point. Its value ranging from 0 to ∞. 0 value indicates a perfect estimation of missing values.
4.8. Correlation Coefficient (Corrl)
This coefficient, correlate actual and predicted value of data set. Correlation of value 1, indicates a good estimation of predicted points with actual ones. Its value near to 0 indicates no or low correlation between the actual and predicted data set, concluding to bad imputation for data set.
4.9. Coefficient of Determination (R2)
A coefficient of determination provides us, the degree of correlation between actual and predicted data points [2] . It takes a value ranging between 0 and 1, with values closer to 1 indicate the best fit to the surface [2] and [7] . Reference [7] mentioned this formula for the coefficient of determination.
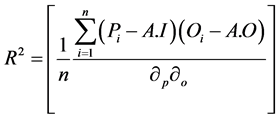 (6)
(6)
In Equation (6), A.I is the average of imputed points and A.O is the average of observation points with 
5. Results
These are the results of performance parameters derived from IDW, Bilinear, Natural and Nearest imputation methods. Performance parameters for each of interpolation method on upper air temperature have explained below over each pressure level.
5.1. Root Mean Square Error (RMSE)
Root mean square error through inverse distance weighting interpolation remains less than 0.2 on all levels except over 70, 100, 150, 250, 300, 400, 500, 600, 700, 850, 925, 1000 hPa where its value vary between 0.2 to 0.7 (see Table 1). RMSE in bilinear interpolation remains <0.03 over 1, 15, 20, 30, 50, 600, 700, 850, 925 hPa while this error little increase to 0.2 and 0.62 over 850, 925, 1000 hPa pressure levels (see Table 2). Same scenario for natural interpolation method, in which RMSE value remains 0.03 at all levels except than 850, 925, 1000 hPa levels (see Table 3). RMSE produce by nearest interpolation method looks somewhat like IDW technique (see Table 4). This RMSE going to increase from 0.1184 on 1 hPa level to 1.066 on 1000 hPa pressure level. This error was more than bilinear and natural interpolation methods on air temperature data (see Tables 1-4).
Table 1. Performance parameters for IDW method.
5.2. Absolute Mean Error (AME)
Absolute mean error with IDW was 0.07256 over 1 hPa and going to increase 0.18522 till 1000 hPa (see Table 1). Although this AME was very less, but other imputation methods like bilinear, produce AME of 0.011 at 1hPa level and this error remains between 0.01 - 0.02 till 925 hPa level (see Table 1). Maximum error with bilinear interpolation method was 0.169 found over 1000 hPa level (see Table 2). Natural interpolation method also produces a very low absolute mean error, which remains from 0.010 to 0.08 till 850 hPa level. At 925, 1000 hPa levels, this error increase to 0.10 and 0.168 respectively (see Table 3). Imputations over 1 hPa to 200 hPa levels were good with very low AME of 0.053 to 0.056. But after 250 to 1000 hPa level this AME value going to increase to 0.263 showing the poor imputations over these pressure levels with the nearest interpolation (see Table 4).
5.3. Correlation Coefficient (Corrl)
Now correlation coefficient tells us what is the correlation between actual air temperature data and imputed data points. Its value close to 1 indicates a strong correlation between actual and predicted value with accurate imputation. Through IDW, this coefficient values was ranging 0.988 to 0.970 overall pressure levels (see Table 1). The correlation coefficient for bilinear interpolation methods remains within the range of 0.999 to 0.992, indicating a good relation between actual and predicted air temperature values (see Table 2). Imputations through natural interpolation methods produce same correlation results as that of bilinear interpolation (see Table 3). Imputations through nearest interpolation method produce worst correlation among all other techniques (see
Table 2. Performance parameters for bilinear interpolation method.
Table 4). This coefficient values vary from 0.993 to 0.971 from 1 hPa to 1000 hPa levels indicating bad imputation of missing data through this method (see Table 4).
5.4. Coefficient of Determination (R2)
The value of 0.971 to 0.93 through IDW interpolation indicating that it was not a good imputation method (see Table 1). In bilinear, its value 0.99 indicating a perfect fit to air temperature overall pressure levels except than 1000 hPa where it has a value of 0.978 (see Table 2). Even this value over 1000 hPa was more accurate then IDW method (see Table 2). The coefficient of determination values closer to 0.99 on all other pressure levels revealing accurate results with natural method (see Table 2). At 1000 hPa level, this coefficient has a value of 0.979. These results of natural interpolation look same as that from the bilinear method. Results through nearest interpolation method were same as that produce from IDW (see Table 4).
6. Discussions
Results indicate that bilinear and natural interpolation methods were best for upper air temperature imputation. Although IDW and nearest, results were also good, but we have to decide best method between bilinear and natural interpolation methods. We adopt the strategy of scatter plots for each of these interpolation methods over each pressure levels on each month of the year. Scatter plot created with plotting actual air temperature with
Table 3. Performance parameters for natural interpolation method.
imputed air temperature through these methods. Trend line which is the best-fit line in the cloud of scatter plot tells us how close the imputed value to its actual one. If clouds of points in scatter plot align perfectly around the trend line, we found it good imputation method.
Figures 2-4 were the scatter plots for each month of air temperature through bilinear interpolation method. After investigating each plot, we have found that over 1 hPa level, scatter plots were poorly fit in February, August, and May. August was the month in 1.5 hPa, where the scatter plots are spread around the trend line. At 3 hPa, in each month, trend line lies close to data points except in February, May, and July. Same spread of scatter plot has investigated in January, March over 7 hPa. Over 11, 20, 30, 200 hPa levels spread of scatter plots clouds was present in February and May. January and February scatter plots were scattered around the trend line over 400, 500, 600, 700, 850, 925 hPa pressure levels. Imputation through bilinear interpolation method of missing air temperature data found align with actual data values over 5, 50, 70, 80, 150, 250, 300, 1000 hPa pressure levels (see Figures 2-4).
Now Figures 5-7 were the scatter plot investigation for natural interpolation method. Imputation through nat-
Table 4. Performance parameters for nearest interpolation method.
ural method seems to be more disturb in certain months over each pressure level. February and May were the months at 1 hPa level, where the scatter plot has spread clouds around the trend line. At 1.5 hPa and 2 hPa levels, February, and May were the months for not providing good scatter plots (see Figure 5). January, February, May and October were the months of not good scatter plot over 3 hPa. 5 hPa seem to be less scatter of data points in April and October. Scatter plot of January, February, October, and February over 7 hPa level was obtuse (see Figure 5). 10 and 15 hPa levels found disturb in January, February, April and May. The large spread of clouds of the points observed in November and June at 20 hPa level (see Figure 5). Scatter plots in months of May, Jun and August found to disperse around trend line over 30 hPa level. 200, 250, 300, 400, 500, 600, 700, 850, 925 hPa were consistently spread around trend line in January, February, March and April (see Figure 6 & Figure 7). Remaining pressure levels found to be best fitted with the trend line, indicating the results for good imputation of missing air temperature through natural interpolation method (see Figures 5-7).
Figure 2. These scatter plots were created with bilinear interpolation method. Actual air temperature (K) with imputed air temperature (K). Top left plot is for 1 hPa level and bottom right is for 20 hPa level.
Figure 3. These scatter plots were created with bilinear interpolation method. Actual air temperature (K) with imputed air temperature (K). Top left plot is for 30 hPa level and bottom right is for 400 hPa level.
Figure 4. These scatter plots were created with bilinear interpolation method. Actual air temperature (K) with imputed air temperature (K). Top left plot is for 500 hPa level and bottom right is for 1000 hPa level.
Figure 5. These scatter plots were created with natural interpolation method. Actual air temperature (K) with imputed air temperature (K). Top left plot is for 1 hPa level and bottom right is for 20 hPa level.
Figure 6. These scatter plots were created with natural interpolation method. Actual air temperature (K) with imputed air temperature (K). Top left plot is for 30 hPa level and bottom right is for 400 hPa level.
Figure 7. These scatter plots were created with natural interpolation method. Actual air temperature (K) with imputed air temperature (K). Top left plot is for 500 hPa level and bottom right is for 1000 hPa level.
7. Conclusion
Performance indicators make a room to reject inverse distance weighting and nearest interpolation methods for imputation (see Table 1 and Table 4). Bilinear and natural interpolation methods were good in imputations over each pressure level. But after investigating scatter plots for each month, we conclude that bilinear interpolation method was the best for air temperature data imputations gathered from AIRS instrument of Aqua Satellite. This method produces an RMSE of only 0.99 in imputation over each pressure level. AME of value 0.01 in the majority of pressure level indicates the reliability of the RMSE, which is very accurate. The coefficient of determination remains >0.99 in all 24 pressure levels, concluding that only bilinear interpolation technique was the best (optimum) for imputation of air temperature data set. Due to very low errors in imputation with natural interpolation, it will be the second best imputation for air temperature data set.
Acknowledgements
I would like to acknowledge AIRS team for providing me air temperature data set. I would like to express my great regards to AIRS team members Edward T Olsen and Thomas Hearty, who guide me in every step to understand AIRS product. My deepest gratitude goes to Alessio Martino, University of the Rome, La Sapienza Italy for assisting me in this research. Also special thanks to Journal of Data Analysis and Information Processing for publication of this effort.
Cite this paper
Muhammad Usman Saleem,Sajid Rashid Ahmed, (2016) Missing Data Imputations for Upper Air Temperature at 24 Standard Pressure Levels over Pakistan Collected from Aqua Satellite. Journal of Data Analysis and Information Processing,04,132-146. doi: 10.4236/jdaip.2016.43012
References
- 1. Price, D., McKenney, D., Nalder, I., Hutchinson, M. and Kesteven, J. (2000) A Comparision of Two Statistical Methods for Spatial Interpoaltion of Canadian Monthly Mean Climate Data. Agricultural and Forest Meterology, 101, 84. http://dx.doi.org/10.1016/S0168-1923(99)00169-0
- 2. Boissonnat, J.-D. and Cazals, F. (2000) Smooth Surface Reconstruction via Natural Neighbour Interpolation of Distance Functions. Proceedings of the 16th Annual Symposium on Computational Geometry, Hong Kong, June 2000, 224. http://dx.doi.org/10.1145/336154.336208
- 3. Langella, G. (2010) File Exchange-MATLAB Central. Mathworks.Com. http://www.mathworks.com/matlabcentral/fileexchange/27562-inverse-distance-weighted--idw--or-simple-moving-average--sma--interpolation/content/gIDW.m
- 4. Pakistan Meteorology Department (2009) Climate Change Indicators of Pakistan. Pakistan Meteorology Department.
- 5. Robeson, M. (1994) Influence of Spatial Sampling and Interpolation on Estimates of Air Temperature Change. Climate Research, 4, 120-124. http://dx.doi.org/10.3354/cr004119
- 6. Yozgatigil, C., Aslan, S., Lyigun, C. and Batmaz, I. (2013) Comparison of Missing Value Imputation Method in Time Series: The Case of Turkish Meteorological Data. Theoretical and Applied Climatology, 112, 144-149.
- 7. Mohammad Noor, N., Mustafa Al Bakri Abdullah, M., Shukri Yahaya, A. and Azam Ramli, N. (2007) Comparison of Linear Interpolation Method and Mean Method to Replace the Missing Values in Environmental Data Set. ICoSM, Penang, 85-87.
- 8. Abbas, Q.S. and Aggarwal, A. (2010) Development of a Structure Framework to Achieve Quality Data. International Journal of Advance Engineering and Application, 193-196.
- 9. Muller, H., Naumann, F. and Freytag, J. (2003) In: Data Quality in Genome Database, Hummboldt Universitt Berlin, Institut fr informatik, Berlin.
- 10. Muraidjar, K., Parsa, R. and Sarathy, R. (1999) A General Additive Data Perturbation Method for Database Security. Management Science, 45, 1399-1415. http://dx.doi.org/10.1287/mnsc.45.10.1399
- 11. Han, J. and Kamber, M. (2006) Data Mining Concepts and Techniques. Morgan Kaufmann, San Meteo, California.
- 12. Rahman, M.G. and Islam, M.Z. (2011) A Decision Tree Based Missing Value Imputation Technique for Data Pre- Processing. Proceedings of the Ninth Australasian Data Mining Conference, Ballarat, 41-50.
- 13. Junninen, H., Naska, H., Tuppurainen, K., Ruuskanen, J. and Kolehmainen, M. (2004) Methods for Imputation of Missing Values in Air Quality Data Set. Atmospheric Environment, 38, 2895-2897, 2899-2900. http://dx.doi.org/10.1016/j.atmosenv.2004.02.026
- 14. Haider, K., Rasul, G. and Afzaal, M. (2008) A Study on Tropical Cyclones of the Arabian Sea in June 2007 and Their Connection with Sea Surface Temperature. Pakistan Journal of Meteorology, 4, 38.
- 15. Iqbal, M. and Quamar, J. (2011) Measuring Temperature Variability of Five Major Cities of Pakistan. Arabian Journal of Geosciences, 4, 595. http://dx.doi.org/10.1007/s12517-010-0224-0
- 16. Saleem, M. (2016) Statistical Investigation and Mapping of Monthly Modified Refractivity Gradient over Pakistan at 700 hecto Pascal Level. Open Journal of Antennas and Propagation, 3.
- 17. Tian, B., Manning, E., Fetzer, E., Olsen, E. and Wong, S. (2014) AIRS Version 6 L3 User Guide: AIRS/AMSU/HSB Version 6 Level 3 Product User Guide. Pasadena, CA.
- 18. AIRS Laboratory Home (2016) http://airs.jpl.nasa.gov/mission_and_instrument/instrument
- 19. Perry, M. and Hollis, D. (2005) The Generation of Monthly Gridded Datasets for a Range of Climatic Variables over the UK. International Journal of Climatology, 25, 1045-1046. http://dx.doi.org/10.1002/joc.1161
- 20. Ozaki, G. (2013) Missing Data Imputation of Climate Datasets: Implications to Modeling Extreme Drought Events. Revista Brasileira de Meteorologia, 29, 23.
- 21. Thiebaux, H.J. and Pedder, M.A. (1987) Spatial Objective Analysis. Academic Press, New York.
- 22. Burrough, P.A. (1986) Principles of Geographical Information Systems for Land Resources Assessment. Oxford University Press, Oxford.
- 23. Ngan Lam, S.N. (1983) Spatial Interpolation Methods: A Review. The American Cartographer, 10, 129-149. http://dx.doi.org/10.1559/152304083783914958
- 24. Franke, R. (1982) Scattered Data Interpolation: Tests of Some Methods. Mathematics of Computation, 38, 181-200.
- 25. Gustavsson, N. (1981) A Review of Methods for Objective Analysis. In: Bengtsson, L., Ghil, M. and Kallen, E., Eds., Dynamic Meterology: Data Assimilation Methods, Springer, New York, 17-76. http://dx.doi.org/10.1007/978-1-4612-5970-1_2
- 26. Shumaker, L.L. (1976) Fitting Surfaces to Scattered Data. In: Lorentz, G.G., et al., Eds., Approxmiation, 2nd Edition, Academic Press, New York, 203-268.
- 27. Stahl, K., Moore, R., Floyer, J., Asplin, M. and McKendry, I. (2006) Comparison of Approaches for Spatial Interpolation of Daily Air Temperature in a Large Region with Complex Topography and Highly Variable Station Density. Agricultural and Forest Meteorology, 139, 224-236. http://dx.doi.org/10.1016/j.agrformet.2006.07.004
- 28. Pyle, D. (1999) Data Preparation for Data Mining. Morgan Kaufmann Publishers, California.
- 29. Little, R. and Rubin, D. (1987) Statistical Analysis with Missing Data. John Wiley and Sons Publishers, New York.
- 30. Schneider, T. (2001) Analysis of Incomplete Climate Data: Estimation of Mean Values and Covariance Matrices and Imputation of Missing Values. Journal of Climate, 14, 853-871. http://dx.doi.org/10.1175/1520-0442(2001)014<0853:AOICDE>2.0.CO;2
- 31. Junnunen, H., Niska, H., Tuppurainen, K., Ruuskanen, J. and Kolehminen, M. (2004) Methods for Imputation for Missing Values in Air Quality Data Sets. Atmospheric Environment, 38, 2895-2807. http://dx.doi.org/10.1016/j.atmosenv.2004.02.026
- 32. Zhan, C., Qin, Y., Zhu, X., Zhang, J. and Zhang, S. (2006) Clustering Based Missing Value Imputation for Data Preprocessing. 2006 4th IEEE International Conference on Industrial Informatics, 16-18 August 2006, 1081-1086. http://dx.doi.org/10.1109/INDIN.2006.275767
- 33. Tseng, S.M., Wang, K.H. and Lee, C.I. (2003) A Preprocessing Method to Deal with Missing Values by Integrating Clustering and Regression Techniques. Applied Artificial Intelligence, 17, 535-544. http://dx.doi.org/10.1080/713827170



















































