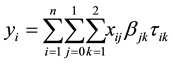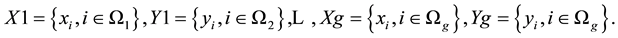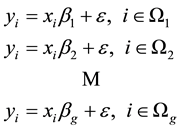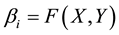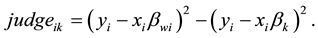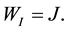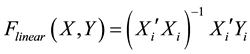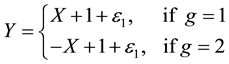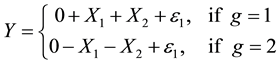Journal of Applied Mathematics and Physics
Vol.03 No.09(2015), Article ID:59467,7 pages
10.4236/jamp.2015.39136
A Fast Iteration Method for Mixture Regression Problem
Dawei Lang, Wanzhou Ye
College of Sciences, Shanghai University, Shanghai, China
Email: wzhy@shu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 July 2015; accepted 5 September 2015; published 8 September 2015
ABSTRACT
In this paper, we propose a Fast Iteration Method for solving mixture regression problem, which can be treated as a model-based clustering. Compared to the EM algorithm, the proposed method is faster, more flexible and can solve mixture regression problem with different error distributions (i.e. Laplace and t distribution). Extensive numeric experiments show that our proposed method has better performance on randomly simulations and real data.
Keywords:
Mixture Regression Problem, Fast Iteration Method, Model-Based Clustering

1. Introduction
In some situations, the data may not be suitable for the linear model, such as nonlinear regression, nonparametric regression, generalized linear model. The mixture regression problem discussed in this paper is a situation with mixed data. Specifically, in the observations, some data are from a model, while others are from other models. As in [1] , mixture regression problem can be treated as a regression or a clustering problem which can be written as:
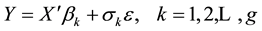
 (1.1)
(1.1)
where  is an independent variable matrix,
is an independent variable matrix, 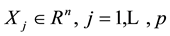 are the observations of the
are the observations of the 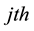 va-
va-
riable. 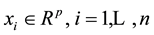 is the ith observation of the data.
is the ith observation of the data. 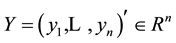 is response variable vector.
is response variable vector.
 and
and 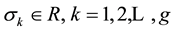 are unknown vectors of regression coefficients and unknown positive scalars, respectively. The random errors
are unknown vectors of regression coefficients and unknown positive scalars, respectively. The random errors 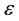 are assumed to be independent of the
are assumed to be independent of the  and
and  is the probability of observation
is the probability of observation 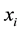 belong to population
belong to population 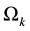 (i.e.
(i.e. . So
. So .
.
The Equation (1.1), a mixture regression model, can also be treated as a model-based clustering [2] , which can be solved by an EM Algorithm [3] -[5] . In fact, EM Algorithm is a statistical method for maximizing the likelihood function by iterative method. The algorithm can be divided into two steps. The one is E-step which is used for estimating the exception for the parameters. The other one is M-step, which is used for maximize the likelihood function under the parameters predicted in E-step. The iteration will continue until the change of likelihood function is less than a given value (i.e. 10−6).
In [6] , Song used an EM algorithm for solving robust mixture regression model. The details of this algorithm are described as follows:
・ Initialize the value of the parameters:
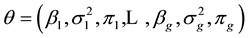
・ E-Step: At the (k + 1)th iteration, calculate:
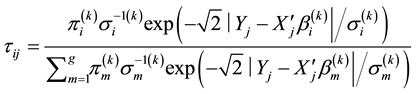
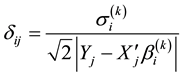
・ M-Step: Use the following value:

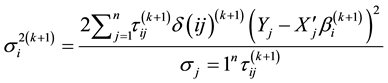
to maximize:
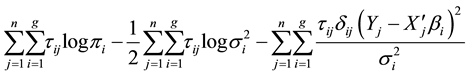
Solving mixture regression problem based on EM algorithm is a complex work with large amount calculation in each iteration. In this paper, we propose a Fast Iteration Method inspired by k-means clustering [7] to solve the mix regression problem. The aim of our method is to fit the data into several linear models. It can also be treated as a model that uses several lines to explain the data (See Figure 1). We will introduce this Fast Iteration Method in the next section.
2. Fast Iteration Method
2.1. Existence of Parameter Matrix
For the situation of the mixture regression problem, the aim of this problem is to find several linear models (i.e. every parameter βk of the model). While, if we known whether an observation is belong to each population, mixture regression model can be treated as a simple linear model. That is: there exist 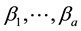
Theorem 2.1 The existence of the parameter matrix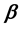
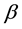
Proof 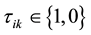
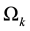
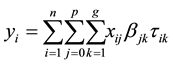
Figure 1. Three lines example for mixture regression problem.
If we know every
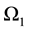
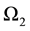
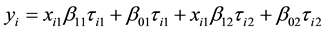
If the elements 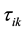
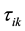
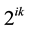
For the limited combinations, there exists a combination which will lead to the minimum square error.
2.2. Fast Iteration Method for Mixture Regression Problem
EM algorithm is meaningful to the mixture regression problem. However, there are still some other methods to solve this question.
The algorithm below is a fast iteration for mixture regression model, which could solve the regression situation with data in different populations. This method is inspired by K-means (the famous clustering algorithm) which calculate the distance between each point to other models and replace the “worst” observation to the suitable model. After finishing this type of calculation for several times, the algorithm will stop until moving any points to other model won’t make the loss-function better, that is, the change of loss function will below a threshold (10−6 or 10−9). In the question of small samples, this stop rules will lead to find a best classifying: moving any observation to any other populations will make things worse. Sometimes set a threshold will avoid the algorithm fall into the endless loop.
Our proposed Fast Iteration Method is similar to K-means algorithm, calculate the MSE for each point to every model and change the point which can decrease the MSE most. We summarize our method as follows.
Algorithm:
1) Calculate the initial value: Group information: 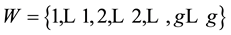
parts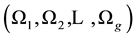
2) Get the subset:
3) Fit g linear models from 
And get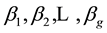
4.) Calculate:
5) 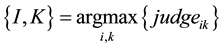
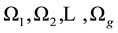
6) Repeat 2 - 5 until stop
For the method of parameter estimating in the algorithm, 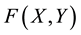
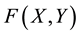
If we need a robust estimation, 
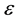
3. Simulation
3.1. Numeric Simulation
In order to validate the rationality of the model, we designed a numeric simulation and generated sample data
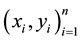
Model 1
Model 2
Model 3
For every model considered above, we generated sample using different kinds of distributions: 1) ε~N(0,1); 2) ε~a Laplace distribution with mean 0 and variance 1; 3) ε~0.95N(0,1) + 0.05N(0,25) Mixture Normal distribution; 4) ε~t3 t-distribution with degree 3.
We used three methods for comparing. Fast Iteration with Linear Model (FI-OLS), Fast Iteration with median regression model (FI-LAE) and EM algorithm are used for solving mixture regression problem for each model.
Repeat the simulation with 1000 times and we got the bias and MSE of every parameter (see Table 1 for
Table 1. Bias (MSE) of point estimates for model 1, n = 100.
model 1, Table 2 for model 2 and Table 3 for model 3)
As we can see in the three tables, simulation shows the Fast Iteration for Matrix Regression with LAE performs better in Laplace distribution and t-distribution. More specifically, in Table 1, FI-LAE has the smaller MSE in Laplace distribution, Mixture normal distribution and t distribution. EM algorithm gets a better estimation in normal distribution. In Table 2, FI-OLS performs better in normal distribution which got a smaller MSE than FI-LAE and EM algorithm. In other distribution in model 2, FI-LAE is better than FI-OLS and EM algorithm got the biggest MSE. In Table 3, we can also see the FI-LAE got a small MSE in mixture and t distribution, while in the situation of Laplace distribution, FI-LAE is a little bit better than EM algorithm.
As we described our model as a “fast” iteration method, the FI-OLS and FI-LAE are calculated faster than EM algorithm. For 100 observations with 2 populations, EM got about 0.07 s for mixture regression (Rpackage: Mixreg), while FI-OLS used about 0.02 s (i5, 8G memory).
3.2. Real Data Simulation
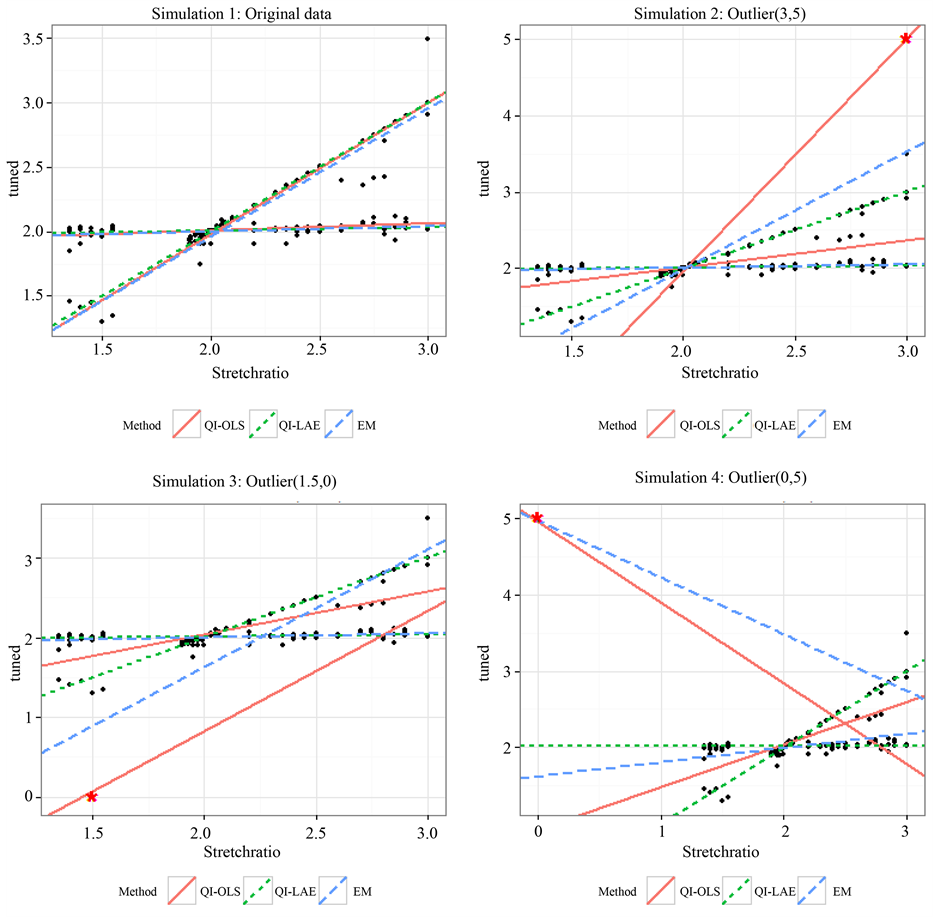
In the data simulation section, we use the data by Cohen (1984) [8] . A data shows pure fundamental tone was played to a trained musician. 150 observations of tuned and stretch ratio are played by the same musician. In this section, we will see the FI-LAE algorithm will handle the mixture regression data with outliers.
・ Situation 1: Original data.
・ Situation 2: Data with 5 outliers at (3,5).
・ Situation 3: Data with 5 outliers at (1.5,0).
・ Situation 4: Data with 5 outliers at (0,5) (Figure 2).
We used three algorithms in these four situations. In the first situation, the original data is used for regression. In other three situations, 5 outliers in different position are places in the data. (3,5) for the Situation 2, (1.5,0 )for the Situation 3 and (0,5) for Situation 4. The algorithms we used are FI-OLS, FI-LAE and EM algorithm. FI-OLS and FI-LAE are mentioned in our Fast Iteration for Mixture Regression model and the Mixreg package in R [9] is used for EM algorithm.
Table 2. Bias (MSE) of point estimates for model 2, n = 100.
Table 3. Bias (MSE) of point estimates for model 3, n = 100.
Figure 2. Real data simulation for FI-OLS, FI-LAE and EM algorithm.
In the situation 1, three algorithms got the similar answers. They all perform really well. In other situations, the FI-LAE shows that if there are some outliers in the data, a robust regression will lead to a closer answer, while the EM and FI-OLS affected by the outliers in different degrees.
4. Conclusion
As the discussion above, we can safely draw the conclusion that the fast iteration for solving mixture regression problem is efficiently and effectively. Compared to ordinary EM algorithm, this method can solve the problem quickly and obtain perfect performance. After changing the method of parameter estimation, the Fast Iteration Method can solve mixture regression when ε is in different distributions.
Cite this paper
DaweiLang,WanzhouYe, (2015) A Fast Iteration Method for Mixture Regression Problem. Journal of Applied Mathematics and Physics,03,1100-1107. doi: 10.4236/jamp.2015.39136
References
- 1. McLachlan, G. and Peel, D. (2004) Finite Mixture Models. John Wiley & Sons, Hoboken.
- 2. Fraley, C. and Raftery, A.E. (2002) Model-Based Clustering, Discriminant Analysis, and Density Estimation. American Statistical Association, 97, 611-631.
http://dx.doi.org/10.1198/016214502760047131 - 3. Ingrassia, S., Minotti, S.C. and Punzoa, A. (2014) Model-Based Clustering via Linear Cluster-Weighted Models. Computational Statistics and Data Analysis, 71, 159-182.
http://dx.doi.org/10.1016/j.csda.2013.02.012 - 4. Gaffney, S. and Smyth, P. (1999) Trajectory Clustering with Mixture Regression Model. Technical Report, No. 99-15.
- 5. Fraley, C. and Raftery, A.E. (1998) How Many Clusters? Which Clustering Method? Answers via Model-Based Cluster Analysis. The Computer Journal, 41, 578-588.
http://dx.doi.org/10.1093/comjnl/41.8.578 - 6. Song, W.X., Yao, W.X. and Xing, Y.R. (2014) Robust Mixture Regression Model Fitting by Laplace Distribution. Computational Statistics and Data Analysis, 71, 128-137.
http://dx.doi.org/10.1016/j.csda.2013.06.022 - 7. MacQueen, J.B. (1967) Some Methods for Classification and Analysis of Multivariate Observations. University of California Press, Oakland, 281-297.
- 8. Cohen, E. (1984) Some Effects of Inharmonic Partials on Interval Perception. Music Perception, 1, 323-349.
http://dx.doi.org/10.2307/40285264 - 9. Rolf Turner Mixreg: Functions to Fit Mixtures of Regressions. R Package Version 0.0-5.
http://CRAN.R-project.org/package=mixreg