Open Journal of Philosophy
Vol.08 No.04(2018), Article ID:86596,7 pages
10.4236/ojpp.2018.84027
Algebraic Structures of Mathematical Foundations
Robert Murray Jones
University of Duesseldorf, Duesseldorf, Germany

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 8, 2018; Accepted: August 7, 2018; Published: August 10, 2018
ABSTRACT
In this paper we undertake to examine how algebra, its tools and its methods, can be used to formulate the mathematics used in applications. We give particular attention to the mathematics used in application to physics. We suggest that methods first proposed by Henry Siggins Leonard are well suited to such an examination.
Keywords:
Functional Analysis, Open Mapping Theorem, Existence Predicate, The EPR Paradox, The Algebraic Resolution of the EPR Paradox by Bub

1. Introduction
In a previous publication (Jones, 2014) , we emphasized the use of a system of logic devised by Henry Siggins Leonard to facilitate the analysis of logical and mathematical structures. In this paper we shift the emphasis from that logic, upon which we continue to rely, to the use of algebra in applied mathematics, and in particular to the formulation of the laws of physics. Many, perhaps all, of the subfields of mathematics are supported by algebra. In few such subfields is this more prominently so than in functional analysis as it is applied to physics. In this paper we explore the structures of algebra that are used in physics and try to discover why they there take on such a very significant role.
1.1. The Tools of Algebra
The plethora of powerful algebras used in funtional analysis is extensive. They defy a comprehensive description. The C* algebras have a particularly central role. (Murphy, 1990) is highly recommended as a textbook of this subject.
1.2. The Problem of the Continuum Hypothesis
The use of the tools of algebra are probably best seen in an example of their use. The Continuum Hypothesis (CH) is a long standing classic mathematical problem.
1.3. The Cantor-Bernstein Theorem
To introduce the tools with which we shall discuss the Continuum Hypothesis, we firstly show these tools used to prove a classic result of set theory: The Cantor-Bernstein Theorem It was conjectured by Cantor, who proved a special case of it, and independently proved by Bernstein. We give below a proof along the lines of the proof by Bernstein.
An accessible modern interpretation of the proof by Bernstein is presented by Thomas Jech in (Jech, 2006: Theorem 3.2, p. 28) .
If X and Y are sets, then indicates that there is a bijection from X to Y.
Theorem (Cantor-Bernstein) If and are both injections, then .
Proof of the Theorem
First, we make use of the injections f and g to define by induction on all positive integers n:
,
,
The sets defined above overlap. To proceed further, we require analogues of them that are pairwise disjoint. To this end, we define
, and
.
By the constructions of these sets, and .
Since the A' sets are pairwise disjoint and the B' sets are also pairwise disjoint. it follows that:
Applying this reasoning on all of the A' and B', we obtain:
Extending the unions of the latter result to all n, we obtain:
To complete the proof, complements must be taken into account.
For the A set, and
For the B set.
Clearly,
,
and
,
from which we conclude,
and lastly,
QED
The Aleph notation of Cantor is a convenient way of expressing assertions concerning infinite quantities. An Aleph, the first letter of the Hebrew alphabet, is normally used with a subscripted index, e.g. , or . The Continuum Hypothesis may be compactly expressed in Cantor’s equation: .
A breakthrough in the conceptual understanding of the CH was made by Georg Kreisel.
What he showed is that, although we do not know whether the CH is true, we know that it is decidable in the set theory of Zermelo. There is an important qualification attached to the latter claim. It is true in second order logic.
Let denote Zermelo’s axiom system for set theory with the axiom of infinity.
See (Kreisel, 1967: p. 150) .
1.4. Applications
We discuss, in Section 2.7, the wide-ranging topic of the applications of functional analysis in physics. Applications of functional analysis in physics, and in particular to quantum theory, were recognized by David Hilbert. In (Reid, 1996) Constance Reid relates how he was surprised and pleased that his mathematics had found application in physics. The subject matter emphases and writing style of a physicist may differ from those of a mathematician. In (Neuenschwander, 2011) the mathematics of functional analysis are presented from the point of view of a physicist. Neuenschwander also relates the life of the mathematician Emmy Noether, who made important contributions to the algebraic foundations of functional analysis.
2. Algebra
2.1. Algebraic Tools
We sketch here some proofs of useful results of algebra that are used later in various other results and theorems. We adopt the notational conventions presented in (Jacobson, 1951) . The latter work was used as a textbook in a course in algebra attended by the author and taught by James Sutherland Frame.
There are several theorems of functional analysis that are fundamental to the subject. Rather than reproducing proofs of them here, we prefer to refer the interested reader to the standard literature of functional analysis. Three such results are: The open mapping theorem, the Banach-Steinhaus theorem, and the Hahn-Banach theorem. These theorems and their proofs are reviewed in (Saxe, 2002: Section 6.3, pp. 151-158) . A few comments on The Open Mapping Theorem are in order. We follow Pietsch (Pietsch, 2007: p. 44) in ascribing credit for the Open Mapping Theorem to Juliusz Schauder (Schauder, 1930) .
Banach algebra is a vast and quite central topic of functional analysis. We regret the extreme brevity of our comments upon it. We recommend the account of Banach algebra presented in (Allan, 2011) to the interested reader. This book, edited by H. Garth Dales, consolidates the course notes used by his late teacher Graham Robert Allen.
2.2. Groups as Applications of Tools
There are many significant interrelations between set theory and algebra. Let H be a set and S be the set of its subsets:
Let us also define the symmetric difference of sets X and Y to be those elements of S that are in X or in Y but not both.
Corollary: S with the operator is a group.
Proof:
, hence, , the empty set, is the unit of the group.
, hence every element of S is its own inverse.
S with the operator is a group
QED
More current information about groups is at (Solomon, 2018) .
2.3. Error-Correcting Codes
We discuss how the group concept is used in error-correcting codes. This application of groups make use of an interpretation of the group operator as exclusive or. Letting 0 and 1 represent binary numbers, this operator may be defined as follows: , , , .
Corollary, The binary digits, with the group operator, as exclusive or, are a group.
Proof.
Zero is the unit of the group: If X is binary number, then
 .
.
Each group element has an inverse;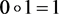 ,
,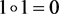 .
.
QED
Error-correcting codes make use of redundancies in strings of binary digits.
2.4. Topology Tools
Here we sketch some of the results of topology that are used in functional analysis and its algebras. We confine ourselves to introductory concepts and results of topology and refer the interested reader to the literature of topology and its application to functional analysis.
A concept of topology that is very nearly omnipresent in functional analysis is separability. A metric space is separable if it contains a countably dense subset. This concept played a remarkable role in an investigation that lasted 36 years and marked a watershed in the subject of functional analysis. In 1936 Stanislaw Mazur offered an award of a live goose for a solution to a question concerning continuous functions in separable spaces. In 1972 he awarded the live goose to Per Enflo for his solution in which he constructed a counter example to resolve the question. This history is well told in (Pietsch, 2007: pp. 285-287) .
2.5. Set Theory and Limitative Results
Set theory is a necessary tool for any examination, such as this, of the underlying reasoning of a mathematical topic. Set theory is not only developing, but also contains certain paradoxical aspects that call for caution and selectivity in foundational assumptions. We recommend the development of the theories which we here examine in the light of a branch of set theory that is called determinacy. Determinacy makes use of the concept of games to define, and found, set theoeretical conepts. We refer to (Jech, 2006: Chapter 33, pp. 627-645) .
2.6. Alternatives to the Full Axiom of Choice
Games of length Omega, that is infinite games, are used to define the concepts of determinacy. The Mycielsky and Steinhaus game plays here a central role. The strongest form of determinacy makes use of the Axiom of Determinacy. This axiom is inconsistent with the axiom of full choice. There are, however, several weaker forms of choice that can be combined with determinacy. Thus determinacy does not exclude all use of choice.
2.7. Applications of Algebra to Physics
Algebra and combinatorics are also applicable to the quantum theory of physics. In the early years of the 20th Century, quantum theory developed in a way that encountered certain paradoxes. One of these was formulated by three authors, Einstein, Podolsky, and Rosen. It came to be known as the EPR paradox, after the three initials of its authors.
The eminent theoretician Niels Bohr discovered an answer to the EPR paradox. His answer was the discovery of entanglement. That answer was thereafter formulated by Jeffrey Bub in terms of Boolean algebra, in (Bub, 1997: Chapter 7) ; thus bringing to bear the resources of algebra to support the answer that Bohr had given.
The formulation that Bub provides for the views of Bohr pertaining to the EPR argument uses a 16-element Boolean algebra. An upward pointing arrow in a subscript indicates a particle with upward spin; a downward pointing arrow in a subscript indicates a particle with downward spin.
Acknowledgements
We wish to again express our indebtedness and thanks to two students of Henry Leonard for their numerous recollections of his teachings in logic. They are: Joanne Eicher (University of Minnesota, Twin Cities) and Rolf George (University of Waterloo, Ontario). We are indebted to Henry S. Leonard for his paper (Leonard, 1969) .
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Jones, R. M. (2018). Algebraic Structures of Mathematical Foundations. Open Journal of Philosophy, 8, 401-407. https://doi.org/10.4236/ojpp.2018.84027
References
- 1. Allan, G. R. (2011). Introduction to Banach Spaces and Algebras. Oxford, UK: Oxford University Press. [Paper reference 1]
- 2. Bub, J. (1997). Interpreting the Quantum World. Cambridge, UK: Cambridge University Press. [Paper reference 1]
- 3. Jacobson, N. (1951). Lectures in Abstract Algebra, 1. Basic Concepts, 2. Linear Algebra, 3. Theory of Fields and Galois Theory. New York: D. Van Nostrand Company. [Paper reference 1]
- 4. Jech, T. (2006). Set Theory: The Third Millenium Edition, Revised and Expanded (3rd ed.). Berlin: Springer-Verlag. (Corrected 4th Printing 2006). [Paper reference 2]
- 5. Jones, R. M. (1962). A Note on Obversion. Mind, LXXI, 541-542. https://doi.org/10.1093/mind/LXXI.284.541 [Paper reference 1]
- 6. Jones, R. M. (1964). Formal Results in the Logic of Existence. Philosophical Studies, 15, 7-10. https://doi.org/10.1007/BF00428091 [Paper reference 1]
- 7. Jones, R. M. (2014). Model Theories of Set Theories and Type Theory. Open Journal of Philosophy, 4, 54-58. [Paper reference 1]
- 8. Kreisel, G. (1967) Informal Rigour and Completeness Proofs. Problems in the Philosophy of Mathematics, 47, 138-186. https://doi.org/10.1016/S0049-237X(08)71525-8 [Paper reference 1]
- 9. Leonard, H. S. (1969) The Logic of Existence. Philosophical Studies, 7, 49-64. https://doi.org/10.1007/BF02221764 [Paper reference 3]
- 10. Murphy, G. (1990). C*-Algebras and Operator Theory. San Diego, CA: Academic Press. [Paper reference 1]
- 11. Neuenschwander, D. (2011). Emmy Noether’s Wonderful Theorem. Baltimore, MD: The John Hopkins University Press. [Paper reference 1]
- 12. Pietsch, A. (2007). History of Banach Spaces and Linear Operators. Berlin: Birkhäuser. [Paper reference 2]
- 13. Reid, C. (1996). Hilbert. New York, NY: Springer-Verlag. https://doi.org/10.1007/978-1-4612-0739-9 [Paper reference 1]
- 14. Saxe, K. (2002). Beginning Functional Analysis. New York, NY: Springer-Verlag. https://doi.org/10.1007/978-1-4757-3687-8 [Paper reference 1]
- 15. Schauder, J. (1930). über die Umkehrung linearer, stetiger Funktionaloperationen. Studia Mathematica, 2, 1-6. [Paper reference 1]
- 16. Solomon, R. (2018). The Classification of Finite Simple Groups: A Progress Report. Notices of the American Mathematical Society, 65, 646-651. [Paper reference 1]
Appendices
A Formula References
In order to make this paper self-contained, we list here formulas from other sources that are referenced in the annotations of proofs.
Formulas from (Leonard, 1969) .
L5 
L6 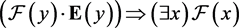
L9 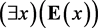
D1 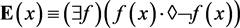
Leonard claimed in (Leonard, 1969: p. 58) that it was fifteen years before he accidentally hit upon L5 as a requisite for his logic.
Formulas for forms of Obversion.
Obversion in Leonard’s logic was discussed in (Jones, 1962) .
Ob1. 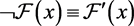
Ob2. 
Formulas from Jones (Jones, 1964) .
Def 2. 
CnX. 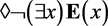
Nc 
The lower-case letter c is used as a non-designating constant term for illustrative purposes.

