Theoretical Economics Letters
Vol.4 No.2(2014), Article ID:43741,11 pages DOI:10.4236/tel.2014.42023
Monopolistic Product Line Competition with Ex Post Consumer Heterogeneity
Nikolaos Georgantzís1,2, Aurora García-Gallego2
1Department of Food Economics and Marketing, University of Reading, Reading, UK
2LEE and Department of Economics, Universitat Jaume I, Castellón, Spain
Email: n.georgantzis@reading.ac.uk, mgarcia@eco.uji.es
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 30 October 2013; revised 30 November 2013; accepted 7 December 2013
ABSTRACT
We model monopolistic competition in product lines, assuming that consumer heterogeneity is the result rather than the cause of product variety. Our results contradict some well-known policy implications yielded by the standard monopolistic competition framework.
Keywords:Consumer Heterogeneity; Product Diversity; Monopolistic Competition

1. Introduction
Economists and marketing scientists1 have recognized the importance of firms’ product line breadth for product choice by the consumer and, thus, for market competition. Although the implications of product line rivalry in the presence of heterogeneous consumers have received some attention2, the role of product line decisions as a cause (rather than as a result) of consumer heterogeneity has been largely ignored. In fact, a similar critique could be extended to the whole literature on product differentiation with few exceptions of spatial competition3 models, which adopt a purely geographical interpretation of “space”, in order for the controversial issue of preference endogeneity to be excluded from the discussion. Generally speaking, this critique applies to economic theory as a whole and, specifically, to the metaphysical perception that consumer preferences for products must have preceded any other economic phenomenon, ignoring any information on the way in which new products can affect preferences. An early critique to this perception was put forward by [9] :
“A theory which can make no use of so much information is a remarkably empty one. Even the technique of supposing the existence of a utility function for all possible goods, including those not yet invented, and regarding the prices of nonexistent goods as infinite—an incredible stretching of the consumers’ powers of imagination—has no predictive value.” ([9] , p. 133)
It is surprising that recent contributors to the theory of monopolistic competition have paid so little (if any) attention to Edward H. Chamberlin [10] , the founder of the theory, who had envisaged an active demand side with buyers choosing “locations” on the (abstract) space:
“If we now recognize that the population, instead of being distributed uniformly, will be most unevenly scattered about, and heavily concentrated in some areas, we have a much closer approach to reality. (...) In such places, shops will be larger or more numerous or both. Of course in all this there is mutual adaptation, action and interaction, and the picture could be developed much further in terms of different types of activity in different types of concentrations, etc., if space permitted. (...).
Tastes exist or are developed for particular products; (...)” ([10] , p. 347).
It seems that, since Chamberlin’s insightful suggestion, space never permitted and even the most path-breaking marketing studies have largely ignored the existence of preference-forming and persuasive business strategies. As we will argue in the following lines, the result is a fairly optimistic approach to the issue of whether product variety provided in an unregulated industry significantly diverges from the socially optimal one.
Monopolistic competition has been the basic theoretical framework in which the (sub) optimality of product variety provision has been studied. The result of divergence between the free-entry (long run) equilibrium and the socially optimal number of varieties is usually obtained in setups where the consumers’ benefits from a broader product variety are weighted against increases in production and setup costs associated with it. A revision of the literature on monopolistic competition is beyond the scope of this note. However, it is important that both the representative and the heterogenous consumer approaches4 assume that the demand side has some ex ante preference for product diversity. In fact, the former directly introduces such a preference into the representative consumer’s utility function, whereas the latter indirectly assumes it, at least at an aggregate level, by considering that consumers are heterogeneous with respect to, say, their “address” on a geographical or an abstract (product characteristics) space. Then, as far as the demand side is concerned, product variety is a consumer welfare-enhancing and thus, —to some extent—desirable market characteristic, whose social costs relate to the negative effect of product variety on production efficiency. All results on the overor under-provision of product varieties5 in a free-entry equilibrium relate to the fact that individual firms’ incentives are incompatible with the objective of social welfare maximization. Although this approach yields insightful implications for the functioning and regulation of many real world markets, it ignores a plausible alternative hypothesis concerning the temporal order and, thus, causality between product diversity and the consumers’ preference for variety.
Consider a potential consumer of banking services shopping every day in a city. Many branches of different banks are located all over the city center. Before opening an account, the consumer is (ex ante) indifferent among all branches, whose services and prices are very similar6. The consumer is more likely to open an account with a bank, if the bank has a higher number of branches in the city. Once all potential clients choose an account in a branch, each bank exploits its monopolistic power over its clients in each one of its branches, accounting for this type of ex post consumer heterogeneity7. Smokers are another good example of ex post heterogeneous consumers. That is, an initially indifferent population of non-smokers is more likely to start smoking the brand of cigarettes which is available in the largest number of varieties. Once some of them are locked-in with a specific variety of a given brand, switching costs are high enough for the manufacturer to behave as a monopolist with respect to the supply of this variety.
An important share of real world examples for our model concerns ex post heterogenous buyers of inter-mediate goods. In cosmetics and para-pharmaceutical product markets, ex ante indifferent retailers become heterogeneous (ex post), after each one of them chooses to become an exclusive distributor of a brand. In these cases, given a usual restriction imposed by manufacturers prohibiting their retailers to distribute rival brands, the latter are more likely to prefer a brand with a more complete product line. Subsequently, the demand by final consumers will reproduce the market shares dictated by retailer choice of brands. With this example it must have, also, been made clear that, when we talk about firms’ variety of products, we do not limit our analysis to demand substitutes. Rather, demand-unrelated and complementary products or components (like is the case of computers and their associated software or peripheral hardware) can also be valid examples of ex ante indifferent buyers who, after choosing one brand become (ex post) loyal to its services.
The features discussed above inspire the model presented in the next section. We should mention, however, that there is a much broader family of qualitatively similar models with these characteristics. Nevertheless, rather than discussing all possible generalizations with respect to functional forms and other details of the modelling strategy, we concentrate on illustrating the consequences of our basic assumptions for market analysis.
2. A Monopolistic Competition Model
In this section we present the assumptions and introduce the notation used to derive the subgame perfect equilibrium of the following four-stage game: In the first stage, a (potentially) multiproduct firm  decides on whether to enter into the market and (if it does) its location on a circular street of a positive length
decides on whether to enter into the market and (if it does) its location on a circular street of a positive length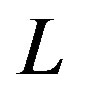 . In the second stage, the firm decides on the breadth of its product line, which is a segment of the circle,
. In the second stage, the firm decides on the breadth of its product line, which is a segment of the circle, 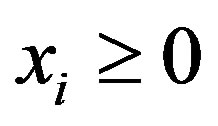 , symmetrically defined around firm i’s central product (the firm’s location on the circle), as shown in Figure 1. In the third stage, the firm (may) sets (potentially) discriminatory prices:
, symmetrically defined around firm i’s central product (the firm’s location on the circle), as shown in Figure 1. In the third stage, the firm (may) sets (potentially) discriminatory prices: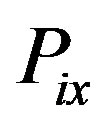 . That is, a price which depends on the distance
. That is, a price which depends on the distance 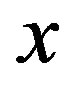 between a variety and its central product. In the fourth stage, a population of ex ante initially indifferent consumers (considering all varieties to be ex ante identical among them) choose the variety which maximizes their utility function given by:
between a variety and its central product. In the fourth stage, a population of ex ante initially indifferent consumers (considering all varieties to be ex ante identical among them) choose the variety which maximizes their utility function given by:
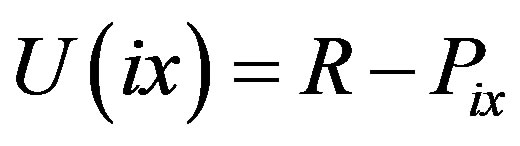 (1)
(1)
where 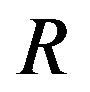 is the consumer’s reservation price for the product and
is the consumer’s reservation price for the product and 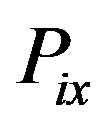 is firm i’s price for a variety lying at distance
is firm i’s price for a variety lying at distance  from the firm’s central product. In order avoid notation that would be abandoned in the symmetric equilibrium studied, this notation anticipates that the firm will set equal prices for varieties lying at equal distances from the central product. However, the possibility of asymmetric outcomes will be discussed too.
from the firm’s central product. In order avoid notation that would be abandoned in the symmetric equilibrium studied, this notation anticipates that the firm will set equal prices for varieties lying at equal distances from the central product. However, the possibility of asymmetric outcomes will be discussed too.
Variety is costly for firms and the further a product lies from a firm’s central variety, the more costly it is to produce a unit of it. We model this cost structure, assuming a linear transportation cost8:  paid by the firm in order to produce up to a variety at
paid by the firm in order to produce up to a variety at  distance from the firm’s central product. We also assume an exogenously given fixed (entry) cost
distance from the firm’s central product. We also assume an exogenously given fixed (entry) cost  for each firm, with
for each firm, with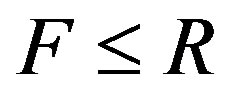 .
.
As already shown in Equation (7), if firms’ product lines overlap, varieties offered by both firms yield homogeneous product Bertrand competition. Furthermore, it is also shown there, that all buyers will agglomerate on varieties lying just in the middle between two adjacent firms’ central products, yielding maximum consumer surplus and zero total profits to the firms. Therefore, as long as a firm can avoid product line overlapping (and for the moment we will assume it does), it will choose locations lying sufficiently apart from adjacent firms in order to create a monopoly for each one of the varieties it produces. In that case, it can behave as a monopolist with respect to each one of its products, extracting  monetary units from each one of its clients.
monetary units from each one of its clients.
Then, a firm’s profit function is obtained as the difference between revenue and cost9:
 (2)
(2)

Figure 1. Firm i’s central variety, product line scope and consumer density.
In fact, our assumptions so far imply that, before choosing a variety, consumers are indifferent among all products in the market, because they consider them as perfect substitutes of each other. This ex ante indifference is maintained ex post, once consumers observe the monopolistic prices of the products, all of which would leave them with zero surplus. Therefore, in the fourth stage, each one of them randomizes among all varieties sold in the market. Thus, consumers will be uniformly distributed along the spectrum of all products sold in the market.
Let the spectrum  of all products sold in the market be the sum of product lines of all firms:
of all products sold in the market be the sum of product lines of all firms: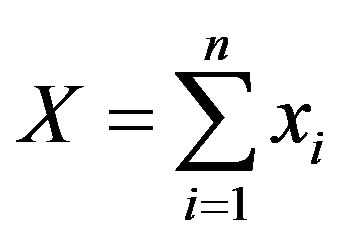 .
.
Given the aforementioned uniformity of consumers along the space of varieties offered by firms, the distribution of consumers will have a constant density:
 which, for our calculations, is more conveniently written as:
which, for our calculations, is more conveniently written as:
 (3)
(3)
In order to define a firm’s market share 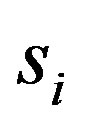 (and demand) for all non-negative product lines (including the case in which all firms set their product line breadth to zero) we assume:
(and demand) for all non-negative product lines (including the case in which all firms set their product line breadth to zero) we assume:
 (4)
(4)
Firms compete, deciding simultaneously on their product line scopes: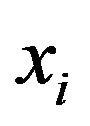 . The corresponding Nash equilibrium will satisfy the first order conditions:
. The corresponding Nash equilibrium will satisfy the first order conditions:
 (5)
(5)
on which it can be easily checked that the second order conditions are also satisfied10. Equation (5) as a unique positive root, leading to the following reaction function for firm :
:
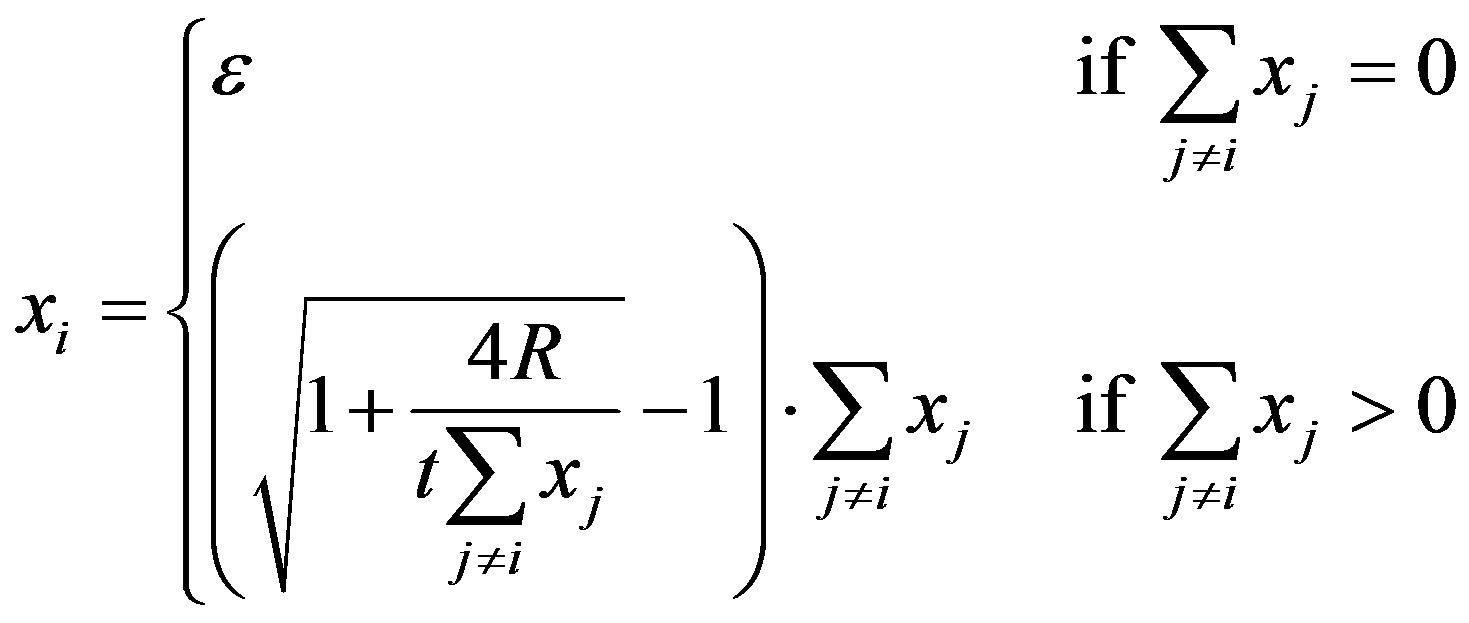 (6)
(6)
where 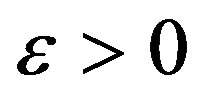 is an infinitesimal expansion of a firm’s product line.
is an infinitesimal expansion of a firm’s product line.
Despite the nonlinear form of the reaction function for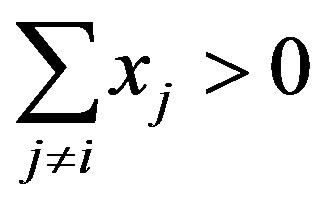 , a clear-cut result is straightforward to obtain concerning strategic complementarity between a firm’s product line scope and that of rival firms. It is also the case that these (concave) reaction functions (see Figure 2) give rise to the following symmetric Nash equilibrium in product line scope11:
, a clear-cut result is straightforward to obtain concerning strategic complementarity between a firm’s product line scope and that of rival firms. It is also the case that these (concave) reaction functions (see Figure 2) give rise to the following symmetric Nash equilibrium in product line scope11:
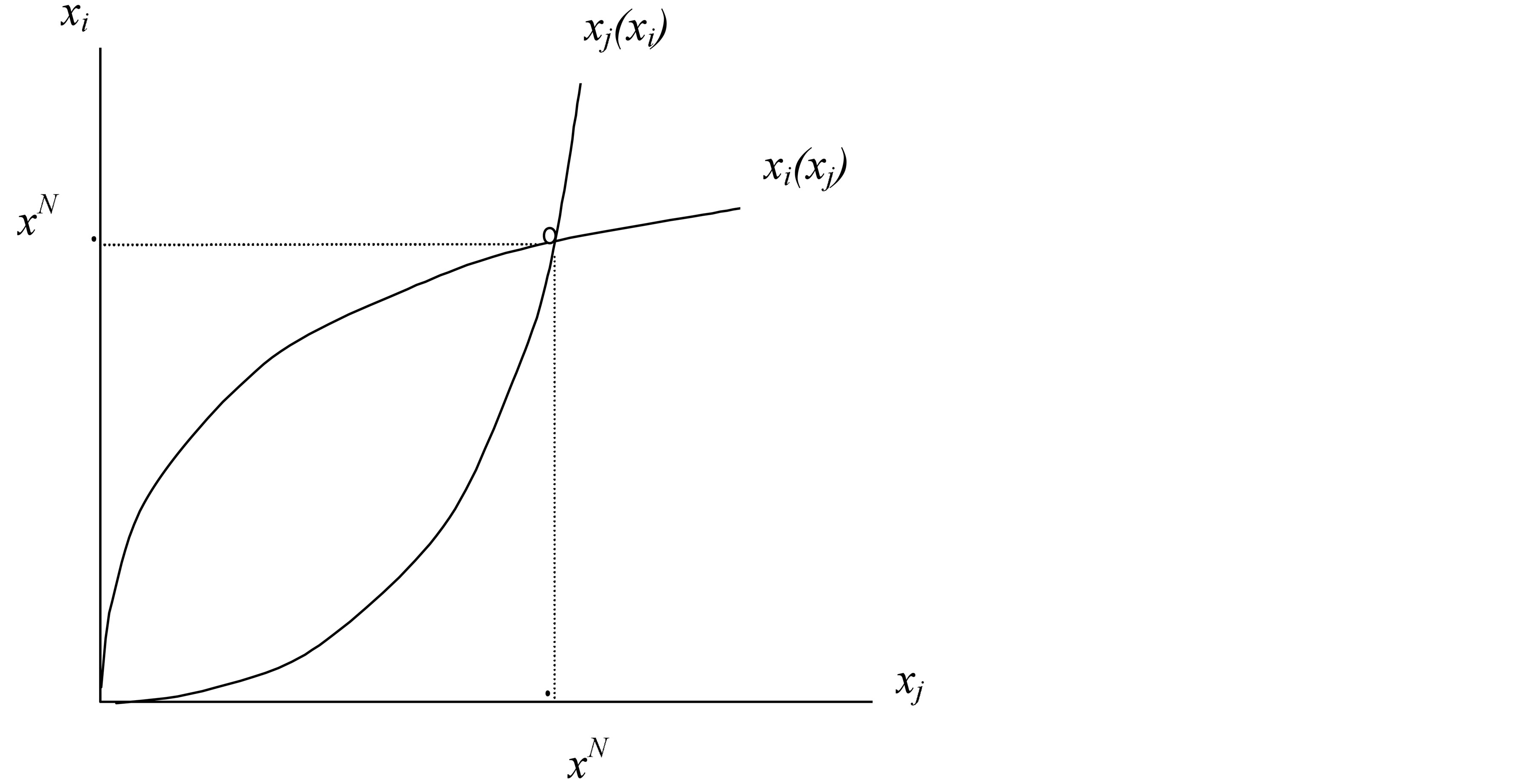
Figure 2. Reaction functions and Nash equilibrium 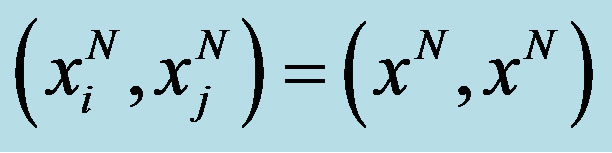 for the duopoly case.
for the duopoly case.
 (7)
(7)
Given the definition of a firm’s demand, it is traightforward to see that the system of reaction curves also intersect with each other at the origin, but this point cannot be an equilibrium of the one shot product-line game, because individual deviations from it are profitable for all  12. Therefore, the positive product line scope
12. Therefore, the positive product line scope 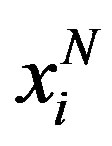 presented here is the unique (stable) equilibrium of the one-shot game. However, it can be checked that, given our demand specification, the outcome in which each firm produces its central variety alone is the joint profit-maximizing solution13. Individual Nash equilibrium profits are given by:
presented here is the unique (stable) equilibrium of the one-shot game. However, it can be checked that, given our demand specification, the outcome in which each firm produces its central variety alone is the joint profit-maximizing solution13. Individual Nash equilibrium profits are given by:
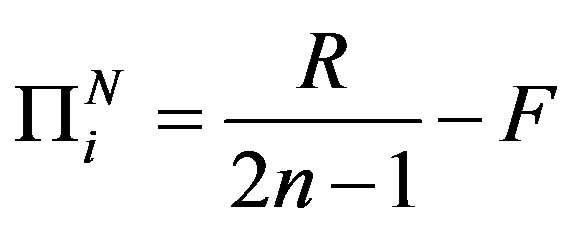 (8)
(8)
which, like in other monopolistic competition models, is strictly decreasing in the number of firms in the market, but does not depend on unit transportation costs. Using the expression of short run equilibrium profits in Equation (8), we can obtain the long run equilibrium number of firms (which satisfies the zero profit condition):
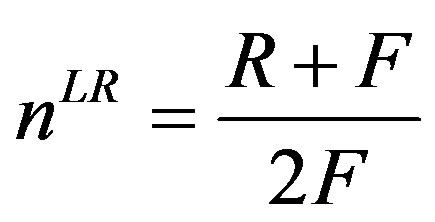 (9)
(9)
implying an individual line scope given by:
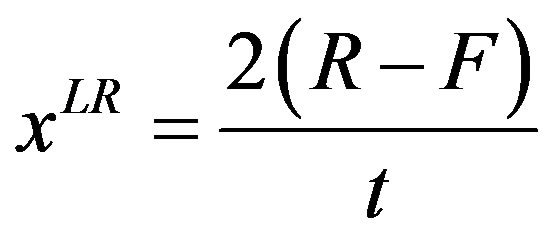 (10)
(10)
and a total spectrum of products given by:
 (11)
(11)
However, the reader should remember that the non-overlapping variety spectrum considered so far should not be taken for granted. In fact, if the total spectrum of products given in Equation (11) exceeded  (the space of product characteristics available, due for example to technological or other exogenous factors), then the long run equilibrium described above would be meaningless. Any number of firms above the one given in Equation (9) would satisfy the zero profit condition.
(the space of product characteristics available, due for example to technological or other exogenous factors), then the long run equilibrium described above would be meaningless. Any number of firms above the one given in Equation (9) would satisfy the zero profit condition.
Formally, if , the total spectrum of varieties in the market would be
, the total spectrum of varieties in the market would be 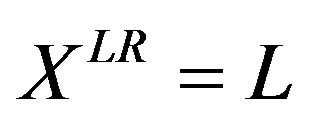 and any number of firms exceeding
and any number of firms exceeding 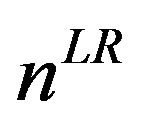 in Equation (9) could be observed in the long run and product lines would be given by:
in Equation (9) could be observed in the long run and product lines would be given by: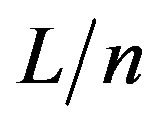 . But the most striking difference of this long run configuration of the industry would be that consumers would agglomerate on varieties lying in the middle between firm locations. In that case, both total transportation costs and consumer surplus would be maximal (conditional on firm locations).
. But the most striking difference of this long run configuration of the industry would be that consumers would agglomerate on varieties lying in the middle between firm locations. In that case, both total transportation costs and consumer surplus would be maximal (conditional on firm locations).
If we add transportation and fixed costs corresponding to the long run industry configuration, we can easily confirm a straightforward consequence of the zero-profit condition. That is, total social costs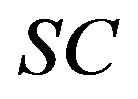 , are equal to the whole amount available to be spent on the product
, are equal to the whole amount available to be spent on the product .
.
A less straightforward to explain result concerns the long run equilibrium total transportation costs, given by:
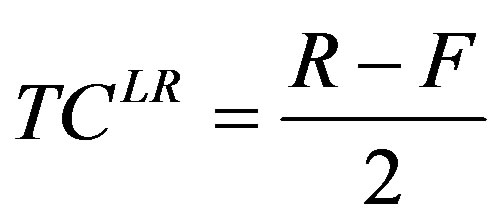 (12)
(12)
which indicates that policies leading to a reduction in unit transportation cost will not be effective, as they leave both the long run number of firms Equation (8) and total transportation costs unaffected.
3. Policy Implications
In our framework, like in other monopolistic competition models, the long run number of firms is a strictly decreasing function of entry costs and an increasing function of market size. However, given that the number of firms increases both product variety (which in its turn increases “transportation costs”) and fixed (entry) costs, industrial policy through entry regulation should aim at restricting the number of firms to the minimum necessary for supplying the market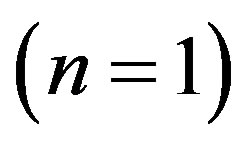 . This contradicts the usual result14 that the socially optimal number of firms is, generally speaking, an interior solution to the problem of minimizing social costs (the sum of transportation and production costs). Based on this result, it can be concluded that entry regulation may be necessary in order to prevent the variety proliferation or variety under-provision outcomes (depending on the specific assumptions) resulting from free entry.
. This contradicts the usual result14 that the socially optimal number of firms is, generally speaking, an interior solution to the problem of minimizing social costs (the sum of transportation and production costs). Based on this result, it can be concluded that entry regulation may be necessary in order to prevent the variety proliferation or variety under-provision outcomes (depending on the specific assumptions) resulting from free entry.
In our setup, entry regulation should aim at establishing a monopoly, or—in the case of competition policy (taking the number of firms as given)—at facilitating collusion among firms in order to limit their product line scopes to a minimum. In fact, an alternative or complementary measure to entry regulation could be the imposition of an entry fee paid to the state until  reaches the value
reaches the value 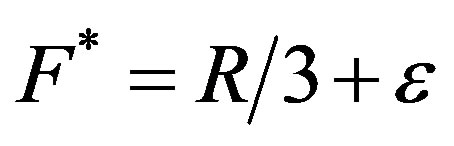 (
( being a very small positive number). This is the minimum entry cost for which the entry of a second firm is unprofitable. This divergence between the present framework and other monopolistic competition models is due to our assumption that product diversity does not satisfy an already existing need of the consumer, but rather, is a costly strategy, adopted by firms in order to preserve and extend their shares in the market.
being a very small positive number). This is the minimum entry cost for which the entry of a second firm is unprofitable. This divergence between the present framework and other monopolistic competition models is due to our assumption that product diversity does not satisfy an already existing need of the consumer, but rather, is a costly strategy, adopted by firms in order to preserve and extend their shares in the market.
4. Conclusions
We have presented one of the simplest monopolistic competition models which can reflect our basic assumptions: 1) Ex post consumer heterogeneity is a result (not a cause) of product diversity, which is a strategy used by firms aiming at preserving their market shares (not satisfying a broader range of pre-existing tastes).
Our model shares many common aspects15 with the models proposed in the papers by [16] and by [17] . However, our assumption of ex post consumer heterogeneity and the essentially horizontal differentiation nature of our framework, as opposed to vertical differentiation used in the aforementioned studies, makes our results not directly comparable to theirs’. Furthermore, our analysis pays special attention to the long run (free-entry) equilibrium.
Therefore, an implicit assumption made here, which should be relaxed in future research, is that firms’ strategies cannot expand the market by attracting new consumers. 2) Before varieties are chosen by ex ante indifferent consumers, all products in the market are treated as perfect substitutes. Regarding the assumption concerning the initial indifference of consumers among existing varieties, it must be noted that it can also be endogenized as the equilibrium of a subgame preceding the stage of pricing, in which consumers correctly anticipate that, irrespective of their variety choice, they will be charged a price leaving them with zero surplus. 3) After products are randomly chosen by consumers in a way which makes each firm’s market share to depend proportionally on the firm’s product line, monopoly (perfectly discriminatory) pricing takes place. It must be stressed that our framework is applicable to cases in which, once a variety is randomly chosen by the consumer, switching costs are sufficiently high for firms to sustain their monopoly pricing in equilibrium.
Together with the hypothesis that product line scope is a determinant of a firm’s market share, an implicit assumption of our framework is that price competition in the ex ante stage is fierce enough to yield competitive (access) pricing, because in this stage consumers consider brands to be perfect substitutes. However, after each consumer chooses a brand, firms can exploit their monopolistic power in the supply of each one of the products. In fact, consumer indifference in the ex ante stage can be justified as a rational anticipation of the fact that in the purchase stage, independently of the brand chosen, the consumer will be left with zero surplus.
Most of our results contradict policy implications obtained in previous studies on monopolistic competition. A major divergence concerns our finding on the benefits from market monopolization (or cartelization), leading to a single product offered by one firm and homogeneous consumers. Other seemingly paradoxical findings indicate that a certain level of a fixed entry cost can be desirable if it leads to a long run industry configuration with one firm in it. Finally, policies aiming at reducing the unit transportation cost may be ineffective.
An obvious critique could be that, contrary to our model, real-world markets always contain a mixture of ex ante and ex post heterogeneous consumers. Although a model combining both types of consumer heterogeneity is an interesting generalization for future research, we feel that the first approach to the effects of product line decisions on consumer heterogeneity should be attempted in a purely ex post model like ours.16 Alternative benchmark solutions which could also be considered in future research are those corresponding to different levels of trust and coordination between sellers and buyers. For example, a consumer who, in the ex ante stage, is guaranteed (by explicit contracts or infinite repetition of the market game) that some percentage of her surplus will be left to her, will endogenize the cost of differentiation and will prefer more efficient (less differentiated) varieties.
A more profound critique could be that our “inefficiency-of-variety” result crucially depends on the assumption of ex post consumer heterogeneity. But, then, would it be fair not to recognize that all previous results on (sub) optimality of product diversity crucially depend on the assumptions of ex ante consumer heterogeneity or a representative consumer’s preference for variety? The question that should be answered in each case is what causes what.
Whether our findings or the conclusions reached in the previous work which should be taken into account by policy makers, depends on whether product variety is the cause or the result of consumer heterogeneity. Although the functioning of real world markets makes it difficult for empirical research to identify the direction of causality between consumer heterogeneity and product diversity (mainly because firms, assisted by mainstream economic theory and marketing science, would hesitate to admit a different causality but the one usually assumed), economists need to play a more active role in the search of evidence against the usual claim that product line expansion aims at following the patterns dictated by existing consumer needs.
Acknowledgements
Financial support by the Spanish Ministerio de Economía y Competitividad (project ECO2011-23634) and UJIBancaixa (project P1-1B2010-17) are gratefully acknowledged. Special thanks go to M. Ginés for useful comments and discussion. All errors are the authors’ responsibility alone.
References
- Johnson, J.P. and Myatt, D.P. (2003) Multiproduct Quality Competition: Fighting Brands and Product Line Pruning. American Economic Review, 93, 748-774. http://dx.doi.org/10.1257/000282803322157070
- Klemperer, P. and Padilla, A.J. (1997) Do Firms’ Product Lines Include too many Varieties. RAND Journal of Economics, 28, 472-488. http://dx.doi.org/10.2307/2556025
- Kuhn, K.U. and Padilla, A.J. (1996) Product Line Decisions and the Coase Conjecture. RAND Journal of Economics, 27, 391-414. http://dx.doi.org/10.2307/2555933
- De Fraja, G. (1996) Product Line Competition in Vertically Differentiated Markets. International Journal of Industrial Organization, 24, 389-414. http://dx.doi.org/10.1016/0167-7187(95)00483-1
- Judd, K.L. (1985) Credible Spatial Preemption. RAND Journal of Economics, 16, 153-166. http://dx.doi.org/10.2307/2555407
- William, P.P. and Bayus, B.L. (2001) An Empirical Analysis of Firms’ Product Line Decisions. Journal of Marketing Research, 38, 103-118.
- Anderson, S.P., de Palma, A. and Thisse, J.F. (1992) Discrete Choice Theory of Product Differentiation. MIT Press, Cambridge.
- Fujita, M. and Thisse, J.F. (1986) Spatial Competition with a Land Market: Hotelling and von Thunen Unified. Review of Economic Studies, 58, 819-841. http://dx.doi.org/10.2307/2297721
- Lancaster, K.J. (1966) A New Approach to Consumer Theory. Journal of Political Economy, 74, 132-157. http://dx.doi.org/10.1086/259131
- Chamberlin, E.H. (1951) Monopolistic Competition Revisited. Economica, 18, 343-362. http://dx.doi.org/10.2307/2549607
- Dixit, A. and Stiglitz, J. (1977) Monopolistic Competition and Optimum Product Diversity. American Economic Review, 67, 297-308.
- Salop, S.C. (1979) Monopolistic Competition with Outside Goods. Bell Journal of Economics, 10, 141-156. http://dx.doi.org/10.2307/3003323
- MacLeod, W.B., Norman, G. and Thisse, J.F. (1988) Price Discrimination and Equilibrium in Monopolistic Competition. Journal of Economic Theory, 4, 429-446.
- Tirole, J. (1985) The Theory of Industrial Organization. MIT Press, Cambridge.
- Champsaur, P. and Rochet, J.C. (1998) Multiproduct Duopolists. Econometrica, 57, 533-357. http://dx.doi.org/10.2307/1911051
- Mussa, M. and Rosen, S. (1978) Monopoly and Product Quality. Journal of Economic Theory, 18, 301-317. http://dx.doi.org/10.1016/0022-0531(78)90085-6
- García-Gallego, A., Georgantzís, N. and Orts, V. (2001) Endogenous Retailer Preferences in Intermediate Good Markets. International Review of Retail Distribution and Consumer Research, 11, 123-139.
Mathematical Appendix
Here, we show that the reaction functions are such that there is a unique Nash equilibrium in product lines.
Let us concentrate first on the case in which  Equation (4) has two roots, given by:
Equation (4) has two roots, given by:
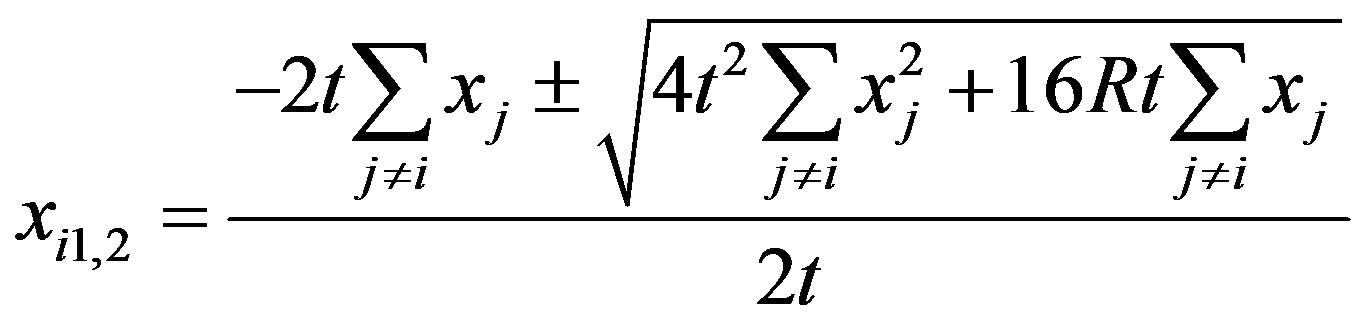 but only one of them is positive (the one with a positive signed square root on the numerator), from which we can derive the following reaction function for firm i:
but only one of them is positive (the one with a positive signed square root on the numerator), from which we can derive the following reaction function for firm i:
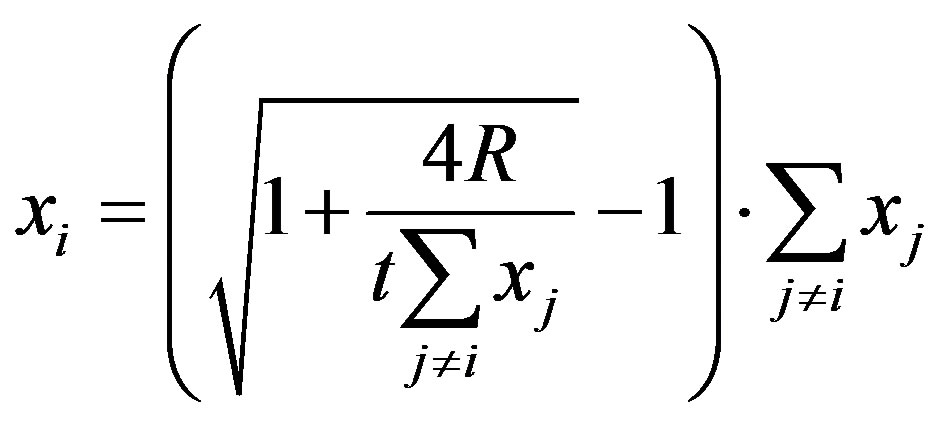 (13)
(13)
The shape of the function (for, say, parameter values R = 10, t = 1) is as depicted in Figure 3.
From the figure it can be seen that Equation (12) implies that firms’ strategies are strategic complements and that the (positive) slope of the reaction function is decreasing as other firms’ product line scopes increase.
We formally show these properties and study the Nash equilibrium in product lines, focusing on the  case, and denoting firms as 1 and 2. Equation (12) becomes:
case, and denoting firms as 1 and 2. Equation (12) becomes:
 (14)
(14)
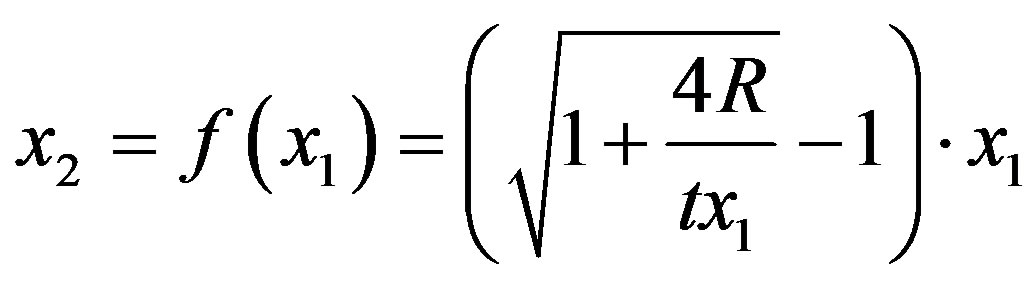 (15)
(15)
In the  axis we show that function in Equation (13) is (continuous) strictly positive and concave in the domain
axis we show that function in Equation (13) is (continuous) strictly positive and concave in the domain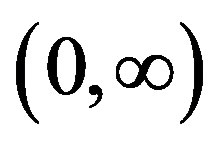 . Observe that the first derivative:
. Observe that the first derivative:
 (16)
(16)
is positive or negative depending on the numerator sign. However, the numerator cannot be zero because if it were, then:

Figure 3. Firm i’s reaction function with respect to rival firms’ product line scopes.
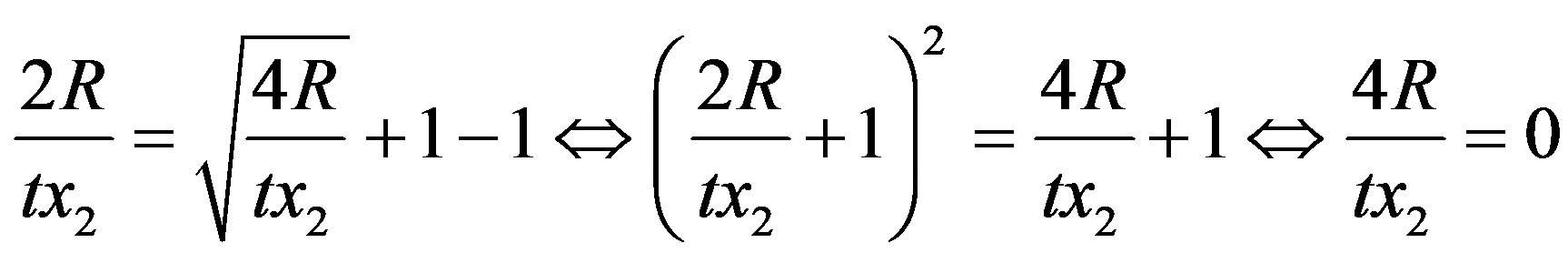
which contradicts . As a result, derivative in Equation (15) is either always positive or negative. For value
. As a result, derivative in Equation (15) is either always positive or negative. For value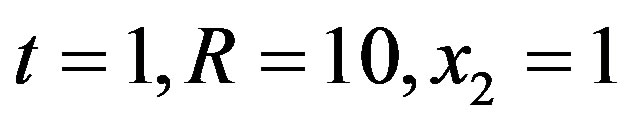 , the value of
, the value of
 which shows that it is always positive.
which shows that it is always positive.
As far as the concavity of function in Equation (13) is concerned, observe that the second derivative is always negative:
 (17)
(17)
With respect to function , in Equation (14), we are interested in its inverse form:
, in Equation (14), we are interested in its inverse form:
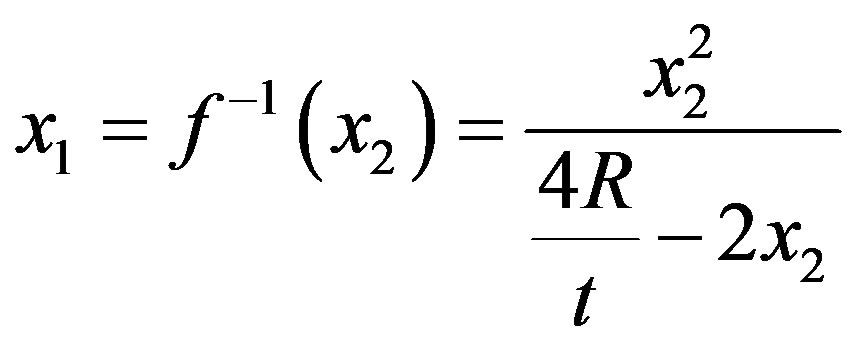 (18)
(18)
where , for the function to be defined—which implies that
, for the function to be defined—which implies that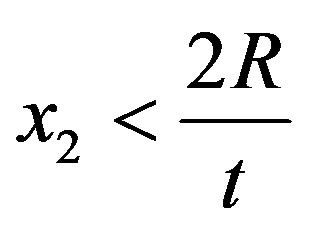 , and that, for
, and that, for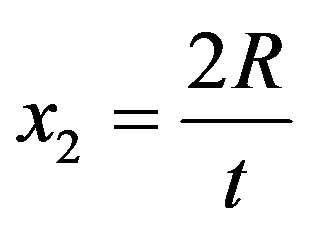 ,
,
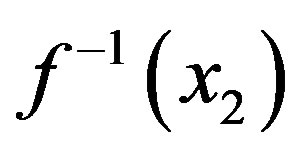 has an asymptotic behavior. We show that function
has an asymptotic behavior. We show that function  is positively sloped and strictly convex in the domain
is positively sloped and strictly convex in the domain . Observe that, since
. Observe that, since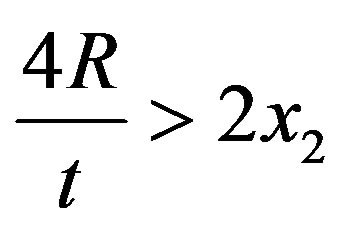 , the first derivative:
, the first derivative:
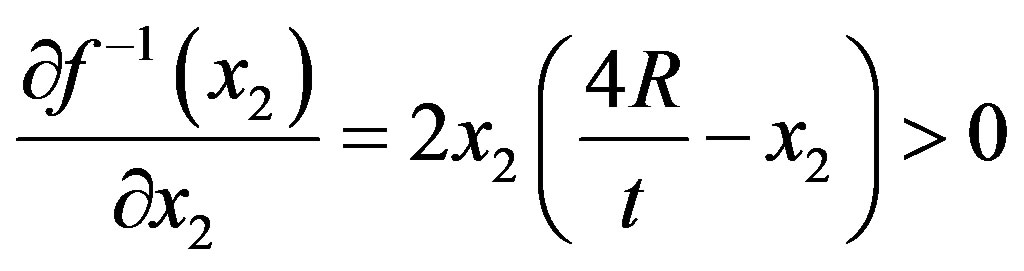 (19)
(19)
is always positive, and so it is the second derivative:
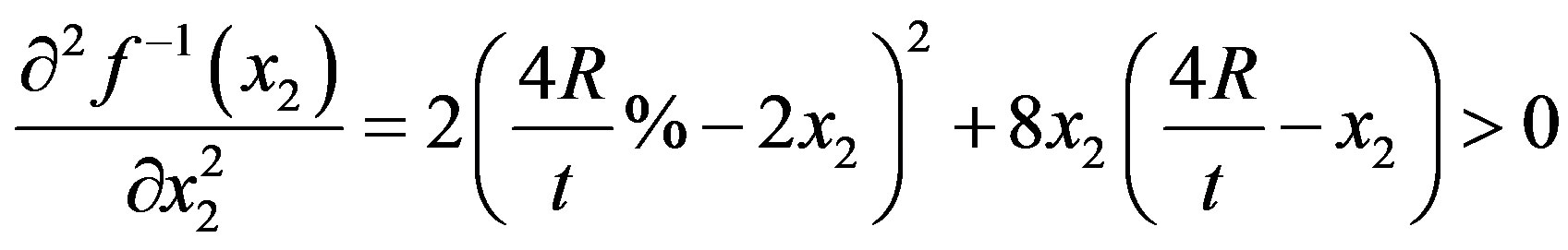 (20)
(20)
Therefore, we have the two reaction functions represented on the same system of axes, one strictly convex and the other strictly concave. We can show now that point

is the only one in which both functions cut each other. To do that, we take the diagonal 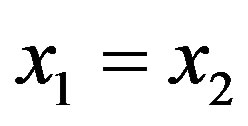 as a reference function. Then, we just have to prove that, for function in Equation (13), values of
as a reference function. Then, we just have to prove that, for function in Equation (13), values of 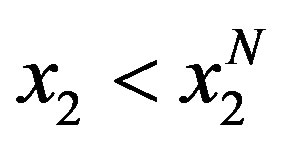 are always above the diagonal and, values of
are always above the diagonal and, values of 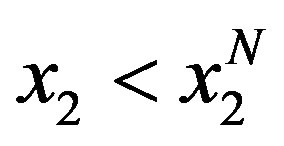 are always below the diagonal. For the case of function in Equation (17) the contrary must be shown. That is, values of
are always below the diagonal. For the case of function in Equation (17) the contrary must be shown. That is, values of  are always below the diagonal
are always below the diagonal , and that values of
, and that values of  are always above the diagonal.
are always above the diagonal.
Consider first  in Equation (13). For values of
in Equation (13). For values of 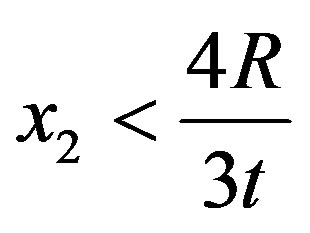 it follows that
it follows that
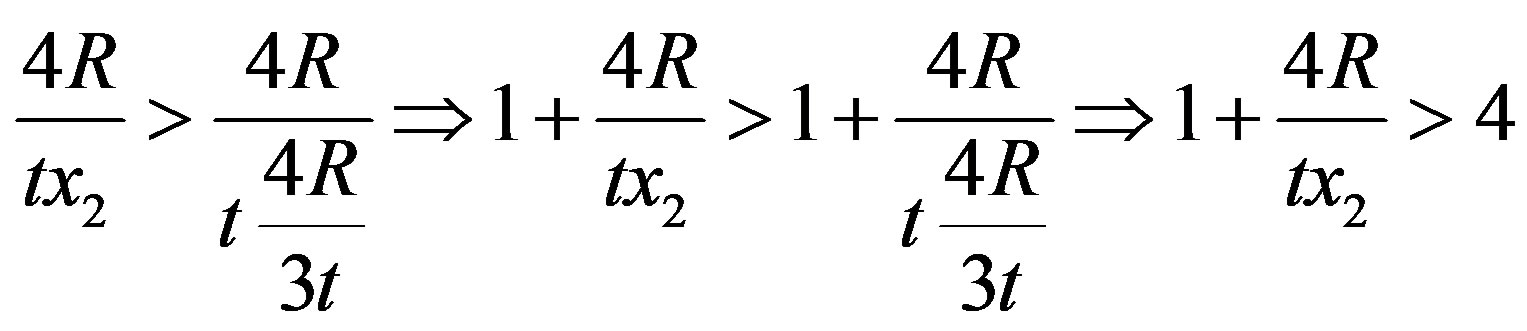
which implies that 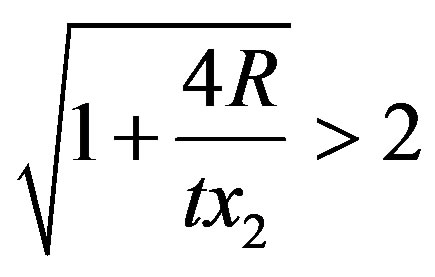 and, therefore, that
and, therefore, that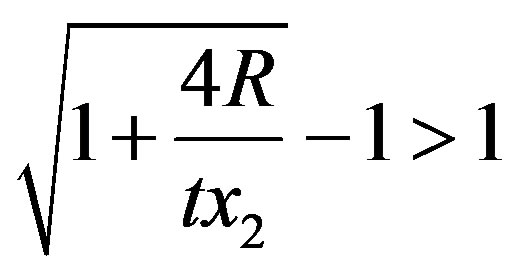 . As a consequence, for values of
. As a consequence, for values of 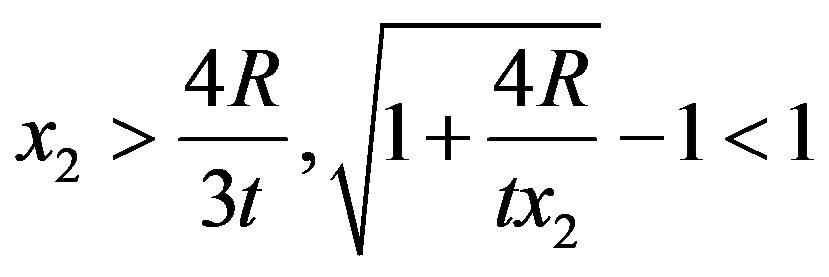 applies.
applies.
Consider now function  in Equation (17). For values of
in Equation (17). For values of 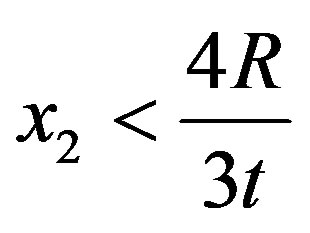 it follows that
it follows that

which implies that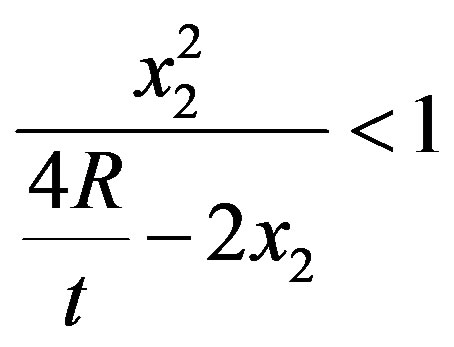 . As a consequence,
. As a consequence,  for values of
for values of .
.
With respect to the case in which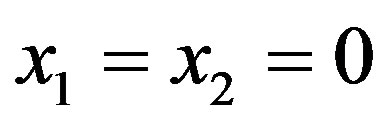 , it can be shown that reaction functions tend to zero. In fact:
, it can be shown that reaction functions tend to zero. In fact:
 .
.
NOTES

1Although with some divergence of focus, with the former analyzing mainly the implications of product line decisions for market competition (see, for example, -) or preemption () and the latter the implications of such strategies on firms’ profitability and success (see, among others, ).
2The main contribution is the nested logit approach by , which—like the model presented here—has been used to determine simultaneously the long-run number of firms and the number of product varieties per firm. It is found that the free entry equilibrium leads to too many firms and too few varieties (both in total number and number of varieties per firm) as compared to the socially optimum.
3 present a model of spatial competition with endogenous consumer location, whose interpretation in terms of consumers’ choice of “ideal” variety has been left unexplored.

4This is a way of referring, in the most generic way, to monopolistic competition models in the fashion of and , respectively.
5In fact, , using a somehow similar framework to ours (in that they assume perfect price discrimination and a circular product characteristics space), show that any result (under-/over-provision and optimal provision) may emerge in equilibrium.
6In fact, indifference could also be due to limited information on the current bankand branch-specific conditions of all products offered and due to ignorance on all future needs she may have to satisfy in the bank.
7Product lines offered to consumers in the market for mobile telephone services and monopolization of buyers by car manufacturers in post-sale services like accessories and mechanical parts also offer good real world examples for our framework.

8Although these costs are associated with the production, they have more similarities to a transportation cost associated with the “distance” between a variety produced by a firm and the firm’s central product. For this reason and an alternative interpretation of these costs offered in the following footnote, we refer to these costs adopting the term transportation costs.
9In fact, this profit function could also correspond to an alternative interpretation of production costs and consumer utility, according to which firms produce all varieties at a constant (zero) unit cost, but consumers of less central varieties suffer some disutility (for example a bank’s branch in the periphery offers less services or less efficiently than the central office in a capital). Given that a firm can perfectly discriminate among its different products, it sets a price 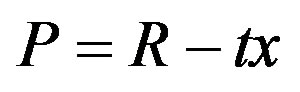 (which is equivalent to the perfectly discriminatory scheme of “extracting all consumer surplus, after utility losses or transportation costs are taken into account”).
(which is equivalent to the perfectly discriminatory scheme of “extracting all consumer surplus, after utility losses or transportation costs are taken into account”).

10From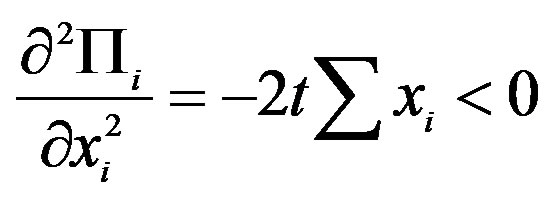 .
.
11In the appendix we demonstrate that this equilibrium is unique.

12Observe that the profit earned by firm i with a zero product line scope when others’ lines are also zero is , while the firm’s profits from an infinitesimal increase in
, while the firm’s profits from an infinitesimal increase in  would approximate
would approximate , from below, which is strictly higher than
, from below, which is strictly higher than , except for the case of a monopoly
, except for the case of a monopoly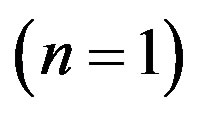 , the only market structure in which any expansion of the firm’s product line beyond the central variety is unprofitable.
, the only market structure in which any expansion of the firm’s product line beyond the central variety is unprofitable.
13This collusive outcome can be tacitly sustained if we consider an infinitely repeated version of the one-shot game studied here with a standard trigger strategy and a discount rate which is higher than a critical value , which is an increasing function of n and
, which is an increasing function of n and .
.

14See and .
15For example, the assumption of perfect price discrimination among different qualities represented on a continuum, and the result by that duopolists have no incentive to compete head-to-head (offering common segments of the quality space). Under a quite different setup of demand and supply specifications, have shown recently that the contrary result may also hold.

16Among other reasons (formality and elegance of the results, etc.), it is a matter of justice to and suggestion, which for approximately half a century have remained totally unexplored.

